Spectral Properties of Effective Dynamics from Conditional Expectations
Abstract
1. Introduction
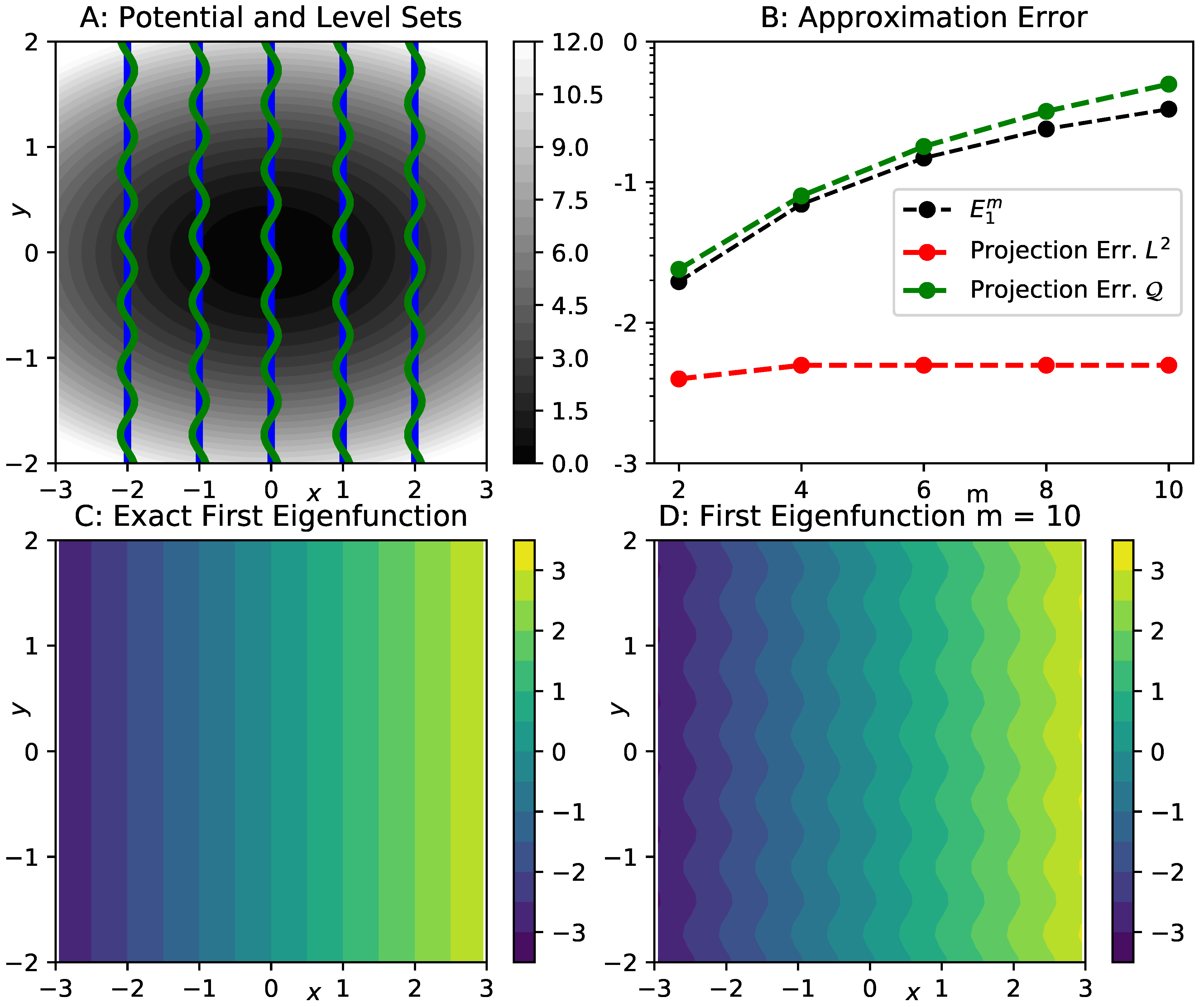
- Concerning the first problem, we prove a new relative error bound for the approximation of generator eigenvalues by the coarse grained generator, if the dynamics is reversible (Proposition 2). This bound shows that a small projection error of the full eigenfunctions with respect to the energy norm is required for a small eigenvalue error. We also derive conditions to ensure that the spectrum of the reduced generator is discrete in the first place (Proposition 1).
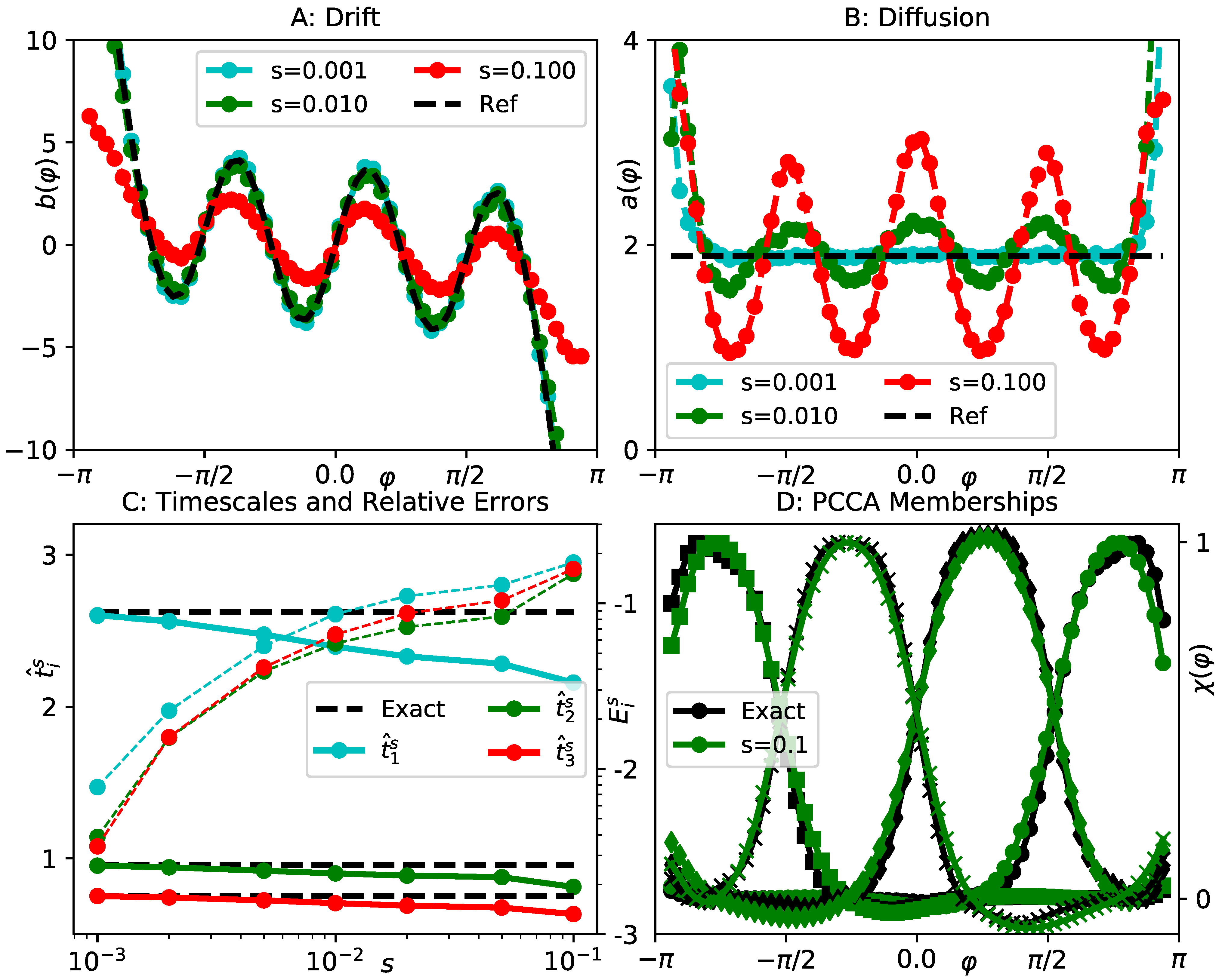
- Concerning the second issue, we present numerical examples indicating that, if KM estimators are used within the gEDMD algorithm for reversible systems, on a good set of reaction coordinates, then the resulting eigenvalue estimates seem to be fairly insensitive to the offset used for the KM estimators (Section 4.2 and Section 4.3, Conjecture 1).
- Thirdly, we suggest that, if the observations of the second part can be confirmed theoretically, it is possible to use KM estimators at large offsets to define meaningful effective equations for underdamped dynamics (Corollary 1). The reason is that the statistics of the underdamped process approach those of an overdamped process after a suitable re-scaling of time. We provide successful illustrations of this idea using a toy example and molecular dynamics simulation data of the alanine dipeptide (Section 5.2 and Section 5.3).
2. Concepts
2.1. SDEs and Generators
2.2. Spectral Decomposition
2.3. Dimensionality Reduction
2.4. Galerkin Approximation
2.5. Kramers–Moyal Estimators
3. Spectral Properties of the Projected Generator
3.1. Summary of Spectral Properties
3.2. Illustration of the Error Bound
4. Spectral Properties and Kramers–Moyal Estimators
4.1. Methods
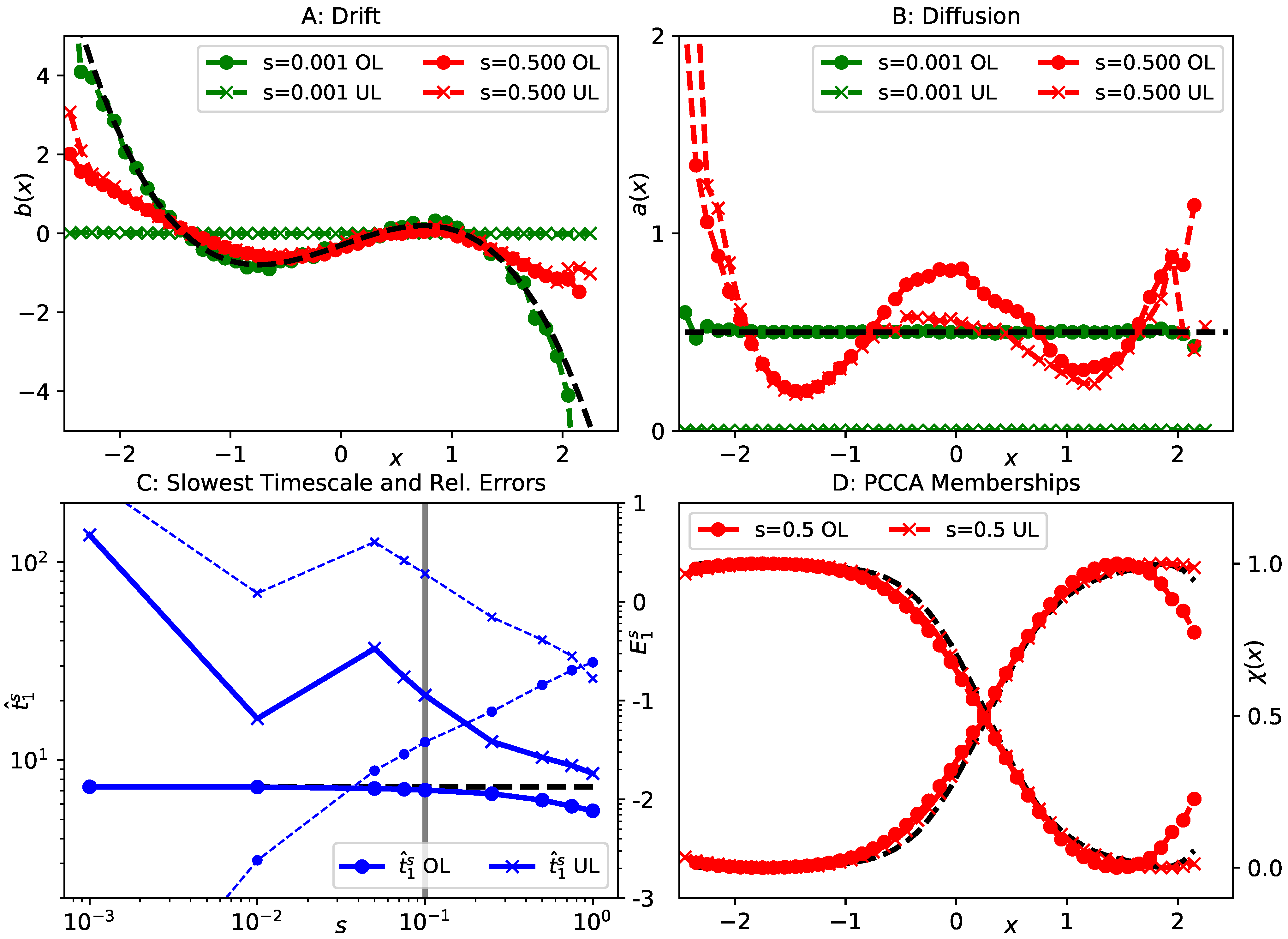
4.2. Lemon Slice Potential
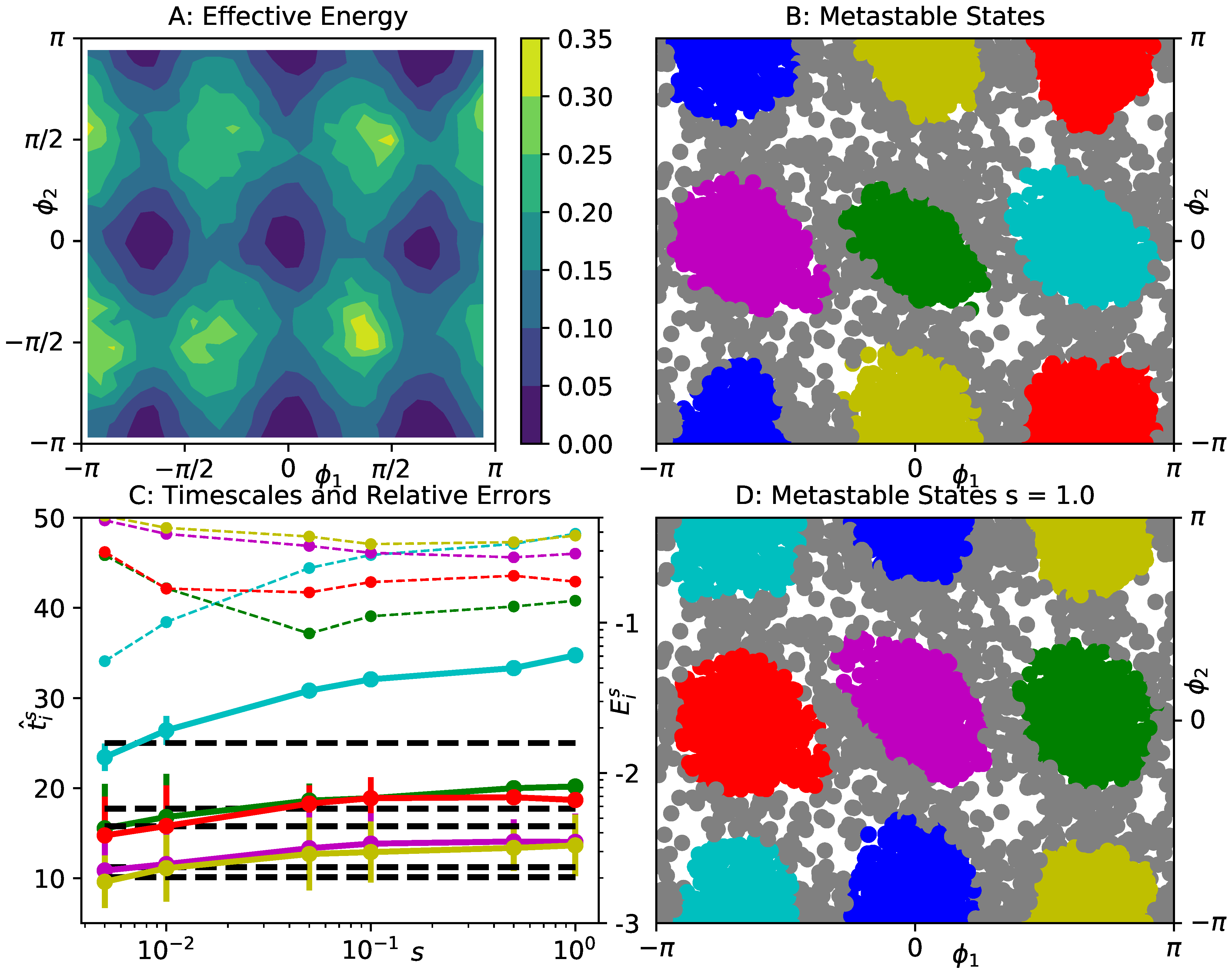
4.3. Prototypical Molecular Potential
4.4. Summary of Observations
5. Underdamped Langevin Dynamics
5.1. Projection and Re-Scaling of the Underdamped Process
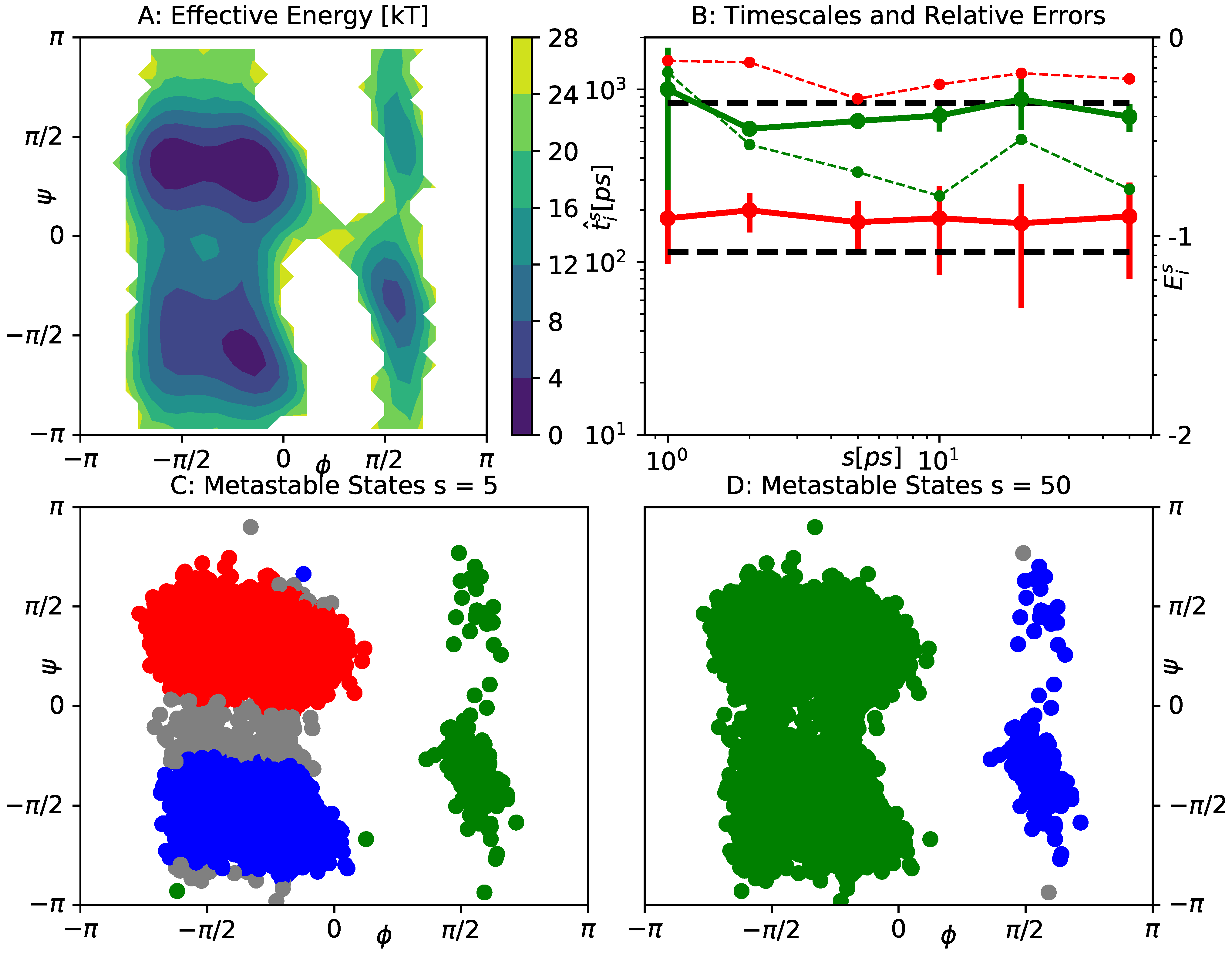
5.2. Langevin Toy Model
5.3. Alanine Dipeptide
6. Precise Statements on Spectral Properties and Their Proofs
6.1. Form Domain
6.2. Solution Operator and Discrete Spectrum
6.3. Coarse Grained Generator and Its Spectrum
6.4. Approximation Result
6.5. Comments
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Lemon Slice Potential: Effective Drift and Diffusion Coefficients
Appendix B. Parameters of Prototypical Molecular Example
References
- Mori, H. Transport, collective motion, and Brownian motion. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonlinear generalized Langevin equations. J. Stat. Phys. 1973, 9, 215–220. [Google Scholar] [CrossRef]
- Chorin, A.J.; Hald, O.H.; Kupferman, R. Optimal prediction and the Mori–Zwanzig representation of irreversible processes. Proc. Natl. Acad. Sci. USA 2000, 97, 2968–2973. [Google Scholar] [CrossRef] [PubMed]
- Chorin, A.J.; Hald, O.H.; Kupferman, R. Optimal prediction with memory. Physica D 2002, 166, 239–257. [Google Scholar] [CrossRef]
- Hijón, C.; Español, P.; Vanden-Eijnden, E.; Delgado-Buscalioni, R. Mori–Zwanzig formalism as a practical computational tool. Faraday Discuss. 2009, 144, 301–322. [Google Scholar] [CrossRef]
- Pavliotis, G.; Stuart, A. Multiscale Methods: Averaging and Homogenization; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Pavliotis, G.A.; Stuart, A.M. Parameter estimation for multiscale diffusions. J. Stat. Phys. 2007, 127, 741–781. [Google Scholar] [CrossRef]
- Clementi, C. Coarse-grained models of protein folding: Tol-models or predictive tools? Curr. Opin. Struct. Biol. 2008, 18, 10–15. [Google Scholar] [CrossRef]
- Noé, F.; Clementi, C. Collective variables for the study of long-time kinetics from molecular trajectories: Theory and methods. Curr. Opin. Struct. Biol. 2017, 43, 141–147. [Google Scholar] [CrossRef]
- Noid, W. Perspective: Coarse-grained models for biomolecular systems. J. Phys. Chem. 2013, 139, 090901. [Google Scholar] [CrossRef]
- Prinz, J.H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and Validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar] [CrossRef]
- Rohrdanz, M.A.; Zheng, W.; Maggioni, M.; Clementi, C. Determination of reaction coordinates via locally scaled diffusion map. J. Chem. Phys. 2011, 134, 124116. [Google Scholar] [CrossRef] [PubMed]
- Saunders, M.G.; Voth, G.A. Coarse-Graining Methods for Computational Biology. Annu. Rev. Biophys. 2013, 42, 73–93. [Google Scholar] [CrossRef] [PubMed]
- Weinan, E.; Vanden-Eijnden, E. Metastability, conformation dynamics, and transition pathways in complex systems. In Multiscale Modelling and Simulation; Springer: Berlin, Germany, 2004; pp. 35–68. [Google Scholar]
- Legoll, F.; Lelièvre, T. Effective dynamics using conditional expectations. Nonlinearity 2010, 23, 2131. [Google Scholar] [CrossRef]
- Froyland, G.; Gottwald, G.A.; Hammerlindl, A. A trajectory-free framework for analysing multiscale systems. Phys. D 2016, 328, 34–43. [Google Scholar] [CrossRef]
- Zhang, W.; Hartmann, C.; Schutte, C. Effective dynamics along given reaction coordinates, and reaction rate theory. Faraday Discuss. 2016, 195, 365–394. [Google Scholar] [CrossRef]
- Zhang, W.; Schütte, C. Reliable Approximation of Long Relaxation Timescales in Molecular Dynamics. Entropy 2017, 19, 367. [Google Scholar] [CrossRef]
- Legoll, F.; Lelièvre, T.; Olla, S. Pathwise estimates for an effective dynamics. Stoch. Process. Appl. 2017, 127, 2841–2863. [Google Scholar] [CrossRef]
- Lelièvre, T.; Zhang, W. Pathwise estimates for effective dynamics: The case of nonlinear vectorial reaction coordinates. Multiscale Model. Simul. 2019, 17, 1019–1051. [Google Scholar] [CrossRef]
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A Direct Approach to Conformational Dynamics Based on Hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar] [CrossRef]
- Dellnitz, M.; Junge, O. On the Approximation of Complicated Dynamical Behavior. SIAM J. Numer. Anal. 1999, 36, 491–515. [Google Scholar] [CrossRef]
- Noé, F.; Nüske, F. A variational approach to modeling slow processes in stochastic dynamical systems. Multiscale Model. Simul. 2013, 11, 635–655. [Google Scholar] [CrossRef]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A Data-Driven Approximation of the Koopman Operator: Extending Dynamic Mode Decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Mardt, A.; Pasquali, L.; Wu, H.; Noé, F. VAMPnets for deep learning of molecular kinetics. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Klus, S.; Nüske, F.; Koltai, P.; Wu, H.; Kevrekidis, I.; Schütte, C.; Noé, F. Data-Driven Model Reduction and Transfer Operator Approximation. J. Nonlinear Sci. 2018, 28, 985–1010. [Google Scholar] [CrossRef]
- Wu, H.; Noé, F. Variational approach for learning Markov processes from time series data. J. Nonlinear Sci. 2020, 30, 23–66. [Google Scholar] [CrossRef]
- Klus, S.; Nüske, F.; Peitz, S.; Niemann, J.H.; Clementi, C.; Schütte, C. Data-driven approximation of the Koopman generator: Model reduction, system identification, and control. Phys. D Nonlinear Phenom. 2020, 406, 132416. [Google Scholar] [CrossRef]
- Kessler, M.; Lindner, A.; Sorensen, M. Statistical Methods for Stochastic Differential Equations; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Gobet, E.; Hoffmann, M.; Reiß, M. Nonparametric estimation of scalar diffusions based on low frequency data. Ann. Stat. 2004, 32, 2223–2253. [Google Scholar]
- Crommelin, D.; Vanden-Eijnden, E. Diffusion Estimation from Multiscale Data by Operator Eigenpairs. Multiscale Model. Simul. 2011, 9, 1588–1623. [Google Scholar] [CrossRef]
- Zhang, L.; Mykland, P.A.; Aït-Sahalia, Y. A tale of two time scales: Determining integrated volatility with noisy high-frequency data. J. Am. Stat. Assoc. 2005, 100, 1394–1411. [Google Scholar] [CrossRef]
- Bittracher, A.; Hartmann, C.; Junge, O.; Koltai, P. Pseudo generators for under-resolved molecular dynamics. Eur. Phys. J. Spec. Top. 2015, 224, 2463–2490. [Google Scholar] [CrossRef][Green Version]
- Bittracher, A.; Koltai, P.; Junge, O. Pseudogenerators of spatial transfer operators. SIAM J. Appl. Dyn. Syst. 2015, 14, 1478–1517. [Google Scholar] [CrossRef][Green Version]
- Duong, M.H.; Lamacz, A.; Peletier, M.A.; Schlichting, A.; Sharma, U. Quantification of coarse-graining error in Langevin and overdamped Langevin dynamics. Nonlinearity 2018, 31, 4517. [Google Scholar] [CrossRef]
- Bakry, D.; Gentil, I.; Ledoux, M. Analysis and Geometry of Markov Diffusion Operators; Springer Science & Business Media: Berlin, Germany, 2013; Volume 348. [Google Scholar]
- Davies, E.B. Metastable states of symmetric Markov semigroups II. J. Lond. Math. Soc. 1982, 2, 541–556. [Google Scholar] [CrossRef]
- Pazy, A. Semigroups of Linear Operators and Applications to Partial Differential Equations; Springer: New York, NY, USA; Berlin, Germany, 1983. [Google Scholar]
- Davies, E.B. Metastable states of symmetric Markov semigroups I. Proc. Lond. Math. Soc. 1982, 45, 133–150. [Google Scholar] [CrossRef]
- Deuflhard, P.; Huisinga, W.; Fischer, A.; Schütte, C. Identification of almost invariant aggregates in reversible nearly uncoupled Markov chains. Linear Algebra Appl. 2000, 315, 39–59. [Google Scholar] [CrossRef]
- Risken, H.; Haken, H. The Fokker–Planck Equation: Methods of Solution and Applications, 2nd ed.; Springer: Berlin, Germany, 1989. [Google Scholar]
- Deuflhard, P.; Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra Appl. 2005, 398, 161–184. [Google Scholar] [CrossRef]
- Schütte, C. Conformational Dynamics: Modelling, Theory, Algorithm, and Application to Biomolecules. Available online: https://opus4.kobv.de/opus4-zib/frontdoor/index/index/docId/406 (accessed on 20 January 2021).
- Nüske, F.; Wu, H.; Prinz, J.H.; Wehmeyer, C.; Clementi, C.; Noé, F. Markov state models from short non-equilibrium simulations—Analysis and correction of estimation bias. J. Chem. Phys. 2017, 146, 094104. [Google Scholar] [CrossRef]
- Wang, J.; Olsson, S.; Wehmeyer, C.; Pérez, A.; Charron, N.E.; De Fabritiis, G.; Noé, F.; Clementi, C. Machine learning of coarse-grained molecular dynamics force fields. ACS Cent. Sci. 2019, 5, 755–767. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef]
- Knyazev, A.V.; Osborn, J.E. New a priori FEM error estimates for eigenvalues. SIAM J. Numer. Anal. 2006, 43, 2647–2667. [Google Scholar] [CrossRef][Green Version]
- Cejas, M.E.; Durán, R.G. Weighted a priori estimates for elliptic equations. arXiv 2017, arXiv:1711.00879. [Google Scholar] [CrossRef]
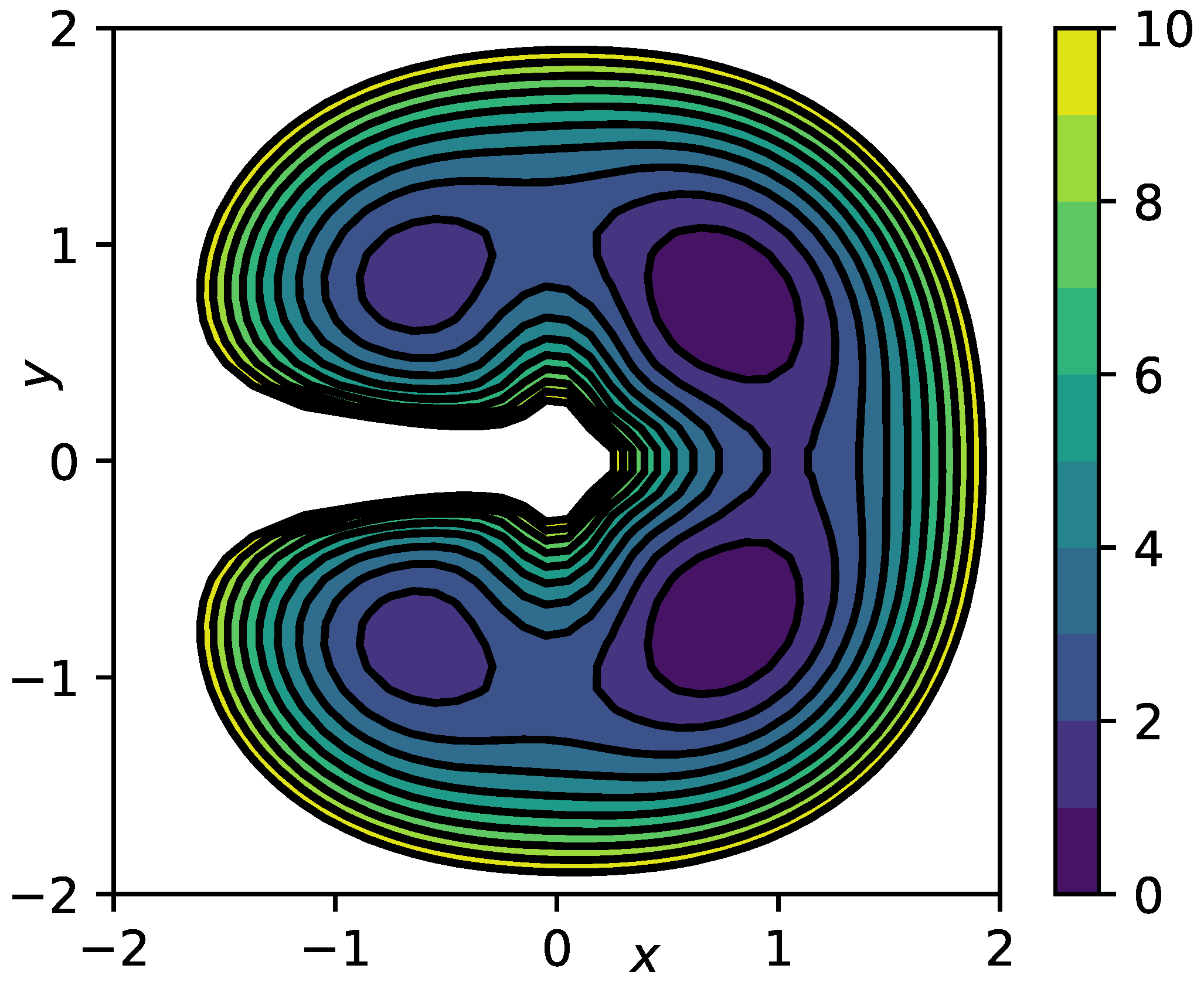

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nüske, F.; Koltai, P.; Boninsegna, L.; Clementi, C. Spectral Properties of Effective Dynamics from Conditional Expectations. Entropy 2021, 23, 134. https://doi.org/10.3390/e23020134
Nüske F, Koltai P, Boninsegna L, Clementi C. Spectral Properties of Effective Dynamics from Conditional Expectations. Entropy. 2021; 23(2):134. https://doi.org/10.3390/e23020134
Chicago/Turabian StyleNüske, Feliks, Péter Koltai, Lorenzo Boninsegna, and Cecilia Clementi. 2021. "Spectral Properties of Effective Dynamics from Conditional Expectations" Entropy 23, no. 2: 134. https://doi.org/10.3390/e23020134
APA StyleNüske, F., Koltai, P., Boninsegna, L., & Clementi, C. (2021). Spectral Properties of Effective Dynamics from Conditional Expectations. Entropy, 23(2), 134. https://doi.org/10.3390/e23020134




