Quantifying the Autonomy of Structurally Diverse Automata: A Comparison of Candidate Measures
Abstract
1. Introduction
2. Quantitative Measures Related to Agency, Autonomy, and Intelligence
2.1. Structural and Graph-Theoretical Measures
2.2. Information Theoretical Measures
2.3. Causal Measures
2.4. Dynamical Measures
3. Evolution Simulation
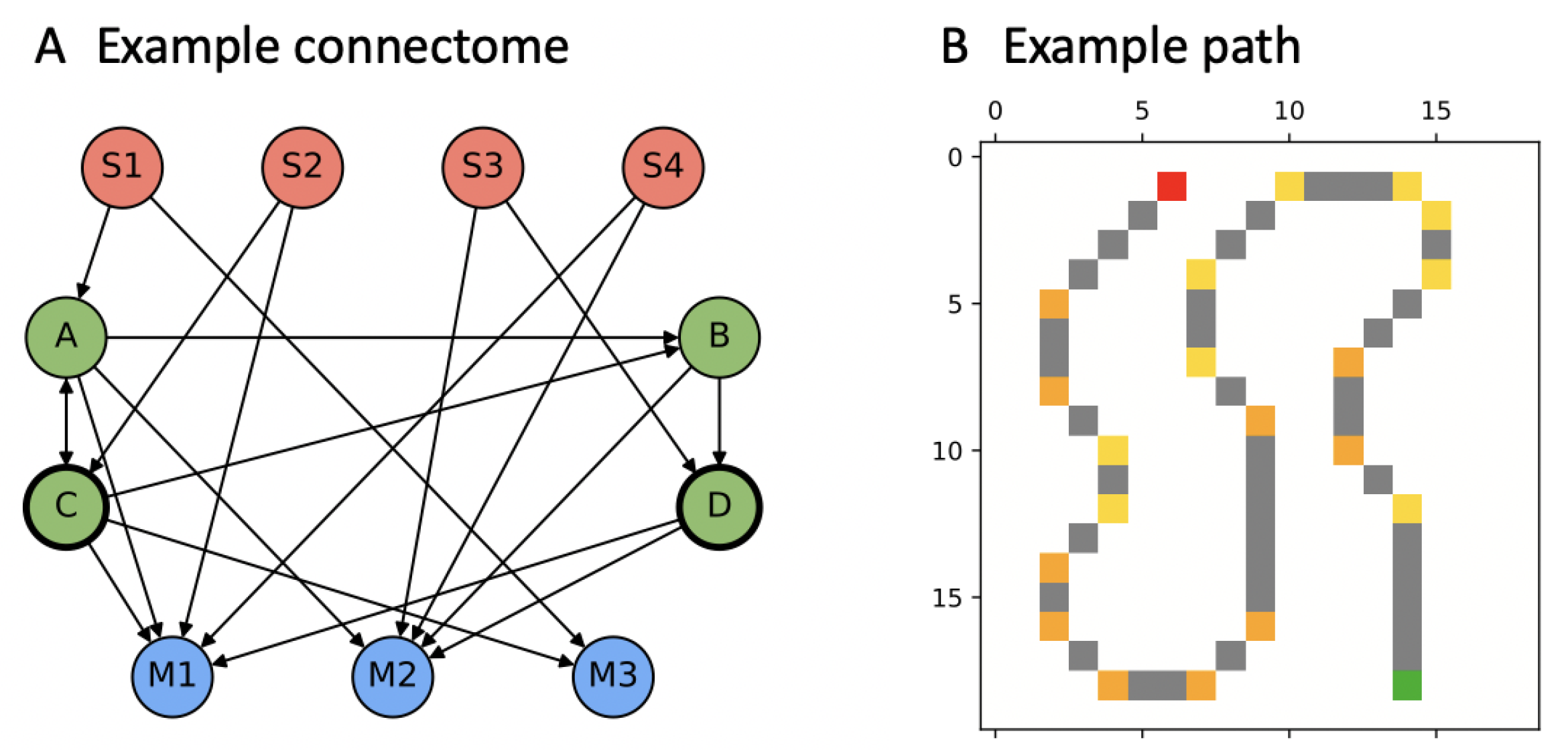
3.1. Markov Brains (MBs)
3.2. “PathFollow” Environment
3.3. Data Analysis
4. Results
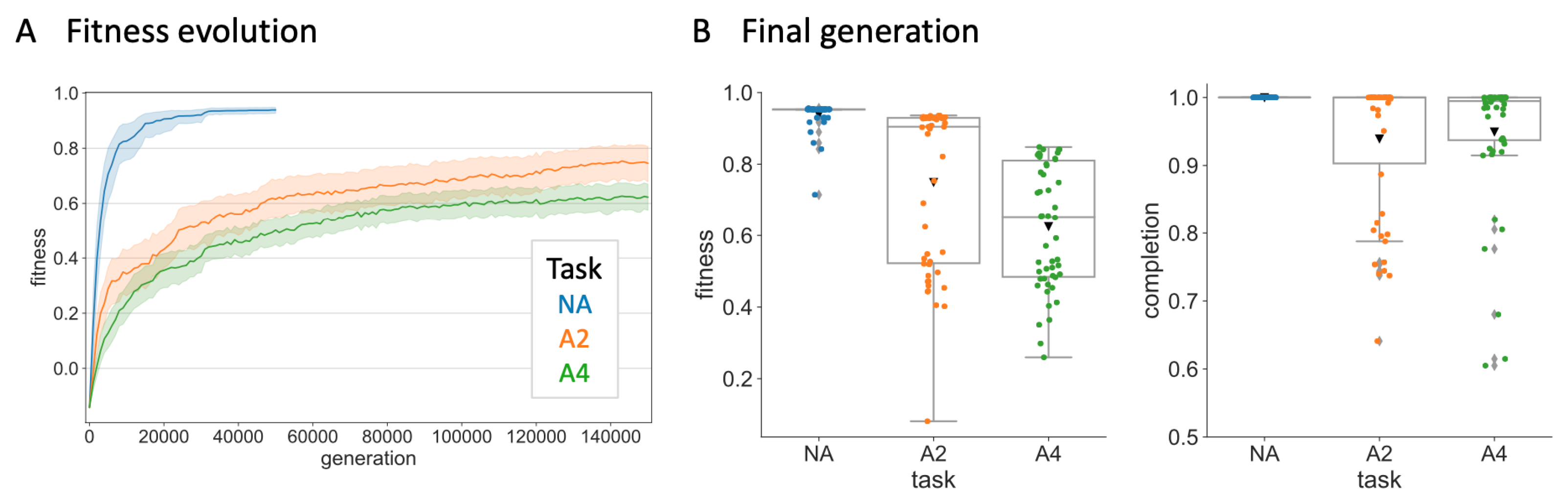
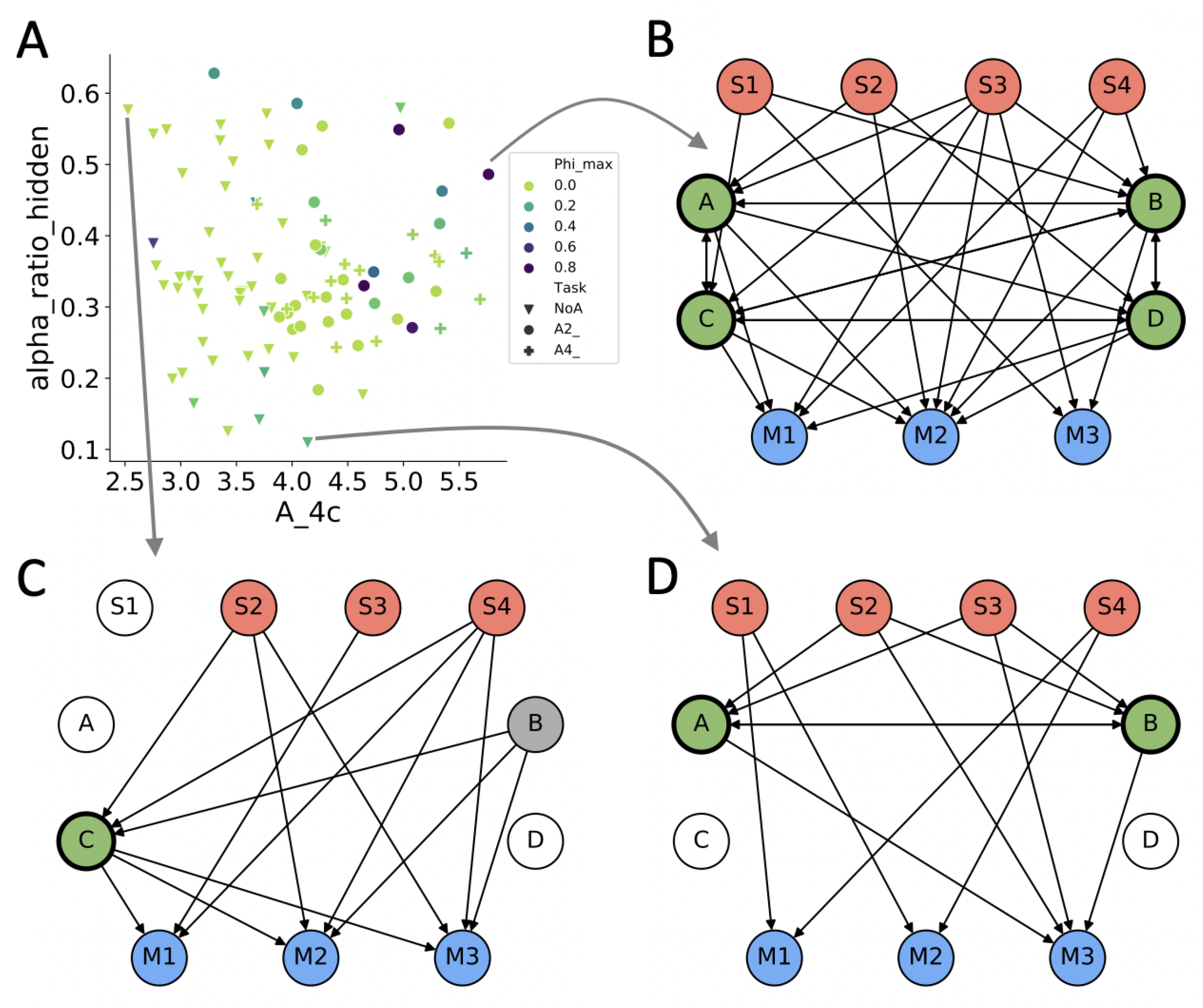
4.1. Evolved Network Structures
4.2. Information Theoretical Analysis
4.3. Causal Analysis
4.4. Dynamical Analysis
5. Discussion
5.1. Scope and Limitations
5.2. Related Work
5.3. Memory and Autonomy
5.4. Correlation, Causation, and Internal Structure
5.5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
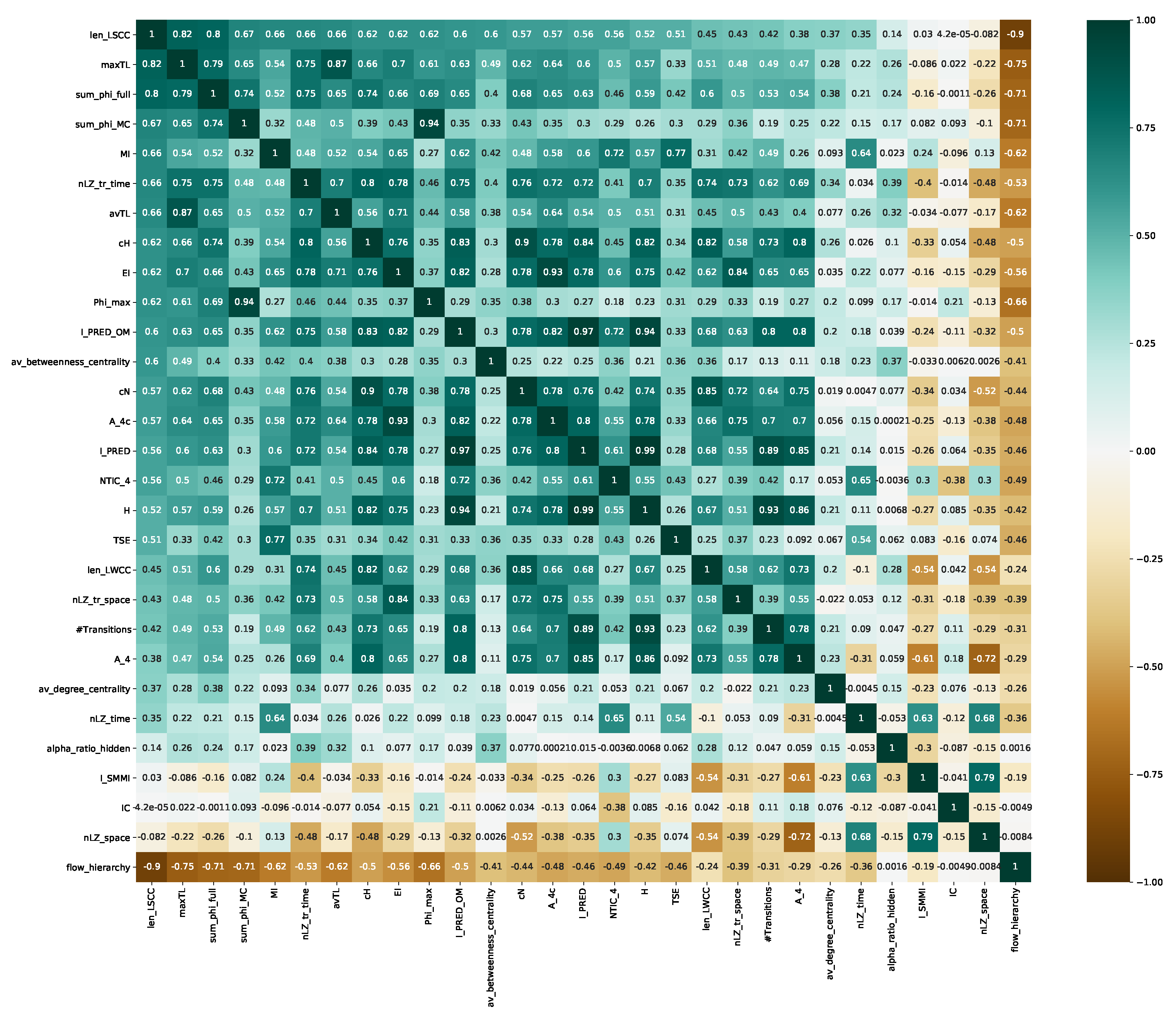
Appendix A
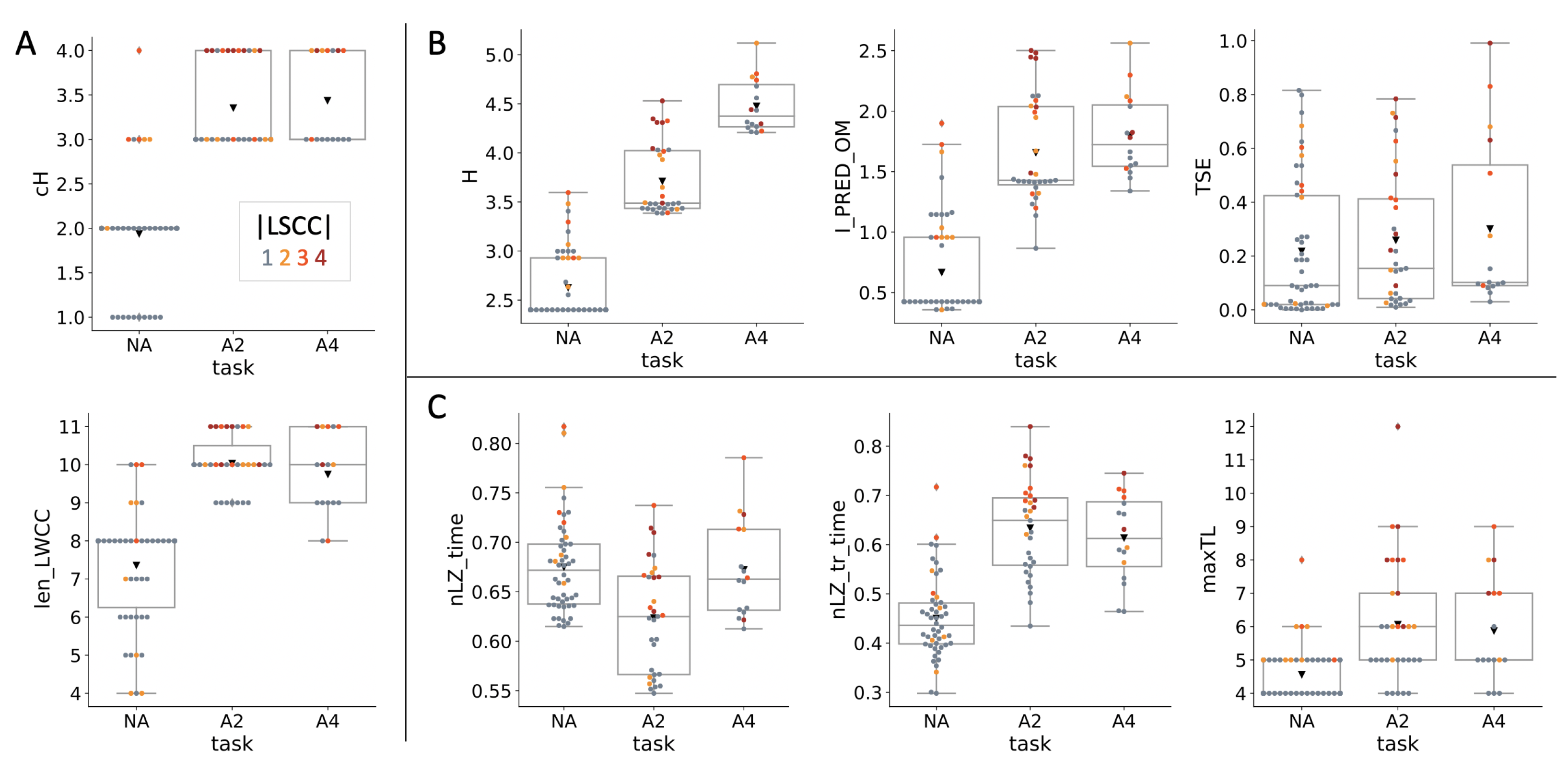
Appendix B
References
- Bertschinger, N.; Olbrich, E.; Ay, N.; Jost, J. Autonomy: An information theoretic perspective. Biosystems 2008, 91, 331–345. [Google Scholar] [CrossRef] [PubMed]
- Boden, M.A. Autonomy: What is it? Biosystems 2008, 91, 305–308. [Google Scholar] [CrossRef]
- Albantakis, L. A Tale of Two Animats: What Does It Take to Have Goas? Springer: Cham, Switzerland, 2018; pp. 5–15. [Google Scholar] [CrossRef]
- Krakauer, D.; Bertschinger, N.; Olbrich, E.; Flack, J.C.; Ay, N. The information theory of individuality. Theory Biosci. 2020, 139, 209–223. [Google Scholar] [CrossRef]
- Vakhrameev, D.; Aguilera, M.; Barandiaran, X.E.; Bedia, M. Measuring Autonomy for Life-Like AI. In Proceedings of the 2020 Conference on Artificial Life, Montréal, QC, Canada, 13–17 July 2020; MIT Press: Cambridge, MA, USA, 2020; pp. 589–591. [Google Scholar] [CrossRef]
- Maturana, H.R.; Varela, F.J. Autopoiesis and Cognition: The Realization of the Living; Boston Studies in the Philosophy and History of Science; Springer: Dordrecht, The Netherlands, 1980. [Google Scholar]
- Tononi, G. On the Irreducibility of Consciousness and Its Relevance to Free Will; Springer New York: New York, NY, USA, 2013; pp. 147–176. [Google Scholar] [CrossRef]
- Marshall, W.; Kim, H.; Walker, S.I.; Tononi, G.; Albantakis, L. How causal analysis can reveal autonomy in models of biological systems. Philos. Trans. Ser. Math. Phys. Eng. Sci. 2017, 375, 20160358. [Google Scholar] [CrossRef]
- Aguilera, M.; Di Paolo, E. Integrated Information and Autonomy in the Thermodynamic Limit. arXiv 2018, arXiv:1805.00393. [Google Scholar]
- Farnsworth, K.D. How Organisms Gained Causal Independence and How It Might Be Quantified. Biology 2018, 7, 38. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Moreno, A.; Etxeberria, A.; Umerez, J. The autonomy of biological individuals and artificial models. BioSystems 2008, 91, 309–319. [Google Scholar] [CrossRef]
- Moreno, A.; Mossio, M. Biological Autonomy. In History, Philosophy and Theory of the Life Sciences; Springer: Dordrecht, The Netherlands, 2015; Volume 12. [Google Scholar] [CrossRef]
- Barandiaran, X.; Ruiz-Mirazo, K. Modelling autonomy: Simulating the essence of life and cognition. BioSystems 2008, 91, 295–304. [Google Scholar] [CrossRef]
- Hintze, A.; Schossau, J.; Bohm, C. The Evolutionary Buffet Method; Springer: Cham, Switzerland, 2019; pp. 17–36. [Google Scholar] [CrossRef]
- Hintze, A.; Edlund, J.A.; Olson, R.S.; Knoester, D.B.; Schossau, J.; Albantakis, L.; Tehrani-Saleh, A.; Kvam, P.; Sheneman, L.; Goldsby, H.; et al. Markov Brains: A Technical Introduction. arXiv 2017, arXiv:1709.05601. [Google Scholar]
- Rocha, L.M. Syntactic Autonomy: Why There Is No Autonomy without Symbols and How Self-Organizing Systems Might Evolve Them; Annals of the New York Academy of Sciences; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2000; Volume 901, pp. 207–223. [Google Scholar] [CrossRef]
- Bertschinger, N.; Olbrich, E. Information and Closure in Systems Theory. In Proceedings of the 7th German Workshop on Artificial Life, Jena, Germany, 26–28 July 2006. [Google Scholar]
- Kirchhoff, M.; Parr, T.; Palacios, E.; Friston, K.; Kiverstein, J. The Markov blankets of life: Autonomy, active inference and the free energy principle. J. R. Soc. Interface 2018, 15, 20170792. [Google Scholar] [CrossRef] [PubMed]
- Pearl, J. Causality: Models, Reasoning and Inference; Cambridge University Press: Cambridge, UK, 2000; Volume 29. [Google Scholar]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef]
- Bruineberg, J.; Dolega, K.; Dewhurst, J.; Baltieri, M. The Emperor’s New Markov Blankets. 2020. Available online: http://philsciarchive.pitt.edu/18467/1/The%20Emperor%27s%20New%20Markov%20Blankets.pdf (accessed on 15 September 2021).
- Kolchinsky, A.; Wolpert, D.H. Semantic information, autonomous agency and non-equilibrium statistical physics. Interface Focus 2018, 8, 20180041. [Google Scholar] [CrossRef] [PubMed]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Freeman, L.C. A Set of Measures of Centrality Based on Betweenness. Sociometry 1977, 40, 35. [Google Scholar] [CrossRef]
- Luo, J.; Magee, C.L. Detecting Evolving Patterns of Self-Organizing Networks by Flow Hierarchy Measurement. Complexity 2011, 16, 53–61. [Google Scholar] [CrossRef]
- Fischer, D.; Mostaghim, S.; Albantakis, L. How swarm size during evolution impacts the behavior, generalizability, and brain complexity of animats performing a spatial navigation task. In Proceedings of the Genetic and Evolutionary Computation Conference on—GECCO 18, Kyoto, Japan, 15–19 July 2018; pp. 77–84. [Google Scholar] [CrossRef]
- Walker, S.I.; Davies, P.C.W. The algorithmic origins of life. J. R. Soc. Interface R. Soc. 2013, 10, 20120869. [Google Scholar] [CrossRef]
- Edlund, J.A.; Chaumont, N.; Hintze, A.; Koch, C.; Tononi, G.; Adami, C. Integrated information increases with fitness in the evolution of animats. PLoS Comput. Biol. 2011, 7, e1002236. [Google Scholar] [CrossRef]
- Albantakis, L.; Hintze, A.; Koch, C.; Adami, C.; Tononi, G. Evolution of Integrated Causal Structures in Animats Exposed to Environments of Increasing Complexity. PLoS Comput. Biol. 2014, 10, e1003966. [Google Scholar] [CrossRef]
- Beer, R.D.; Williams, P.L. Information processing and dynamics in minimally cognitive agents. Cogn. Sci. 2015, 39, 1–38. [Google Scholar] [CrossRef] [PubMed]
- Salge, C.; Glackin, C.; Polani, D. Empowerment—An Introduction. arXiv 2013, arXiv:cs.AI/1310.1863. [Google Scholar]
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, complexity, and learning. Neural. Comput. 2001, 13, 2409–2463. [Google Scholar] [CrossRef] [PubMed]
- Schwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Marstaller, L.; Hintze, A.; Adami, C. The evolution of representation in simple cognitive networks. Neural. Comput. 2013, 25, 2079–2107. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Generalized Measures of Information Transfer. arXiv 2011, arXiv:1102.1507. [Google Scholar]
- Mediano, P.A.; Seth, A.K.; Barrett, A.B. Measuring integrated information: Comparison of candidate measures in theory and simulation. Entropy 2019, 21, 17. [Google Scholar] [CrossRef]
- Krakauer, D.C.; Zanotto, P. Viral individuality and limitations of the life concept. In Protocells: Bridging Nonliving and Living Matter; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Krakauer, D.; Bertschinger, N.; Olbrich, E.; Ay, N.; Flack, J.C. The Information Theory of Individuality. arXiv 2014, arXiv:1412.2447. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Chang, A.Y.C.; Biehl, M.; Yu, Y.; Kanai, R. Information Closure Theory of Consciousness. Front. Psychol. 2020, 11, 1504. [Google Scholar] [CrossRef]
- Kanwal, M.; Grochow, J.; Ay, N. Comparing Information-Theoretic Measures of Complexity in Boltzmann Machines. Entropy 2017, 19, 310. [Google Scholar] [CrossRef]
- Oizumi, M.; Tsuchiya, N.; Amari, S.I. A unified framework for information integration based on information geometry. Proc. Natl. Acad. Sci. USA 2015, 113, 14817–14822. [Google Scholar] [CrossRef]
- Tegmark, M. Improved Measures of Integrated Information. PLoS Comput. Biol. 2016, 12, e1005123. [Google Scholar] [CrossRef]
- Tononi, G.; Sporns, O. Measuring information integration. BMC Neurosci. 2003, 4, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Balduzzi, D.; Tononi, G. Integrated information in discrete dynamical systems: Motivation and theoretical framework. PLoS Comput. Biol. 2008, 4, e1000091. [Google Scholar] [CrossRef]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, L.S.; Marshall, W.; Albantakis, L.; Tononi, G. Mechanism Integrated Information. Entropy 2021, 23, 362. [Google Scholar] [CrossRef]
- McGill, W. Multivariate information transmission. Trans. Ire Prof. Group Inf. Theory 1954, 4, 93–111. [Google Scholar] [CrossRef]
- Watanabe, S. Information Theoretical Analysis of Multivariate Correlation. IBM J. Res. Dev. 1960, 4, 66–82. [Google Scholar] [CrossRef]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994, 91, 5033–5037. [Google Scholar] [CrossRef]
- Olbrich, E.; Bertschinger, N.; Ay, N.; Jost, J. How should complexity scale with system size? Eur. Phys. J. 2008, 63, 407–415. [Google Scholar] [CrossRef]
- Timme, N.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2014, 36, 119–140. [Google Scholar] [CrossRef]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Harder, M.; Salge, C.; Polani, D. Bivariate measure of redundant information. Phys. Rev. -Stat. Nonlinear Soft Matter Phys. 2013, 87, 012130. [Google Scholar] [CrossRef] [PubMed]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying Unique Information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Chicharro, D. Quantifying Multivariate Redundancy with Maximum Entropy Decompositions of Mutual Information. arXiv 2017, arXiv:1708.03845. [Google Scholar]
- Kolchinsky, A. A novel Approach to Multivariate Redundancy and Synergy. arXiv 2019, arXiv:1908.08642. [Google Scholar]
- Tax, T.; Mediano, P.; Shanahan, M.; Tax, T.M.; Mediano, P.A.; Shanahan, M. The Partial Information Decomposition of Generative Neural Network Models. Entropy 2017, 19, 474. [Google Scholar] [CrossRef]
- Yu, S.; Wickstrøm, K.; Jenssen, R.; Principe, J.C. Understanding Convolutional Neural Network Training with Information Theory. arXiv 2018, arXiv:1804.06537. [Google Scholar]
- Mediano, P.A.M.; Rosas, F.; Carhart-Harris, R.L.; Seth, A.K.; Barrett, A.B. Beyond Integrated Information: A Taxonomy of Information Dynamics Phenomena. arXiv 2019, arXiv:1909.02297. [Google Scholar]
- Ay, N.; Polani, D. Information Flows in Causal Networks. Adv. Complex Syst. 2008, 11, 17–41. [Google Scholar] [CrossRef]
- Hoel, E.P.; Albantakis, L.; Tononi, G. Quantifying causal emergence shows that macro can beat micro. Proc. Natl. Acad. Sci. USA 2013, 110, 19790–19795. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Tononi, G. Integrated information theory. Scholarpedia 2015, 10, 4164. [Google Scholar] [CrossRef]
- Albantakis, L.; Tononi, G. Causal Composition: Structural Differences among Dynamically Equivalent Systems. Entropy 2019, 21, 989. [Google Scholar] [CrossRef]
- Albantakis, L.; Tononi, G. The Intrinsic Cause-Effect Power of Discrete Dynamical Systems—From Elementary Cellular Automata to Adapting Animats. Entropy 2015, 17, 5472–5502. [Google Scholar] [CrossRef]
- Mayner, W.G.; Marshall, W.; Albantakis, L.; Findlay, G.; Marchman, R.; Tononi, G. PyPhi: A toolbox for integrated information theory. PLoS Comput. Biol. 2018, 14, e1006343. [Google Scholar] [CrossRef]
- Albantakis, L.; Marshall, W.; Hoel, E.; Tononi, G. What caused what? A quantitative account of actual causation using dynamical causal networks. Entropy 2019, 21, 459. [Google Scholar] [CrossRef]
- Korb, K.B.; Nyberg, E.P.; Hope, L. A new causal power theory. In Causality in the Sciences; Oxford University Press: Oxford, UK, 2011. [Google Scholar] [CrossRef]
- Juel, B.E.; Comolatti, R.; Tononi, G.; Albantakis, L. When is an action caused from within? Quantifying the causal chain leading to actions in simulated agents. arXiv 2019, arXiv:1904.02995. [Google Scholar]
- Shapley, L.S. Contributions to the Theory of Games, Chapter A Value for n-person Games; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Albantakis, L. Integrated information theory. In Beyond Neural Correlates of Consciousness; Overgaard, M., Mogensen, J., Kirkeby-Hinrup, A., Eds.; Routledge: London, UK, 2020; pp. 87–103. [Google Scholar] [CrossRef]
- Strogatz, S.H.; Dichter, M. Nonlinear Dynamics and Chaos, 2nd ed.; SET with Student Solutions Manual; Studies in Nonlinearity; Avalon Publishing: New York, NY, USA, 2016. [Google Scholar]
- Adamatzky, A.; Martinez, G.J. On generative morphological diversity of elementary cellular automata. Kybernetes 2010, 39, 72–82. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the Complexity of Finite Sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Zenil, H.; Villarreal-Zapata, E. Asymptotic Behaviour and Ratios of Complexity in Cellular Automata. arXiv 2013, arXiv:1304.2816. [Google Scholar]
- Gauvrit, N.; Zenil, H.; Tegnér, J. The Information-theoretic and Algorithmic Approach to Human, Animal and Artificial Cognition. In Representation and Reality in Humans, Other Living Organisms and Intelligent Machines; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Zenil, H. Compression-based investigation of the dynamical properties of cellular automata and other systems. arXiv 2009, arXiv:0910.4042. [Google Scholar] [CrossRef]
- Nilsen, A.S.; Juel, B.E.; Marshall, W.; Storm, J.F. Evaluating Approximations and Heuristic Measures of Integrated Information. Entropy 2019, 21, 525. [Google Scholar] [CrossRef] [PubMed]
- Casali, A.G.; Gosseries, O.; Rosanova, M.; Boly, M.; Sarasso, S.; Casali, K.R.; Casarotto, S.; Bruno, M.A.; Laureys, S.; Tononi, G.; et al. A theoretically based index of consciousness independent of sensory processing and behavior. Sci. Transl. Med. 2013, 5, 198ra105. [Google Scholar] [CrossRef]
- Bohm, C.; Hintze, A. MABE (Modular Agent Based Evolver): A framework for digital evolution research. In Proceedings of the 14th European Conference on Artificial Life ECAL, Lyon, France, 4–8 September 2017; MIT Press: Cambridge, MA, USA, 2017; pp. 76–83. [Google Scholar] [CrossRef]
- Olson, R.S.; Hintze, A.; Dyer, F.C.; Knoester, D.B.; Adami, C. Predator confusion is sufficient to evolve swarming behaviour. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Fischer, D.; Mostaghim, S.; Albantakis, L. How cognitive and environmental constraints influence the reliability of simulated animats in groups. PLoS ONE 2020, 15, e0228879. [Google Scholar] [CrossRef] [PubMed]
- Boden, M.A. Autonomy and artificiality. In The Philosophy of Artificial Life; Oxford University Press: Oxford, UK, 1996; pp. 95–108. [Google Scholar]
- Varela, F.; Maturana, H.; Uribe, R. Autopoiesis: The organization of living systems, its characterization and a model. Biosystems 1974, 5, 187–196. [Google Scholar] [CrossRef]
- Varela, F.J. Principles of Biological Autonomy; North Holland: Amsterdam, The Netherlands, 1979. [Google Scholar]
- Letelier, J.C.; Soto-Andrade, J.; Guíñez Abarzúa, F.; Cornish-Bowden, A.; Luz Cárdenas, M. Organizational invariance and metabolic closure: Analysis in terms of (M,R) systems. J. Theor. Biol. 2006, 238, 949–961. [Google Scholar] [CrossRef]
- Clark, A. How to Knit Your Own Markov Blanket. In Philosophy and Predictive Processing; Metzinger, T.K., Wiese, W., Eds.; MIND Group: Frankfurt, Germany, 2017. [Google Scholar]
- Rovelli, C. Agency in Physics. arXiv 2020, arXiv:2007.05300. [Google Scholar]
- Waade, P.T.; Olesen, C.L.; Ito, M.M.; Mathys, C. Consciousness Fluctuates with Surprise: An empirical pre-study for the synthesis of the Free Energy Principle and Integrated Information Theory. PsyArXiv 2020. [Google Scholar] [CrossRef]
- Friston, K.J.; Wiese, W.; Hobson, J.A. Sentience and the origins of consciousness: From cartesian duality to Markovian monism. Entropy 2020, 22, 516. [Google Scholar] [CrossRef]
- Safron, A. An Integrated World Modeling Theory (IWMT) of Consciousness: Combining Integrated Information and Global Neuronal Workspace Theories With the Free Energy Principle and Active Inference Framework; Toward Solving the Hard Problem and Characterizing Agentic Causation. Front. Artif. Intell. 2020, 3, 30. [Google Scholar] [CrossRef] [PubMed]
- Albantakis, L. Review of Sentience and the Origins of Consciousness: From Cartesian Duality to Markovian Monism. 2020. Available online: https://www.consciousnessrealist.com/sentience-and-the-origins-of-consciousness/ (accessed on 15 September 2021).
- Shalizi, C.; Crutchfield, J. Computational mechanics: Pattern and prediction, structure and simplicity. J. Stat. Phys. 2001, 104, 817–879. [Google Scholar] [CrossRef]
- Marshall, W.; Gomez-Ramirez, J.; Tononi, G. Integrated Information and State Differentiation. Front. Psychol. 2016, 7, 926. [Google Scholar] [CrossRef]
- Lizier, J.; Prokopenko, M.; Zomaya, A. A framework for the local information dynamics of distributed computation in complex systems. In Guided Self-Organization: Inception; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lizier, J.T. JIDT: An Information-Theoretic Toolkit for Studying the Dynamics of Complex Systems. Front. Robot. AI 2014, 1, 37. [Google Scholar] [CrossRef]
- Shalizi, C.R.; Haslinger, R.; Rouquier, J.B.; Klinkner, K.L.; Moore, C. Automatic filters for the detection of coherent structure in spatiotemporal systems. Phys. Rev. 2006, 73, 036104. [Google Scholar] [CrossRef] [PubMed]
- Biehl, M.; Ikegami, T.; Polani, D. Towards information based spatiotemporal patterns as a foundation for agent representation in dynamical systems. In Proceedings of the Artificial Life Conference 2016, Cancun, Mexico, 4–6 July 2016. [Google Scholar] [CrossRef]
- Biehl, M.; Polani, D. Action and perception for spatiotemporal patterns. arXiv 2017, arXiv:1706.03576. [Google Scholar]
- Hintze, A.; Kirkpatrick, D.; Adami, C. The structure of evolved representations across different substrates for artificial intelligence. arXiv 2018, arXiv:1804.01660. [Google Scholar]
- Chicharro, D.; Ledberg, A.; Robins, J.; J, T.; Corbetta, M. When two become one: The limits of causality analysis of brain dynamics. PLoS ONE 2012, 7, e32466. [Google Scholar] [CrossRef]
- Rohde, M.; Stewart, J. Ascriptional and ‘genuine’ autonomy. Biosystems 2008, 91, 424–433. [Google Scholar] [CrossRef]
- Albantakis, L. The Greek Cave: Why a Little Bit of Causal Structure Is Necessary... Even for Functionalist, 2020. Available online: https://www.consciousnessrealist.com/greek-cave/ (accessed on 15 September 2021).
- Doerig, A.; Schurger, A.; Hess, K.; Herzog, M.H. The unfolding argument: Why IIT and other causal structure theories cannot explain consciousness. Conscious. Cogn. 2019, 72, 49–59. [Google Scholar] [CrossRef]
- Dale, R.; Spivey, M.J. From apples and oranges to symbolic dynamics: A framework for conciliating notions of cognitive representation. J. Exp. Theor. Artif. Intell. 2005, 17, 317–342. [Google Scholar] [CrossRef]

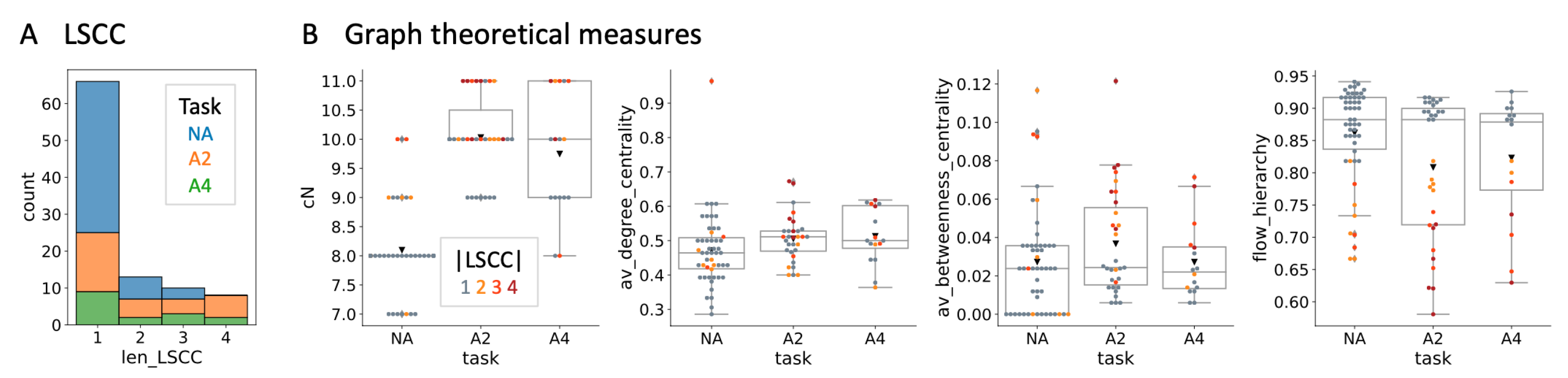
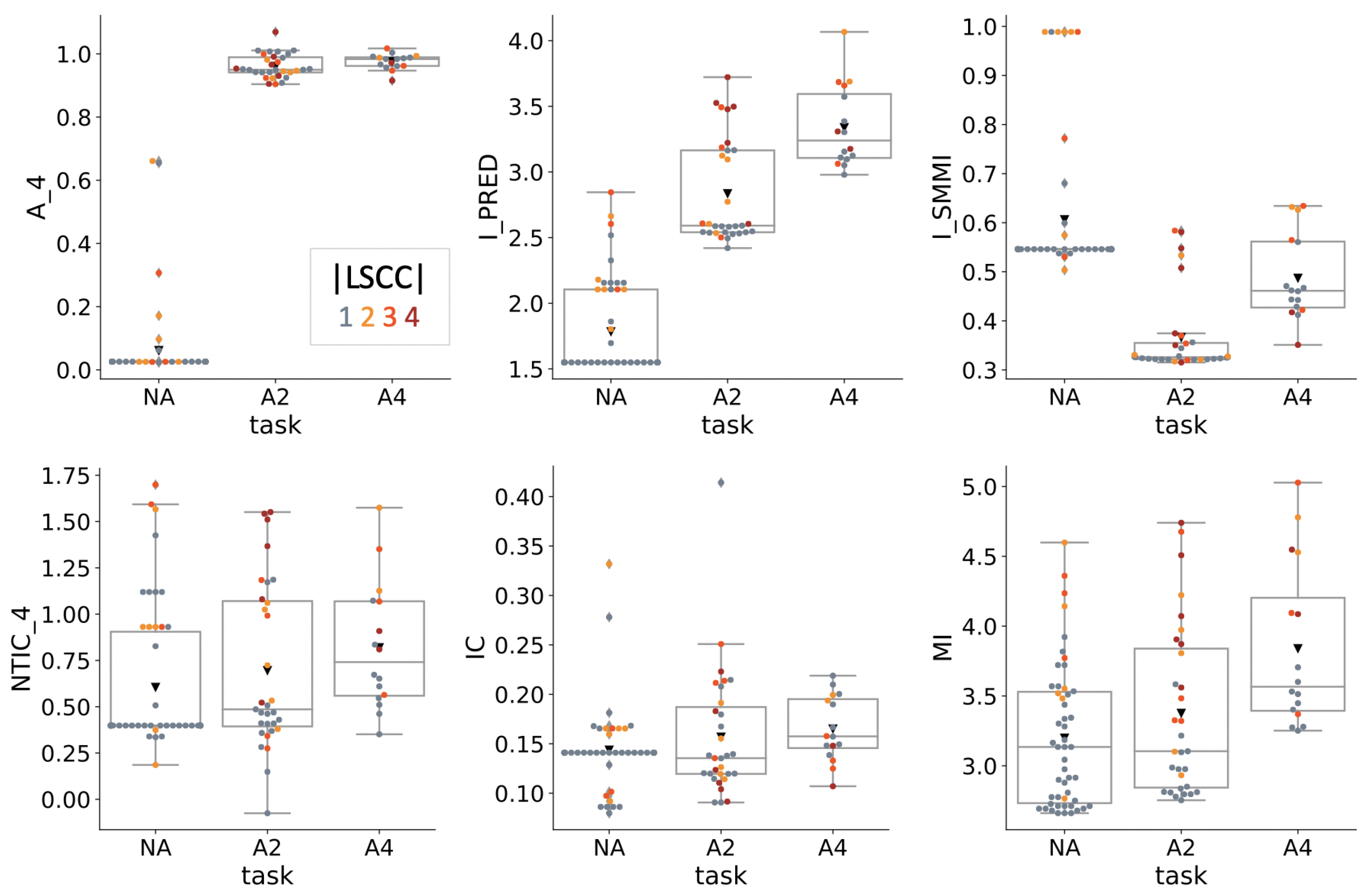
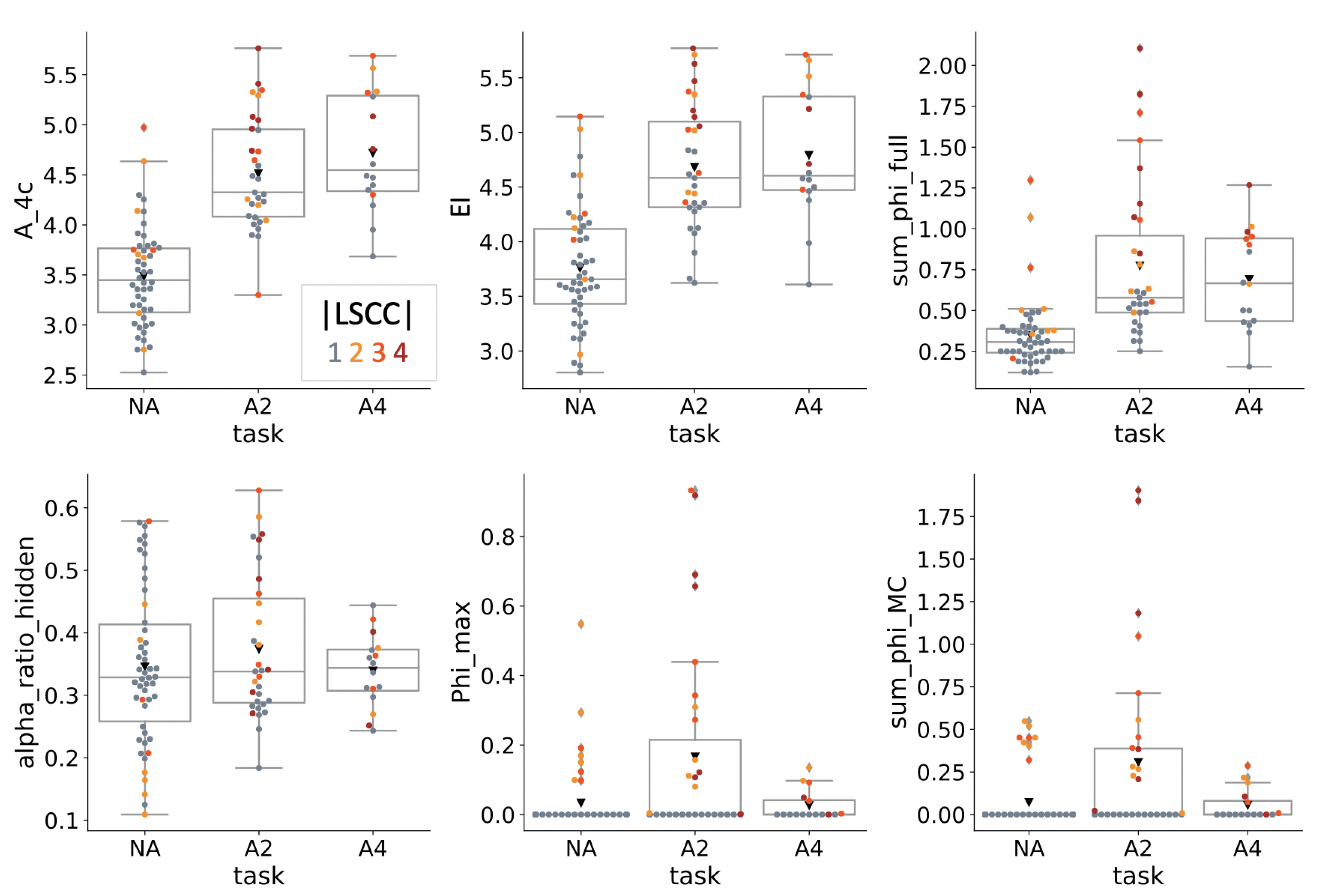
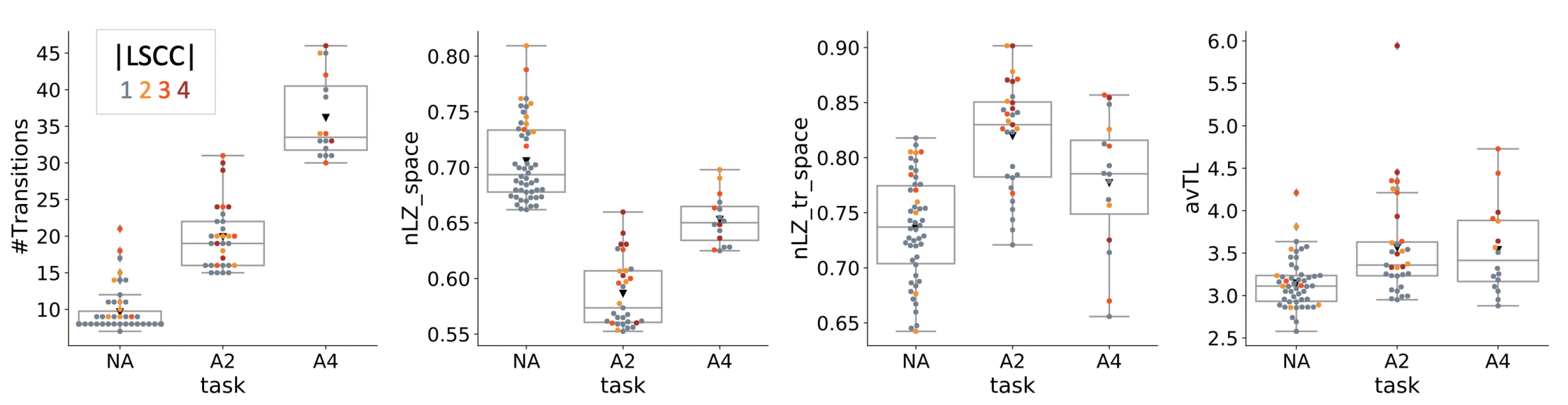
| Condition | NA | A2 | A4 |
|---|---|---|---|
| Number of generations | 50 k | 150 k | 150 k |
| Number of turn symbols | 2 | 2 | 4 |
| Random turn symbols | No | Yes | Yes |
| Number of evaluations per generation | 1 | 10 | 10 |
| Number of available sensors | 4 | 4 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Albantakis, L. Quantifying the Autonomy of Structurally Diverse Automata: A Comparison of Candidate Measures. Entropy 2021, 23, 1415. https://doi.org/10.3390/e23111415
Albantakis L. Quantifying the Autonomy of Structurally Diverse Automata: A Comparison of Candidate Measures. Entropy. 2021; 23(11):1415. https://doi.org/10.3390/e23111415
Chicago/Turabian StyleAlbantakis, Larissa. 2021. "Quantifying the Autonomy of Structurally Diverse Automata: A Comparison of Candidate Measures" Entropy 23, no. 11: 1415. https://doi.org/10.3390/e23111415
APA StyleAlbantakis, L. (2021). Quantifying the Autonomy of Structurally Diverse Automata: A Comparison of Candidate Measures. Entropy, 23(11), 1415. https://doi.org/10.3390/e23111415






