Microstructural Characteristics of the Weighted and Directed International Crop Trade Networks
Abstract
:1. Introduction
2. Datasets and Network Construction
2.1. Data Description
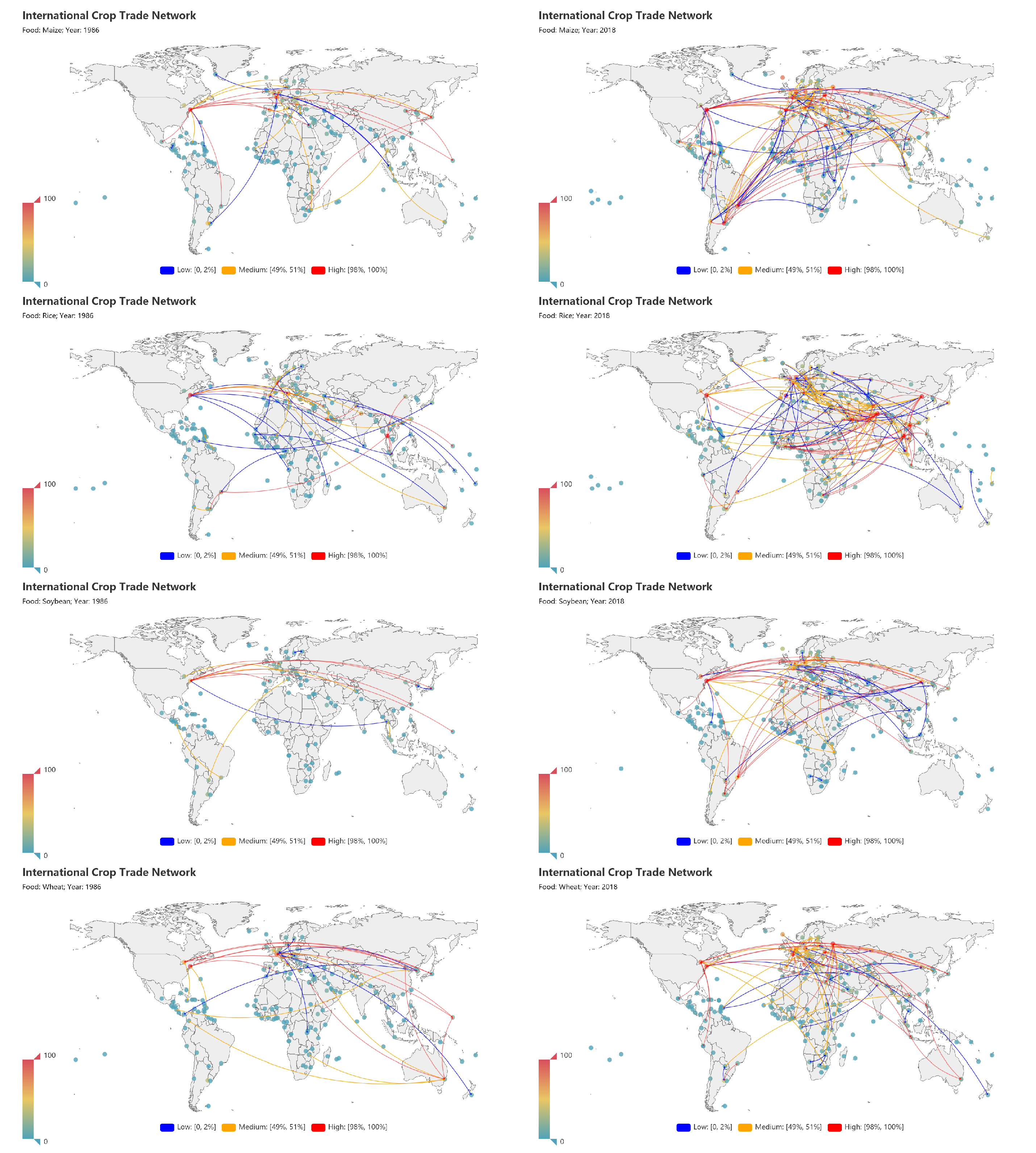
2.2. Network Construction
3. Empirical Results
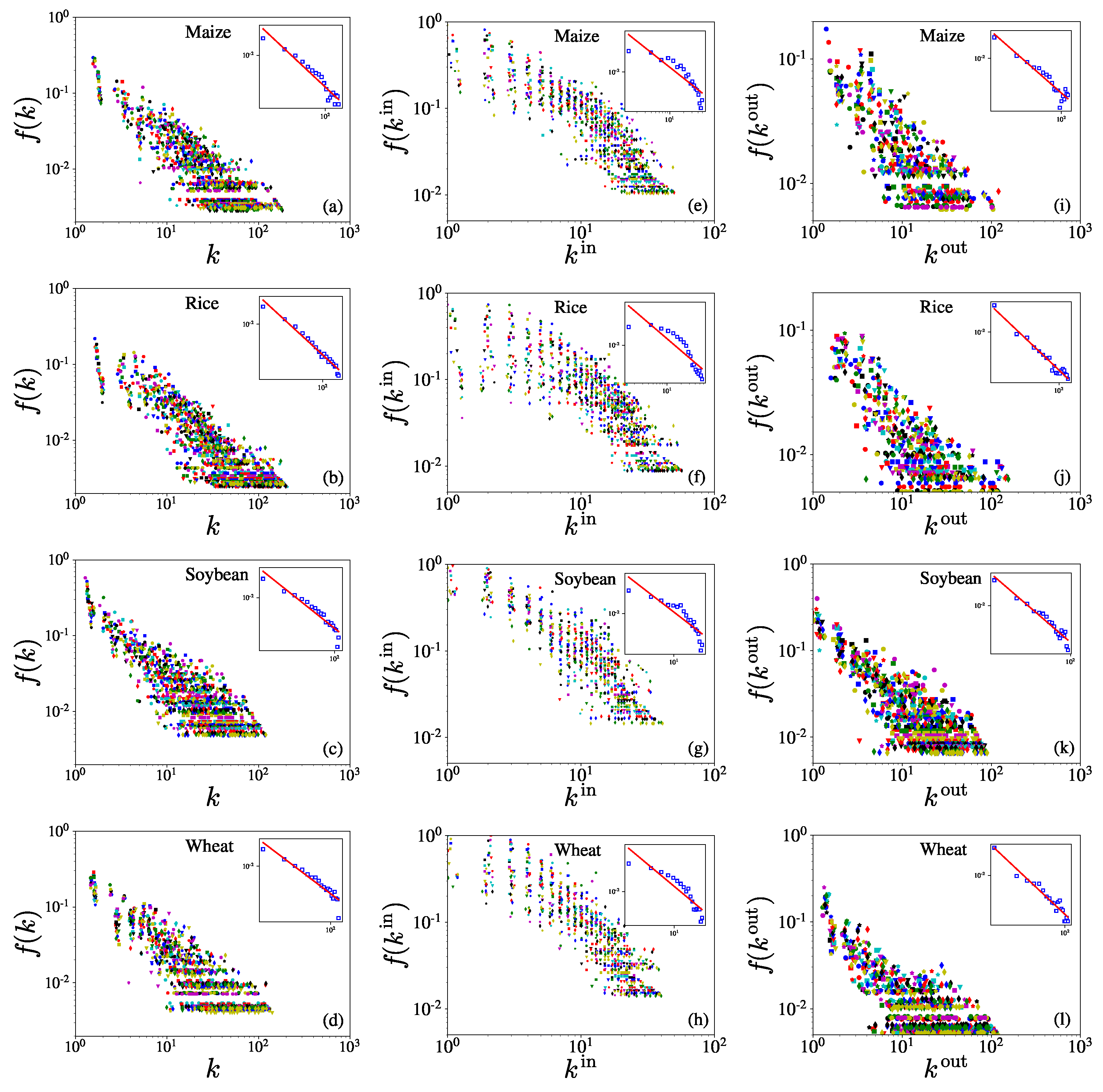
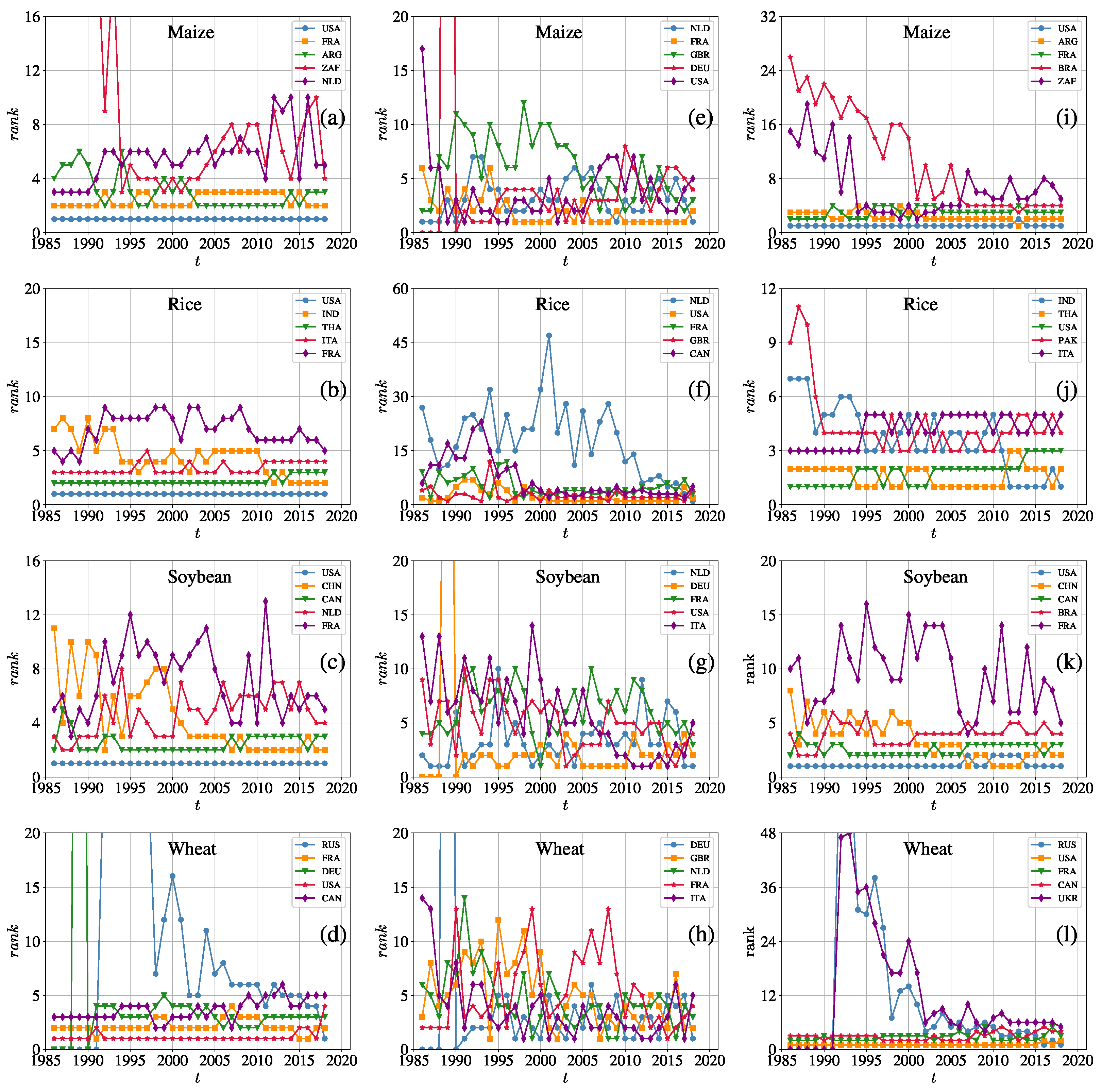
3.1. Node Degrees
3.2. Node Strengths
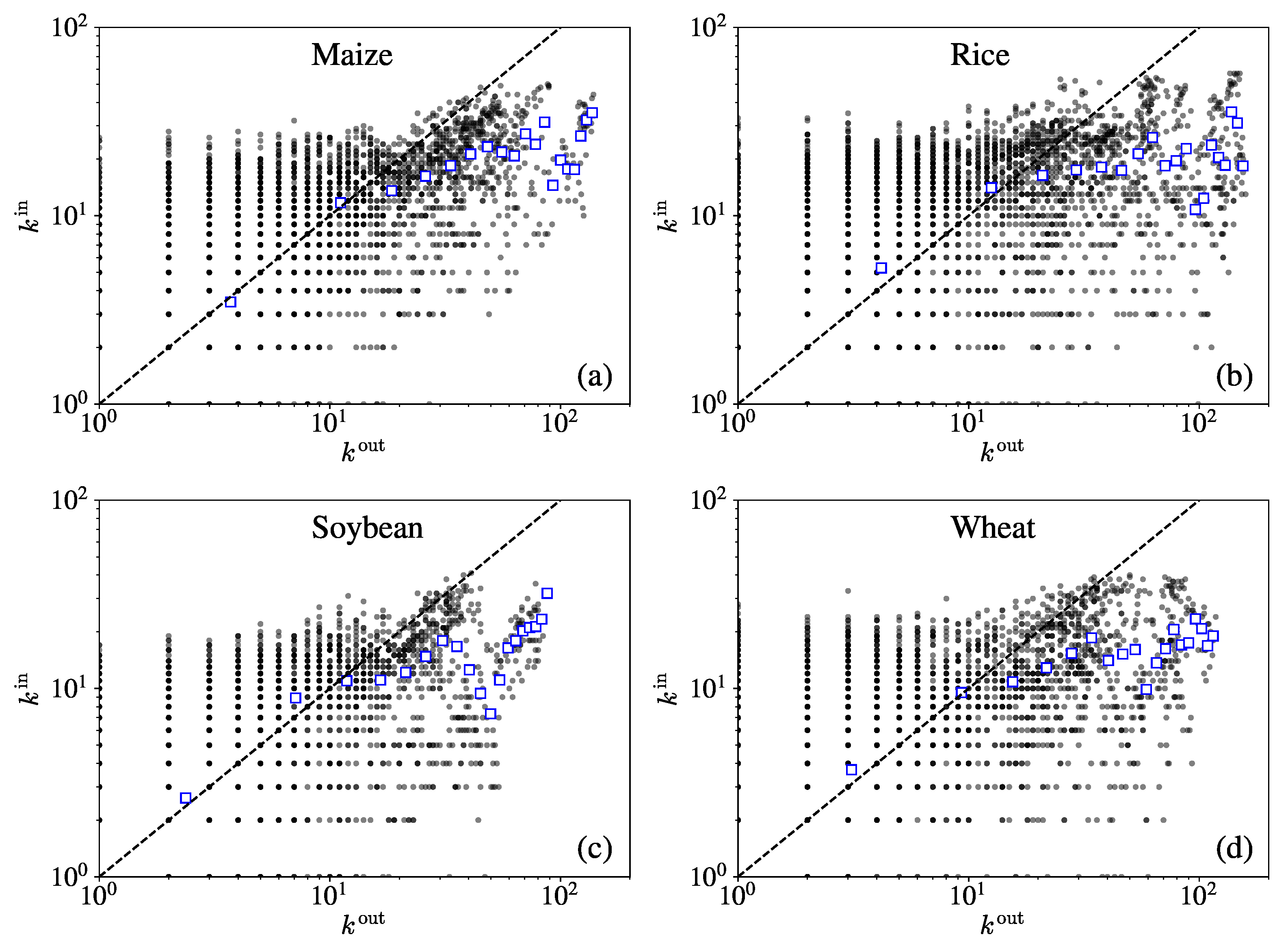
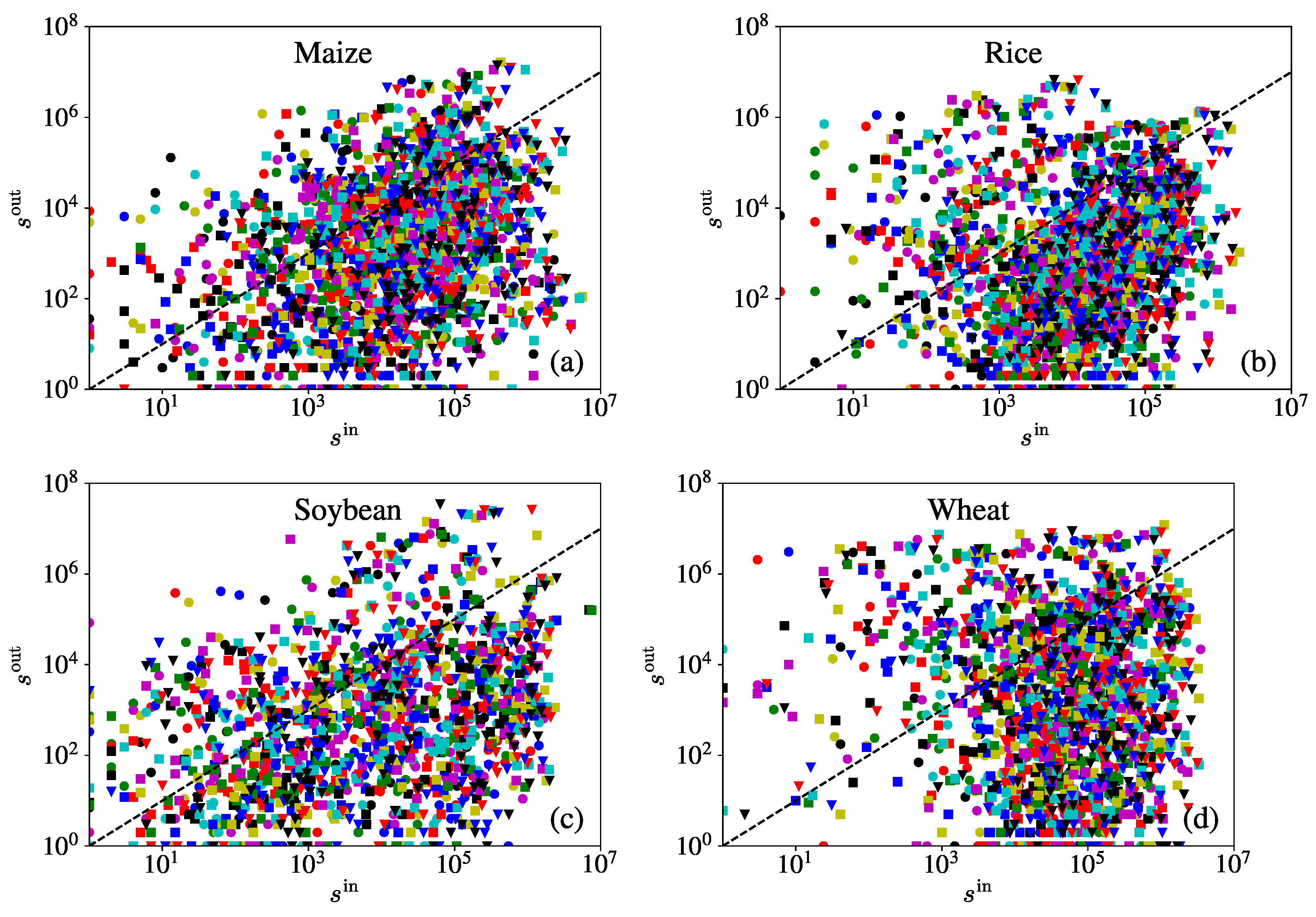
3.3. Degree vs. Strength
3.4. Link Weight
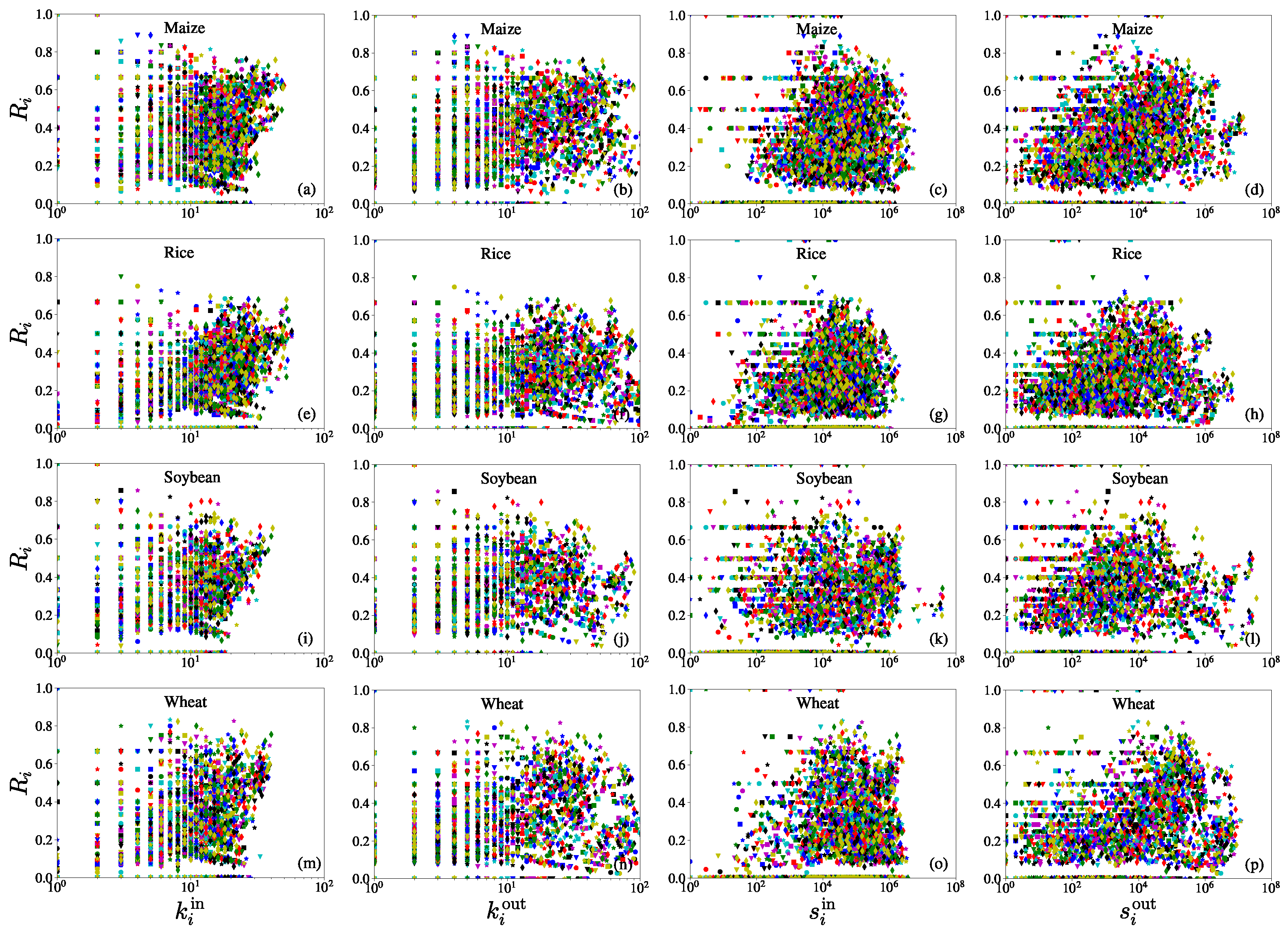
3.5. Reciprocity
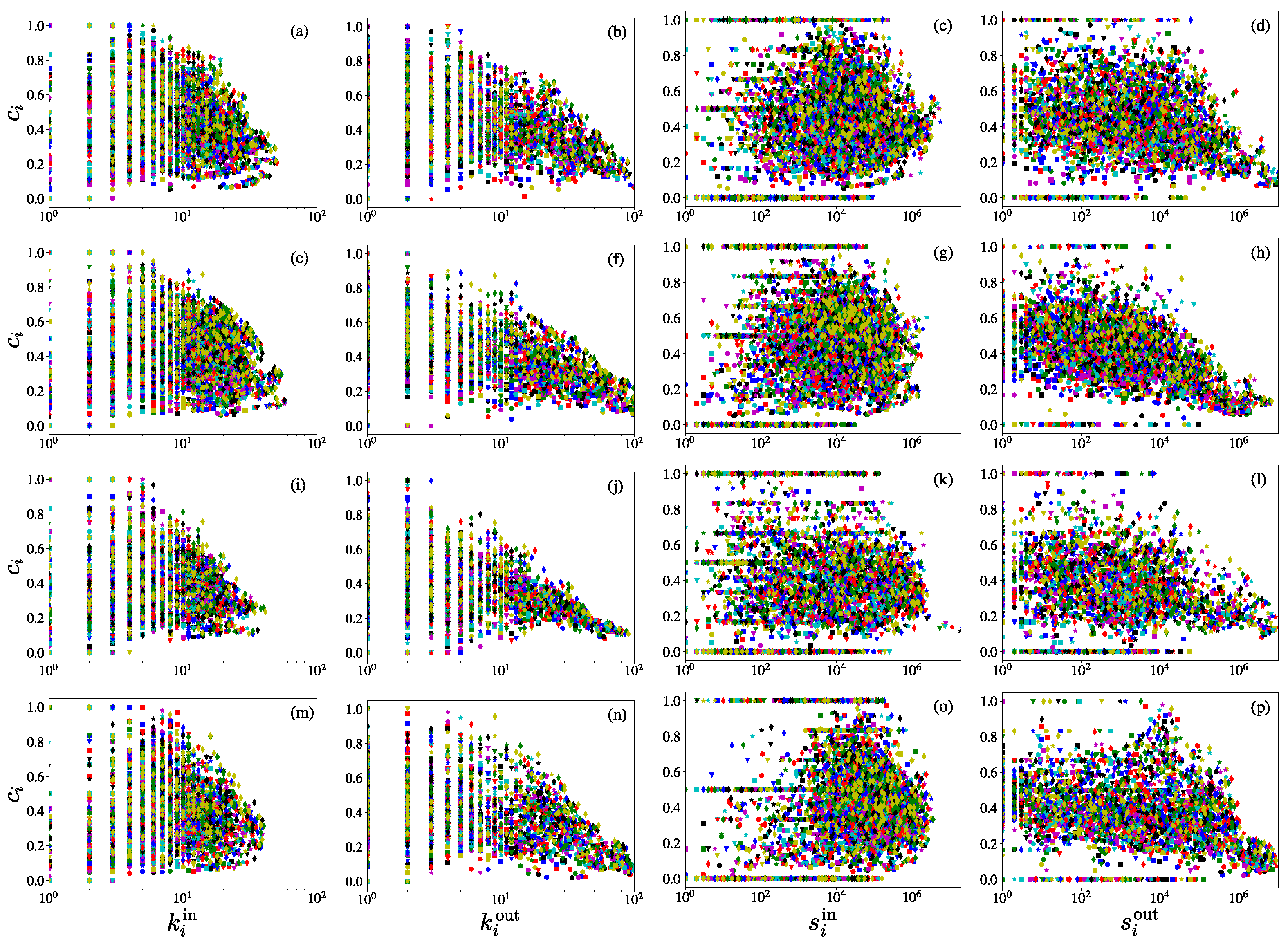
3.6. Clustering Coefficient
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- UN. Transforming Our World: The 2030 Agenda for Sustainable Development; UN Publishing: NewYork, NY, USA, 2015. [Google Scholar]
- Gutierrez-Moya, E.; Adenso-Diaz, B.; Lozano, S. Analysis and vulnerability of the international wheat trade network. Food Secur. 2021, 13, 113–128. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; Carr, J.A.; Laio, F.; Ridolfi, L.; Vandoni, S. Feeding humanity through global food trade. Earth Future 2014, 2, 458–469. [Google Scholar] [CrossRef]
- Hanjra, M.A.; Qureshi, M.E. Global water crisis and future food security in an era of climate change. Food Policy 2010, 35, 365–377. [Google Scholar] [CrossRef]
- Fair, K.R.; Bauch, C.T.; Anand, M. Dynamics of the global wheat trade network and resilience to shocks. Sci. Rep. 2017, 7, 7177. [Google Scholar] [CrossRef] [Green Version]
- FAO. The State of Agricultural Commodity Markets; FAO: Rome, Italy, 2015; Available online: http://www.fao.org (accessed on 15 September 2021).
- Lin, X.; Dang, Q.; Konar, M. A network analysis of food flows within the united states of America. Environ. Sci. Technol. 2014, 48, 5439–5447. [Google Scholar] [CrossRef]
- Torreggiani, S.; Mangioni, G.; Puma, M.J.; Fagiolo, G. Identifying the community structure of the food-trade international multi-network. Environ. Res. Lett. 2018, 13, 054026. [Google Scholar] [CrossRef]
- Dong, C.; Yin, Q.; Lane, K.J.; Yan, Z.; Shi, T.; Liu, Y.; Bell, M.L. Competition and transmission evolution of global food trade: A case study of wheat. Phys. A 2018, 509, 998–1008. [Google Scholar] [CrossRef]
- Suweis, S.; Carr, J.A.; Maritan, A.; Rinaldo, A.; D’Odorico, P. Resilience and reactivity of global food security. Proc. Natl. Acad. Sci. USA 2015, 112, 6902–6907. [Google Scholar] [CrossRef] [Green Version]
- Marchand, P.; Carr, J.A.; Dell’Angelo, J.; Fader, M.; Gephart, J.A.; Kummu, M.; Magliocca, N.R.; Porkka, M.; Puma, M.J.; Ratajczak, Z.; et al. Reserves and trade jointly determine exposure to food supply shocks. Environ. Res. Lett. 2016, 11, 095009. [Google Scholar] [CrossRef] [Green Version]
- Gephart, J.A.; Pace, M.L. Structure and evolution of the global seafood trade network. Environ. Res. Lett. 2015, 10, 125014. [Google Scholar] [CrossRef] [Green Version]
- Gephart, J.A.; Rovenskaya, E.; Dieckmann, U.; Pace, M.L.; Braennstroem, A. Vulnerability to shocks in the global seafood trade network. Environ. Res. Lett. 2016, 11, 035008. [Google Scholar] [CrossRef]
- Stoll, J.S.; Crona, B.I.; Fabinyi, M.; Farr, E.R. Seafood trade routes for lobster obscure teleconnected vulnerabilities. Front. Mar. Sci. 2018, 5, 239. [Google Scholar] [CrossRef]
- Chung, M.G.; Kapsar, K.; Frank, K.A.; Liu, J.G. The spatial and temporal dynamics of global meat trade networks. Sci. Rep. 2020, 10, 16657. [Google Scholar] [CrossRef] [PubMed]
- Raynolds, L.T. The globalization of organic agro-food networks. World Dev. 2004, 32, 725–743. [Google Scholar] [CrossRef]
- Ercsey-Ravasz, M.; Toroczkai, Z.; Lakner, Z.; Baranyi, J. Complexity of the international agro-food trade network and its impact on food safety. PLoS ONE 2012, 7, e37810. [Google Scholar] [CrossRef]
- Wu, F.; Guclu, H. Global maize trade and food security: Implications from a social network model. Risk Anal. 2013, 33, 2168–2178. [Google Scholar] [CrossRef] [Green Version]
- Puma, M.J.; Bose, S.; Chon, S.Y.; Cook, B.I. Assessing the evolving fragility of the global food system. Environ. Res. Lett. 2015, 10, 024007. [Google Scholar] [CrossRef]
- Schaffer-Smith, D.; Tomscha, S.A.; Jarvis, K.J.; Maguire, D.Y.; Treglia, M.L.; Liu, J. Network analysis as a tool for quantifying the dynamics of metacoupled systems: An example using global soybean trade. Ecol. Soc. 2018, 23, 3. [Google Scholar] [CrossRef] [Green Version]
- Wellesley, L.; Preston, F.; Lehne, J.; Bailey, R. Chokepoints in global food trade: Assessing the risk. Res. Transp. Bus. Manag. 2017, 25, 15–28. [Google Scholar] [CrossRef]
- Serrano, M.A.; Boguñá, M. Topology of the world trade web. Phys. Rev. E 2003, 68, 015101(R). [Google Scholar] [CrossRef] [Green Version]
- Hou, W.; Liu, H.; Wang, H.; Wu, F. Structure and patterns of the international rare earths trade: A complex network analysis. Resour. Policy 2018, 55, 133–142. [Google Scholar] [CrossRef]
- Dupas, M.C.; Halloy, J.; Chatzimpiros, P. Time dynamics and invariant subnetwork structures in the world cereals trade network. PLoS ONE 2019, 14, e0216318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, X.; Wu, X.; Guan, C.; Ma, R.; Nielsen, C.P.; Zhang, B. Linking agricultural GHG emissions to global trade network. Earth Future 2020, 8, e2019EF001361. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Liu, G.; Pu, G.; Chen, Y.; Chen, W.Q.; Shi, L. Spatiotemporal evolution of the international plastic resin trade network. J. Clean Prod. 2020, 276, 124221. [Google Scholar] [CrossRef]
- Guo, S.Z.; Lu, Z.M.; Chen, Z.; Luo, H. Strength-strength and strength-degree correlation measures for directed weighted complex network analysis. IEICE Trans. Inf. Syst. 2011, E94D, 2284–2287. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 313, 1–101. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Gao, Z.; Sun, H. Strength dynamics of weighted evolving networks. Chin. Phys. 2007, 16, 47–50. [Google Scholar] [CrossRef]
- Konar, M.; Dalin, C.; Suweis, S.; Hanasaki, N.; Rinaldo, A.; Rodriguez-Iturbe, I. Water for food: The global virtual water trade network. Water Resour. Res. 2011, 47, W05520. [Google Scholar] [CrossRef] [Green Version]
- Albert, R.; Barabasi, A. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef] [Green Version]
- Burkholz, R.; Schweitzer, F. International crop trade networks: The impact of shocks and cascades. Environ. Res. Lett. 2019, 14, 114013. [Google Scholar] [CrossRef] [Green Version]
- Garlaschelli, D.; Loffredo, M. Patterns of link reciprocity in directed networks. Phys. Rev. Lett. 2004, 93, 268701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Newman, M.E.J.; Forrest, S.; Balthrop, J. Email networks and the spread of computer viruses. Phys. Rev. E 2002, 66, 035101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, P.; Wang, J.; Li, X.; Li, M.; Di, Z.; Fan, Y. Clustering coefficient and community structure of bipartite networks. Phys. A 2008, 387, 6869–6875. [Google Scholar] [CrossRef] [Green Version]
- Ji, Q.; Li, D.; Jin, Z. Divisive algorithm based on node clustering coefficient for community detection. IEEE Access 2020, 6, 142337–142347. [Google Scholar] [CrossRef]
- Robins, G.; Alexander, M. Small worlds among interlocking directors: Network structure and distance in bipartite graphs. Comput. Math. Organ. Theory 2004, 10, 69–94. [Google Scholar] [CrossRef]
- Lind, P.G.; Gonzalez, M.C.; Herrmann, H.J. Cycles and clustering in bipartite networks. Phys. Rev. E 2005, 72, 056127. [Google Scholar] [CrossRef] [Green Version]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Fagiolo, G. Clustering in complex directed networks. Phys. Rev. E 2007, 76, 026107. [Google Scholar] [CrossRef] [Green Version]
- Peng, P.; Yang, Y.; Cheng, S.; Lu, F.; Yuan, Z. Hub-and-spoke structure: Characterizing the global crude oil transport network with mass vessel trajectories. Energy 2019, 168, 966–974. [Google Scholar] [CrossRef]
- Garlaschelli, D.; Loffredo, M.I. Structure and evolution of the world trade network. Phys. A 2005, 355, 138–144. [Google Scholar] [CrossRef] [Green Version]
- Fagiolo, G.; Reyes, J.; Schiavo, S. The evolution of the world trade web: A weighted-network analysis. J. Evol. Econ. 2010, 20, 479–514. [Google Scholar] [CrossRef]
- Saramäki, J.; Kivela, M.; Onnela, J.P.; Kaski, K.; Kertész, J. Generalizations of the clustering coefficient to weighted complex networks. Phys. Rev. E 2007, 75, 027105. [Google Scholar] [CrossRef] [Green Version]

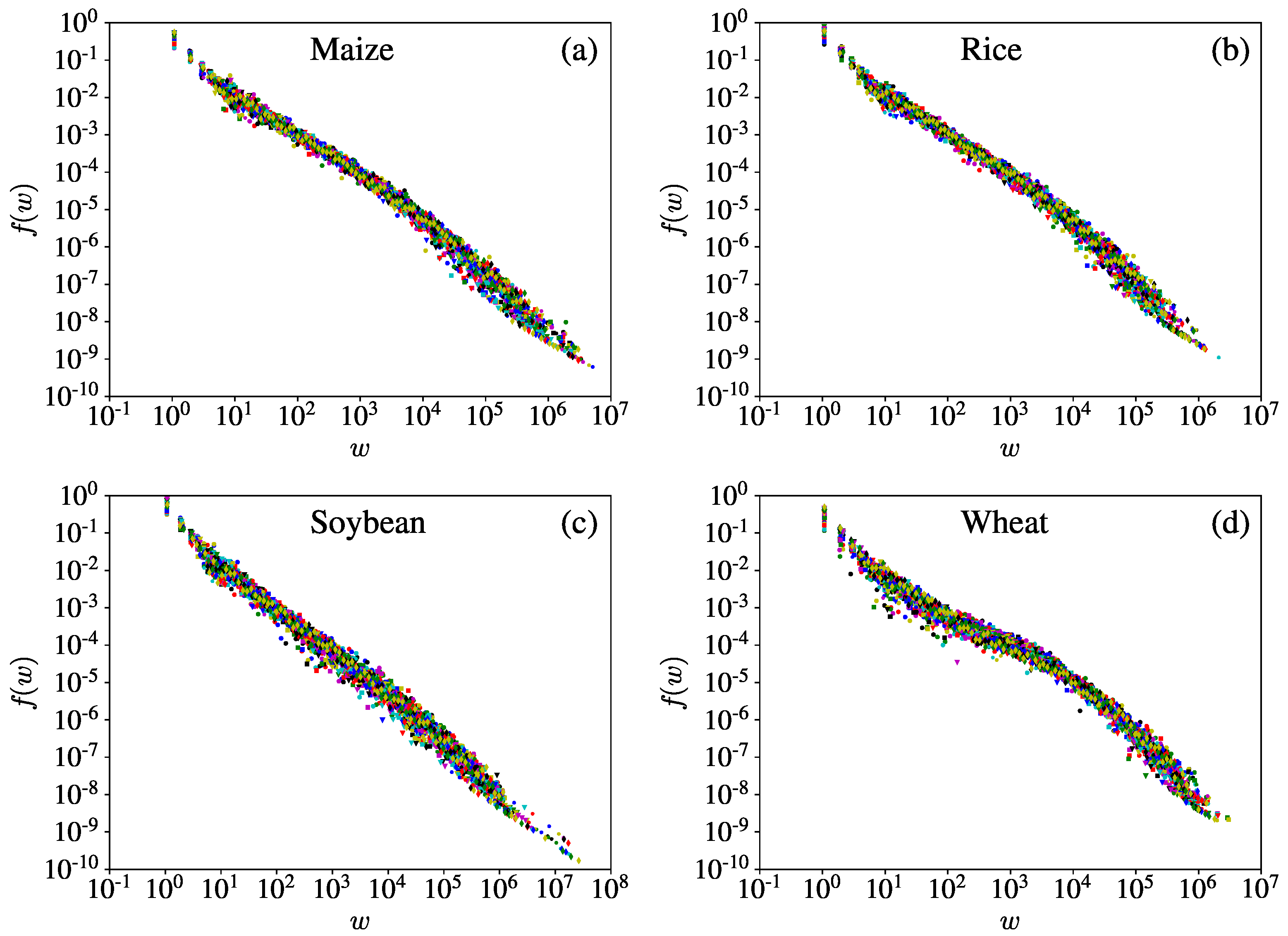
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.-T.; Zhou, W.-X. Microstructural Characteristics of the Weighted and Directed International Crop Trade Networks. Entropy 2021, 23, 1250. https://doi.org/10.3390/e23101250
Zhang Y-T, Zhou W-X. Microstructural Characteristics of the Weighted and Directed International Crop Trade Networks. Entropy. 2021; 23(10):1250. https://doi.org/10.3390/e23101250
Chicago/Turabian StyleZhang, Yin-Ting, and Wei-Xing Zhou. 2021. "Microstructural Characteristics of the Weighted and Directed International Crop Trade Networks" Entropy 23, no. 10: 1250. https://doi.org/10.3390/e23101250
APA StyleZhang, Y.-T., & Zhou, W.-X. (2021). Microstructural Characteristics of the Weighted and Directed International Crop Trade Networks. Entropy, 23(10), 1250. https://doi.org/10.3390/e23101250






