Network-Based Driving Force of National Economic Development: A Social Capital Perspective
Abstract
:1. Introduction
2. Literature Review
3. Data
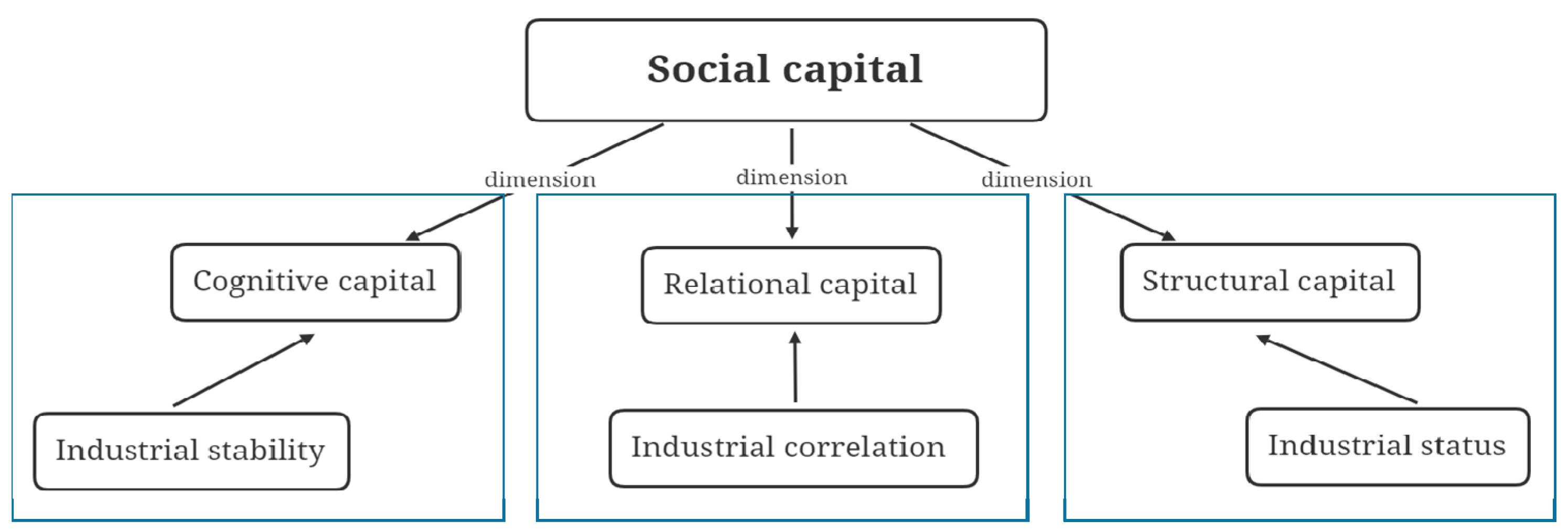
4. Methodology
4.1. Structural Capital: Industrial Status
4.2. Relational Capital: Industrial Correlation
4.3. Cognitive Capital: Industrial Stability
4.4. Econometric Model
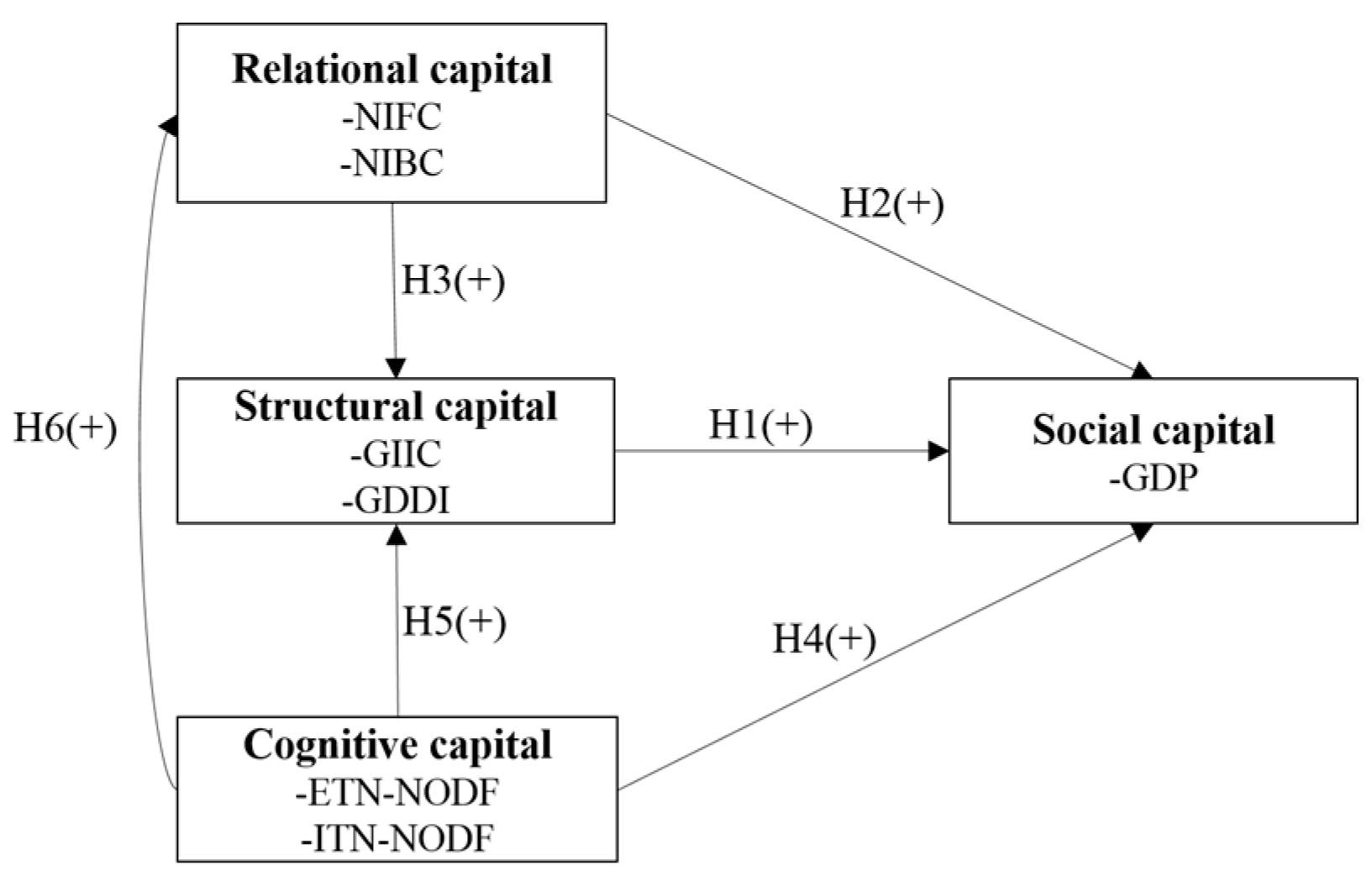
5. Hypotheses
5.1. Hypothesis Formulation
5.2. Hypothesis Testing
6. Results and Discussions
6.1. The Effects of Structural Capital
6.2. The Effects of Relational Capital
6.3. The Effects of Cognitive Capital
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Basic Information about WIOD2016
| No. | Abbreviation | Country | No. | Abbreviation | Country |
|---|---|---|---|---|---|
| 1 | AUS | Australia | 23 | IRL | Ireland |
| 2 | AUT | Austria | 24 | ITA | Italy |
| 3 | BEL | Belgium | 25 | JPN | Japan |
| 4 | BGR | Bulgaria | 26 | KOR | Korea |
| 5 | BRA | Brazil | 27 | LTU | Lithuania |
| 6 | CAN | Canada | 28 | LUX | Luxembourg |
| 7 | CHE | Switzerland | 29 | LVA | Latvia |
| 8 | CHN | China | 30 | MEX | Mexico |
| 9 | CYP | Cyprus | 31 | MLT | Malta |
| 10 | CZE | Czech | 32 | NLD | Netherlands |
| 11 | DEU | Germany | 33 | NOR | Norway |
| 12 | DNK | Denmark | 34 | POL | Poland |
| 13 | ESP | Spain | 35 | PRT | Portugal |
| 14 | EST | Estonia | 36 | ROU | Romania |
| 15 | FIN | Finland | 37 | RUS | Russia |
| 16 | FRA | France | 38 | SVK | Slovak |
| 17 | GBR | United Kingdom | 39 | SVN | Slovenia |
| 18 | GRC | Hellenic | 40 | SWE | Sweden |
| 19 | HRV | Croatia | 41 | TUR | Turkey |
| 20 | HUN | Hungary | 42 | TWN | Chinese Taipai |
| 21 | IDN | Indonesia | 43 | USA | United States |
| 22 | IND | India | 44 | ROW | Rest of the world |
| Abbreviation | Industrial Sector |
|---|---|
| S1 | Crop and animal production, hunting, and related service activities |
| S2 | Forestry and logging |
| S3 | Fishing and aquaculture |
| S4 | Mining and quarrying |
| S5 | Manufacture of food products, beverages, and tobacco products |
| S6 | Manufacture of textiles, wearing apparel, and leather products |
| S7 | Manufacture of wood and of products of wood and cork, except furniture; manufacture of articles of straw and plaiting materials |
| S8 | Manufacture of paper and paper products |
| S9 | Printing and reproduction of recorded media |
| S10 | Manufacture of coke and refined petroleum products |
| S11 | Manufacture of chemicals and chemical products |
| S12 | Manufacture of basic pharmaceutical products and pharmaceutical preparations |
| S13 | Manufacture of rubber and plastic products |
| S14 | Manufacture of other non-metallic mineral products |
| S15 | Manufacture of basic metals |
| S16 | Manufacture of fabricated metal products, except machinery and equipment |
| S17 | Manufacture of computer, electronic, and optical products |
| S18 | Manufacture of electrical equipment |
| S19 | Manufacture of machinery and equipment n.e.c. |
| S20 | Manufacture of motor vehicles, trailers and semi-trailers |
| S21 | Manufacture of other transport equipment |
| S22 | Manufacture of furniture; other manufacturing |
| S23 | Repair and installation of machinery and equipment |
| S24 | Electricity, gas, steam, and air conditioning supply |
| S25 | Water collection, treatment, and supply |
| S26 | Sewerage; waste collection, treatment, and disposal activities; materials recovery; remediation activities and other waste management services |
| S27 | Construction |
| S28 | Wholesale and retail trade and repair of motor vehicles and motorcycles |
| S29 | Wholesale trade, except of motor vehicles and motorcycles |
| S30 | Retail trade, except of motor vehicles and motorcycles |
| S31 | Land transport and transport via pipelines |
| S32 | Water transport |
| S33 | Air transport |
| S34 | Warehousing and support activities for transportation |
| S35 | Postal and courier activities |
| S36 | Accommodation and food service activities |
| S37 | Publishing activities |
| S38 | Motion picture, video and television programme production, sound recording and music publishing activities; programming and broadcasting activities |
| S39 | Telecommunications |
| S40 | Computer programming, consultancy and related activities; information service activities |
| S41 | Financial service activities, except insurance and pension funding |
| S42 | Insurance, reinsurance and pension funding, except compulsory social security |
| S43 | Activities auxiliary to financial services and insurance activities |
| S44 | Real estate activities |
| S45 | Legal and accounting activities; activities of head offices; management consultancy activities |
| S46 | Architectural and engineering activities; technical testing and analysis |
| S47 | Scientific research and development |
| S48 | Advertising and market research |
| S49 | Other professional, scientific and technical activities; veterinary activities |
| S50 | Administrative and support service activities |
| S51 | Public administration and defence; compulsory social security |
| S52 | Education |
| S53 | Human health and social work activities |
| S54 | Other service activities |
| S55 | Activities of households as employers; undifferentiated goods- and services-producing activities of households for own use |
| S56 | Activities of extraterritorial organizations and bodies |
Appendix B. Supplementary Description of Methodology
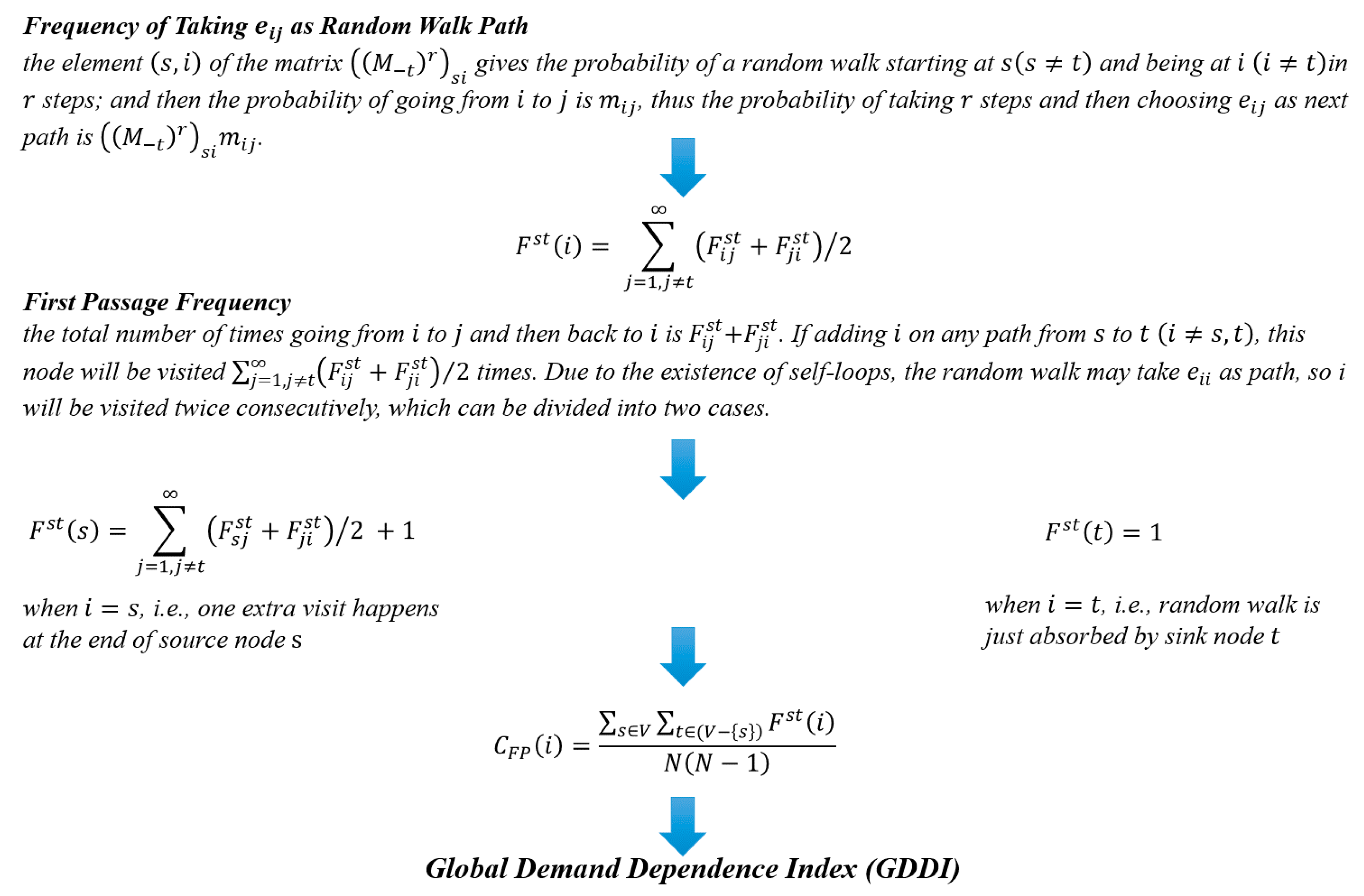
Appendix B.1. Supplementary Description of GIIC
Appendix B.2. Supplementary Description of GDDI
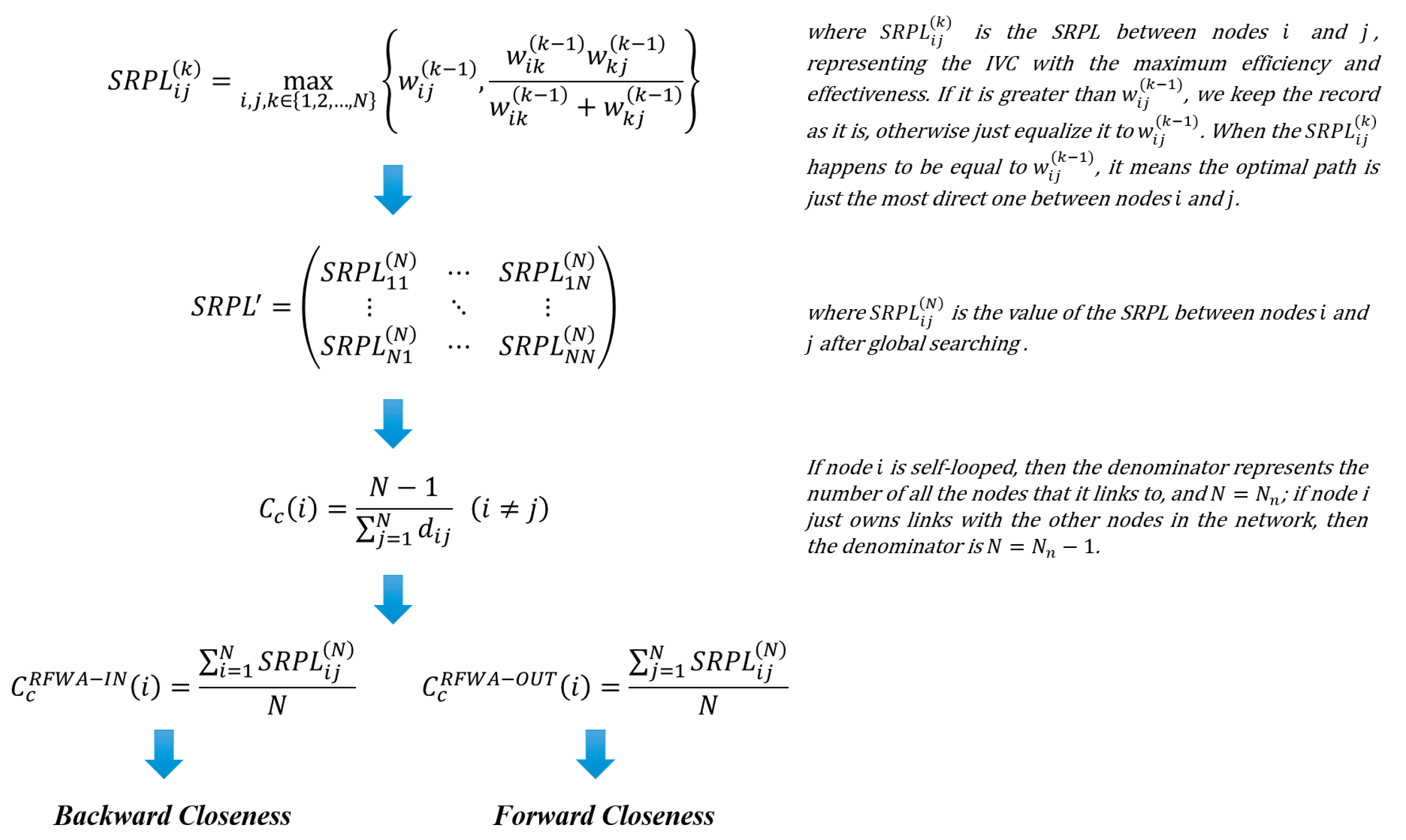
Appendix B.3. Supplementary Description of Backward Closeness and Forward Closeness
Appendix B.4. Supplementary Description of NODF
References
- Nahapiet, J.; Ghoshal, S. Social Capital, Intellectual Capital, and the Organizational Advantage. Acad. Manag. Rev. 1998, 23, 242–266. [Google Scholar] [CrossRef]
- Chen, L. New Horizon of Capital Research: Research Review on Social Capital. J. Yunnan Univ. Financ. Econ. 2007, 4, 12–20. [Google Scholar]
- Burt, R.S. Structural Holes; Harvard University Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Putnam, R.D. The Prosperous Community: Social Capital and Public Life. Am. Prospects 1993, 13, 35–42. [Google Scholar]
- Zhao, Y.; Luo, J. How to measure social capital: An empirical research review. Soc. Sci. Abroad 2005, 2, 18–24. [Google Scholar]
- Coleman, J.S. Social Capital in the Creation of Human Capital. Am. J. Sociol. 1988, 94, S95–S120. [Google Scholar] [CrossRef]
- Burton, N.; Mai, C.V. The Light and the Dark of Mindful Social Capital: Right Mindfulness and Social Capital Development. Eur. Manag. Rev. 2020, 18, 137–150. [Google Scholar] [CrossRef]
- Xing, L.; Guan, J.; Wu, S. Measuring the impact of final demand on global production system based on Markov process. Phys. A Stat. Mech. Appl. 2018, 502, 148–163. [Google Scholar] [CrossRef]
- Zhang, Q.; Zeng, A.; Shang, M. Extracting the Information Backbone in Online System. PLoS ONE 2013, 8, e62624. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, S.J.; Yu, X.; Zhu, K. Characterizing global value chains: Production length and upstreamness. NBER Work. Pap. 23261 2017. [Google Scholar] [CrossRef]
- Timmer, M.P.; Los, B.; Stehrer, R.; Vries, G.D. An Anatomy of the Global Trade Slowdown based on the WIOD 2016 Release. In GGDC Research Memorandum Number 162; University of Groningen: Groningen, The Netherlands, 2016. [Google Scholar]
- Xing, L.; Dong, X.; Guan, J. Global industrial impact coefficient based on random walk process and inter-country input–output table. Phys. A Stat. Mech. Appl. 2017, 471, 576–591. [Google Scholar] [CrossRef]
- Guan, J.; Li, Y.; Xing, L.; Liang, G. Closeness centrality for similarity-weight network and its application to measuring industrial sectors’ position on the global value chain. Phys. A Stat. Mech. Appl. 2020, 541, 123337. [Google Scholar] [CrossRef]
- Ren, J.; Xing, L.; Han, Y.; Dong, X. Nestedness-Based Measurement of Evolutionarily Stable Equilibrium of Global Production System. Entropy 2021, 23, 1077. [Google Scholar] [CrossRef]
- Alves, L.; Mangioni, G.; Cingolani, I.; Rodrigues, F.A.; Panzarasa, P.; Moreno, Y. The nested structural organization of the worldwide trade multi-layer network. Sci. Rep. 2019, 9, 373–382. [Google Scholar] [CrossRef] [Green Version]
- Almeida-Neto, M.; Guimares, P.; Guimares, P.R.; Loyola, R.D.; Ulrich, W. A consistent metric for nestedness analysis in ecological systems: Reconciling concept and measurement. Oikos 2008, 117, 1227–1239. [Google Scholar] [CrossRef]
- Hair, J.F.; Hult, G.; Ringle, C.M.; Sarstedt, M.; Kai, O.T. Mirror, Mirror on the Wall: A Comparative Evaluation of Composite-based Structural Equation Modeling Methods. J. Acad. Mark. Sci. 2017, 45, 616–632. [Google Scholar] [CrossRef]
- Wold, H. Model construction and evaluation when theoretical knowledge is scarce: Theory and application of partial least squares. In Evaluation of Econometric Models; Kmenta, J., Ramsey, J.B., Eds.; Academic Press: New York, NY, USA, 1980; pp. 47–74. [Google Scholar]
- Chin, W.W. How to write up and report PLS analyses. In Handbook of Partial Least Squares: Concepts, Methods and Applications; Vinzi, V.E., Chin, W.W., Henseler, J., Wang, H., Eds.; Springer: Berlin, Germany, 2010; pp. 655–690. [Google Scholar]
- Nitzl, C.; Roldàn, J.L.; Carrión, G.C. Mediation Analysis in Partial Least Squares Path Modeling: Helping Researchers Discuss More Sophisticated Models. Ind. Manag. Data Syst. 2016, 116, 1849–1864. [Google Scholar] [CrossRef]
- Ringle, C.M.; Sarstedt, M. Gain More Insight from Your PLS-SEM Results: The Importance-Performance Map Analysis. Ind. Manag. Data Syst. 2016, 116, 1865–1886. [Google Scholar] [CrossRef]
- Sarstedt, M.; Ringle, C.M.; Hair, J.F. Partial Least Squares Structural Equation Modeling. In Handbook of Market Research; Homburg, C., Klarmann, M., Vomberg, A., Eds.; Springer: Cham, Switzerland, 2017; pp. 1–40. [Google Scholar]
- Ringle, C.M.; Wende, S.; Becker, J.M. SmartPLS 3. SmartPLS GmbH, Boenningstedt. 2015. Available online: http://www.smartpls.com (accessed on 28 June 2021).
- Hair, J.F.; Sarstedt, M.; Matthews, L.; Ringle, C.M. Identifying and treating unobserved heterogeneity with FIMIX-PLS: Part I—Method. Eur. Bus. Rev. 2016, 28, 63–76. [Google Scholar] [CrossRef]
- Matthews, L.; Sarstedt, M.; Hair, J.F.; Ringle, C.M. Identifying and treating unobserved heterogeneity with FIMIX-PLS: Part II—A Case Study. Eur. Bus. Rev. 2016, 28, 208–224. [Google Scholar] [CrossRef]
- Sarstedt, M.; Hair, J.F.; Cheah, J.H.; Becker, J.M.; Ringle, C.M. How to specify, estimate, and validate higher-order constructs in PLS-SEM. Australas. Mark. J. 2019, 27, 197–211. [Google Scholar] [CrossRef]
- Nitzl, C. The use of partial least squares structural equation modelling (PLS-SEM) in management accounting research: Directions for future theory development. J. Account. Lit. 2016, 37, 19–35. [Google Scholar] [CrossRef]
- Hair, J.F.; Risher, J.J.; Sarstedt, M.; Ringle, C.M. When to use and how to report the results of PLS-SEM. Eur. Bus. Rev. 2019, 31, 2–24. [Google Scholar] [CrossRef]
- Chin, W.W.; Cheah, J.H.; Liu, Y.; Ting, H. Demystifying the Role of Causal-predictive Modeling Using Partial Least Squares Structural Equation Modeling in Information Systems Research. Ind. Manag. Data Syst. 2020, 120, 2161–2209. [Google Scholar] [CrossRef]
- Khan, G.F.; Sarstedt, M.; Shiau, W.L.; Hair, J.F.; Ringle, C.M.; Fritze, M.P. Methodological Research on Partial Least Squares Structural Equation Modeling (PLS-SEM): An Analysis Based on Social Network Approaches. Internet Res. 2019, 29, 407–429. [Google Scholar] [CrossRef]
- Hair, J.F.; Ringle, C.M.; Sarstedt, M. PLS-SEM: Indeed a Silver Bullet. J. Mark. Theory Pract. 2011, 19, 139–152. [Google Scholar] [CrossRef]
- Li, E.Y.; Liao, C.H.; Yen, H.R. Co-authorship networks and research impact: A social capital perspective. Res. Policy 2013, 42, 1515–1530. [Google Scholar] [CrossRef]
- Hair, J.F.; Anderson, R.E.; Tatham, R.L.; Black, W.C. Multivariate Data Analysis, 5th ed.; All Publications: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Cohen, J. A Power Primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C. “German Development Report (2020)”—Germany in Transition; Social Sciences Academic Press: Beijing, China, 2020. [Google Scholar]
- Motwani, R.; Raghavan, P. Randomized algorithms. ACM Comput. Surv. 1996, 28, 33–37. [Google Scholar] [CrossRef]


| Output | Intermediate Use | Final Demand | Total Output | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Input | Country | Country A | Country B | ROW | Country A | Country B | ROW | |||
| Sector | A1, …, An | B1, …, Bn | R1, …, Rn | A1, …, An | B1, …, Bn | R1, …, Rn | ||||
| Intermediate Inputs | Country A | A1, …, An | ZAA | ZAB | ZAR | YAA | YAB | YAR | XA | |
| Country B | B1, …, Bn | ZBA | ZBB | ZBR | YBA | YBB | YBR | XB | ||
| ROW | R1, …, Rn | ZRA | ZRB | ZRR | YRA | YRB | YRR | XR | ||
| Value-Added | VAA | VAB | VAR | Notes:;;. | ||||||
| Total Input | XA | XB | XR | |||||||
| ID | Mean | S.D. | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | GDP | 11.497 | 0.768 | 1.000 | |||||
| 2 | GDDI | 3.706 | 0.773 | 0.966 | 1.000 | ||||
| 3 | GIIC | 1.615 | 0.714 | 0.946 | 0.969 | 1.000 | |||
| 4 | NIFC | 3.698 | 0.491 | 0.959 | 0.952 | 0.912 | 1.000 | ||
| 5 | NIBC | 3.710 | 0.470 | 0.957 | 0.956 | 0.910 | 0.985 | 1.000 | |
| 6 | ETN-NODF | 0.815 | 0.384 | 0.418 | 0.449 | 0.447 | 0.449 | 0.421 | 1.000 |
| 7 | ITN-NODF | 0.435 | 0.395 | 0.397 | 0.476 | 0.463 | 0.446 | 0.415 | 0.856 |
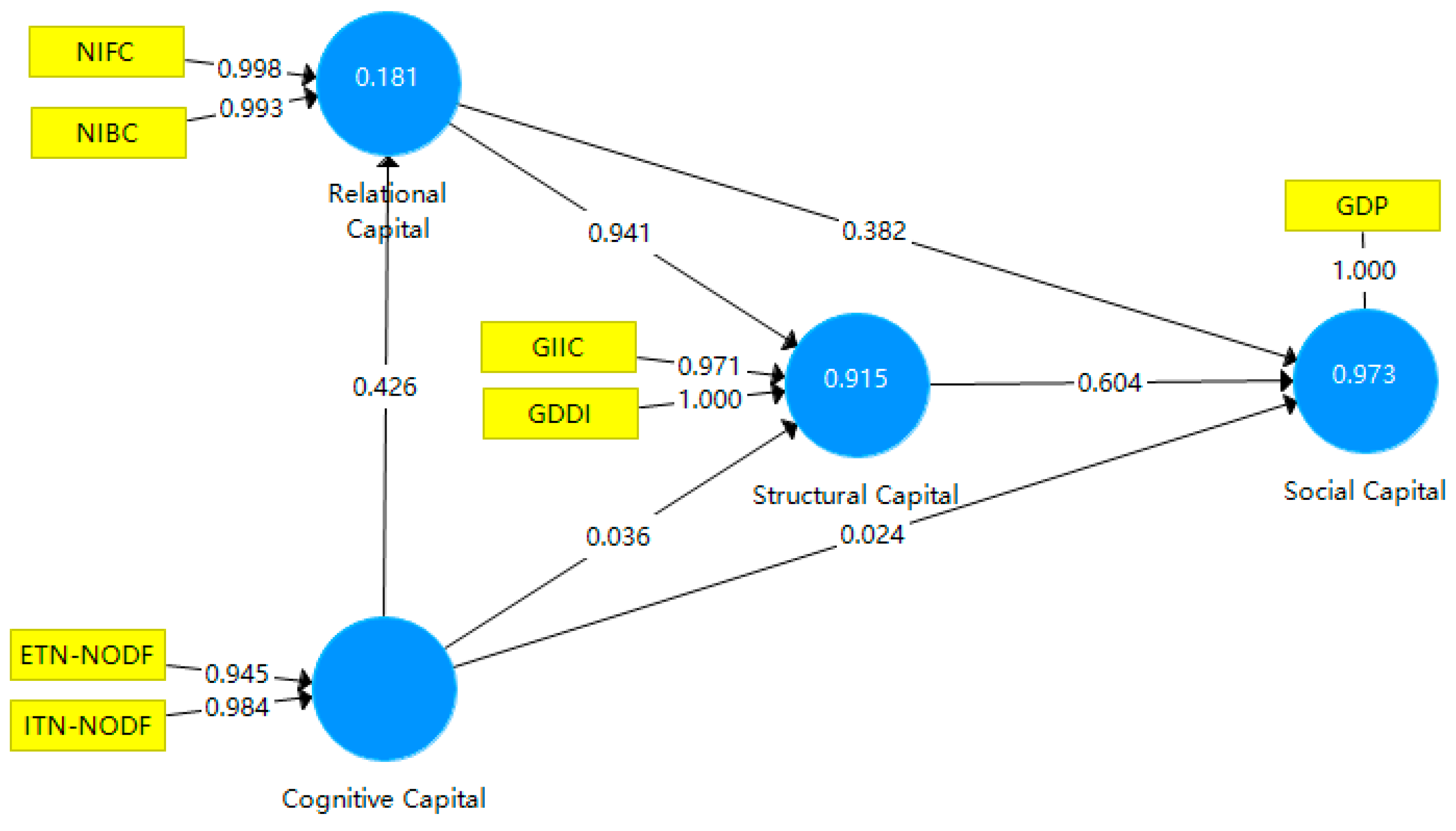
| Hypothesis | β a | T-Statistic | p-Values | Effect Size b | Decision | |
|---|---|---|---|---|---|---|
| H1: Structural capital→Social capital | 0.604 | 30.028 | 0.000 *** | 1.142 | large | Supported |
| H2: Relational capital→Social capital | 0.382 | 18.560 | 0.000 *** | 0.464 | large | Supported |
| H3: Relational capital→Structural capital | 0.941 | 142.094 | 0.000 *** | 8.545 | large | Supported |
| H4: Cognitive capital→Social capital | 0.024 | 3.525 | 0.000 *** | 0.017 | small | Supported |
| H5: Cognitive capital→Structural capital | 0.036 | 2.764 | 0.006 ** | 0.013 | small | Supported |
| H6: Cognitive capital→Relational capital | 0.426 | 14.899 | 0.000 *** | 0.221 | medium | Supported |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, L.; Ai, X.; Ren, J.; Wang, D. Network-Based Driving Force of National Economic Development: A Social Capital Perspective. Entropy 2021, 23, 1276. https://doi.org/10.3390/e23101276
Xing L, Ai X, Ren J, Wang D. Network-Based Driving Force of National Economic Development: A Social Capital Perspective. Entropy. 2021; 23(10):1276. https://doi.org/10.3390/e23101276
Chicago/Turabian StyleXing, Lizhi, Xi Ai, Jiaqi Ren, and Dawei Wang. 2021. "Network-Based Driving Force of National Economic Development: A Social Capital Perspective" Entropy 23, no. 10: 1276. https://doi.org/10.3390/e23101276
APA StyleXing, L., Ai, X., Ren, J., & Wang, D. (2021). Network-Based Driving Force of National Economic Development: A Social Capital Perspective. Entropy, 23(10), 1276. https://doi.org/10.3390/e23101276






