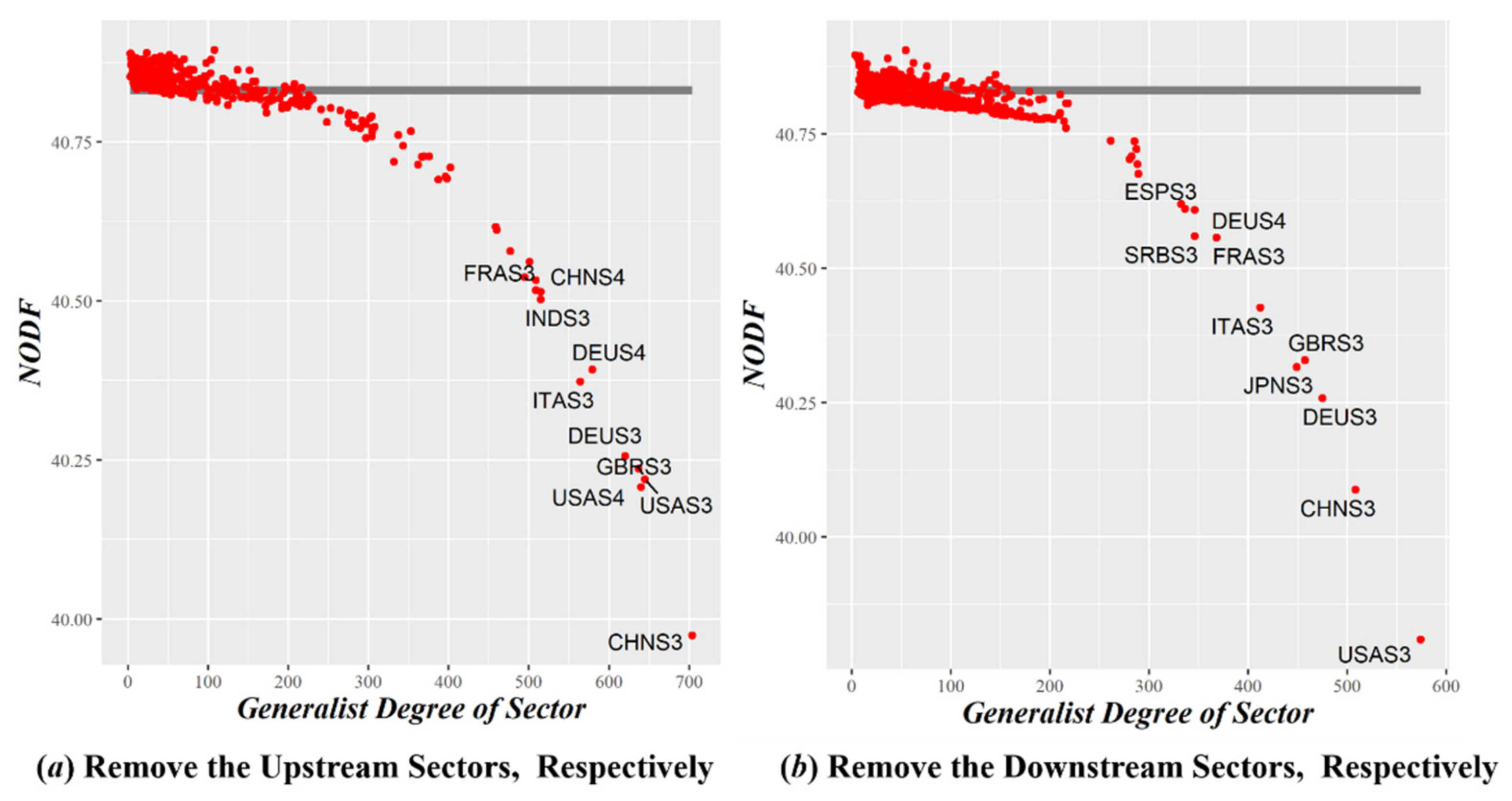
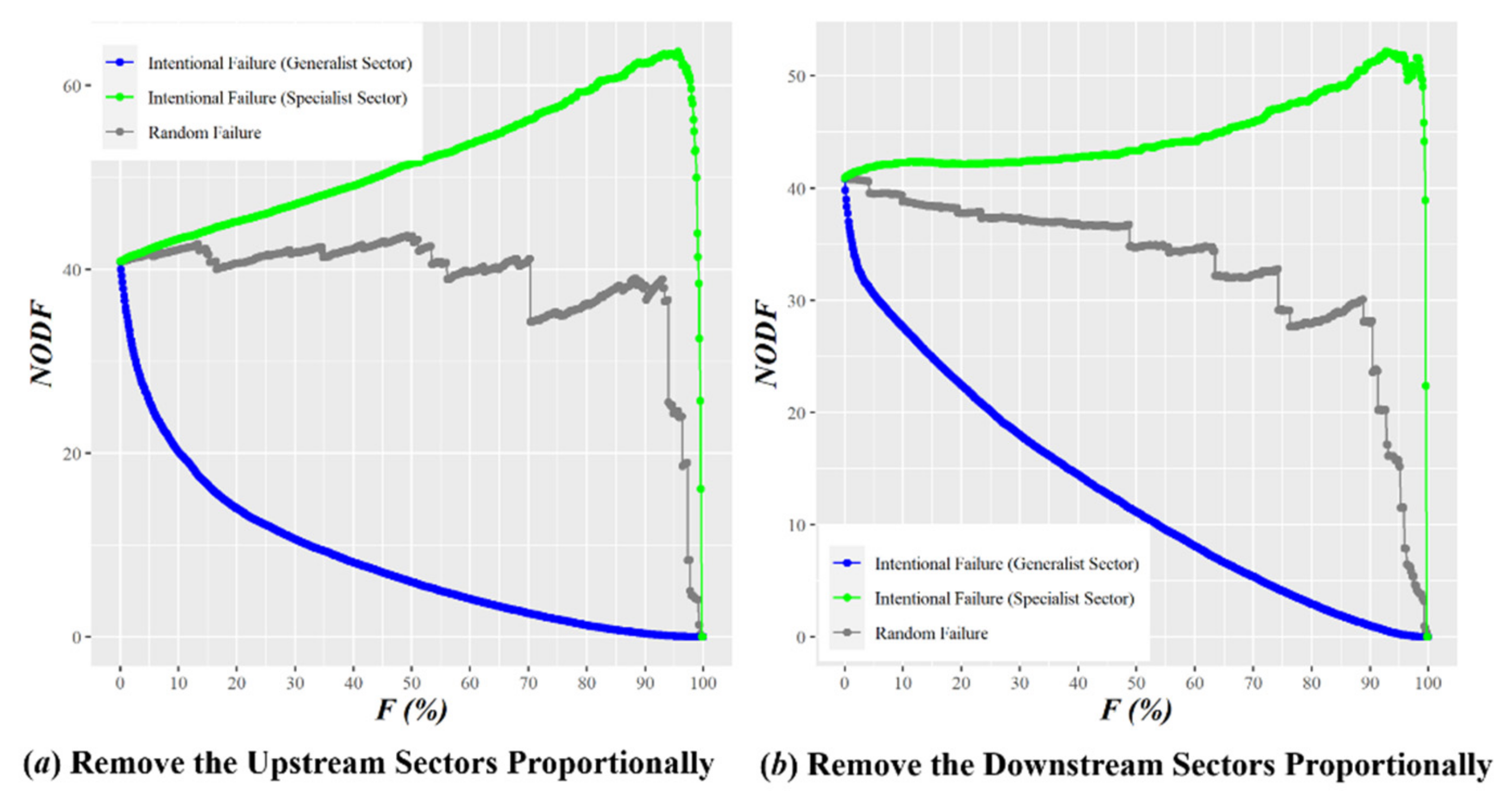
Appendix B. Network Pruning
The GIVCNBG model is a very dense weighted network, and there is a more or less value flow between each upstream sector and downstream sector. Therefore, before analyzing the nested structure, the network needs to be pruned to extract the backbone. In order to find an effectual way to extract the backbone of weighted network, two questions are proposed. The first question is that the information content of network should be retained as much as possible with the decline of number of edges (Q1). In other words, the nature of network pruning is a trade-off between the number of retained edges and the gross of the retained weights. The second question is that only the truly important edges linking nodes are worthy to be retained during downsizing of the network (Q2). Sometimes, a weighted edge is numerically insignificant but functionally significant, and reckless deletion will result in a useless broken structure.
It is common in the weighted networks that, even at the local level defined by edges linking to a given node, only a few of those edges carry a disproportionate fraction of its strength, and the remaining edges take a very small percentage that is left. Enlightened by H-Index, the Pareto Principle and the idea of the Disparity Filter proposed by Vespignani, we present a novel heuristic algorithm to effectively prune the dense and weighted GIVCN model, which is named X-Index Filtering Algorithm (XIFA).
As we all know, Hirsch proposed that a scientist has index if of his or her paper have at least citations each and the other papers have citations each. Obviously, this mixed quantitative index takes both the quantity and quality of papers into account, which can be used as an algorithm framework to solve Q1 of this paper by weighing the pros and cons, namely the number and weights of edges. According to the Pareto principle, it makes sense that 80% of consequences come from 20% of the causes, asserting an unequal relationship between inputs and outputs. We hence assume that a minority of edges hold the most weight in the network, which are regarded as the so-called important edges as mentioned in Q2.
Therefore, the core idea of XIFA is as follows: An industrial sector has backward index
(
)/forward index
(
) if top
percent of its relations to all upstream/downstream sectors occupy at least
of its total input/output amount of intermediate goods. The formula deduction and practical calculation process is shown in
Figure A1. According to the induction hypothesis, the X-index of a node is measured by the number of crucial edges with big to small weights, and a smaller X-index value indicates that the edge weight distribution of this node is more heterogeneous. In the directed networks, the XIFA is initiated by removing all indegree edges of each node that are insufficient to show the local influence, and the pruning process is then repeated for the outdegree edges. It should be noted that the existence of some edges tended to be overlooked, for instance, certain edges are important in terms of indegree but unimportant in terms of outdegree and vice versa, and one more rule is hence set, that is, the weighted edges that are worthy to be reserved in either direction will stay.
A special subgraph is extracted from the GIVCNBG model based on XIFA, which is named the GIVCNBG-FE model (FE refers to filtering edges). The remaining MRIO relations are different from those deleted depending on how heterogeneous the industrial sectors’ inputs or outputs are all over the world. We can assume that around 20% of the most important input or output relations of a given sector are supposed to cover 80% of its input or output amount of intermediate goods, which addresses Q1 favorably.
Table A4.
The Procedure of Pruning GIVCN Model Based on XIFA.
Table A4.
The Procedure of Pruning GIVCN Model Based on XIFA.
| Procedure | Column Deletion of Input Relations | Row Deletion of Output Relations |
|---|
| Network | |
| Refactoring |
|
|
| Conditions |
|
|
| Definition |
|
|
| Pruning | | |
| Merging | |
| Result | |
The XIFA algorithm is a mixed quantitative indicator, which takes into account the scope and intensity of the influence of the industrial sector, extracting the main topology of the industrial network according to the heterogeneity of input and output among the industrial sectors. From the perspective of complex networks, for nodes with strong edge weight heterogeneity, only a small number of connections with extremely large weights are needed to be kept, while for nodes with weak edge weight heterogeneity, the number of connections needed to be kept is greater but not more than 50%.
From the perspective of industrial economics, the integrity of the GVC must be considered. In consequence, a method of pruning separately from the aspect of output and input, then integrating, was finally adopted. This prevents certain industrial sectors from being too marginalized from the GVC.
Moreover, overlapping two subnetworks via the input relations (columns) and output relations (rows) pruning process is only a partial solution to Q2 because this pruning method is still based on the relations with adjacent nodes rather than global information. Therefore, to solve Q1 and Q2 at the same time a hybrid strategy needs to be adopted, a specific part in our other paper “Extracting the Backbone of Global Value Chain from High-Dimensional Multi-Region Input–Output Network”. For the nested structure to be studied in this article, the GIVCNBG-FE model has extracted enough GVC network topology information.
Figure A1.
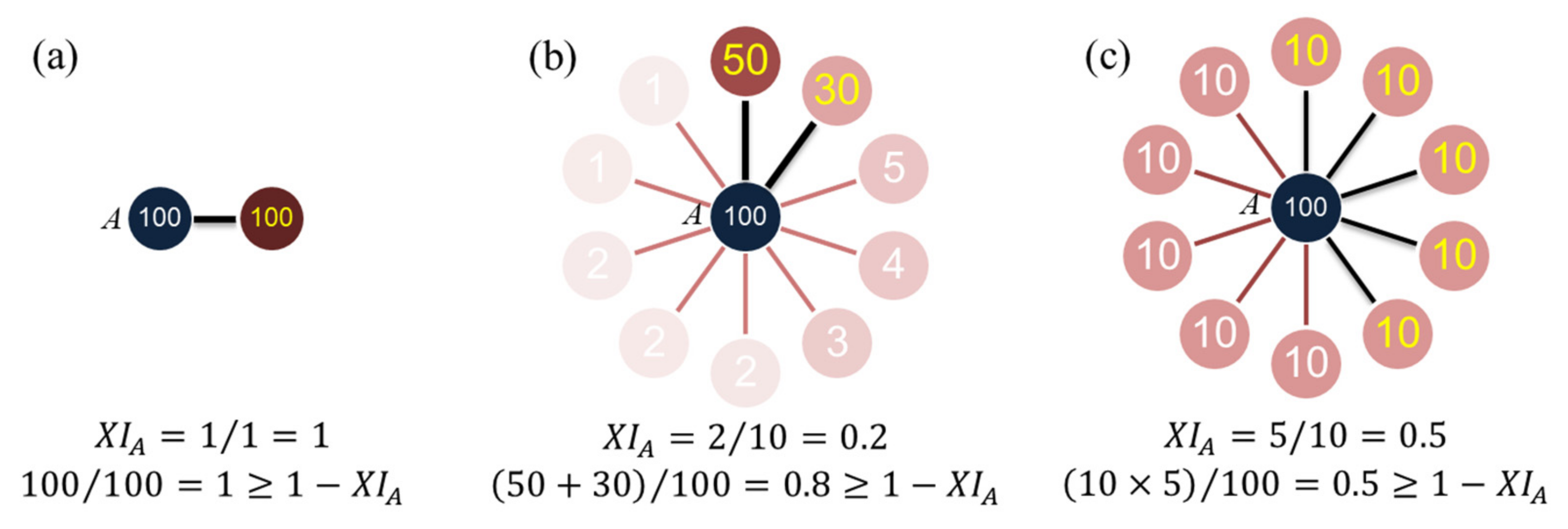
Three possible situations in the application of XIFA algorithm. (a) The source node has only one weighted edge connected to it, and 100% of its strength is allocated on it; (b) Top 20% of weighted edges carry 80% of the strength of source node. (c) Any 50% of weighted edges carry 50% of the strength of source node.
Figure A1.
Three possible situations in the application of XIFA algorithm. (a) The source node has only one weighted edge connected to it, and 100% of its strength is allocated on it; (b) Top 20% of weighted edges carry 80% of the strength of source node. (c) Any 50% of weighted edges carry 50% of the strength of source node.
Appendix C. Sorting Algorithms
- 1.
SBD Algorithm
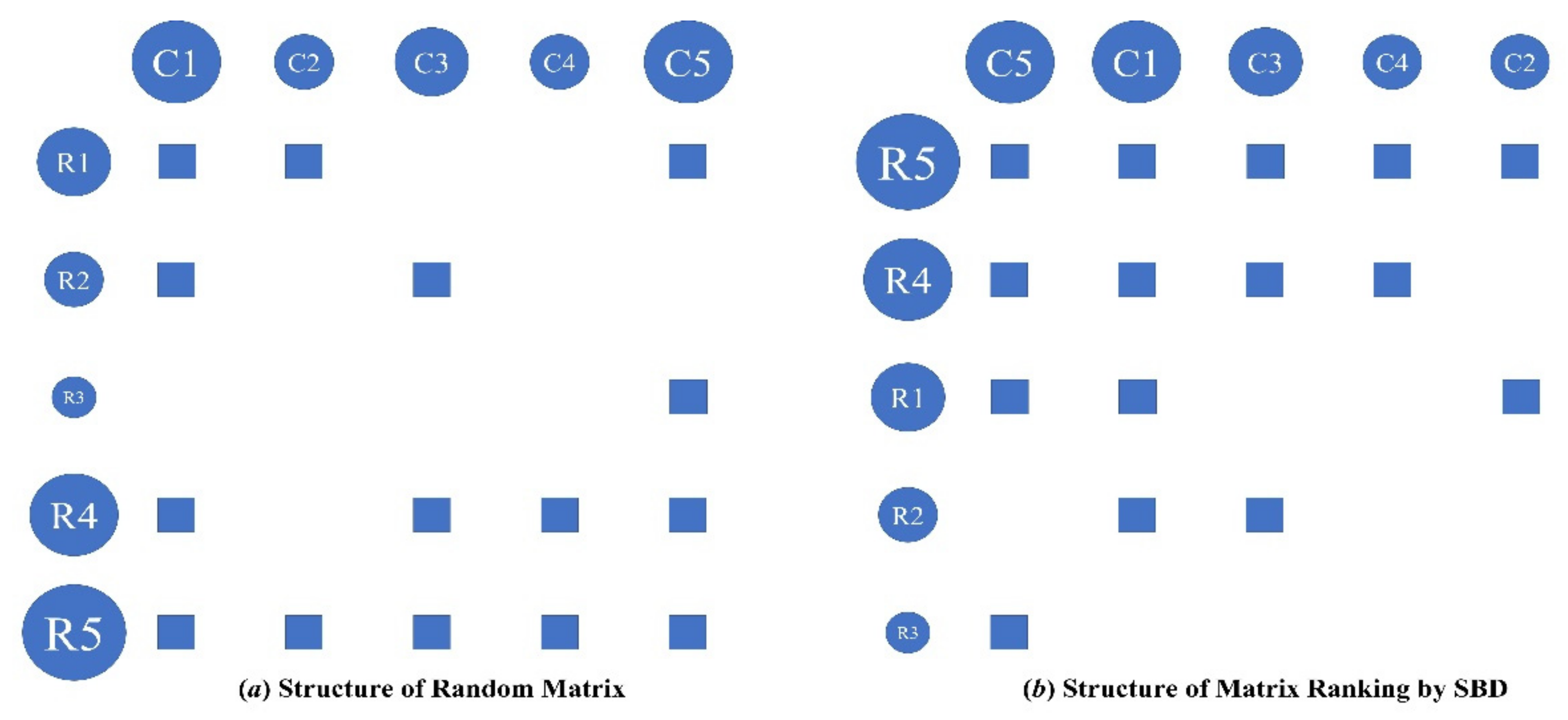
Sorted by Degree, or the SBD Algorithm, based on the concept of nestedness, sorts the adjacency matrix according to the degree of the network node (see
Figure A2). It is prescribed in the nested structure that the neighborhood of lower-degree nodes is a subset of the neighborhood of higher degree nodes. Accordingly, the SBD algorithm basically rearranges the adjacency matrix’s rows and columns in the descending order of the node’s degree from top to bottom and from left to right respectively. In the rearranged network adjacency matrix, the topmost upstream sector boasts the largest number of downstream sectors, while the leftmost downstream sector boasts the largest number of the most upstream sectors.
- 2.
NTC Algorithm
The Nestedness Temperature Calculator (NTC Algorithm) is a thermodynamics-based algorithm proposed by Atmar, focusing on the degree of disorder of the measurement matrix [
46]. The nested structure features ordered arrangement of nodes, therefore, the more disordered the adjacency matrix, the higher its temperature, and the lower the level of nestedness. The NTC Algorithm lines out a perfect nested region at the top left of the adjacency matrix, and the unexpected absence of any element above the line and the unexpected appearance of any element below the line results in an increase in the temperature of the adjacency matrix.
Figure A2.
Sorting Adjacency Matrix Based on SBD Algorithm. This is a schematic diagram of the process of ordering nodes by degree. The solid blue circles represent each industrial sector, the rows represent the upstream industrial sectors, the columns represent the downstream industry sectors, the blue squares represent the existence of interdependence between upstream and downstream industries, and the size of the solid circles is proportional to the node’s degree.
Figure A2.
Sorting Adjacency Matrix Based on SBD Algorithm. This is a schematic diagram of the process of ordering nodes by degree. The solid blue circles represent each industrial sector, the rows represent the upstream industrial sectors, the columns represent the downstream industry sectors, the blue squares represent the existence of interdependence between upstream and downstream industries, and the size of the solid circles is proportional to the node’s degree.
- 3.
BIN Algorithm
BINMATNEST Algorithm (the BIN Algorithm) was proposed by Rodrı’guez-Girone´s et al., which compensates for the shortcomings of the NTC, e.g., the non-uniqueness of the perfect order line and the inadequacy of null model selection [
47]. In design, the BIN Algorithm is a genetic algorithm that minimizes the matrix temperature by rearranging the rows and columns. It first generates some alternative solutions and then lets the well-performing matrix generate “Offspring”, thus, iteratively filtering out the best-performing solution. Unlike the NTC algorithm, the BIN algorithm is capable of screening out the optimal matrix with lower temperature. The matrix reaches the lowest temperature after reordering and is therefore more well-organized, with stabler connections between industrial sectors concentrated at the upper left corner. Under the circumstances, the NTC algorithm is not worth discussing anymore.
- 4.
FCA Algorithm
The Fitness-Complexity Algorithm (FCA Algorithm) applies a nonlinear iterative method originally designed to measure economic complexity [
48]. The mechanism is that the higher the fitness of a country, the higher its productive capacity or competitiveness; the higher the complexity of a certain product, then, the higher the productive capacity required from other countries producing that product. In the adjacency matrix of the country-product network, the rows represent countries and the columns the export products. After reordering the matrix in the descending order of fitness from top to bottom and product complexity from left to right, the new matrix exhibits distinct nestedness. The FCA therefore can be used to explore the maximum nestedness of a network.
We apply the GIVCNBG-FE-Eora26SC4 model to calculate the nestedness of the GVC network at intervals of five years, and compare the sorting results of the SBD, BIN and FCA algorithms and their NODF metrics, as shown in
Figure A3.
Figure A3.
Sorting Adjacency Matrix of GVC Network Based on Three Algorithms and Its Corresponding NODF Variation Trend. (a–c) are the adjacency matrix ranking results obtained according to the SBD, BIN, and FCA algorithms, respectively. Where the vertical axis represents the upstream sector and the horizontal axis represents the downstream sector, and each non-empty position reflects the transfer of intermediate products from the upstream sector to the downstream sector. This input–output relationship between industrial sectors resembles predation in an ecosystem: the upstream sector, as the provider of energy (products and services), can be regarded as the prey; the downstream sector, as the consumer of energy (products and services), can be regarded as the predator, and each industry sector plays dual role in the industrial ecosystem.
Figure A3.
Sorting Adjacency Matrix of GVC Network Based on Three Algorithms and Its Corresponding NODF Variation Trend. (a–c) are the adjacency matrix ranking results obtained according to the SBD, BIN, and FCA algorithms, respectively. Where the vertical axis represents the upstream sector and the horizontal axis represents the downstream sector, and each non-empty position reflects the transfer of intermediate products from the upstream sector to the downstream sector. This input–output relationship between industrial sectors resembles predation in an ecosystem: the upstream sector, as the provider of energy (products and services), can be regarded as the prey; the downstream sector, as the consumer of energy (products and services), can be regarded as the predator, and each industry sector plays dual role in the industrial ecosystem.
The SBD algorithm sorts the adjacency matrix in a way that most of the non-zero elements are clustered at the upper left corner. The results obtained by the BIN algorithm resemble that of the SBD algorithm, with the upper left corner being sparser. The results obtained by the FCA algorithm are computationally weaker than the other two algorithms. Given the above analysis (see
Figure A3d), the SBD algorithm is thus used in this paper to sort the nested structure of the adjacency matrix. The overall smooth NODF values indicate temporal stability of the nested structure, which means the topology of the GVC network does not change drastically during a normal economic cycle.