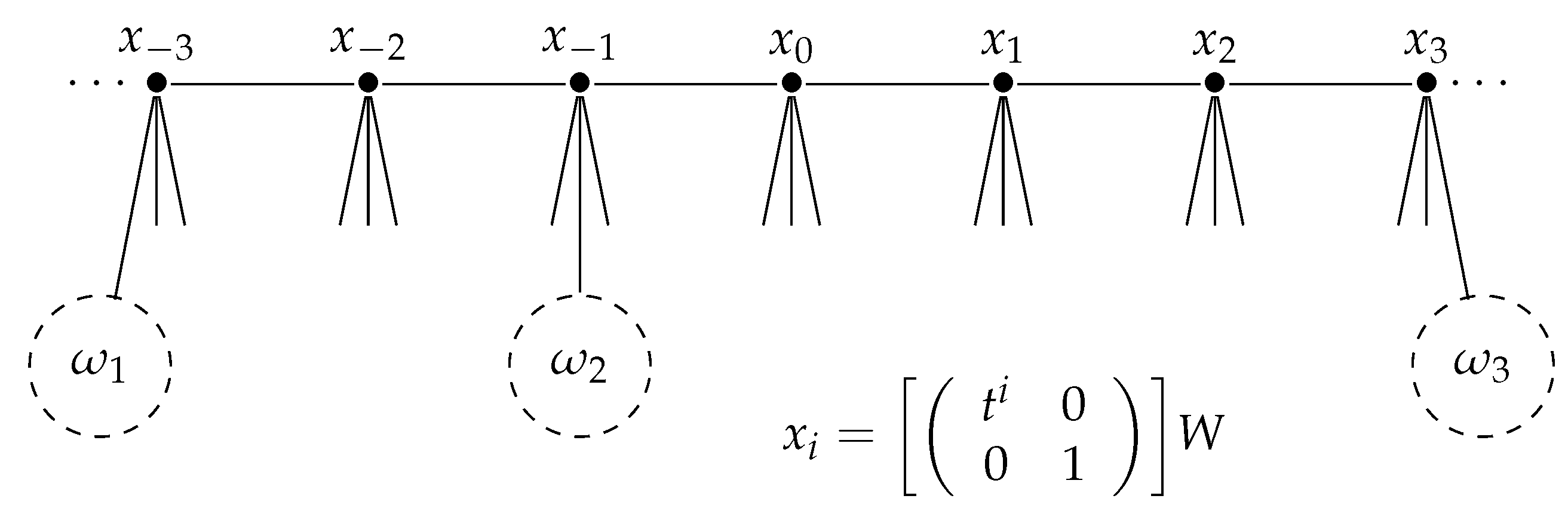1. Introduction
Let
be a probability space and let
be a measurable map. We say that
T is measure-preserving if
for every
. In this case we say that
is a
measure-preserving system. To a measure-preserving system is associated a numerical invariant called measure-theoretic entropy (see
Section 2 for the precise definition). Since it is preserved by measurable isomorphism, it can be used in order to distinguish special measures like Haar measure from other invariant measures.
One of the most important dynamical systems in homogeneous dynamics is the geodesic flow on the quotient
of the unit tangent bundle
of hyperbolic plane by modular group. It is an Anosov flow on a three-dimensional non-compact manifold and has wide application on the theory of Diophantine approximation and analytic number theory. Using the Mobius transformation of
on
, it may be identified with
on
given by
with
Unlike in the case of unipotent flow (right multiplication by one-parameter unipotent group), there is a great variety of invariant probability measures and orbit closures of
on
X. Furthermore, according to Sullivan [
1], its supremum of measure theoretic entropy is equal to 1, which is the measure-theoretic entropy of the Haar measure.
Meanwhile, the discrete version of the geodesic flow is also explored by several authors ([
2,
3,
4]). They considered the behavior of discrete geodesic flow system on and its application on Diophantine approximation over a positive characteristic field of formal series. Following these literatures, we investigate the measure-theoretic entropy of the discrete geodesic flow on positive characteristic setting in this paper. More precisely, we compute the measure-theoretic entropy of the right translation by diagonal elements on the non-compact quotient
of the space of bi-infinite geodesics
of
-regular tree by modular group. It also may be viewed as a diagonal action on the positive characteristic homogeneous space
. (See
Section 3 for the action of the group on the tree.)
In the sequel, let
,
,
a be the diagonal element
in
G and
. We denote by
the right translation map given by
.
As in the real case, there are a lot of -invariant probability measures on . In this article, we describe these invariant probability measure with respect to a family of measures on and discuss a formula of the measure-theoretic entropy of with respect to . We give the main theorem of the paper.
Theorem 1. Let be the right translation map given as above. For each , let . If μ is the -invariant measure on , then there are measures on and a function such that the following holds.
It is well known that the Haar measure (the unique
G-invariant probability measure)
m is the measure of maximal entropy for
on
(see Reference [
5]). For the Haar measure
m on
, we can explicitly compute
and
of the Theorem 1. Namely, we have (see
Section 5)
From the above description, we achieve the measure-theoretic entropy of
with respect to
m.
Corollary 1. Let be as above. Then, we haveand the measure of maximal entropy is the unique G-invariant probability measure. Here, supremum runs over the set of -invariant probability measures on . This article is organized as follows. In
Section 2, we review elementary definition and some properties of measure-theoretic entropy in view of ergodic theory and dynamical systems. We study some arithmetic and geometry of
in
Section 3. There we mainly present the brief theory of simple continued fraction of
and describe the Bruhat-Tits tree of
. In
Section 4, we investigate the dynamical system
, describing
on the
-quotient of the space of parametrized bi-infinite geodesics over the Bruhat-Tits tree of
G by a suspension map of a shift map. Finally, we prove Theorem 1 and Corollary 1 in
Section 5.
3. Continued Fraction of and the Tree of
In this section, we discuss arithmetic and geometry of a field of formal series
over a finite field
. In particular, we review simple continued fraction expansion of
and the Bruhat-Tits tree of
. We refer to Reference [
7] and Reference [
4] for more details of the theory of continued fraction of a field of formal series.
3.1. Continued Fraction of a Field of Formal Series
Given an arbitrary field
with an absolute value
, we define the finite simple continued fraction
as
for
and
. We define the
infinite simple continued fraction , if exists, by
where the limit is taken with respect to the absolute value
.
Let
be the field
of Laurent series in
over a finite field
and
be the subring
, of polynomials in
t over
, of
. Given an element
of
with
, let us define
the degree, the polynomial part and fractional part of
, respectively. Then,
is a normed field with the associated absolute value given by
We further denote by
the local ring
of
which consists of power series in
over
. More precisely, let
Contrary to the usual absolute value on
, the norm
on
is non-Archimedean, that is,
holds for every
and in particular equality holds if
.
While there is no general algorithm to compute the sum, difference or product of continued fractions, we state a useful lemma on an absolute value of difference of two continued fractions.
Lemma 1 (Lemma 1.2.21 of Reference [
7]).
For with , let i be the integer such that for and . If , then . If , then where . The non-Archimedean property of the norm on yields that if and only if with the above notation. We conclude that the infinite simple continued fraction expansion of a Laurent series is always unique.
3.2. Tree of
We recall the notion of
Bruhat-Tits tree of
G in this subsection. See also Reference [
5] for the detail. Let
W the maximal compact subgroup
of
G. The vertices of
are defined to be the elements of
. We note that right multiplication of elements in
W corresponds to an iteration of elementary
-column operations. Let us recall that there are three types of elementary
-column operations.
A column within the matrix can be switched with another column.
Each column can be multiplied by an invertible element of (hence by a non-zero element of ).
A column can be replaced by the sum of that column and a -multiple of another column.
Using these three types of operations, we can understand every vertex of
as
for some integer
n (may be negative) and a rational function
. Let
be the projection map which forgets the
term. Two vertices
are defined to be adjacent to each other (there is an edge between two vertices) if and only if
and
and
satisfy
for some
. It follows that the degree (the number of edges attached to the vertex) of each vertex of
is equal to
. We also note that the visual boundary
at infinity of
can be identified with
(cf. Section 2 of Reference [
8]). Let
be the set
of distinct ordered triple points in
. Since two by two projective general linear group
over a field
F acts simply transitively on
by Möbius transformation
we have a bijection
given by
Let us finish this section with introducing notation for special vertices of
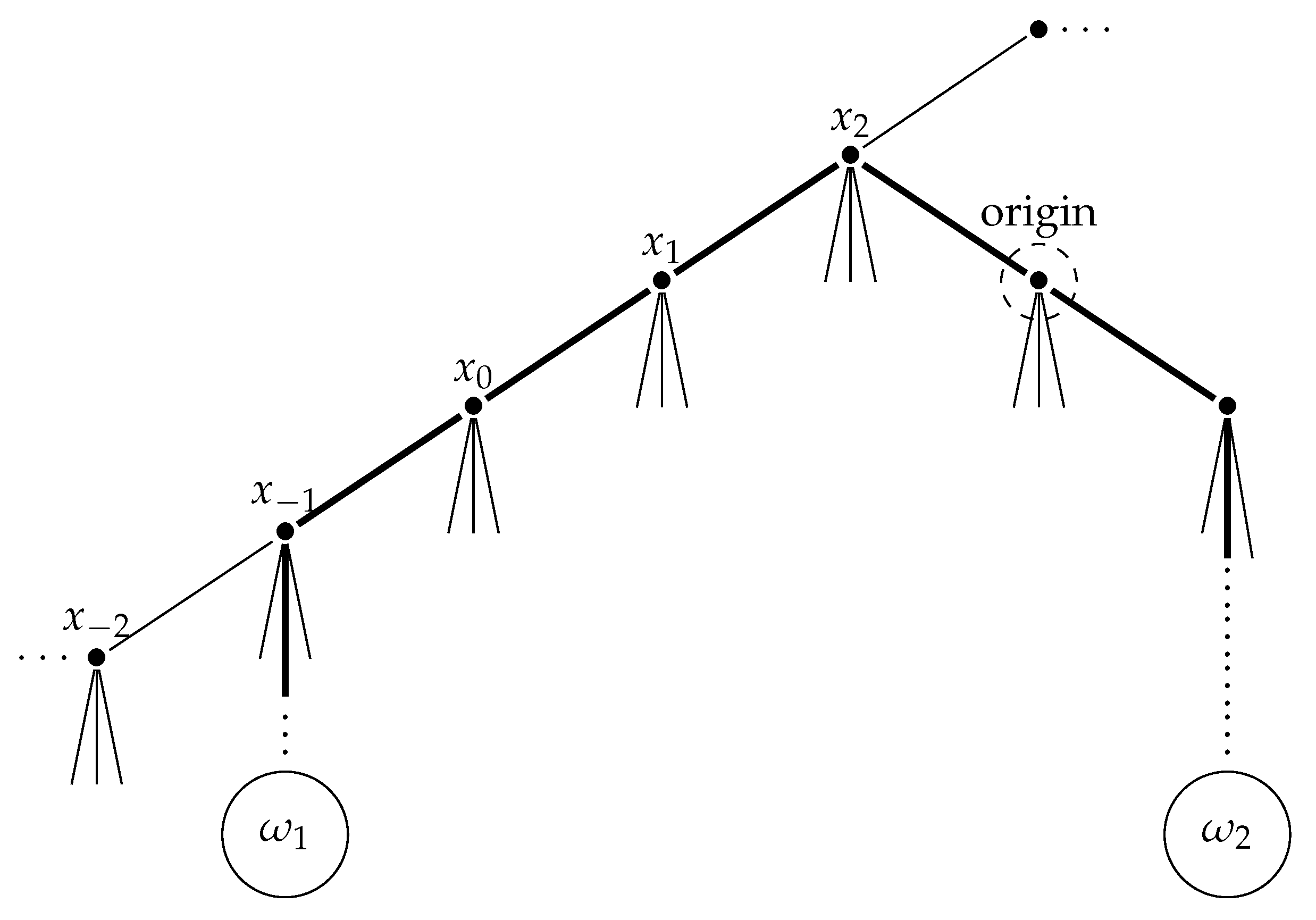
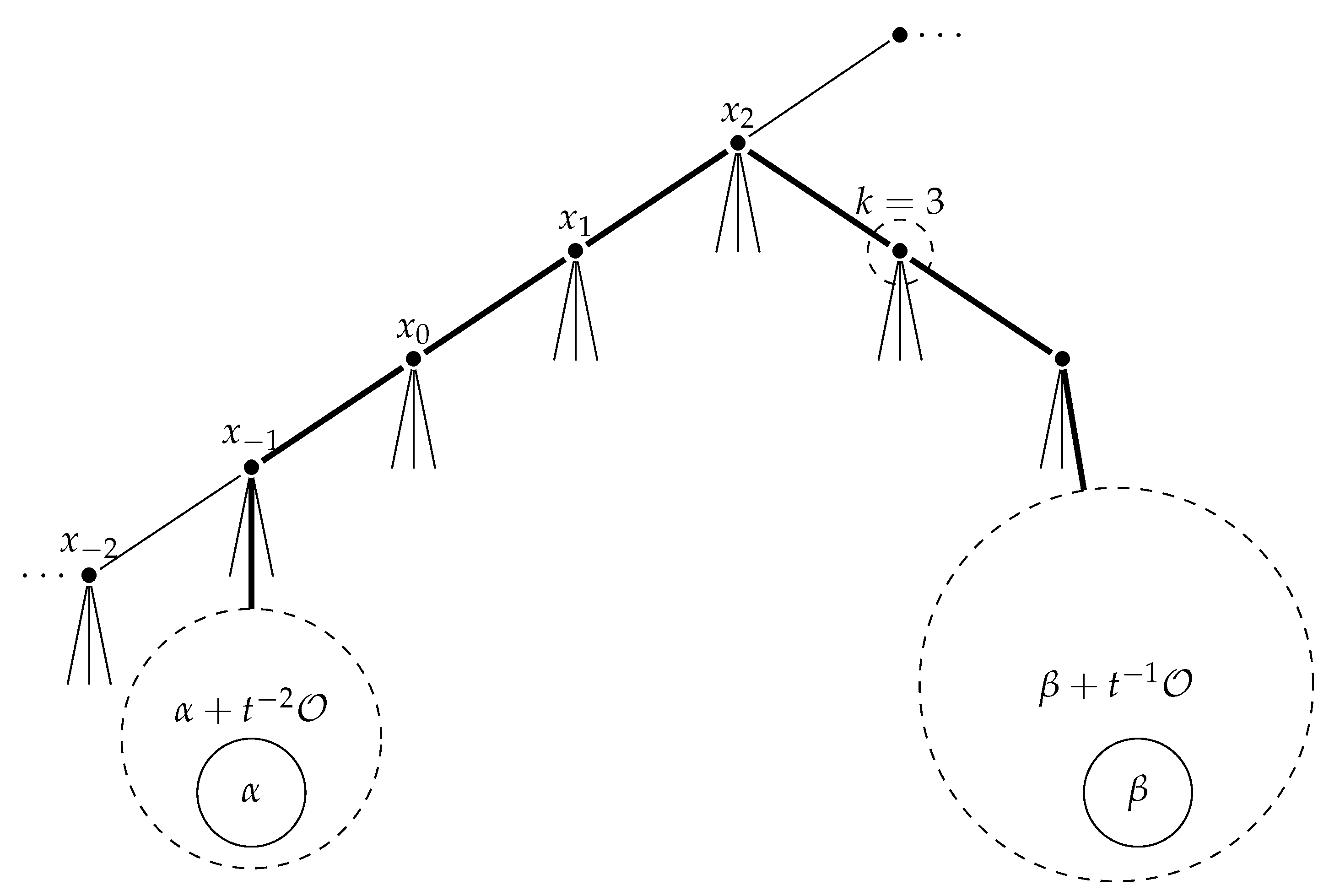
. Let
be the vertex of
defined by
Then, the sequence
forms a bi-infinite parametrized geodesic on
, which we call the
standard geodesic of
. See
Figure 1 which describes the vertices
of
and an example of ordered triple points
.
6. Discussion
From the above theorem, we may distinguish the Haar measure with other -invariant probability measures. It would be very interesting to discuss the effective uniqueness of the maximal measure m. Namely, we would like to answer to the following question: For a compactly supported locally constant function f on , is is essentially bounded by ?
This type of question can be answered via achieving ‘Einsiedler inequality’. It is known for a shift of finite type [
9], diagonal action on
p-adic and
S-arithmetic homogeneous spaces ([
10,
11]). In the positive characteristic setting, the main difficulty is that the associated countable Markov shift does not have the ‘big images and preimages’ (BIP) property.
7. Conclusions
Measure-theoretic entropy is a numerical invariant associated to a measure-preserving system. It is preserved by measurable isomorphism, and hence it can be used in order to distinguish special measures from other invariant measures. Motivated by the case of geodesic flow on modular surface , we addressed a positive characteristic homogeneous space.
We investigated arbitrary invariant probability measures of the discrete geodesic flow on . Especially, we interpreted these invariant probability measures with respect to a family of measures on a field of formal series. The formula of the mesure-theoretic entropy with respect to general -invariant measure on is also given. Moreover, we conclude that the entropy of with respect to the Haar measure m, which is the measure of maximal entropy, is .