Spatiotemporal Intermittency in Pulsatile Pipe Flow
Abstract
1. Introduction
2. Numerical Methodology
2.1. Governing Equations
2.2. Direct Numerical Simulation
2.3. Transient Growth Analysis
2.4. Modelling Geometric Imperfections in Our DNS
3. Results
3.1. Temporal Modulation of Statistically Steady Puff Dynamics
3.2. Optimal Infinitesimal Perturbations of Pulsatile Pipe Flow
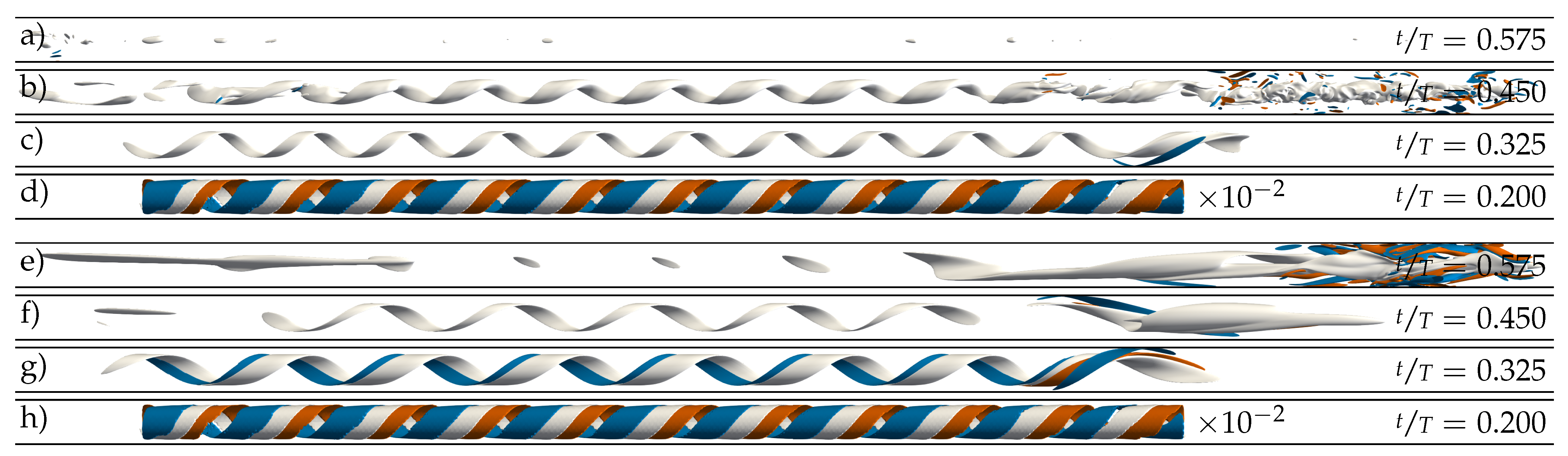
3.3. Nonlinear Dynamics of Helical Perturbations
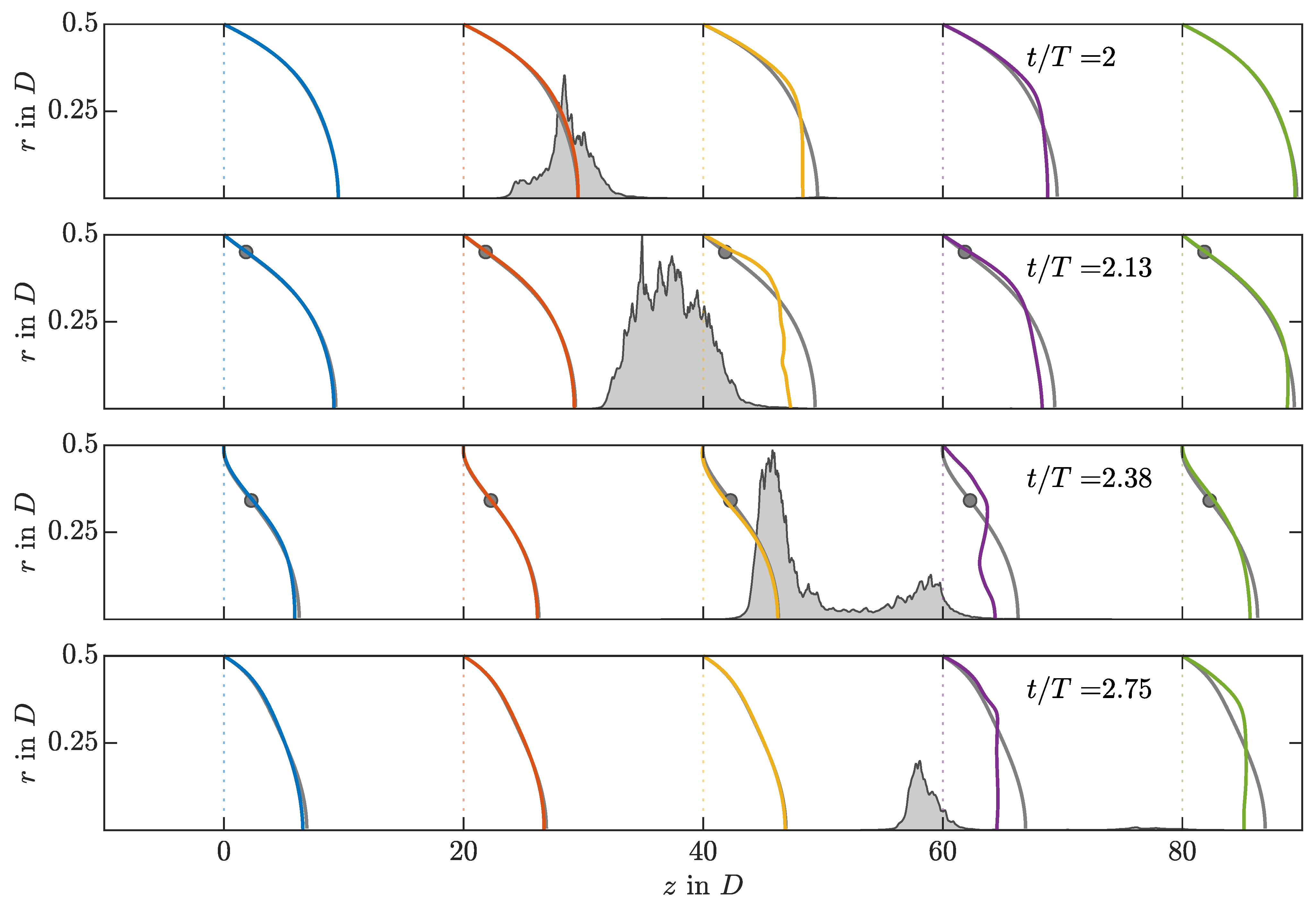
3.4. Puff Recovery Length
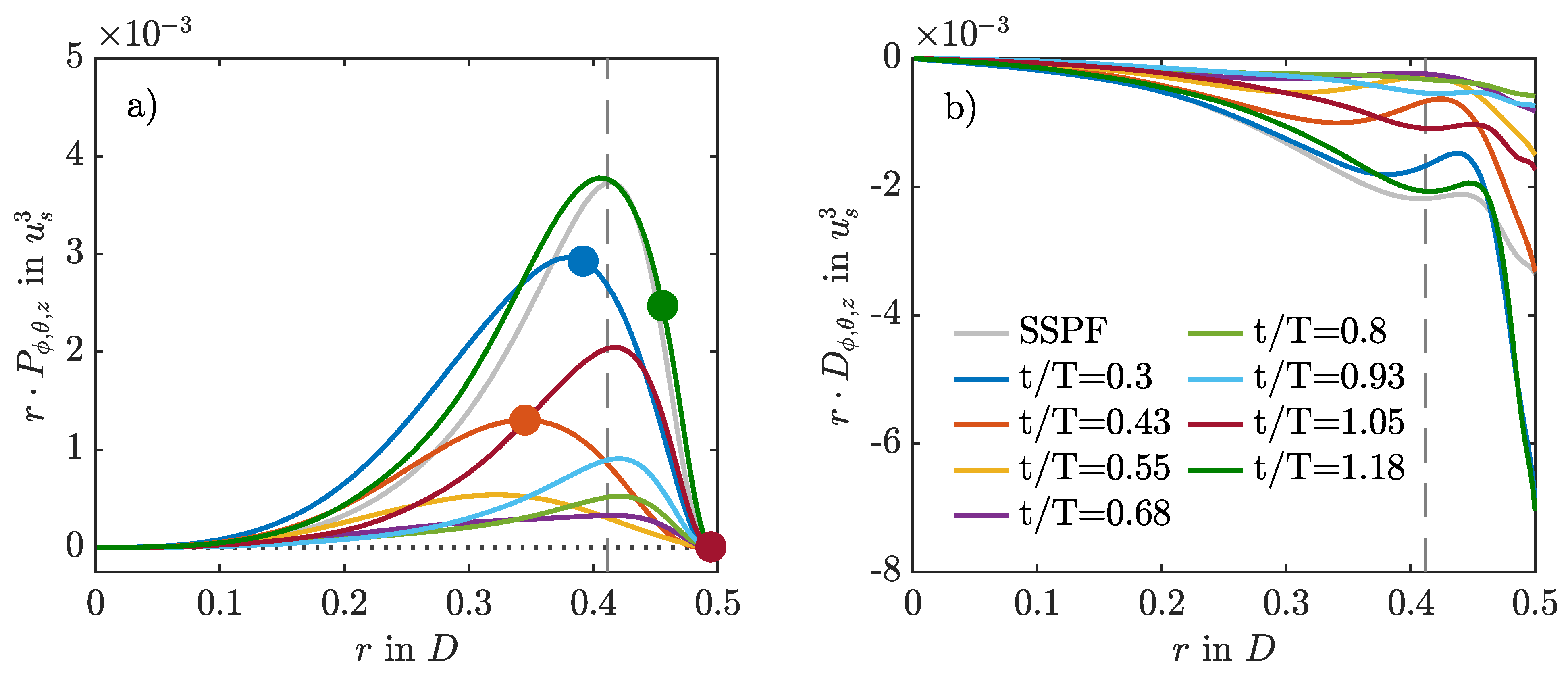
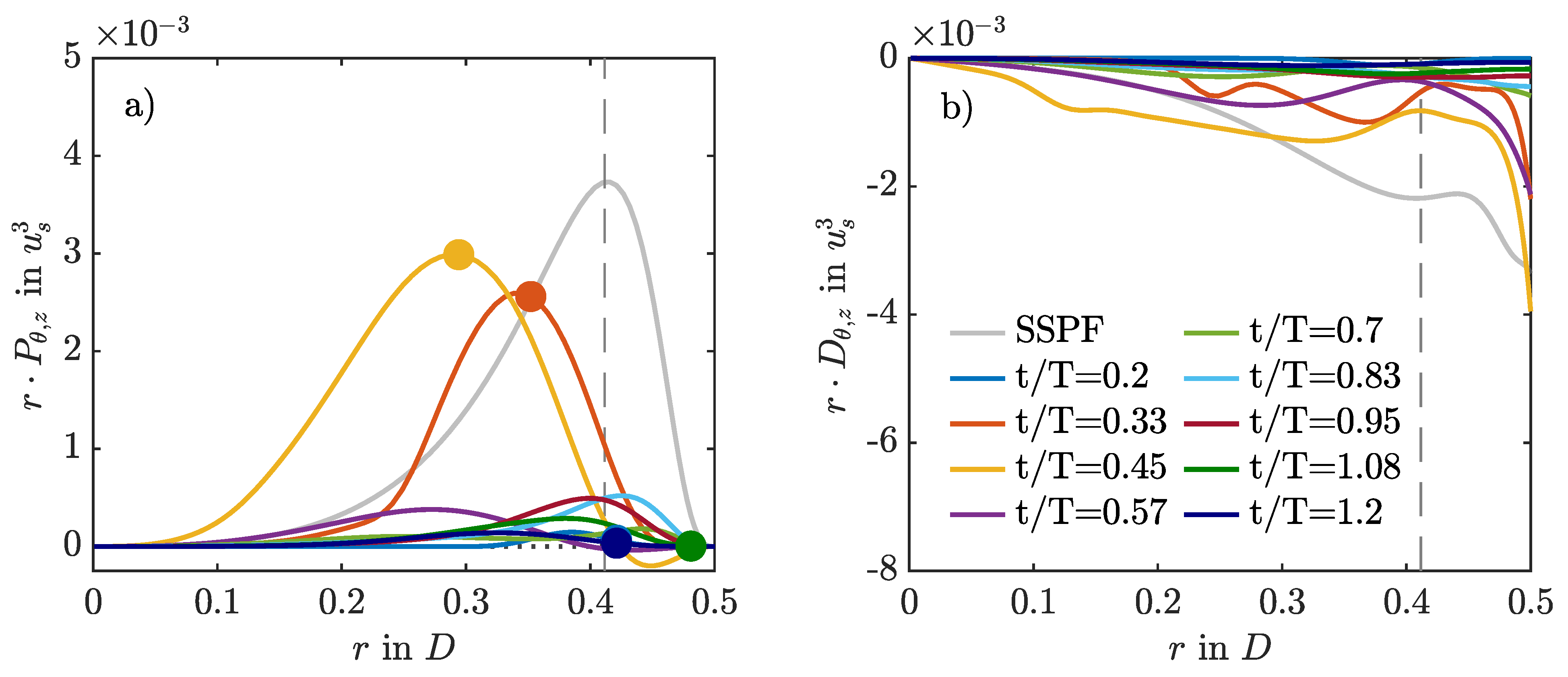
3.5. Intermittent Production and Dissipation
3.6. Effect of Local Geometric Imperfections
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AC | Acceleration |
| DC | Deceleration |
| SW | Sexl–Womersley |
| NSE | Navier–Stokes equations |
| TGA | Transient growth analysis |
| DNS | Direct numerical simulation |
| SSPF | Statistically steady pipe flow |
| IC SSPF | Cases with a SSPF initial condition |
| IC SWOP | Cases with a SW profile and optimum perturbation initial condition |
References
- Reynolds, O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Proc. R. Soc. Lond. 1883, 35, 84–99. [Google Scholar]
- Rotta, J.C. Experimenteller Beitrag zur Entstehung turbulenter Strömung im Rohr. Ing. Arch. 1956, 24, 258–281. [Google Scholar] [CrossRef]
- Wygnanski, I.J.; Champagne, F.H. On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 1973, 59, 281–335. [Google Scholar] [CrossRef]
- Wygnanski, I.; Sokolov, M.; Friedman, D. On transition in a pipe. Part 2. The equilibrium puff. J. Fluid Mech. 1975, 69, 283–304. [Google Scholar] [CrossRef]
- Avila, K.; Moxey, D.; De Lozar, A.; Avila, M.; Barkley, D.; Hof, B. The onset of turbulence in pipe flow. Science 2011, 333, 192–196. [Google Scholar] [CrossRef]
- Schmid, P.J.; Henningson, D.S. Stability and Transition in Shear Flows; Applied Mathematical Sciences; Springer: New York, NY, USA, 2001; Volume 142. [Google Scholar] [CrossRef]
- Meseguer, A.; Trefethen, L. Linearized pipe flow to Reynolds number 107. J. Comput. Phys. 2003, 186, 178–197. [Google Scholar] [CrossRef]
- Darbyshire, A.G.; Mullin, T. Transition to turbulence in constant-mass-flux pipe flow. J. Fluid Mech. 1995, 289, 83–114. [Google Scholar] [CrossRef]
- de Lozar, A.; Hof, B. An experimental study of the decay of turbulent puffs in pipe flow. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 589–599. [Google Scholar] [CrossRef]
- Barkley, D.; Song, B.; Mukund, V.; Lemoult, G.; Avila, M.; Hof, B. The rise of fully turbulent flow. Nature 2015, 526, 550–553. [Google Scholar] [CrossRef]
- Mukund, V.; Hof, B. The critical point of the transition to turbulence in pipe flow. J. Fluid Mech. 2018, 839, 76–94. [Google Scholar] [CrossRef]
- Avila, M.; Hof, B. Nature of laminar-turbulence intermittency in shear flows. Phys. Rev. E 2013, 87, 063012. [Google Scholar] [CrossRef] [PubMed]
- Sexl, T. Über den von E. G. Richardson entdeckten “Annulareffekt”. Z. Phys. 1930, 61, 349–362. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Warnecke, S.; Song, B.; Ma, X.; Hof, B. Transition to turbulence in pulsating pipe flow. J. Fluid Mech. 2017, 831, 418–432. [Google Scholar] [CrossRef]
- Xu, D.; Avila, M. The effect of pulsation frequency on transition in pulsatile pipe flow. J. Fluid Mech. 2018, 857, 937–951. [Google Scholar] [CrossRef]
- Xu, D.; Varshney, A.; Ma, X.; Song, B.; Riedl, M.; Avila, M.; Hof, B. Nonlinear hydrodynamic instability and turbulence in pulsatile flow. Proc. Natl. Acad. Sci. USA 2020, 117, 11233–11239. [Google Scholar] [CrossRef]
- Stettler, J.C.; Hussain, A.K.M.F. On transition of the pulsatile pipe flow. J. Fluid Mech. 1986, 170, 169–197. [Google Scholar] [CrossRef]
- Trip, R.; Kuik, D.J.; Westerweel, J.; Poelma, C. An experimental study of transitional pulsatile pipe flow. Phys. Fluids 2012, 24, 1–17. [Google Scholar] [CrossRef]
- Xu, D.; Song, B.; Avila, M. Non-modal transient growth of disturbances in pulsatile and oscillatory pipe flow. J. Fluid Mech. 2020, in press. [Google Scholar]
- Truckenmüller, K.E. Stabilitätstheorie für die Oszillierende Rohrströmung. Ph.D. Thesis, Helmut-Schmidt-Universität, Hamburg, Germany, 2006. [Google Scholar]
- López, J.M.; Feldmann, D.; Rampp, M.; Vela-Martín, A.; Shi, L.; Avila, M. nsCouette—A high-performance code for direct numerical simulations of turbulent Taylor–Couette flow. SoftwareX 2020, 11, 100395. [Google Scholar] [CrossRef]
- Barkley, D.; Blackburn, H.M.; Sherwin, S.J. Direct optimal growth analysis for timesteppers. Int. J. Numer. Methods Fluids 2008, 57, 1435–1458. [Google Scholar] [CrossRef]
- Marensi, E.; Ding, Z.; Willis, A.P.; Kerswell, R.R. Designing a minimal baffle to destabilise turbulence in pipe flows. J. Fluid Mech. 2020, 900. [Google Scholar] [CrossRef]
- Blackburn, H.M.; Sherwin, S.J.; Barkley, D. Convective instability and transient growth in steady and pulsatile stenotic flows. J. Fluid Mech. 2008, 607, 267–277. [Google Scholar] [CrossRef][Green Version]
- Hof, B.; de Lozar, A.; Avila, M.; Tu, X.; Schneider, T.M. Eliminating Turbulence in Spatially Intermittent Flows. Science 2010, 327, 1491–1494. [Google Scholar] [CrossRef] [PubMed]
- Kerswell, R. Nonlinear Nonmodal Stability Theory. Annu. Rev. Fluid Mech. 2018, 50, 319–345. [Google Scholar] [CrossRef]
- Barkley, D. Simplifying the complexity of pipe flow. Phys. Rev. E 2011, 84, 016309. [Google Scholar] [CrossRef]
- Feldmann, D. Eine Numerische Studie zur Turbulenten Bewegungsform in der oszillierenden Rohrströmung. Ph.D. Thesis, Technische Universität Ilmenau, Ilmenau, Germany, 2015. urn:urn:nbn:de:gbv:ilm1-2015000634. [Google Scholar]
- Kühnen, J.; Song, B.; Scarselli, D.; Budanur, N.B.; Riedl, M.; Willis, A.P.; Avila, M.; Hof, B. Destabilizing turbulence in pipe flow. Nat. Phys. 2018, 14, 386–390. [Google Scholar] [CrossRef]





| in | inD | inD | in | inD | |||||
|---|---|---|---|---|---|---|---|---|---|
| Contraction | 0.25 | 4 | 2.5 | 10 | 100 | 0.45 | 20 | ≥1 | 0 |
| Bump | 0.25 | 4 | 2.5 | 10 | 100 | 0.45 | 20 | 0.25 | 0 |
| Tilted Bump | 0.25 | 4 | 2.5 | 10 | 100 | 0.45 | 20 | 0.0625 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feldmann, D.; Morón, D.; Avila, M. Spatiotemporal Intermittency in Pulsatile Pipe Flow. Entropy 2021, 23, 46. https://doi.org/10.3390/e23010046
Feldmann D, Morón D, Avila M. Spatiotemporal Intermittency in Pulsatile Pipe Flow. Entropy. 2021; 23(1):46. https://doi.org/10.3390/e23010046
Chicago/Turabian StyleFeldmann, Daniel, Daniel Morón, and Marc Avila. 2021. "Spatiotemporal Intermittency in Pulsatile Pipe Flow" Entropy 23, no. 1: 46. https://doi.org/10.3390/e23010046
APA StyleFeldmann, D., Morón, D., & Avila, M. (2021). Spatiotemporal Intermittency in Pulsatile Pipe Flow. Entropy, 23(1), 46. https://doi.org/10.3390/e23010046





