Coupled Criticality Analysis of Inflation and Unemployment
Abstract
1. Introduction
2. Methods
2.1. Multifractal Random Walk (MRW)
2.2. Joint Multifractal Approach: The Bi-MRW Method
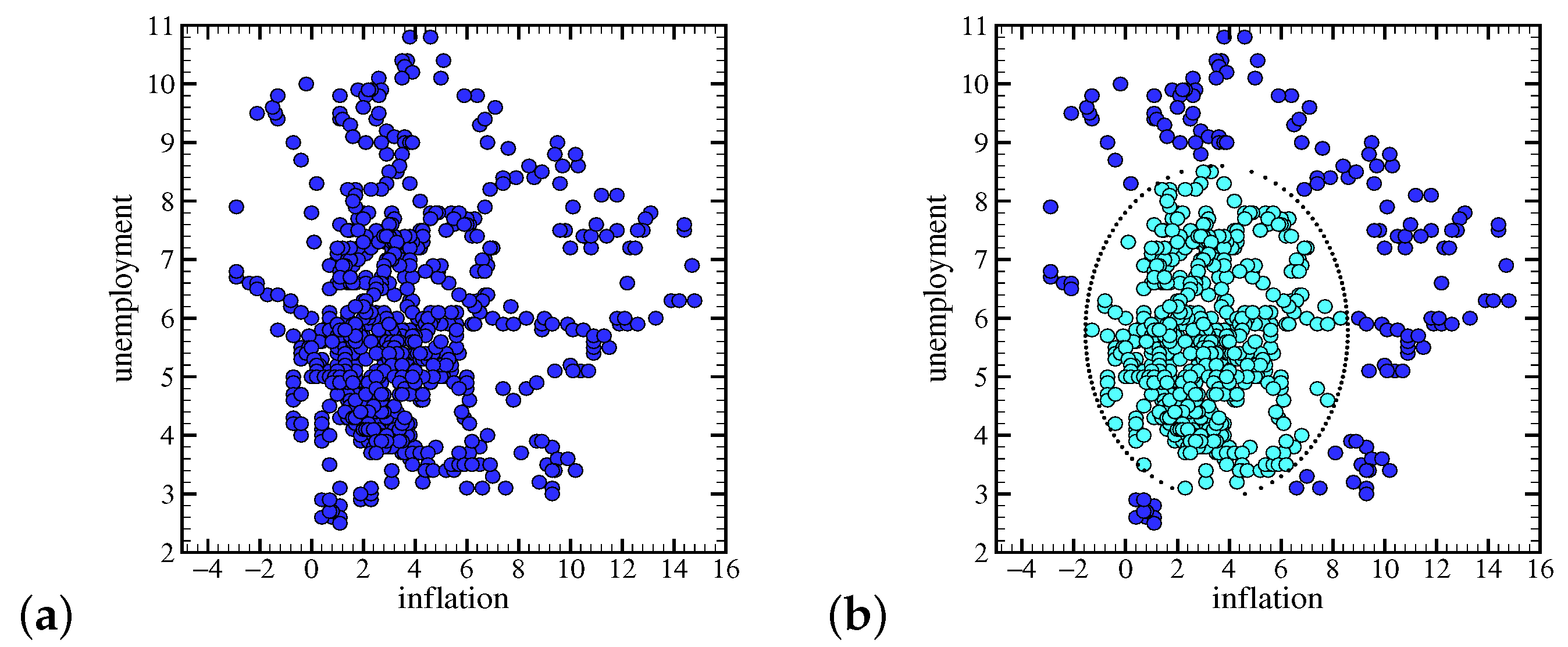
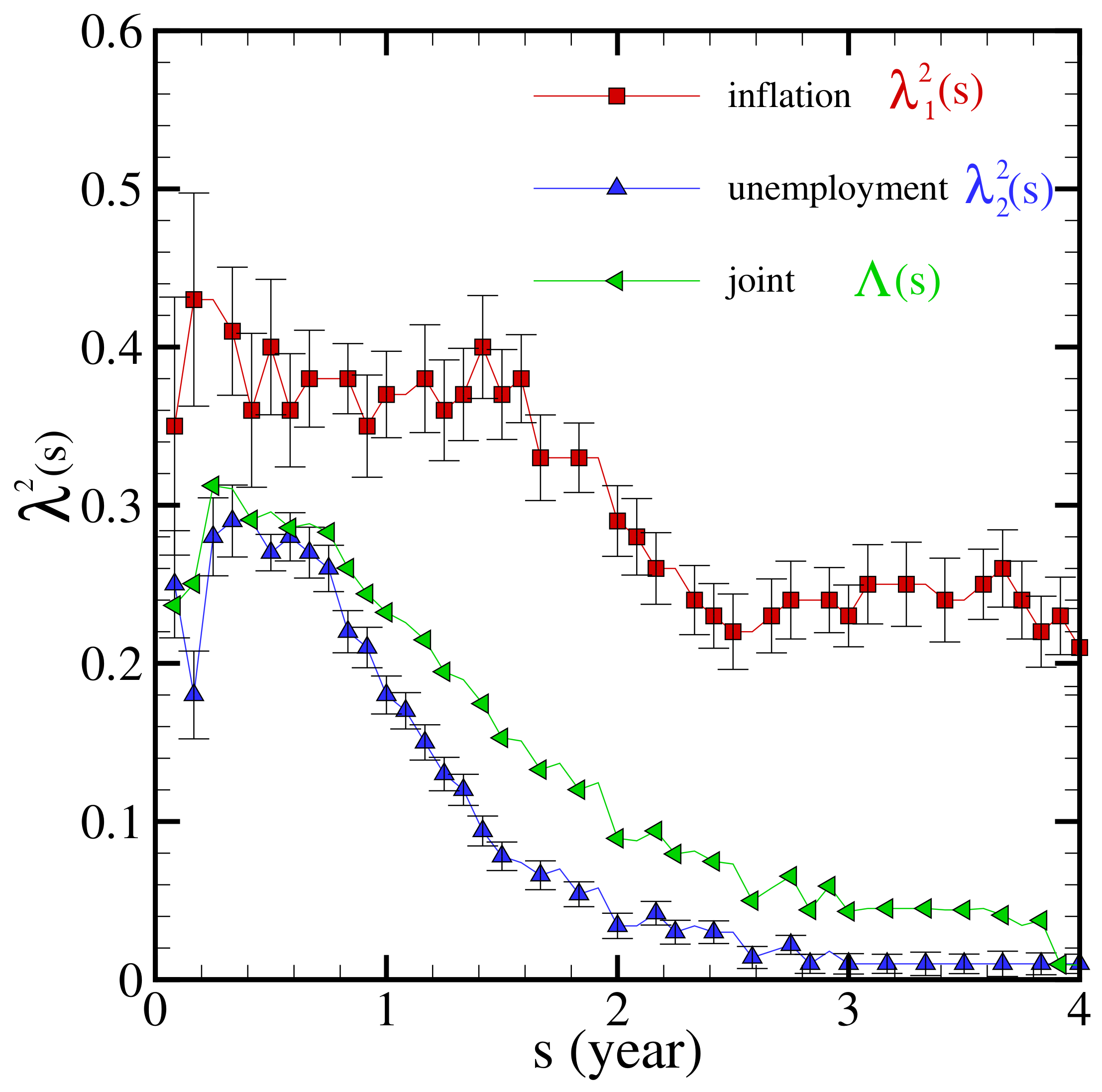
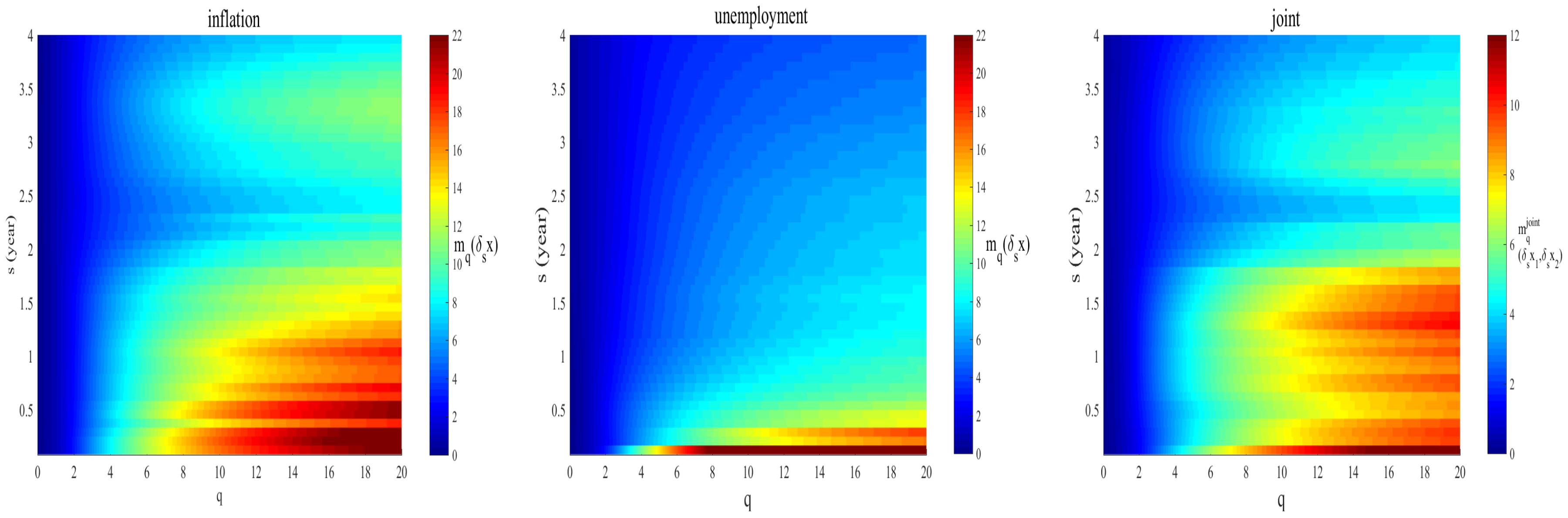
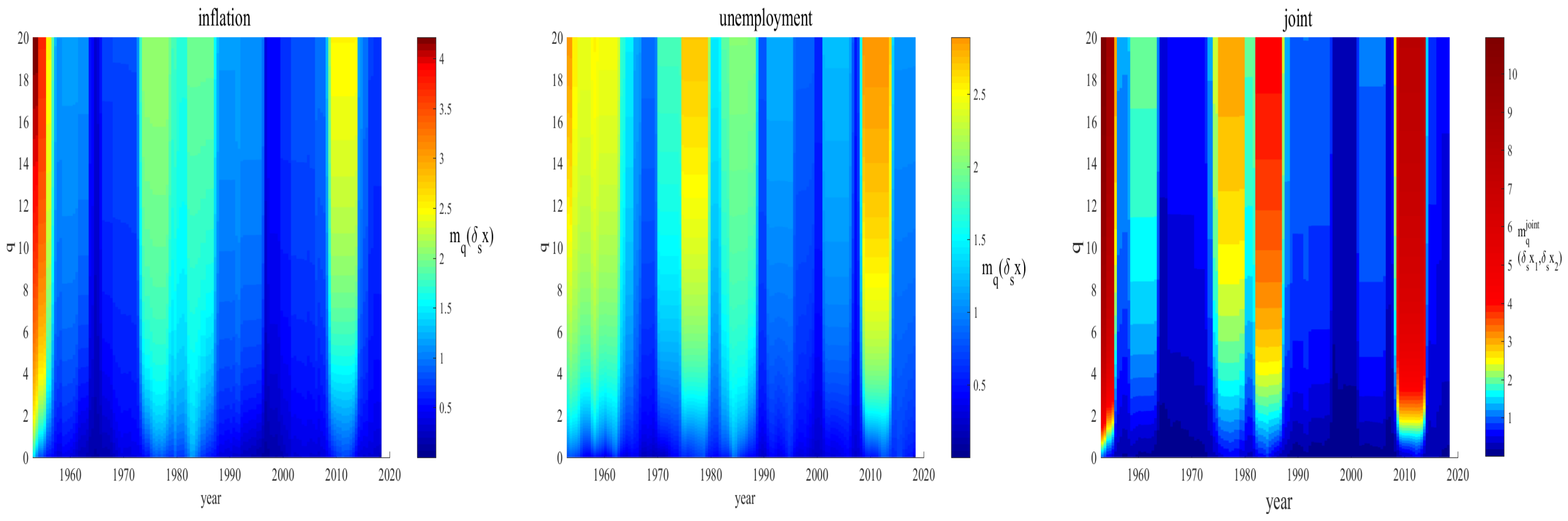
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MRW | Multifractal Random Walk |
| Probability Density Function | |
| Bi-MRW | Bivariate Multifractal Random Walk |
References
- Phillips, A.W. The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom. Economica 1958, 25, 283. [Google Scholar]
- Phelps, E.S. Phillips curves, expectations of inflation and optimal unemployment over time. Economica 1967, 34, 254. [Google Scholar] [CrossRef]
- Samuelson, P.A.; Solow, R.M. Analytical aspects of anti-inflation policy. Am. Econ. Rev. 1960, 40, 177. [Google Scholar]
- Friedman, M. The role of monetary policy. Am. Econ. Rev. 1968, 58, 1. [Google Scholar]
- Friedman, M. Nobel lecture: Inflation and unemployment. J. Political Econ. 1977, 85, 451. [Google Scholar] [CrossRef]
- Phelps, E.S. Money Wage Dynamics and Labor Market Equilibrium. J. Political Econ. 1968, 76, 678. [Google Scholar] [CrossRef]
- Lucas, R.E., Jr.; Sargent, T.J. After Keynesian Macroeconomics. In Rational Expectations and Econometric Practice; University of Minnesota Press: Minneapolis, MN, USA, 1981; pp. 295–320. [Google Scholar]
- Akerlof, G.A.; Dickens, W.T.; Perry, G.L.; Bewley, T.F.; Blinder, A.S. Near-Rational Wage and Price Setting and the Long-Run Phillips Curve. Brook. Pap. Econ. Act. 2000, 31, 1. [Google Scholar] [CrossRef]
- Gali, J.; Gertler, M.; Lopez-Salido, J.D. Robustness of the estimates of the hybrid New Keynesian Phillips curve. J. Monet. 2005, 52, 1107. [Google Scholar] [CrossRef]
- Tobin, J. Inflation and unemployment. In Essential Readings in Economics; Estrin, S., Marin, A., Eds.; Palgrave: London, UK, 1995; pp. 232–254. [Google Scholar]
- Mankiw, N.G. The inexorable and mysterious tradeoff between inflation and unemployment. Econ. J. 2001, 111, 45. [Google Scholar] [CrossRef]
- Rochon, L.-P.; Rossi, S. The relationship between inflation and unemployment: A critique of Friedman and Phelps. Rev. Keynes. Econ. 2018, 6, 533. [Google Scholar] [CrossRef]
- Taylor, J.B. The Role of Policy in the Great Recession and the Weak Recovery. Am. Econ. Rev. 2014, 104, 61. [Google Scholar] [CrossRef]
- Mishkin, F.S. Monetary policy strategy: Lessons from the crisis. NBER Work. Pap. 2011, 16755. [Google Scholar] [CrossRef]
- Kitov, I. Inflation, Unemployment, Labor Force Change in the USA. 2006. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=886662 (accessed on 2 March 2006).
- Ribba, A. Short-run and long-run interaction between inflation and unemployment in the USA. Appl. Econ. Lett. 2003, 10, 373. [Google Scholar] [CrossRef]
- Rao, B.B. A model of income, unemployment and inflation for the USA. Appl. Econ. 1992, 24, 597. [Google Scholar] [CrossRef]
- Donayre, L.; Panovska, I.U.S. wage growth and nonlinearities: The roles of inflation and unemployment. Econ. Model. 2018, 68, 273. [Google Scholar] [CrossRef]
- Nada, D.W. Analysis of the relationship between inflation and unemployment rate: Case study USA. Int. J. Bus. Adm. Manag. Res. 2018, 4, 1. [Google Scholar] [CrossRef]
- Binder, C. Coronavirus fears and macroeconomic expectations. Rev. Econ. Stat. 2020, 102, 721–730. [Google Scholar] [CrossRef]
- Fetzer, T.; Hensel, L.; Hermle, J.; Roth, C. Coronavirus perceptions and economic anxiety. Rev. Econ. Stat. 2020, 1–36. [Google Scholar] [CrossRef]
- Safdari, H.; Hosseiny, A.; Farahani, S.V.; Jafari, G.R. A picture for the coupling of unemployment and inflation. Phys. A Stat. Mech. Its Appl. 2016, 444, 744. [Google Scholar] [CrossRef]
- Kartika, M.; Kurniasih, E.P. Does Phillips Curve Apply in ASEAN Countries. Int. J. Sci. Res. Publ. 2020, 10, 253. [Google Scholar] [CrossRef]
- Arthur, W.B. Complexity and the Economy. Science 1999, 284, 107. [Google Scholar] [CrossRef] [PubMed]
- Namaki, A.; Shirazi, A.H.; Raei, R.; Jafari, G.R. Network analysis of a financial market based on genuine correlation and threshold method. Phys. A Stat. Mech. Its Appl. 2011, 390, 3835. [Google Scholar] [CrossRef]
- Raei, R.; Namaki, A.; Vahabi, H. Analysis of Collective Behavior of Iran Banking Sector by Random Matrix Theory. Iran. J. Financ. 2019, 3, 60. [Google Scholar]
- Hosseiny, A.; Bahrami, M.; Palestrini, A.; Gallegati, M. Metastable Features of Economic Networks and Responses to Exogenous Shocks. PLoS ONE 2016, 11, e0160363. [Google Scholar] [CrossRef] [PubMed]
- Shirazi, A.H.; Saberi, A.A.; Hosseiny, A.; Amirzadeh, E.; Simin, P.T. Non-criticality of interaction network over system’s crises: A percolation analysis. Sci. Rep. 2017, 7, 15855. [Google Scholar] [CrossRef]
- Namaki, A.; Raei, R.; Asadi, N.; Hajihasani, A. Analysis of Iran Banking Sector by Multi-Layer Approach. Iran. J. Financ. 2019, 3, 73. [Google Scholar]
- Pearce, D. Complexity theory and economics. Agenda A J. Policy Anal. Reform 1994, 1, 101–106. [Google Scholar] [CrossRef]
- Helbing, D.; Kirman, A. Rethinking economics using complexity theory. Real-World Econ. Rev. 2013, 64. [Google Scholar] [CrossRef]
- Hosseiny, A.; Absalan, M.; Sherafati, M.; Gallegati, M. Hysteresis of economic networks in an XY model. Phys. A Stat. Mech. Its Appl. 2019, 513, 644–652. [Google Scholar] [CrossRef]
- Bahrami, M.; Chinichian, N.; Hosseiny, A.; Jafari, G.; Ausloos, M. Optimization of the post-crisis recovery plans in scale-free networks. Phys. A Stat. Mech. Its Appl. 2020, 540, 123203. [Google Scholar] [CrossRef]
- Varela, L.M.; Rotundo, G.; Ausloos, M.; Carrete, J. Complex networks analysis in socio-economic models. In Complexity and Geographical Economics. Topics and Tools; Commendatore, P., Kayam, S.S., Kubin, I., Eds.; Springer: Berlin, Germany, 2015; pp. 209–245. [Google Scholar]
- Ausloos, M.; Dawid, H.; Merlone, U. Spatial interactions in Agent Based Modeling. In Complexity and Geographical Economics. Topics and Tools; Commendatore, P., Kayam, S.S., Kubin, I., Eds.; Springer: Berlin, Germany, 2015; pp. 353–377. [Google Scholar]
- Schweitzer, F.; Fagiolo, G.; Sornette, D.; Vega-Redondo, F.; Vespignani, A.; White, D.R. Economic networks: The new challenges. Science 2009, 325, 422. [Google Scholar] [CrossRef]
- Rotundo, G.; D’Arcangelis, A.M. Ownership and control in shareholding networks. J. Econ. Interact. Coord. 2010, 5, 191–219. [Google Scholar] [CrossRef]
- Chakraborti, A.; Challet, D.; Chatterjee, A.; Marsili, M.; Zhang, Y.C.; Chakrabarti, B.K. Statistical mechanics of competitive resource allocation using agent-based models. Phys. Rep. 2015, 552, 1. [Google Scholar] [CrossRef]
- Namaki, A.; Raei, R.; Jafari, G.R. Comparing Tehran stock exchange as an emerging market with a mature market by random matrix approach. Int. J. Mod. Phys. C 2011, 22, 371. [Google Scholar] [CrossRef]
- Dragulescu, A.; Yakovenko, V.M. Statistical mechanics of money. Eur. Phys. J. B-Condens. Matter Complex Syst. 2000, 17, 723. [Google Scholar] [CrossRef]
- Vandewalle, N.; Ausloos, M.; Boveroux, P.; Minguet, A. How the financial crash of October 1997 could have been predicted. Eur. Phys. J. B 1998, 4, 139. [Google Scholar] [CrossRef]
- Hosseiny, A.; Gallegati, M. Role of intensive and extensive variables in a soup of firms in economy to address long run prices and aggregate data. Phys. A Stat. Mech. Its Appl. 2017, 470, 51. [Google Scholar] [CrossRef]
- Hosseiny, A. Geometrical Imaging of the Real Gap between Economies of China and the United States. Phys. A Stat. Mech. Its Appl. 2017, 479, 151. [Google Scholar] [CrossRef]
- Ivanova, K.; Shirer, H.N.; Clothiaux, E.E.; Kitova, N.; Mikhalev, M.A.; Ackerman, T.P.; Ausloos, M. A case study of stratus cloud base height multifractal fluctuations. Phys. A Stat. Mech. Its Appl. 2002, 308, 518. [Google Scholar] [CrossRef]
- Ausloos, M. Generalized Hurst exponent and multifractal function of original and translated texts mapped into frequency and length time series. Phys. Rev. E 2012, 86, 031108. [Google Scholar] [CrossRef]
- Ye, Y.; Hang, X.R.; Koh, J.M.; Miszczak, J.A.; Cheong, K.H.; Xie, N. Passive network evolution promotes group welfare in complex networks. Chaos Solitons Fractals 2020, 130, 109464. [Google Scholar] [CrossRef]
- Rybak, M.; Malarz, K.; Kułakowski, K. Competing contact processes in the Watts-Strogatz network. Eur. Phys. J. B 2016, 89, 145. [Google Scholar] [CrossRef][Green Version]
- Vandewalle, N.; Ausloos, M. Fractals in Finance. In Fractals and Beyond Complexity in the Sciences; Novak, M.M., Ed.; World Scient.: Singapore, 1998; pp. 355–356. [Google Scholar]
- Ivanova, K.; Ausloos, M. Low q-moment multifractal analysis of Gold price, Dow Jones Industrial Average and BGL-USD exchange rate. Eur. Phys. J. B 1999, 8, 665. [Google Scholar] [CrossRef]
- Zhou, W.-X. Finite-size effect and the components of multifractality in financial volatility. Chaos Solitons Fractals 2012, 45, 147. [Google Scholar] [CrossRef]
- Kukacka, J.; Kristoufek, L. Do ‘complex’ financial models really lead to complex dynamics Agent-based models and multifractality. J. Econ. Dyn. Control 2020, 113, 103855. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Phys. A Stat. Mech. Its Appl. 2002, 316, 87. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J.; Feng, J. Understanding the Fractal Dimensions of Urban Forms through Spatial Entropy. Entropy 2017, 19, 600. [Google Scholar] [CrossRef]
- Chen, Y.; Huang, L. Spatial Measures of Urban Systems: From Entropy to Fractal Dimension. Entropy 2018, 20, 991. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, D.; Ma, K.; Gao, K. Descriptions of Entropy with Fractal Dynamics and Their Applications to the Flow Pressure of Centrifugal Compressor. Entropy 2019, 21, 266. [Google Scholar] [CrossRef]
- Shayeganfar, F.; Jabbari-Farouji, S.; Sadegh Movahed, M.; Jafari, G.R.; Reza Rahimi Tabar, M. Multifractal analysis of light scattering-intensity fluctuations. Phys. Rev. E 2009, 80, 061126. [Google Scholar] [CrossRef]
- Saakian, D.B. The calculation of multifractal properties of directed random walks on hierarchic trees with continuous branching. J. Stat. Mech. Theory Exp. 2012, 4, P04007. [Google Scholar] [CrossRef]
- Saakian, D.B.; Martirosyan, A.; Hu, C.K.; Struzik, Z.R. Exact probability distribution function for multifractal random walk models of stocks. Europhys. Lett. 2011, 95, 28007. [Google Scholar] [CrossRef]
- Buonocore, R.J.; Brandi, G.; Mantegna, R.N.; Di Matteo, T. On the interplay between multiscaling and stock dependence. Quant. Financ. 2020, 20, 133. [Google Scholar] [CrossRef]
- Matteo, T.D.; Aste, T.; Dacorogna, M.M.; Di Matteo, T.; Aste, T.; Dacorogna, M.M. Long-term memories of developed and emerging markets: Using the scaling analysis to characterize their stage of development. J. Bank. Financ. 2005, 29, 827. [Google Scholar] [CrossRef]
- Bariviera, A.F. One model is not enough: Heterogeneity in cryptocurrencies’ multifractal profiles. Financ. Res. Lett. 2020, 101649. [Google Scholar] [CrossRef]
- Lux, T.; Ausloos, M. Market fluctuations I: Scaling, multiscaling, and their possible origins. In The Science of Disasters; Springer: Berlin/Heidelberg, Germany, 2002; pp. 372–409. [Google Scholar]
- Beghdadi, A.; Andraud, C.; Lafait, J.; Peiro, J.; Perreau, M. Entropic and multifractal analysis of disordered morphologies. Fractals 1993, 1, 360. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141. [Google Scholar] [CrossRef]
- Kohmoto, M. Entropy function for multifractals. Phys. Rev. A 1988, 37, 1345. [Google Scholar] [CrossRef]
- US Inflation Calculator. Available online: http://www.usinflationcalculator.com (accessed on 11 December 2020).
- US Bureau of Labor Statistics. Available online: https://www.bls.gov/bls/unemployment.htm (accessed on 11 December 2020).
- Sayeed, J.; Islam, M.D.; Yasmin, S. Does the U.S. economy face a long run trade off between inflation and unemployment. Int. J. Monet. Econ. Financ. 2019, 12, 118. [Google Scholar] [CrossRef]
- Chabaud, B.; Naert, A.; Peinke, J.; Chillá, F.; Castaing, B.; Hébral, B. Transition towards developed turbulence. Phys. Rev. Lett. 1994, 73, 3227. [Google Scholar] [CrossRef]
- Bacry, E.; Delour, J.; Muzy, J.F. Multifractal random walk. Phys. Rev. E 2001, 64, 026103. [Google Scholar] [CrossRef]
- Muzy, J.F.; Sornette, D.; Delour, J.; Arneodo, A. Multifractal returns and hierarchical portfolio theory. Quant. Financ. 2001, 1, 131. [Google Scholar] [CrossRef]
- Muzy, J.F.; Delour, J.; Bacry, E. Modelling fluctuations of financial time series: From cascade process to stochastic volatility model. Eur. Phys. B 2000, 17, 537. [Google Scholar] [CrossRef]
- Agostini, G.D. Bayesian Inference in Processing Experimental Data: Principles and Basic Applications. Rep. Prog. Phys. 2003, 66, 1383. [Google Scholar] [CrossRef]
- Sivia, D.S.; Skilling, J. Data Analysis: A Bayesian Tutorial; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Ball, L.; Mankiw, N.G.; Romer, D.; Akerlof, G.A.; Rose, A.; Yellen, J.; Sims, C.A. The new Keynesian economics and the output-inflation trade-off. Brook. Pap. Econ. Act. 1988, 1, 1. [Google Scholar] [CrossRef]
- Mortensen, D.T.; Pissarides, C.A. Job reallocation, employment fluctuations and unemployment. Handb. Macroecon. 1999, 1, 1171. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koohi Lai, Z.; Namaki, A.; Hosseiny, A.; Jafari, G.; Ausloos, M. Coupled Criticality Analysis of Inflation and Unemployment. Entropy 2021, 23, 42. https://doi.org/10.3390/e23010042
Koohi Lai Z, Namaki A, Hosseiny A, Jafari G, Ausloos M. Coupled Criticality Analysis of Inflation and Unemployment. Entropy. 2021; 23(1):42. https://doi.org/10.3390/e23010042
Chicago/Turabian StyleKoohi Lai, Zahra, Ali Namaki, Ali Hosseiny, Gholamreza Jafari, and Marcel Ausloos. 2021. "Coupled Criticality Analysis of Inflation and Unemployment" Entropy 23, no. 1: 42. https://doi.org/10.3390/e23010042
APA StyleKoohi Lai, Z., Namaki, A., Hosseiny, A., Jafari, G., & Ausloos, M. (2021). Coupled Criticality Analysis of Inflation and Unemployment. Entropy, 23(1), 42. https://doi.org/10.3390/e23010042





