1. Introduction
Modern cities are diverse in their spatial structures: Some cities are monocentric, with a single centre of business, retail, and other types of activity, while some exhibit polycentric patterns in which multiple activity clusters are distributed across space [
1,
2,
3,
4,
5]. It is well known that a city’s structure affects economic productivity, environmental conditions, and other aspects of human life [
6,
7,
8,
9,
10]. Importantly, spatial structures of cities change over time in intricate ways, with the process of intra-urban migration being one of the main drivers of a city’s evolution [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. However, there is a lack of models that can quantitatively explain and accurately predict a city’s evolution in terms of intra-urban migration and the resultant patterns of an urban spatial structure.
In existing models of cities, intra-urban migration is usually considered as a fast process in which an
equilibrium is reached very quickly [
19,
20,
21,
22,
23,
24]. Such an equilibrium is typically defined by the spatial distribution of infrastructure and employment [
19,
21,
23,
25,
26,
27], and the intra-urban dynamics are typically not considered as an example of a non-equilibrium process in the thermodynamic sense. A non-equilibrium approach is also hard to explicitly validate due to the difficulty of collecting the data.
In this work, we consider intra-urban migration as an irreversible process, and explicitly derive the dynamics of the corresponding non-equilibrium evolution. In doing so, we shall draw on an analogy with diffusive relaxation. This opens a way towards a systematic and coherent framework describing human migration within cities (both temporally and spatially), as opposed to an unconstrained evolution of cities through expansion.
Human relocation has been widely considered as diffusion in open systems [
28,
29]. This approach employs an apparent and direct analogy between human migration and molecular diffusion, and has shown good predictions at different scales [
15,
16,
17,
30,
31,
32], from city growth [
23,
33,
34] and epidemic spread [
31,
35,
36] to inter-continental migration [
28]. These migration processes can be characterised as expansive, as they increase the area of human habitat, viewing the human society as an open system. In the modern world, however, most of the migration processes result in a redistribution of the population across already occupied locations, rather than expanding to non-occupied areas. This constraint essentially confines the migration to happening in a closed system with a fixed area and population. In this paper, we propose a diffusion model describing migration processes in a
closed system from the perspective of non-equilibrium thermodynamics.
In general, migration from rural to urban areas, as well as expansion of metropolitan boundaries, is a relatively slow and long-term process. In contrast, intra-urban migration happens at a much faster rate [
19,
20,
26,
27,
37,
38,
39]. Nevertheless, we argue that intra-urban migration is a fundamental driving force shaping the long-term evolution of the urban spatial structure, with external migration and spatial expansion playing only a secondary role. Thus, we aim to model urban transitions as dynamics developing in a closed system, at least in the first approximation.
Typically, intra-urban human mobility has been considered as a process driven by certain attractiveness of various locations within a city, perceived in terms of proximity to schools, business centres, recreational facilities, etc. [
19,
24]. This notion of attractiveness was modelled both explicitly, using specific socio-economic indicators [
40,
41], and implicitly, being reconstructed directly from migration data [
26]. The latter approaches can be classified as “microscopic” [
42,
43], as they focus on a specific mechanism of human relocation.
In this paper, we propose a concise “phenomenological” approach that considers the migration flows from the perspective of diffusion. Importantly, we do not make any assumptions about particular choices that may motivate individuals to relocate. Instead, we analyse their collective movement and show that this process is similar to diffusion. As a result, we reveal the trends of population movement analogously to the macroscopic movement of a fluid. In doing so, we introduce a rigorous definition of an equilibrium state as the spatial configuration to which the apparent evolution relaxes, and a decomposition of the population into two distinct groups with different relocation frequencies.
This paper is organised as follows. In
Section 2, we present a general framework of the irreversible evolution of a city driven by residential relocation. In
Section 3, we apply this framework to the Australian capital cities. In particular, we analyse the dynamic relocation patterns in
Section 3.1, develop the analogy between intra-urban resettlement and diffusion in
Section 3.2, and predict the equilibrium population distribution in
Section 3.3. In
Section 4, we analyse the robustness of the model. Finally, in
Section 5, we summarise the findings of this work.
2. Dynamics of Intra-Urban Migration
We consider an urban area as a set of N suburbs i with a certain residential population at time t. The total population at any time is fixed: . We assume that time is discrete, and the choice of the time step is dictated by the resolution of the available data. A migration flow is defined as a change in residential location from suburb i to suburb j. This flow is uni-directional, so that, in general, , and the net flow . Non-zero net flow indicates that the system is out of equilibrium. In a diffusive system, the net flow gradually decays to zero with time as the system evolves towards an equilibrium. Such an equilibrium state is stationary on the “macroscopic” level, showing no change in the population of each suburb. However, on the “microscopic” level, there still exists some movement of people, resulting in non-zero uni-directional flows . In an equilibrium, these uni-directional flows satisfy a microscopic detailed balance, so that , resulting in zero net flow between each pair of suburbs.
The uni-directional flow matrix allows one to predict the future population of any suburb. In particular, the population at the next time step
can be expressed through the migration flow
at the current time step
t as
, where the sum includes the term
accounting for immobile population. Introducing the fraction of relocated people as
, we can write the population evolution equation as
where
X is the (row) vector of the suburbs’ population and
P is the relocation matrix denoting the fractions of relocating people between each pair of suburbs, with the diagonal elements
denoting the fraction of non-relocating residents. The column sum for each row of the relocation matrix is equal to
, so
P is a row-stochastic matrix [
44].
The population evolution Equation (
1) represents a simple Markov process, converging to a distinct stationary state
, which we identify as the equilibrium state. In equilibrium, the population of each suburb
does not change in time, such that
where
. We assume that the urban area is a closed system with no external shocks and, thus, the relocation matrix does not change in time, i.e.,
. Since matrix
P is row-stochastic, it has a unit eigenvalue [
44], and the vector
can be found as a left eigenvector of matrix
P that corresponds to the unit eigenvalue. This eigenvector is unique (up to a constant multiplier) if some power of matrix
P has strictly positive elements [
44].
Our next step is to explicitly represent the relocation dynamics in both spatial and temporal terms. We decompose the relocation matrix according to the following structure:
where
is the share of people who relocate to a different suburb within a period of time. Such a decomposition is known as the mover–stayer model [
45], which has been used to describe relocation phenomena in biology, economics, and social sciences [
46,
47,
48,
49].
Here, matrix H shows the relocation structure of those residents who moved to a different suburb (i.e., have not stayed in the same suburb). The matrix H shows the spatial structure of the system and characterises the variation in microscopic “attractiveness” between different suburbs. Without loss of generality, we assume that . Furthermore, the coefficient can be alternatively written as , where is the characteristic relocation time. We will refer to it as the relocation frequency or the population mobility.
We next extend the simple decomposition (
3), so that the population mobility has a more complex structure than a single frequency
. Without loss of generality, we assume that the relocation dynamics are governed by a discrete set of relocation frequencies
, where
. In the context of the population structure, this would suggest that the urban population comprises several distinct groups, which differ in their mobility. There may exist a number of classifications that differentiate population groups by their mobility, based on their ownership status (renters and home-owners), family status (singles and families), and employment status (students, professionals, retirees). In this work, we abstract away from the specific nature of these groups, assuming only their existence.
Expanding the structure of the population mobility does not affect the spatial structure of the relocation, i.e., the matrix
H. We therefore assume that the spatial structure of the relocation dynamics is the same for each population group. Although this is, in principle, a strong condition, we show in
Section 4.3 that it does not affect the results in practice.
The equilibrium population of each component is obtained similarly to Equation (
2), as
We show in
Appendix A.1 that the population of each component
converges to the equilibrium population structure
where
is the total fraction of the city population belonging to the component
k, so that
and
is the total equilibrium population structure that is independent of
and
. This is also illustrated in
Figure A1. Thus, the total equilibrium
can be obtained using the full spatial matrix
H, without the component-specific relocation matrices
or even the component’s fractions
. This is very convenient, as the component structure of the population is not known a priori, and in practice, it is only matrix
H that can be obtained from the data directly.
4. Robustness Evaluation
In the previous section, we showed that our non-equilibrium framework of diffusive intra-urban relaxation explains the short-term migration data and is able to provide long-term predictions. The important element of the model is the assumption that the population comprises multiple components with different relocation frequencies, which, in the context of our framework, correspond to different relaxation rates. In this section, we investigate the robustness of this claim, analysing the extent of its applicability. In particular, in
Section 4.2, we study the two-component model, arguing that this case is sufficient to consistently describe the short-term migration. In
Section 4.3 and
Section 4.4, we explore the sensitivity of the equilibrium configuration to the spatial migration patterns (captured by matrix
H), varying between different population components. In
Section 4.3, we do this for an abstract city with extreme migration patterns, while in
Section 4.4, we extend this analysis to a specific case (Sydney).
4.1. Heterogeneity of the Population
In
Section 3.1, we reported that the baseline one-component model systematically predicts higher rates of five-year migration than those observed in reality. Here, we show that having a homogeneous population mobility can not produce consistent migration predictions; hence, the population has to be heterogeneous with respect to its mobility. The population, which is comprised of two groups with two distinct relocation frequencies, is a minimal realisation of such heterogeneity.
One may expect that the five-year relocation rate observed in reality is lower than the one predicted from the one-year relocation rate due to the low mobility of recently relocated people. Indeed, if an individual has recently moved into a new home, there might be not much incentive for them to move further relatively quickly. To represent this constraint, we assume that people do not relocate for
years after their last relocation (immobility assumption), and calculate the share of those who have not relocated for different values of this parameter,
.
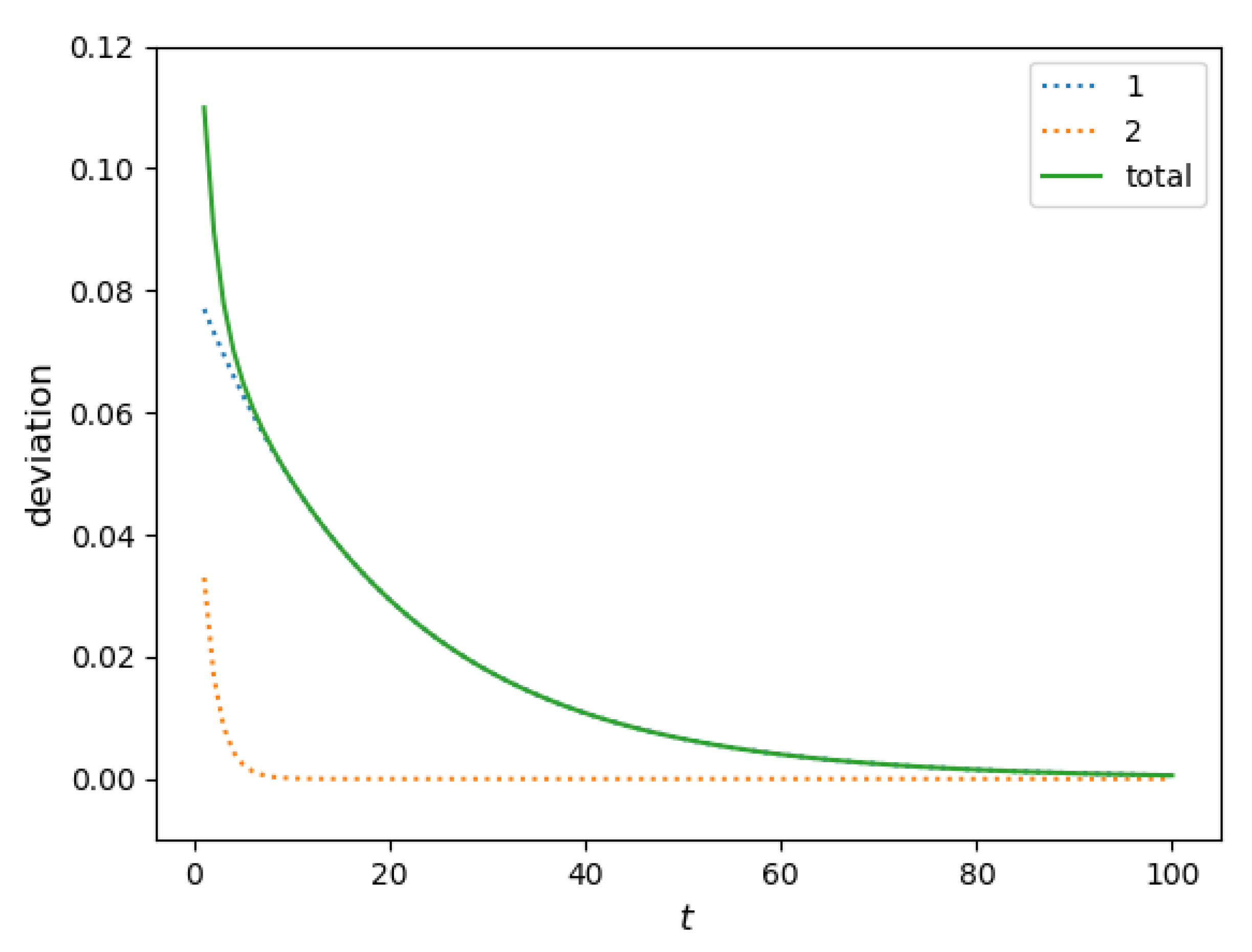
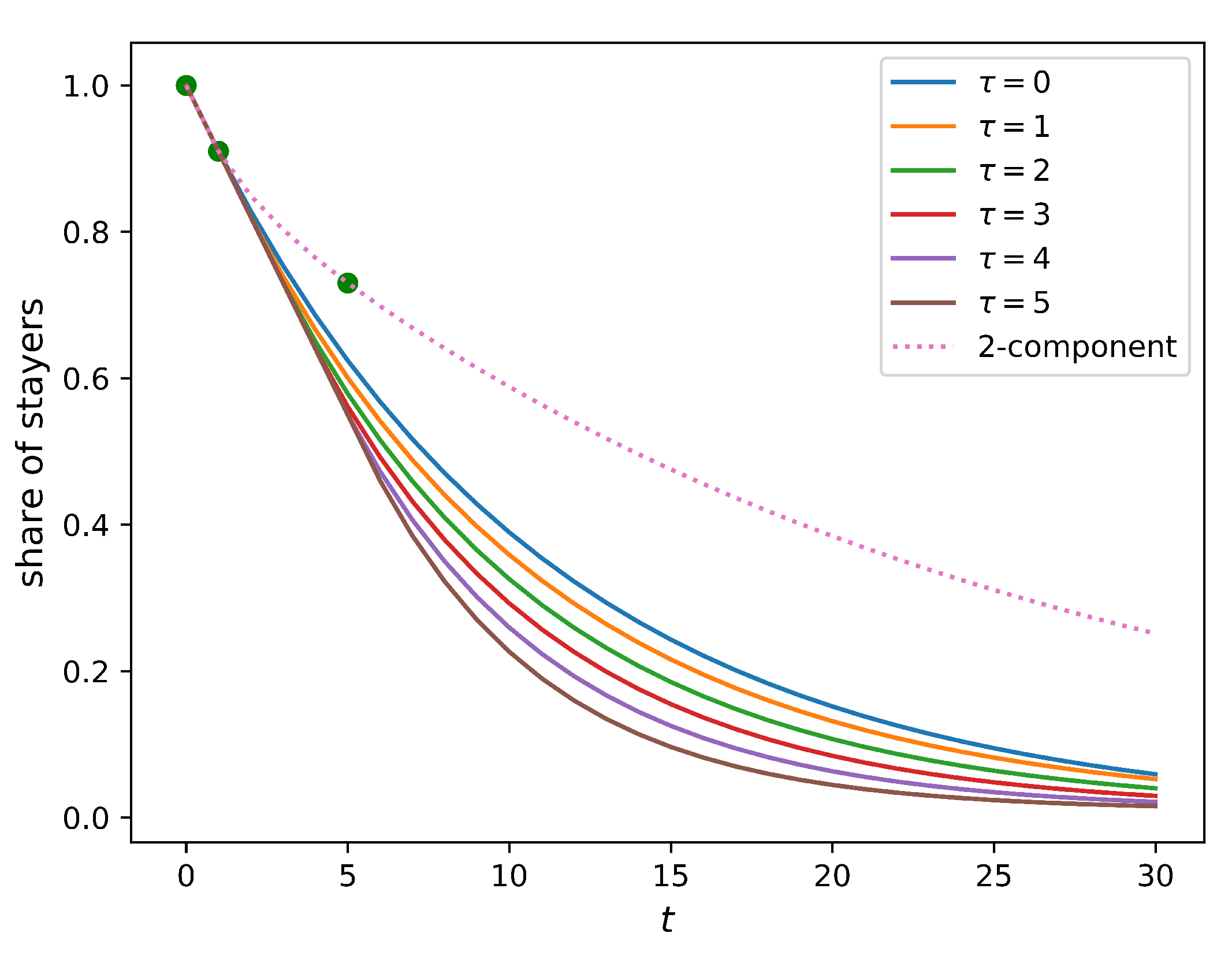
Figure 4 compares how this share changes in time for homogeneous populations (full solution of this model is provided in
Appendix A.3) and a two-component population without an immobility assumption. It is evident from the figure that the immobility assumption does not improve the model. Indeed, no value of the immobility period
can match the five-year relocation flow. In such a setting, the presence of the residents that do not relocate within a certain period implies a higher relocation frequency for those who do. As a result, the five-year relocation rate predicted by the homogeneous model with the immobility assumption is higher than that produced by the simple homogeneous model (the baseline model), leading to an outcome opposite to the one that was expected.
This analysis shows that a lower mobility of the recently relocated people cannot be a valid explanation for the lower actual five-year relocation rate. Therefore, we conclude that having a homogeneous population comprised of only one component is not sufficient to make the model consistent with the data.
4.2. Solution Space of the Two-Component Model
In
Section 3.1, we calculated
and
using the average shares of stayers within a one-year period (
), within a five-year period (
), and with conditions (
8). The values of
and
depend on
, which is not known without specifying the nature of the groups. This, however, does not affect the possibility of splitting the population into two groups and obtaining consistent predictions of the five-year migration patterns from the one-year migration patterns.
The non-linear system of algebraic Equation (
8) allows one to calculate the relocation frequencies
and
for a given composition
. It consists of two equations while containing three unknown variables (
,
, and
), and for a given
, it can have up to five real roots. Some of the roots may not belong to the range from 0 to 1 and, therefore, cannot be valid solutions for
and
.
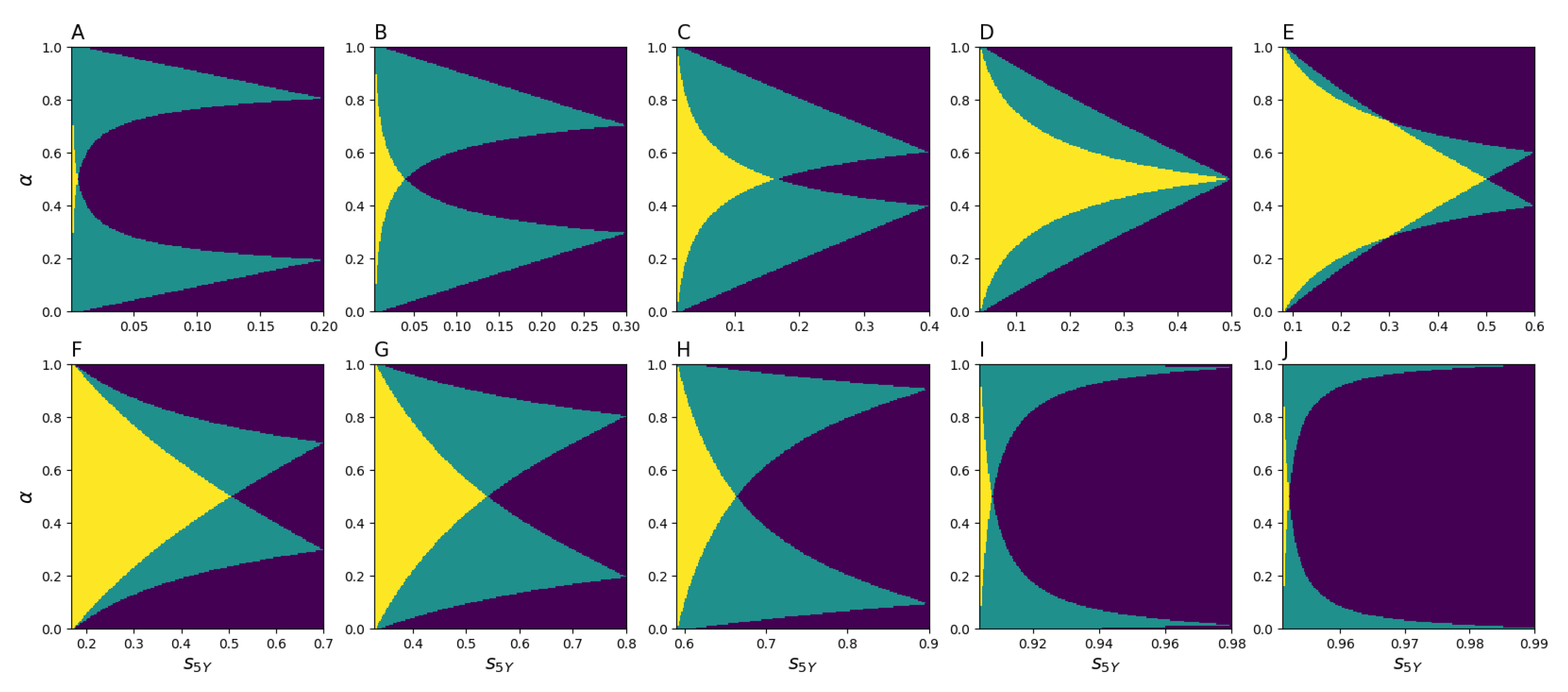
Figure 5 demonstrates that, depending on
,
, and
, there exist two, one, or zero solutions. Furthermore, it is evident from
Figure 5 that, for any
ranging from
to
, there exists at least one solution for the pair
and
. This means that it is always possible to calibrate the model (
8) as long as
(the other inequality,
, holds automatically), which is the case for the actual migration data.
Although it is not feasible to estimate
directly from the current data set, it would be possible to do so with a longer record of internal migration. In particular, if we also knew people’s places of residence 10 years ago, 15 years ago, etc., we would be able to determine the value of
, which predicts the share of movers and stayers with a higher precision. This idea is illustrated in
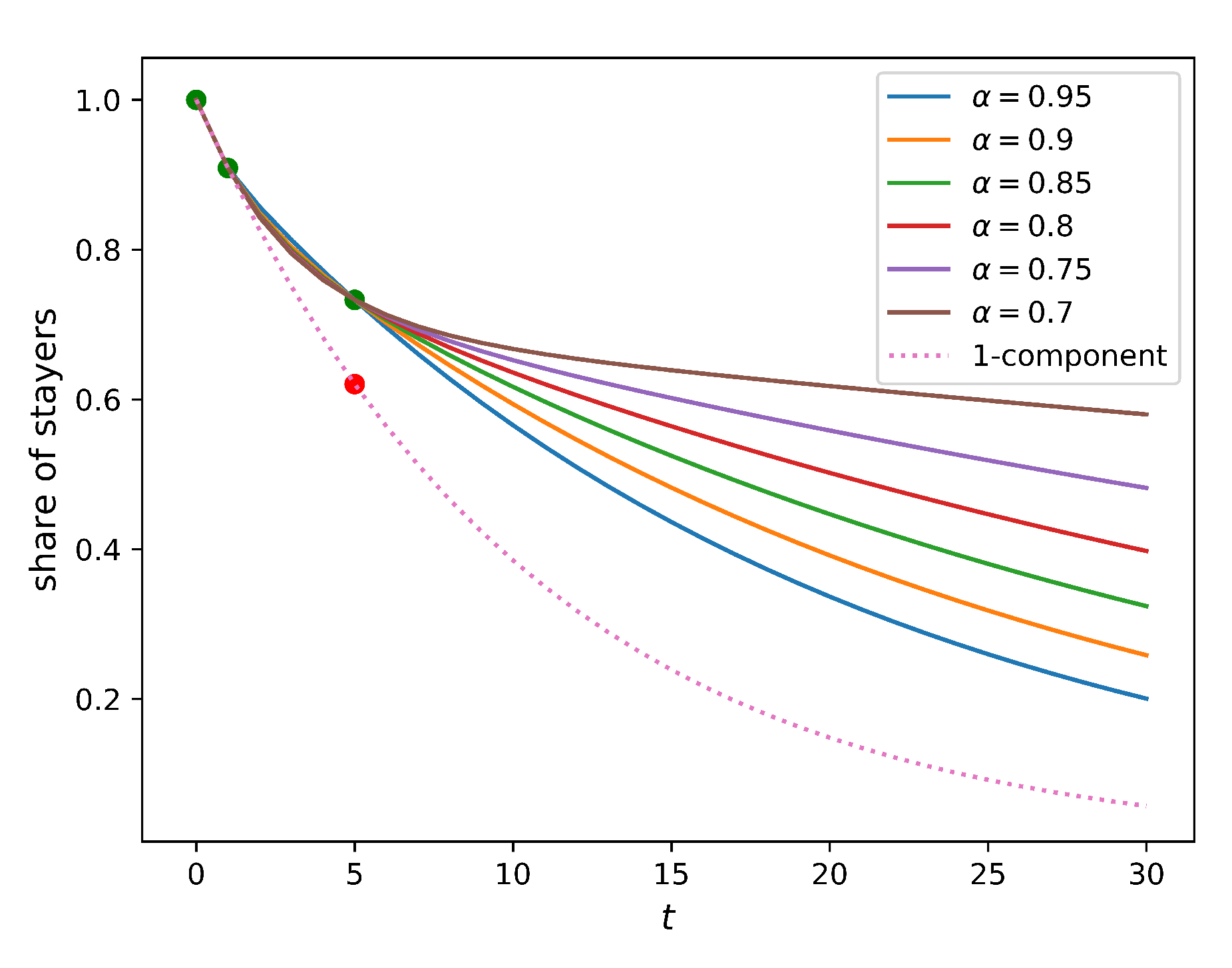
Figure 6, which demonstrates the stayer share values predicted by the two-component model. Parameters
and
are calibrated to
and
(Sydney values are used as an example). The values of
vary from 0.7 to 0.95 (the solution of (
8) exists and is unique if
and
, but the solutions for
and
are equivalent due to symmetry). For the 30-year horizon, the predictions for the share vary from 0.2 (if
) to 0.6 (if
). This means that the two-component model can consistently calibrate a larger variety of data than the one-component model. If, however, the actual structure of the population is more complex, e.g., is made of a larger number of components, the two-component model would not be able to adequately account for the corresponding data.
4.3. Component-Specific Relocation Matrix
As has been shown previously, heterogeneity in mobility rates
does not affect the equilibrium structure of the city as long as all groups have the same relocation matrix
H. This assumption, however, may not be valid if we do not observe
H for each group directly. This might be important, as there exists empirical evidence that different social groups (such as renters and mortgagors) have different migration patterns [
27]. Thus, it is important to assess the possibility for the matrices
to be component-specific, or in other words, heterogeneous.
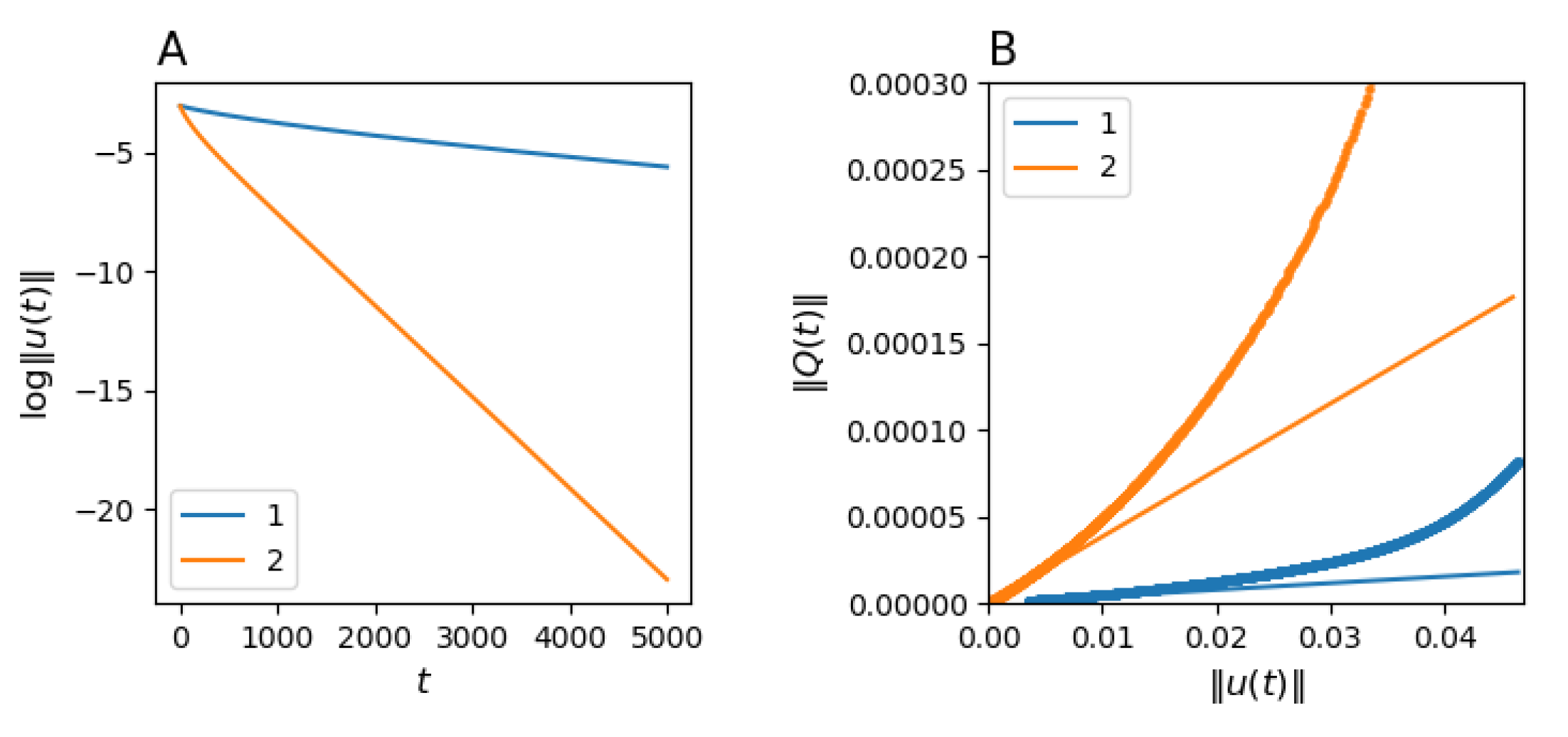
If matrices are heterogeneous, the equilibrium population structure is no longer independent of the compositions and relocation rates . In particular, matrices may have different stationary vectors , in which case it is impossible to estimate the stationary population structure unless matrices are observed directly. The equilibrium structure depends on the individual matrices and cannot be expressed via the aggregated relocation matrix .
In this section, we show that the structure calculated using the aggregated matrix can still give a reasonable approximation for the stationary population structure , even if the individual vectors differ drastically. To demonstrate this, we consider two artificial examples. In the first example, the population components 1 and 2 generate the migration flows with opposite directions. In the second example, there are two groups of suburbs (A and B), and the members of component 1 always relocate to the suburbs within A, while the members of component 2 always relocate to suburbs within B. These two examples are considered for a linear toy city comprising 99 suburbs. All suburbs are located along a line, such that suburb 50 is the “central” one.
In the first example, matrix
consists of elements
given by:
where
is the distance from
i to the “central” suburb (suburb 50),
. Elements of
are defined as follows:
This form of
and
means that the members of component 1 prefer to relocate to more central suburbs (that are close to suburb 50), while the members of component 2 relocate to the peripheral suburbs (which are far from suburb 50) more frequently. The equilibrium population distributions
and
are displayed in
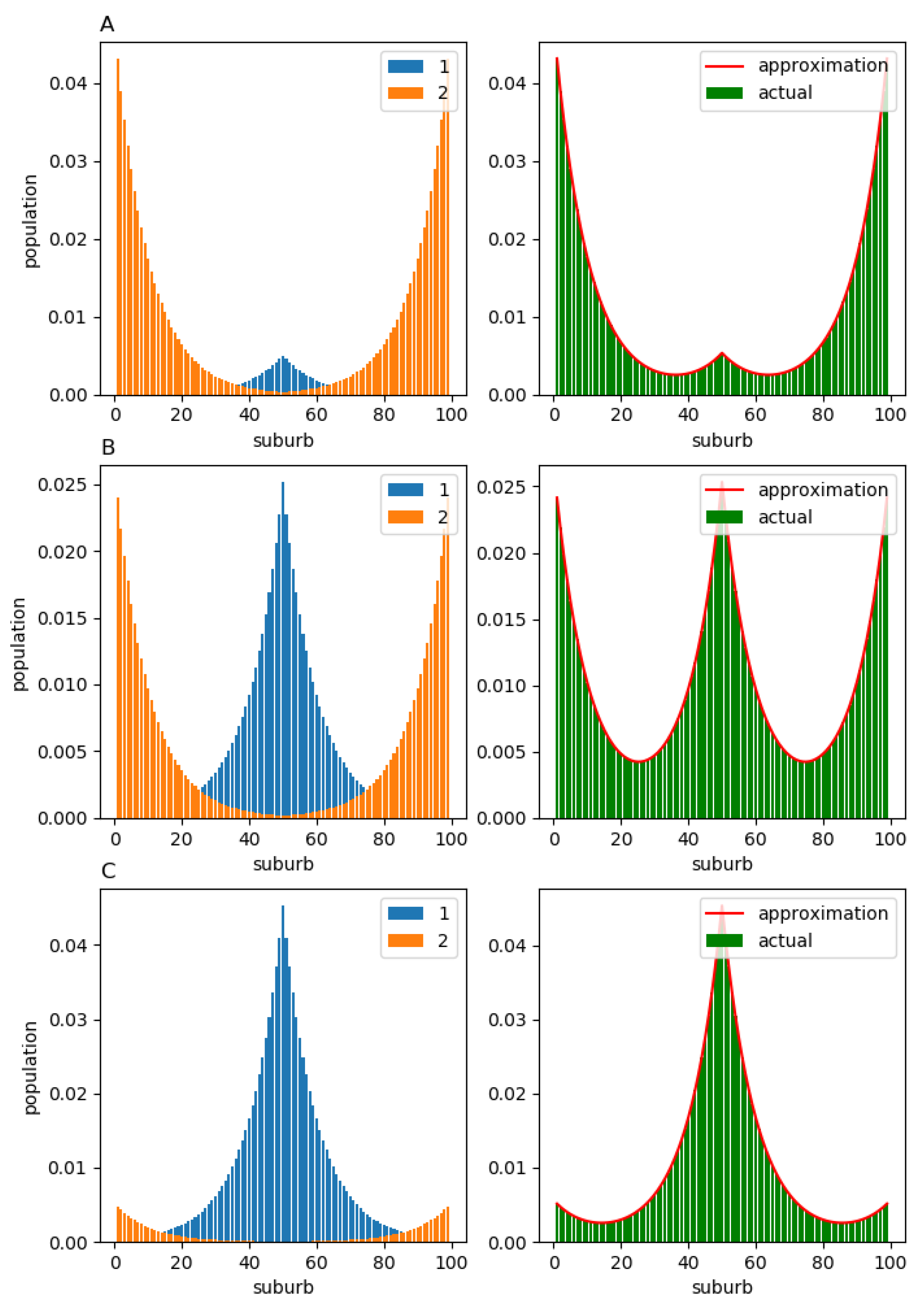
Figure 7 (left column). As one might have anticipated, the population of component 1 forms a monocentric structure around the “central” suburb, while the population of component 2 predominantly inhabits the peripheral suburbs. The corresponding total population structure
and its approximation
obtained from matrix
are shown in the right column. In all three cases, (A)
, (B)
, and (C)
, the actual population structures
(green bars) lie very close to the corresponding approximations
(red solid line).
In the second example, we fill columns 26–74 of matrix with positive random numbers, and the other columns are filled with zeros. In contrast, to fill matrix , we assign zero values to columns 26–74 and positive random numbers to columns 1–25 and 75–99. Each row in both matrices is normalised so that its elements sum to one.
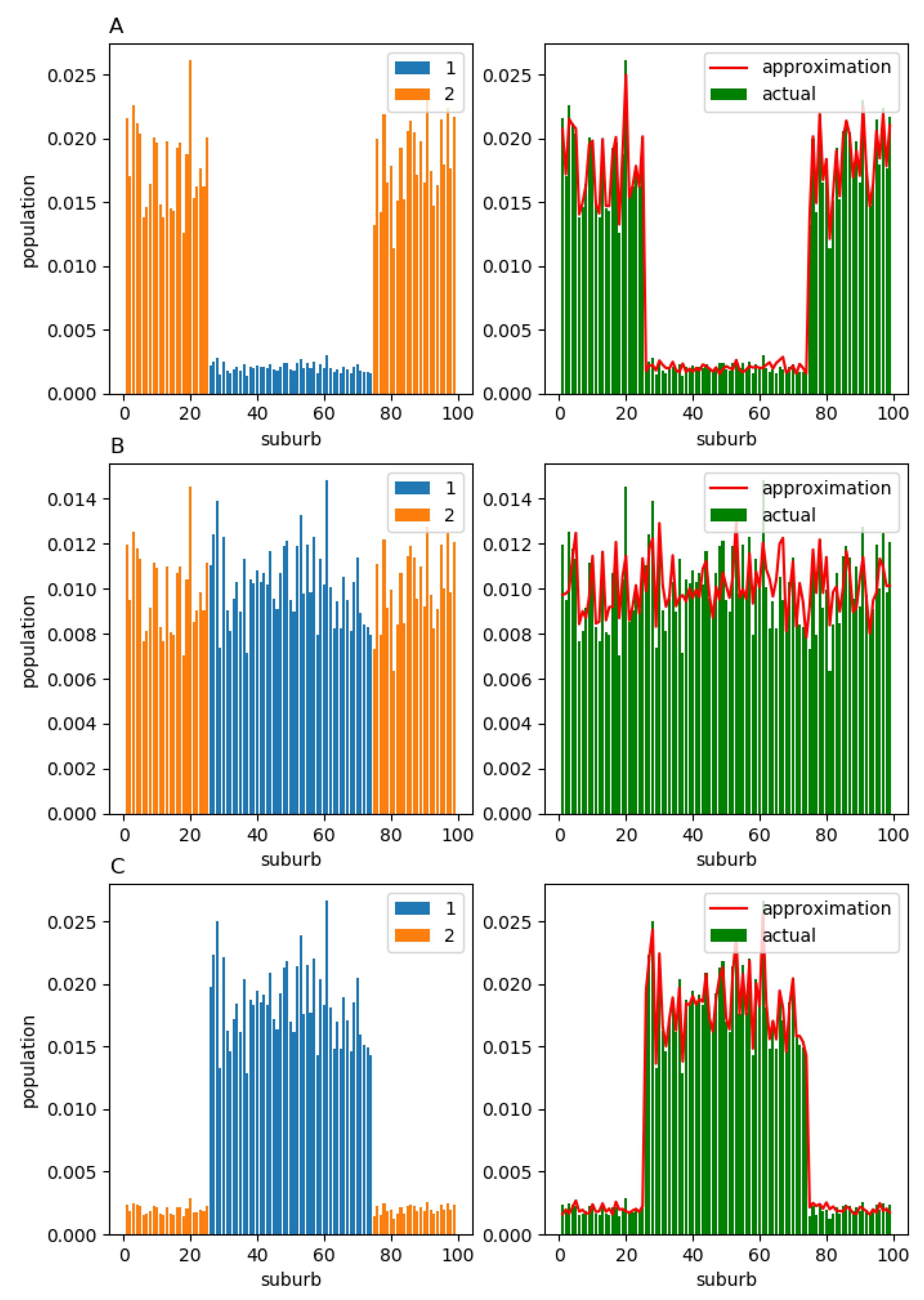
It is natural to anticipate that, in the equilibrium, all members of component 2 will live in suburbs 26–74, while the members of component 1 will live in suburbs 1–25 and 75–99 (left column in
Figure 8; cases A, B, and C correspond to
, respectively). In the right column of
Figure 8, we again observe that, regardless of
, the actual equilibrium structure
(green bars) does not deviate significantly from its approximation
(red solid line).
4.4. Sydney Case Study
To demonstrate the robustness of the results presented in
Section 3.3 with respect to the heterogeneity of relocation patterns, we extend this analysis to the Greater Sydney Capital Area. In a real city, the migration matrices
and
are not normally observed separately. Moreover, these matrices cannot be assigned arbitrarily, as they need to be consistent with the actual migration data. In particular, following the procedure suggested in
Section 4.3, the component-specific matrices have to be defined such that
, with
accounting for the relocations flowing primarily into central districts, and
corresponding to the relocations flowing primarily into the peripheral areas.
To accomplish this task, we choose a distance threshold
, and select suburb groups
and
so that
contains only suburbs with the distance to the central business district being less than
, while
contains the rest of the suburbs. Next, we assume that when relocating, the members of component 1 almost always choose suburbs from set
, while group 2 members choose suburbs from set
. Finally, we calibrate
and
to actual relocation data denoting
in each row
i, and define elements
of
as follows:
if
, and
if
. The elements of
are then given by:
In other words, all members of the first component move to areas inside and all members of the second component move to areas inside , but the total share of people from i who move to suburbs inside might differ from . If , we assume that all the people who relocate from i to belong to the first component, and so does the proportion of the people migrating to the other suburbs, while the rest of i’s residents belong to the second component. Conversely, if , we assume that only the proportion of those who relocate to belong to the first component, while others belong to the second component.
It is easy to see that, in that case,
, and that all elements
and
are positive; in each row
i, we have
and
, which is required by construction. The resulting equilibrium structure of the population density is shown in
Figure 9 for
,
km (median distance to the central business district). Similarly to the previous examples, the approximated
(
Figure 9D) does not differ significantly from the actual value
(
Figure 9C), although
and
do differ drastically (
Figure 9A,B).
From these examples, we can conclude that the heterogeneity in matrices has a limited effect on the long-term population structure, and it is possible to obtain an accurate prediction by using only the aggregate relocation matrix .
5. Conclusions
We have introduced a diffusive migration framework that describes intra-urban migration as an irreversible evolution of the urban population. The results have been tested with residential relocation data available from the Australian Census for eight Greater Capital areas over 10 years.
Using this framework, we were able to explain the medium-term (five years) migration patterns using the short-term (one year) migration patterns. We have shown that this is possible to achieve only if the population is not homogeneous and has an internal structure. In particular, such a population should be comprised of at least two components, with each component having a distinct relocation frequency. Such a relocation frequency corresponds to a particular relaxation time of the component.
This heterogeneity of migration frequencies has an intuitive interpretation. For example, the group of residents that migrate more often can be interpreted as renters (who are less attached to their places of residence, and are relatively free to change them as soon as they identify a better option), and the other group could be interpreted as homeowners (for whom it may be more problematic to change the place of residence due to the transaction costs, peculiarities of the housing market, and individual circumstances).
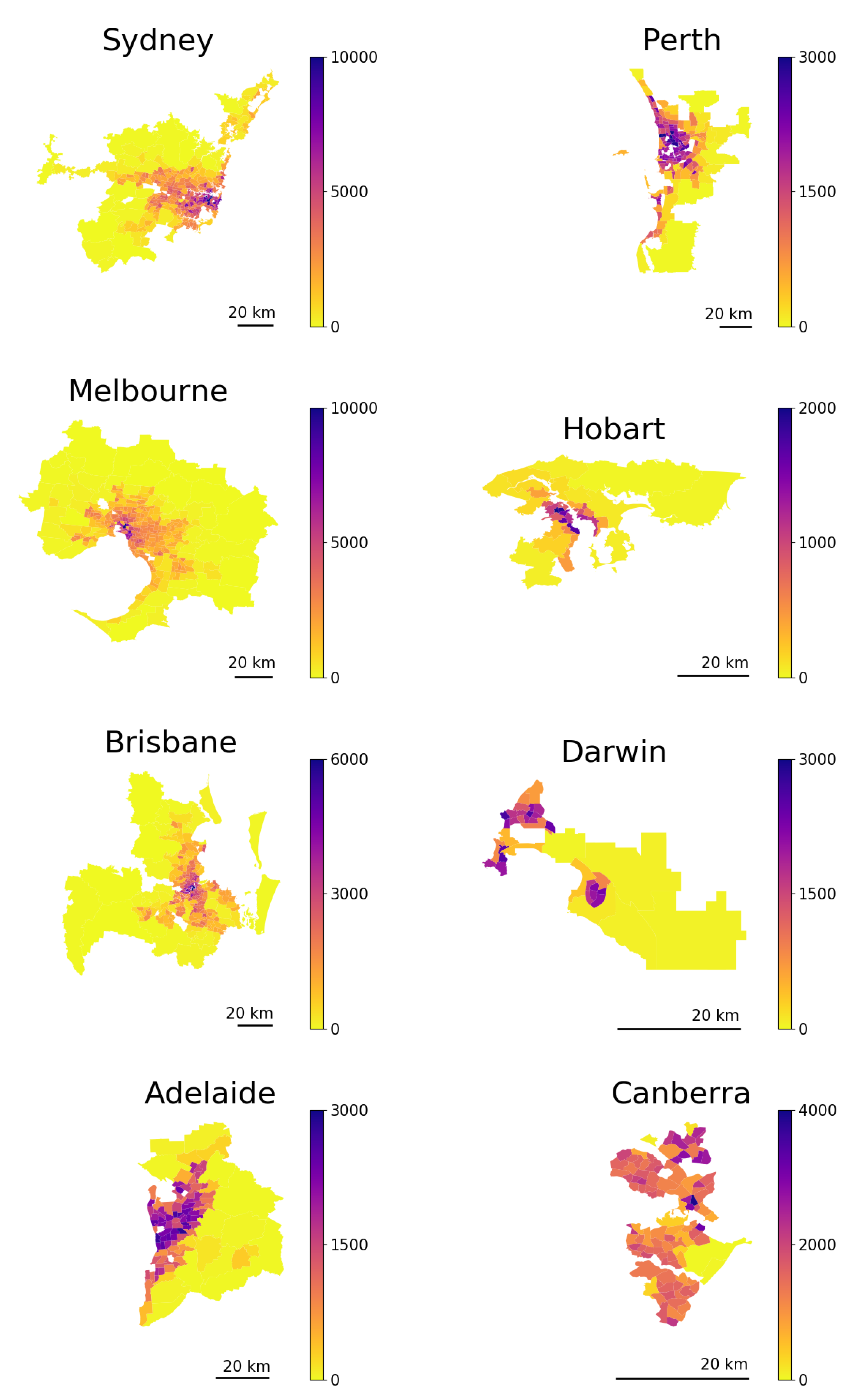
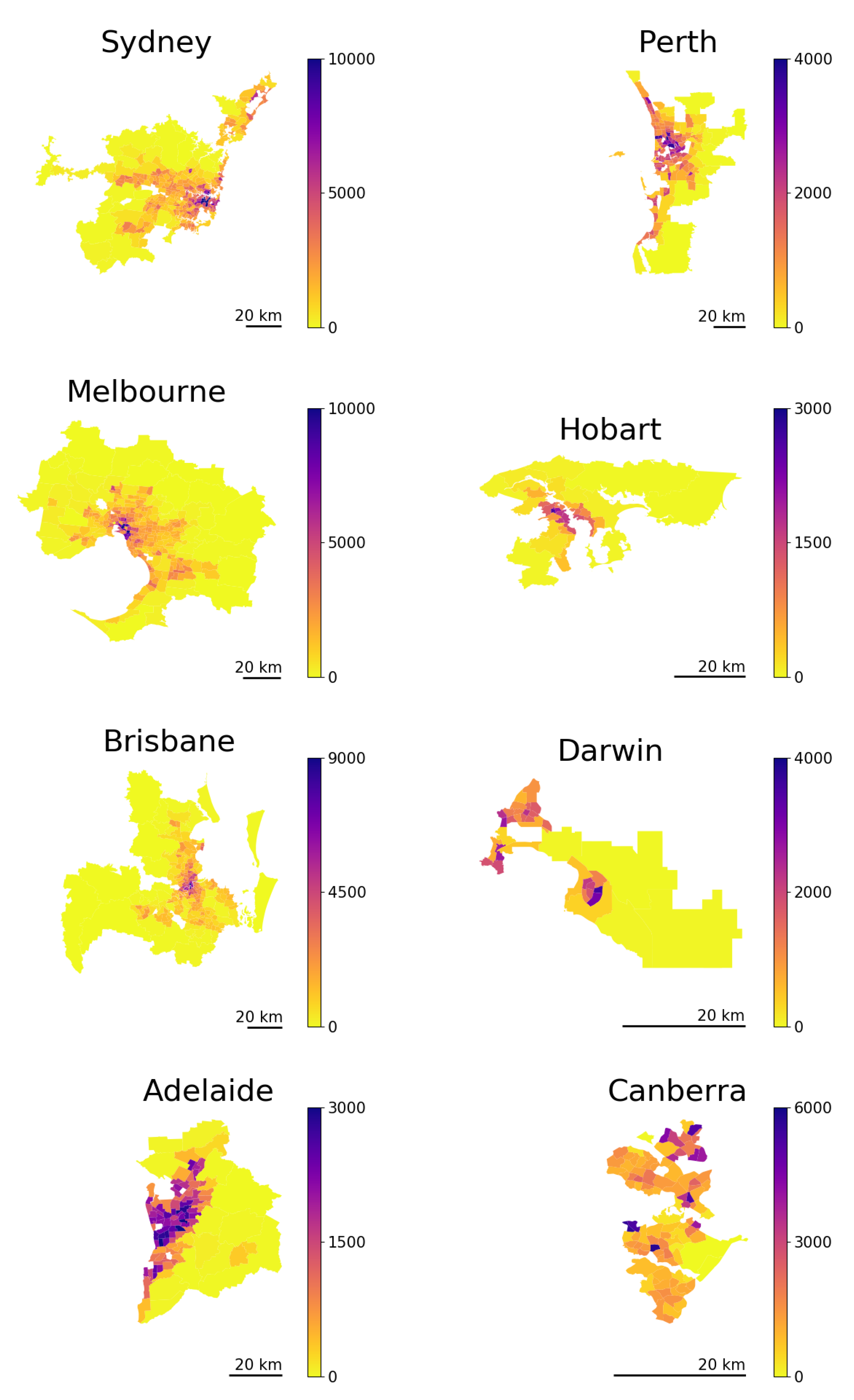
Using this diffusive migration framework, we produced a long-term prediction for the Australian capital cities’ structures based on the short-term migration data, with only an assumption about the temporal stability of the migration rates. According to our predictions, the largest capital cities (Sydney, Melbourne, and Perth) are moving towards more spread-out configurations, while Hobart and Canberra exhibit a more compact structure in equilibrium. The other capitals, Brisbane, Adelaide, and Darwin, are likely to preserve their current configurations in the long run. These results are consistent with those of previous studies predicting the possibility of polycentric transition in Sydney and Melbourne [
19,
27].
Our predictions are robust with respect to the composition of the migration components, as well as the possible heterogeneity of their relocation patterns, both dynamically and spatially. In particular, we have analytically shown that the long-run equilibrium is independent of the size of each community and their relocation rates. The robustness with respect to the spatial heterogeneity of relocation has been shown numerically through an abstract illustrative example. In this example, the relocation communities have opposite preferences regarding their destinations: Members of the first group prefer central districts, while their counterparts prefer the peripheral ones.
The temporal stability of the migration flows is a crucial element of our long-term analysis. Despite being consistent within the period of observation (2006–2016), they may be affected by multiple factors in future: Human migration is a complicated non-linear process involving multiple interdependent factors, often leading to various phase transitions and critical phenomena [
19,
20,
22,
27,
43,
56,
57]. However, the relocation data may contain some unique features that are not captured in other static human mobility and land-use data (e.g., [
13,
19,
24,
27,
58]). Thus, we believe that the proposed dynamic framework for intra-urban migration, which enables robust long-term predictions, offers a principled approach to modelling out-of-equilibrium urban development.