ML-Based Analysis of Particle Distributions in High-Intensity Laser Experiments: Role of Binning Strategy
Abstract
1. Introduction
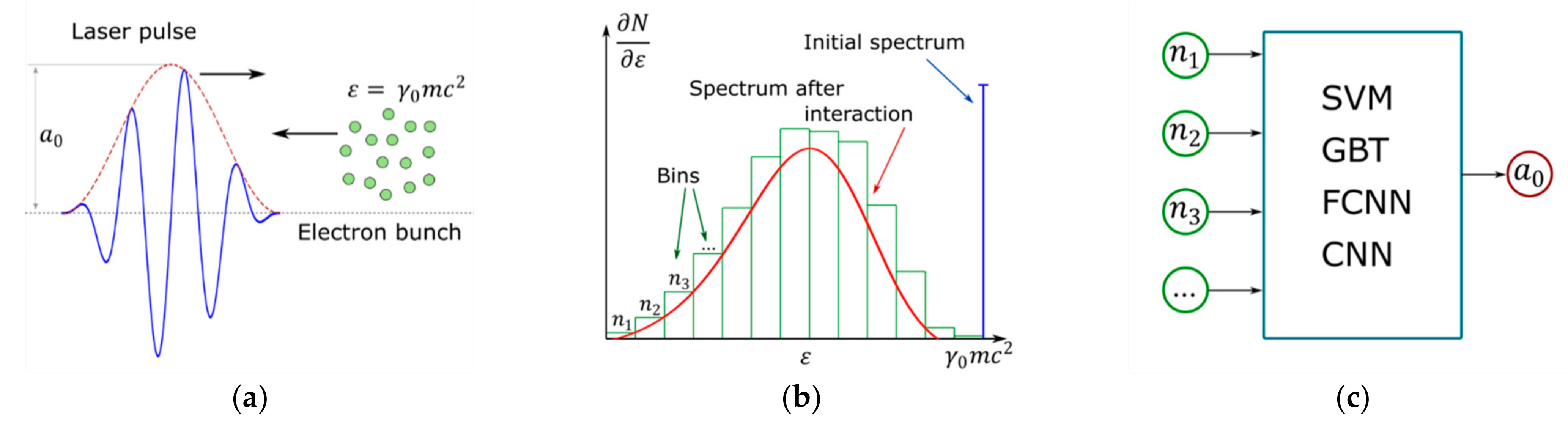
2. Problem Statement
3. Methods
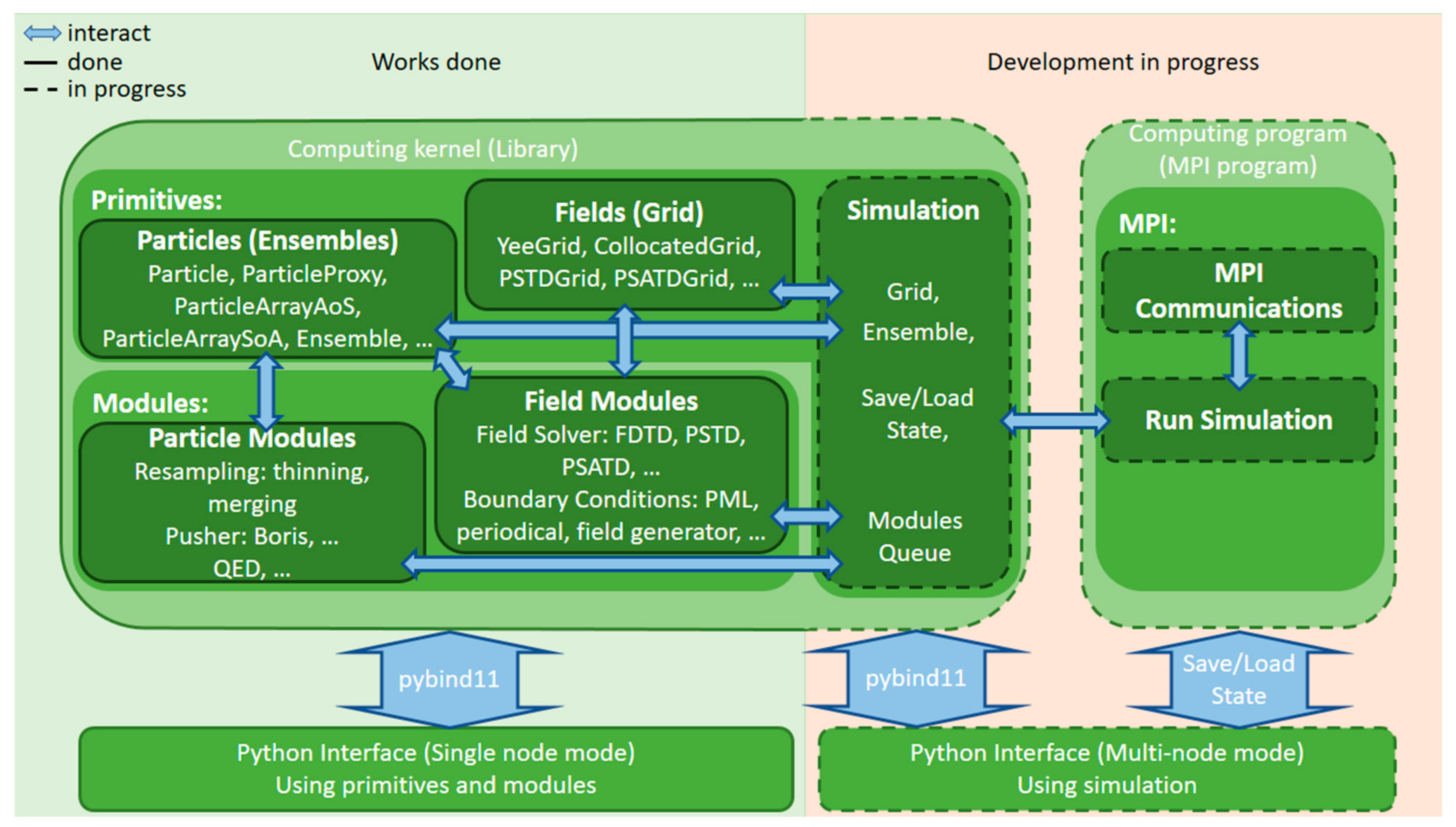
3.1. Hi-Chi Project Overview
3.2. Data Generation
3.3. Machine Learning Techniques
4. Experimental Results
4.1. Methodology
4.2. Results and Discussion
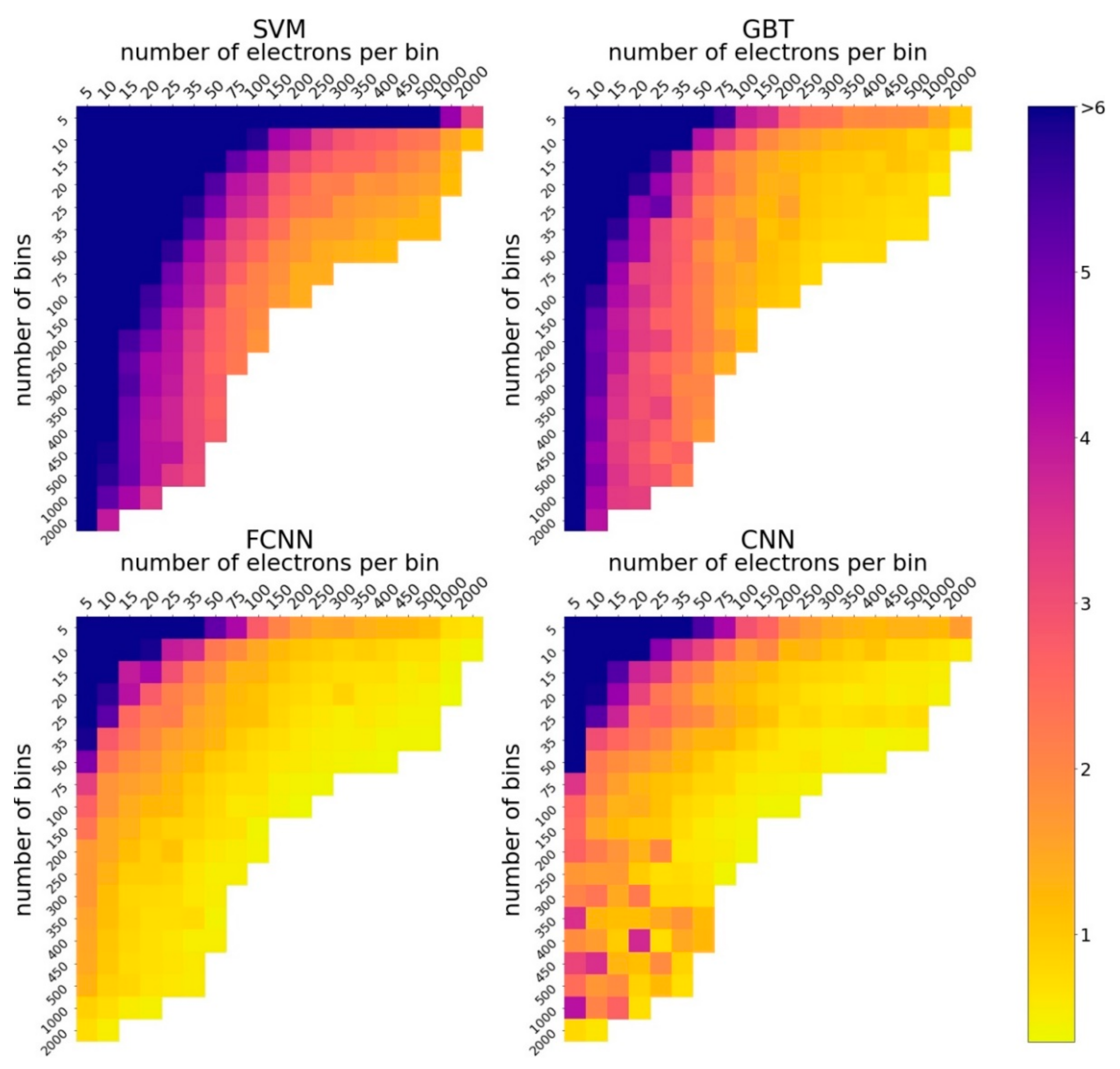
4.2.1. How Accuracy of ML Models Depends on the Number of Bins and the Number of Electrons per Bin?
4.2.2. Optimal Configuration of the Parameters
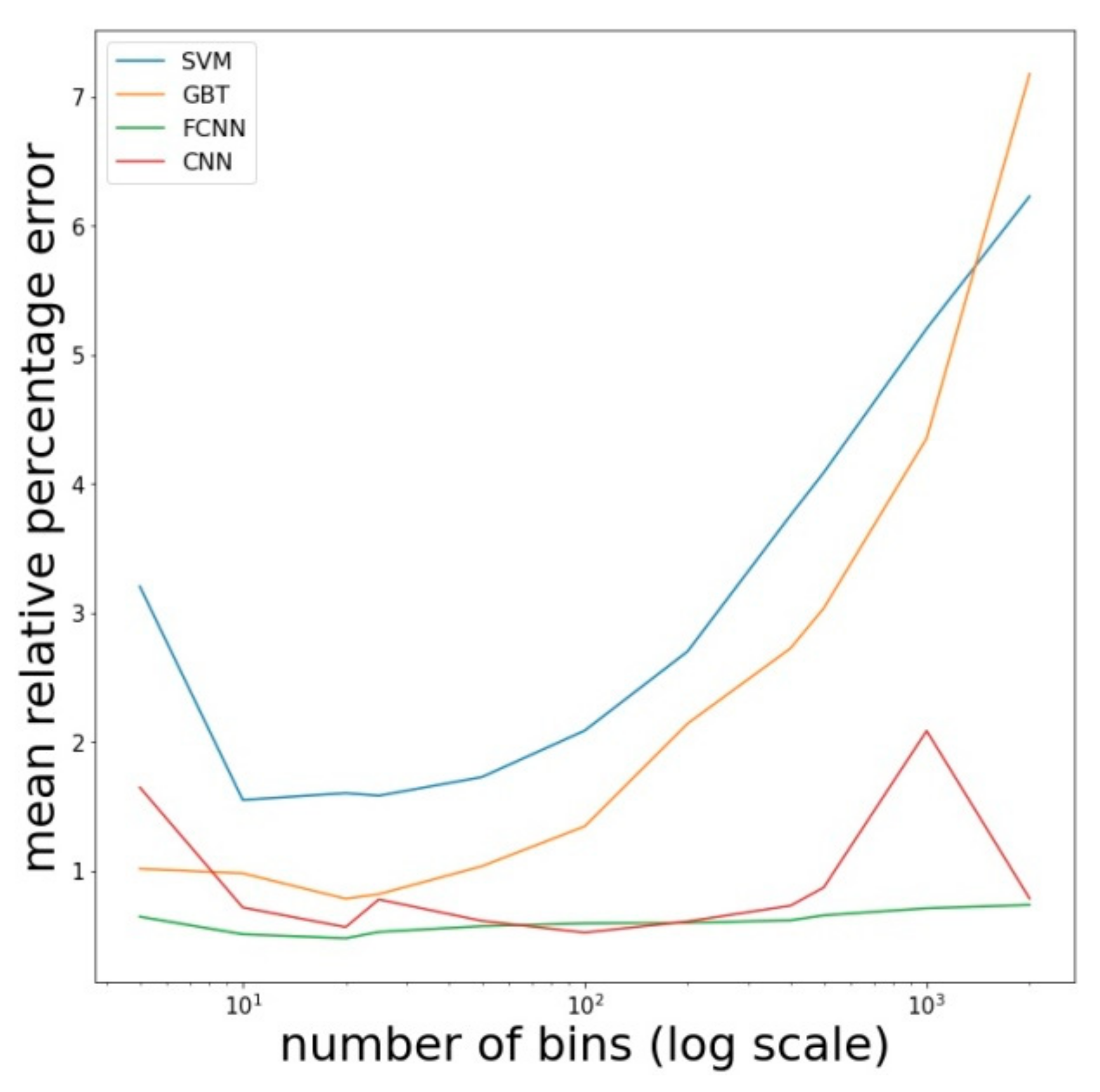
4.2.3. Final Comparison
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mehta, P.; Bukov, M.; Wang, C.H.; Day, A.G.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to machine learning for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Cirac, I.; Cranmer, K.; Daudet, L.; Schuld, M.; Tishby, N.; Vogt-Maranto, L.; Zdeborová, L. Machine learning and the physical sciences. Rev. Mod. Phys. 2019, 91, 045002. [Google Scholar] [CrossRef]
- Gonoskov, A.; Wallin, E.; Polovinkin, A.; Meyerov, I. Employing machine learning for theory validation and identification of experimental conditions in laser-plasma physics. Sci. Rep. 2019, 9, 7043. [Google Scholar] [CrossRef] [PubMed]
- Rubin, D.B. Bayesianly justifiable and relevant frequency calculations for the applies statistician. Ann. Stat. 1984, 12, 1151–1172. [Google Scholar] [CrossRef]
- Beaumont, M.A.; Zhang, W.; Balding, D.J. Approximate Bayesian computation in population genetics. Genetics 2002, 162, 2025–2035. [Google Scholar] [PubMed]
- Marjoram, P.; Molitor, J.; Plagnol, V.; Tavaré, S. Markov chain Monte Carlo without likelihoods. Proc. Natl. Acad. Sci. USA 2003, 100, 15324–15328. [Google Scholar] [CrossRef] [PubMed]
- Sisson, S.A.; Fan, Y.; Beaumont, M. Handbook of Approximate Bayesian Computation; Sisson, S.A., Fan, Y., Beaumont, M.A., Eds.; CRC Press: Boca-Raton, FL, USA, 2019. [Google Scholar]
- Alsing, J.; Wandelt, B.; Feeney, S. Massive optimal data compression and density estimation for scalable, likelihood-free inference in cosmology. MNRAS 2018, 477, 2874–2885. [Google Scholar] [CrossRef]
- Charnock, T.; Lavaux, G.; Wandelt, B.D. Automatic physical inference with information maximizing neural networks. Phys. Rev. D 2018, 97, 083004. [Google Scholar] [CrossRef]
- di Piazza, A.; Müller, C.; Hatsagortsyan, K.Z.; Keitel, C.H. Extremely high-intensity laser interactions with fundamental quantum systems. Rev. Mod. Phys. 2012, 84, 1177. [Google Scholar] [CrossRef]
- Cole, J.M.; Behm, K.T.; Gerstmayr, E.; Blackburn, T.G.; Wood, J.C.; Baird, C.D.; Duff, M.J.; Harvey, C.; Ilderton, A.; Joglekar, A.S.; et al. Experimental evidence of radiation reaction in the collision of a high-intensity laser pulse with a laser-wakefield accelerated electron beam. Phys. Rev. X 2018, 8, 011020. [Google Scholar] [CrossRef]
- Poder, K.; Tamburini, M.; Sarri, G.; di Piazza, A.; Kuschel, S.; Baird, C.D.; Behm, K.; Bohlen, S.; Cole, J.M.; Corvan, D.J.; et al. Experimental signatures of the quantum nature of radiation reaction in the field of an ultraintense laser. Phys. Rev. X 2018, 8, 031004. [Google Scholar] [CrossRef]
- Harvey, C.N.; Gonoskov, A.; Ilderton, A.; Marklund, M. Quantum quenching of radiation losses in short laser pulses. Phys. Rev. Lett. 2017, 118, 105004. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Lee, M.; Lee, H.J. Machine learning analysis for the soliton formation in resonant nonlinear three-wave interactions. J. Korean Phys. Soc. 2019, 75, 909–916. [Google Scholar] [CrossRef]
- Gonoskov, A.; Bastrakov, S.; Efimenko, E.; Ilderton, A.; Marklund, M.; Meyerov, I.; Muraviev, A.; Sergeev, A.; Surmin, I.; Wallin, E. Extended particle-in-cell schemes for physics in ultrastrong laser fields: Review and developments. Phys. Rev. E 2015, 92, 023305. [Google Scholar] [CrossRef] [PubMed]
- Arran, C.; Cole, J.M.; Gerstmayr, E.; Blackburn, T.G.; Mangles, S.P.D.; Ridgers, C.P. Optimal parameters for radiation reaction experiments. Plasma Phys. Control. Fusion 2019, 61, 074009. [Google Scholar] [CrossRef]
- Hi-Chi Project. Available online: https://github.com/hi-chi/pyHiChi (accessed on 5 December 2020).
- Taflove, A.; Hagness, S.C. Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed.; Artech house: Boston, MA, USA, 2005. [Google Scholar]
- Liu, Q.H. The PSTD algorithm: A time-domain method requiring only two cells per wavelength. Microw. Opt. Technol. Lett. 1997, 15, 158–165. [Google Scholar] [CrossRef]
- Haber, I.; Lee, R.; Klein, H.; Boris, J. Advances in electromagnetic simulation techniques. In Proceedings of the Sixth Conference on Numerical Simulation of Plasmas, Berkeley, CA, USA, 16–18 July 1973; pp. 46–48. [Google Scholar]
- Vay, J.L.; Haber, I.; Godfrey, B.B. A domain decomposition method for pseudo-spectral electromagnetic simulations of plasmas. J. Comput. Phys. 2013, 243, 260–268. [Google Scholar] [CrossRef]
- Lehé, R.; Vay, J.L. Review of spectral maxwell solvers for electromagnetic particle-in-cell: Algorithms and advantages. In Proceedings of the 13th International Computational Accelerator Physics Conference, Key West, FL, USA, 20–24 October 2018; pp. 345–349. [Google Scholar]
- Muraviev, A.; Bashinov, A.; Efimenko, E.; Volokitin, V.; Meyerov, I.; Gonoskov, A. Strategies for particle resampling in PIC simulations. arXiv 2020, arXiv:2006.08593. [Google Scholar]
- Surmin, I.A.; Bastrakov, S.I.; Efimenko, E.S.; Gonoskov, A.A.; Korzhimanov, A.V.; Meyerov, I.B. Particle-in-Cell laser-plasma simulation on Xeon Phi coprocessors. Comput. Phys. Commun. 2016, 202, 204–210. [Google Scholar] [CrossRef]
- Surmin, I.; Bastrakov, S.; Matveev, Z.; Efimenko, E.; Gonoskov, A.; Meyerov, I. Co-design of a particle-in-cell plasma simulation code for Intel Xeon Phi: A first look at Knights Landing. In Lecture Notes in Computer Science, Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, Granada, Spain, 14–16 December 2016; Springer: Cham, Switzerland, 2016; Volume 10049, pp. 319–329. [Google Scholar] [CrossRef]
- Hager, G.; Wellein, G. Introduction to High Performance Computing for Scientists and Engineers; CRC Press: Boca-Raton, FL, USA, 2010. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, New York, NY, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Wadsworth, Inc.: Monterey, CA, USA, 1984. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control. Syst. 1992, 5, 455. [Google Scholar] [CrossRef]
- Lu, Z.; Pu, H.; Wang, F.; Hu, Z.; Wang, L. The expressive power of neural networks: A view from the width. Adv. Neural Inf. Process. Syst. 2017, 30, 6231–6239. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- XGBoost Documentation. Available online: https://xgboost.readthedocs.io/ (accessed on 5 December 2020).
- Scikit-Learn Documentation. Available online: https://scikit-learn.org/ (accessed on 5 December 2020).
- XGBoost Documentation. Python API. Available online: https://xgboost.readthedocs.io/en/latest/python/python_api.html (accessed on 21 December 2020).
- Scikit-Learn Documentation. Python API (SVR). Available online: https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html (accessed on 21 December 2020).
- Keras Documentation. Available online: https://keras.io/ (accessed on 5 December 2020).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Scikit-Learn Documentation. Python API (PCA). Available online: https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html (accessed on 5 December 2020).
- Gorban, A.; Kégl, B.; Wunsch, D.; Zinovyev, A. Principal manifolds for data visualization and dimension reduction. Lect. Notes Comput. Sci. Eng. 2008, 58. [Google Scholar] [CrossRef]

| Measure | SVM | GBT | FCNN | CNN | PCA+FCNN |
|---|---|---|---|---|---|
| Mean absolute error | 4.050 | 2.453 | 1.784 | 1.827 | 2.000 |
| Mean relative percentage error | 1.062 | 0.661 | 0.512 | 0.496 | 0.709 |
| Coefficient of determination | 0.99930 | 0.99967 | 0.99993 | 0.99992 | 0.99991 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodimkov, Y.; Efimenko, E.; Volokitin, V.; Panova, E.; Polovinkin, A.; Meyerov, I.; Gonoskov, A. ML-Based Analysis of Particle Distributions in High-Intensity Laser Experiments: Role of Binning Strategy. Entropy 2021, 23, 21. https://doi.org/10.3390/e23010021
Rodimkov Y, Efimenko E, Volokitin V, Panova E, Polovinkin A, Meyerov I, Gonoskov A. ML-Based Analysis of Particle Distributions in High-Intensity Laser Experiments: Role of Binning Strategy. Entropy. 2021; 23(1):21. https://doi.org/10.3390/e23010021
Chicago/Turabian StyleRodimkov, Yury, Evgeny Efimenko, Valentin Volokitin, Elena Panova, Alexey Polovinkin, Iosif Meyerov, and Arkady Gonoskov. 2021. "ML-Based Analysis of Particle Distributions in High-Intensity Laser Experiments: Role of Binning Strategy" Entropy 23, no. 1: 21. https://doi.org/10.3390/e23010021
APA StyleRodimkov, Y., Efimenko, E., Volokitin, V., Panova, E., Polovinkin, A., Meyerov, I., & Gonoskov, A. (2021). ML-Based Analysis of Particle Distributions in High-Intensity Laser Experiments: Role of Binning Strategy. Entropy, 23(1), 21. https://doi.org/10.3390/e23010021





