The Conditional Entropy Bottleneck
Abstract
1. Introduction
- Vulnerability to adversarial examples. Most machine-learned systems are vulnerable to adversarial examples. Many defenses have been proposed, but few have demonstrated robustness against a powerful, general-purpose adversary. Many proposed defenses are ad-hoc and fail in the presence of a concerted attacker [1,2].
- Poor out-of-distribution detection. Most models do a poor job of signaling that they have received data that is substantially different from the data they were trained on. Even generative models can report that an entirely different dataset has higher likelihood than the dataset they were trained on [3]. Ideally, a trained model would give less confident predictions for data that was far from the training distribution (as well as for adversarial examples). Barring that, there would be a clear, principled statistic that could be extracted from the model to tell whether the model should have made a low-confidence prediction. Many different approaches to providing such a statistic have been proposed [4,5,6,7,8,9], but most seem to do poorly on what humans intuitively view as obviously different data.
- Miscalibrated predictions. Related to the issues above, classifiers tend to be overconfident in their predictions [4]. Miscalibration reduces confidence that a model’s output is fair and trustworthy.
- Overfitting to the training data. Zhang et al. [10] demonstrated that classifiers can memorize fixed random labelings of training data, which means that it is possible to learn a classifier with perfect inability to generalize. This critical observation makes it clear that a fundamental test of generalization is that the model should fail to learn when given what we call information-free datasets.
- Better classification accuracy. MNI models can achieve superior accuracy on classification tasks than models that capture either more or less information than the minimum necessary information (Section 3.1.1 and Section 3.1.6).
- Improved robustness to adversarial examples. Retaining excessive information about the training data results in vulnerability to a variety of whitebox and transfer adversarial examples. MNI models are substantially more robust to these attacks (Section 3.1.2 and Section 3.1.6).
- Strong out-of-distribution detection. The CEB objective provides a useful metric for out-of-distribution (OoD) detection, and CEB models can detect OoD examples as well or better than non-MNI models (Section 3.1.3).
- Better calibration. MNI models are better calibrated than non-MNI models (Section 3.1.4).
- No memorization of information-free datasets. MNI models fail to learn in information-free settings, which we view as a minimum bar for demonstrating robust generalization (Section 3.1.5).
2. Materials and Methods
2.1. Robust Generalization
2.2. The Minimum Necessary Information
- Information. We would like a representation Z that captures useful information about a dataset . Entropy is the unique measure of information [20], so the criterion prefers information-theoretic approaches. (We assume familiarity with the mutual information and its relationships to entropy and conditional entropy: [21] (p. 20).)
- Necessity. The semantic value of information is given by a task, which is specified by the set of variables in the dataset. Here we will assume that the task of interest is to predict Y given X, as in any supervised learning dataset. The information we capture in our representation Z must be necessary to solve this task. As a variable X may have redundant information that is useful for predicting Y, a representation Z that captures the necessary information may not be minimal or unique (the MNI criterion does not require uniqueness of Z).
- Minimality. Given all representations that can solve the task, we require one that retains the smallest amount of information about the task: .
MNI and Robust Generalization
2.3. The Conditional Entropy Bottleneck
2.4. Variational Bound on CEB
2.5. Comparison to the Information Bottleneck
Amortized IB
2.6. Model Variants
2.6.1. Bidirectional CEB
2.6.2. Consistent Classifier
2.6.3. CatGen Decoder
3. Results
3.1. (RG1), (RG2), and (RG3): Fashion MNIST
3.1.1. (RG1): Accuracy and Compression
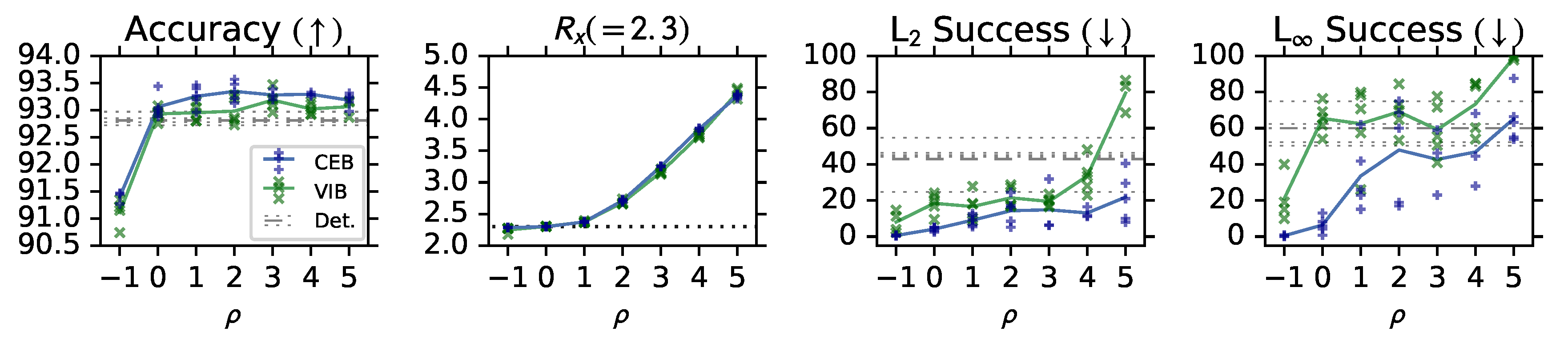
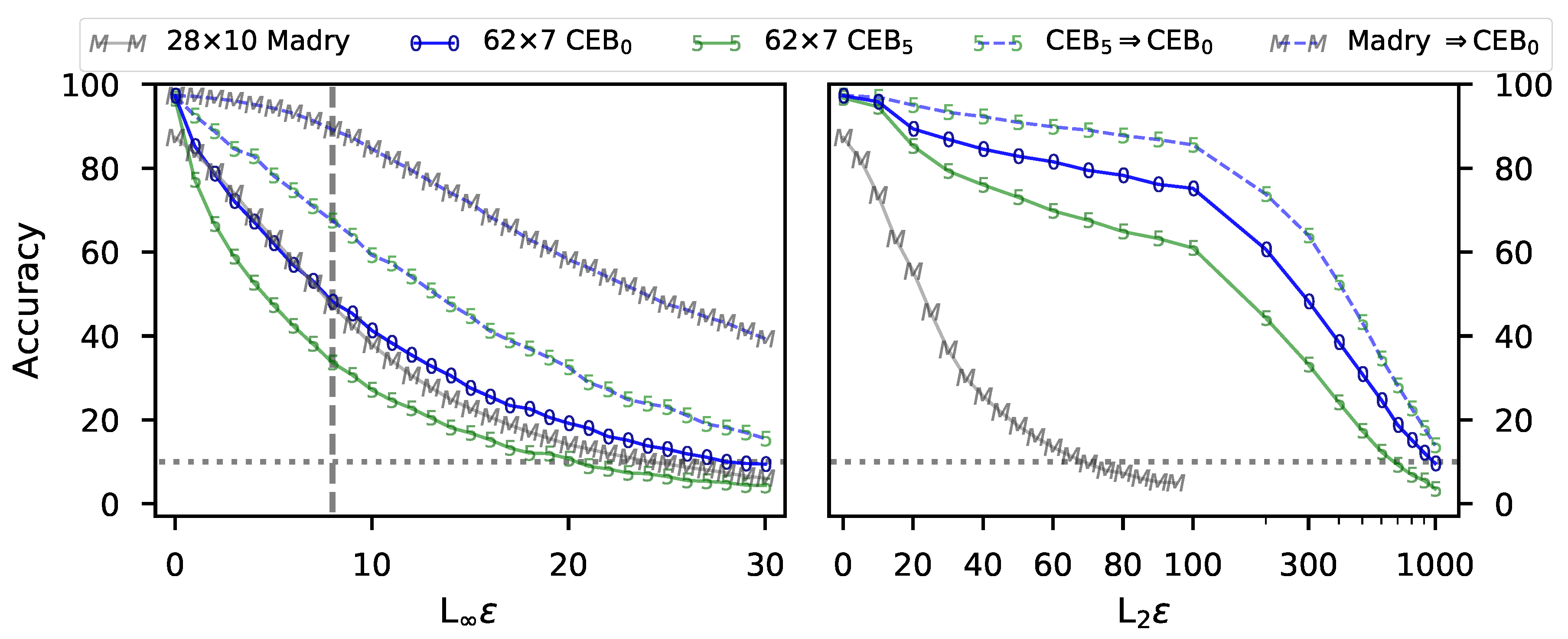
3.1.2. (RG2): Adversarial Robustness
3.1.3. (RG3): Out-of-Distribution Detection
3.1.4. (RG3): Calibration
3.1.5. (RG1): Overfitting Experiments
3.1.6. (RG1) and (RG2): CIFAR10 Experiments
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Model Details
Appendix A.1. Fashion MNIST
Appendix A.2. CIFAR-10
Appendix A.3. Distributional Families
Appendix B. Mutual Information Optimization
Appendix B.1. Finiteness of the Mutual Information
Appendix C. Additional CEB Objectives
Appendix C.1. Hierarchical CEB
Appendix C.2. Sequence Learning
Appendix C.2.1. Modeling and Architectural Choices
Appendix C.2.2. Multi-Scale Sequence Learning
Appendix C.3. Unsupervised CEB
Appendix C.3.1. Denoising CEB Autoencoder
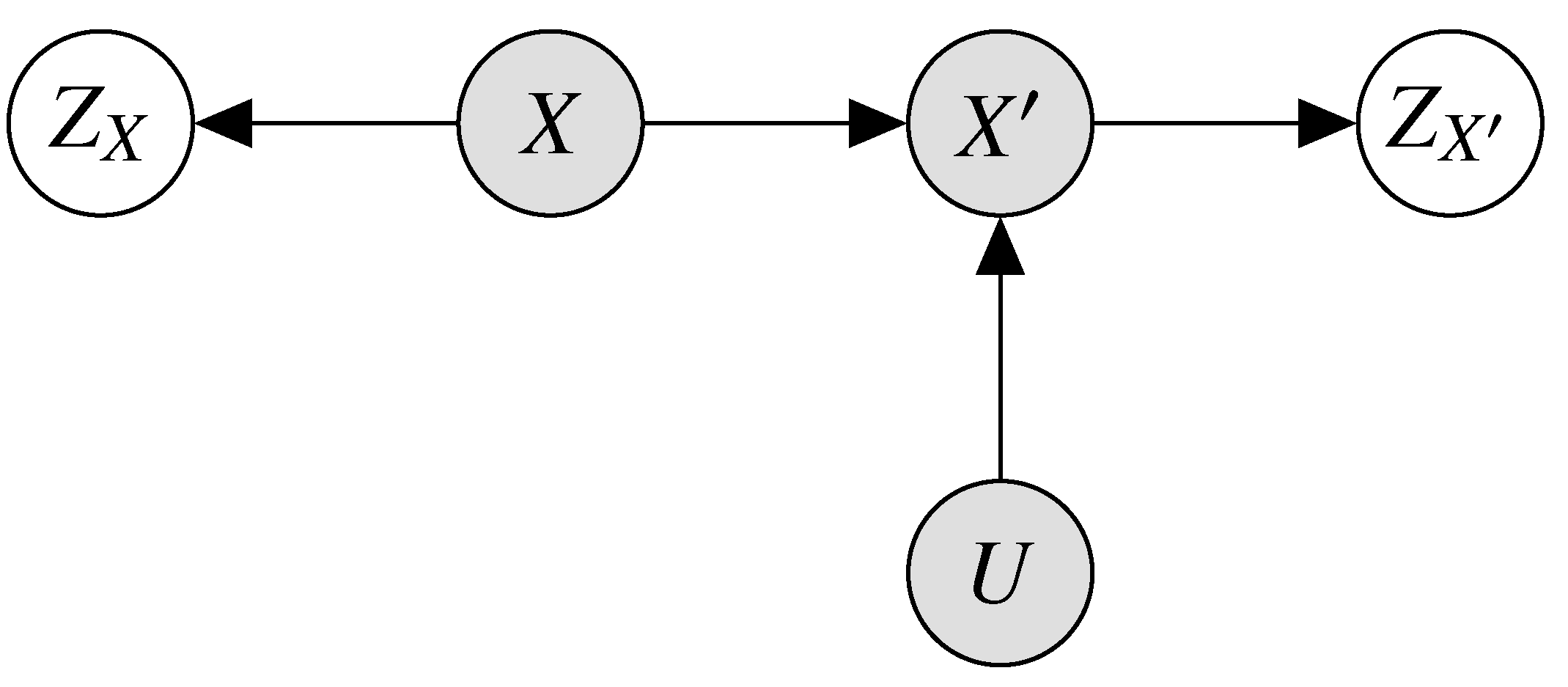
Theoretical Optimality of Noise Functions
References
- Carlini, N.; Wagner, D. Adversarial examples are not easily detected: Bypassing ten detection methods. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 10–17 August 2017; pp. 3–14. [Google Scholar]
- Athalye, A.; Carlini, N.; Wagner, D. Obfuscated Gradients Give a False Sense of Security: Circumventing Defenses to Adversarial Examples. In Proceedings of the 35th International Conference on Machine Learning (ICML), Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Nalisnick, E.; Matsukawa, A.; Teh, Y.W.; Gorur, D.; Lakshminarayanan, B. Do deep generative models know what they don’t know? In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On Calibration of Modern Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Lakshminarayanan, B.; Pritzel, A.; Blundell, C. Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles. In Advances in Neural Information Processing Systems 30; Guyon, I., Luxburg, U.V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; MIT Press: Cambridge, MA, USA, 2017; pp. 6402–6413. Available online: https://papers.nips.cc/paper/7219-simple-and-scalable-predictive-uncertainty-estimation-using-deep-ensembles (accessed on 7 September 2020).
- Hendrycks, D.; Gimpel, K. A Baseline for Detecting Misclassified and Out-of-Distribution Examples in Neural Networks. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Liang, S.; Li, Y.; Srikant, R. Enhancing The Reliability of Out-of-distribution Image Detection in Neural Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lee, K.; Lee, H.; Lee, K.; Shin, J. Training Confidence-calibrated Classifiers for Detecting Out-of-Distribution Samples. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Devries, T.; Taylor, G.W. Learning Confidence for Out-of-Distribution Detection in Neural Networks. arXiv 2018, arXiv:1802.04865. [Google Scholar]
- Zhang, C.; Bengio, S.; Hardt, M.; Recht, B.; Vinyals, O. Understanding deep learning requires rethinking generalization. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Tishby, N.; Pereira, F.C.; Bialek, W. The information bottleneck method. In Proceedings of the 37th annual Allerton Conference on Communication, Control, and Computing, Allerton, IL, USA, 22–24 September 1999; pp. 368–377. [Google Scholar]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. arXiv 2014, arXiv:1412.6572. Available online: https://arxiv.org/abs/1412.6572 (accessed on 7 September 2020).
- Kurakin, A.; Goodfellow, I.; Bengio, S. Adversarial machine learning at scale. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Madry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards Deep Learning Models Resistant to Adversarial Attacks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Cohen, J.M.; Rosenfeld, E.; Kolter, J.Z. Certified adversarial robustness via randomized smoothing. arXiv 2019, arXiv:1902.02918. [Google Scholar]
- Wong, E.; Schmidt, F.; Metzen, J.H.; Kolter, J.Z. Scaling provable adversarial defenses. In Advances in Neural Information Processing Systems; NIPS: La Jolla, CA, USA, 2018; Available online: https://papers.nips.cc/paper/8060-scaling-provable-adversarial-defenses (accessed on 7 September 2020).
- Alemi, A.A.; Fischer, I.; Dillon, J.V.; Murphy, K. Deep Variational Information Bottleneck. In Proceedings of the International Conference on Learning Representations, Toulon, France, 24–26 April 2017. [Google Scholar]
- Alemi, A.A.; Fischer, I.; Dillon, J.V. Uncertainty in the Variational Information Bottleneck. arXiv 2018, arXiv:1807.00906. Available online: https://arxiv.org/abs/1807.00906 (accessed on 7 September 2020).
- Achille, A.; Soatto, S. Information dropout: Learning optimal representations through noisy computation. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2897–2905. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Fischer, I. Bounding the Multivariate Mutual Information. Information Theory and Machine Learning Workshop. 2019. Available online: https://drive.google.com/file/d/17lJiJ4v_6h0p-ist_jCrr-o1ODi7yELx/view (accessed on 7 September 2020).
- Anantharam, V.; Gohari, A.; Kamath, S.; Nair, C. On hypercontractivity and a data processing inequality. In Proceedings of the 2014 IEEE International Symposium on Information Theory, Honolulu, HI, USA, 29 June–4 July 2014; pp. 3022–3026. [Google Scholar]
- Polyanskiy, Y.; Wu, Y. Strong data-processing inequalities for channels and Bayesian networks. In Convexity and Concentration; Springer: New York, NY, USA, 2017; pp. 211–249. [Google Scholar]
- Wu, T.; Fischer, I.; Chuang, I.L.; Tegmark, M. Learnability for the Information Bottleneck. Entropy 2019, 21, 924. [Google Scholar] [CrossRef]
- Shamir, O.; Sabato, S.; Tishby, N. Learning and generalization with the information bottleneck. Theor. Comput. Sci. 2010, 411, 2696–2711. [Google Scholar] [CrossRef]
- Bassily, R.; Moran, S.; Nachum, I.; Shafer, J.; Yehudayoff, A. Learners that Use Little Information. In Proceedings of the Machine Learning Research, New York, NY, USA, 23–24 February 2018; Janoos, F., Mohri, M., Sridharan, K., Eds.; 2018; Volume 83, pp. 25–55. Available online: http://proceedings.mlr.press/v83/bassily18a.html (accessed on 7 September 2020).
- Ilyas, A.; Santurkar, S.; Tsipras, D.; Engstrom, L.; Tran, B.; Madry, A. Adversarial examples are not bugs, they are features. In Advances in Neural Information Processing Systems; NIPS: La Jolla, CA, USA, 2019; pp. 125–136. Available online: https://papers.nips.cc/paper/8307-adversarial-examples-are-not-bugs-they-are-features (accessed on 7 September 2020).
- Kingma, D.P.; Welling, M. Auto-encoding variational Bayes. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Yeung, R.W. A new outlook on Shannon’s information measures. IEEE Trans. Inf. Theory 1991, 37, 466–474. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Alemi, A.A.; Poole, B.; Fischer, I.; Dillon, J.V.; Saurous, R.A.; Murphy, K. Fixing a Broken ELBO. In ICML2018; 2018; Available online: https://icml.cc/Conferences/2018/ScheduleMultitrack?event=2442 (accessed on 7 September 2020).
- Vedantam, R.; Fischer, I.; Huang, J.; Murphy, K. Generative Models of Visually Grounded Imagination. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Higgins, I.; Sonnerat, N.; Matthey, L.; Pal, A.; Burgess, C.P.; Bošnjak, M.; Shanahan, M.; Botvinick, M.; Hassabis, D.; Lerchner, A. SCAN: Learning Hierarchical Compositional Visual Concepts. arXiv 2018, arXiv:1707.03389. [Google Scholar]
- Oord, A.V.D.; Li, Y.; Vinyals, O. Representation learning with contrastive predictive coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Poole, B.; Ozair, S.; van den Oord, A.; Alemi, A.A.; Tucker, G. On Variational Bounds of Mutual Information. In Proceedings of the ICML2019, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Goyal, P.; Dollár, P.; Girshick, R.; Noordhuis, P.; Wesolowski, L.; Kyrola, A.; Tulloch, A.; Jia, Y.; He, K. Accurate, large minibatch SGD: Training imagenet in 1 hour. arXiv 2017, arXiv:1706.02677. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features From Tiny Images; Technical Report; University of Toronto: Toronto, ON, USA, 2009; Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 7 September 2020).
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Papernot, N.; Faghri, F.; Carlini, N.; Goodfellow, I.; Feinman, R.; Kurakin, A.; Xie, C.; Sharma, Y.; Brown, T.; Roy, A.; et al. Technical Report on the CleverHans v2.1.0 Adversarial Examples Library. arXiv 2018, arXiv:1610.00768. [Google Scholar]
- Lee, K.; Lee, K.; Lee, H.; Shin, J. A Simple Unified Framework for Detecting Out-of-Distribution Samples and Adversarial Attacks. In Advances in Neural Information Processing Systems 31; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; NIPS: La Jolla, CA, USA, 2018; pp. 7167–7177. Available online: https://papers.nips.cc/paper/7947-a-simple-unified-framework-for-detecting-out-of-distribution-samples-and-adversarial-attacks (accessed on 7 September 2020).
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. In Proceedings of the British Machine Vision Conference (BMVC), York, UK, 9–12 September 2019; Richard, C., Wilson, E.R.H., Smith, W.A.P., Eds.; BMVA Press: London, UK, 2016; pp. 87.1–87.12. Available online: http://www.bmva.org/bmvc/2016/papers/paper087/ (accessed on 7 September 2020).
- Cubuk, E.D.; Zoph, B.; Mane, D.; Vasudevan, V.; Le, Q.V. AutoAugment: Learning Augmentation Strategies From Data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Recht, B.; Roelofs, R.; Schmidt, L.; Shankar, V. Do CIFAR-10 classifiers generalize to CIFAR-10? arXiv 2018, arXiv:1806.00451. [Google Scholar]
- Clevert, D.A.; Unterthiner, T.; Hochreiter, S. Fast and accurate deep network learning by exponential linear units (elus). In Proceedings of the International Conference on Learning Representations Workshop, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the Machine Learning Research, Lille, France, 7–9 July 2015; Bach, F., Blei, D., Eds.; PMLR: Lille, France, 2015; Volume 37, pp. 448–456. Available online: http://proceedings.mlr.press/v37/ioffe15 (accessed on 7 September 2020).
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 4–8 May 2015. [Google Scholar]
- Figurnov, M.; Mohamed, S.; Mnih, A. Implicit Reparameterization Gradients. In Advances in Neural Information Processing Systems 31; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; NIPS: La Jolla, CA, USA, 2018; pp. 441–452. Available online: https://papers.nips.cc/paper/7326-implicit-reparameterization-gradients (accessed on 7 September 2020).
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef]
- Hjelm, R.D.; Fedorov, A.; Lavoie-Marchildon, S.; Grewal, K.; Bachman, P.; Trischler, A.; Bengio, Y. Learning deep representations by mutual information estimation and maximization. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Amjad, R.A.; Geiger, B.C. Learning Representations for Neural Network-Based Classification Using the Information Bottleneck Principle. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2225–2239. [Google Scholar] [CrossRef] [PubMed]
- Bialek, W.; Nemenman, I.; Tishby, N. Predictability, complexity, and learning. Neural Comput. 2001, 13. [Google Scholar] [CrossRef] [PubMed]
- Van Den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.W.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. arXiv 2016, arXiv:1609.03499. Available online: https://arxiv.org/abs/1609.03499 (accessed on 7 September 2020).
- Vincent, P.; Larochelle, H.; Bengio, Y.; Manzagol, P.A. Extracting and composing robust features with denoising autoencoders. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 1096–1103. [Google Scholar]
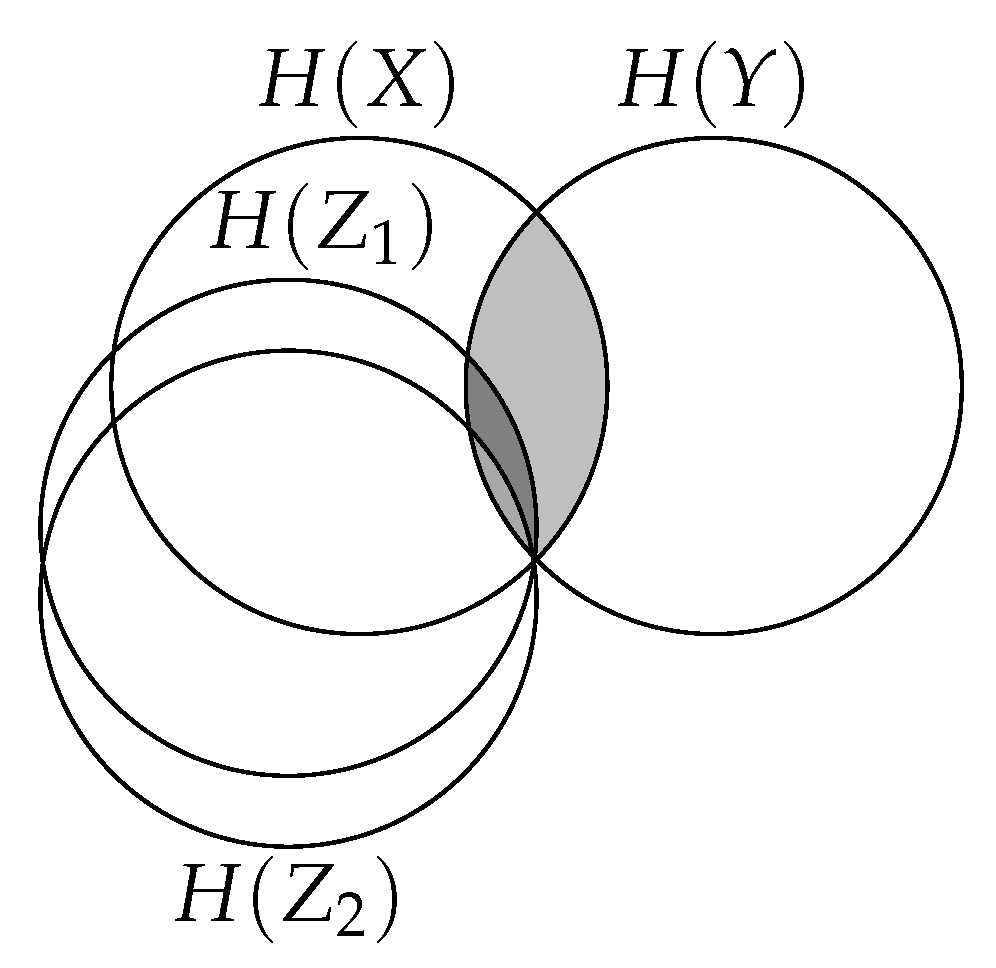
 regions inaccessible to the objective due to the Markov chain .
regions inaccessible to the objective due to the Markov chain .  regions being maximized by the objective ( in both cases).
regions being maximized by the objective ( in both cases).  regions being minimized by the objective. IB minimizes the intersection between Z and both and . CEB only minimizes the intersection between Z and .
regions being minimized by the objective. IB minimizes the intersection between Z and both and . CEB only minimizes the intersection between Z and .
 regions inaccessible to the objective due to the Markov chain .
regions inaccessible to the objective due to the Markov chain . 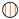 regions being maximized by the objective ( in both cases).
regions being maximized by the objective ( in both cases).  regions being minimized by the objective. IB minimizes the intersection between Z and both and . CEB only minimizes the intersection between Z and .
regions being minimized by the objective. IB minimizes the intersection between Z and both and . CEB only minimizes the intersection between Z and .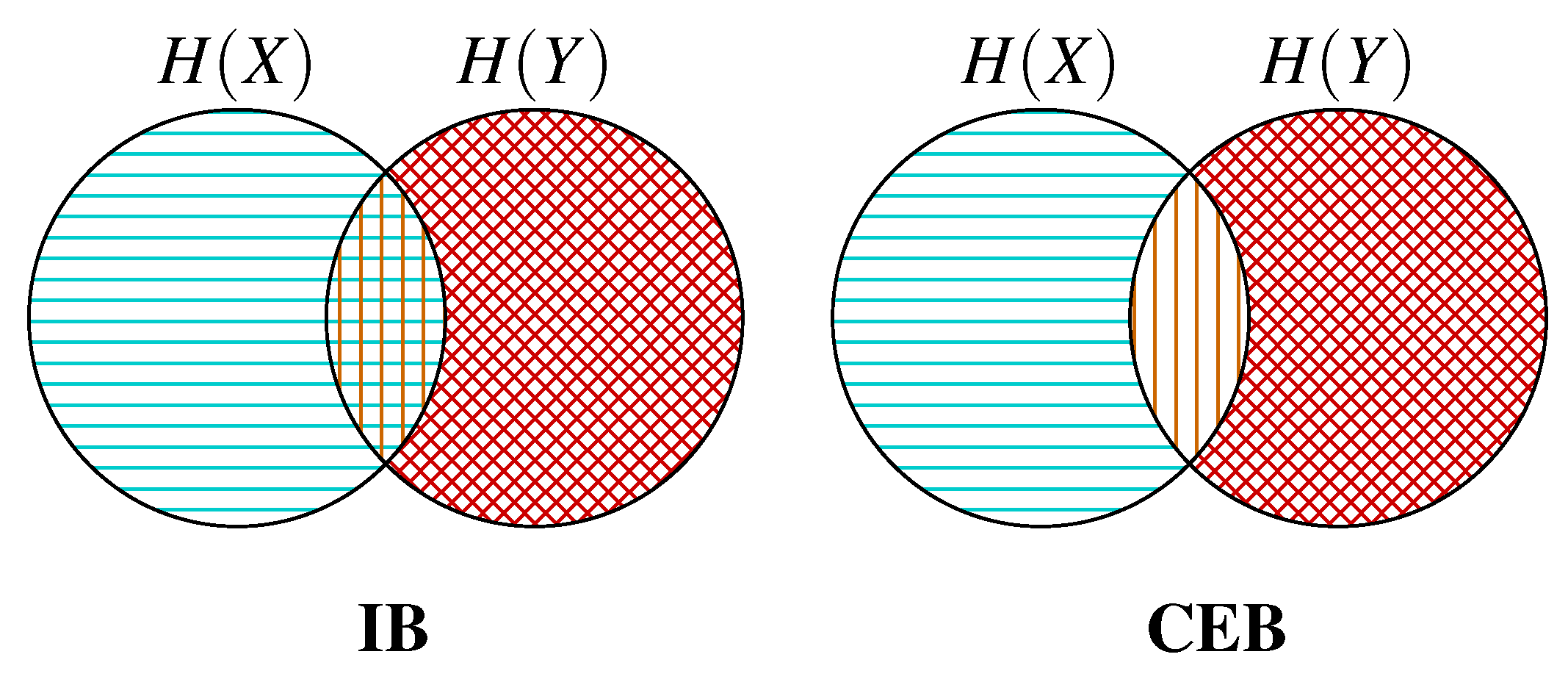

| OoD | Model | Thrsh. | FPR @ 95% TPR ↓ | AUROC ↑ | AUPR In ↑ | Adv. Success ↓ |
|---|---|---|---|---|---|---|
| U(0,1) | Determ | H | 35.8 | 93.5 | 97.1 | N/A |
| VIB | R | 0.0 | 100.0 | 100.0 | N/A | |
| VIB | R | 80.6 | 57.1 | 51.4 | N/A | |
| CEB | R | 0.0 | 100.0 | 100.0 | N/A | |
| MNIST | Determ | H | 59.0 | 88.4 | 90.0 | N/A |
| VIB | R | 0.0 | 100.0 | 100.0 | N/A | |
| VIB | R | 12.3 | 66.7 | 91.1 | N/A | |
| CEB | R | 0.1 | 94.4 | 99.9 | N/A | |
| Vertical Flip | Determ | H | 66.8 | 88.6 | 90.2 | N/A |
| VIB | R | 0.0 | 100.0 | 100.0 | N/A | |
| VIB | R | 17.3 | 52.7 | 91.3 | N/A | |
| CEB | R | 0.0 | 90.7 | 100.0 | N/A | |
| CW | Determ | H | 15.4 | 90.7 | 86.0 | 100.0% |
| VIB | R | 0.0 | 100.0 | 100.0 | 55.2% | |
| VIB | R | 0.0 | 98.7 | 100.0 | 35.8% | |
| CEB | R | 0.0 | 99.7 | 100.0 | 35.8% |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, I. The Conditional Entropy Bottleneck. Entropy 2020, 22, 999. https://doi.org/10.3390/e22090999
Fischer I. The Conditional Entropy Bottleneck. Entropy. 2020; 22(9):999. https://doi.org/10.3390/e22090999
Chicago/Turabian StyleFischer, Ian. 2020. "The Conditional Entropy Bottleneck" Entropy 22, no. 9: 999. https://doi.org/10.3390/e22090999
APA StyleFischer, I. (2020). The Conditional Entropy Bottleneck. Entropy, 22(9), 999. https://doi.org/10.3390/e22090999





