Composition Classification of Ultra-High Energy Cosmic Rays
Abstract
1. Introduction
2. Data Description
- : total number of particles generated by the event at the ground level.
- : total number of muons, at the ground level.
- : total number of electromagnetic particles, at the ground level.
- : zenith angle of the primary particle [degrees].
- : primary particle energy [GeV].
3. Methods
3.1. Classification Methods
3.1.1. Artificial Neural Network
- Number of layers: configurations containing from 2 up to 7 hidden layers were considered. ReLu units were taken for the these [27]. For the output layer, softmax units (one per class) were used.
- Number of neurons: configurations containing from five up to 50 neurons per layer were considered for the hidden layers.
- Constant weight initialization to 0.025 (for the sake of reproducibility).
- Optimisation algorithm: Adam [28] with default parameters (after analysing the behaviour of higher and lower learning rate and beta values) and a maximum of 500 epochs. Batch size was set fixed to 256.
- Loss function: crossentropy for classification [29].
3.1.2. XGBoost
3.1.3. Support Vector Machines
3.1.4. K-Nearest Neighbors
3.1.5. Classifiers Comparison
3.2. Markov Blanket Feature Selection (MBFS) Algorithm
4. Results
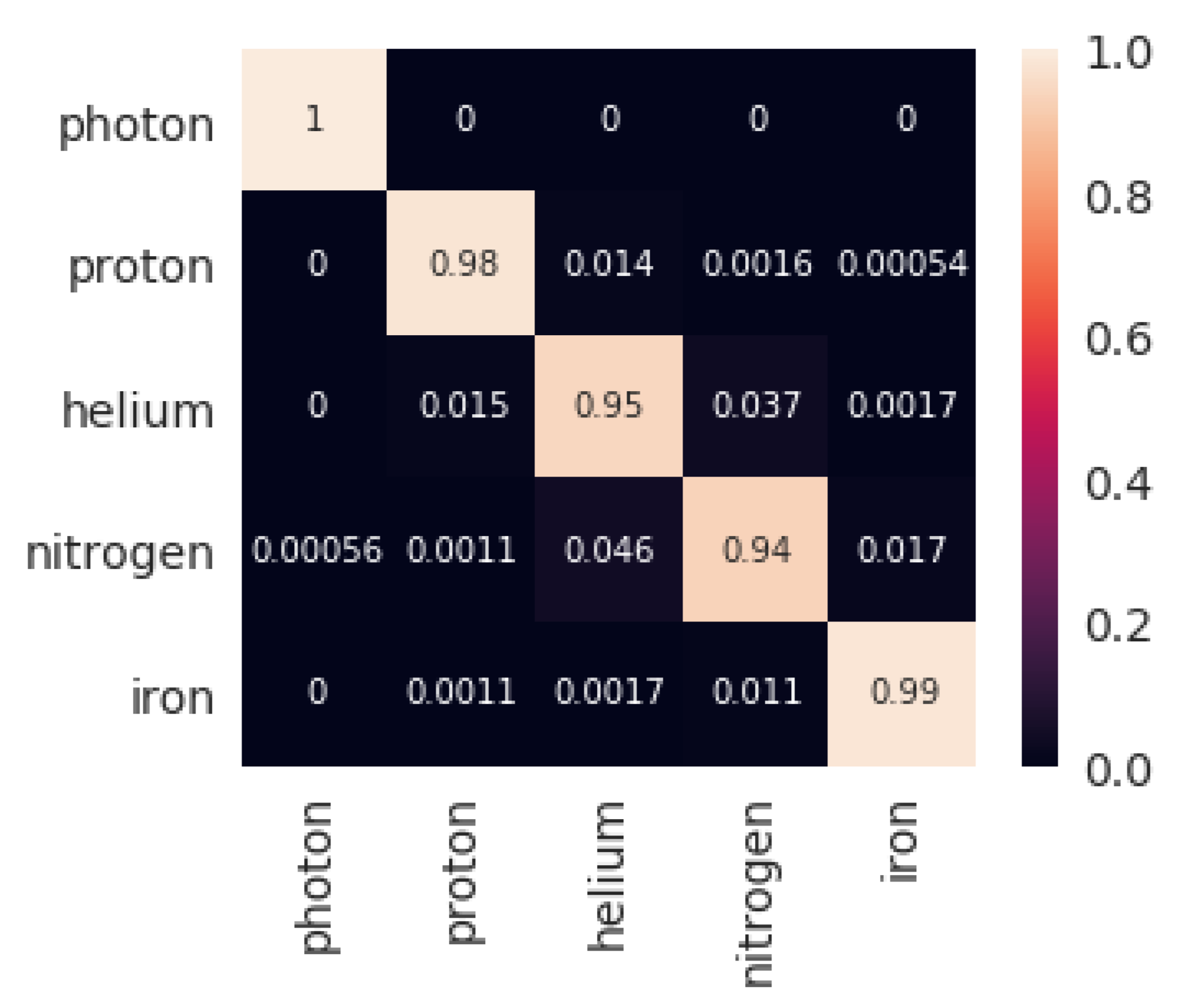
4.1. Classification
- 5 features: , , , ,
- 3 features: , ,
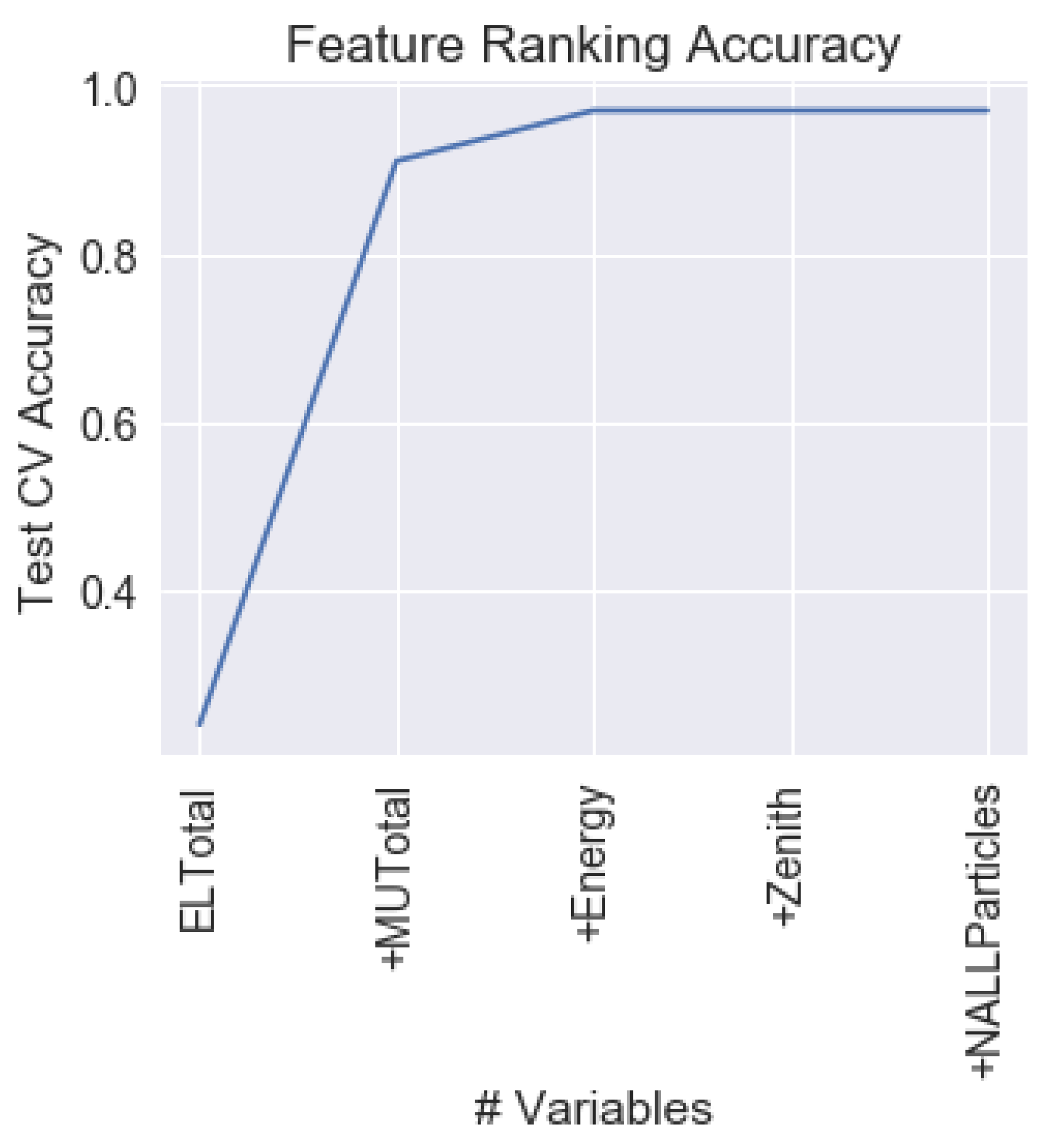
4.2. Feature Ranking
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- The Pierre Auger Collaboration. Measurement of the cosmic ray spectrum above 4 × 1018 eV using inclined events detected with the Pierre Auger Observatory. J. Cosmol Astropart. P 2015, 2015, 049. [Google Scholar] [CrossRef]
- Gaisser, T.K. Cosmic Rays and Particle Physics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- The Pierre Auger Collaboration. Depth of maximum of air-shower profiles at the Pierre Auger Observatory. I. Measurements at energies above 1017.8 eV. Phys. Rev. D 2014, 90, 122005. [Google Scholar] [CrossRef]
- The Pierre Auger Collaboration. Inferences on mass composition and tests of hadronic interactions from 0.3 to 100 EeV using the water-Cherenkov detectors of the Pierre Auger Observatory. Phys. Rev. D 2017, 96, 122003. [Google Scholar] [CrossRef]
- Auger, P.; Maze, R.; Ehrenfest, P.; Freon, A. Les grandes gerbes de rayons cosmiques. J. Phys. Radium 1939, 10, 39–48. [Google Scholar] [CrossRef]
- Guillén, A.; Bueno, A.; Carceller, J.; Martínez-Velázquez, J.; Rubio, G.; Peixoto, C.T.; Sanchez-Lucas, P. Deep learning techniques applied to the physics of extensive air showers. Astropart. Phys. 2019, 111, 12–22. [Google Scholar] [CrossRef]
- Guillén, A.; Todero, C.; Martínez, J.C.; Herrera, L.J. A Preliminary Approach to Composition Classification of Ultra-High Energy Cosmic Rays. In Proceedings of the 3rd International Conference on: Applied Physics, System Science and Computers (APSAC 2018), Lectures Notes in Electrical Engineering, Dubrovnik, Croatia, 26–28 September 2018; pp. 196–202. [Google Scholar]
- Heck, D.; Knapp, J.; Capdevielle, J.; Schatz, G.; Thouw, T. CORSIKA: A Monte Carlo Code to Simulate Extensive Air Showers; Technical report; 51.02.03; LK 01; Wissenschaftliche Berichte, FZKA-6019 (Februar 98); Forschungszentrum Karlsruhe GmbH: Karlsruhe, Germany, 1998. [Google Scholar] [CrossRef]
- Institute for Nuclear Physics (IKP). CORSIKA—An Air Shower Simulation Program. Available online: https://www.ikp.kit.edu/corsika/index.php (accessed on 3 September 2020).
- Koller, D.; Sahami, M. Toward optimal feature selection. In Proceedings of the Thirteenth International Conference on Machine Learning (ICML’96), Bari, Italy, 3–6 July 1996; pp. 284–292. [Google Scholar]
- Herrera, L.J.; Pomares, H.; Rojas, I.; Verleysen, M.; Guillén, A. Effective input variable selection for function approximation. In Proceedings of the 16th International Conference on Artificial Neural Networks, ICANN’2006–LNCS 4131, Athens, Greece, 10–14 September 2006; pp. 41–50. [Google Scholar] [CrossRef]
- Lafuente, V.; Herrera, L.J.; del Mar Pérez, M.; Val, J.; Negueruela, I. Firmness prediction in Prunus persica ‘Calrico’ peaches by visible/short-wave near infrared spectroscopy and acoustic measurements using optimised linear and non-linear chemometric models. J. Sci. Food Agric. 2014, 111, 2033–2040. [Google Scholar]
- Upasana, R.; Chouhan Usha, V.N. Comparative study of machine learning approaches for classification and prediction of selective caspase-3 antagonist for Zika virus drugs. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Del Falco, I.; De Pietro, G.S. Evaluation of artificial intelligence techniques for the classification of different activities of daily living and falls. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Qin, P.; Shi, X. Evaluation of Feature Extraction and Classification for Lower Limb Motion Based on sEMG Signal. Entropy 2020, 22, 852. [Google Scholar] [CrossRef]
- Fanjul-Vélez, F.; Pampín-Suárez, S.; Arce-Diego, J.L. Application of Classification Algorithms to Diffuse Reflectance Spectroscopy Measurements for Ex Vivo Characterization of Biological Tissues. Entropy 2020, 22, 736. [Google Scholar] [CrossRef]
- The FCC Collaboration. FCC-hh: The Hadron Collider. Eur. Phys. J. Spec. Top. 2019, 228, 755–1107. [Google Scholar] [CrossRef]
- Ostapchenko, S. Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: QGSJET-II model. Phys. Rev. D 2011, 83, 014018. [Google Scholar] [CrossRef]
- Fletcher, R.S.; Gaisser, T.K.; Lipari, P.; Stanev, T. SIBYLL: An event generator for simulation of high energy cosmic ray cascades. Phys. Rev. D 1994, 50, 5710–5731. [Google Scholar] [CrossRef] [PubMed]
- Pierog, T.; Karpenko, I.; Katzy, J.M.; Yatsenko, E.; Werner, K. EPOS LHC: Test of collective hadronization with data measured at the CERN Large Hadron Collider. Phys. Rev. C 2015, 92, 034906. [Google Scholar] [CrossRef]
- Fesefeldt, H. The Simulation of Hadronic Showers: Physics and Applications; Cern Libraries: Geneva, Switzerland, 1985. [Google Scholar]
- Ferrari, A.; Sala, P.; Fasso, A.; Ranft, J. FLUKA: A Multi-Particle Transport Code; Stanford Linear Accelerator Center (SLAC): Menlo Park, CA, USA, 2005. [Google Scholar] [CrossRef]
- Bass, S.; Belkacem, M.; Bleicher, M.; Brandstetter, M.; Bravina, L.; Ernst, C.; Gerland, L.; Hofmann, M.; Hofmann, S.; Konopka, J.; et al. Microscopic models for ultrarelativistic heavy ion collisions. Prog. Part. Nucl. Phys. 1998, 41, 255–369. [Google Scholar] [CrossRef]
- Nelson, W.; Hirayama, H.; Rogers, D. EGS4 Code System (No. SLAC-265); Technical report; Stanford Linear Accelerator Center: Menlo Park, CA, USA, 1985.
- Asif, A.; Dawood, M.; Jan, B.; Khurshid, J.; DeMaria, M.; Minhas, F.U.A.A. PHURIE: Hurricane intensity estimation from infrared satellite imagery using machine learning. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Jamil, M.; Zeeshan, M. A comparative analysis of ANN and chaotic approach-based wind speed prediction in India. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Glorot, X.; Bordes, A.; Bengio, Y. Deep Sparse Rectifier Neural Networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, 11–13 April 2011; pp. 315–323. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv Preprint 2014, arXiv:1412.6980. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 3 September 2020).
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the KDD ’16, 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Scholkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Keerthi, S.S.; Lin, C.J. Asymptotic Behaviors of Support Vector Machines with Gaussian Kernel. Neural Comput. 2003, 15, 1667–1689. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. 2005, 27, 1226–1238. [Google Scholar] [CrossRef] [PubMed]
- Estévez, P.A.; Tesmer, M.; Perez, C.A.; Zurada, J.M. Normalized Mutual Information Feature Selection. IEEE Trans. Neural Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef] [PubMed]

| 5 Features | 3 Features | |||||
|---|---|---|---|---|---|---|
| trn. Time (s.) | Accuracy | f1-Score | trn. Time (s.) | Accuracy | f1-Score | |
| ANN | 48,715 | 0.91 (0.015) | 0.92 (0.012) | 23,957 | 0.76 (0.14) | 0.77 (0.017) |
| XGBoost | 909 | 0.97 (0.002) | 0.97 (0.002) | 843 | 0.87 (0.002) | 0.87 (0.002) |
| SVMs | 9536 | 0.94 (0.003) | 0.94 (0.003) | 10,677 | 0.83 (0.004) | 0.83 (0.004) |
| KNN | 3.59 | 0.78 (0.003) | 0.79 (0.003) | 2.75 | 0.62 (0.006) | 0.63(0.005) |
| Classifier | 5 Features | 3 Features |
|---|---|---|
| ANN | 2 layers, | 2 layers, |
| XGBoost | ||
| SVMs | ||
| KNN |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrera, L.J.; Todero Peixoto, C.J.; Baños, O.; Carceller, J.M.; Carrillo, F.; Guillén, A. Composition Classification of Ultra-High Energy Cosmic Rays. Entropy 2020, 22, 998. https://doi.org/10.3390/e22090998
Herrera LJ, Todero Peixoto CJ, Baños O, Carceller JM, Carrillo F, Guillén A. Composition Classification of Ultra-High Energy Cosmic Rays. Entropy. 2020; 22(9):998. https://doi.org/10.3390/e22090998
Chicago/Turabian StyleHerrera, Luis Javier, Carlos José Todero Peixoto, Oresti Baños, Juan Miguel Carceller, Francisco Carrillo, and Alberto Guillén. 2020. "Composition Classification of Ultra-High Energy Cosmic Rays" Entropy 22, no. 9: 998. https://doi.org/10.3390/e22090998
APA StyleHerrera, L. J., Todero Peixoto, C. J., Baños, O., Carceller, J. M., Carrillo, F., & Guillén, A. (2020). Composition Classification of Ultra-High Energy Cosmic Rays. Entropy, 22(9), 998. https://doi.org/10.3390/e22090998







