Synergistic Information Transfer in the Global System of Financial Markets
Abstract
1. Introduction
2. Data
3. Methods
3.1. Bivariate Granger Causality
3.2. Global Granger Causality
3.3. Partial Information Decomposition
4. Results
4.1. Pairwise and Global Granger Causality
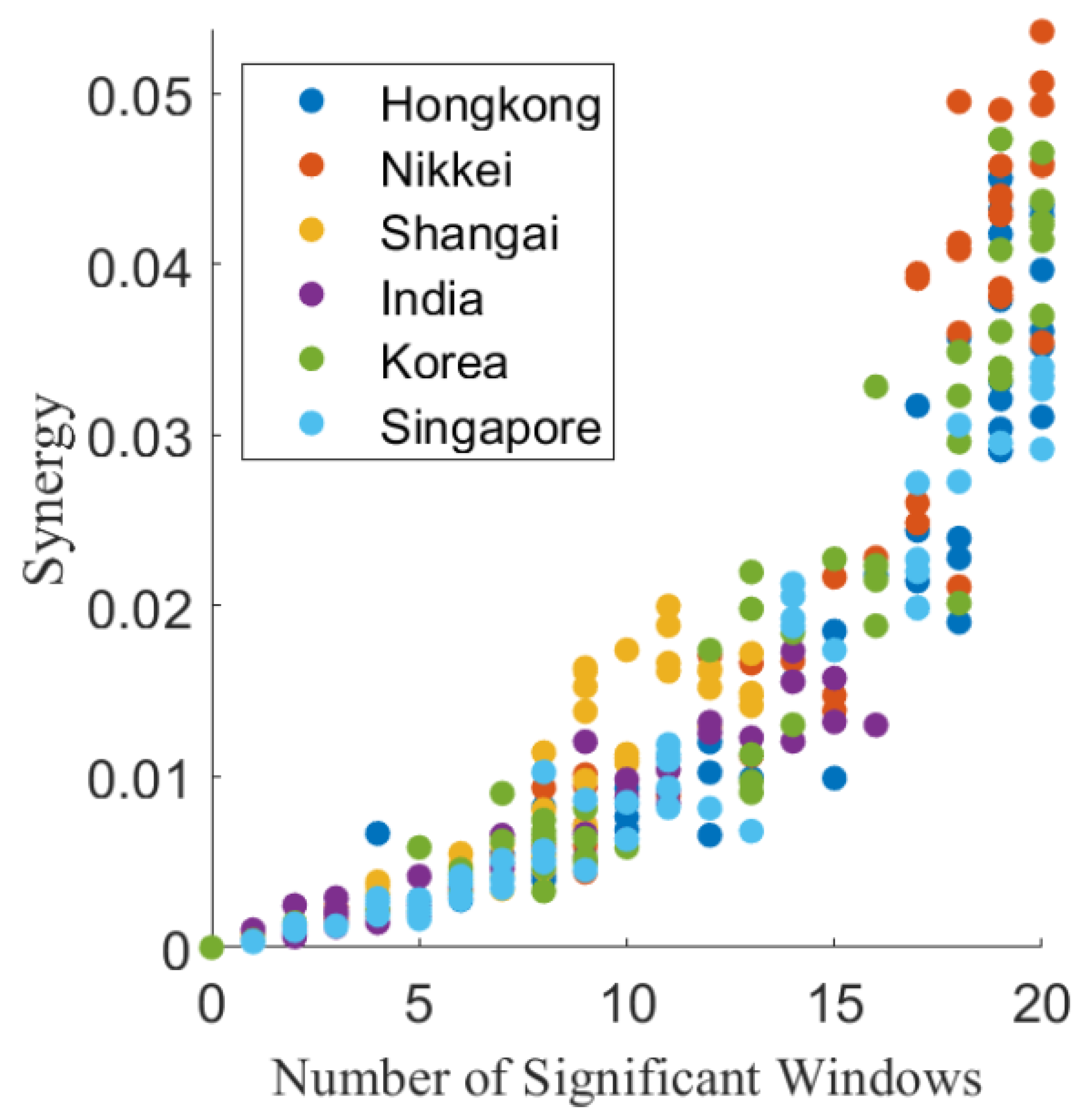
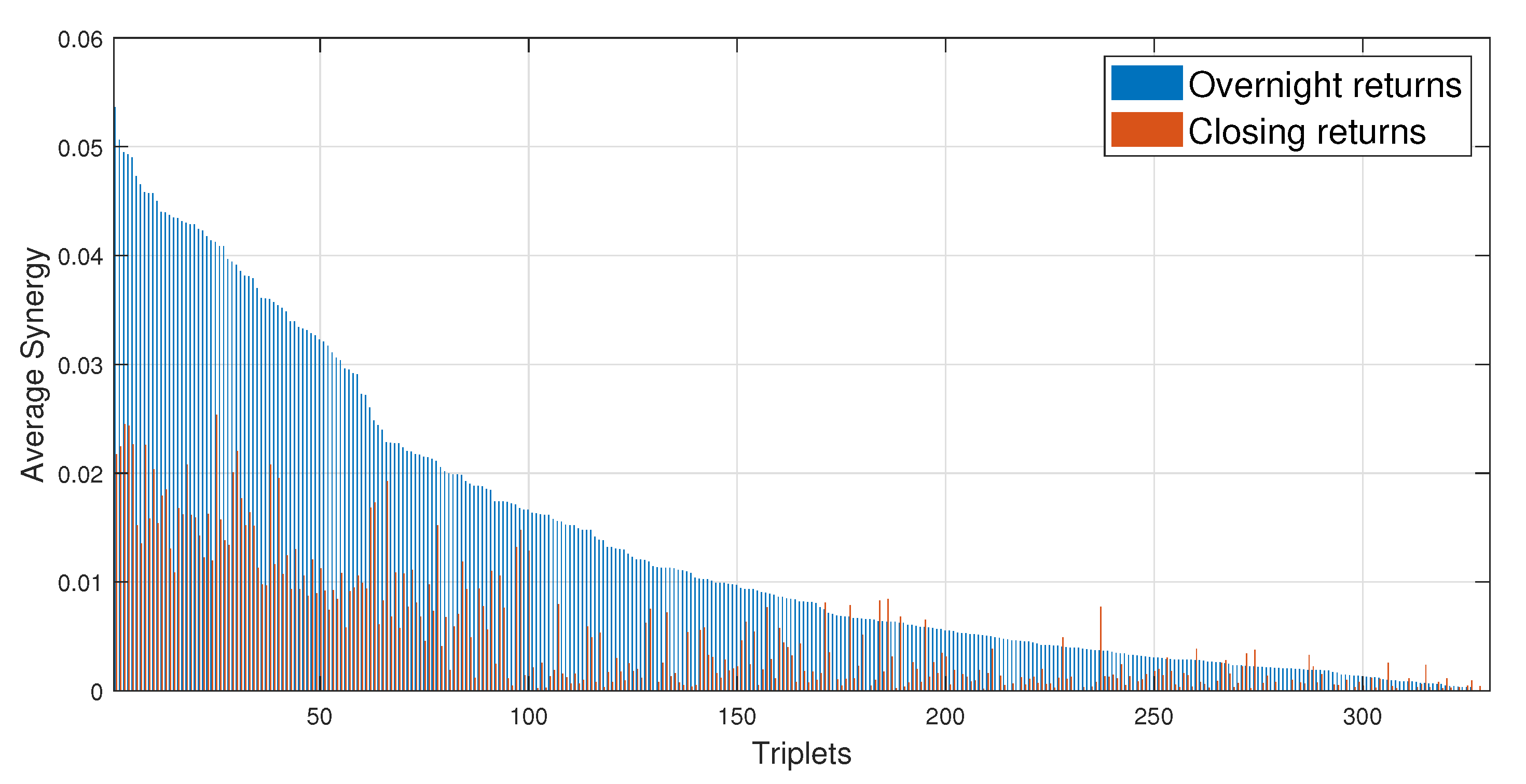
4.2. Synergy
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wooldridge, D.P.; Domanski, D.; Cobau, A. Changing Links between Mature and Emerging Financial Markets. BIS Q. Rev. 2003. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1971684 (accessed on 7 September 2020).
- Chinn David, M.; Frankel, J.A. Financial Links around the Pacific Rim: 1982–1992; No. 1554-2016-132500; UC Berkeley: Berkeley, CA, USA, 1993. [Google Scholar]
- Bonanno, G.; Vandewalle, N.; Mantegna, R.N. Taxonomy of stock market indices. Phys. Rev. 2000, E62, R7615. [Google Scholar] [CrossRef] [PubMed]
- Maslov, S. Measures of globalization based on cross-correlations of world financial indices. Phys. A Stat. Mech. Its Appl. 2001, 301, 397–406. [Google Scholar] [CrossRef]
- Drozdz, S.; Grümmer, F.; Ruf, F.; Speth, J. Towards identifying the world stock market cross-correlations: DAX versus Dow Jones. Phys. A Stat. Mech. Its Appl. 2001, 294, 226–234. [Google Scholar] [CrossRef]
- Coelho, R.; Gilmore, C.G.; Lucey, B.; Richmond, P.; Hutzler, S. The evolution of interdependence in world equity markets? Evidence from minimum spanning trees. Phys. A Stat. Mech. Its Appl. 2007, 376, 455–466. [Google Scholar] [CrossRef]
- Eryigit, M.; Eryigit, R. Network structure of cross-correlations among the world market indices. Phys. A Stat. Mech. Its Appl. 2009, 388, 3551–3562. [Google Scholar] [CrossRef]
- Song, D.M.; Tumminello, M.; Zhou, W.X.; Mantegna, R.N. Evolution of worldwide stock markets, correlation structure, and correlation-based graphs. Phys. Rev. E 2011, 84, 026108. [Google Scholar] [CrossRef]
- Sandoval, L., Jr.; Franca, I.D.P. Correlation of financial markets in times of crisis. Phys. A Stat. Mech. Its Appl. 2012, 391, 187–208. [Google Scholar] [CrossRef]
- Agbloyor, E.K.; Abor, J.; Adjasi, C.K.D.; Yawson, A. Exploring the causality links between financial markets and foreign direct investment in Africa. Res. Int. Bus. Financ. 2013, 28, 118–134. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef]
- Marschinski, R.; Kantz, H. Analysing the information flow between financial time series. Eur. Phys. J. B Condens. Matter Complex Syst. 2002, 30, 275–281. [Google Scholar] [CrossRef]
- Baek, S.K.; Jung, W.S.; Kwon, O.; Moon, H.T. Transfer entropy analysis of the stock market. arXiv 2005, arXiv:physics/0509014. [Google Scholar]
- Kwon, O.; Yang, J.S. Information flow between composite stock index and individual stocks. Phys. A Stat. Mech. Its Appl. 2008, 387, 2851–2856. [Google Scholar] [CrossRef]
- Kwon, O.; Yang, J.S. Information flow between stock indices. EPL Europhys. Lett. 2008, 82, 68003. [Google Scholar] [CrossRef]
- Jizba, P.; Kleinert, H.; Shefaat, M. Rényi’s information transfer between financial time series. Phys. A Stat. Mech. Its Appl. 2012, 391, 2971–2989. [Google Scholar] [CrossRef]
- Dimpfl, T.; Peter, F.J. The impact of the financial crisis on transatlantic information flows: An intraday analysis. J. Int. Financ. Mark. Inst. Money 2014, 31, 1–13. [Google Scholar] [CrossRef]
- Sandoval, L. Structure of a global network of financial companies based on transfer entropy. Entropy 2014, 16, 4443–4482. [Google Scholar] [CrossRef]
- Zhou, L.; Qiu, L.; Gu, C.; Yang, H. Immediate causality network of stock markets. EPL Europhys. Lett. 2017, 121, 48002. [Google Scholar] [CrossRef]
- Bossomaier, T.; Barnett, L.; Steen, A.; Harré, M.; d’Alessandro, S.; Duncan, R. Information flow around stock market collapse. Account. Financ. 2018, 58, 45–58. [Google Scholar] [CrossRef]
- Yue, P.; Fan, Y.; Batten, J.A.; Zhou, W.X. Information transfer between stock market sectors: A comparison between the USA and China. Entropy 2020, 22, 194. [Google Scholar] [CrossRef]
- Bossomaier, T.; Barnett, L.; Harré, M.; Lizier, J.T. An Introduction to Tranfer Entropy; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Granger, C.W.J. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Billio, M.; Getmansky, M.; Lo, A.W.; Pelizzon, L. Econometric measures of connectedness and systemic risk in the finance and insurance sectors. J. Financ. Econ. 2012, 104, 535–559. [Google Scholar] [CrossRef]
- Výrost, T.; Lyócsa, Š.; Baumöhl, E. Granger causality stock market networks: Temporal proximity and preferential attachment. Phys. A Stat. Mech. Its Appl. 2015, 427, 262–276. [Google Scholar] [CrossRef]
- Papana, A.; Kyrtsou, C.; Kugiumtzis, D.; Diks, C. Financial networks based on Granger causality: A case study. Phys. A Stat. Mech. Its Appl. 2017, 482, 65–73. [Google Scholar] [CrossRef]
- Tang, Y.; Xiong, J.J.; Luo, Y.; Zhang, Y.C. How do the global stock markets Influence one another? Evidence from finance big data and granger causality directed network. Int. J. Electron. Commer. 2019, 23, 85–109. [Google Scholar]
- Lizier, J.T.; Bertschinger, N.; Jost, J.; Wibral, M. Information Decomposition of Target Effects from Multi-Source Interactions: Perspectives on Previous, Current and Future Work. Entropy 2018, 20, 307. [Google Scholar] [CrossRef]
- Bertschinger, N.; Rauh, J.; Olbrich, E.; Jost, J.; Ay, N. Quantifying unique information. Entropy 2014, 16, 2161–2183. [Google Scholar] [CrossRef]
- Stramaglia, S.; Cortes, J.M.; Marinazzo, D. Synergy and redundancy in the Granger causal analysis of dynamical networks. New J. Phys. 2014, 16, 105003. [Google Scholar] [CrossRef]
- Stramaglia, S.; Wu, G.R.; Pellicoro, M.; Marinazzo, D. Expanding the transfer entropy to identify information circuits in complex systems. Phys. Rev. E 2012, 86, 066211. [Google Scholar] [CrossRef]
- Faes, L.; Marinazzo, D.; Stramaglia, S. Multiscale Information Decomposition: Exact Computation for Multivariate Gaussian Processes. Entropy 2017, 19, 408. [Google Scholar] [CrossRef]
- Marinazzo, D.; Angelini, L.; Pellicoro, M.; Stramaglia, S. Synergy as a warning sign of transitions: The case of the two-dimensional Ising model. Phys. Rev. E 2019, 99, 040101. [Google Scholar] [CrossRef] [PubMed]
- Krohova, J.; Faes, L.; Czippelova, B.; Turianikova, Z.; Mazgutova, N.; Pernice, R.; Busacca, A.; Marinazzo, D.; Stramaglia, S.; Javorka, M. Multiscale Information Decomposition Dissects Control Mechanisms of Heart Rate Variability at Rest and During Physiological Stress. Entropy 2019, 21, 526. [Google Scholar] [CrossRef]
- Camino-Pontes, B.; Diez, I.; Jimenez-Marin, A.; Rasero, J.; Erramuzpe, A.; Bonifazi, P.; Stramaglia, S.; Swinnen, S.; Cortes, J.M. Interaction Information Along Lifespan of the Resting Brain Dynamics Reveals a Major Redundant Role of the Default Mode Network. Entropy 2018, 20, 742. [Google Scholar] [CrossRef]
- Boonstra, T.W.; Faes, L.; Kerkman, J.N.; Marinazzo, D. Information decomposition of multichannel EMG to map functional interactions in the distributed motor system. NeuroImage 2019, 202, 116093. [Google Scholar] [CrossRef] [PubMed]
- Quandl. Available online: https://www.quandl.com/ (accessed on 7 September 2020).
- Yahoo Finance. Available online: http://finance.yahoo.com/ (accessed on 7 September 2020).
- Geweke, J. Measurement of linear dependence and feedback between multiple time series. J. Am. Stat. Assoc. 1982, 77, 304–313. [Google Scholar] [CrossRef]
- Marinazzo, D.; Pellicoro, M.; Stramaglia, S. Kernel method for nonlinear Granger causaliy. Phys. Rev. Lett. 2008, 100, 144103. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved Surrogate Data for Nonlinearity Tests. Phys. Rev. Lett. 1996, 77, 636. [Google Scholar] [CrossRef]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2015, 91, 052802. [Google Scholar] [CrossRef]
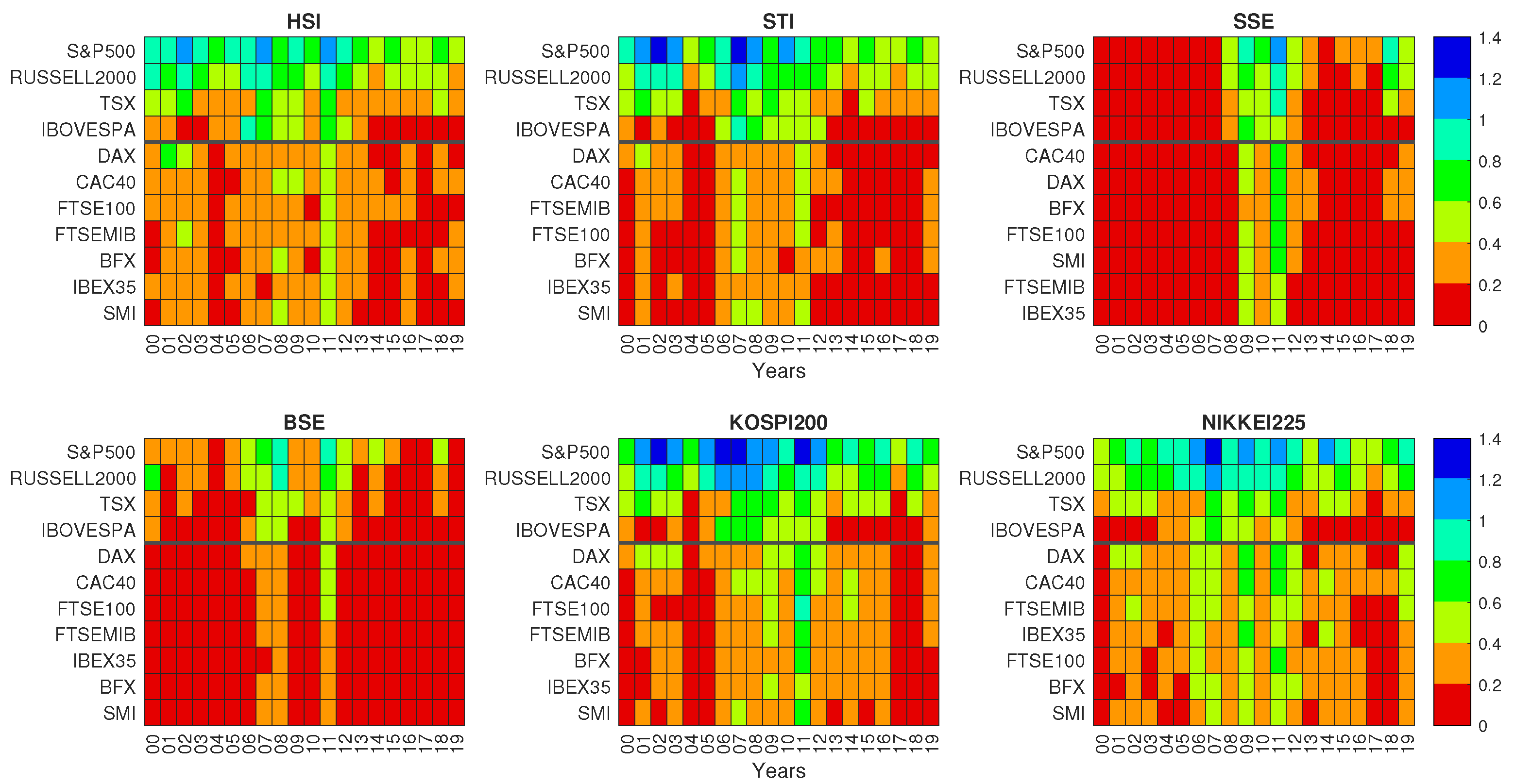

| SSE | KOSPI 200 | BSE | HSI | Nikkei 225 | STI | |
|---|---|---|---|---|---|---|
| 2000 | ||||||
| 2001 | ||||||
| 2002 | ||||||
| 2003 | ||||||
| 2004 | ||||||
| 2005 | ||||||
| 2006 | ||||||
| 2007 | ||||||
| 2008 | ||||||
| 2009 | ||||||
| 2010 | ||||||
| 2011 | ||||||
| 2012 | ||||||
| 2013 | ||||||
| 2014 | ||||||
| 2015 | ||||||
| 2016 | ||||||
| 2017 | ||||||
| 2018 | ||||||
| 2019 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scagliarini, T.; Faes, L.; Marinazzo, D.; Stramaglia, S.; Mantegna, R.N. Synergistic Information Transfer in the Global System of Financial Markets. Entropy 2020, 22, 1000. https://doi.org/10.3390/e22091000
Scagliarini T, Faes L, Marinazzo D, Stramaglia S, Mantegna RN. Synergistic Information Transfer in the Global System of Financial Markets. Entropy. 2020; 22(9):1000. https://doi.org/10.3390/e22091000
Chicago/Turabian StyleScagliarini, Tomas, Luca Faes, Daniele Marinazzo, Sebastiano Stramaglia, and Rosario N. Mantegna. 2020. "Synergistic Information Transfer in the Global System of Financial Markets" Entropy 22, no. 9: 1000. https://doi.org/10.3390/e22091000
APA StyleScagliarini, T., Faes, L., Marinazzo, D., Stramaglia, S., & Mantegna, R. N. (2020). Synergistic Information Transfer in the Global System of Financial Markets. Entropy, 22(9), 1000. https://doi.org/10.3390/e22091000








