Analysis of Information-Based Nonparametric Variable Selection Criteria
Abstract
1. Introduction
2. Preliminaries
2.1. Information-Theoretic Measures of Dependence
2.2. Information-Based Feature Selection
2.3. Approximations of CMI: CIFE and JMI Criteria
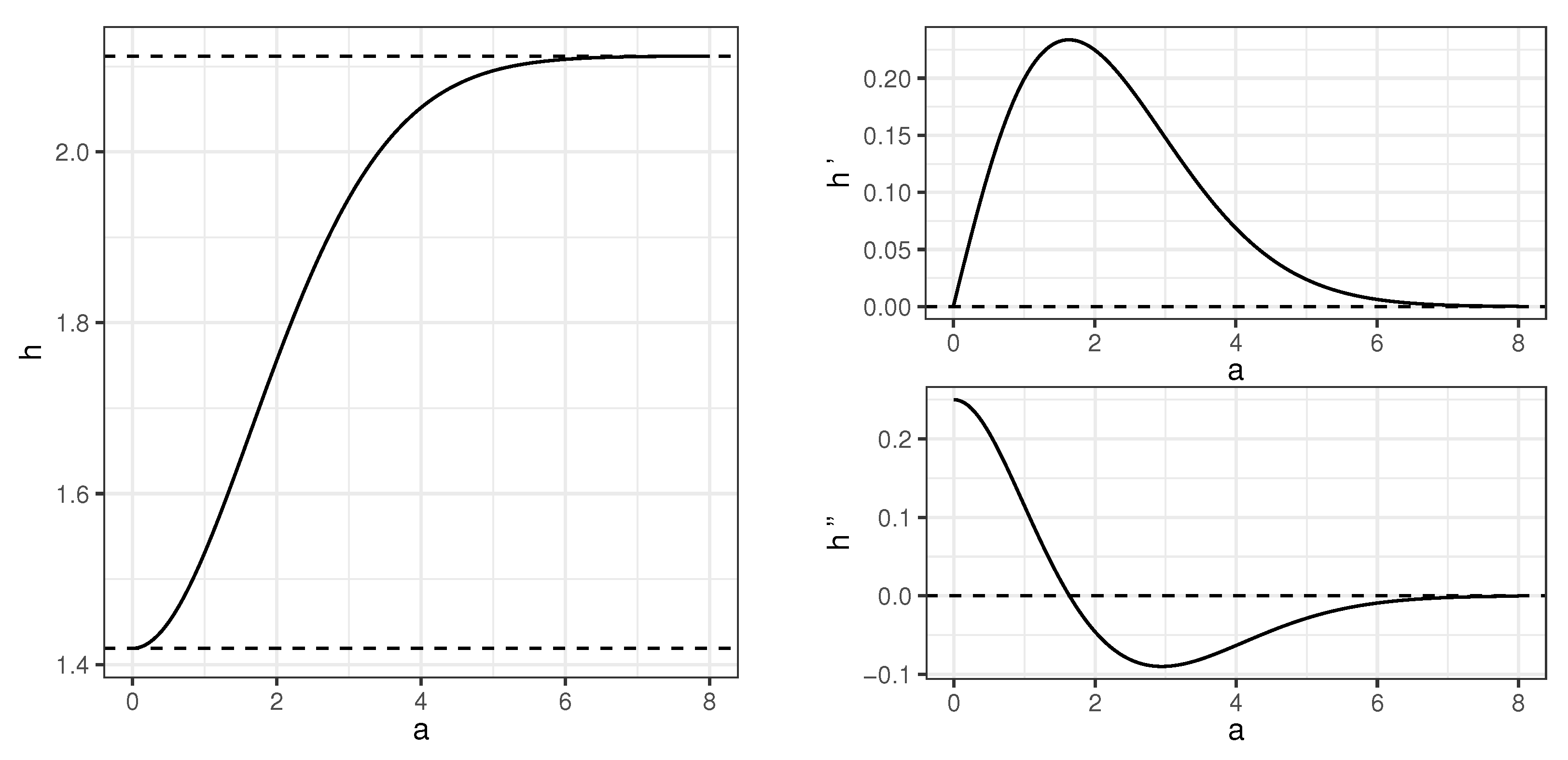
3. Auxiliary Results: Information Measures for Gaussian Mixtures
4. Main Results: Behavior of Information-Based Criteria in Generative Tree Model
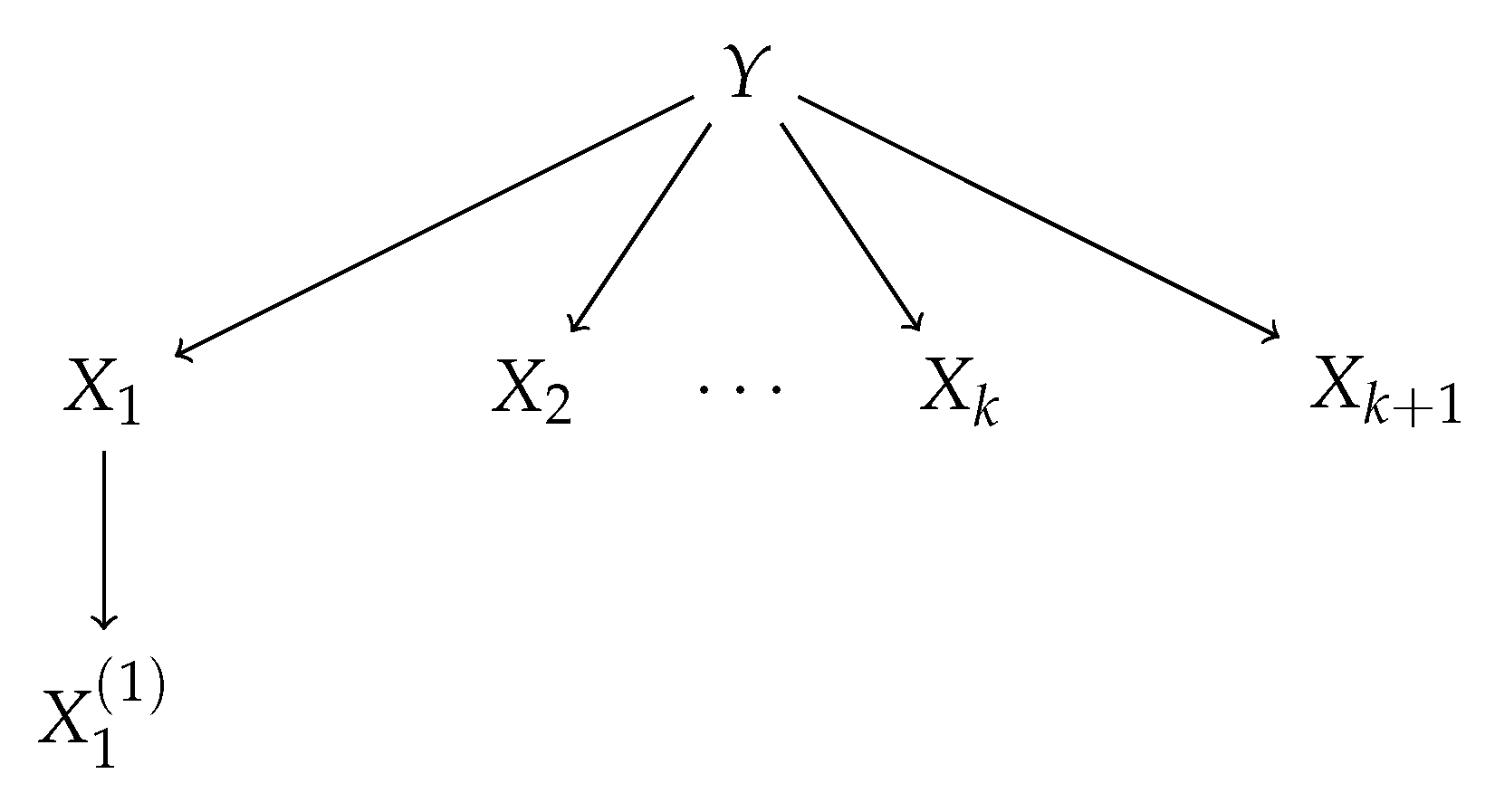
4.1. Generative Tree Model
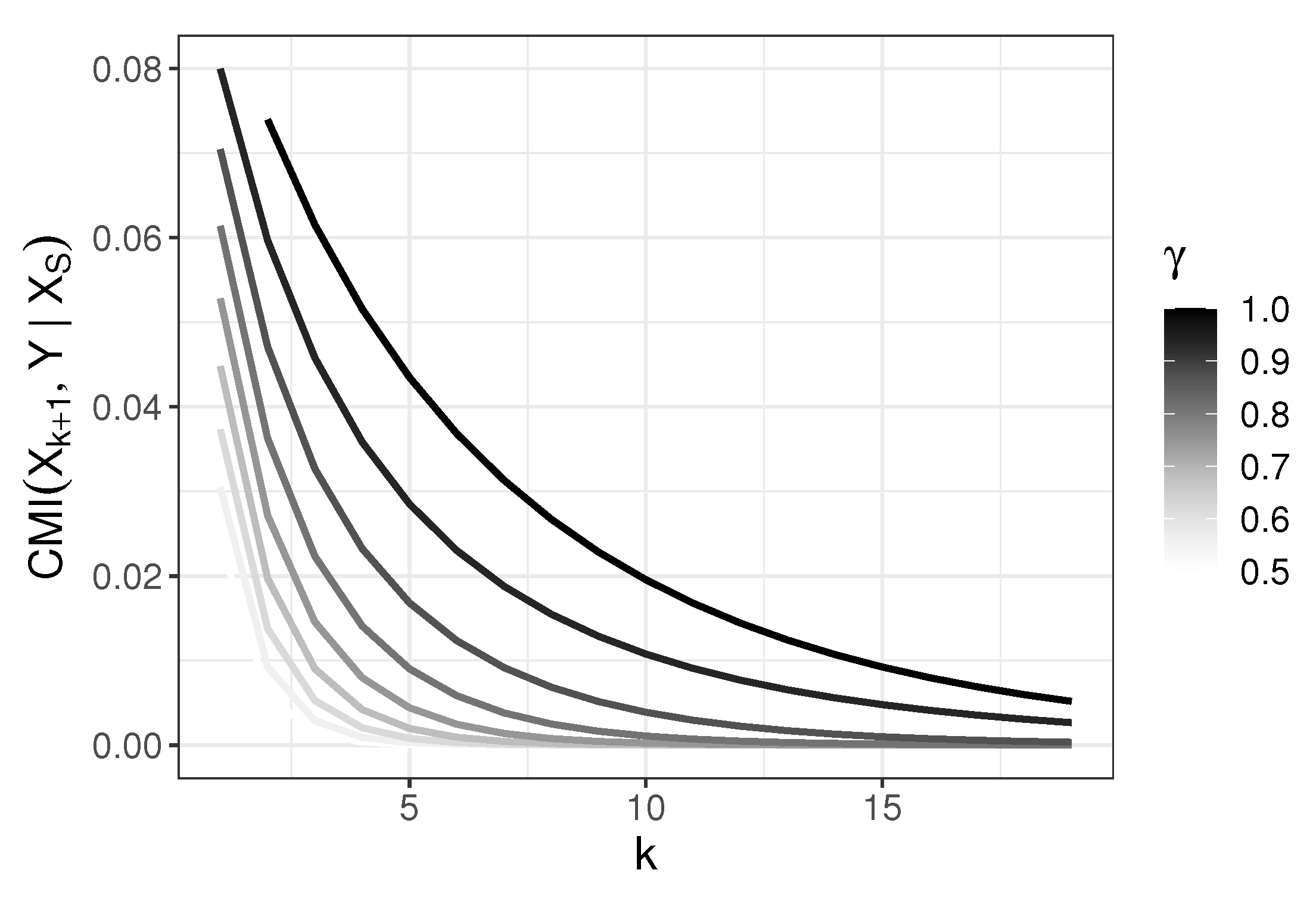
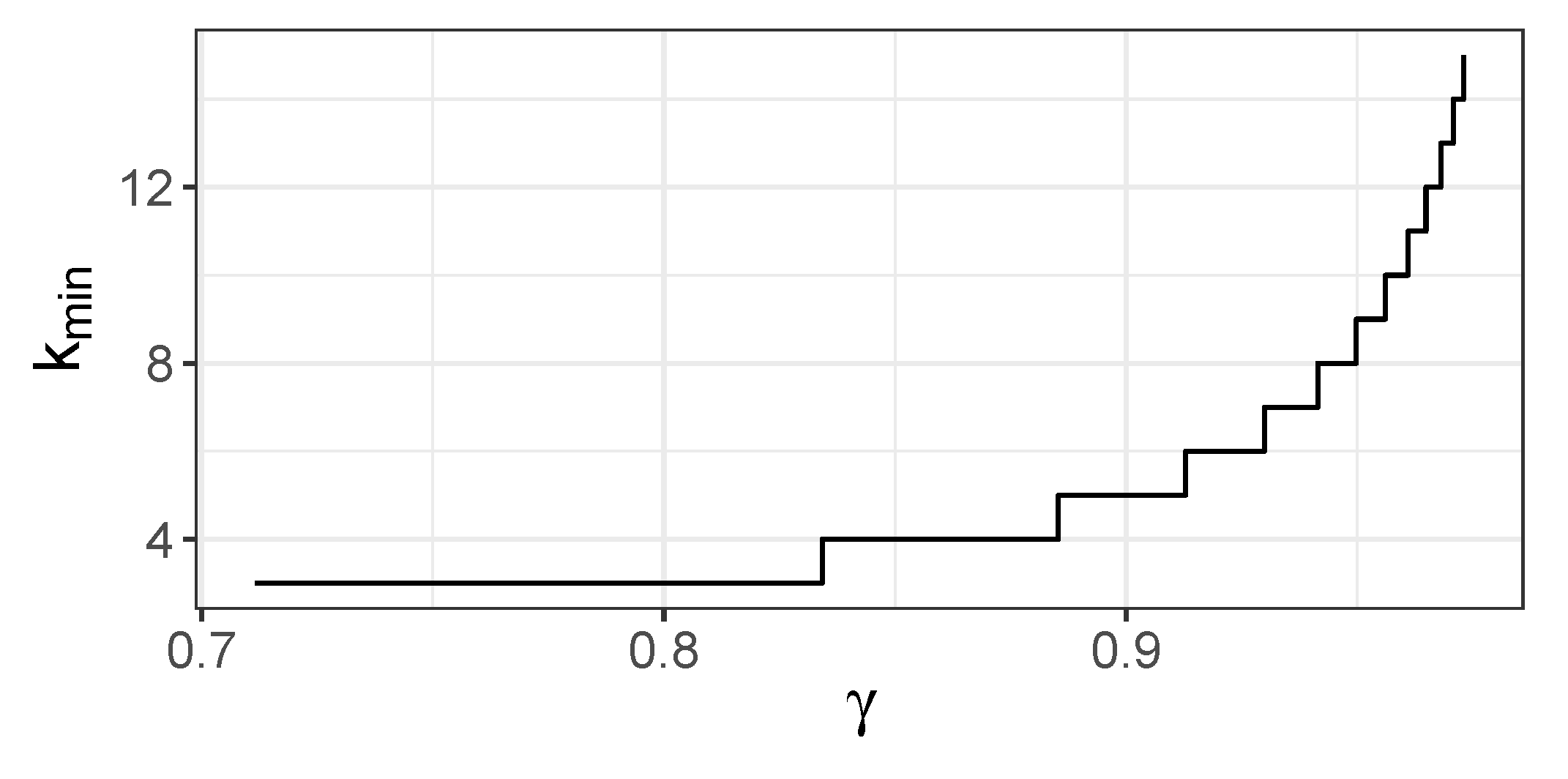
4.2. Behavior of CMI
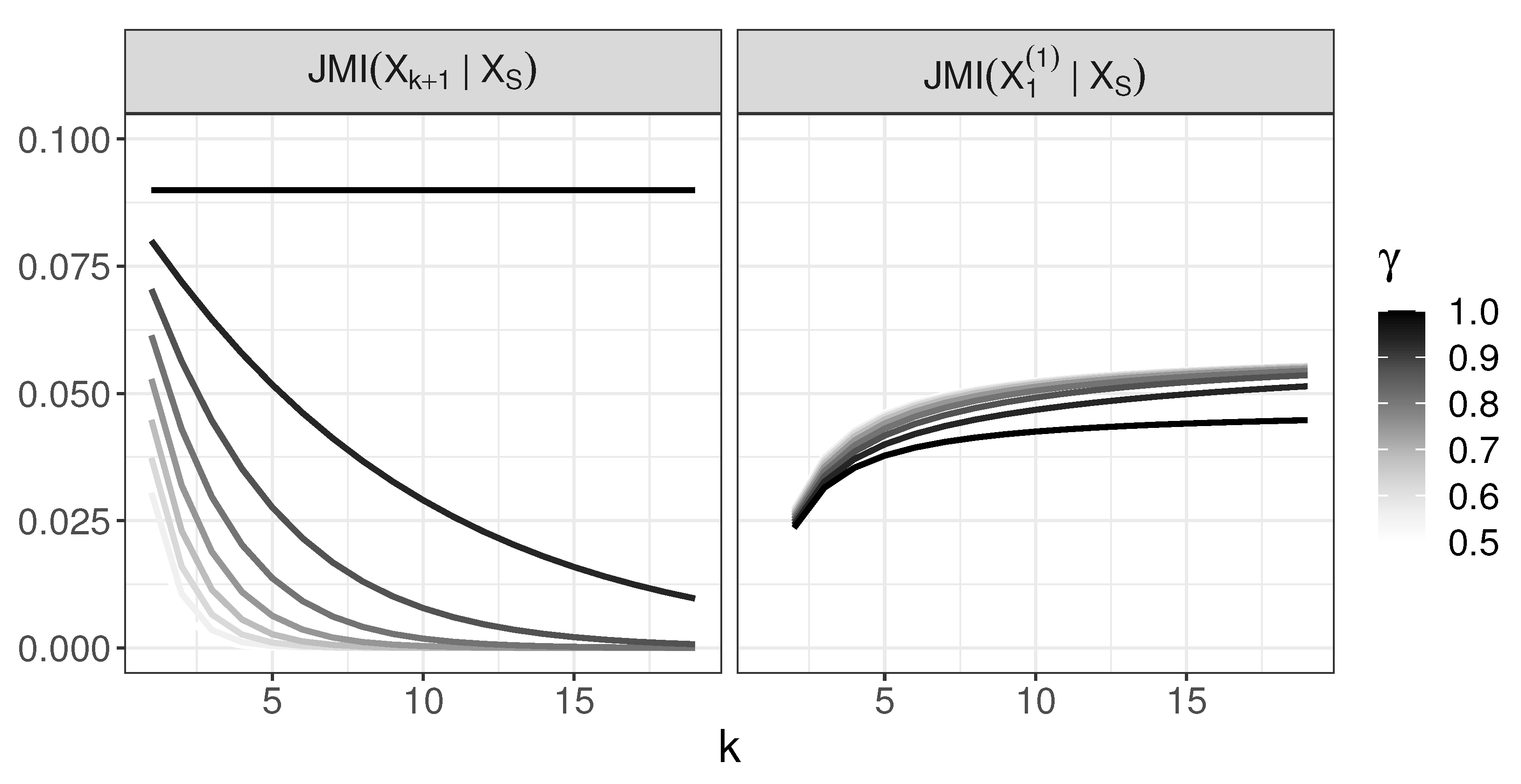
4.3. Behavior of JMI
- For active predictors are chosen in the right order and is not chosen before them;
- For , variable is chosen at a certain step before all are chosen, and we evaluate a moment when this situation occurs.
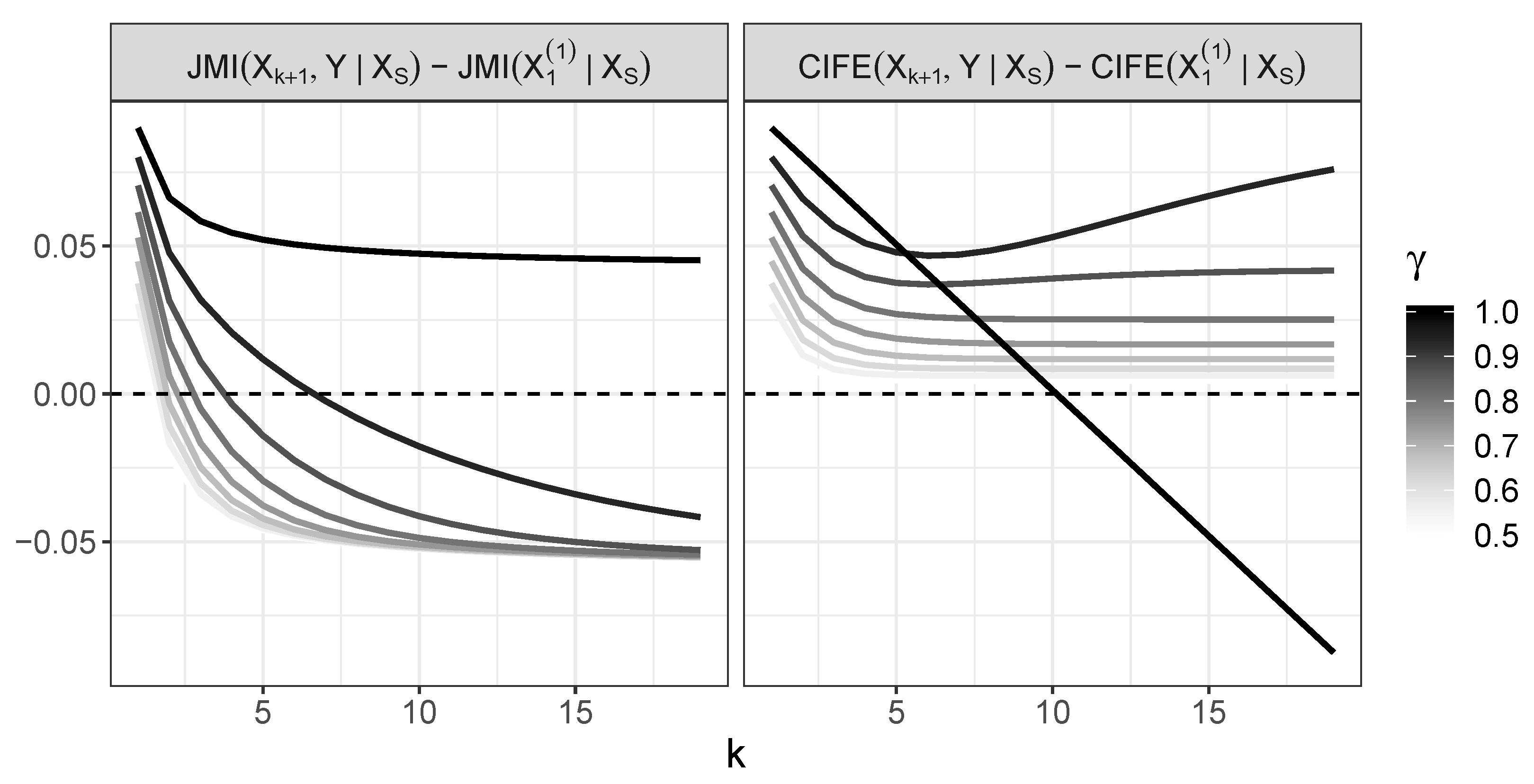
4.4. Behavior of CIFE and Its Comparison with JMI
- For , CIFE incorrectly chooses at some point;
- For , CIFE selects variables in the right order.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guyon, I.; Elyseeff, A. An introduction to feature selection. In Feature Extraction, Foundations and Applications; Springer: Berlin/Heidelberger, Germany, 2006; Volume 207, pp. 1–25. [Google Scholar]
- Brown, G.; Pocock, A.; Zhao, M.; Luján, M. Conditional likelihood maximisation: A unifying framework for information theoretic feature selection. J. Mach. Learn. Res. 2012, 13, 27–66. [Google Scholar]
- Gao, S.; Ver Steeg, G.; Galstyan, A. Variational Information Maximization for Feature Selection. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; pp. 487–495. [Google Scholar]
- Lafferty, J.; Liu, H.; Wasserman, L. parse nonparametric graphical models. Stat. Sci. 2012, 27, 519–537. [Google Scholar] [CrossRef]
- Liu, H.; Xu, M.; Gu, H.; Gupta, A.; Lafferty, J.; Wasserman, L. Forest density estimation. J. Mach. Learn. Res. 2011, 12, 907–951. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-VCH: Hoboken, NJ, USA, 2006. [Google Scholar]
- Yeung, R.W. A First Course in Information Theory; Kluwer: South Holland, The Netherlands, 2002. [Google Scholar]
- McGill, W.J. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Ting, H.K. On the Amount of Information. Theory Probab. Appl. 1960, 7, 439–447. [Google Scholar] [CrossRef]
- Han, T.S. Multiple mutual informations and multiple interactions in frequency data. Inform. Control 1980, 46, 26–45. [Google Scholar] [CrossRef]
- Meyer, P.; Schretter, C.; Bontempi, G. Information-theoretic feature selection in microarray data using variable complementarity. IEEE J. Sel. Top. Signal Process. 2008, 2, 261–274. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural. Comput. Appl. 2014, 24, 175–186. [Google Scholar] [CrossRef]
- Lin, D.; Tang, X. Conditional infomax learning: An integrated framework for feature extraction and fusion. In European Conference on Computer Vision 2006 May 7; Springer: Berlin/Heidelberg, Germany, 2006; pp. 68–82. [Google Scholar]
- Mielniczuk, J.; Teisseyre, P. Stopping rules for information-based feature selection. Neurocomputing 2019, 358, 255–274. [Google Scholar] [CrossRef]
- Yang, H.H.; Moody, J. Data visualization and feature selection: New algorithms for nongaussian data. Adv. Neural. Inf. Process Syst. 1999, 12, 687–693. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1226–1238. [Google Scholar] [CrossRef]
- Michalowicz, J.; Nichols, J.M.; Bucholtz, F. Calculation of differential entropy for a mixed gaussian distribution. Entropy 2008, 10, 200–206. [Google Scholar] [CrossRef]
- Moshkar, K.; Khandani, A. Arbitrarily tight bound on differential entropy of gaussian mixtures. IEEE Trans. Inf. Theory 2016, 62, 3340–3354. [Google Scholar] [CrossRef]
- Huber, M.; Bailey, T.; Durrant-Whyte, H.; Hanebeck, U. On entropy approximation for gaussian mixture random vectors. In Proceedings of the 2008 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems, Seoul, Korea, 20–22 August 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 181–189. [Google Scholar]
- Singh, S.; Póczos, B. Nonparanormal information estimation. arXiv 2017, arXiv:1702.07803. [Google Scholar]
- Watanabe, S. Iformation theoretical analysis of multivariate correlation. IBM J. Res. Dev. 1960, 45, 211–232. [Google Scholar]
- Pena, J.M.; Nilsson, R.; Bjoerkegren, J.; Tegner, J. Towards scalable and data efficient learning of Markov boundaries. Int. J. Approx. Reason. 2007, 45, 211–232. [Google Scholar] [CrossRef]
- Achille, A.; Soatto, S. Emergence of invariance and disentanglements in deep representations. J. Mach. Learn. Res. 2018, 19, 1948–1980. [Google Scholar]
- Macedo, F.; Oliveira, M.; Pacecho, A.; Valadas, R. Theoretical foundations of forward feature selection based on mutual information. Neurocomputing 2019, 325, 67–89. [Google Scholar] [CrossRef]

| (a) , , | ||||
| 0.1114 | ||||
| 0.0527 | 0.0422 | |||
| 0.0241 | 0.0192 | 0.0176 | ||
| 0.0589 | 0.0000 | 0.0000 | 0.0000 | |
| (b) , , | ||||
| 0.1114 | ||||
| 0.0527 | 0.0422 | |||
| 0.0241 | 0.0192 | 0.0205 | 0.0208 | |
| 0.0589 | 0.0000 | 0.0266 | ||
| (c) , , | ||||
| 0.1114 | ||||
| 0.0527 | 0.0422 | |||
| 0.0241 | 0.0192 | 0.0169 | ||
| 0.0589 | 0.0000 | −0.0083 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Łazęcka, M.; Mielniczuk, J. Analysis of Information-Based Nonparametric Variable Selection Criteria. Entropy 2020, 22, 974. https://doi.org/10.3390/e22090974
Łazęcka M, Mielniczuk J. Analysis of Information-Based Nonparametric Variable Selection Criteria. Entropy. 2020; 22(9):974. https://doi.org/10.3390/e22090974
Chicago/Turabian StyleŁazęcka, Małgorzata, and Jan Mielniczuk. 2020. "Analysis of Information-Based Nonparametric Variable Selection Criteria" Entropy 22, no. 9: 974. https://doi.org/10.3390/e22090974
APA StyleŁazęcka, M., & Mielniczuk, J. (2020). Analysis of Information-Based Nonparametric Variable Selection Criteria. Entropy, 22(9), 974. https://doi.org/10.3390/e22090974





