Composite Multiscale Partial Cross-Sample Entropy Analysis for Quantifying Intrinsic Similarity of Two Time Series Affected by Common External Factors
Abstract
1. Introduction
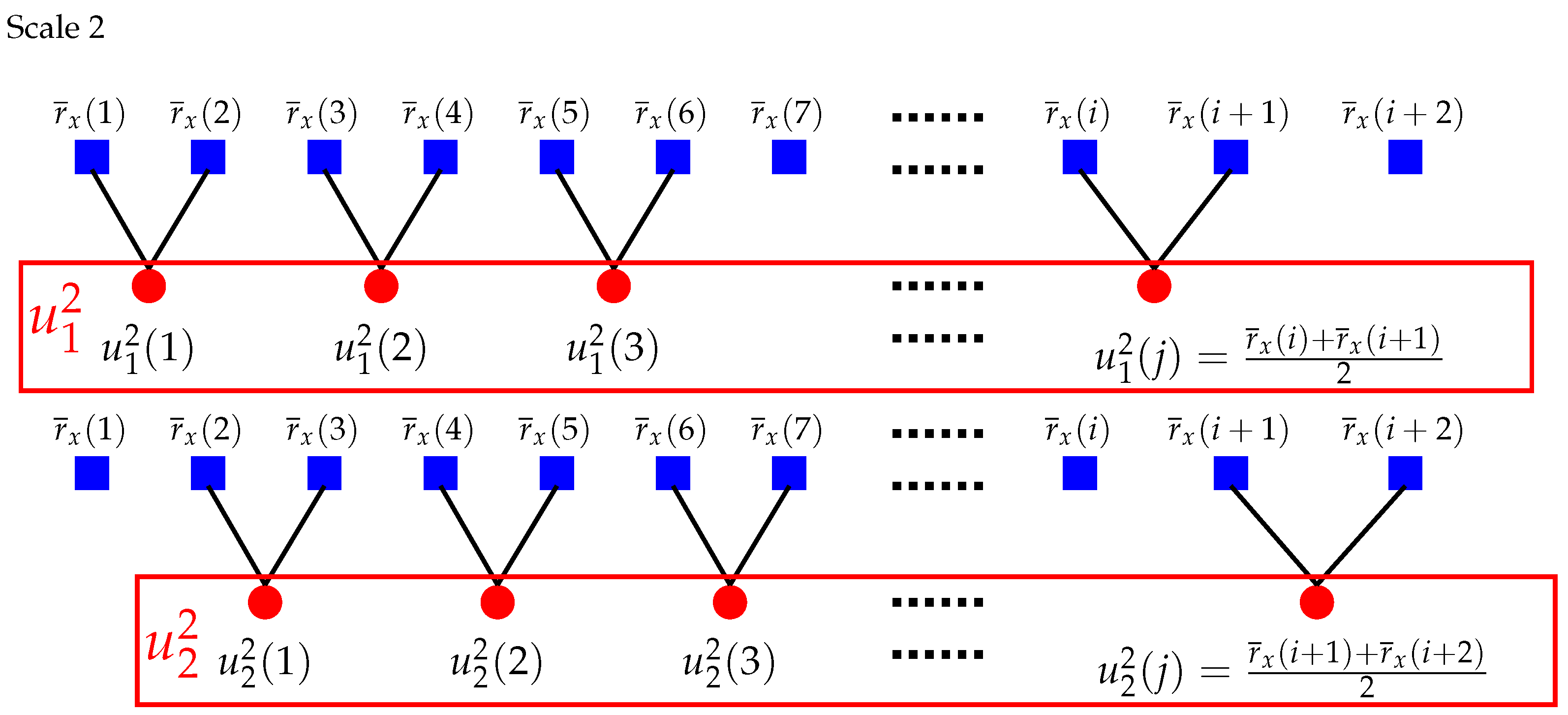
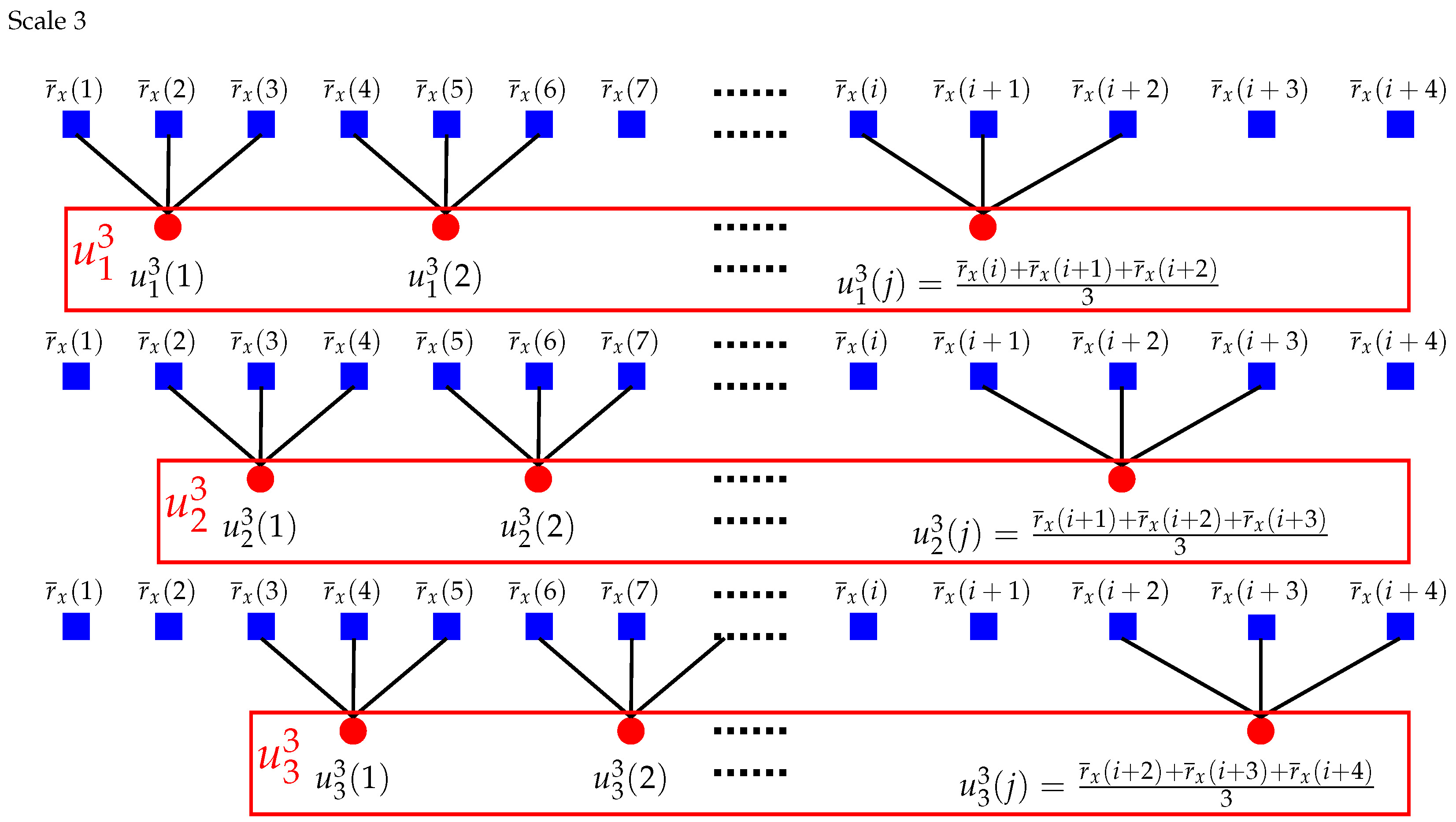
2. Composite Multiscale Partial Cross-Sample Entropy
3. Numerical Experiments for Artificial Time Series
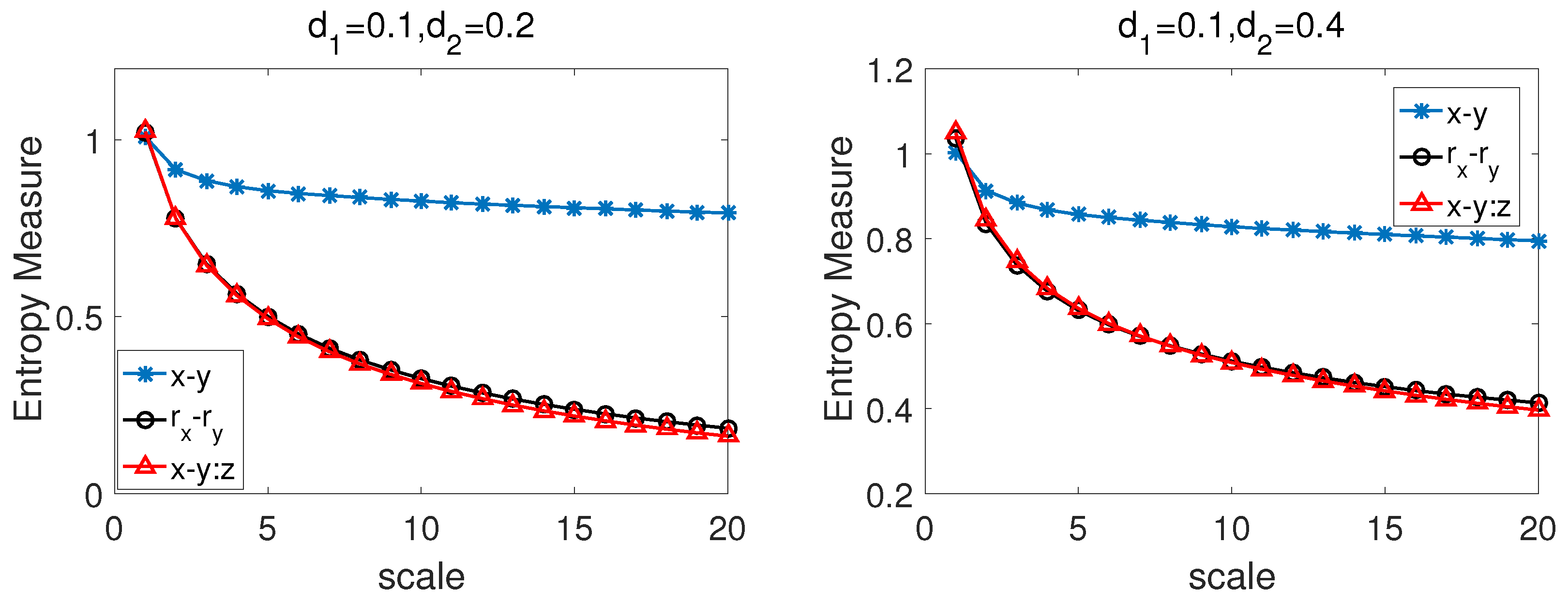
3.1. Bivariate Fractional Brownian Motion (BFBMs)
3.2. TWO-Component ARFIMA Process
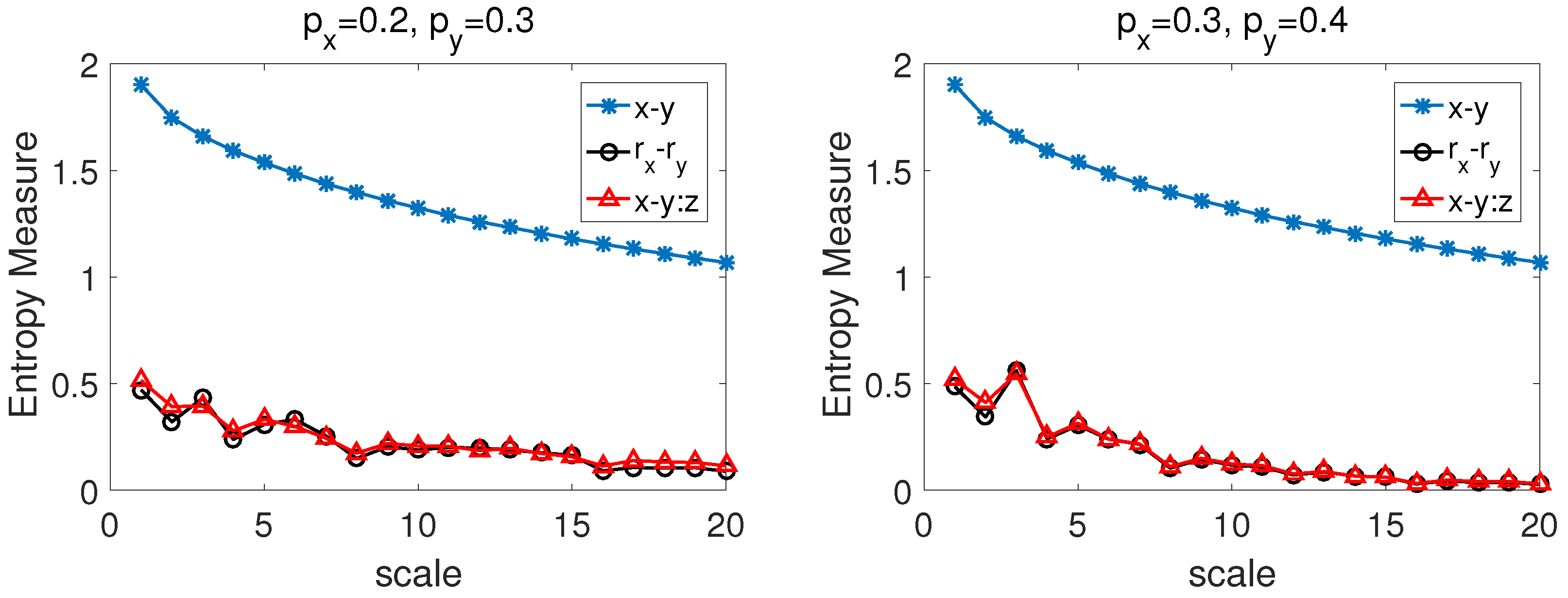
3.3. Multifractal Binomial Measures
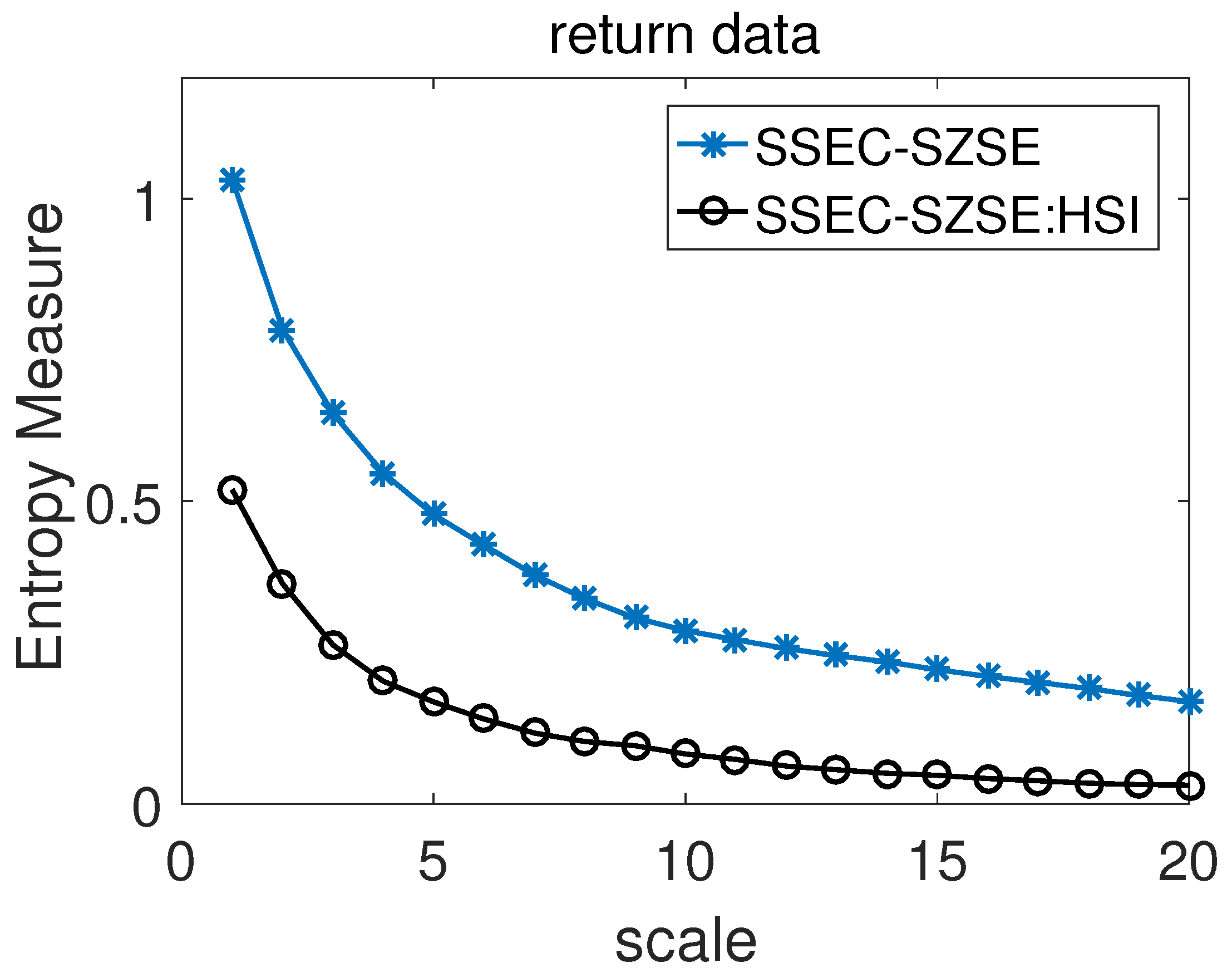
4. Application to Stock Market Index
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Campillo, M.; Paul, A. Long-Range Correlations in the Diffuse Seismic Coda. Science 2003, 299, 547–549. [Google Scholar] [CrossRef] [PubMed]
- Auyang, S.Y. Foundations of Complex-System Theories: In Economics, Evolutionary Biology, and Statistical Physics; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Plerou, V.; Stanley, H.E. Stock return distributions: Tests of scaling and universality from three distinct stock markets. Phys. Rev. E 2008, 77, 037101. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rényi, A. On measures of entropy and information. In Proceedings of the 4th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1960; University of California Press: Berkeley, CA, USA, 1961; Volume 5073, pp. 547–561. [Google Scholar]
- Tsallis, C. Possible Generalization of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tribus, M. The Maximum Entropy Formalism; MIT Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Grassberger, P.; Procaccia, I. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar] [CrossRef]
- Eckmann, J.P.; Ruelle, D.; Ruelle, D. Ergodic theory of chaos and strange attractors. Rev. Mod. Phys. 1985, 57, 617–656. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Pincus, S.M. Approximate entropy (ApEn) as a complexity measure. Chaos 1995, 5, 110–117. [Google Scholar] [CrossRef]
- Pincus, S.M. Quantifying complexity and regularity of neurobiological systems. Methods Neurosci. 1995, 28, 336–363. [Google Scholar]
- Pincus, S.M.; Viscarello, R.R. Approximate entropy: A regularity measure for fetal heart rate analysis. Obstet. Gynecol. 1992, 79, 249–255. [Google Scholar]
- Schuckers, S.A.C. Use of approximate entropy measurements to classify ventricular tachycardia and fibrillation. J. Electrocardiol. 1998, 31, 101–105. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time–series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef] [PubMed]
- Lake, D.E.; Richman, J.S.; Griffin, M.P.; Moorman, J.R. Sample entropy analysis of neonatal heart rate variability. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2002, 283, R789–R797. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.Z.; Qian, X.Y.; Lu, H.Y. Cross-sample entropy of foreign exchange time series. Physica A 2010, 389, 4785–4792. [Google Scholar] [CrossRef]
- Costa, M.; Peng, C.K.; Goldberger, A.L.; Hausdorff, J.M. Multiscale entropy analysis of human gait dynamics. Physica A 2003, 330, 53–60. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of biological signals. Phys. Rev. E 2005, 71, 021906. [Google Scholar] [CrossRef]
- Thuraisingham, R.A.; Gottwald, G.A. On multiscale entropy analysis for physiological data. Physica A 2006, 366, 323–332. [Google Scholar] [CrossRef]
- Peng, C.K.; Costa, M.; Goldberger, A.L. Adaptive data analysis of complex fluctuations in physiologic time series. Adv. Adapt. Data Anal. 2009, 1, 61–70. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, G.L.; Liu, H.S.; Zou, H.J.; Guo, W.Z. Bearing fault diagnosis using multi-scale entropy and adaptive neuro–fuzzy inference. Expert Syst. Appl. 2010, 37, 6077–6085. [Google Scholar] [CrossRef]
- Lin, J.L.; Liu, J.Y.C.; Li, C.W.; Tsai, L.F.; Chung, H.Y. Motor shaft misalignment detection using multiscale entropy with wavelet denoising. Expert Syst. Appl. 2010, 37, 7200–7204. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Wang, C.C.; Lee, K.Y. Time series analysis using composite multiscale entropy. Entropy 2013, 15, 1069–1084. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Lin, S.G.; Lee, K.Y.; Peng, C.K. Analysis of complex time series using refined composite multiscale entropy. Phys. Lett. A 2014, 378, 1369–1374. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P.J.; Feng, G.C. Modified multiscale cross-sample entropy for complex time series. Appl. Math. Comput. 2016, 289, 98–110. [Google Scholar]
- Lin, T.K.; Chien, Y.H. Performance evaluation of an entropy-based structural health monitoring system utilizing composite multiscale cross-sample entropy. Entropy 2019, 21, 41. [Google Scholar] [CrossRef]
- Wu, Y.; Shang, P.J.; Li, Y.L. Multiscale sample entropy and cross-sample entropy based on symbolic representation and similarity of stock markets. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 49–61. [Google Scholar] [CrossRef]
- Wang, F.; Zhao, W.C.; Jiang, S. Detecting asynchrony of two series using multiscale cross–trend sample entropy. Nonlinear Dyn. 2020, 99, 1451–1465. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Li, L.; Cao, J.; Mandic, D.P. Multivariate multiscale entropy for brain consciousness analysis. In Proceedings of the IEEE Engineering in Medicine and Biology Society (EMBC), Boston, MA, USA, 30 August–3 September 2011; pp. 810–813. [Google Scholar]
- Ahmed, M.U.; Mandic, D.P. Multivariate multiscale entropy: A tool for complexity analysis of multichannel data. Phys. Rev. E 2011, 84, 061918. [Google Scholar] [CrossRef]
- Looney, D.; Adjei, T.; Mandic, D.P. A Novel Multivariate Sample Entropy Algorithm for Modeling Time Series Synchronization. Entropy 2018, 20, 82. [Google Scholar] [CrossRef]
- Jamin, A.; Humeau-Heurtier, A. (Multiscale) Cross-Entropy Methods: A Review. Entropy 2020, 22, 45. [Google Scholar] [CrossRef]
- Kenett, D.Y.; Shapira, Y.; Ben-Jacob, E. RMT assessments of the market latent information embedded in the stocks’ raw, normalized, and partial correlations. J. Probab. Stat. 2009, 2009, 249370. [Google Scholar] [CrossRef]
- Kenett, D.Y.; Tumminello, M.; Madi, A.; Gur-Gershgoren, G.; Mantegna, R.N.; Ben-Jacob, E. Dominating clasp of the financial sector revealed by partial correlation analysis of the stock market. PLoS ONE 2010, 5, e15032. [Google Scholar] [CrossRef] [PubMed]
- Shapira, Y.; Kenett, D.Y.; Ben-Jacob, E. The index cohesive effect on stock market correlations. Eur. Phys. J. B 2009, 72, 657. [Google Scholar] [CrossRef]
- Baba, K.; Shibata, R.; Sibuya, M. Partial correlation and conditional correlation as measures of conditional independence. Aust. N. Z. J. Stat. 2004, 46, 657–664. [Google Scholar] [CrossRef]
- Yuan, N.M.; Fu, Z.T.; Zhang, H.; Piao, L.; Xoplak, E.I.; Luterbacher, J. Detrended Partial-Cross-Correlation Analysis: A New Method for Analyzing Correlations in Complex System. Sci. Rep. 2015, 5, 8143. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.Y.; Liu, Y.M.; Jiang, Z.Q.; Podobnik, B.; Zhou, W.X.; Stanley, H.E. Detrended partial cross-correlation analysis of two nonstationary time series influenced by common external forces. Phys. Rev. E 2015, 91, 062816. [Google Scholar] [CrossRef]
- Wei, Y.L.; Yu, Z.G.; Zou, H.L.; Anh, V.V. Multifractal temporally weighted detrended cross-correlation analysis to quantify power-law cross-correlation and its application to stock markets. Chaos 2017, 27, 063111. [Google Scholar]
- Lavancier, F.; Philippe, A.; Surgailis, D. Covariance function of vector self–similar processes. Stat. Probab. Lett. 2009, 79, 2415–2421. [Google Scholar] [CrossRef][Green Version]
- Coeurjolly, J.F.; Amblard, P.O.; Achard, S. On multivariate fractional Brownian motion and multivariate fractional Gaussian noise. In Proceedings of the 2010 18th European Signal Processing Conference, Aalborg, Denmark, 23–27 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 1567–1571. [Google Scholar]
- Amblard, P.O.; Coeurjolly, J.F. Identification of the multivariate fractional Brownian motion. IEEE Trans. Signal Process. 2011, 59, 5152–5168. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Fractional differencing. Biometrika 1981, 68, 165–176. [Google Scholar] [CrossRef]
- Podobnik, B.; Ivanov, P.; Biljakovic, K.; Horvatic, D.; Stanley, H.E.; Grosse, I. Fractionally integrated process with power-law correlations in variables and magnitudes. Phys. Rev. E 2005, 72, 026121. [Google Scholar] [CrossRef]
- Podobnik, B.; Stanley, H.E. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [PubMed]
- Podobnik, B.; Horvatic, D.; Ng, A.L.; Stanley, H.E.; Ivanov, P.C. Modeling long-range cross-correlations in two-component ARFIMA and FIARCH processes. Physica A 2008, 387, 3954–3959. [Google Scholar] [CrossRef]
- Shi, W.B.; Shang, P.J. The multiscale analysis between stock market time series. Int. J. Mod. Phys. C 2015, 26, 1550071. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Han, G.; Jiang, S.; Yu, Z. Composite Multiscale Partial Cross-Sample Entropy Analysis for Quantifying Intrinsic Similarity of Two Time Series Affected by Common External Factors. Entropy 2020, 22, 1003. https://doi.org/10.3390/e22091003
Li B, Han G, Jiang S, Yu Z. Composite Multiscale Partial Cross-Sample Entropy Analysis for Quantifying Intrinsic Similarity of Two Time Series Affected by Common External Factors. Entropy. 2020; 22(9):1003. https://doi.org/10.3390/e22091003
Chicago/Turabian StyleLi, Baogen, Guosheng Han, Shan Jiang, and Zuguo Yu. 2020. "Composite Multiscale Partial Cross-Sample Entropy Analysis for Quantifying Intrinsic Similarity of Two Time Series Affected by Common External Factors" Entropy 22, no. 9: 1003. https://doi.org/10.3390/e22091003
APA StyleLi, B., Han, G., Jiang, S., & Yu, Z. (2020). Composite Multiscale Partial Cross-Sample Entropy Analysis for Quantifying Intrinsic Similarity of Two Time Series Affected by Common External Factors. Entropy, 22(9), 1003. https://doi.org/10.3390/e22091003




