1. Introduction
Artificial Bee Colony (ABC) is a swarm intelligence (SI) heuristic for optimization problems inspired by the foraging behavior of honeybees. It was initially designed to solve box-constrained continuous problems [
1]. The algorithm consists of three main steps–employed bees, onlooker bees and scout bees–that perform local and global search. In the original implementation of the ABC, at the employed and onlooker bees steps, a single component from each solution is chosen to be updated by a position update rule.
Following its conception, improvements to the search capabilities of the original ABC were proposed by many researchers. The great majority of these propositions centered around changes to the initialization of solutions in the solution space, update procedure of the first two phases and selection method in the onlooker phase [
2]. Despite differences between each variant, they all share a common trait: the solution update rule chooses one to
n decision variables with equal probability under a random uniform distribution. This may allow for a better exploration of the search space and prevent solutions to collapse in the same subspace at later iterations. However, issues to the consistency and convergence of the algorithm may arise due to this design choice.
Besides the uniformity of choice of decision variables, it has been observed that most ABC variants handle problems whose objective functions are multimodal poorly. Adaptations of the ABC to solve problems from this family include changes to the main update equation; adoption of a self-adaptive solution set growth/shrink scheme; and adaptations to the re-sampling step of stagnated solutions [
2]. Despite efforts, the ABC still lacks a way to understand how the solutions are fitted and how apart they are in the objective function landscape.
Taking into account the deficiencies observed in the ABC mentioned above, we propose the Adaptive Decision Variable Matrix (A-DVM), a self-adaptive decision variable selection procedure that is an extension of a deterministic solution variable scheme developed in Mollinetti et al. [
3]. A-DVM builds an augmented binary matrix that automatically balances deterministic and random decision variable selection to maintain a healthy amount of exploration in the early iterations while emphasizing exploitation in later stages. Levels of exploration and exploitation are monitored by an indicator of how many solutions cover the search space. The chosen estimator is the
value, a measure proposed by Morrison [
4], which provides a reliable assessment of the shape of the distribution of the solutions along the main and peripheral axes of search. To validate the proposed approach, A-DVM is incorporated into the original ABC and several state-of-the-art variants and evaluated in a test set that features 15 multimodal unconstrained problems. Results are compared to the original counterparts of the ABCs, as well as to some well-established optimization algorithms such as the Particle Swarm Optimization (PSO) and Differential Evolution (DE).
The contributions that the A-DVM brings is twofold. First, a selection scheme that attempts to establish a balance between the global and local search along with the iterations so that the search can be conducted more efficiently. Naturally, it can be incorporated into any version of the ABC without interfering with any other mechanism. Second, a mean to assess how solutions of the solution set are spread throughout the search space and how well they fit the objective function value landscape. Such information is very beneficial in guiding solutions out of deceptive local optima when considering multimodal problems.
This work is organized as follows:
Section 2 describes the original ABC.
Section 3 discusses the main issues behind the fully randomized selection.
Section 4 explains the idea behind the A-DVM.
Section 5 reports the experiments and discusses the results. Lastly,
Section 6 outlines the conclusion of the paper and points some future directions.
3. Issues Of Randomization
Population-based optimization methods usually employ randomization. By choosing step sizes, decision variables or even target solutions at random during the update steps, population-based optimization methods can “cover more ground” in the search space effortlessly. This is a key element to the success of population-based heuristics, but not without some unintended side effects.
For the sake of clarity, we refer in accordance to [
14] to a neighborhood
as the classical definition of a Euclidean ball centered at a point
,
where
is the
norm and
. Assume that a stochastic heuristic, such as the Artificial Bee Colony (ABC), runs infinitely on a problem
, where
f is the objective function,
S is the feasible set, and
is a problem family. Moreover, borrowing some concepts explained in [
15], let
denote the infinite sequence of iterates generated by the heuristic where
is a sequence of random numbers distributed independently from
. Let
and
denote the set of accumulation points and the closure of the sequence
. Lastly, let
denote the set of global optima. Clearly no
can be “seen” if
or
.
In the following section, we will see how randomization affects the performance of the ABC.
An Analysis of the ABC Decision Variable Selection
Often overlooked, a common aspect of the ABC variants is that decision variable is chosen according to the same uniform distribution with for all during the Onlooker and Employed bees steps.
Let
be the probability that
is chosen in (
3). For each situation below, we assume that
and
is monotonically decreasing, i.e.,
. The original ABC chooses a single
each time it calls (
3) during the Onlooker and Employed bees step. We need to notice the following issues brought by the process of selecting
j randomly.
Failed update steps cause solutions to be trapped in basins of attraction: Choosing the same wrong decision variable many times fails to move solutions out of basins of attraction, contributing to wasteful iterations, premature convergence and needless flagging of solutions at the scout bees step. Let . Suppose that and . Also suppose , , , and and are adjacent to .
Lastly, let
be a component of
such that a successful update moves
to
while an update to
for any
moves
to
.
is moved in (
3) one axis at a time, if
is chosen, then (
4) accepts
and
. Otherwise,
is incremented by 1 every time
is rejected by (
4). If each component is chosen in (
3) with equal probability, then the probability of
to be chosen is
. Therefore,
has a probability of
to move to a basin of attraction
similar to
, and probability
to move to a more promising region
.
Decision variables may never be chosen: If the problem is of high-dimensional
or the evaluation function
is so expensive that only a limited number of objective function calls are allowed, there will be at least a component
that may never be chosen in (
3). Let
be the probability of
not to be chosen at (
3). Then the probability of
not to be chosen be at the end of
iterations is
. It is clear that
converges to 0 as the number of iterations goes to infinity. If
and ABC runs
iterations, then
, so
is not chosen in (
3).
At first glance, there would be two ways to resolve these issues. Either assign a non-equal probability to choose the decision variable or choose more than one
at (
3) to be updated simultaneously. We disprove the effectiveness of these “quick fixes” through following arguments.
Changing the choice probabilities of decision variables to be unequal would not solve issue in high-dimensional problems because still converges to 0. A sufficient measure, in this case, would keep previously chosen components in memory. This only increases the complexity of the Onlooker and Employed bees phase from to if non-visited components are kept in a separate list for each solution in X in an efficient way
Changing (
3) to choose multiple components from
would not improve issue
. Let
and suppose that
is chosen for each
to update. Update rule (
3) is an affine transformation in the
j-th axis along the line segment between
and
. If
, then
simultaneous affine transformations in the
-dimensional subspace between
and
would be performed. In terms of complexity, there would be no burden
j decision variables are updated at once by means of a matrix product operation. However, in terms of performance, there would be no improvement because of two reasons. First, moving along many axes at once does not reduce the possibility of
to remain in
if
. Secondly, setting
in (
3) has been shown to be not as good as
in later iterations due to the coarseness of the search when most of the solutions have converged to a single accumulation point [
2].
In the following section, we present a method that provides a solution to the issues stated above, the Adaptive Decision Variable Matrix (A-DVM). A-DVM is a decision selection variable scheme proposed to the ABC.
4. A Novel Decision Variable Selection Mechanism
We propose a method for selecting decision variables efficiently without any additional memory nor simultaneous update of multiple components. The Adaptive Decision Variable Matrix (A-DVM) is an extension of the decision variable selection procedure of Mollinetti et al. [
3]. It exploits the same modular nature as the Artificial Bee Colony (ABC), and thereby it can be integrated to the employed and/or onlooker bees phase without interfering with any additional steps of the original or any variant. To emphasize the difference between the A-DVM and Mollinetti et al. [
3] deterministic selection, we briefly explain their proposition as follows.
4.1. Fully Deterministic Decision Variable Selection
The selection scheme proposed by Mollinetti et al. [
3] is inspired by Cantor’s Diagonalization argument used to prove the non-existence of bijection from the set of natural numbers to the set of real numbers [
16,
17]. Cantor’s argument state that any binary square matrix
T does not have the same column as the vector consisting of the complements of the diagonal elements of
T. The authors extended this notion to generate new solutions
in the solution set
X. For any given problem, the deterministic decision variable selection arranges the solution set
X into a
matrix:
If
A is a square matrix, the entries on the main diagonal are stored in an
m-vector
and undergo the update step. In general, the higher the number of solutions, the better the exploration of the search, and so
holds. If
A is wide, then vector
c consists of entries on the main diagonal and the superdiagonals of
A offset
d units to the right. For instance, if
A is a
matrix, then
c will be:
The vector
c allows (
3) to be performed simultaneously for all columns of
A by means of a simple vector multiplication:
where ⊙ is the Hadamard product,
is a
column vector of values sampled from
,
, and
is a function similar to (
4) defined as:
Suppose in the matrix A of the above example that if and , then . Thus, entries and are replaced with in A, and the corresponding values of f are updated.
Lastly, a safeguard step is performed so that every decision variable of each candidate solution can be updated at least once before the algorithm termination. The last column
of
A is moved to the first position and the remaining columns are shifted one position to the right. Referring to the example, the matrix
A is now:
This step ensures that every decision variable is updated by (
8) every
d iterations.
The results in Mollinetti et al. [
3] indicate that eliminating the randomness in the choice of the decision variable in (
3) boosted the performance of the original ABC in multimodal problems of up to 30 decision variables. However, it is observed that the diversity of solutions was compromised because local search was more emphasized over global search. From this result, we suppose that the bias towards local search brought by the fully deterministic parameter selection has yet not solved
issue . In fact, if anything, the fully deterministic selection made it worse. Therefore, reintroducing a small degree of randomness while guaranteeing that every solution is chosen at some iteration is a step in the right direction to refocus global search.
4.2. A Self-Adaptive Decision Variable Selection Procedure (A-DVM)
Let us change the focus to a partially deterministic selection, and reintroduce an adaptive degree of randomness to the selection process based on the “spread” of solutions throughout the search space. The variables
are chosen via a binary decision matrix. The goal of the A-DVM is not only to provide an acceptable solution to the issues discussed in
Section 3, but to improve the overall performance of the state-of-the-art of ABC for the multimodal and high-dimensional problem of the form of (
1).
The main piece of the A-DVM is the
binary matrix
that represents which
has been chosen to be updated by (
3) or (
8). The matrix
is a composition of two matrices,
, a binary matrix with a single 1 in each column, whose row is determined randomly according to a uniform distribution; and
, a matrix with 0 or 2 in each entry generated by the fully deterministic scheme of Mollinetti et al. [
3]. For example,
and
are matrices of the form:
The matrix
is the result of a composition of
into
. That means some solutions
have their
j-th component randomly selected when updated by (
3) or (
8) while the rest have their
j-th component chosen by the fully deterministic scheme. We write
when
of the columns of
are from
and the remaining
are from
. An example of
based on the above example is as follows:
The degree of how much
is favored over
is represented by the coefficient
that is iteratively adjusted as follows, to maintain a healthy diversity of solutions while balancing between local search and local search:
where
is the measure of the dispersion of the population at the current iteration and
and
are scaling parameters set to
and
in accordance to McGinley et al. [
18]. Values of
close to 1 signify high population diversity and activate exploitation by the deterministic selection. On the other hand, values close to 0 boost exploration using random selection. Because solutions in population-based algorithms tend to concentrate around accumulation points
after a considerable amount of iterations [
14],
is increased by a growth function
defined as follows, to intensify local search around
after
iterations:
where
is set to
. The value of
is given by:
where an acceptable value for
was empirically verified to be
.
To ensure that every decision variable is chosen in at least every
d iterations, we introduce a history
that stores which columns of
were put into
, and give a chance to the remaining columns of
to be contained in
at the next iteration. We enforce a bound on the number of iterations that solutions are chosen by the fully deterministic selection to be no more than
and no less than
(refer to (
10)). When the entries in
H are all ones,
H is reinitialized and the whole process runs again. The overall steps of the A-DVM are outlined in Algorithm 2.
| Algorithm 2: Steps of the A-DVM |
![Entropy 22 01004 i002 Entropy 22 01004 i002]() |
4.3. The Dispersion Estimate
Estimating the dispersion of the solutions in the search space is specifically effective for population-based algorithms to deal with multimodal or high-dimensional problems. Measuring how far apart solutions in
X are from each other is very helpful to guide them towards accumulation points or free them from local optima. Significant contributions related to this subject can be found in Ursem [
19] and Back et al. [
20] which introduced the Sparse Population Diversity (SPD) metric, a method for estimating the variation of the solution set by measuring the distance from each solution in relation to the centroid. McGinley et al. [
18] proposed the Healthy Population Diversity (HPD), an extension of the SPD that introduces the concept of individual contribution to the computation of the centroid.
Metrics like SPD and HPD may accurately and inexpensively identify differences between the solutions in
X by measuring the distances to each
. However, this kind of measurement does not take into account how the solutions are distributed in the search space, which is problematic since the same measurement values from SPD and HPD may indicate different search-space coverage of solution of
X. Because of that, we employ the
dispersion measure introduced in Morrisson [
4], initially proposed for Evolutionary Algorithms with binary solution encoding, and adapt it to continuous problems in the form of (
1). Computation of
is as follows:
where
,
and
. The values of
and
are obtained by measuring the moment of inertia of the solution centroid in relation to each solution. We denote as
as the number of solutions
. The centroid
of the
jth components and the moment of inertia
of centroid
are
The first measure
involves a quantitative assessment of the solutions around the distribution centroid. Assuming the distribution around the centroid to be uniform,
is
where
represents the inertia of a uniform distribution:
Measure
indicates how much the calculation of
is misleading when the distribution is not uniform in the search-space, since
only verifies non-uniformity along the principal diagonal of the search space. The second measure
is
where
,
is the characteristic function that returns either 0 or 1 whether a solution belongs to
or
, respectively, and
is the range between
, so that
for an
N-dimensional unit volume.
4.4. Remarks On Complexity
As for the complexity,
function evaluations are done in each employed and onlooker bees phase, so the addition of A-DVM preserves the same
function evaluations per iteration as the classical ABC. The effort to compute the sum of moments of inertia and
dispersion is proportional to the solution set size
[
4]. Updates of solutions (
3) during the employed or onlooker bees is done one by one in a loop require
time for the size
of solution set
X. On the other hand, offline update (
8) can be done in a linear time due to the vector multiplication. We recommend (
8) for parallel versions of the ABC, when
is large or the evaluation of
is expensive.
Regarding lookup table H, it is verified in time which columns of were not chosen to be a part of . Lastly, about binary matrix , because the deterministic parameter selection extracts the diagonal of solution set X, it is recommended to set to ensure that every decision variable of each solution is chosen in at most d iterations.
5. Experiment and Results
A numerical experiment was carried out to answer the following research questions: “Does incorporating the Adaptive Decision Variable Matrix (A-DVM) improve the Artificial Bee Colony (ABC) and its variants overall performance on multimodal problems?”. To provide an answer to that question, we chose 15 instances of (
1), each of which is designed to validate the capability of metaheuristics to handle multimodal and non-smooth objective functions. The instances are ranked in the top 30 hardest continuous optimization functions in the Global Optimization Benchmarks suite [
21]. The number of variables ranges from 2 to 30 to test the robustness of the solvers when dealing with many as well as few variables. Each algorithm is executed 30 times with the same seed interchangeably in a random fashion to avoid bias in the machine load. The number of variables, the box constraint range
and the global optimum of each instance are listed in
Table 1.
Testing involves the incorporation of the A-DVM to the onlooker and employed bees phase of the following versions of the ABC: the original ABC from Karaboga [
22] (ABC+A-DVM), two versions of the global best guided ABC (gbestABC) from Gao et al. [
23] (GBESTABC+A-DVM, GBESTABC2+A-DVM) and two versions of the ABC-X from [
2] for multimodal problems (ABC-XM1+A-DVM, ABC-XM2+A-DVM). The original counterparts were also used for the baseline (ABC, GBESTABC, GBESTABC2, ABC-XM1, ABC-XM5) together with the modified ABC for multidimensional functions (MABC) from Akay and Karaboga [
8] and its version with the A-DVM (MABC+A-DVM). Comparison is not limited only to ABCs and variants, but popular population-based algorithms, such as the Particle Swarm Optimization from Kennedy and Eberhart [
24], Evolutionary Particle Swarm Optimization by Miranda and Fonseca [
25] and Differential Evolution (DE) [
26], were also included in the experiment.
The stopping criteria for each algorithm was set to
function evaluations (FE’s) or if the difference between the best value found so far and the global optimum
is less than
. The population size was common to all algorithms and fixed at 30. For PSO, the inertia factor (
) was set to
and both cognitive and social parameters (
,
) to
. For Differential Evolution (DE) [
26] with
best1bin strategy,
F value was
and
CR . For each version of the ABC:
. For MABC,
,
and
m were
,
, and
of maximum FE’s, respectively. ABC-X parameters were
, maximum population of 66 and minimum of 15 for ABC-Xm1 and
, while for ABC-Xm5, maximum population of 78 and minimum of 17. Lastly, parameters
and
of the A-DVM were set to
.
The experiment was conducted in a machine with the following hardware configuration: Intel core i7-6700 “Skylake” 3.4 GHz CPU; 16 GB RAM DDR4 3200 clocked at 3000 MHz. The running operating system (OS) is UbuntuOS 18.04. All algorithms were written in the python 3 programming language. Floating point operations were handled by the numpy package, version 1.19.1.
Table 2,
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7 show the computational results obtained from this experiment. The statistics used for comparison are the mean, standard deviation, median, and best-worst results obtained from 30 runs with distinct random seeds shown in
Table 6 and
Table 7. Statistical significance between pairs is verified by the Mann-Whitney U-test for non-parametric data, with confidence interval
set to
as shown in
Table 2,
Table 3,
Table 4 and
Table 5. Entries where
denotes no statistical difference between the algorithms. For better legibility, the precision of decimals is set to 5 digits and values lower than
are rounded to 0. Plots of the behavior of each algorithm are shown in
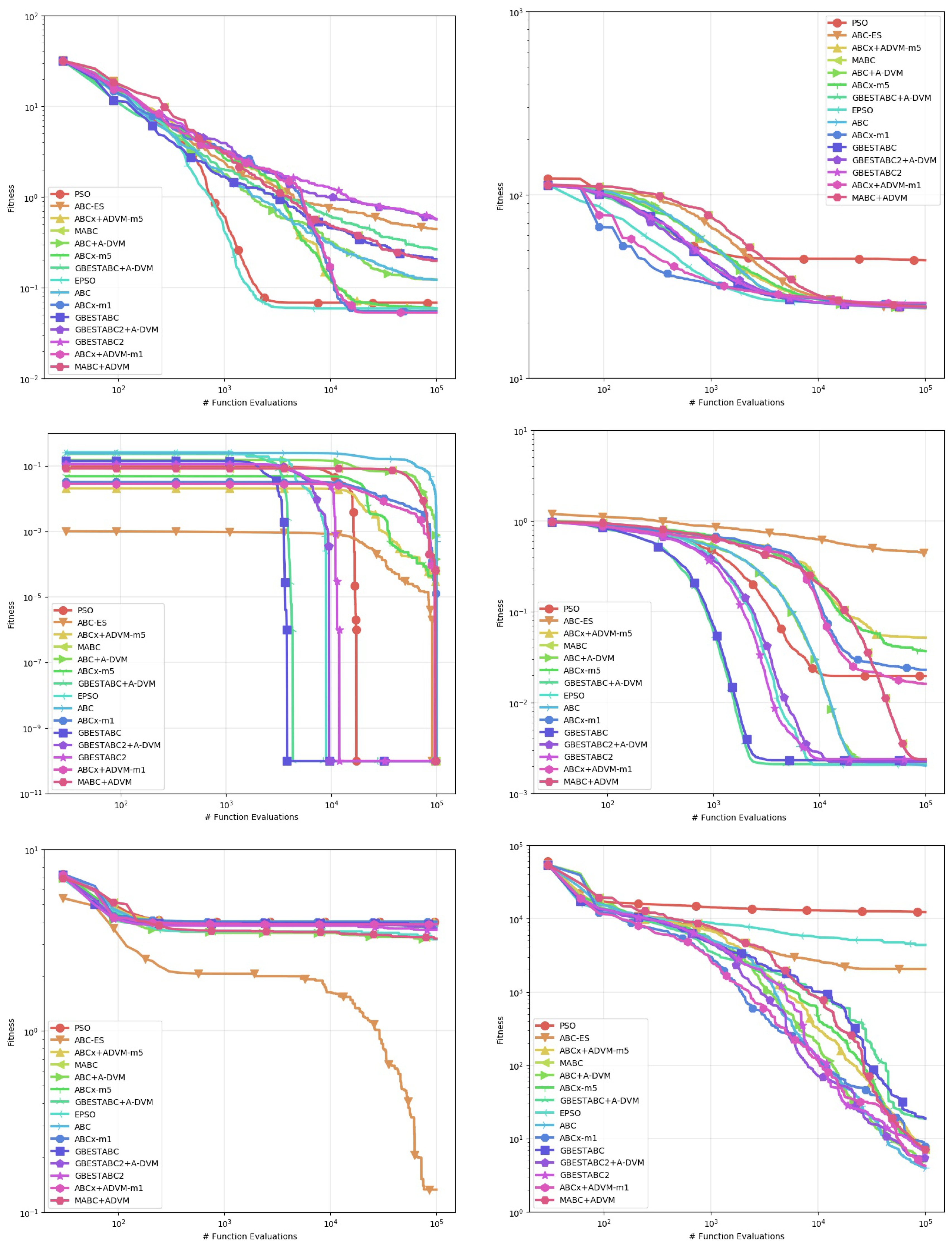
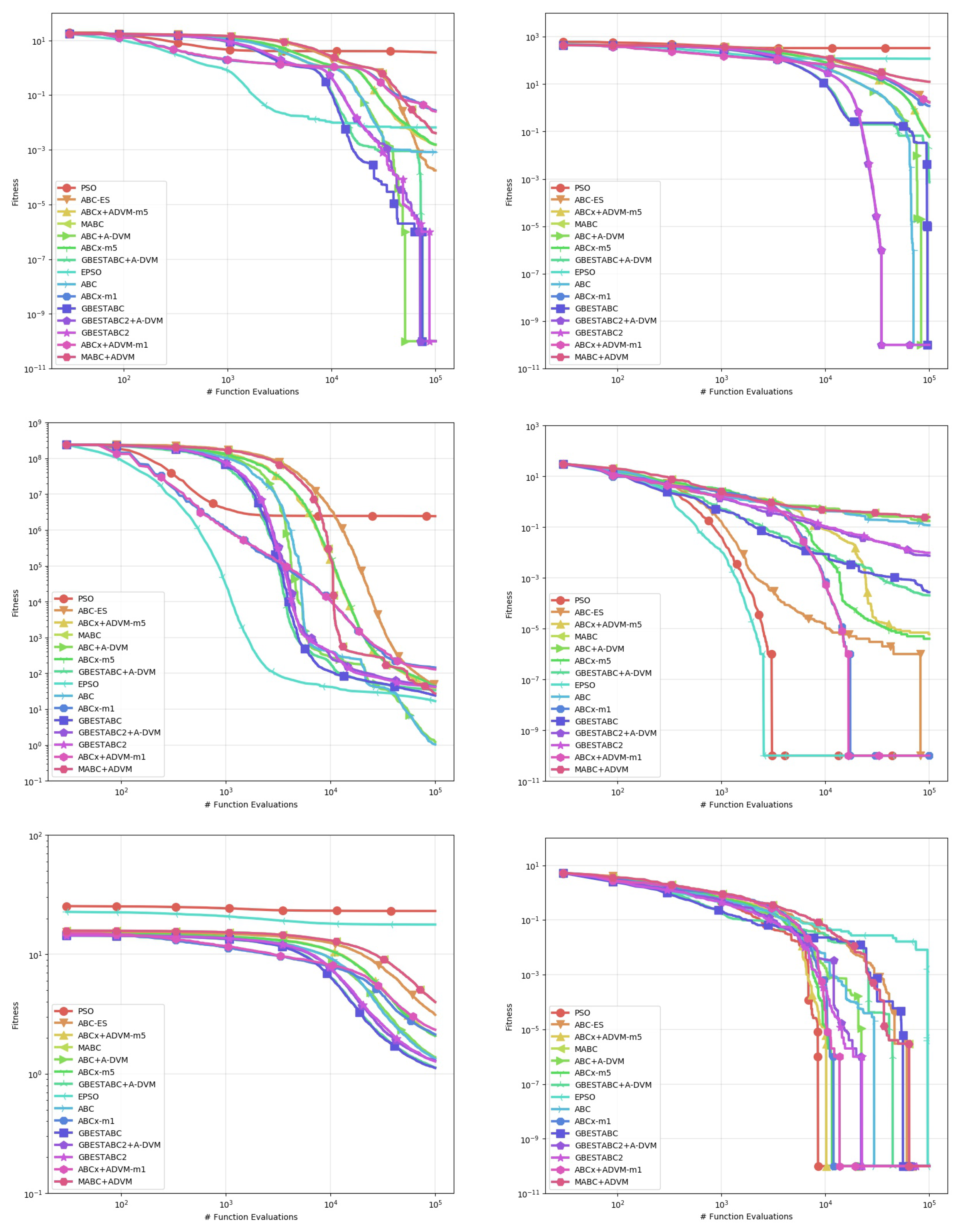
Figure 1,
Figure 2 and
Figure 3. Each line represents the mean of the best solution of all executions for each function evaluation call. All plots were log-scaled for better legibility. If the performance of any algorithm for a particular instance is statistically significant, it means that its
p-value in the U-test is less than
in the pairwise comparison against all other algorithms. The bold numbers in the tables indicate the least value for that particular statistic and instance.
First, we discuss the Rosenbrock, Whitley and Zimmerman function instances where the A-DVM resulted in overall worse performance than all their original counterparts. The A-DVM was indeed able to guide the functions towards a valley, but a thorough local search mechanism was lacking due to the parabolic surface of the Rosenbrock function [
27]. The same behavior is observed in the Whitley and Zimmerman functions, which share the same property as Rosenbrock instance. The poor results in these functions imply a failure of the A-DVM to properly address issues
and
discussed in
Section 3. Additionally, we can relate this case to the no-free-lunch theorem of Wolpert [
28], saying that no algorithm can be strictly better than the others in every problem instance. The inferior results of the A-DVM are also seen for the Rastrigin function in the ABC-X variants. The Cause of such behavior could be due to intensification of the local search mechanism that forced solutions to stay far from the local attractors of the surface of the functions.
Strong evidence of the robustness of the A-DVM against strongly multimodal surfaces was found in the Damavandi, DeVilliersGlasser02 and CrossLegTable instances, ranked as the three hardest functions in the benchmark suite [
21]. Both functions feature large basins of attraction for bad local optima, the number of which is directly proportional to the problem dimensionality. There are two possible causes explaining why the A-DVM versions were not superior to all other versions in these particular instances. First, a small number of dimensions means that a square matrix can be built, providing a thorough exploration of the search space. Second, exploration in the early stages allowed solutions to escape from the basins of attraction.
Evidence that the A-DVM improved the search process in comparison to their counterparts without the search can be seen in the Bukin06, SineEnvelope, CrownedCross and Schwefel06. Although the ABCs with A-DVM were not the best solvers, their robustness was statistically significant in comparison to the versions without A-DVM. Lastly, in the Cola, Griewank, XinSheYang03 and Trefethen, no statistical significance that corroborated that the incorporation of the A-DVM improved or worsened the performance of the original algorithm was found.
6. Conclusions
In this paper, a decision variable selection scheme named Adaptive Decision Variable Matrix (A-DVM) was proposed to be incorporated in the Artificial Bee Colony (ABC) algorithm. A-DVM can be incorporated in both employed and or onlooker bees phases and can be used with any variant of the ABC. A-DVM attempts to balance exploration and exploitation throughout the execution of the algorithm by constructing an augmented binary matrix that represents the choice of components of solutions in the solution set. The binary matrix is composed of a deterministic selection binary matrix that chooses matrix diagonals according to the proposal in [
3] and another binary matrix whose components were selected by a random uniform distribution. The number of columns to be used from the deterministic matrix is determined by a self-adaptive parameter that is based on the
value, a measure of the sparsity of the actual solution set in the search space. Introducing a lookup table of chosen solutions of
guarantees that every solution is a part of
in the update step at least once before termination.
Effects of the A-DVM to the performance of the ABC is verified by a numerical experiment including several versions of the ABC with the A-DVM included and their original counterparts. Representative heuristics such as the Particle Swarm Optimization (PSO), Evolutionary Particle Swarm Optimization (EPSO) and Differential Evolution (DE) are included in the experiment to provide a baseline for the results. For the sake of brevity and to narrow the scope of this work, other prominent Swarm Intelligence (SI) algorithms suited to the multimodal family of problem, such as the monarch butterfly optimization (MBO) [
29]; earthworm optimization algorithm (EWA) [
30]; elephant herding optimization (EHO) [
31]; and moth search (MS) algorithm [
32], were not part of the experiment.
The results indicate that the A-DVM enhances the ability of the ABC to adapt to highly multimodal functions. However, the elimination of the full global search of the stochastic selection resulted in solutions not converging towards accumulation points that are located in basins, as seen in some instances where the A-DVM performed poorly. Integration with ABC variants with smart restart procedures in the scout bees phase may be a possible direction to improve this issue.
Future works include in-depth sensitivity analysis and integration of the selection mechanism to the state-of-the-art ABC used for optimization competitions and testing on large scale problems, mechanical design and power systems to further investigate the performance of the selection. Moreover, a thorough comparative study of multimodal problems using only SI algorithms including the aforementioned examples is due. Another research direction includes applying the proposed method for weight tuning of shallow networks [
33,
34]. Such networks may benefit from the proposed optimization mechanism since it tackles small sample size problems featuring rough objective function landscapes.