Power Conversion and Its Efficiency in Thermoelectric Materials
Abstract
1. Introduction
1.1. Controversial Points of View
1.2. Implications of Natural Philosophy
1.3. Evolution of Thermodynamics
1.4. Modern Thermodynamics
1.5. Entropy in Thermoelectrics
1.6. Aim of This Work
2. Results
2.1. Categories
- Section 2.2: Coupling currents of entropy and charge in thermoelectric materials
- Section 2.3: Material’s voltage–electrical current and electrical power–electrical current characteristics
- Section 2.4: Material’s thermal conductivity–electrical current characteristics
- Section 2.5: Thermoelectric material in generator mode
- Section 2.5.1: Working point for maximum electrical power
- Section 2.5.2: Thermal conductivity
- Section 2.5.3: Thermal power
- Section 2.5.4: Power conversion efficiency (thermal to electrical)
- Section 2.5.5: Working points for maximum conversion efficiency and maximum electrical power
- Section 2.6: Thermoelectric material in entropy pump mode
- Section 2.6.1: Power conversion efficiency (electrical to thermal)
- Section 2.6.2: Electrical and thermal power
- Section 2.7: Complete picture
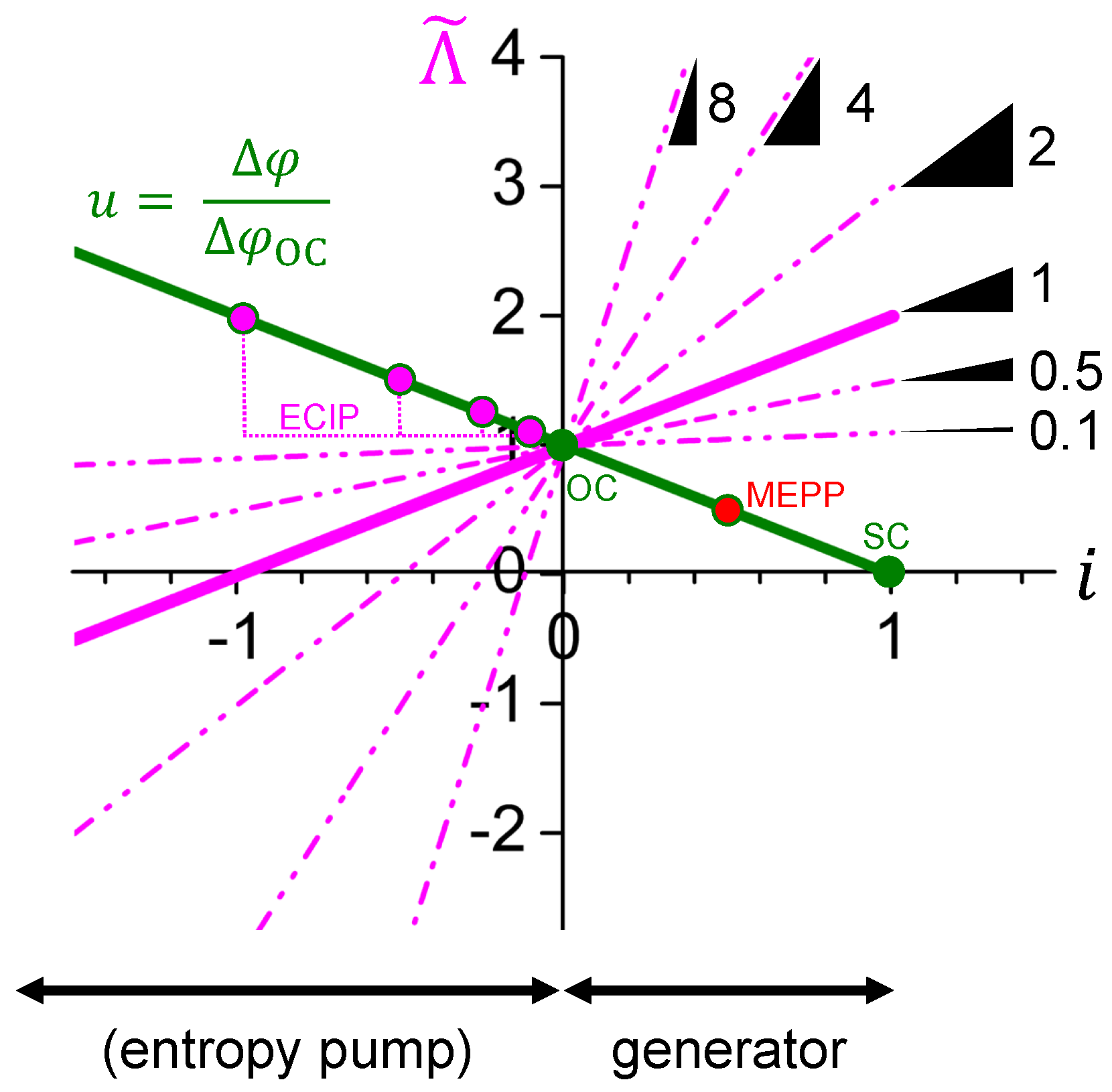
2.2. Coupling Currents of Entropy and Charge in Thermoelectric Materials
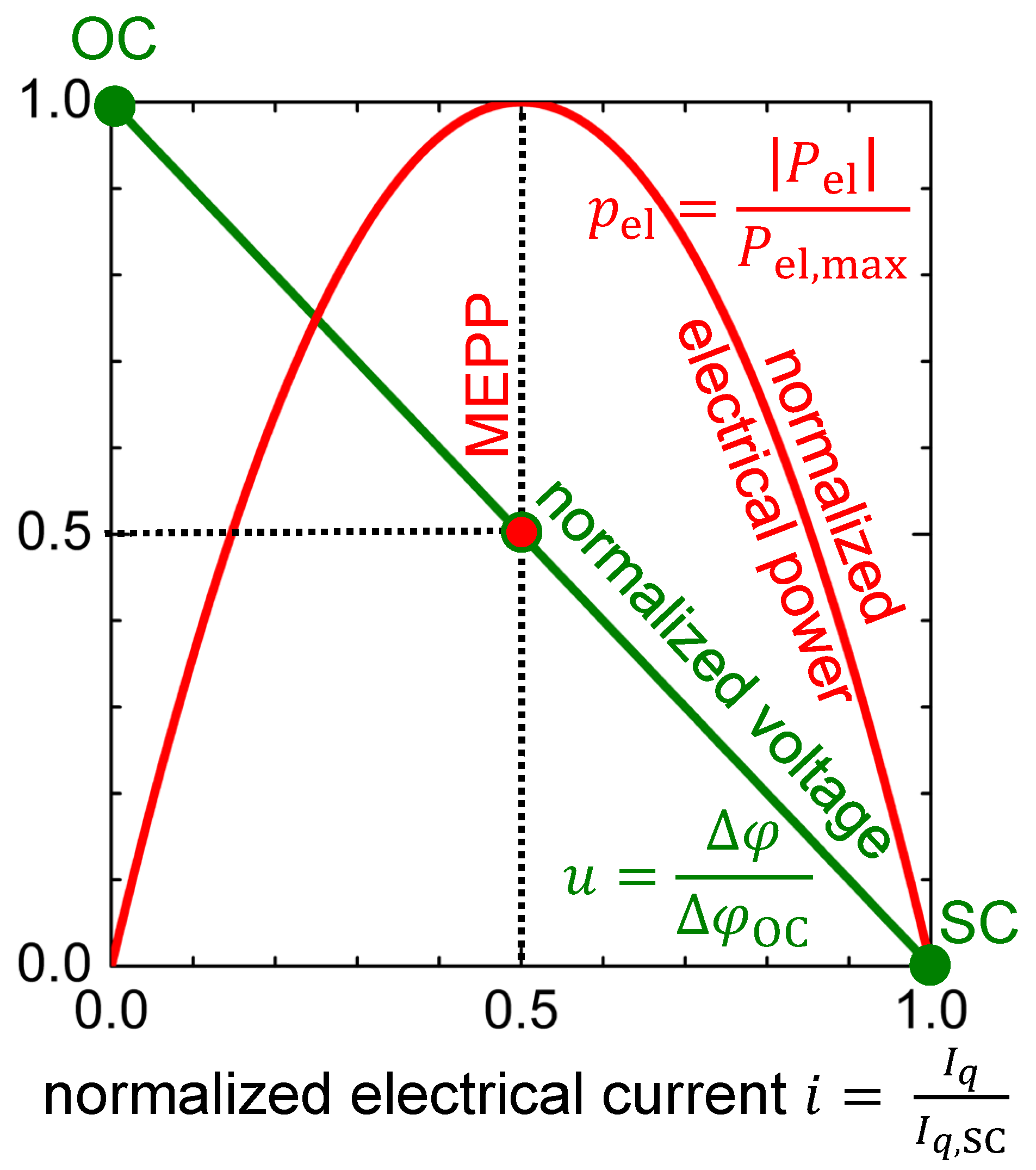
2.3. Material’s Voltage—Electrical Current and Electrical Power—Electrical Current Characteristics
2.4. Material’s Thermal Conductivity—Electrical Current Characteristics
2.5. Thermoelectric Material in Generator Mode
2.5.1. Working Point for Maximum Electrical Power
2.5.2. Thermal Conductivity
2.5.3. Thermal Power
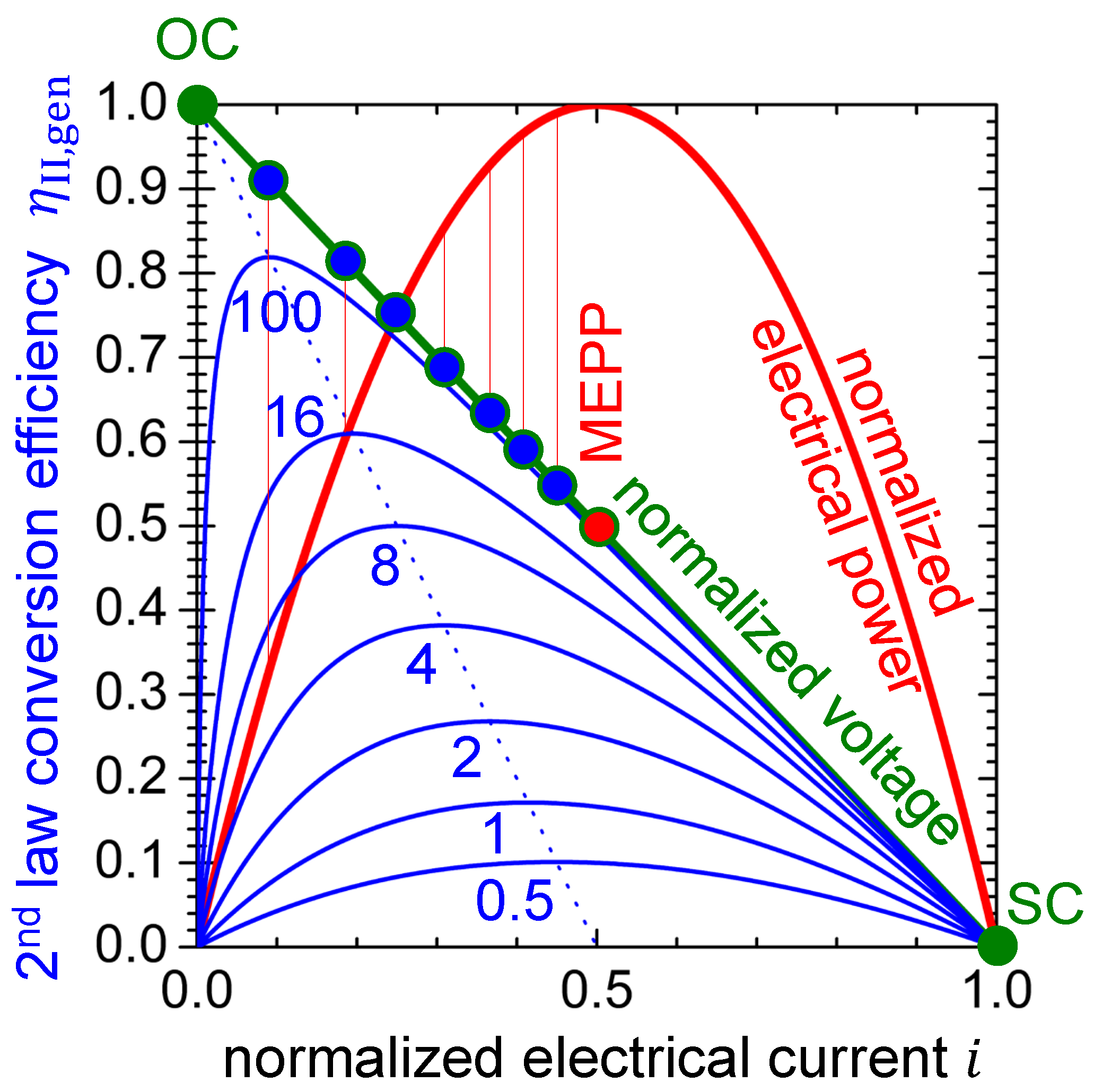
2.5.4. Power Conversion Efficiency (Thermal to Electrical)
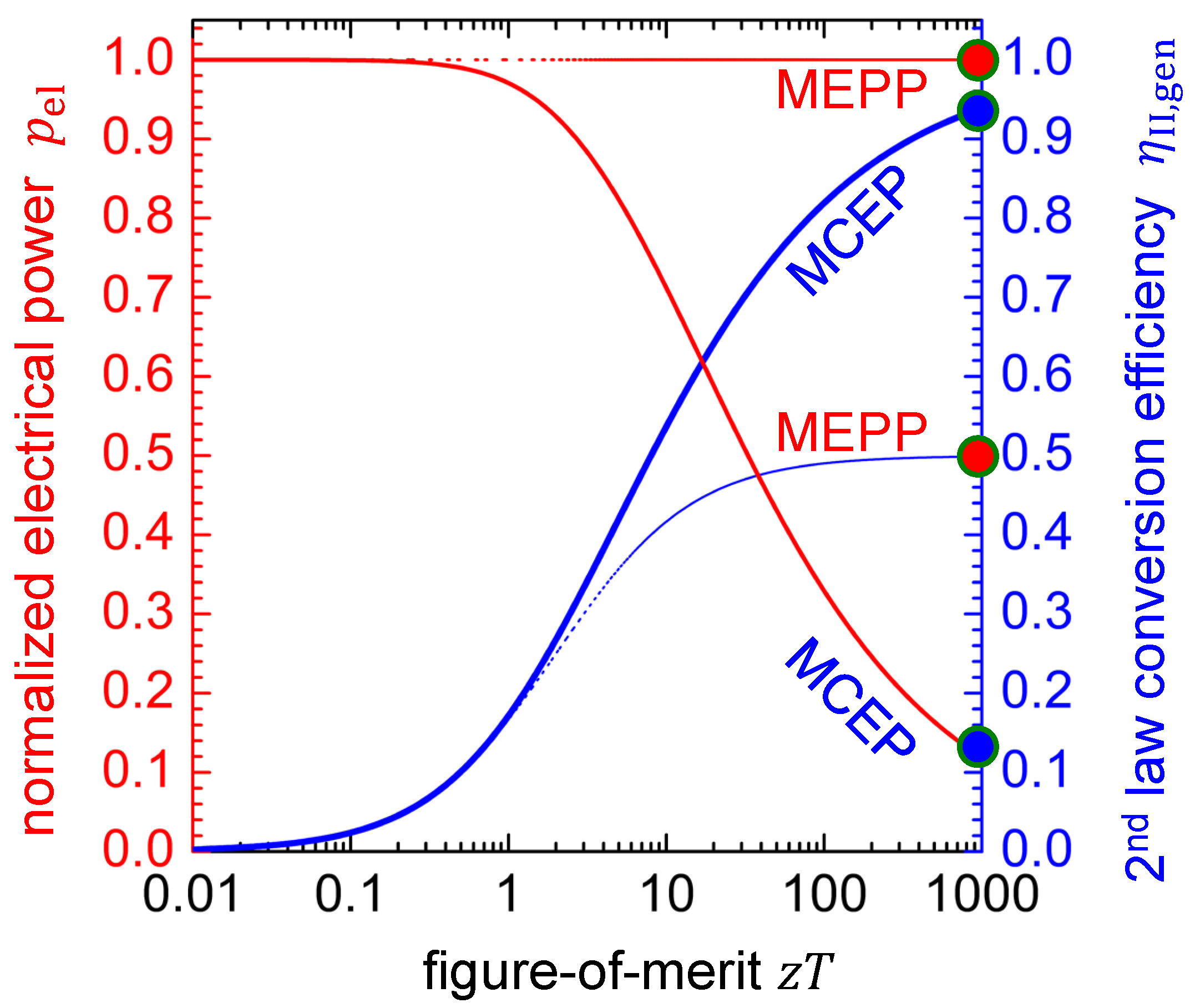
2.5.5. Working Points for Maximum Conversion Efficiency and Maximum Electrical Power
2.6. Thermoelectric Material in Entropy Pump Mode
2.6.1. Power Conversion Efficiency (Electrical to Thermal)
2.6.2. Electrical and Thermal Power
2.7. Complete Picture
3. Materials and Methods
4. Discussion
4.1. Remarks on the Use of Working Points
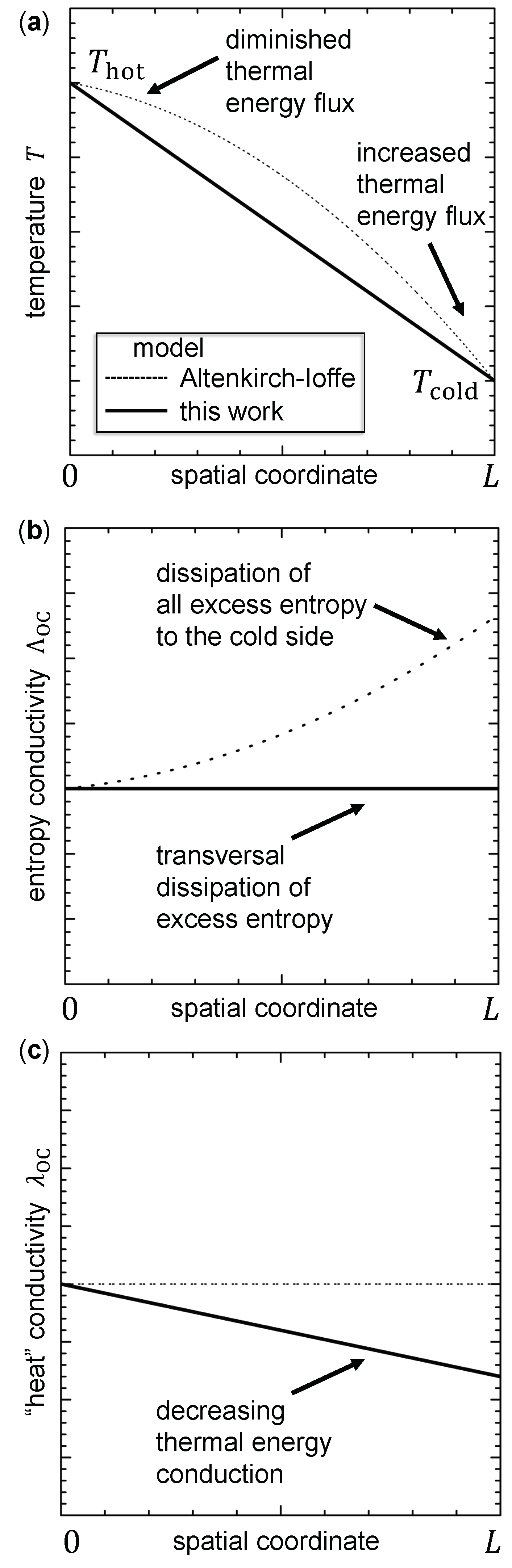
4.2. Remarks on the Altenkirch-Ioffe Model
4.3. Remarks on Narducci’s Model
4.4. Remarks on
4.5. Remarks on Figure-of-Merit
4.6. Remarks on State-of-the-Art and Emerging Thermoelectric Materials
4.7. Remarks on the Importance of the Power Factor and Choice of Materials for Thermogenerators
4.8. Remarks on the Second-Law Power Conversion Efficiency vs. Coefficient of Performance for Entropy Pumps
4.9. Remarks on the Choice of Materials for Entropy Pumps
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ECIP | Entropy Conductivity Inversion Point |
| MCEP | Maximum Conversion Efficiency Point (either in generator mode or entropy pump mode) |
| MEPP | Maximum Electrical Power Point (in generator mode) |
| OC | (Electrical) Open Circuit |
| SC | (Electrical) Short Circuit |
| Symbols | |
| The following symbols are used in this manuscript: | |
| Geometry | |
| A | cross-sectional area of thermoelectric material |
| L | length of thermoelectric material |
| Material properties | |
| Seebeck coefficient | |
| f | figure-of-merit (as proposed by Zener [67]) |
| “heat” conductivity | |
| “heat” conductivity under electrically open-circuited (OC) conditions | |
| entropy conductivity | |
| entropy conductivity under electrically open-circuited (OC) conditions | |
| entropy conductivity under electrically open-circuited (SC) conditions | |
| normalized entropy conductivity | |
| tensor element (of the thermoelectric material tensor) | |
| R | electrical resistance (of thermoelectric material) |
| isothermal electrical conductivity | |
| z | thermoelectric factor (as introduced by Ioffe [56]) |
| figure-of-merit (as introduced by Ioffe [56]) | |
| maximum figure-of-merit | |
| Thermodynamic potentials | |
| chemical potential | |
| electrochemical potential () | |
| gradient of the electrochemical potential | |
| gradient of the electrochemical potential per electric charge () | |
| electrical potential | |
| gradient of the electrical potential | |
| difference of electrical potential (along the thermoelectric material) | |
| voltage under electrically open-circuited (OC) conditions | |
| T | absolute temperature |
| temperature of the thermoelectric material at its cold side | |
| temperature of the thermoelectric material at its hot side | |
| gradient of the temperature | |
| difference of temperature (along the thermoelectric material) | |
| u | normalized voltage |
| normalized voltage at the maximum electrical power point (MEPP) | |
| Fluxes | |
| A | cross-sectional area of thermoelectric material |
| L | length of thermoelectric material |
| i | normalized electrical current |
| normalized electrical current at the maximum conversion efficiency point (MCEP) in entropy pump mode | |
| normalized electrical current at the maximum conversion efficiency point (MCEP) in generator mode | |
| normalized electrical current at the maximum electrical power point (MEPP) | |
| electrical current | |
| electrical current at electrically short-circuited (SC) conditions | |
| entropy current | |
| electrical flux density | |
| entropy flux density | |
| q | electric charge |
| S | entropy |
| Performance | |
| coefficient of performance of the thermoelectric material when used in a cooler | |
| coefficient of performance of the thermoelectric material when used in a heater | |
| first-law power conversion efficiency of the thermoelectric material in generator mode | |
| second-law power conversion efficiency of the thermoelectric material in generator mode | |
| maximum second-law power conversion efficiency of the thermoelectric material in generator mode | |
| second-law power conversion efficiency of the thermoelectric material in entropy pump mode | |
| maximum second-law power conversion efficiency of the thermoelectric material in entropy pump mode | |
| Carnot’s efficiency | |
| normalized electrical power | |
| electrical power, needed for lifting electrical charge (generator mode) | |
| or made available by the fall of electric charge (entropy pump mode); | |
| simplified called output (generator mode) or input (entropy pump mode), | |
| when the electrical potential on one side of the thermoelectric material is set to zero | |
| maximum electrical power output of the thermoelectric material in generator mode (at the MEPP) | |
| electrical power output, of the thermoelectric material in generator mode, at the MCEP | |
| thermal power, made available by the fall of entropy (generator mode) | |
| or needed for lifting entropy (entropy pump mode) | |
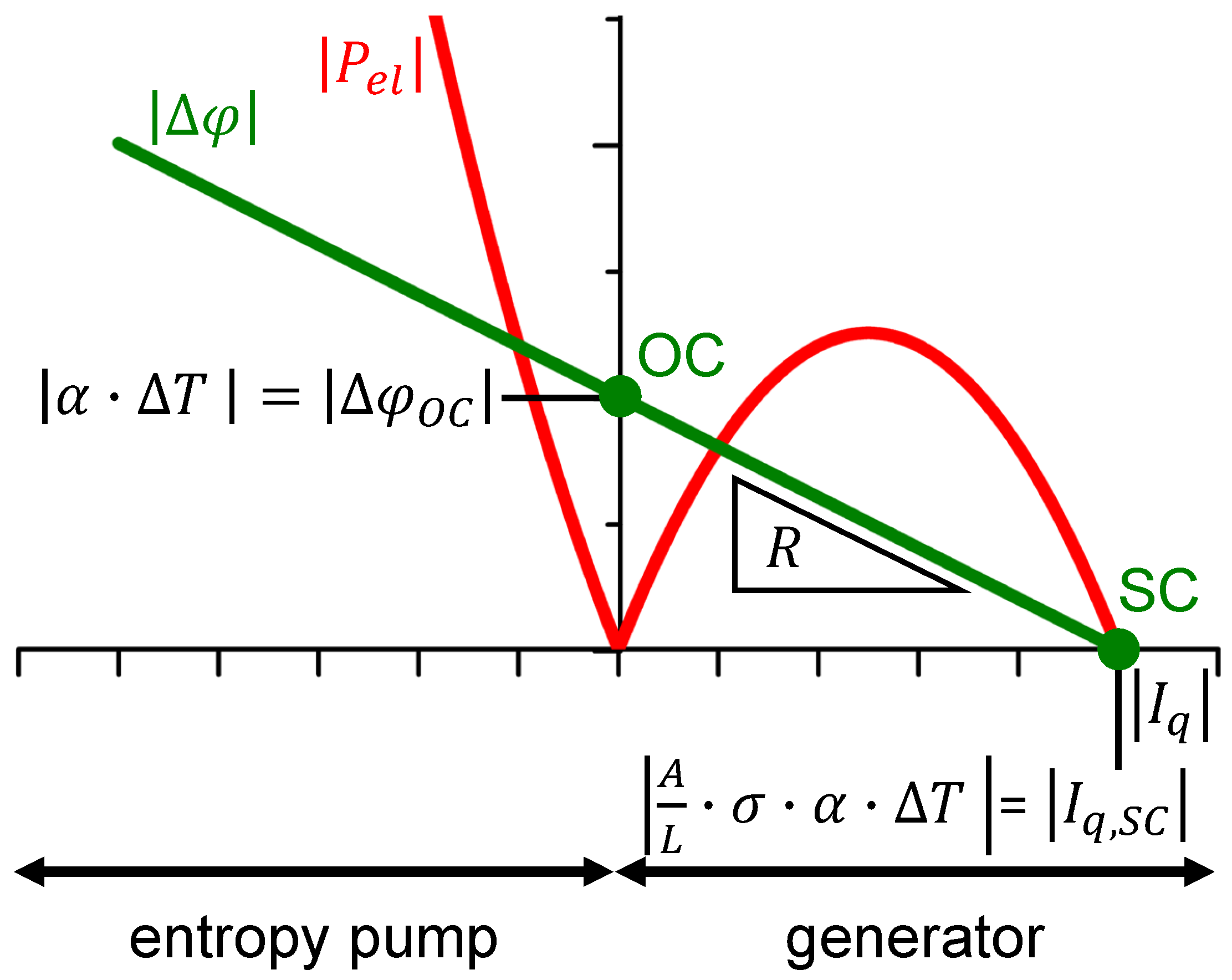
Appendix A. Voltage–Electrical Current and Electrical Power–Electrical Current Characteristics: p- and n-Type Materials
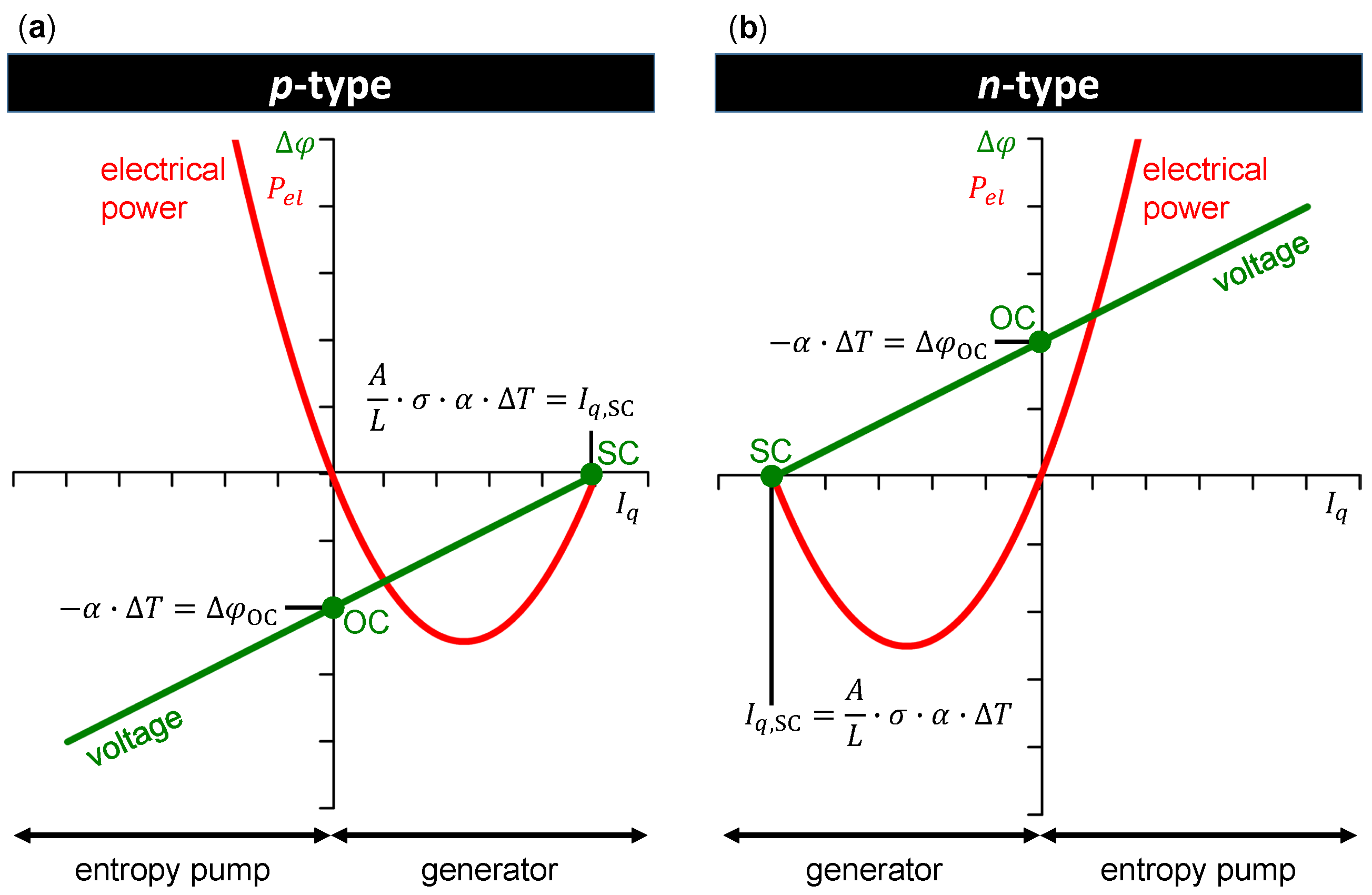
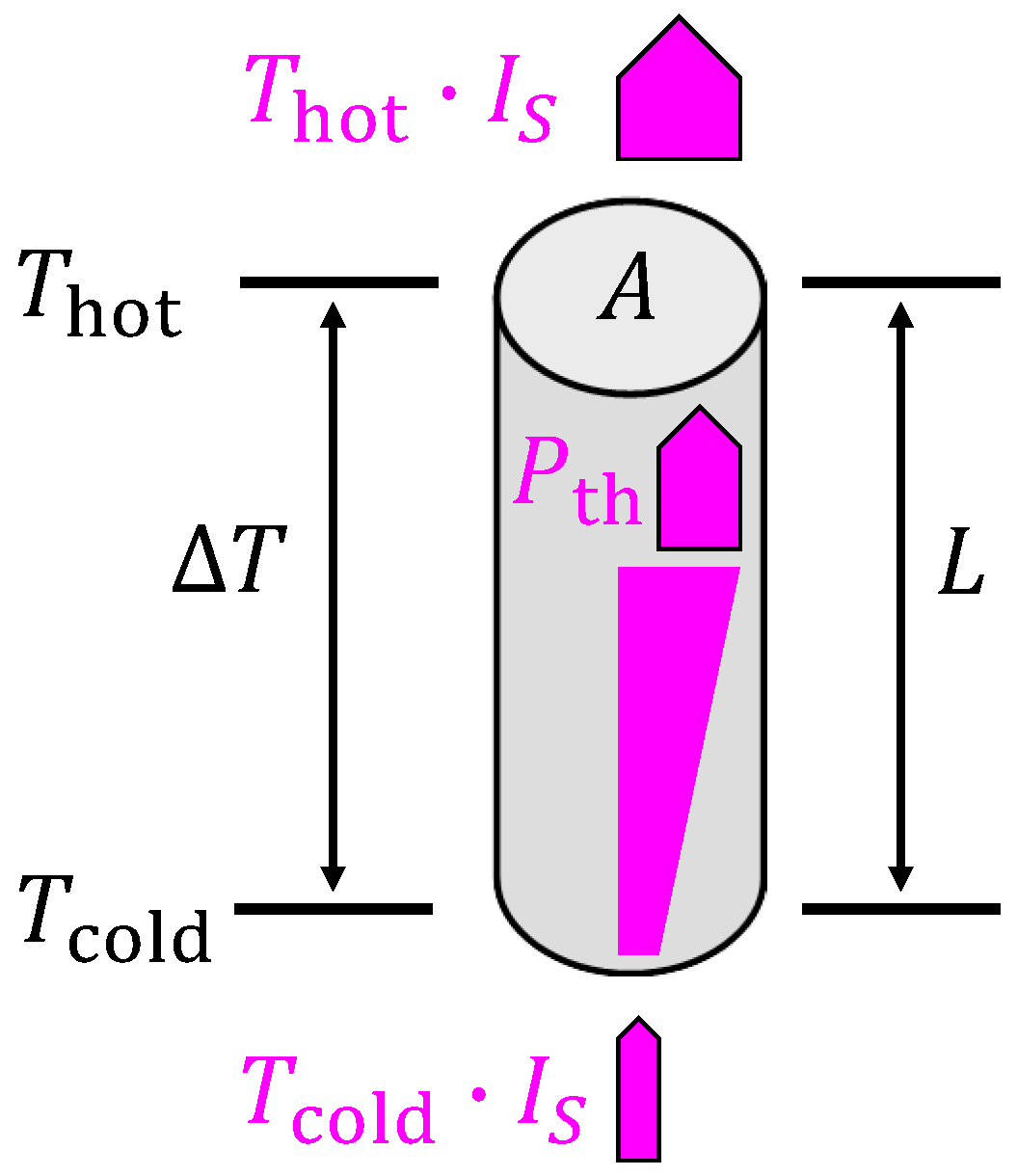
Appendix B. Thermal-to-Electrical Power Conversion: Calculations and Established Models
Appendix B.1. Maximum Electrical Power Point (MEPP): Material in Generator Mode
Appendix B.2. Maximum Conversion Efficiency Point (MCEP): Material in Generator Mode
Appendix B.3. Comparison to Power Conversion Efficiency after Fuchs: Thermogenerator Device
Appendix B.4. Comparison to Power Conversion Efficiency after Altenkirch: Thermogenerator Device
Appendix B.5. Comparison to Power Conversion Efficiency after Ioffe: Thermogenerator Device
Appendix C. Electrical-to-Thermal Power Conversion: Calculations and Established Models
Appendix C.1. Power Conversion Efficiency
Appendix C.2. Maximum Conversion Efficiency Point (MCEP): Material in Entropy Pump Mode
Appendix C.3. Normalized Thermal Power
Appendix C.4. Comparison to Power Conversion Efficiency after Altenkirch: Thermoelectric Cooler Device
Appendix C.5. Comparison to Power Conversion Efficiency after Ioffe: Thermoelectric Cooler Device
References and Notes
- Clausius, R. Abhandlungen über die mechanische Wärmetheorie; Friedrich Vieweg und Sohn: Braunschweig, Germany, 1864. [Google Scholar]
- Clausius, R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie. Poggendorffs Ann. Phys. Chem. 1865, 125, 353–400. [Google Scholar] [CrossRef]
- Clausius, R. Mechanical Theory of Heat; John van Voorst: London, UK, 1867. [Google Scholar]
- Boltzmann, L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung. Wiener Berichte 1877, 76, 373–435. [Google Scholar]
- Boltzmann, L. Wissenschaftliche Abhandlungen, Band 2; J. A. Barth: Leipzig, Germany, 1909. [Google Scholar]
- Flamm, D. Ludwig Boltzmann and his influence on science. Stud. Hist. Phil. Sci. 1983, 14, 225–278. [Google Scholar] [CrossRef]
- Truesdell, C.A. The Tragicomical History of Thermodynamics 1822-1854; Springer: New York, NY, USA, 1980. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the equilibrium of heterogeneous substances. Trans. Conn. Acad. 1875, 3, 108–248. [Google Scholar] [CrossRef]
- Gibbs, J.W. The Collected Works of J. Willard Gibbs, Volume 1, Thermodynamics; Longmans, Green and Co.: New York, NY, USA, 1928. [Google Scholar]
- The monism of the “Energeticist” school should not be confused with “energetics” of the British pioneers in thermodynamics [11].
- Smith, C. The Science of Energy: A Cultural History of Energy Physics in Victorian Britain; The University of Chicago Press: Chicago, IL, USA, 1998. [Google Scholar]
- Ostwald, W. Studien zur Energetik: 2. Grundlinien der allgemeinen Energetik. Berichte über die Verhandlungen der Königlich-Sächsischen Gesellschaft der Wissenschaften zu Leipzig, Mathematisch-Physische Klasse 1892, 44, 211–237. [Google Scholar]
- Helm, G. Die Lehre von der Energie; Arthur Felix: Leipzig, Germany, 1887. [Google Scholar]
- Sommerfeld, A. Ludwig Boltzmann zum Gedächtnis. Wien.-Chem.-Ztg. 1944, 3-4, 25–28. [Google Scholar]
- The aim here is not to discredit Wilhelm Ostwald or Ernst Mach who both have made remarkable contributions to science, but instead to give an understanding of how the actual perception of entropy in the scientific community has developed. Readers who are interested in more background information, including the impact of Mach’s natural philosophy on the development of quantum mechanics, are referred to Flamm [6].
- The late William Thomson [Lord Kelvin] wrote in 1906: “Young persons who have grown up in scientific work within the last fifteen years seem to have forgotten that energy is not an absolute existence. Even the Germans laugh on the ‘Energetikers’ [11]”.
- Boltzmann, L. Ein Wort der Mathematik an die Energetik. Ann. Phys. 1896, 39, 39–71. [Google Scholar] [CrossRef]
- Boltzmann, L. Zur Energetik. Ann. Phys. 1896, 39, 595–598. [Google Scholar] [CrossRef]
- Müller, I. Max Planck – a life for thermodynamics. Ann. Phys. 2008, 17, 73–87. [Google Scholar] [CrossRef]
- Müller, I. Ein Leben für die Thermodynamik. Physik Journal 2008, 7, 39–45. [Google Scholar]
- Herrmann, F. The Karlsruhe Physics Course. Eur. J. Phys. 2000, 21, 49–58. [Google Scholar] [CrossRef]
- Jorda, S. Kontroverse um Karlsruher Physikkurs [Controverse about the Karlsruhe Physiscs Course]. Phys. J. 2013, 12, 6–7. [Google Scholar]
- Strunk, C. Moderne Thermodynamik—Band 2: Quantenstatistik aus experimenteller Sicht, 2 ed.; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- It is worth noting that there was another dispute. Max Planck, together with his scholar Ernst Zermelo, also agitated heavily against Ludwig Boltzmann’s atomistic-statistical principle, which has been fought also in the pages of the Annalen der Physik [19,20] Only later did Planck became an aglow follower of Boltzmann, and Zermelo translated Gibb’s book on statistical mechanics [19,20]. Planck used Boltzmann’s principle to estimate the entropy of the electromagnetic field in his formulation of the spectrum of black body radiation [19,20].
- Planck, M. Über den zweiten Hauptsatz der mechanischen Wärmetheorie; Theodor Ackermann: München, Germany, 1879. [Google Scholar] [CrossRef]
- Callen, H. The application of Onsager’s reciprocal relations to thermoelectric, thermomagnetic, and galvanomagnetic effects. Phys. Rev. 1948, 489, 414–418. [Google Scholar] [CrossRef]
- Callen, H.B. Thermodynamics—An Introduction to the Physical Theories of Equilibrium Thermostatics and Irreversible Thermodynamics; John Wiley and Son: New York, NY, USA, 1960. [Google Scholar]
- de Groot, G. Thermodynamics of Irreversible Processes, 1 ed.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1951. [Google Scholar]
- Callendar, H. The caloric theory of heat and Carnot’s principle. Proc. Phys. Soc. London 1911, 23, 153–189. [Google Scholar] [CrossRef]
- Carnot, S. Réflexions sur la puissance motrice du feu; Bachelier: Paris, France, 1824. [Google Scholar]
- Strunk, C. Moderne Thermodynamik – Band 1: Physikalische Systeme und ihre Beschreibung, 2 ed.; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Fuchs, H.U. The Dynamics of Heat—A Unified Approach to Thermodynamics and Heat Transfer, 2 ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Fuchs, H.U. A direct entropic approach to uniform and spatially continuous dynamical models of thermoelectric devices. Energy Harvest. Syst. 2014, 1, 253–265. [Google Scholar] [CrossRef][Green Version]
- Feldhoff, A. Thermoelectric material tensor derived from the Onsager – de Groot – Callen model. Energy Harvest. Syst. 2015, 2, 5–13. [Google Scholar] [CrossRef]
- Falk, G. Physik—Zahl und Realität, 1 ed.; Birkhäuser: Basel, Switzerland, 1990. [Google Scholar]
- Job, G. Neudarstellung der Wärmelehre—Die Entropie als Wärme; Akademische Verlagsgesellschaft: Frankfurt, Germany, 1972. [Google Scholar]
- Job, G.; Rüffler, R. Physical Chemistry from a Different Angle, 1 ed.; Springer: Berlin/Heidelberger, Germany, 2016. [Google Scholar]
- Strunk [23,31] has shaped the conceptional approach by Falk [35] to put thermodynamics first and assign the statistical behaviour not to an ensemble, but to the individual quantum state itself. Strunk’s approach solves the paradox of doubled statistics, which has been inherent to the traditional approach, and it overcomes attempts to interpret quantum statistics as a modified variant of Newtonian mechanics-based kinetic gas theory. Strunk [23,31] suggests to consider heat as to involve entropy and energy. In his approach, entropy is a basic quantity.
- Neave, E. Joseph Black’s lectures on the elements of chemistry. Isis 1936, 25, 372–390. [Google Scholar] [CrossRef]
- Falk, G. Entropy, a resurrection of caloric—A look at the history of thermodynamics. Eur. J. Phys. 1985, 6, 108–115. [Google Scholar] [CrossRef]
- Robison, J. Lectures on the Elements of Chemistry—Delivered in the University of Edinburgh by the Late Joseph Black; William Creech Edinburgh: Edinburgh, UK, 1803; Volume 1. [Google Scholar]
- To not offend his readers, Strunk has chosen a slightly different point of view by stating that heat comprises entropy and energy and that its use should be avoided when it addresses thermal energy solely.
- Koshibae, W.; Maekawa, S. Effects of spin and orbital degeneracy on the thermopower of strongly correlated systems. Phys. Rev. Lett. 2001, 87, 236603-1–236603-4. [Google Scholar] [CrossRef]
- Wang, Y.; Rogado, N.S.; Cava, R.; Ong, O. Spin entropy as the likely source of enhanced thermopower in NaxCo2O4. Phys. Rev. Lett. 2003, 423, 425–428. [Google Scholar] [CrossRef]
- Falk, G.; Herrmann, F.; Schmid, G. Energy forms or energy carriers? Am. J. Phys. 1983, 51, 1074–1077. [Google Scholar] [CrossRef]
- Treating a device, Fuchs has derived a corresponding equation [32,33].
- Wolf, M.; Menekse, K.; Mundstock, A.; Hinterding, R.; Nietschke, F.; Oeckler, O.; Feldhoff, A. Low thermal conductivity in thermoelectric oxide-based multiphase composites. J. Electron. Mater. 2019, 48, 7551–7561. [Google Scholar] [CrossRef]
- Wolf, M.; Hinterding, R.; Feldhoff, A. High power factor vs. high zT—A review of thermoelectric materials for high-temperature application. Entropy 2019, 21, 1058. [Google Scholar] [CrossRef]
- Geppert, B.; Brittner, A.; Helmich, L.; Bittner, M.; Feldhoff, A. Enhanced flexible thermoelectric generators based on oxide-metal composite materials. J. Electron. Mater. 2017, 46, 2356–2365. [Google Scholar] [CrossRef]
- A constant Seebeck coefficient α of the thermoelectric material being in a temperature gradient implies that the Thomson coefficient is negligible.
- Peltier, J.C.A. Nouvelles expériences sur la caloricité des courants électrique. Ann. Chim. Phys. 1834, 56, 371–386. [Google Scholar]
- Seebeck, T.J. Magnetische Polarisation der Metalle und Erze durch Temperatur-Differenz. Physicalische und medicinische Abhandlungen der königlichen Academie der Wissenschaften zu Berlin 1822, 1820–21, 265–373. [Google Scholar]
- Velmre, E. Thomas Johann Seebeck (1770–1831). Proc. Estonian Acad. Sci. Eng. 2007, 13, 276–282. [Google Scholar]
- Ohmic losses are often referred to as Joule heating.
- Altenkirch, E. Über den Nutzeffekt der Thermosäule. Physikalische Zeitschrift 1909, 10, 560–568. [Google Scholar]
- Ioffe, A.F. Semiconductor Thermoelements and Thermoelectric Cooling, 1 ed.; Infosearch Ltd.: London, UK, 1957. [Google Scholar]
- Altenkirch, E. Elektrothermische Kälteerzeugung und reversible elektrische Heizung. Physikalische Zeitschrift 1911, 12, 920–924. [Google Scholar]
- Wolf, M.; Rybakov, A.; Feldhoff, A. Understanding and improving thermoelectric generators via optimized material working points. Entropy. in preparation.
- Walstrom, P. Satial dependence of thermoelectric voltages and reversible heats. Am. J. Phys. 1988, 56, 890–894. [Google Scholar] [CrossRef]
- Heikes, R.R.; Ure, R.W. Thermoelectricity: Science and Engineering; Interscience Publishers: New York, NY, USA, 1961. [Google Scholar]
- This has confused Ioffe [56], who misinterpreted the situation as an uphill “heat” flow: “Of the total Joule ‘heat’ Iq2 · RTEG generated in the thermoelement, half passes to the hot junction, returning the power · Iq2 · RTEG and the rest is transferred to the cold junction.”
- Fuchs, H.U. Personal communication, 8 December 2018.
- Gryasnov, O.; Moizhes, B.; Nemchinskii, V. Generalized thermoelectric effectivness. J. Tech. Phys. 1978, 48, 1720–1728. [Google Scholar]
- Narducci, D. Do we really need high thermoelectric figures of merit? A critical appraisal to the power conversion efficiency of thermoelectric materials. Appl. Phys. Lett. 2011, 99, 102104:1–102104:3. [Google Scholar] [CrossRef]
- Slack, A. New Materials and Performance Limits for Thermoelectric Cooling. In CRC Handbook of Thermoelectrics; Rowe, D., Ed.; CRC Press: New York, NY, USA, 1994. [Google Scholar]
- Goupil, C.; Seifert, W.; Zabrocki, K.; Müller, E.; Snyder, G.J. Thermodynamics of thermoelectric phenomena and applications. Entropy 2011, 13, 1481–1517. [Google Scholar] [CrossRef]
- Zener, C. Putting electrons to work. Trans. ASM 1961, 53, 1052–1068. [Google Scholar]
- Wu, H.J.; Zhao, L.D.; Zheng, F.S.; Wu, D.; Pei, Y.L.; Tong, X.; Kanatzidis, M.G. Broad temperature plateau for thermoelectric figure of merit zT > 2 in phase-separated PbTe0.7S0.3. Nat. Commun. 2014, 5, 4515. [Google Scholar] [CrossRef]
- Risseh, A.E.; Nee, H.P.; Goupil, C. Electrical power conditioning system for thermoelectric waste heat recovery in commercial vehicles. IEEE Trans. Transp. Electrif. 2018, 4, 548–562. [Google Scholar] [CrossRef]
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D.; et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef]
- He, R.; Kraemer, D.; Mao, J.; Zeng, L.; Jie, Q.; Lan, Y.; Li, C.; Shuai, J.; Kim, H.S.; Liu, Y.; et al. Power factor and output power density in p-type half-Heuslers Nb1–xTixFeSb. Proc. Natl. Acad. Sci. USA 2016, 113, 13576–13581. [Google Scholar] [CrossRef]
- Chen, L.; Gao, S.; Zeng, X.; Mehdizadeh Dehkordi, A.; Tritt, T.; Poon, S. Uncovering high thermoelectric figure of merit in (Hf,Zr)NiSn half-Heusler alloys. Appl. Phys. Lett. 2015, 107, 041902. [Google Scholar] [CrossRef]
- Yamashita, O.; Ochi, T.; Odahara, H. Effect of the cooling rate on the thermoelectric properties of p-type (Bi0.25Sb0.75)2Te3 and n-type Bi2(Te0.94Se0.06)3 after melting in the bismuth-telluride system. Mater. Res. Bull. 2009, 44, 1352–1359. [Google Scholar] [CrossRef]
- Zhu, H.; He, R.; Mao, J.; Zhu, Q.; Li, C.; Sun, J.; Ren, W.; Wang, Y.; Liu, Z.; Tang, Z.; et al. Discovery of ZrCoBi based half-Heuslers with high thermoelectric conversion efficiency. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Pei, Y.; Shi, X.; Lalonde, A.; Wang, H.; Chen, L.; Snyder, G. Convergence of electronic bands for high performance bulk thermoelectrics. Nature 2011, 473, 66–69. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, L.D.; Zhu, Y.; Liu, Y.; Li, F.; Yu, M.; Liu, D.B.; Xu, W.; Lin, Y.H.; Nan, C.W. Synergistically optimizing electrical and thermal transport properties of BiCuSeO via a dual-doping approach. Adv. Energy Mater. 2016, 6, 1502423. [Google Scholar] [CrossRef]
- Liu, H.; Shi, X.; Xu, F.; Zhang, L.; Zhang, W.; Chen, L.; Li, Q.; Uher, C.; Day, T.; Snyder, G.J. Copper ion liquid-like thermoelectrics. Nat. Mater. 2012, 11, 422–425. [Google Scholar] [CrossRef] [PubMed]
- Shutoh, N.; Sakurada, S. Thermoelectric properties of the Tix(Zr0.5Hf0.5)1–xNiSn half-Heusler compounds. J. Alloys Compd. 2005, 389, 204–208. [Google Scholar] [CrossRef]
- Zhang, J.; Song, L.; Pedersen, S.H.; Yin, H.; Hung, L.T.; Iversen, B.B. Discovery of high-performance low-cost n-type Mg3Sb2-based thermoelectric materials with multi-valley conduction bands. Nat. Commun. 2017, 8, 13901. [Google Scholar] [CrossRef]
- Shi, X.; Yang, J.; Salvador, J.R.; Chi, M.; Cho, J.Y.; Wang, H.; Bai, S.; Yang, J.; Zhang, W.; Chen, L. Multiple-filled skutterudites: High thermoelectric figure of merit through separately optimizing electrical and thermal transports. J. Am. Chem. Soc. 2011, 133, 7837–7846. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Cui, J.; Xiao, Y.; Zhang, Y.; He, J.; Chen, Y.; Cao, J.; Cai, W.; Pennycook, S.J.; et al. Extraordinary thermoelectric performance in n-type manganese doped Mg3Sb2 Zintl: High band degeneracy, tuned carrier scattering mechanism and hierarchical microstructure. Nano Energy 2018, 52, 246–255. [Google Scholar] [CrossRef]
- Ahmad, S.; Singh, A.; Bohra, A.; Basu, R.; Bhattacharya, S.; Bhatt, R.; Meshram, K.N.; Roy, M.; Sarkar, S.K.; Hayakawa, Y.; et al. Boosting thermoelectric performance of p-type SiGe alloys through in-situ metallic YSi2 nanoinclusions. Nano Energy 2016, 527, 282–297. [Google Scholar] [CrossRef]
- Zhao, K.; Zhu, C.; Qiu, P.; Qiu, P.; Blichfeld, A.B.; Eikeland, E.; Ren, D.; Iversen, B.B.; Xu, F.; Shi, X.; et al. High thermoelectric performance and low thermal conductivity in Cu2–yS1/3Se1/3Te1/3 liquid-like materials with nanoscale mosaic structures. Nano Energy 2017, 42, 43–50. [Google Scholar] [CrossRef]
- Hsu, K.F.; Loo, S.; Guo, F.; Chen, W.; Dyck, J.S.; Uher, C.; Hogan, T.; Polychroniadis, E.K.; Kanatzidis, M.G. Cubic AgPbmSbTe2+m: Bulk thermoelectric materials with high figure of merit. Science 2014, 303, 818–821. [Google Scholar] [CrossRef] [PubMed]
- Biswas, K.; He, J.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Dravid, V.P.; Kanatzidis, M.G. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature 2012, 489, 414–418. [Google Scholar] [CrossRef] [PubMed]
- Hong, M.; Chen, Z.G.; Yang, L.; Zou, Y.C.; Dargusch, M.S.; Wang, H.; Zou, J. Realizing zT of 2.3 in Ge1–x–ySbxInyTe via Reducing the phase-transition temperature and introducing resonant energy doping. Adv. Mater. 2018, 30, 1705942. [Google Scholar] [CrossRef]
- Tan, G.; Shi, F.; Hao, S.; Zhao, L.D.; Chi, H.; Zhang, X.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Non-equilibrium processing leads to record high thermoelectric figure of merit in PbTe-SrTe. Nat. Commun. 2016, 7, 12167. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.D.; Lo, S.H.; Zhang, Y.; Sun, H.; Tan, G.; Uher, C.; Wolverton, C.; Dravid, V.P.; Kanatzidis, M.G. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 2014, 508, 373. [Google Scholar] [CrossRef]
- Olvera, A.A.; Moroz, N.A.; Sahoo, P.; Ren, P.; Bailey, T.P.; Page, A.A.; Uher, C.; Poudeu, P.F.P. Partial indium solubility induces chemical stability and colossal thermoelectric figure of merit in Cu2Se. Energy Environ. Sci. 2017, 10, 1668–1676. [Google Scholar] [CrossRef]
- Chang, C.; Wu, M.; He, D.; Pei, Y.; Wu, C.F.; Wu, X.; Yu, H.; Zhu, F.; Wang, K.; Chen, Y. 3D charge and 2D phonon transports leading to high out-of-plane zT in n-type SnSe crystals. Science 2018, 360, 778–782. [Google Scholar] [CrossRef]
- Curzon, F.; Ahlborn, B. Efficiency of a Carnot engine at maximum power output. Am. J. Phys. 1975, 43, 22–24. [Google Scholar] [CrossRef]
- Leff, H.S. Thermal efficiency at maximum work ouptut: New results for old heat engines. Am. J. Phys. 1987, 55, 602–610. [Google Scholar] [CrossRef]
- Ioffe (see [56], p. 45) has introduced it as “heat” conductivity–electrical conductivity plot (λOC–σ).
- Bittner, M.; Kanas, N.; Hinterding, R.; Steinbach, F.; Räthel, J.; Schrade, M.; Wiik, K.; Einarsrud, M.A.; Feldhoff, A. A comprehensive study on improved power materials for high-temperature thermoelectric generators. J. Power Sources 2019, 410–411, 143–151. [Google Scholar] [CrossRef]

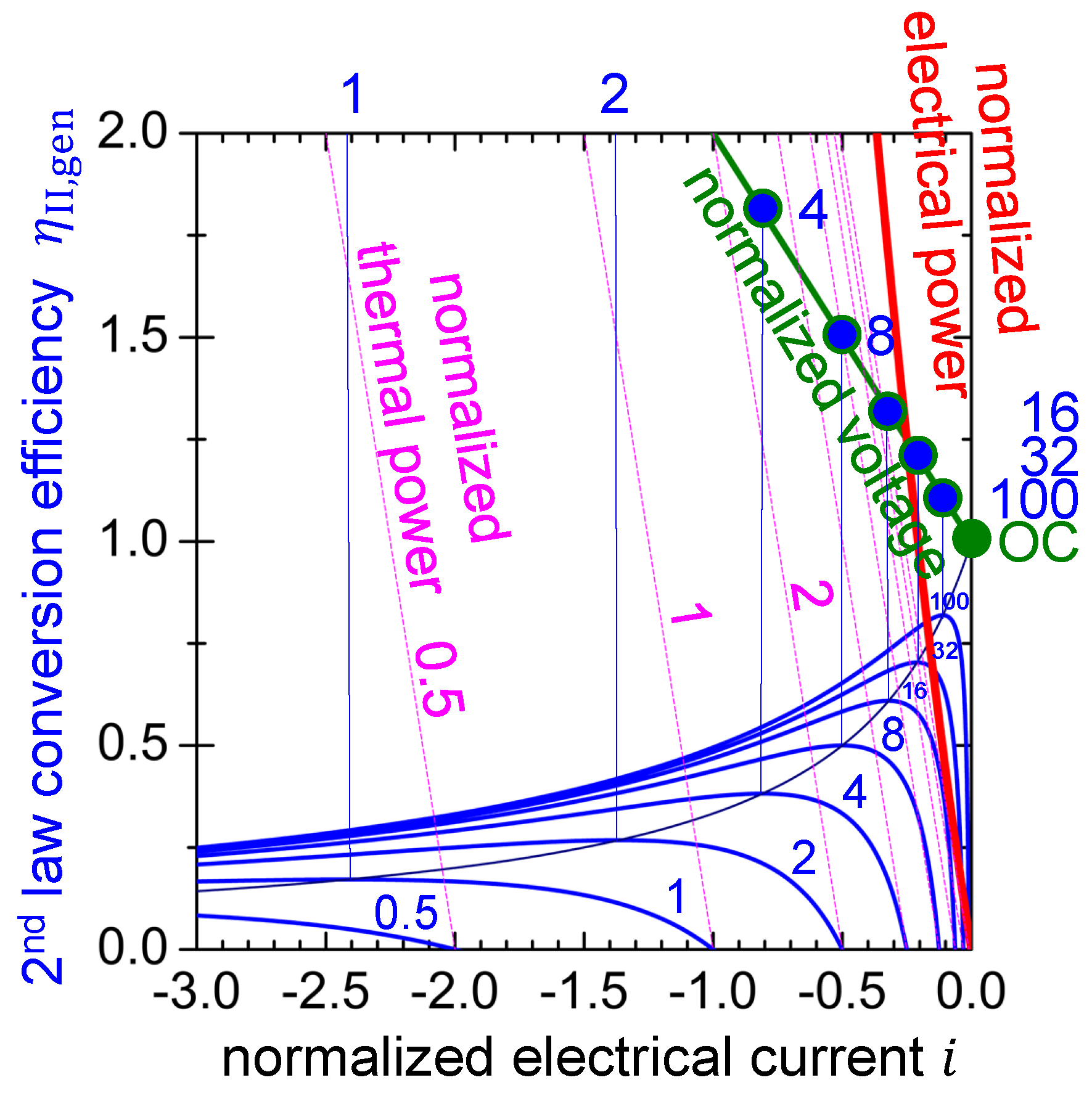
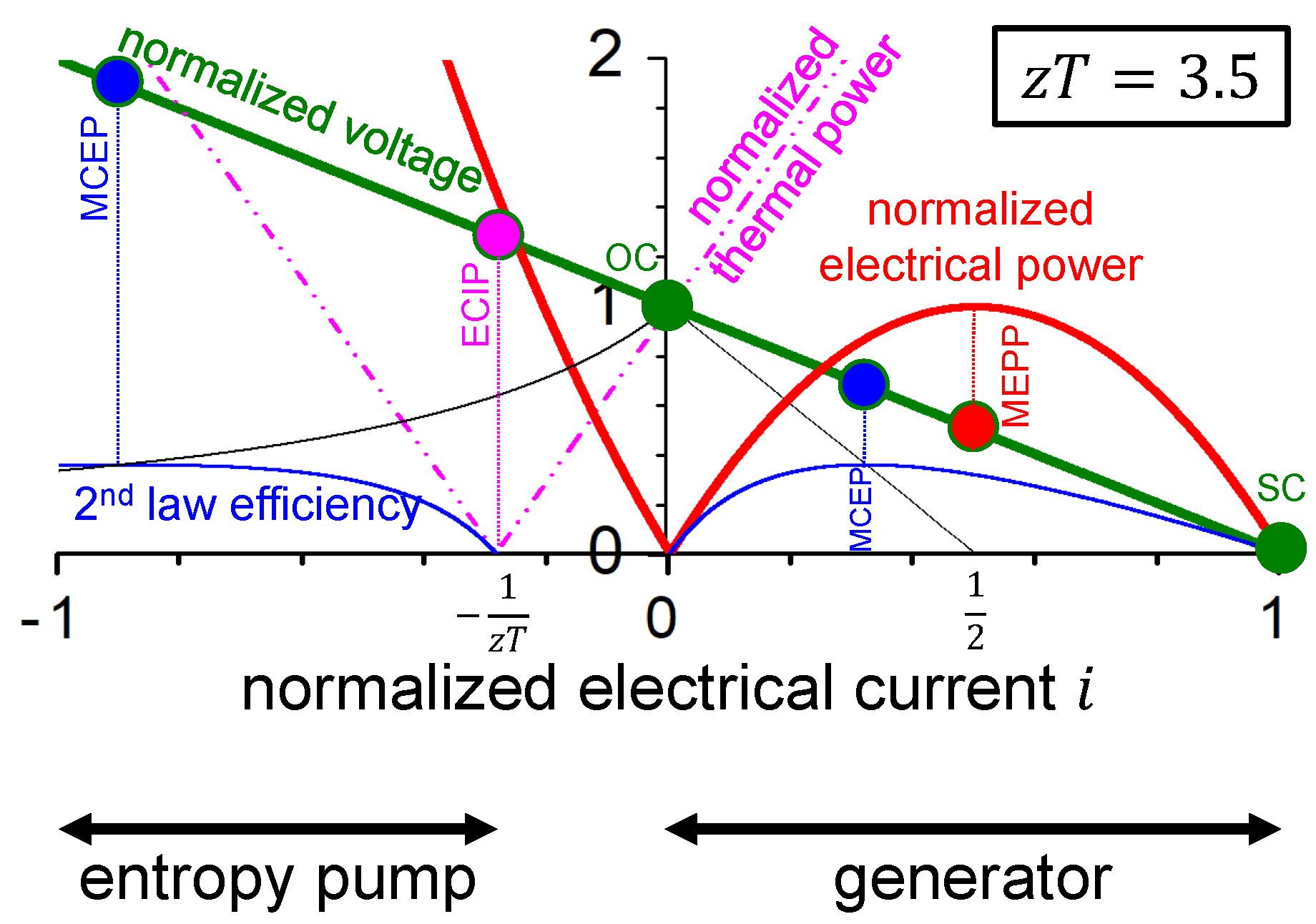
| Abbreviation | Working Point | Operational Mode |
|---|---|---|
| MCEP | Maximum (power) conversion efficiency point | entropy pump mode |
| EICP | Entropy conductivity inversion point | entropy pump mode |
| OC | (electrical) open circuit | generator mode |
| MCEP | (see above) | generator mode |
| MEPP | Maximum (electrical) power point | generator mode |
| SC | (electrical) short circuit | generator mode |
| Maximum 2nd Law Efficiency | 2nd Law Efficiency at MEPP | |
|---|---|---|
| 0.1 | 0.02 | 0.02 |
| 0.5 | 0.1 | 0.1 |
| 1 | 0.17 | 0.17 |
| 1.5 | 0.23 | 0.21 |
| 2 | 0.27 | 0.25 |
| 2.5 | 0.30 | 0.28 |
| 3 | 0.33 | 0.3 |
| 3.5 | 0.36 | 0.32 |
| 4 | 0.38 | 0.33 |
| 8 | 0.5 | 0.4 |
| 16 | 0.61 | 0.44 |
| 32 | 0.70 | 0.47 |
| 100 | 0.82 | 0.49 |
| 0.1 | 41.95 | 1761.32 | |
| 0.5 | 9.80 | 97.01 | |
| 1 | 5.66 | 32.87 | |
| 1.5 | 4.22 | 19.67 | |
| 2 | 3.46 | 12.83 | |
| 2.5 | 2.99 | 10.77 | |
| 3.0 | 2.68 | 8.93 | |
| 3.5 | 2.42 | 7.56 | |
| 4 | 2.2 | 5.76 | |
| 8 | 1.5 | 3.00 | |
| 16 | 1.03 | 1.69 | |
| 32 | 0.71 | 1.02 | |
| 100 | 0.40 | 0.49 |
| Material | Type | T | Ref. | ||
|---|---|---|---|---|---|
| [WcmK] | [K] | ||||
| (BiSb)Te | p | 1.05 | 43 | 323 | [70] |
| FeNbTiSb | p | 1.10 | 53 | 973 | [48,71] |
| HfZrHfNiSnSb | n | 1.20 | 47 | 900 | [48,72] |
| Bi(TeSe) (0.017 wt.% Te, 0.068 wt.% I) | n | 1.25 | 57 | 298 | [73] |
| (BiSb)Te (8wt.% Te) | p | 1.27 | 58 | 298 | [73] |
| nano (BiSb)Te | p | 1.4 | 38 | 373 | [70] |
| ZrCoBiSbSn | p | 1.42 | 38 | 973 | [48,74] |
| FeNbHfSb | p | 1.45 | 51 | 1200 | [48,75] |
| BiCaPbCuSeO | p | 1.5 | 8 | 873 | [48,76] |
| -CuSe | p | 1.5 | 12 | 1000 | [77] |
| TiZrHfNiSnSbSe | n | 1.5 | 62 | 700 | [48,78] |
| MgSbBiTe | n | 1.65 | 13 | 725 | [79] |
| BaLaYbCoSb | n | 1.7 | 51 | 850 | [80] |
| MgMnSbBiTe | n | 1.71 | 20 | 700 | [48,81] |
| B-doped SiGe + YSi | p | 1.81 | 39 | 1073 | [48,82] |
| CuSSeTe | p | 1.9 | 8 | 1000 | [83] |
| AgPbSbTe | n | 2.2 | 11 | 800 | [84] |
| PbTeS-2.5%K | p | 2.2 | 14 | 923 | [68] |
| PbTe-4%SrTe-2%Na | p | 2.2 | 24 | 915 | [85] |
| GeSbInTe | p | 2.3 | 37 | 650 | [86] |
| PbTe-8%SrTe | p | 2.5 | 30 | 923 | [87] |
| SnSe single crystal’s b-axis | p | 2.6 | 10 | 923 | [88] |
| -CuSe/CuInSe (1% In) | p | 2.6 | 12.5 | 850 | [89] |
| SnSeBr single crystal’s a-axis | n | 2.8 | 9 | 773 | [90] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feldhoff, A. Power Conversion and Its Efficiency in Thermoelectric Materials. Entropy 2020, 22, 803. https://doi.org/10.3390/e22080803
Feldhoff A. Power Conversion and Its Efficiency in Thermoelectric Materials. Entropy. 2020; 22(8):803. https://doi.org/10.3390/e22080803
Chicago/Turabian StyleFeldhoff, Armin. 2020. "Power Conversion and Its Efficiency in Thermoelectric Materials" Entropy 22, no. 8: 803. https://doi.org/10.3390/e22080803
APA StyleFeldhoff, A. (2020). Power Conversion and Its Efficiency in Thermoelectric Materials. Entropy, 22(8), 803. https://doi.org/10.3390/e22080803





