A Method to Present and Analyze Ensembles of Information Sources
Abstract
1. Introduction
2. Materials and Methods
2.1. Individual Information Source
2.2. Information Source Ensemble Analysis
2.3. Software
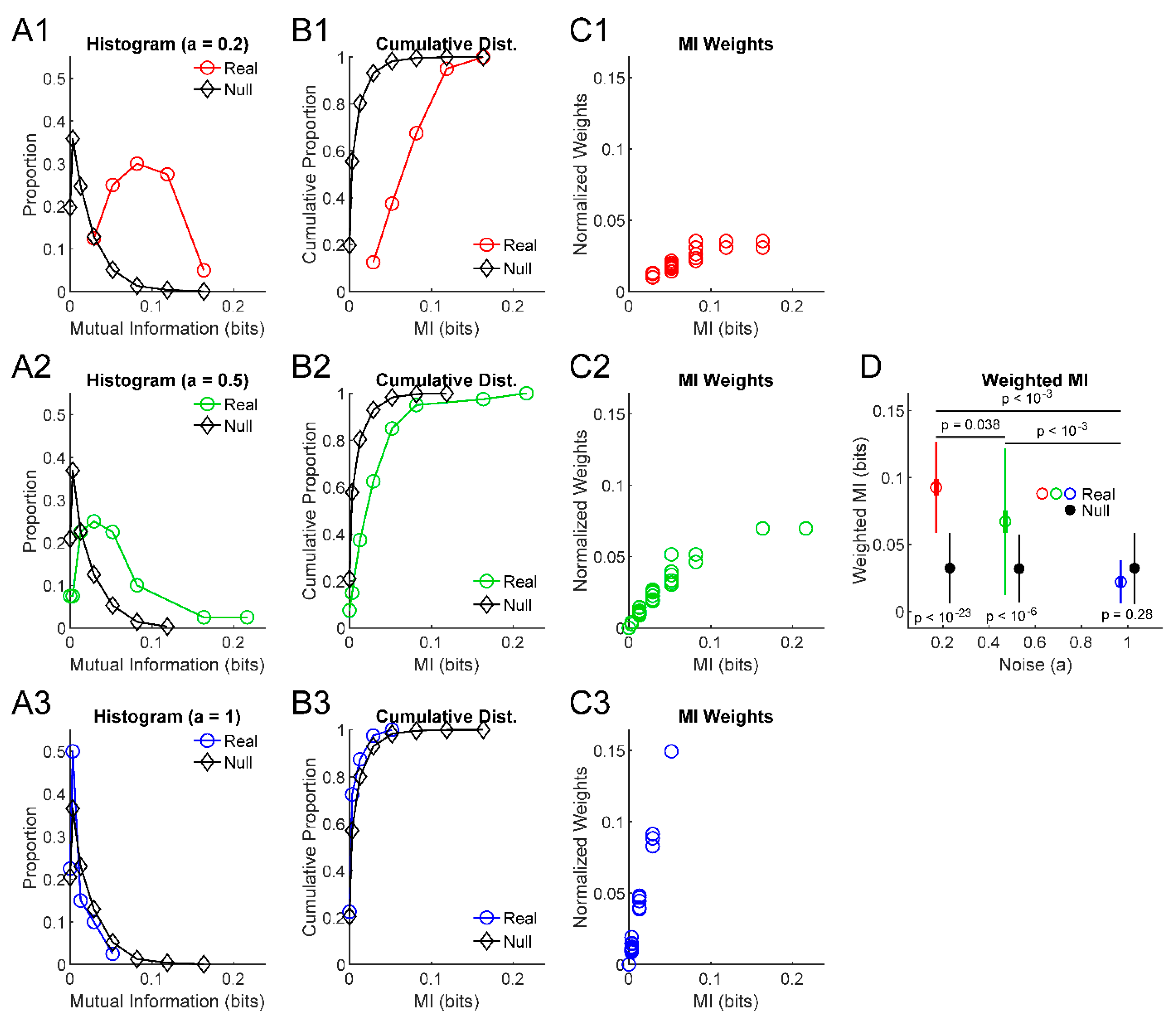
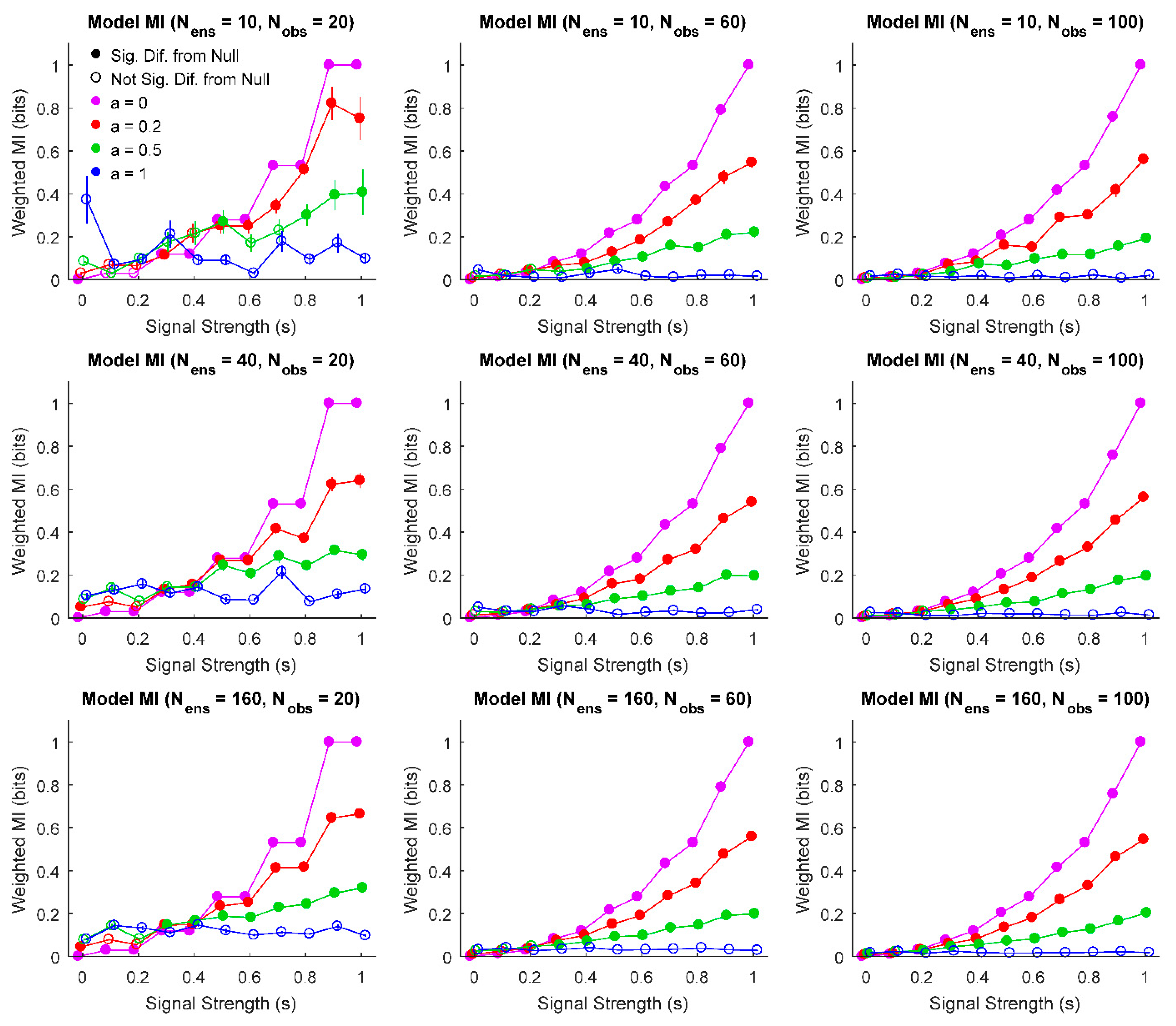
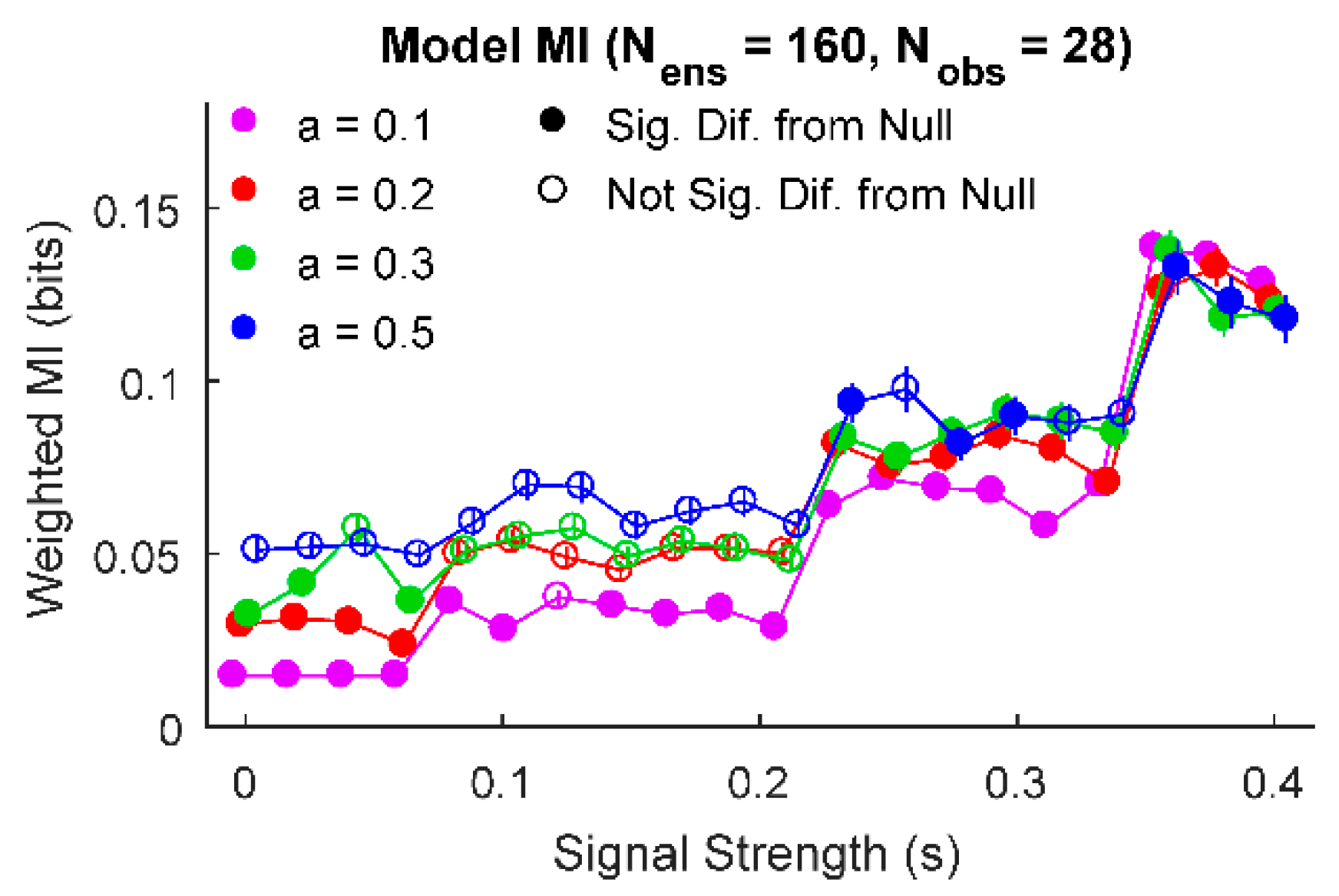
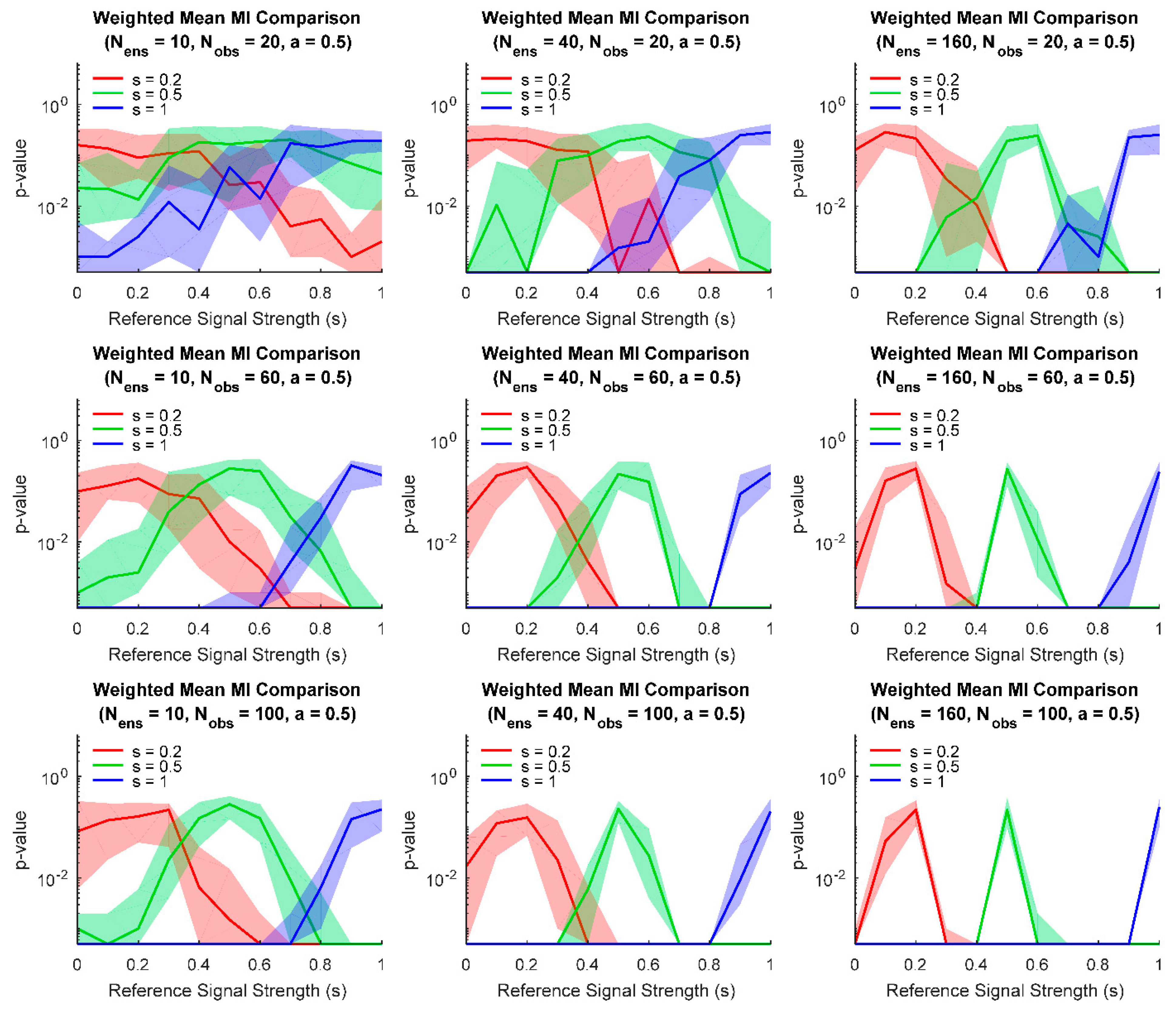
3. Results
4. Discussion
4.1. Method Generalizability
4.2. Relationship to Neural Systems and Neural Networks
4.3. Limitations and Future Research
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: New York, NY, USA, 2006. [Google Scholar]
- Cunningham, J.P.; Yu, B.M. Dimensionality reduction for large-scale neural recordings. Nat. Neurosci. 2014, 17, 1500–1509. [Google Scholar] [CrossRef] [PubMed]
- Dadarlat, M.; Stryker, M.P. Locomotion Enhances Neural Encoding of Visual Stimuli in Mouse V1. J. Neurosci. 2017, 37, 3764–3775. [Google Scholar] [CrossRef] [PubMed]
- Fagerholm, E.D.; Scott, G.; Shew, W.L.; Song, C.; Leech, R.; Knöpfel, T.; Sharp, D.J. Cortical Entropy, Mutual Information and Scale-Free Dynamics in Waking Mice. Cereb. Cortex 2016, 26, 3945–3952. [Google Scholar] [CrossRef] [PubMed]
- Ito, S.; Hansen, M.E.; Heiland, R.; Lumsdaine, A.; Litke, A.M.; Beggs, J.M. Extending Transfer Entropy Improves Identification of Effective Connectivity in a Spiking Cortical Network Model. PLoS ONE 2011, 6, e27431. [Google Scholar] [CrossRef] [PubMed]
- Nigam, S.; Shimono, M.; Ito, S.; Yeh, F.-C.; Timme, N.; Myroshnychenko, M.; Lapish, C.C.; Tosi, Z.; Hottowy, P.; Smith, W.C.; et al. Rich-Club Organization in Effective Connectivity among Cortical Neurons. J. Neurosci. 2016, 36, 670–684. [Google Scholar] [CrossRef] [PubMed]
- Rolls, E.T.; Treves, A.; Robertson, R.G.; Georges-François, P.; Panzeri, S. Information about spatial view in an ensemble of primate hippocampal cells. J. Neurophysiol. 1998, 79, 1797–1813. [Google Scholar] [CrossRef]
- Timme, N.; Ito, S.; Myroshnychenko, M.; Yeh, F.-C.; Hiolski, E.; Hottowy, P.; Beggs, J.M. Multiplex Networks of Cortical and Hippocampal Neurons Revealed at Different Timescales. PLoS ONE 2014, 9, e115764. [Google Scholar] [CrossRef]
- Timme, N.M.; Ito, S.; Myroshnychenko, M.; Nigam, S.; Shimono, M.; Yeh, F.-C.; Hottowy, P.; Litke, A.M.; Beggs, J.M. High-Degree Neurons Feed Cortical Computations. PLoS Comput. Biol. 2016, 12, e1004858. [Google Scholar] [CrossRef]
- Damoiseaux, J.S.; Greicius, M.D. Greater than the sum of its parts: A review of studies combining structural connectivity and resting-state functional connectivity. Anat. Embryol. 2009, 213, 525–533. [Google Scholar] [CrossRef]
- Greicius, M.D.; Krasnow, B.; Reiss, A.L.; Menon, V. Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. USA 2002, 100, 253–258. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O.; Bullmore, E.T. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Quiroga, R.Q.; Panzeri, S. Extracting information from neuronal populations: Information theory and decoding approaches. Nat. Rev. Neurosci. 2009, 10, 173–185. [Google Scholar] [CrossRef] [PubMed]
- Novelli, L.; Wollstadt, P.; Mediano, P.A.; Wibral, M.; Lizier, J.T. Large-scale directed network inference with multivariate transfer entropy and hierarchical statistical testing. Netw. Neurosci. 2019, 3, 827–847. [Google Scholar] [CrossRef] [PubMed]
- Rubinov, M.; Sporns, O. Complex network measures of brain connectivity: Uses and interpretations. Neurolmage 2010, 52, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Panzeri, S.; Senatore, R.; Montemurro, M.; Petersen, R.S. Correcting for the Sampling Bias Problem in Spike Train Information Measures. J. Neurophysiol. 2007, 98, 1064–1072. [Google Scholar] [CrossRef]
- Treves, A.; Panzeri, S. The Upward Bias in Measures of Information Derived from Limited Data Samples. Neural Comput. 1995, 7, 399–407. [Google Scholar] [CrossRef]
- Paninski, L. Estimation of Entropy and Mutual Information. Neural Comput. 2003, 15, 1191–1253. [Google Scholar] [CrossRef]
- Victor, J.D. Binless strategies for estimation of information from neural data. Phys. Rev. E 2002, 66. [Google Scholar] [CrossRef]
- Wibral, M.; Lizier, J.T.; Priesemann, V. Bits from Brains for Biologically Inspired Computing. Front. Robot. AI 2015, 2, 1–25. [Google Scholar] [CrossRef]
- Lindner, M.; Vicente, R.; Priesemann, V.; Wibral, M. Tretnool: A Matlab open source toolbox to analyse information flow in time series data with transfer entropy. BMC Neurosci. 2011, 12, 119. [Google Scholar] [CrossRef]
- Timme, N.M. GitHub: Information Theory Ensemble Analysis. Available online: https://github.com/nmtimme/Information-Theory-Ensemble-Analysis (accessed on 20 May 2020).
- Timme, N.M. Personal Website. Available online: www.nicholastimme.com (accessed on 20 May 2020).
- Linsenbardt, D.N.; Timme, N.M.; Lapish, C.C. Encoding of the Intent to Drink Alcohol by the Prefrontal Cortex Is Blunted in Rats with a Family History of Excessive Drinking. Eneuro 2019, 6. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Sys. Tech. J. 1948, 27, 379–423. [Google Scholar]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar]
- Timme, N.M.; Alford, W.; Flecker, B.; Beggs, J.M. Synergy, redundancy, and multivariate information measures: An experimentalist’s perspective. J. Comput. Neurosci. 2013, 36, 119–140. [Google Scholar] [CrossRef]
- Runge, J.; Heitzig, J.; Petoukhov, V.; Kurths, J. Escaping the Curse of Dimensionality in Estimating Multivariate Transfer Entropy. Phys. Rev. Lett. 2012, 108, 258701. [Google Scholar] [CrossRef]
- Montalto, A.; Faes, L.; Marinazzo, D. Mute: A Matlab Toolbox to Compare Established and Novel Estimators of the Multivariate Transfer Entropy. PLoS ONE 2014, 9, e109462. [Google Scholar] [CrossRef]
- Wollstadt, P.; Lizier, J.T.; Vicente, R.; Finn, C.; Martínez-Zarzuela, M.; Mediano, P.A.; Novelli, L.; Wibral, M. IDTxl: The Information Dynamics Toolkit xl: A Python package for the efficient analysis of multivariate information dynamics in networks. J. Open Source Softw. 2019, 4. [Google Scholar] [CrossRef]
| y = 0 | ||
| y = 1 |
| Meaning | |
|---|---|
| s | The strength of the interaction (0: no interaction, 1: strongest possible interaction) |
| a | The noise level (0: no noise, 1: only noise) |
| Number of information sources in the ensemble | |
| Number of randomization (Monte Carlo) trials in the null data comparison |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Timme, N.M.; Linsenbardt, D.; Lapish, C.C. A Method to Present and Analyze Ensembles of Information Sources. Entropy 2020, 22, 580. https://doi.org/10.3390/e22050580
Timme NM, Linsenbardt D, Lapish CC. A Method to Present and Analyze Ensembles of Information Sources. Entropy. 2020; 22(5):580. https://doi.org/10.3390/e22050580
Chicago/Turabian StyleTimme, Nicholas M., David Linsenbardt, and Christopher C. Lapish. 2020. "A Method to Present and Analyze Ensembles of Information Sources" Entropy 22, no. 5: 580. https://doi.org/10.3390/e22050580
APA StyleTimme, N. M., Linsenbardt, D., & Lapish, C. C. (2020). A Method to Present and Analyze Ensembles of Information Sources. Entropy, 22(5), 580. https://doi.org/10.3390/e22050580





