Dynamical Complexity of the 2015 St. Patrick’s Day Magnetic Storm at Swarm Altitudes Using Entropy Measures
Abstract
:1. Introduction
2. Methodology
2.1. Shannon Entropy
2.2. Symbolic Dynamics and Block Entropy
2.3. Alternative Entropy Formulations
2.4. Approximate Entropy
2.5. Sample Entropy
2.6. Fuzzy Entropy
- The uncertainty of an open system state can be quantified by the Boltzmann-Gibbs (B-G) entropy, which is the widest known uncertainty measure in statistical mechanics. B-G entropy cannot, however, describe nonequilibrium physical systems characterized by long-range interactions or long-term memory or being of a multi-fractal nature. Inspired by multi-fractal concepts, Tsallis [38,39] has proposed a generalization of the B-G statistics, that is, the Tsallis Entropy, .
- Approximate entropy () has been introduced by Pincus as a measure for characterizing the regularity in relatively short and potentially noisy data. More specifically, examines time series for detecting the presence of similar epochs; more similar and more frequent epochs lead to lower values of .
- Sample entropy () was proposed by Richman and Moorman as an alternative that would provide an improvement of the intrinsic bias of .
- Fuzzy entropy (), like its ancestors, and , is a “regularity statistic” that quantifies the (un)predictability of fluctuations in a time series. For the calculation of , the similarity between vectors is defined based on fuzzy membership functions and the vectors’ shapes. can be considered as an upgraded alternative of (and ) for the evaluation of complexity, especially for short time series contaminated by noise.
3. Data and Analysis
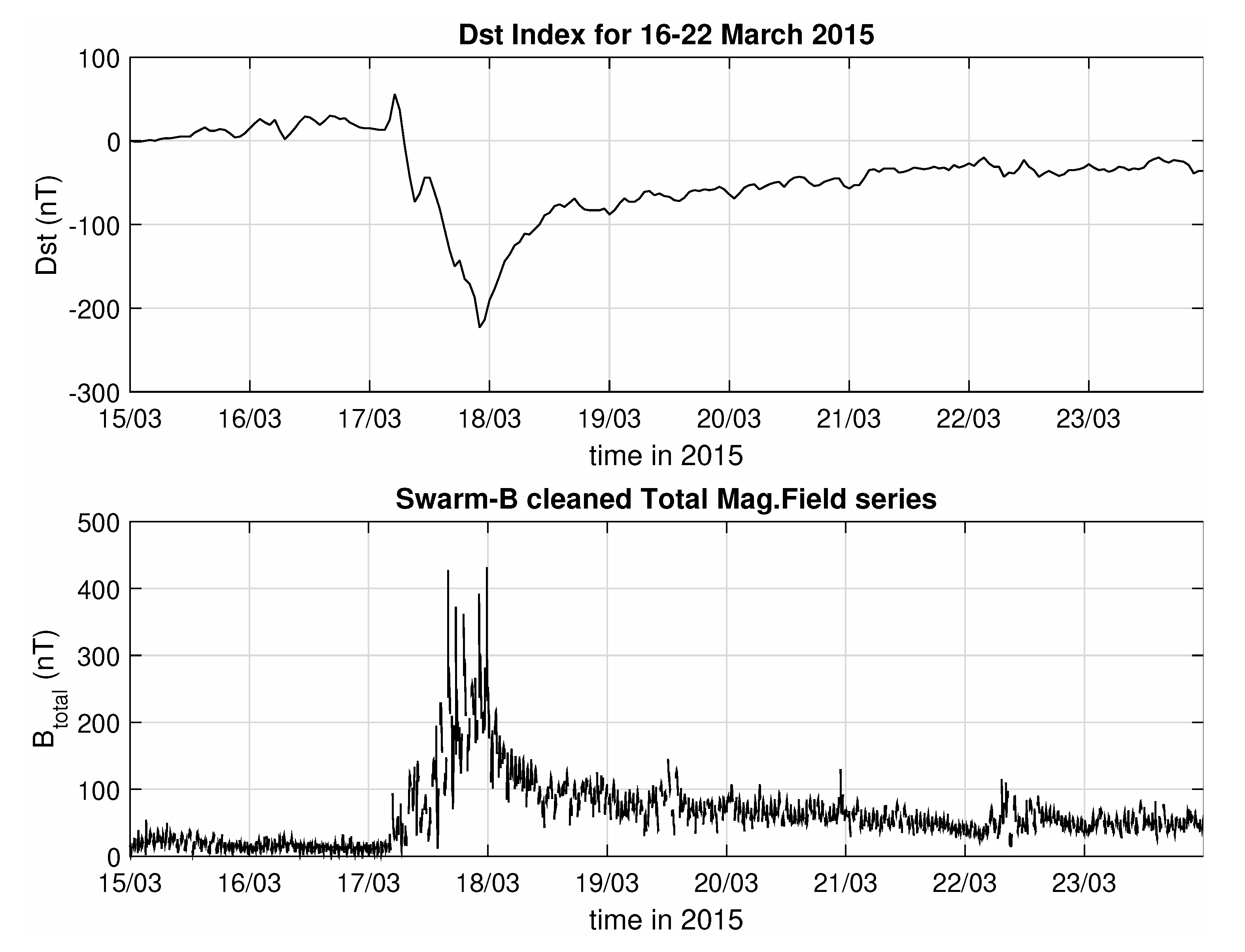
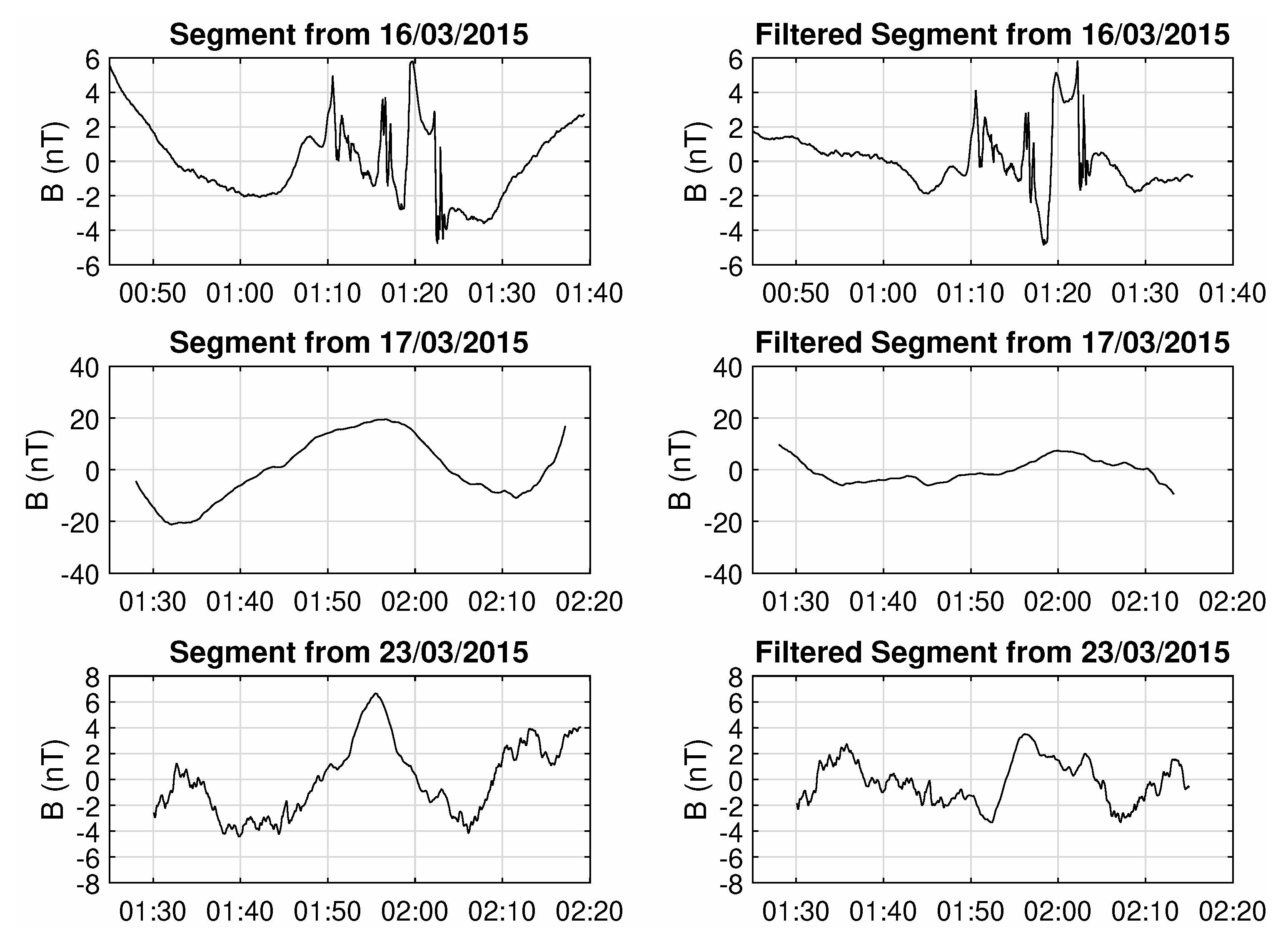
3.1. Swarm Magnetic Field Data
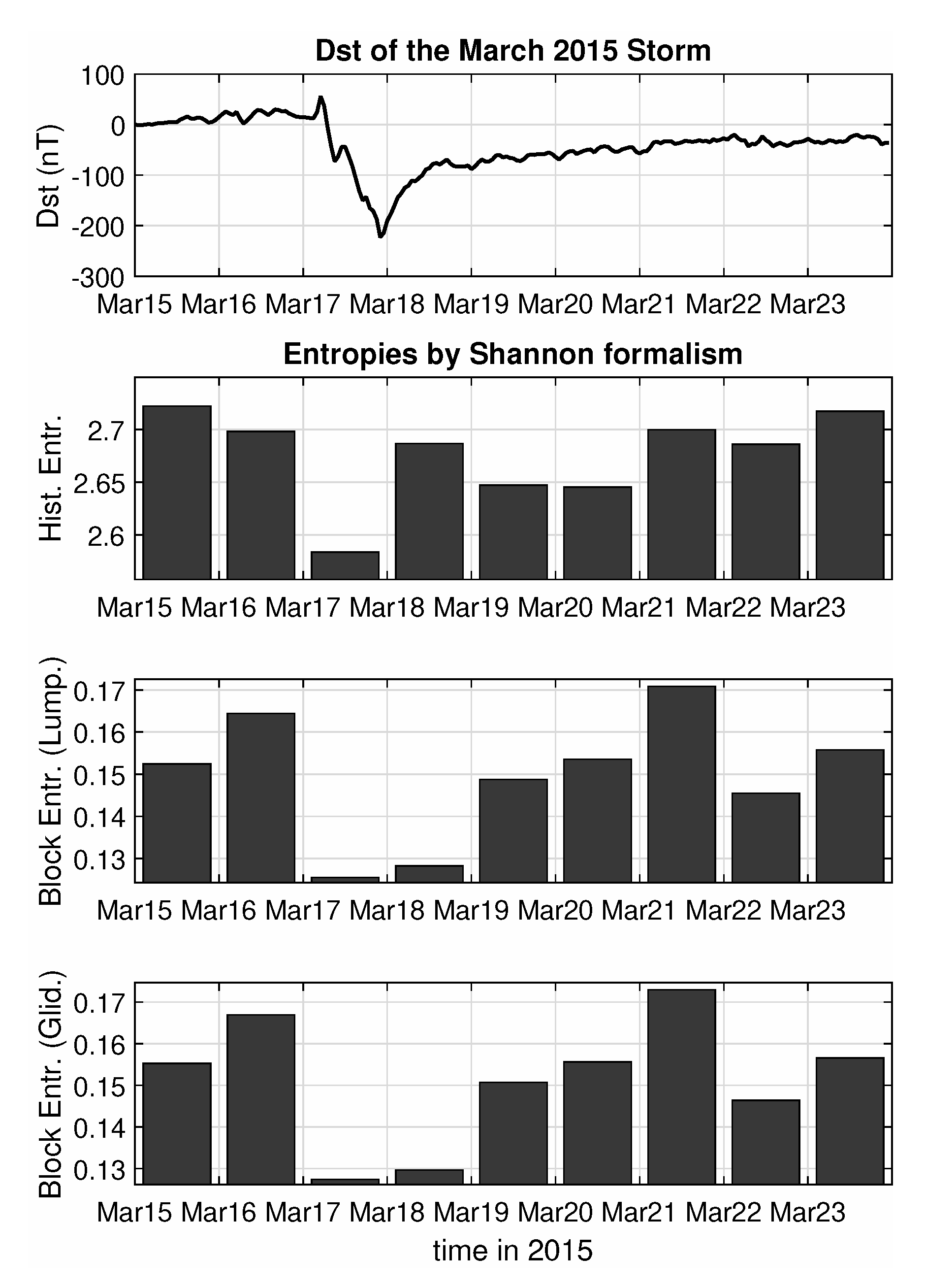
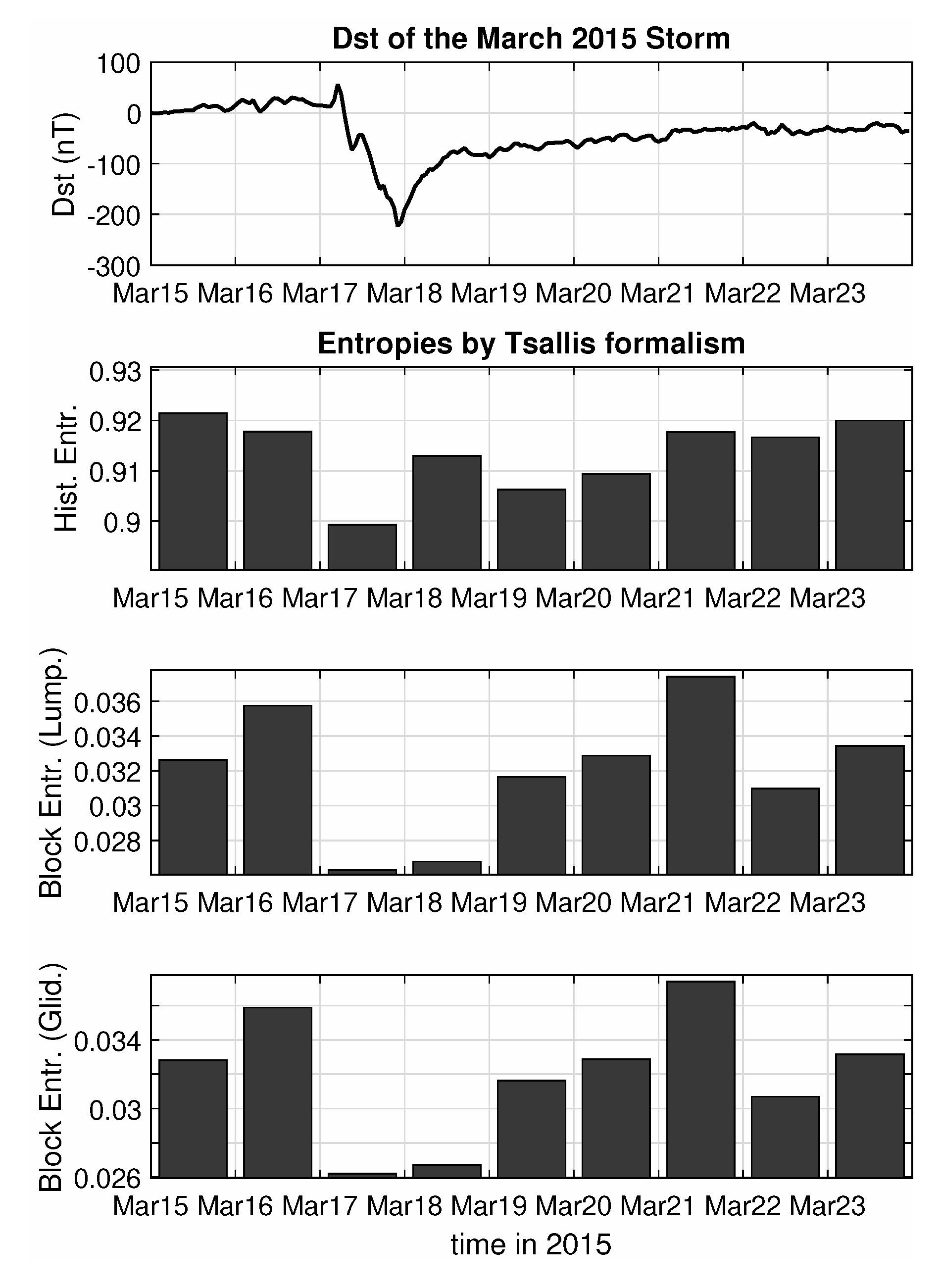
3.2. Entropy Analysis of the Swarm B Magnetic Field Data for the St. Patrick’s 2015 Storm
4. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tsurutani, B.T.; Sugiura, M.; Iyemori, T.; Goldstein, B.E.; Gonzalez, W.D.; Akasofu, S.I.; Smith, E.J. The nonlinear response of AE to the IMF BS driver: A spectral break at 5 hours. Geophys. Res. Lett. 1990, 17, 279–282. [Google Scholar] [CrossRef] [Green Version]
- Baker, D.N.; Klimas, A.J.; McPherron, R.L.; Büchner, J. The evolution from weak to strong geomagnetic activity: An interpretation in terms of deterministic chaos. Geophys. Res. Lett. 1990, 17, 41–44. [Google Scholar] [CrossRef]
- Vassiliadis, D.V.; Sharma, A.S.; Eastman, T.E.; Papadopoulos, K. Low-dimensional chaos in magnetospheric activity from AE time series. Geophys. Res. Lett. 1990, 17, 1841–1844. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.S.; Vassiliadis, D.V.; Papadopoulos, K. Reconstruction of low-dimensional magnetospheric dynamics by singular spectrum analysis. Geophys. Res. Lett. 1993, 20, 355–358. [Google Scholar] [CrossRef]
- Vörös, Z.; Baumjohann, W.; Nakamura, R.; Runov, A.; Zhang, T.L.; Volwerk, M.; Eichelberger, H.U.; Balogh, A.; Horbury, T.S.; Glaßmeier, K.-H.; et al. Multi-scale magnetic field intermittence in the plasma sheet. Ann. Geophys. 2003, 21, 1955–1964. [Google Scholar] [CrossRef] [Green Version]
- Klimas, A.J.; Vassiliadis, D.; Baker, D.N.; Roberts, D.A. The organized nonlinear dynamics of the magnetosphere. J. Geophys. Res. 1996, 101, 13089–13113. [Google Scholar] [CrossRef]
- Consolini, G.; Marcucci, M.F.; Candidi, M. Multifractal Structure of Auroral Electrojet Index Data. Phys. Rev. Lett. 1996, 76, 4082–4085. [Google Scholar] [CrossRef]
- Angelopoulos, V.; Mukai, T.; Kokubun, S. Evidence for intermittency in Earth’s plasma sheet and implications for self-organized criticality. Phys. Plasmas 1999, 6, 4161–4168. [Google Scholar] [CrossRef]
- Wanliss, J.A. Fractal properties of SYM-H during quiet and active times. J. Geophys. Res. 2005, 110, A03202. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Kapiris, P.; Mandea, M.; Vassiliadis, D.; Eftaxias, K. From pre-storm activity to magnetic storms: A transition described in terms of fractal dynamics. Ann. Geophys. 2006, 24, 3557–3567. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.; Wu, C.C.; Podesta, J.; Echim, M.; Lamy, H.; Tam, S.W.Y. ROMA (Rank-Ordered Multifractal Analyses) of intermittency in space plasmas – a brief tutorial review. Nonlin. Processes Geophys. 2010, 17, 545–551. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Tozzi, R. On the multi-scale nature of large geomagnetic storms: An empirical mode decomposition analysis. Nonlin Proc. Geophys. 2012, 19, 667–673. [Google Scholar] [CrossRef]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Dynamical complexity in Dst time series using non-extensive Tsallis entropy. Geophys. Res. Lett. 2008, 35, L14102. [Google Scholar] [CrossRef] [Green Version]
- Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Kalimeri, M.; Anastasiadis, A.; Eftaxias, K. Investigating dynamical complexity in the magnetosphere using various entropy measures. J. Geophys. Res. 2009, 114, A00D06. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Materassi, M.; Tozzi, R. An information theory approach to the storm-substorm relationship. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Runge, J.; Balasis, G.; Daglis, I.A.; Papadimitriou, C.; Donner, R.V. Common solar wind drivers behind magnetic storm–magnetospheric substorm dependency. Sci. Rep. 2018, 8, 16987. [Google Scholar] [CrossRef]
- Wing, S.; Johnson, J.R.; Camporeale, E.; Reeves, G.D. Information theoretical approach to discovering solar wind drivers of the outer radiation belt. J. Geophys. Res. Space Phys. 2016, 121, 9378–9399. [Google Scholar] [CrossRef]
- Balasis, G.; Donner, R.V.; Potirakis, S.M.; Runge, J.; Papadimitriou, C.; Daglis, I.A.; Kurths, J. Statistical Mechanics and Information-Theoretic Perspectives on Complexity in the Earth system. Entropy 2013, 15, 4844–4888. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1997, 28, 656–715. [Google Scholar] [CrossRef]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Frechet, M. Methode des fonctions arbitraires, théorie des événements en chaîne dans le cas d’un nombre fini d’états possibles. In Gauthier-Villars; AMS: Paris, France, 1938. [Google Scholar]
- Tolman, R.C. Principles of Statistical Mechanics; Clarendon: Oxford, UK, 1938. [Google Scholar]
- Kotsiantis, S.; Kanellopoulos, D. Discretization Techniques: A recent survey. GESTS Int. Trans. Comput. Sci. Eng. 2006, 32, 47–58. [Google Scholar]
- Hao, B.-L. Elementary Symbolic Dynamics and Chaos in Dissipative Systems; World Scientific: Singapore, 1989. [Google Scholar]
- Karamanos, K.; Nicolis, G. Symbolic dynamics and entropy analysis of Feigenbaum limit sets. Chaos Solitons Fractals 1999, 10, 1135–1150. [Google Scholar] [CrossRef]
- Karamanos, K. Entropy Analysis of Automatic Sequences Revisited: An Entropy Diagnostic for Automaticity. AIP Conf. Proc. 2001, 573, 278. [Google Scholar] [CrossRef]
- Ebeling, W.; Nicolis, G. Word frequency and entropy of symbolic sequences: A dynamical perspective. Chaos Solitons Fractals 1992, 2, 635–650. [Google Scholar] [CrossRef]
- Nicolis, G.; Gaspard, P. Toward a probabilistic approach to complex systems. Chaos Solitons Fractals 1994, 4, 41–57. [Google Scholar] [CrossRef]
- Khinchin, A.I. Mathematical Foundations of Information Theory; Dover: New York, NY, USA, 1957. [Google Scholar]
- McMillan, B. The basic theorems of information theory. Ann. Math. Stat. 1953, 24, 196–219. [Google Scholar] [CrossRef]
- Hartley, R.V.L. Transmission of information. Bell Syst. Tech. J. 1928, 7, 535–563. [Google Scholar] [CrossRef]
- Rényi, A. On Measures of Entropy and Information. In Proceedings of the fourth Berkeley Symposium on Mathematics, Statistics and Probability, Berkeley, CA, USA, 1 January 1961; pp. 547–561. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics, Approaching a Complex World; Springer: New York, NY, USA, 2009. [Google Scholar]
- Anastasiadis, A. Editorial of Special Issue: Tsallis Entropy. Entropy 2012, 14, 174–176. [Google Scholar] [CrossRef] [Green Version]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef] [Green Version]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of surface EMG signal based on fuzzy entropy. IEEE Trans. Neural Syst. Rehab. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Generalized entropy-based criterion for consistent testing. Phys. Rev. E. 1998, 58, 1442–1445. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Hulot, G. Swarm: A constellation to study the Earth’s magnetic field. Earth Planets Space 2006, 58, 351–358. [Google Scholar] [CrossRef] [Green Version]
- Finlay, C.C.; Dumberry, M.; Chulliat, A.; Pais, M.A. Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model. Earth Planets Space 2016, 68, 112. [Google Scholar] [CrossRef] [Green Version]
- Upton, G.; Cook, I. Understanding Statistics; Oxford University Press: Oxford, UK, 1996; p. 55. [Google Scholar]
- Daglis, I. The storm-time ring current. Space Sci. Rev. 2001, 98, 343–363. [Google Scholar] [CrossRef]
- De Michelis, P.; Consolini, G.; Tozzi, R.; Marcucci, M.F. Observations of high-latitude geomagnetic field fluctuations during St. Patrick storm: Swarm and SuperDARN measurements. Earth Planets Space 2016. [Google Scholar] [CrossRef] [Green Version]
- Balasis, G.; Daglis, I.A.; Contoyiannis, Y.; Potirakis, S.M.; Papadimitriou, C.; Melis, N.S.; Kontoes, C. Observation of intermittency-induced critical dynamics in geomagnetic field time series prior to the intense magnetic storms of March, June, and December 2015. J. Geophys. Res. Space Phys. 2018, 123, 4594–4613. [Google Scholar] [CrossRef] [Green Version]
- Balasis, G.; Papadimitriou, C.; Boutsi, A.Z. Ionospheric response to solar and interplanetary disturbances: A Swarm perspective. Philos. Trans. A Math. Phys. Eng. Sci. 2019, 377. [Google Scholar] [CrossRef]
- Balasis, G.; Potirakis, S.M.; Mandea, M. Investigating Dynamical Complexity of Geomagnetic Jerks using Various Entropy Measures. Front. Earth Sci. 2016, 4, 71. [Google Scholar] [CrossRef] [Green Version]
- Davis, T.N.; Sugiura, M. Auroral electrojet activity index AE and its universal time variations. J. Geophys. Res. 1966, 71, 785. [Google Scholar] [CrossRef] [Green Version]
- Gjerloev, J.W.; Hoffman, R.A.; Friel, M.M.; Frank, L.A.; Sigwarth, J.B. Substorm behavior of the auroral electrojet indices. Ann. Geophys. 2004, 22, 2135–2149. [Google Scholar] [CrossRef]
- Mannucci, A.J.; Tsurutani, B.T. Chapter 20-Ionosphere and Thermosphere Responses to Extreme Geomagnetic Storms. In Extreme Events in Geospace; Buzulukova, N., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 493–511. ISBN 9780128127001. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadimitriou, C.; Balasis, G.; Boutsi, A.Z.; Daglis, I.A.; Giannakis, O.; Anastasiadis, A.; Michelis, P.D.; Consolini, G. Dynamical Complexity of the 2015 St. Patrick’s Day Magnetic Storm at Swarm Altitudes Using Entropy Measures. Entropy 2020, 22, 574. https://doi.org/10.3390/e22050574
Papadimitriou C, Balasis G, Boutsi AZ, Daglis IA, Giannakis O, Anastasiadis A, Michelis PD, Consolini G. Dynamical Complexity of the 2015 St. Patrick’s Day Magnetic Storm at Swarm Altitudes Using Entropy Measures. Entropy. 2020; 22(5):574. https://doi.org/10.3390/e22050574
Chicago/Turabian StylePapadimitriou, Constantinos, Georgios Balasis, Adamantia Zoe Boutsi, Ioannis A. Daglis, Omiros Giannakis, Anastasios Anastasiadis, Paola De Michelis, and Giuseppe Consolini. 2020. "Dynamical Complexity of the 2015 St. Patrick’s Day Magnetic Storm at Swarm Altitudes Using Entropy Measures" Entropy 22, no. 5: 574. https://doi.org/10.3390/e22050574
APA StylePapadimitriou, C., Balasis, G., Boutsi, A. Z., Daglis, I. A., Giannakis, O., Anastasiadis, A., Michelis, P. D., & Consolini, G. (2020). Dynamical Complexity of the 2015 St. Patrick’s Day Magnetic Storm at Swarm Altitudes Using Entropy Measures. Entropy, 22(5), 574. https://doi.org/10.3390/e22050574






