Improving Underwater Continuous-Variable Measurement-Device-Independent Quantum Key Distribution via Zero-Photon Catalysis
Abstract
:1. Introduction
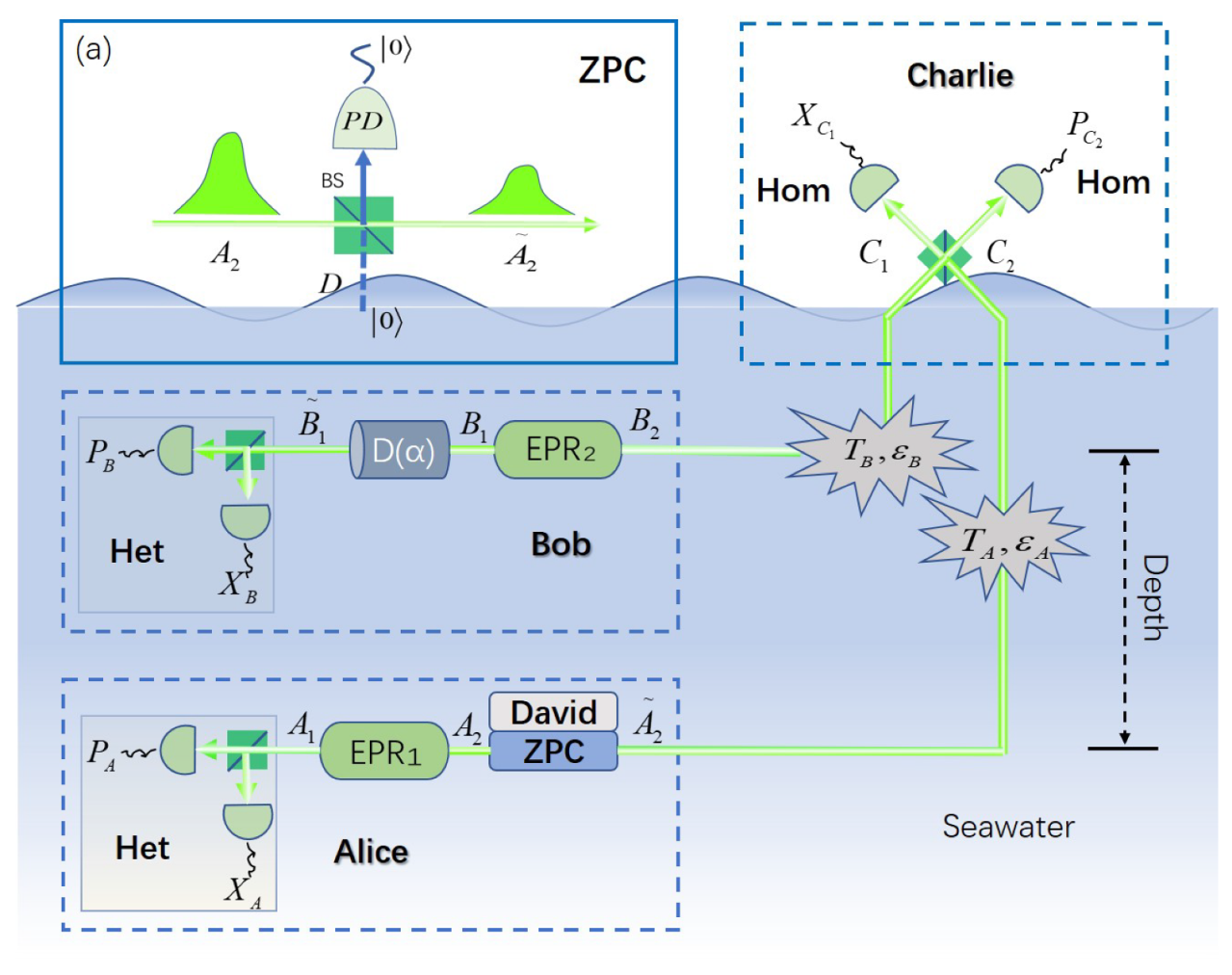
2. The ZPC-Based MDI-CVQKD Protocol
3. Security Analysis
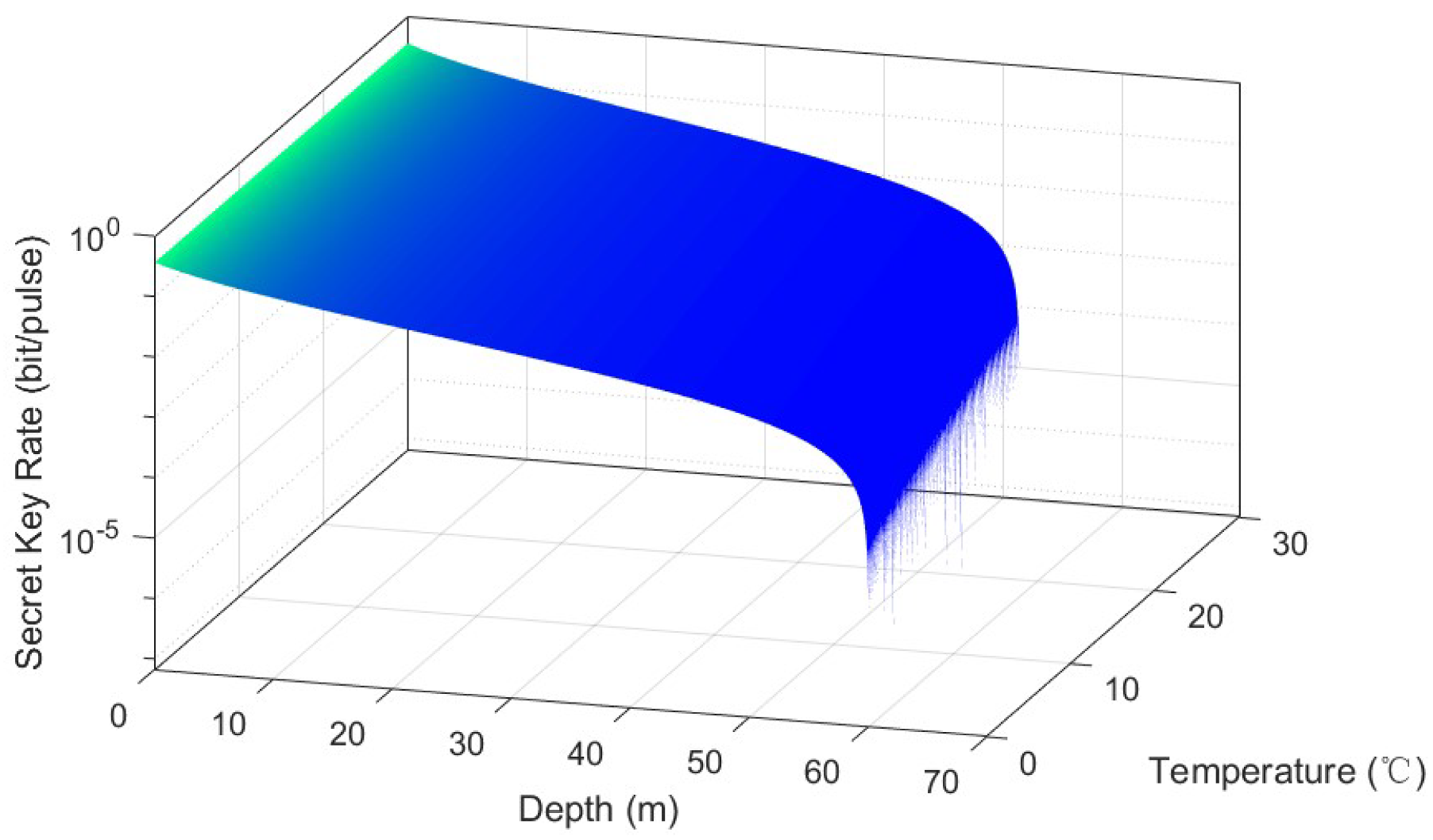
3.1. Derivation of the Secret Key Rate
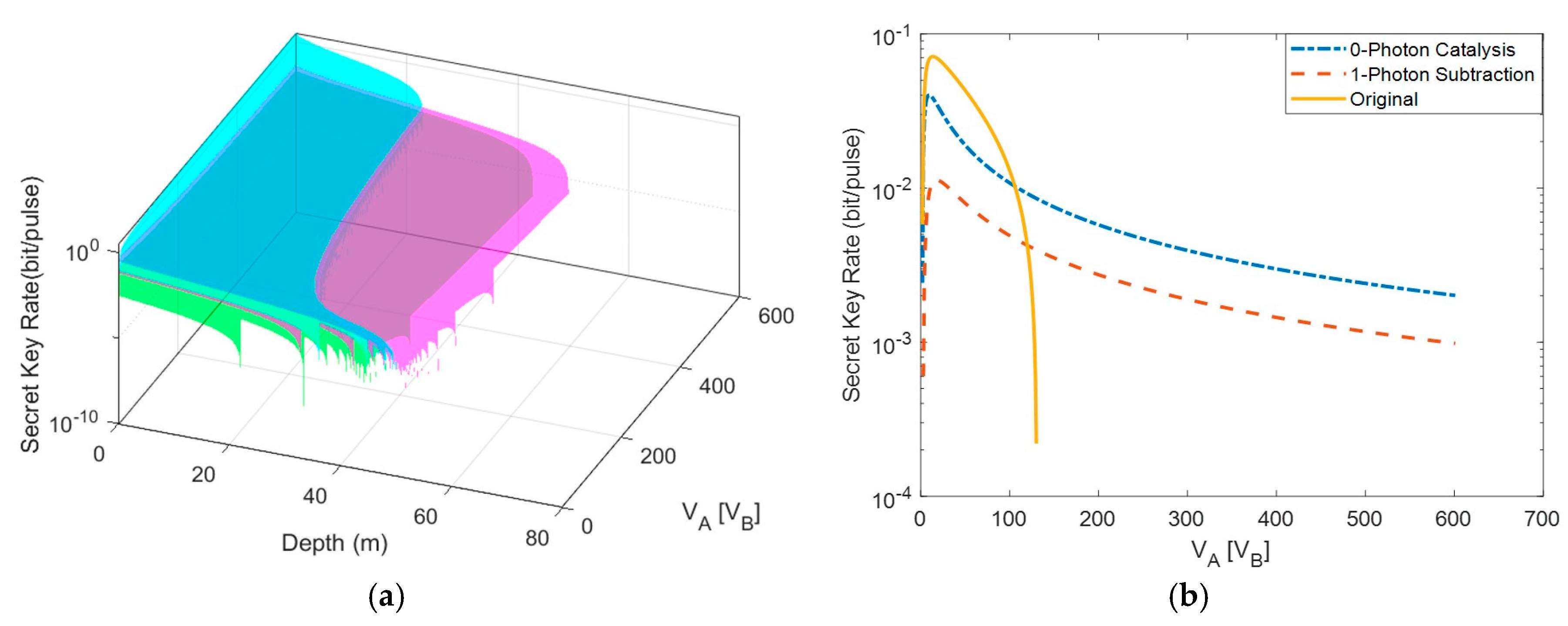
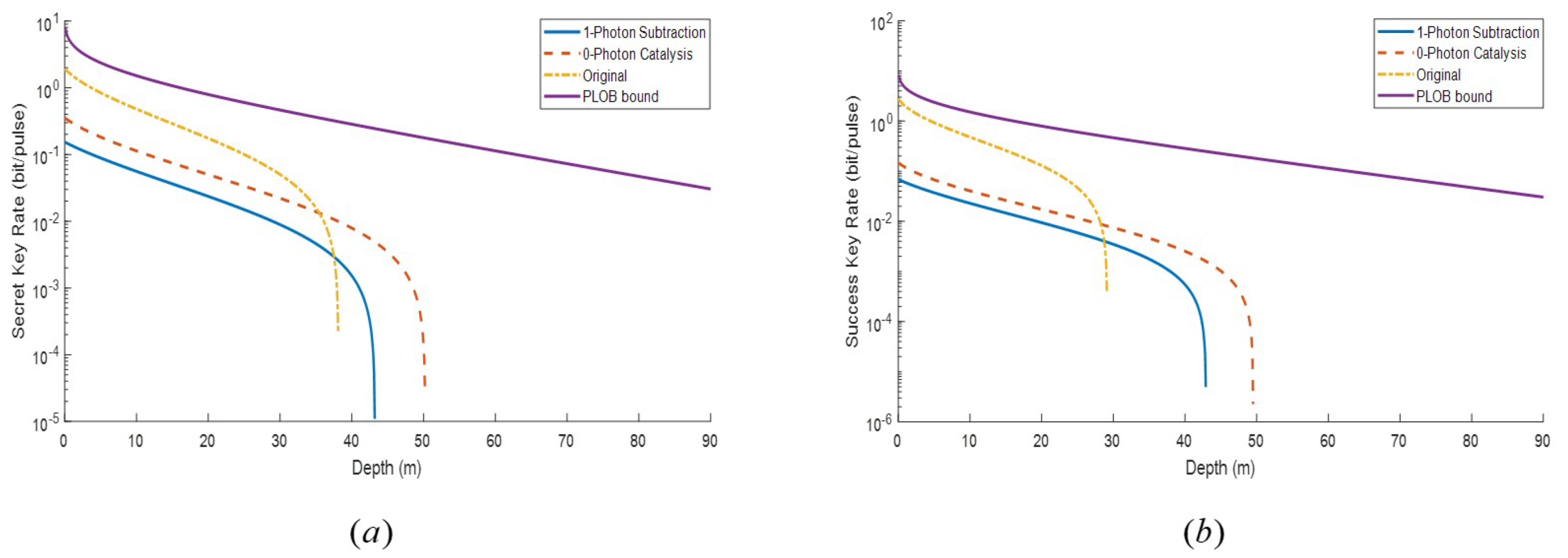
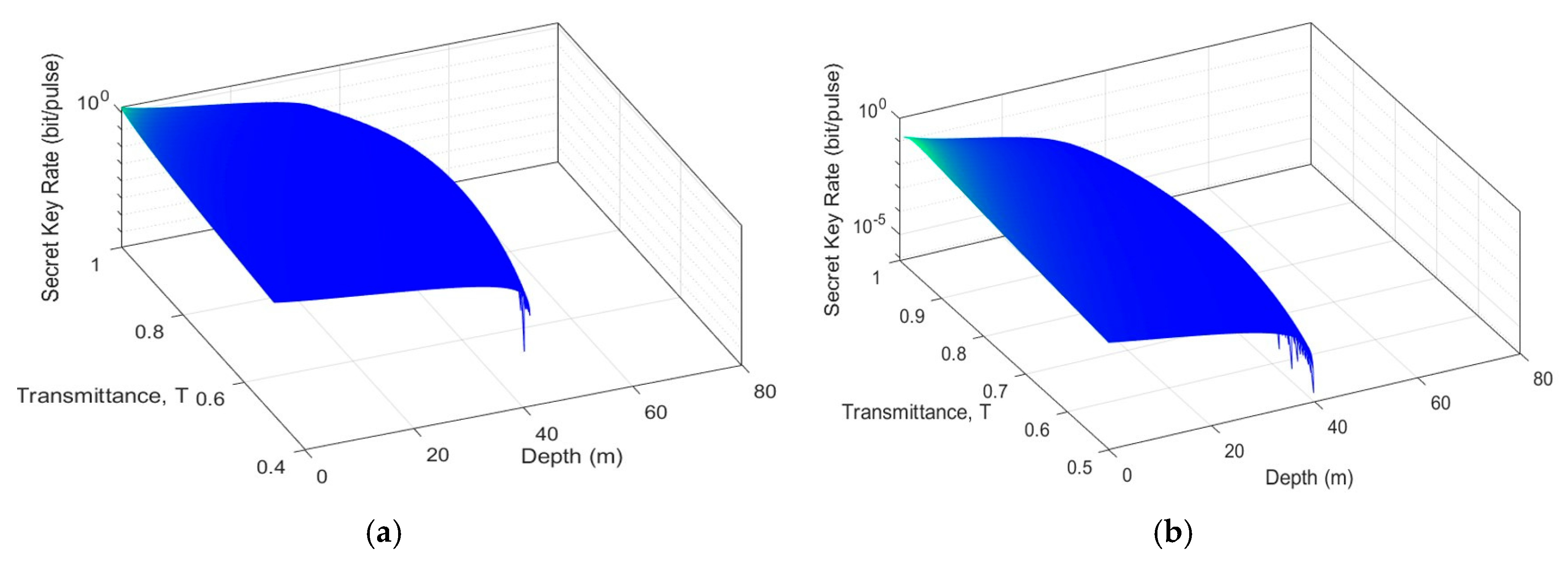
3.2. Numerical Simulations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| QKD | Quantum key Distribution |
| DVQKD | Discrete-variable Quantum key Distribution |
| CVQKD | Continuous-variable Quantum key Distribution |
| MDI | Measurement-device-independent |
| TMSV | Two-mode squeezed vacuum |
| SPS | Single-photon subtraction |
| ZPC | Zero-photon catalysis |
| EB | Entanglement-based |
| PM | Prepare- and-measure |
| Het | Heterodyne detection |
| Hom | Homodyne detection |
| BS | Beam splitter |
Appendix A. A: Seawater Channel
Appendix A.1. Mixing Effects of Temperature and Salinity

Appendix A.2. Effects of Sun Elevation Angle
References
- Vazirani, U.; Vidick, T. Fully Device Independent Quantum Key Distribution. Commun. ACM 2019, 62, 133. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, T.; Hirano, T.; Puttnam, B.; Rademacher, G.; Luís, R.; Fujiwara, M.; Namiki, R.; Awaji, Y.; Takeoka, M.; Wada, N.; et al. Wavelength division multiplexing of continuous variable quantum key distribution and 18.3 Tbit/s data channels. Commun. Phys. 2019, 2, 1301–1350. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.J.; Mao, Y.Y.; Huang, W.T.; Huang, D.; Guo, Y. Optical frequency comb-based multichannel parallel continuous-variable quantum key distribution. Opt. Express 2019, 27, 25314–25329. [Google Scholar] [CrossRef]
- Gessner, M.; Pezzè, L.; Smerzi, A. Efficient entanglement criteria for discrete, continuous, and hybrid variables. Phys. Rev. A 2016, 94, 020101. [Google Scholar] [CrossRef] [Green Version]
- Pirandola, S.; Andersen, U.L.; Banchi, L.; Berta, M.; Bunandar, D.; Colbeck, R.; Englund, D.; Gehring, T.; Lupo, C.; Ottaviani, C.; et al. Advances in Quantum Cryptography. arXiv 2019, 1906, 01645. [Google Scholar] [CrossRef] [Green Version]
- Ye, W.; Zhong, H.; Liao, Q.; Huang, D.; Hu, L.Y.; Guo, Y. Improvement of self-referenced continuous-variable quantum key distribution with quantum photon catalysis. Opt. Express 2019, 27, 17186–17198. [Google Scholar] [CrossRef] [PubMed]
- Liao, Q.; Guo, Y.; Huang, D.; Huang, P.; Zeng, G. Long-distance continuous-variable quantum key distribution using non-Gaussian state-discrimination detection. New J. Phys. 2018, 20, 023015. [Google Scholar] [CrossRef]
- Zhao, W.; Guo, Y.; Zhang, L.; Huang, D. Coherent communications; Phase compensation; Phase estimation; Phase noise; Phase shift; Quantum key distribution. Opt. Express 2019, 27, 1838–1853. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.; Preskill, J. Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Phys. Rev. Lett. 2000, 85, 441–444. [Google Scholar] [CrossRef] [Green Version]
- Braunstein, S.; Pirandola, S. Side-Channel-Free Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar] [CrossRef] [Green Version]
- Lo, H.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.; Lloyd, S.; Gehring, T.; Jacobsen, C.; Andersen, U. High-rate measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 397–402. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Sun, S.; Jiang, M.; Liang, L. Local oscillator fluctuation opens a loophole for Eve in practical continuous-variable quantum-key-distribution systems. Phys. Rev. A 2013, 88, 022339. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Weedbrook, C.; Yin, Z.; Wang, S.; Li, H.; Chen, W.; Guo, G.; Han, Z. Quantum hacking of a continuous-variable quantum-key-distribution system using a wavelength attack. Phys. Rev. A 2013, 87, 062329. [Google Scholar] [CrossRef] [Green Version]
- Qin, H.; Kumar, R.; Alléaume, R. Quantum hacking: Saturation attack on practical continuous-variable quantum key distribution. Phys. Rev. A 2016, 94, 012325. [Google Scholar] [CrossRef] [Green Version]
- Paterson, C. Atmospheric Turbulence and Orbital Angular Momentum of Single Photons for Optical Communication. Phys. Rev. Lett. 2005, 94, 153901. [Google Scholar] [CrossRef]
- Berman, G.; Chumak, A. Photon distribution function for long-distance propagation of partially coherent beams through the turbulent atmosphere. Phys. Rev. A 2006, 74, 013805. [Google Scholar] [CrossRef] [Green Version]
- Semenov, A.; Töppel, F.; Vasylyev, D.; Gomonay, H.; Vogel, W. Homodyne detection for atmosphere channels. Phys. Rev. A 2012, 85, 013826. [Google Scholar] [CrossRef] [Green Version]
- Gariano, J.; Djordjevic, I. Theoretical study of a submarine to submarine quantum key distribution systems. Opt. Express 2019, 27, 3055–3064. [Google Scholar] [CrossRef]
- Bouchard, F.; Sit, A.; Hufnagel, F.; Abbas, A.; Zhang, Y.; Heshami, K.; Fickler, R.; Marquardt, C.; Leuchs, G.; Boyd, R.; et al. Underwater Quantum Key Distribution in Outdoor Conditions with Twisted Photons. arXiv 2018, 1801, 10299. [Google Scholar]
- Ruan, X.; Zhang, H.; Zhao, W.; Wang, X.; Li, X.; Guo, Y. Discrete-Modulated Continuous-Variable Quantum Key Distribution over Seawater Channel. Appl. Sci. 2019, 9, 4956. [Google Scholar] [CrossRef] [Green Version]
- Kitagawa, A.; Takeoka, M.; Sasaki, M.; Chefles, A. Entanglement evaluation of non-Gaussian states generated by photon subtraction from squeezed states. Phys. Rev. A 2006, 73, 042310. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Liao, Q.; Wang, Y.; Huang, D.; Huang, P.; Zeng, G. Performance improvement of continuous-variable quantum key distribution with an entangled source in the middle via photon subtraction. Phys. Rev. A 2017, 95, 032304. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Ye, W.; Zhong, H.; Liao, Q. Continuous-variable quantum key distribution with non-Gaussian quantum catalysis. Phys. Rev. A 2019, 99, 032327. [Google Scholar] [CrossRef] [Green Version]
- Peng, Q.; Chen, G.; Li, X.; Liao, Q.; Guo, Y. Performance Improvement of Underwater Continuous-Variable Quantum Key Distribution via Photon Subtraction. Entropy 2019, 21, 1011. [Google Scholar] [CrossRef] [Green Version]
- Bennett, C.; Brassard, G.; Mermin, N. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557–559. [Google Scholar] [CrossRef]
- Yang, R.H.; He, G.Q. The Influence of Faraday Mirror’s Imperfection in Continuous Variable Quantum Key Distribution System. Acta Photonica Sinica 2015, 44, 2. [Google Scholar]
- Pirandola, S.; Laurenza, R.; Ottaviani, C.; Banchi, L. Fundamental limits of repeaterless quantum communications. Nat. Commun. 2017, 8, 15043. [Google Scholar] [CrossRef] [Green Version]
- Tian, B.; Zhang, F.; Tan, X. Design and development of an LED-based optical communication system for autonomous underwater robots. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 1558–1563. [Google Scholar]
- Doniec, M.; Detweiler, C.; Vasilescu, I.; Rus, D. Using optical communication for remote underwater robot operation. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4017–4022. [Google Scholar]
- Sun, X.; Kang, C.; Kong, M.; Alkhazragi, O.; Guo, Y.; Ouhssain, M.; Weng, Y.; Jones, B.; Ng, T.; Ooi, B. A Review on Practical Considerations and Solutions in Underwater Wireless Optical Communication. OSA 2020, 38, 421–431. [Google Scholar] [CrossRef] [Green Version]
- Wiscombe, W. Improved Mie scattering algorithms. Appl. Opt. 1980, 19, 1505–1509. [Google Scholar] [CrossRef]
- Lock, J.; Gérard, G. Generalized Lorenz–Mie theory and applications. J QUANT SPECTROSC RA 2009, 110, 800–807. [Google Scholar] [CrossRef]
- Zeng, Z.; Fu, S.; Zhang, H.; Dong, Y.; Cheng, J. A Survey of Underwater Optical Wireless Communications. IEEE Commun. Surv. Tutor. 2017, 19, 204–238. [Google Scholar] [CrossRef]
- Danielewicz-Ferchmin, I. Phase Diagram of Hydration Shells in Ionic Solutions. J. Phys. Chem. 1995, 99, 5658–5665. [Google Scholar] [CrossRef]
- Shvab, I. Sadus, R. Structure and polarization properties of water: Molecular dynamics with a nonadditive intermolecular potential. Phys. Rev. E 2012, 85, 051509. [Google Scholar] [CrossRef] [PubMed]
- Coker, H. Empirical free-ion polarizabilities of the alkali metal, alkaline earth metal, and halide ions. J. Phys. Chem. 1976, 80, 2078–2084. [Google Scholar] [CrossRef]
- Farinato, R.; Rowell, R. New values of the light scattering depolarization and anisotropy of water. J. Chem. Phys. 1976, 65, 593. [Google Scholar] [CrossRef]
- Duntley, S. Light in the Sea*. J. Opt. Soc. Am. 1963, 53, 214–233. [Google Scholar] [CrossRef]
- Pegau, W.; Gray, D.; Zaneveld, J. Absorption and attenuation of visible and near-infrared light in water: Dependence on temperature and salinity. OSA 1997, 36, 6035–6046. [Google Scholar] [CrossRef] [Green Version]
- Haltrin, V. Apparent optical properties of the sea illuminated by sun and sky: Case of the optically deep sea. Appl. Opt. 1998, 37, 8336–8340. [Google Scholar] [CrossRef]
- Zaneveld, J.; Barnard, Z.; Boss, E. Theoretical derivation of the depth average of remotely sensed optical parameters. Opt. Express 2005, 13, 9052–9061. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Xie, C.; Huang, P.; Li, J.; Zhang, L.; Huang, D.; Zeng, G. Channel-parameter estimation for satellite-to-submarine continuous-variable quantum key distribution. Phys. Rev. A 2018, 97, 052326. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zou, S.; Mao, Y.; Guo, Y. Improving Underwater Continuous-Variable Measurement-Device-Independent Quantum Key Distribution via Zero-Photon Catalysis. Entropy 2020, 22, 571. https://doi.org/10.3390/e22050571
Wang Y, Zou S, Mao Y, Guo Y. Improving Underwater Continuous-Variable Measurement-Device-Independent Quantum Key Distribution via Zero-Photon Catalysis. Entropy. 2020; 22(5):571. https://doi.org/10.3390/e22050571
Chicago/Turabian StyleWang, Yuang, Shanhua Zou, Yun Mao, and Ying Guo. 2020. "Improving Underwater Continuous-Variable Measurement-Device-Independent Quantum Key Distribution via Zero-Photon Catalysis" Entropy 22, no. 5: 571. https://doi.org/10.3390/e22050571
APA StyleWang, Y., Zou, S., Mao, Y., & Guo, Y. (2020). Improving Underwater Continuous-Variable Measurement-Device-Independent Quantum Key Distribution via Zero-Photon Catalysis. Entropy, 22(5), 571. https://doi.org/10.3390/e22050571




