Estimation of Autoregressive Parameters from Noisy Observations Using Iterated Covariance Updates
Abstract
1. Introduction
2. Scalar Parameter Estimation in Noise
| Algorithm 1: AR Parameter estimation with noisy data. |
Input: , , Previous Conditions: , Compute
Update the covariance to obtain and compute . Return , , . |
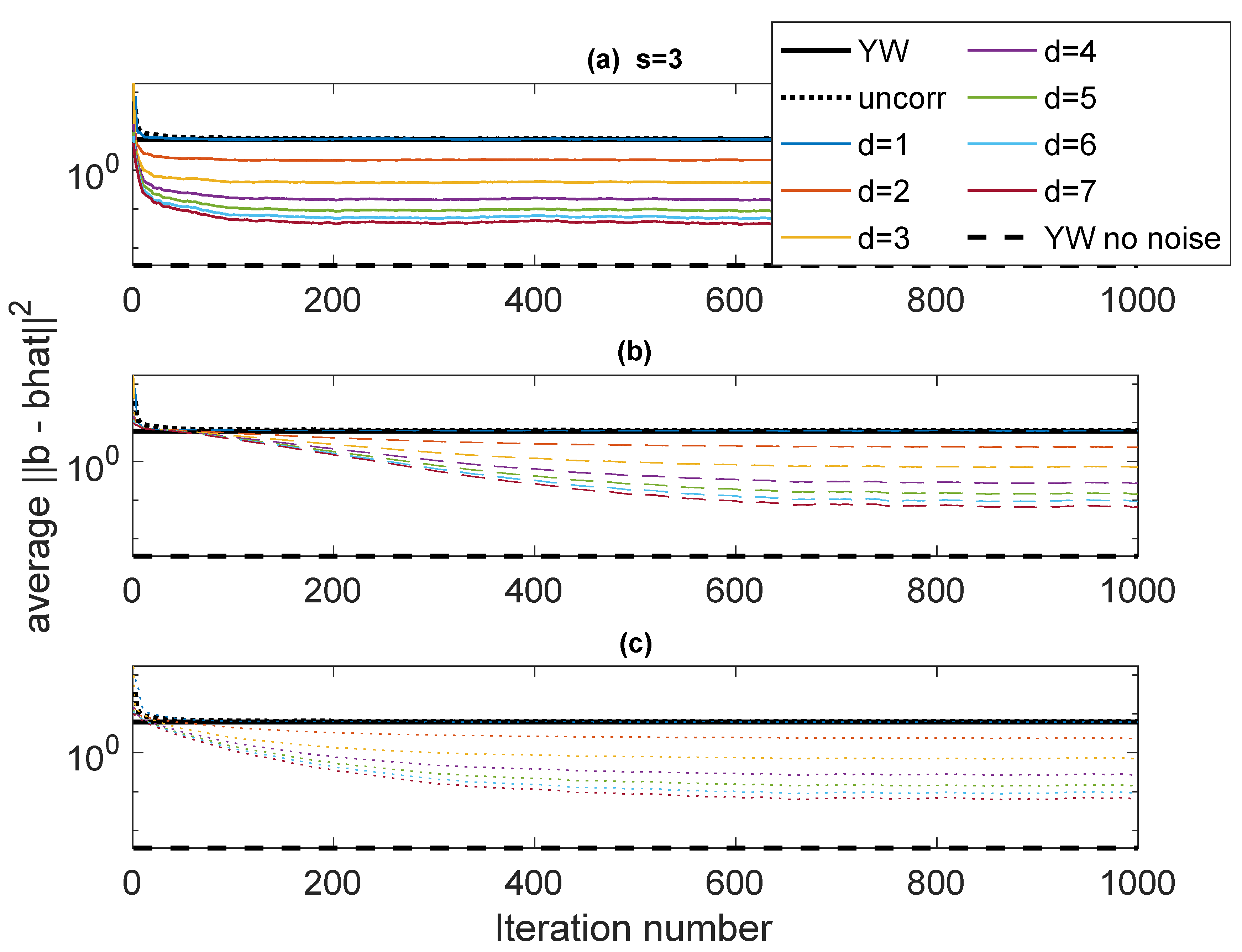
- Ignore : Neglect the correlation structure and simply assume that . This gives the equivalent of taking a scalar measurement and is used as a sort of worst-case basis for comparison among the different algorithms.
- Use the correct value of : That is, assume that and and are known and compute according to (6). This provides a limit on best-case performance against which other methods can be compared.
- Use the estimate of : Using the correct values of and , compute the autocorrelation matrix using in (6).
- Estimate , fix and : With assumed values of and , compute the autocorrelation matrix using in (6).
- Estimate everything: Estimate the values of and , then use them with in (6).
3. Estimating the Variances
4. Vector Autoregressive Formulation
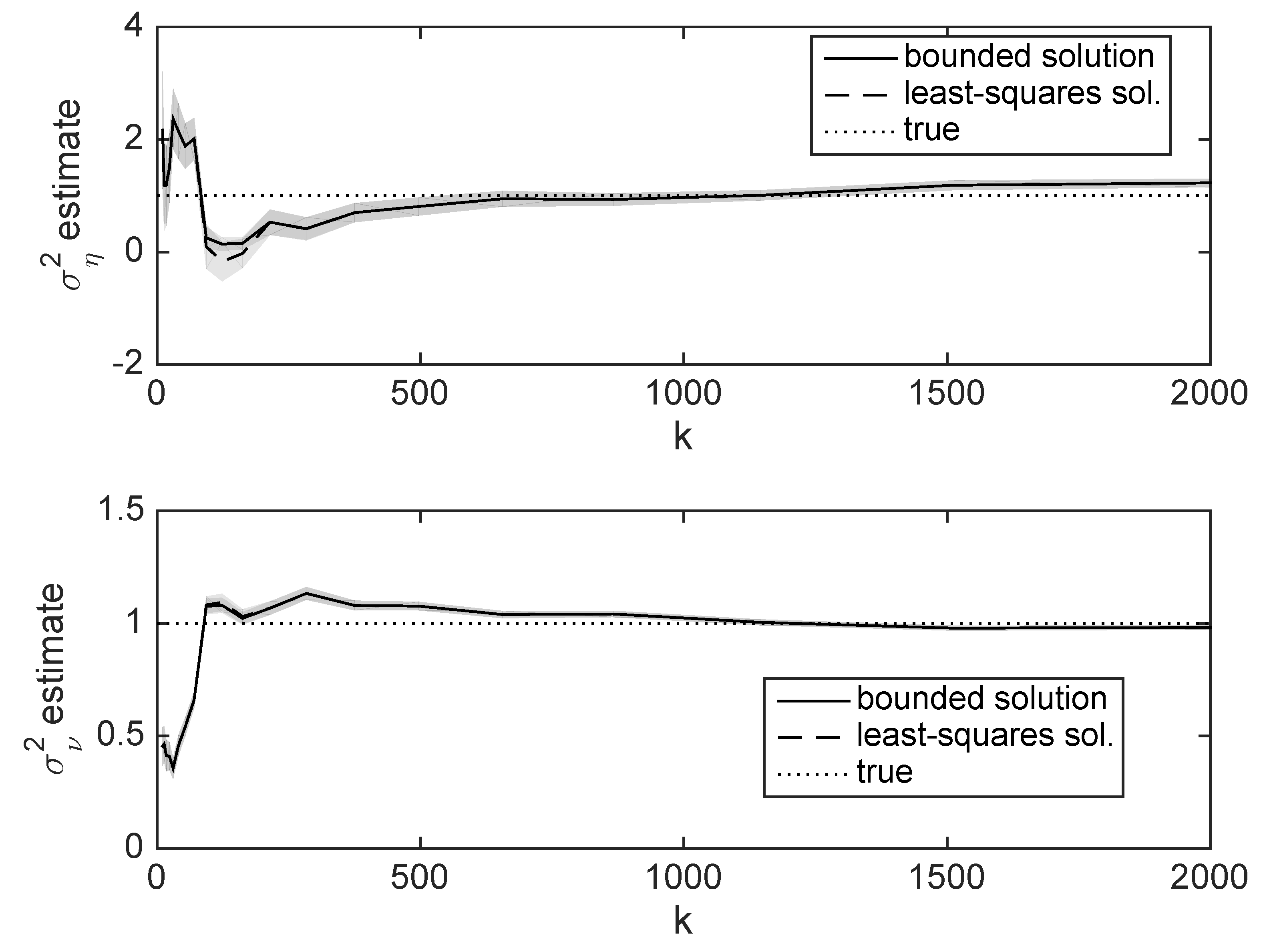
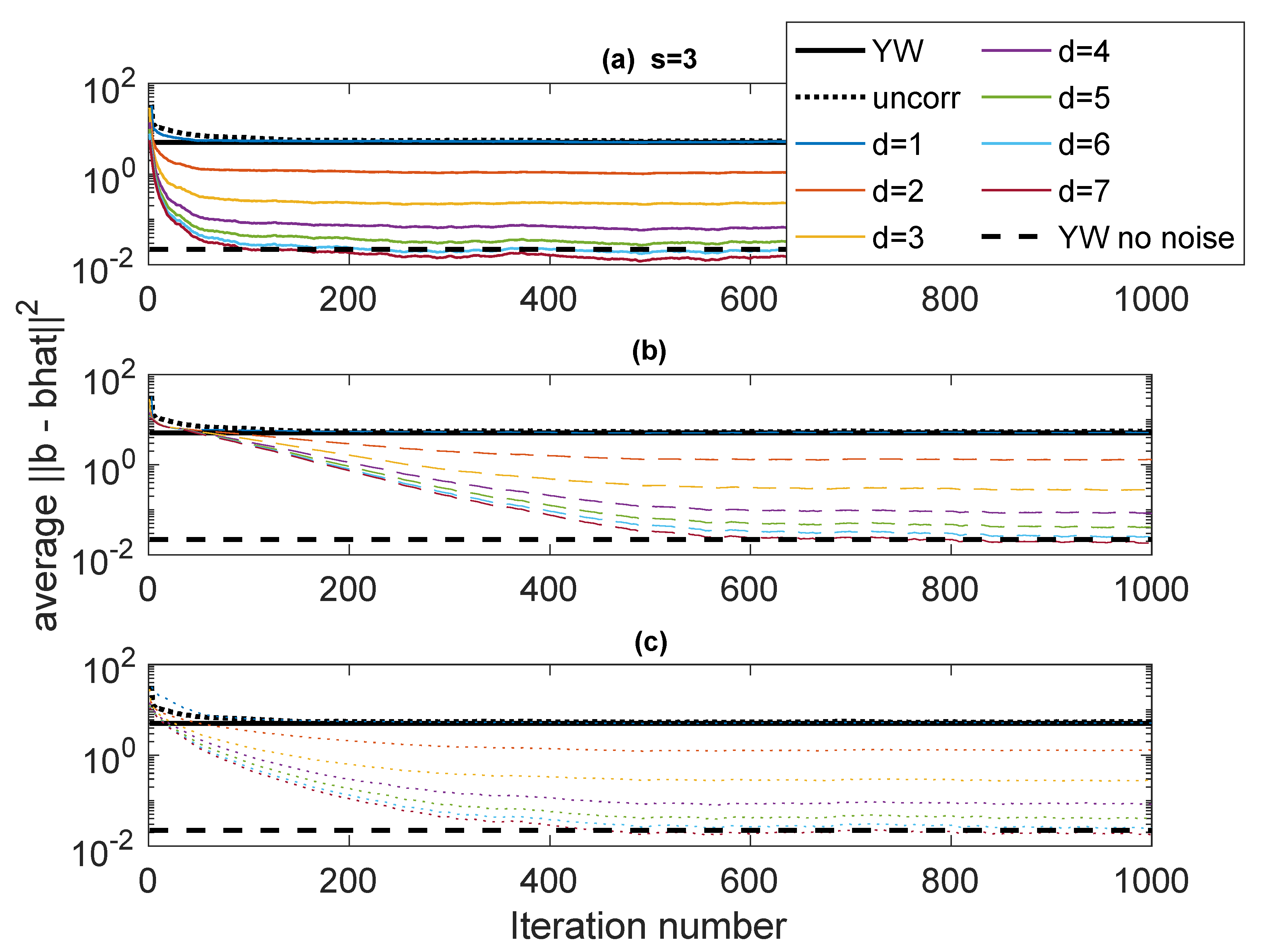
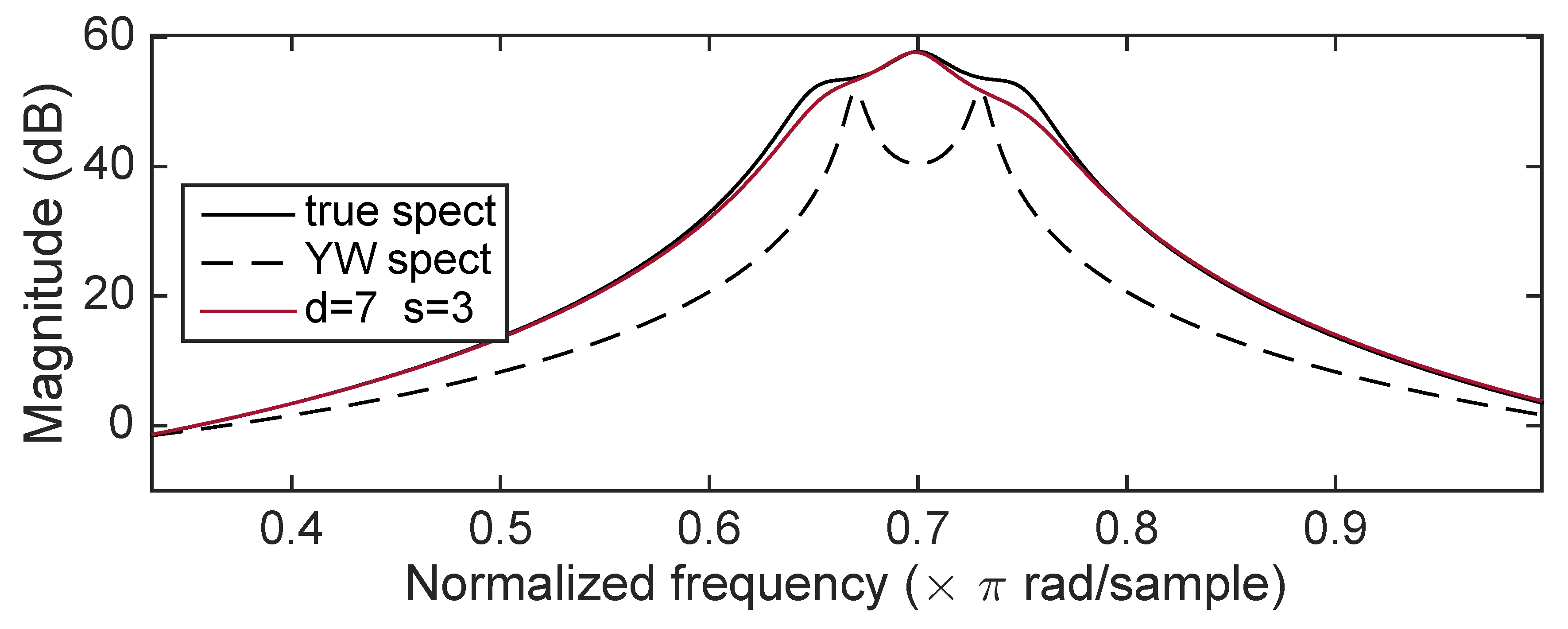
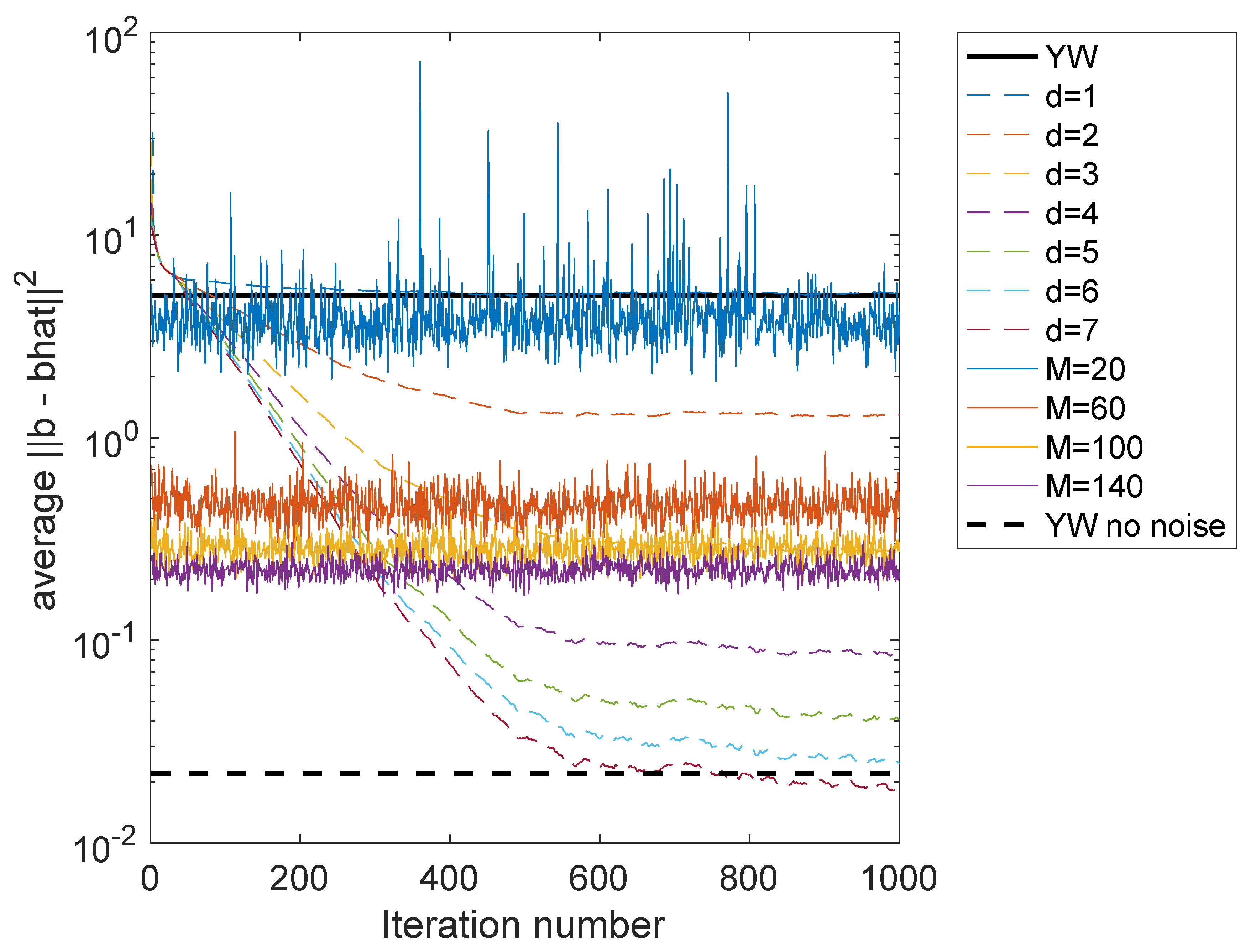
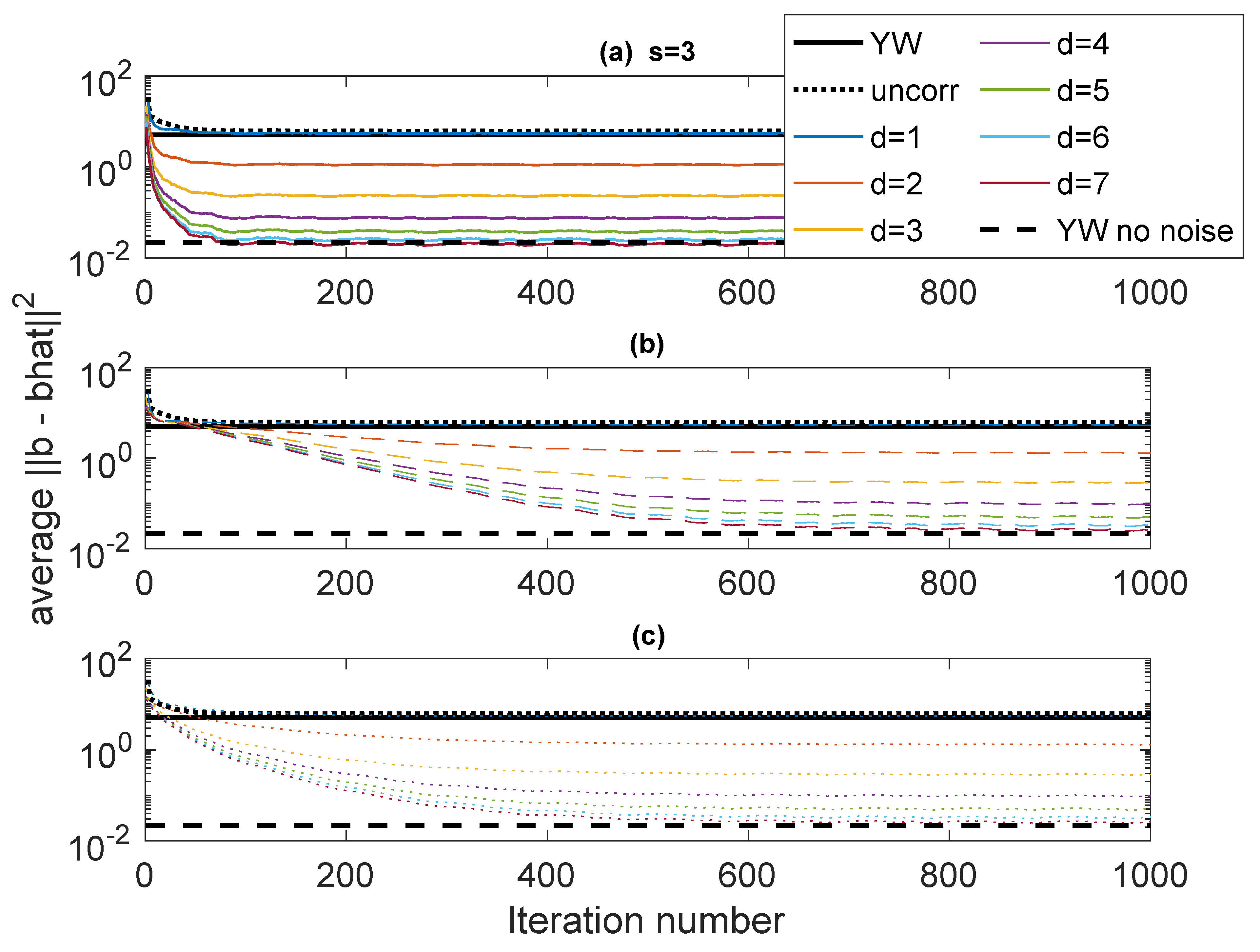
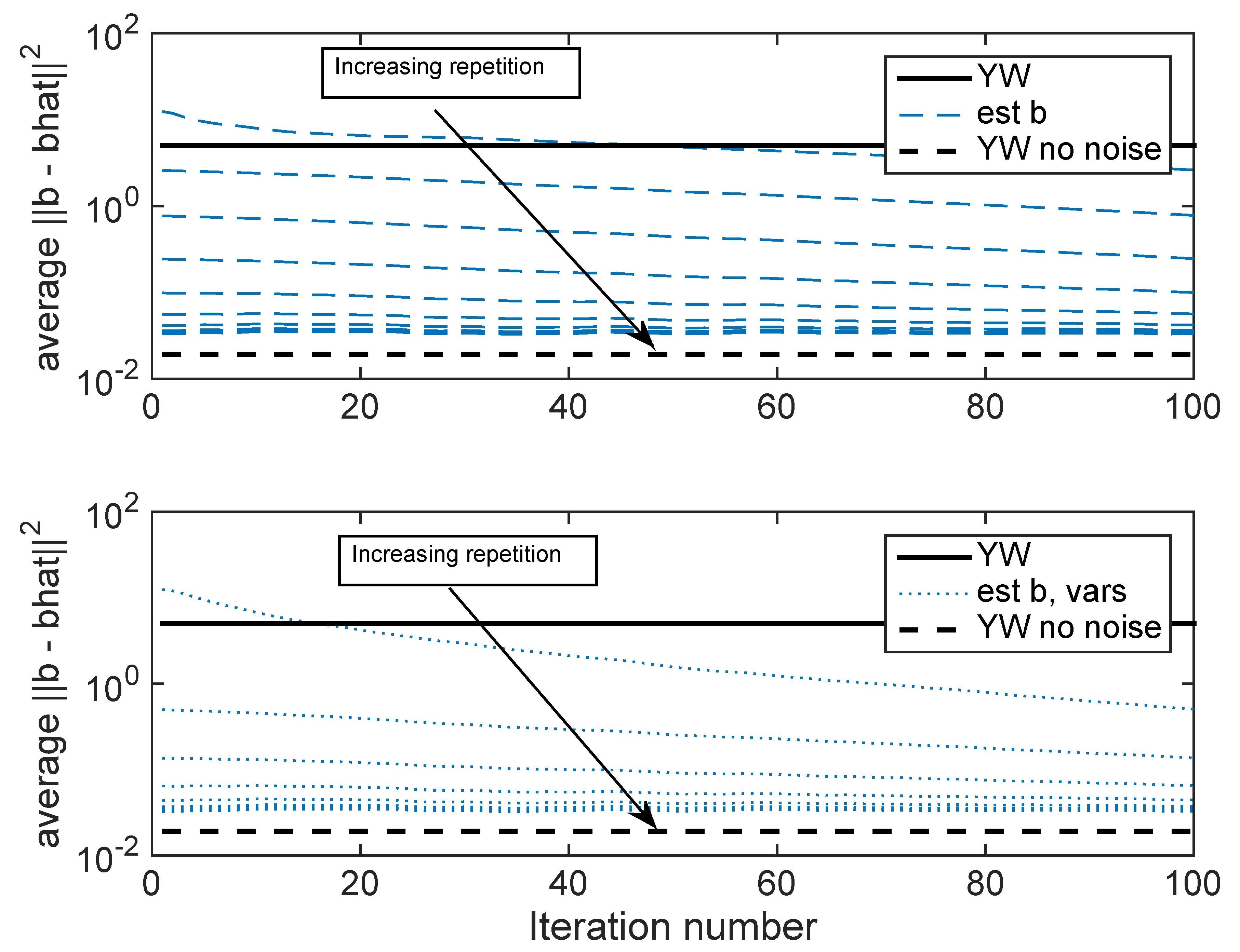
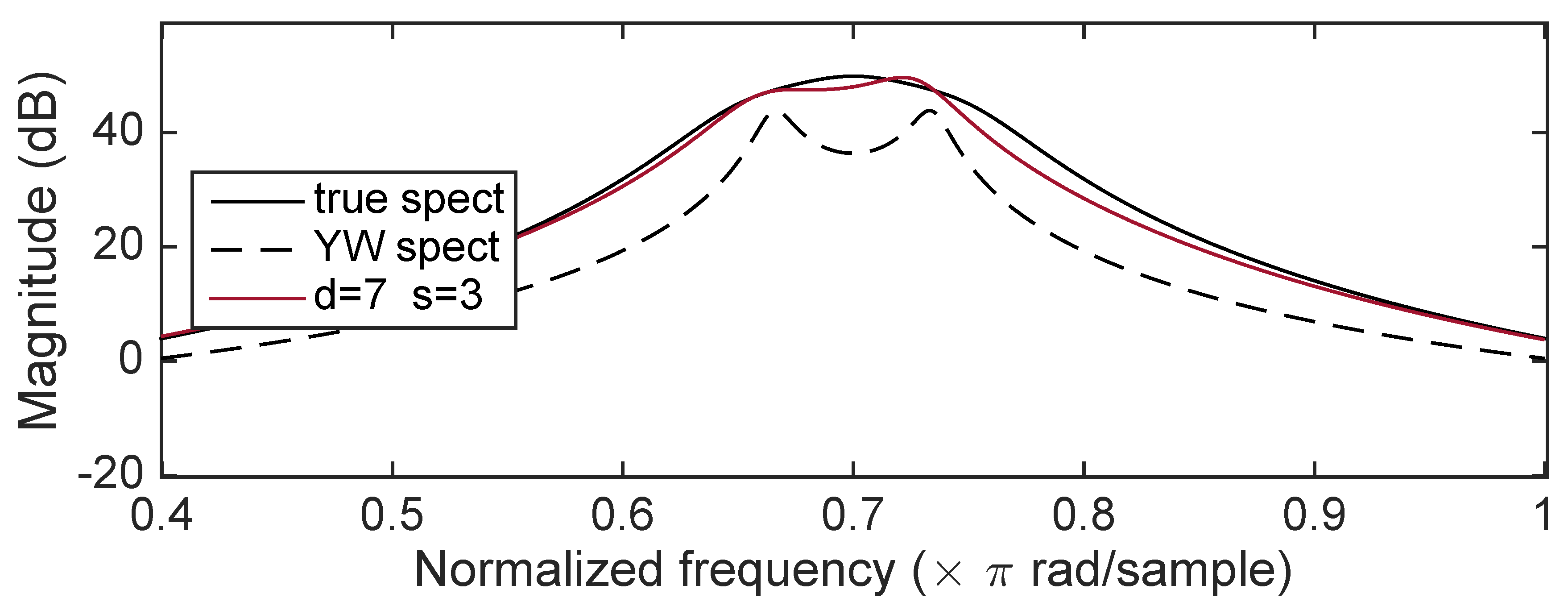
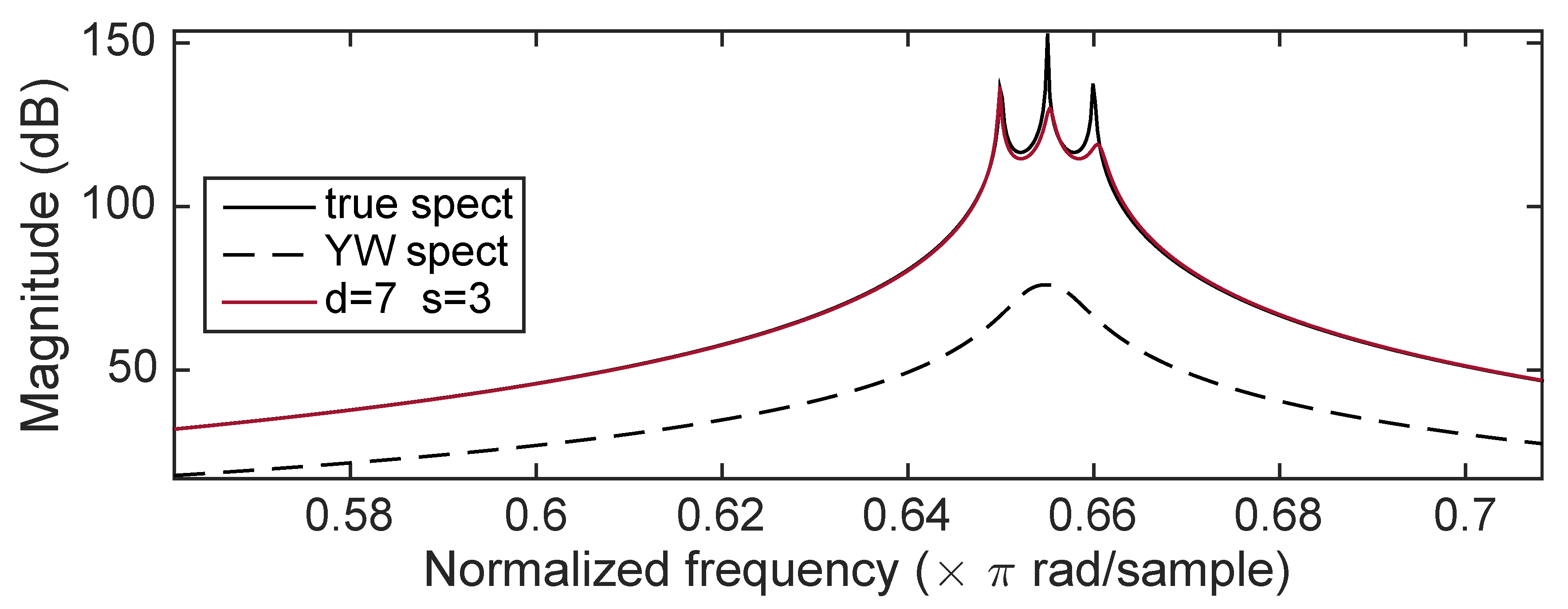
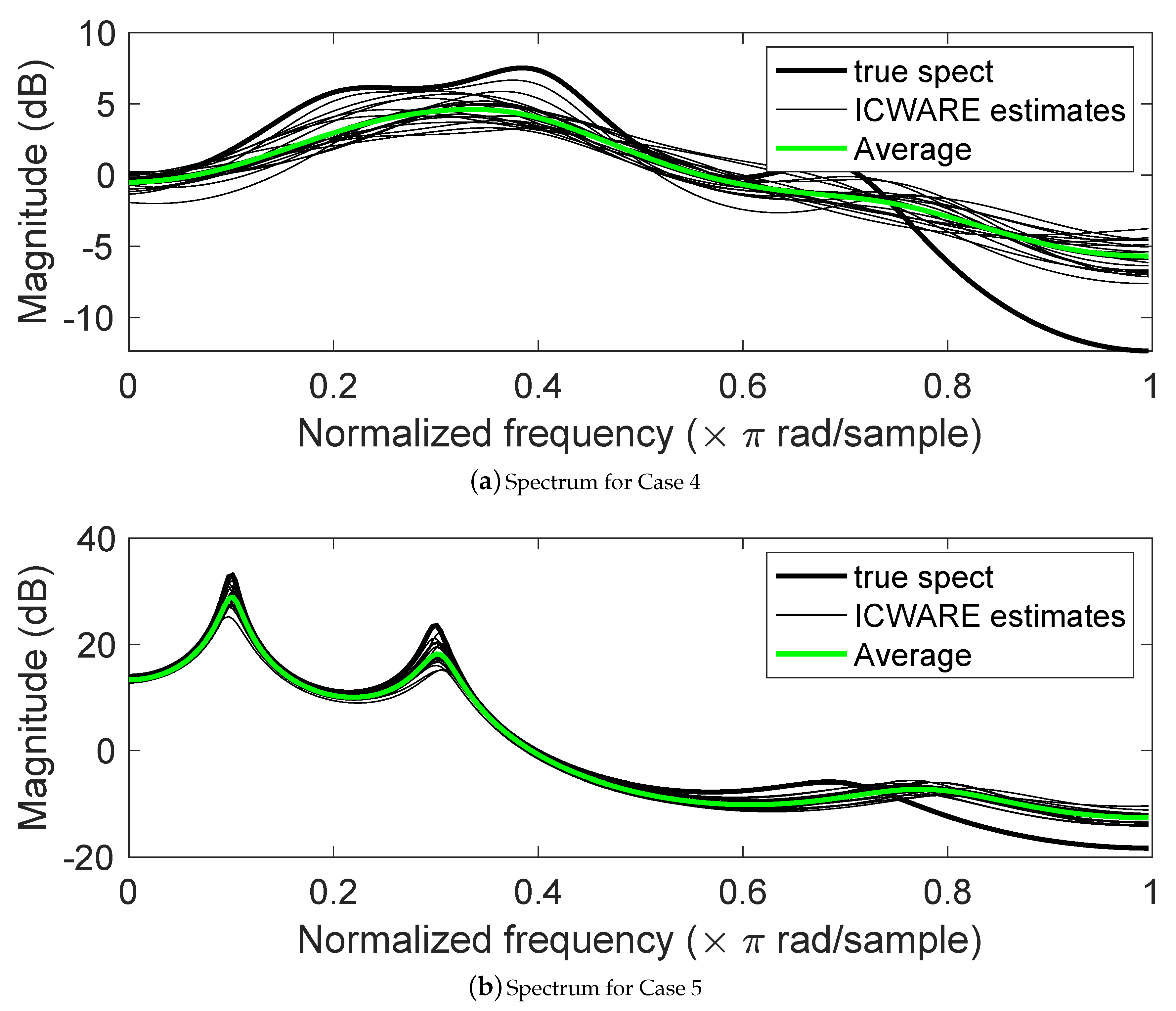
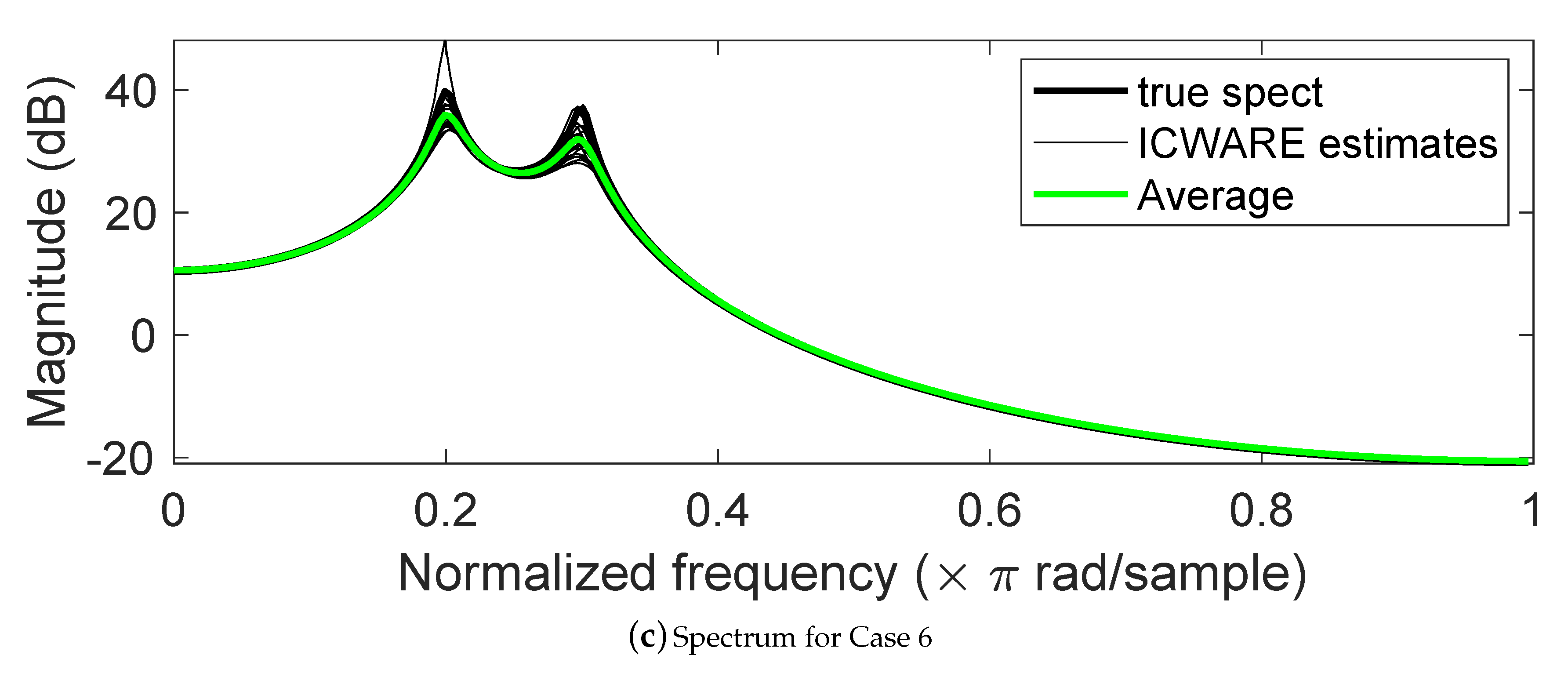
5. Some Results
6. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Maximizing The Log Likelihood Function for Estimating Variances
References
- Makhoul, J. Spectral analysis of speech by linear prediction. IEEE Trans. Audio Electroacoust. 1973, 21, 140–148. [Google Scholar] [CrossRef]
- Lim, J.; Oppenheim, A. All-pole modeling of degraded speech. IEEE Trans. Signal Process. 1978, 26, 197–210. [Google Scholar] [CrossRef]
- Lim, J.; Oppenheim, A. Enhancement and bandwidth compression of noisy speech. Proc. IEEE Inst. Electr. Electron. Eng. 1979, 67, 1586–1604. [Google Scholar] [CrossRef]
- Wrench, A.; Cowan, C. A new approach to noise-robust LPC. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP ’87, New York, NY, USA, 6–9 April 1987; Volume 12, pp. 305–307. [Google Scholar] [CrossRef]
- Kay, S. Modern Spectral Estimation: Theory and Application; Prentice-Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Deller, J.R.; Proakis, J.G.; Hansen, J.H.L. Discrete–Time Processing of Speech Signals; Macmillan: New York, NY, USA, 1993. [Google Scholar]
- Ramamurthy, K.N.; Spanias, A.S. Matlab Software for The Code Excited Linear Prediction Algorithm: The Federal Standard 1016; Morgan & Claypool: San Rafael, CA, USA, 2009. [Google Scholar]
- de Prony, B.R. Essai Expérimental et Analytique: Sur les Lois de la Dilatabilité de Fluides Élastiques et sur Celles de la Force Exapnsive de la Vapeur de l’eau et de la Vapeur de l’alcool, à Différentes Températures. J. l’École Polytech. 1795, 1, 24–76. [Google Scholar]
- Ulrich, T.; Clayton, R. Time series modeling and maximum entropy. Phys. Earth Planetary Interiors 1976, 12, 188–200. [Google Scholar]
- Capon, J. High-Resolution Frequency-Wavenumber Spectrum Analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar] [CrossRef]
- Burg, J. Maximum entropy spectral analysis. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1975. [Google Scholar]
- Marple, L. High Resolution Autoregressive Spectrum Analysis Using Noise Power Cancellation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP ’78, Tulsa, OK, USA, 10–12 April 1978; Volume 3, pp. 345–348. [Google Scholar] [CrossRef]
- Marple, L. A New Autoregressive Spectrum Analysis Algorithm. IEEE Trans. ASSP 1980, 28, 441–454. [Google Scholar] [CrossRef]
- Nuttall, A. Spectral Analysis of a Univariate Process with Bad Data Points, Via Maximum Entropy and Linear Predictive Techniques; Technical Report NUSC Tech. Rep. 5303; Naval Underwater Systems Center: New London, CT, USA, 1976. [Google Scholar]
- Helmut Lütkepohl. New Introduction fo Multiple Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Guler, I.; Kiymik, M.; Akin, M.; Alkan, A. AR spectral analysis of EEG signals by using maximum likelihood estimation. Comput. Biol. Med. 2001, 31, 441–450. [Google Scholar] [CrossRef]
- Baddour, K.; Beaulieu, N. Autoregressive modeling for fading channel simulation. IEEE Trans. Wireless Comm. 2005, 4, 1650–1662. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1978. [Google Scholar]
- Makhoul, J. Linear Prediction: A Tutorial Review. Proc. IEEE 1975, 63, 561–580. [Google Scholar] [CrossRef]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Anderson, B.D.O.; Moore, J.B. Optimal Filtering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Kay, S. The Effects of Noise on the Autoregressive Spectral Estimator. IEEE Trans. Acoust. Speech Signal Process. 1979, 27, 478–485. [Google Scholar] [CrossRef]
- Lacoss, R.T. Data adaptive spectral analysis methods. Geophysics 1971, 36, 661–675. [Google Scholar] [CrossRef]
- Tufts, D.; Kumaresan, R. Improved spectral resolution. Proc. IEEE 1980, 68, 419–420. [Google Scholar] [CrossRef]
- Tufts, D.; Kumaresan, R. Improved spectral resolution II. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP ’80, Denver, CO, USA, 9–11 April 1980; Volume 5, pp. 592–597. [Google Scholar]
- Kumaresan, R.; Tufts, D. Improved spectral resolution III: Efficient realization. Proc. IEEE 1980, 68, 1354–1355. [Google Scholar] [CrossRef]
- Kumaresan, R.; Tufts, D. Accurate parameter estimation of noisy speech-like signals. In Proceedings of the Acoustics, Speech, and Signal Processing, IEEE International Conference on ICASSP ’82, Paris, France, 3–5 May 1982; Volume 7, pp. 1357–1361. [Google Scholar]
- Kumaresan, R.; Tufts, D. Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise. IEEE Trans. Acoust. Speech Signal Process. 1982, 30, 833–840. [Google Scholar] [CrossRef]
- Tufts, D.; Kumaresan, R. Estimation of frequencies of multiple sinusoids: Making linear prediction perform like maximum likelihood. Proc. IEEE 1982, 70, 975–989. [Google Scholar] [CrossRef]
- Kumaresan, R.; Tufts, D.; Scharf, L. A Prony method for noisy data: Choosing the signal components and selecting the order in exponential signal models. Proc. IEEE 1984, 72, 230–233. [Google Scholar] [CrossRef]
- Cadzow, J. High Performance Spectral Estimation: A New ARMA Method. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 524–529. [Google Scholar] [CrossRef]
- Zheng, W.X. On TLS estimation of autoregressive signals with noisy measurements. In Proceedings of the SSeventh International Symposium on Signal Processing and Its Applications, Paris, France, 4 July 2003; Volume 2, pp. 287–290. [Google Scholar] [CrossRef]
- Huffel, S.V.; Vandewalle, J. The Use of Total Linear Least Squares Technique for Identification and Parameter Estimation. In Proceedings of the IFAC/IFORS Symposium on Identification and Parameter Estimation, York, UK, 3–7 July 1985; pp. 1167–1172. [Google Scholar]
- van Huffel, S.J.; Vandewalle, S.J.; Haegemans, A. An Efficient and Reliable Algorithm for Computing the Singular Subspace of a Matrix, Associated with Its Smallest Singular Values. J. Comput. Appl. Math. 1987, 21, 313–320. [Google Scholar] [CrossRef]
- Huffel, S.V.; Vandewalle, J. The Partial Total Least Squares Algorithm. J. Comput. Appl. Math. 1988, 21, 333–341. [Google Scholar] [CrossRef]
- Zheng, W. Identification of Autoregressive Signals Observed in Noise. In Proceedings of the American Control Conference, San Francisco, CA, USA, 2–4 June 1993; pp. 1229–1230. [Google Scholar]
- Zheng, W.X. An efficient algorithm for parameter estimation of noisy AR processes. In Proceedings of the 1997 IEEE International Symposium on Circuits and Systems, ISCAS ’97, Hong Kong, China, 12 June 1997; Volume 4, pp. 2509–2512. [Google Scholar]
- Zheng, W. Estimation of autoregressive signals from noisy measurements. IEEE Proc. Vis. Image Signal Process. 1997, 144, 39–45. [Google Scholar] [CrossRef]
- Zheng, W.X. Unbiased identification of autoregressive signals observed in colored noise. In Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing, Seattle, WA, USA, 15 May 1998; Volume 4, pp. 2329–2332. [Google Scholar]
- Zheng, W.X. Adaptive parameter estimation of autoregressive signals from noisy observations. In Proceedings of the ICSP ’98. 1998 Fourth International Conference on Signal Processing Proceedings, Beijing, China, 12–16 October 1998; Volume 1, pp. 449–452. [Google Scholar]
- Zheng, W.X. On implementation of a least-squares based algorithm for noisy autoregressive signals. In Proceedings of the ISCAS ’98, 1998 IEEE International Symposium on Circuits and Systems, Monterey, CA, USA, 31 May–3 June 1998; Volume 5, pp. 21–24. [Google Scholar]
- Zheng, W.X. A least-squares based method for autoregressive signals in the presence of noise. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1999, 46, 81–85. [Google Scholar] [CrossRef]
- Zheng, W.X. Adaptive linear prediction of autoregressive models in the presence of noise. In Proceedings of the WCCC-ICSP 2000, 5th International Conference on Signal Processing Proceedings, Beijing, China, 21–25 August 2000; Volume 1, pp. 555–558. [Google Scholar]
- Zheng, W.X. Autoregressive parameter estimation from noisy data. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 2000, 47, 71–75. [Google Scholar] [CrossRef]
- Zheng, W.X. Estimation of the parameters of autoregressive signals from colored noise-corrupted measurements. IEEE Signal Process. Lett. 2000, 7, 201–204. [Google Scholar] [CrossRef]
- Zheng, W.X. A fast convergent algorithm for identification of noisy autoregressive signals. In Proceedings of the ISCAS 2000 Geneva. The 2000 IEEE International Symposium on Circuits and Systems, Geneva, Switzerland, 28–31 May 2000; Volume 4, pp. 497–500. [Google Scholar]
- Zheng, W.X. A new estimation algorithm for AR signals measured in noise. In Proceedings of the 2002 6th International Conference on Signal Processing, Beijing, China, 26–30 August 2002; Volume 1, pp. 186–189. [Google Scholar]
- Zheng, W.X. An alternative method for noisy autoregressive signal estimation. In Proceedings of the ISCAS 2002. IEEE International Symposium on Circuits and Systems, Phoenix-Scottsdale, AZ, USA, 26–29 May 2002; Volume 5, pp. V–349–V–352. [Google Scholar]
- Zheng, W.X. On unbiased parameter estimation of autoregressive signals observed in noise. In Proceedings of the 2003 International Symposium on Circuits and Systems, ISCAS ’03, Bangkok, Thailand, 25–28 May 2003; Volume 4, pp. IV–261–IV–264. [Google Scholar]
- Zheng, W.X. Fast adaptive identification of autoregressive signals subject to noise. In Proceedings of the 2004 International Symposium on Circuits and Systems, ISCAS ’04, Vancouver, BC, Canada, 23–26 May 2004; Volume 3, pp. III–313–16. [Google Scholar]
- Zheng, W.X. An efficient method for estimation of autoregressive signals in noise. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems, ISCAS 2005, Kobe, Japan, 23–26 May 2005; Volume 2, pp. 1433–1436. [Google Scholar]
- Zheng, W.X. A new look at parameter estimation of autoregressive signals from noisy observations. In Proceedings of the 2006 IEEE International Symposium on Circuits and Systems, ISCAS 2006, Island of Kos, Greece, 21–24 May 2006; p. 4. [Google Scholar]
- Zheng, W.X. On Estimation of Autoregressive Signals in the Presence of Noise. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 1471–1475. [Google Scholar] [CrossRef]
- Zheng, W.X. An Efficient Method for Estimation of Autoregressive Signals Subject to Colored Noise. In Proceedings of the 2007 IEEE International Symposium on Circuits and Systems, ISCAS 2007, New Orleans, LA, USA, 27–20 May 2007; pp. 2291–2294. [Google Scholar]
- Xia, Y.; Zheng, W.X. On unbiased identification of autoregressive signals with noisy measurements. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 2157–2160. [Google Scholar]
- Arablouei, R.; Dogancay, K.; Adali, T. Unbiased RLS identification of errors-in-variables models in the presence of correlated noise. In Proceedings of the 2014 22nd European Signal Processing Conference (EUSIPCO), Lisbon, Portugal, 1–5 September 2014; pp. 261–265. [Google Scholar]
- Ai-guo, W.; Fan, Y.; Yang-Yang, Q. Bias compensation based recursive least squares identification for equation error models with colored noises. In Proceedings of the 2014 33rd Chinese Control Conference (CCC), Nanjing, China, 28–30 July 2014; pp. 6715–6720. [Google Scholar]
- Arablouei, R.; Dogancay, K.; Adali, T. Unbiased Recursive Least-Squares Estimation Utilizing Dichotomous Coordinate-Descent Iterations. IEEE Trans. Signal Process. 2014, 62, 2973–2983. [Google Scholar]
- Yong, Z.; Hai, T.; Zhaojing, Z. A modified bias compensation method for output error systems with colored noises. In Proceedings of the 2011 30th Chinese Control Conference (CCC), Yantai, China, 1–30 April 2011; pp. 1565–1569. [Google Scholar]
- Wu, A.G.; Qian, Y.Y.; Wu, W.J. Bias compensation-based recursive least-squares estimation with forgetting factors for output error moving average systems. IET Signal Process. 2014, 8, 483–494. [Google Scholar] [CrossRef]
- Arablouei, R.; Dogancay, K.; Werner, S. Recursive Total Least-Squares Algorithm Based on Inverse Power Method and Dichotomous Coordinate-Descent Iterations. IEEE Trans. Signal Process. 2015, 63, 1941–1949. [Google Scholar] [CrossRef]
- Tomcik, J.; Melsa, J. Least squares estimation of predictor coefficients from noisy observations. In Proceedings of the 1977 IEEE Conference on Decision and Control including the 16th Symposium on Adaptive Processes and A Special Symposium on Fuzzy Set Theory and Applications, New Orleans, LA, USA, 7–9 December 1977; pp. 3–6. [Google Scholar]
- Lee, T.S. Identification and spectral estimation of noisy multivariate autoregressive processes. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP ’81, Atlanta, GA, USA, 30 March–1 April 1981; Volume 6, pp. 503–507. [Google Scholar]
- Cadzow, J.A. Autoregressive Moving Average Spectral Estimation: A Model Equation Error Procedure. IEEE Trans. Geosci. Remote Sens. 1981, GE-19, 24–28. [Google Scholar] [CrossRef]
- Gingras, D. Estimation of the autoregressive parameters from observations of a noise corrupted autoregressive time series. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP ’82, Paris, France, 3–5 May 1982; Volume 7, pp. 228–231. [Google Scholar]
- Ahmed, M. Estimating the parameters of a noisy AR-process by using a bootstrap estimator. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP ’82, Paris, France, 3–5 May 1982; Volume 7, pp. 152–155. [Google Scholar]
- Tugnait, J. Recursive parameter estimation for noisy autoregressive signals. IEEE Trans. Inform. Theory 1986, 32, 426–430. [Google Scholar] [CrossRef]
- Paliwal, K. A noise-compensated long correlation matching method for AR spectral estimation of noisy signals. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP ’86, Tokyo, Japan, 7–11 April 1986; Volume 11, pp. 1369–1372. [Google Scholar]
- Cernuschi-Frias, B.; Rogers, J. On the exact maximum likelihood estimation of Gaussian autoregressive processes. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 922–924. [Google Scholar] [CrossRef]
- Gingras, D.; Masry, E. Autoregressive spectral estimation in additive noise. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 490–501. [Google Scholar] [CrossRef]
- Masry, E. Almost sure convergence analysis of autoregressive spectral estimation in additive noise. IEEE Trans. Inform. Theory 1991, 37, 36–42. [Google Scholar] [CrossRef]
- Deriche, M. AR parameter estimation from noisy data using the EM algorithm. In Proceedings of the 1994 IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP-94, South Australia, Australia, 19–22 April 1994; Volume iv, pp. IV/69–IV/72. [Google Scholar]
- Lee, L.M.; Wang, H.C. An extended Levinson-Durbin algorithm for the analysis of noisy autoregressive process. IEEE Signal Process. Lett. 1996, 3, 13–15. [Google Scholar]
- Hasan, T.; Yahagi, T. Accurate noise compensation technique for the identification of multichannel AR processes with noise. In Proceedings of the 1996 IEEE International Symposium on Circuits and Systems Connecting the World, ISCAS ’96, Atlanta, GA, USA, 15 May 1996; Volume 2, pp. 401–404. [Google Scholar] [CrossRef]
- Doblinger, G. An adaptive Kalman filter for the enhancement of noisy AR signals. In Proceedings of the 1998 IEEE International Symposium on Circuits and Systems, ISCAS ’98, Monterey, CA, USA, 31 May–3 June 1998; Volume 5, pp. 305–308. [Google Scholar]
- Hasan, T.; Hossain, J. Multichannel autoregressive spectral estimation from noisy observations. In Proceedings of the TENCON 2000, Kuala Lumpur, Malaysia, 24–27 September 2000; Volume 1, pp. 327–332. [Google Scholar]
- Hasan, T.; Ahmed, K. A joint technique for autoregressive spectral estimation from noisy observations. In Proceedings of the TENCON 2000, Kuala Lumpur, Malaysia, 24–27 September 2000; Volume 2, pp. 120–125. [Google Scholar]
- Davila, C. On the noise-compensated Yule-Walker equations. IEEE Trans. Signal Process. 2001, 49, 1119–1121. [Google Scholar] [CrossRef][Green Version]
- So, H. LMS algorithm for unbiased parameter estimation of noisy autoregressive signals. Electron. Lett. 2001, 37, 536–537. [Google Scholar] [CrossRef]
- Jin, C.Z.; Jia, L.J.; Yang, Z.J.; Wada, K. On convergence of a BCLS algorithm for noisy autoregressive process estimation. In Proceedings of the 41st IEEE Conference on Decision and Control, Las Vegas, NV, USA, 10–13 December 2002; Volume 4, pp. 4252–4257. [Google Scholar]
- Hasan, M.; Rahim Chowdhury, A.; Adnan, R.; Rahman Bhuiyan, M.; Khan, M. A new method for parameter estimation of autoregressive signals in colored noise. In Proceedings of the 2002 11th European Signal Processing Conference, Toulouse, France, 3–6 September 2002; pp. 1–4. [Google Scholar]
- Hasan, T.; Fattah, S.; Khan, M. Identification of noisy AR systems using damped sinusoidal model of autocorrelation function. IEEE Signal Process. Lett. 2003, 10, 157–160. [Google Scholar] [CrossRef]
- Hasan, M.; Chowdhury, A.; Khan, M. Identification of autoregressive signals in colored noise using damped sinusoidal model. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2003, 50, 966–969. [Google Scholar] [CrossRef]
- Diversi, R.; Guidorzi, R.; Soverini, U. Identification of ARX models with noisy input and output. In Proceedings of the 2007 European Control Conference (ECC), Kos, Greece, 2–5 July 2007; pp. 4073–4078. [Google Scholar]
- Fattah, S.; Zhu, W.; Ahmad, M. Identification of autoregressive moving average systems from noise-corrupted observations. In Proceedings of the 2008 Joint 6th International IEEE Northeast Workshop on Circuits and Systems and TAISA Conference, NEWCAS-TAISA 2008, Montreal, QC, Canada, 22–25 June 2008; pp. 69–72. [Google Scholar]
- Fattah, S.; Zhu, W.; Ahmad, M. A correlation domain algorithm for autoregressive system identification from noisy observations. In Proceedings of the 51st Midwest Symposium on Circuits and Systems, MWSCAS 2008, Knoxville, TN, USA, 10–13 August 2008; pp. 934–937. [Google Scholar]
- Babu, P.; Stoica, P.; Marzetta, T. An IQML type algorithm for AR parameter estimation from noisy covariance sequences. In Proceedings of the 2009 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 1022–1026. [Google Scholar]
- Qu, X.; Zhou, J.; Luo, Y. An Advanced Parameter Estimator of Multichannel Autoregressive Signals from Noisy Observations. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, ICIECS 2009, Wuhan, China, 19–20 December 2009; pp. 1–4. [Google Scholar]
- Weruaga, L.; Al-Ahmad, H. Frequency-selective autoregressive estimation in noise. In Proceedings of the 2010 IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP), Dallas, TX, USA, 15–19 March 2010; pp. 3854–3857. [Google Scholar]
- Mahmoudi, A.; Karimi, M. Parameter estimation of noisy autoregressive signals. In Proceedings of the 2010 18th Iranian Conference on Electrical Engineering (ICEE), Isfahan, Iran, 11–13 May 2010; pp. 145–149. [Google Scholar]
- Weruaga, L. Two methods for autoregressive estimation in noise. In Proceedings of the 2011 IEEE GCC Conference and Exhibition (GCC), Dubai, United Arab Emirates, 19–22 February 2011; pp. 501–504. [Google Scholar] [CrossRef]
- Youcef, A.; Diversi, R.; Grivel, E. Errors-in-variables identification of noisy moving average models. In Proceedings of the 2015 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 968–972. [Google Scholar]
- Hamilton, J.D. Time Series Analysis; Princeton University Press: Princeton, NJ, USA, 1994. [Google Scholar]
- Kay, S. Recursive Maximum Likelihood Estimation of Autoregressive Processes. IEEE Trans. Acoust. Speech Signal Process. 1983, 31, 292–303. [Google Scholar] [CrossRef]
- Evans, A.; Fischl, R. Optimal least squares time-domain synthesis of recursive digital filters. IEEE Trans. Audio Electroacoust. 1973. [Google Scholar] [CrossRef]
- Bresler, Y.; Macovski, A. Exact maximum likelihood parameter estimation of superimposed exponentials in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1081–1089. [Google Scholar] [CrossRef]
- Steiglitz, K.; McBride, L. A technique for the identification of linear systems. IEEE Trans. Autom. Control 1965, 10, 461–464. [Google Scholar] [CrossRef]
- Kumaresan, R.; Scharf, L.; Shaw, A. An Algorithm for pole-zero modeling and spectral analysis. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 637–640. [Google Scholar] [CrossRef]
- Anderson, J.; Giannakis, G. Noisy input/output system identification using cumulants and the Steiglitz-McBride algorithm. In Proceedings of the 1991 Conference Record of the Twenty-Fifth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 4–6 November 1991; Volume 1, pp. 608–612. [Google Scholar]
- Fuller, W.A. Measurement Error Models; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Petitjean, J.; Grivel, E.; Bobillet, W.; Roussilhe, P. Multichannel AR parameter estimation from noisy observations as an errors-in-variables issue. In Proceedings of the 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2008; pp. 1–5. [Google Scholar]
- Petitjean, J.; Diversi, R.; Grivel, E.; Guidorzi, R.; Roussilhe, P. Recursive errors-in-variables approach for AR parameter estimation from noisy observations. Application to radar sea clutter rejection. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP 2009, Taipei, Taiwan, 19–24 April 2009; pp. 3401–3404. [Google Scholar]
- Petitjean, J.; Grivel, E.; Diversi, R.; Guidorzi, R. A recursive errors-in-variables method for tracking time varying autoregressive parameters from noisy observations. In Proceedings of the 2010 18th European Signal Processing Conference, Aalborg, Denmark, 23–27 August 2010; pp. 840–844. [Google Scholar]
- Labarre, D.; Grivel, E.; Berthoumieu, Y.; Todini, E.; Najim, M. Consistent estimation of autoregressive parameters from noisy observations based on two interacting Kalman filters. Signal Process. 2006, 86, 2863–2876. [Google Scholar] [CrossRef]
- Jamoos, A.; Grivel, E.; Christov, N.; Najim, M. Estimation of autoregressive fading channels based on two cross-coupled H∞ filters. Signal Image Video Process. J. Springer 2009, 3, 209–216. [Google Scholar] [CrossRef]
- Jamoos, A.; Grivel, E.; Shakarneh, N.; Abdel-Nour, H. Dual Optimal filters for parameter estimation of a multivariate autoregressive process from noisy observations. IET Signal Processing 2011, 5, 471–479. [Google Scholar] [CrossRef]
- Bugallo, M.F.; Martino, L.; Corander, J. Adaptive importance sampling in signal procesing. Digit. Signal Process. 2015, 47, 36–49. [Google Scholar] [CrossRef]
- Urteaga, I.; Djuric, P.M. Sequential estimation of Hidden ARMA Processes by Particle Filtering—Part I. IEEE Trans. Signal Process. 2017, 65, 482–493. [Google Scholar] [CrossRef]
- Urteaga, I.; Djuric, P.M. Sequential estimation of Hidden ARMA Processes by Particle Filtering—Part II. IEEE Trans. Signal Process. 2017, 65, 494–504. [Google Scholar] [CrossRef]
- Martino, L.; Elvira, V.; Camps-Valls, G. Distributed Particle Metropolis-Hastings Schemes. In IEEE Statistical Signal Processing Workshop; IEEE: Piscataway, NJ, USA, 2018; pp. 553–557. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Farahmand, S.; Giannakis, G.B. Robust RLS in the Presence of Correlated Noise Using Outlier Sparsity. IEEE Trans. Signal Process. 2012, 60, 3308–3313. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 1.21. 2011. Available online: http://cvxr.com/cvx (accessed on 19 May 2020).
- Moon, T.K.; Stirling, W.C. Mathematical Methods and Algorithms for Signal Processing; Prentice-Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
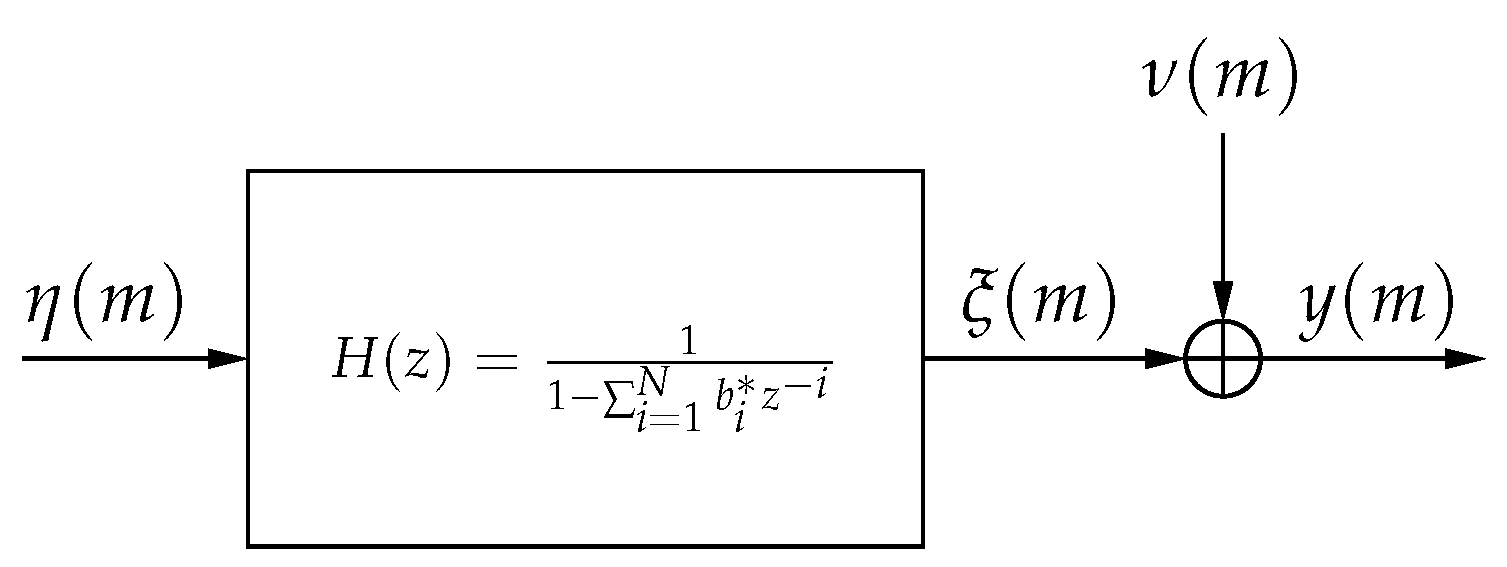

| Case | Order | Pole Locations |
|---|---|---|
| 1 | 3 | , , |
| 2 | 3 | , , |
| 3 | 3 | , , |
| 4 | 6 | , , |
| 5 | 6 | , , |
| 6 | 6 | , , |
| d | |||
|---|---|---|---|
| 2 | −5.9 | −5.8 | 11.1 |
| 3 | −12.4 | −12.5 | 4.5 |
| 4 | −17.5 | −17.5 | −0.6 |
| 5 | −20.6 | −20.6 | −3.9 |
| 6 | −22.6 | −22.7 | −5.9 |
| 7 | −23.9 | −24.0 | −7.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moon, T.K.; Gunther, J.H. Estimation of Autoregressive Parameters from Noisy Observations Using Iterated Covariance Updates. Entropy 2020, 22, 572. https://doi.org/10.3390/e22050572
Moon TK, Gunther JH. Estimation of Autoregressive Parameters from Noisy Observations Using Iterated Covariance Updates. Entropy. 2020; 22(5):572. https://doi.org/10.3390/e22050572
Chicago/Turabian StyleMoon, Todd K., and Jacob H. Gunther. 2020. "Estimation of Autoregressive Parameters from Noisy Observations Using Iterated Covariance Updates" Entropy 22, no. 5: 572. https://doi.org/10.3390/e22050572
APA StyleMoon, T. K., & Gunther, J. H. (2020). Estimation of Autoregressive Parameters from Noisy Observations Using Iterated Covariance Updates. Entropy, 22(5), 572. https://doi.org/10.3390/e22050572






