Figure 1.
(a) The forward model (FM) and (b) the predictive coding and active inference framework where and represent the current latent state and prediction of the next sensory state in terms of the exteroception and proprioception. The predicted proprioception can then be converted into a motor control signal as necessary, such as by using an inverse model as depicted in (b).
Figure 1.
(a) The forward model (FM) and (b) the predictive coding and active inference framework where and represent the current latent state and prediction of the next sensory state in terms of the exteroception and proprioception. The predicted proprioception can then be converted into a motor control signal as necessary, such as by using an inverse model as depicted in (b).
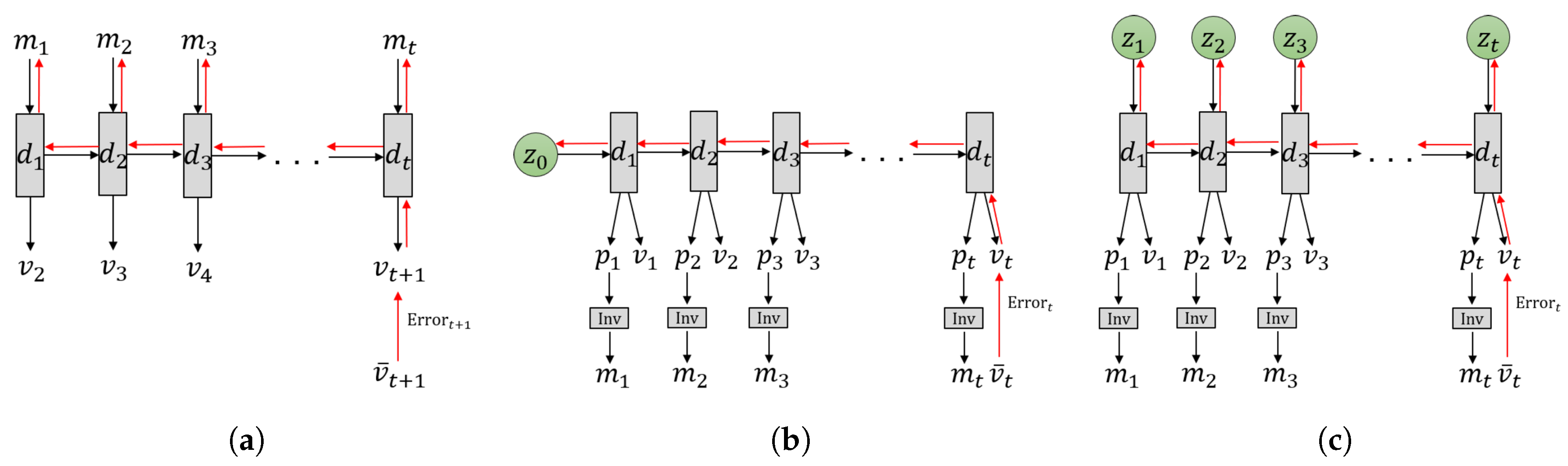
Figure 2.
Three different models for learning-based goal-directed motor planning. (a) The forward model implemented in an RNN, (b) predictive coding (PC) and active inference (AIF) frameworks implemented in a recurrent neural network (RNN) using initial sensitivity by latent random variables at the initial step, either by the stochastic or the deterministic , and (c) the proposed GLean scheme based on the PC and AIF framework implemented in a variational RNN. In each case, the horizontal axis indicates progression through time (left to right). The black arrows represent computation in the forward pass, while the red arrows represent prediction error being propagated during backpropagation through time (BPTT).
Figure 2.
Three different models for learning-based goal-directed motor planning. (a) The forward model implemented in an RNN, (b) predictive coding (PC) and active inference (AIF) frameworks implemented in a recurrent neural network (RNN) using initial sensitivity by latent random variables at the initial step, either by the stochastic or the deterministic , and (c) the proposed GLean scheme based on the PC and AIF framework implemented in a variational RNN. In each case, the horizontal axis indicates progression through time (left to right). The black arrows represent computation in the forward pass, while the red arrows represent prediction error being propagated during backpropagation through time (BPTT).
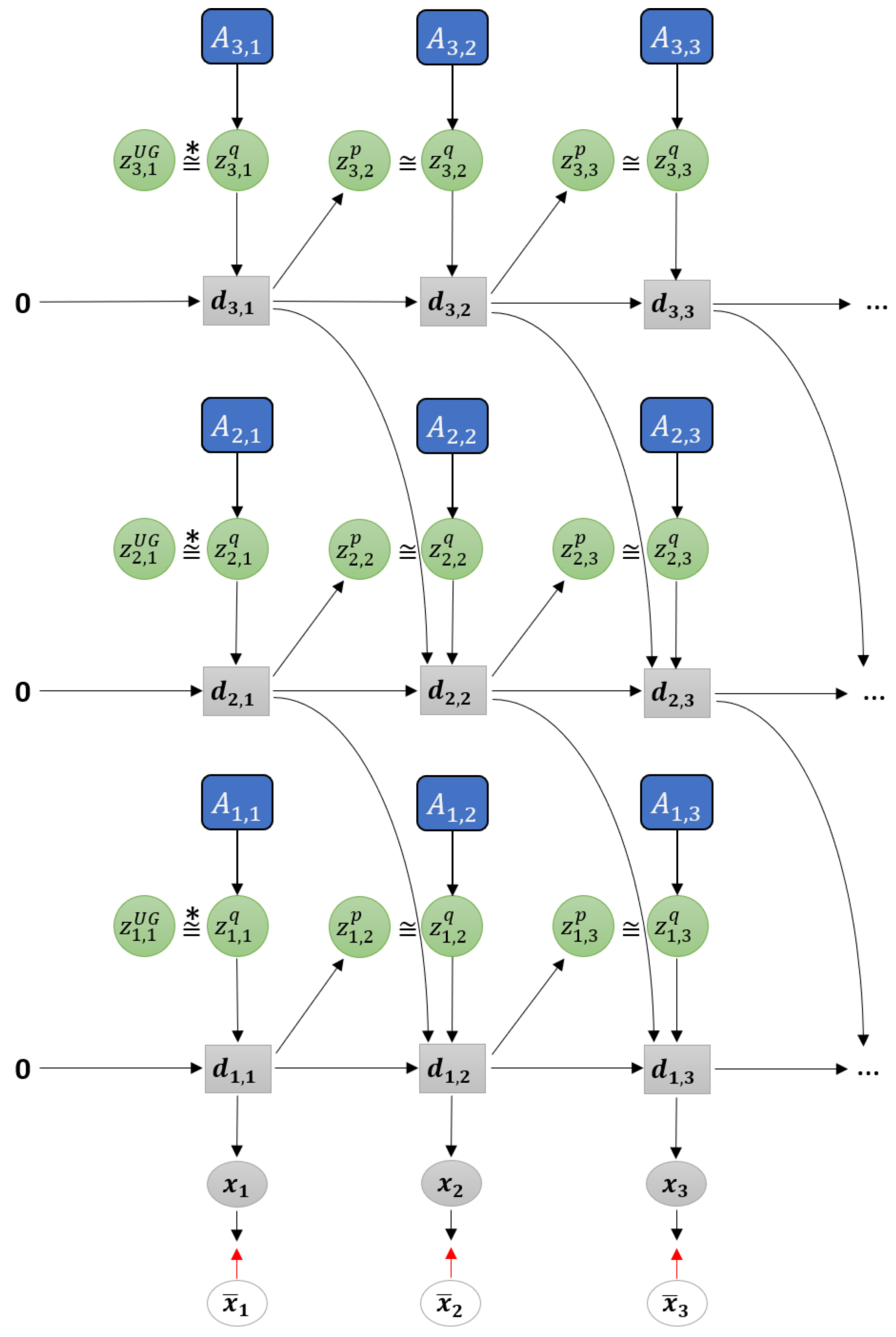
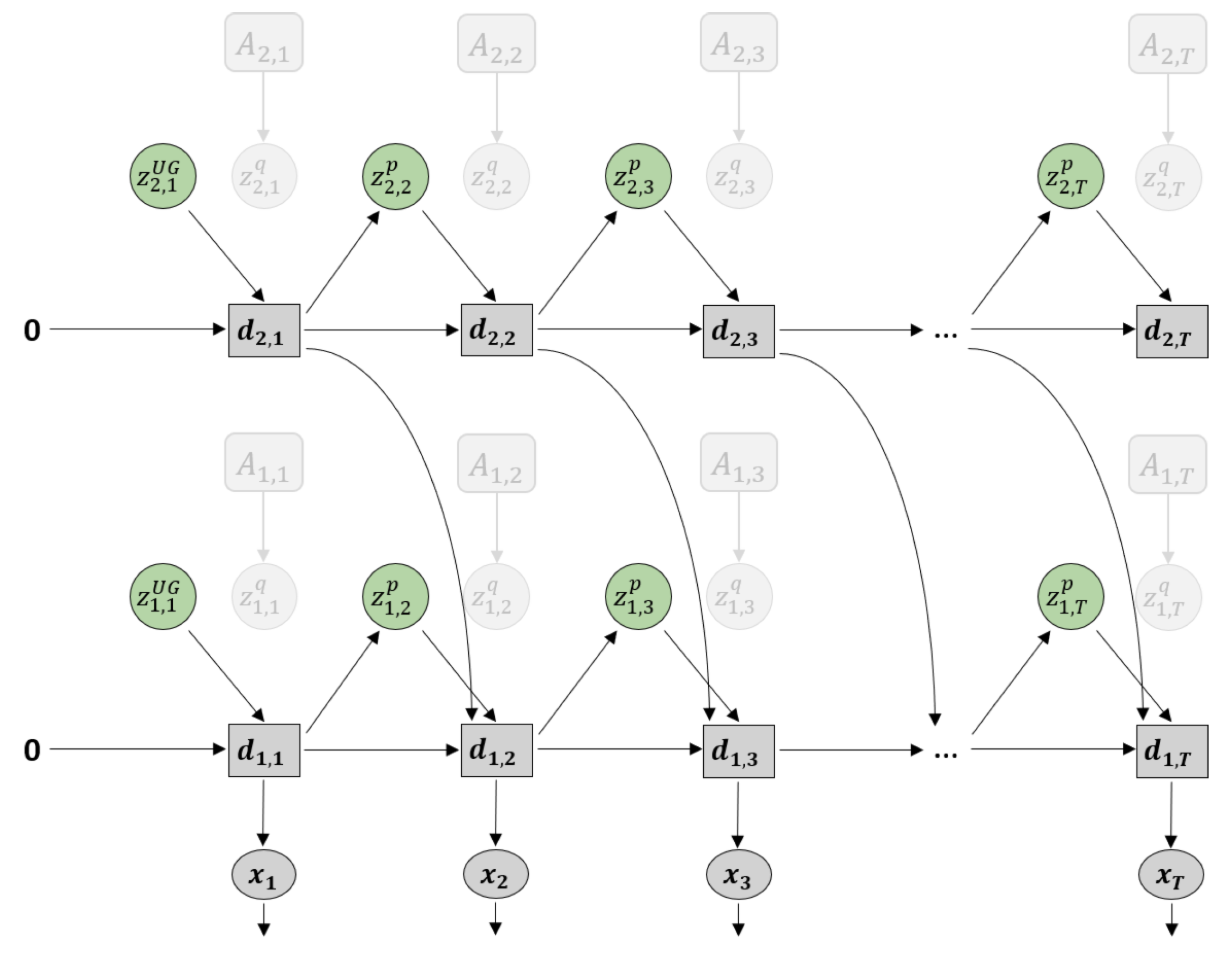
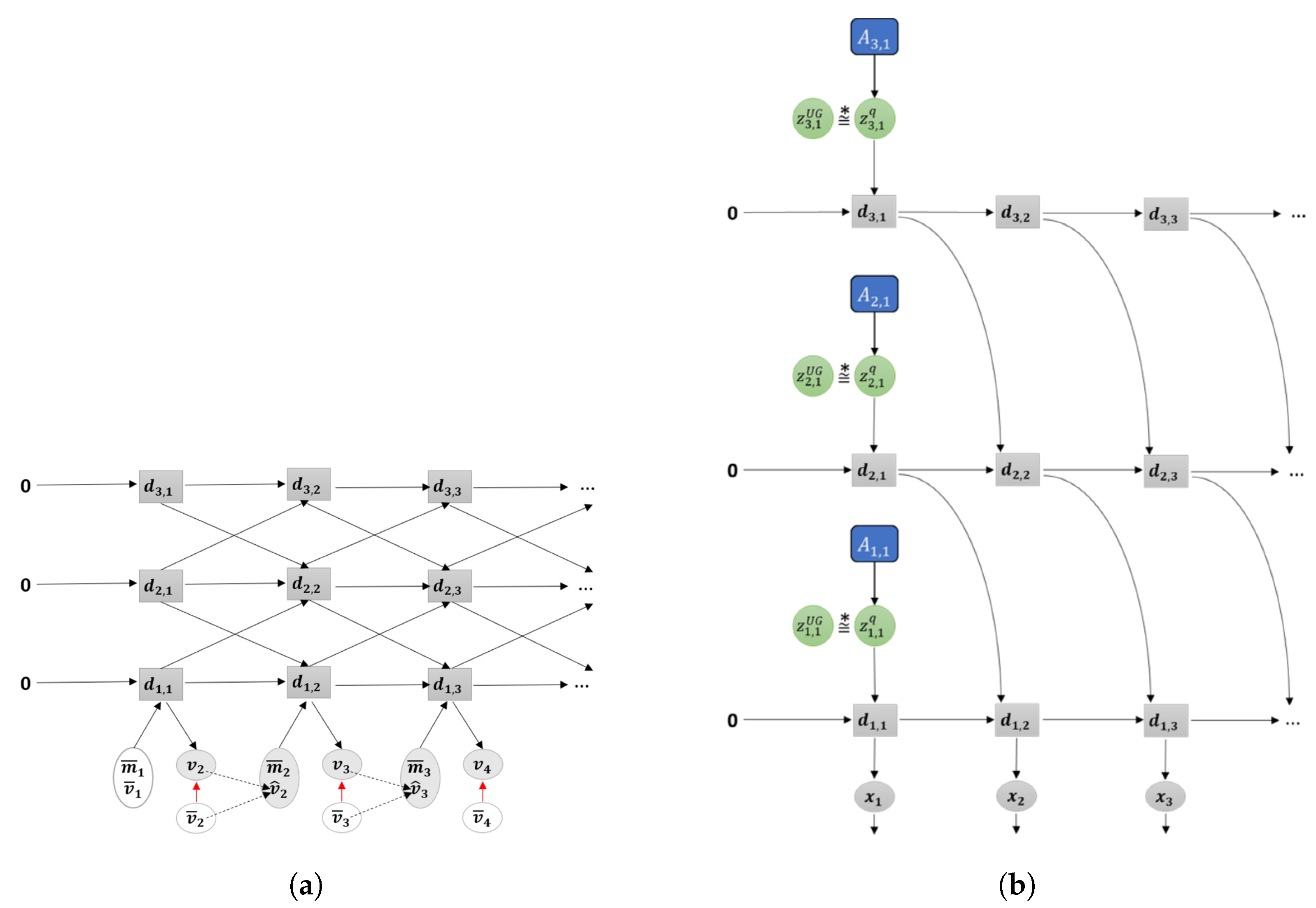
Figure 3.
Graphical representation of predictive-coding inspired variational RNN (PV-RNN) as implemented in this paper.
Figure 3.
Graphical representation of predictive-coding inspired variational RNN (PV-RNN) as implemented in this paper.
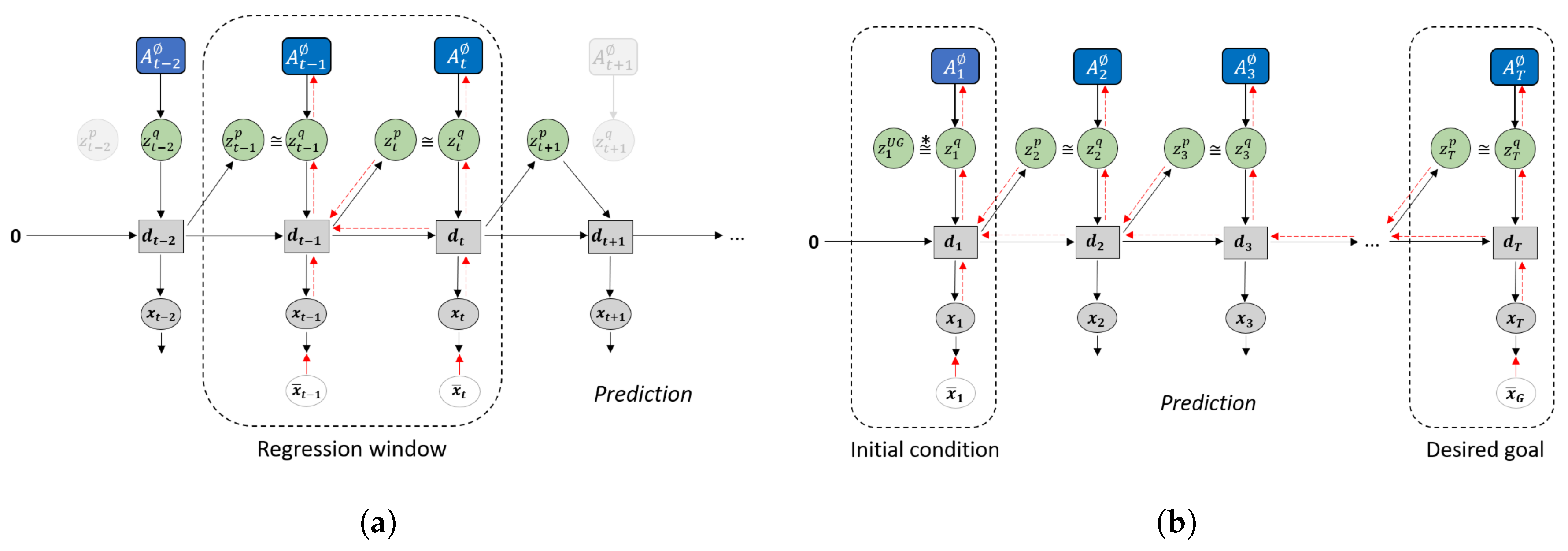
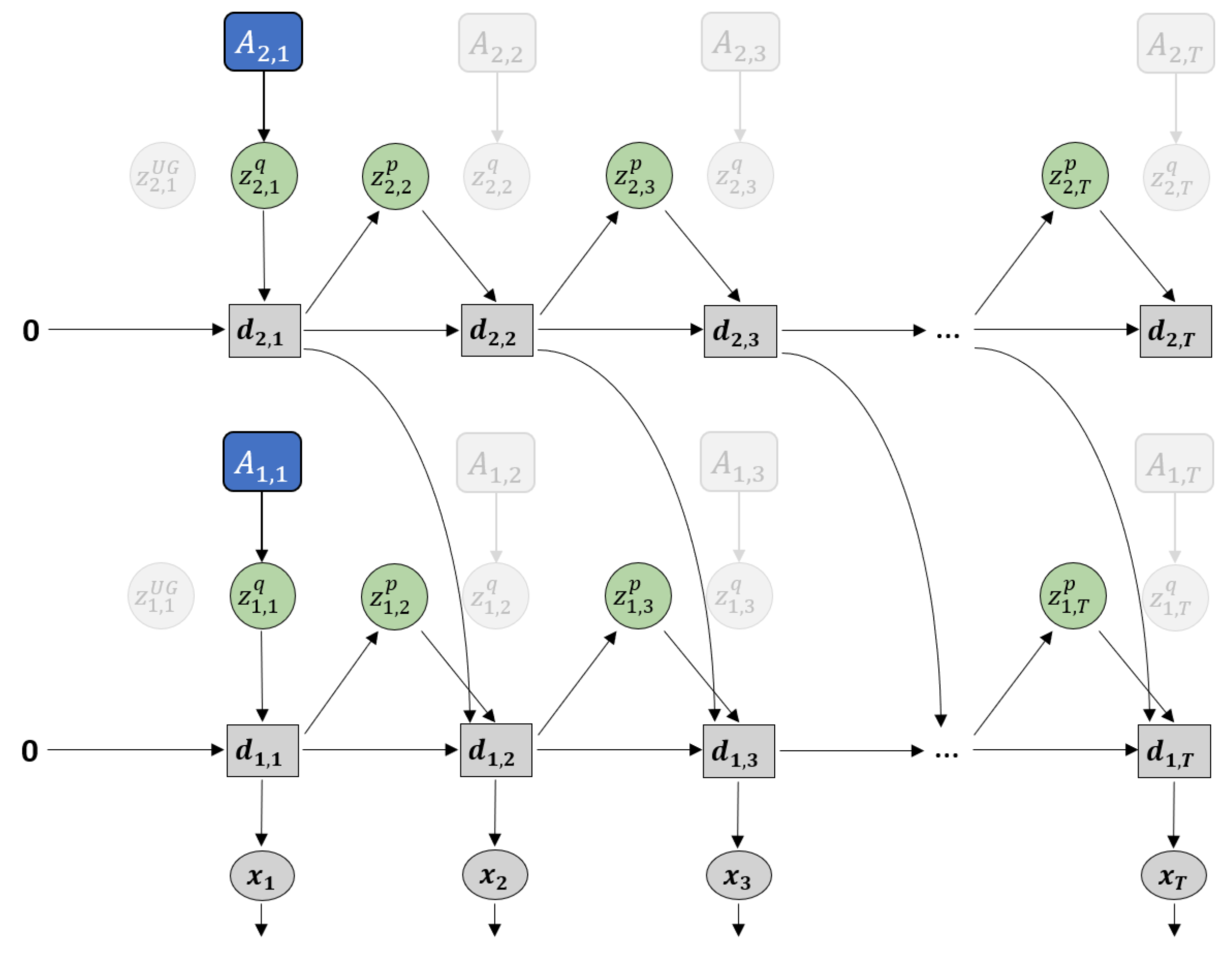
Figure 4.
Difference in how error regression is employed in (a) future sequence prediction and (b) goal-directed planning. Solid black lines represent the forward generative model while the dashed red lines represent back-propagation through time used to update .
Figure 4.
Difference in how error regression is employed in (a) future sequence prediction and (b) goal-directed planning. Solid black lines represent the forward generative model while the dashed red lines represent back-propagation through time used to update .
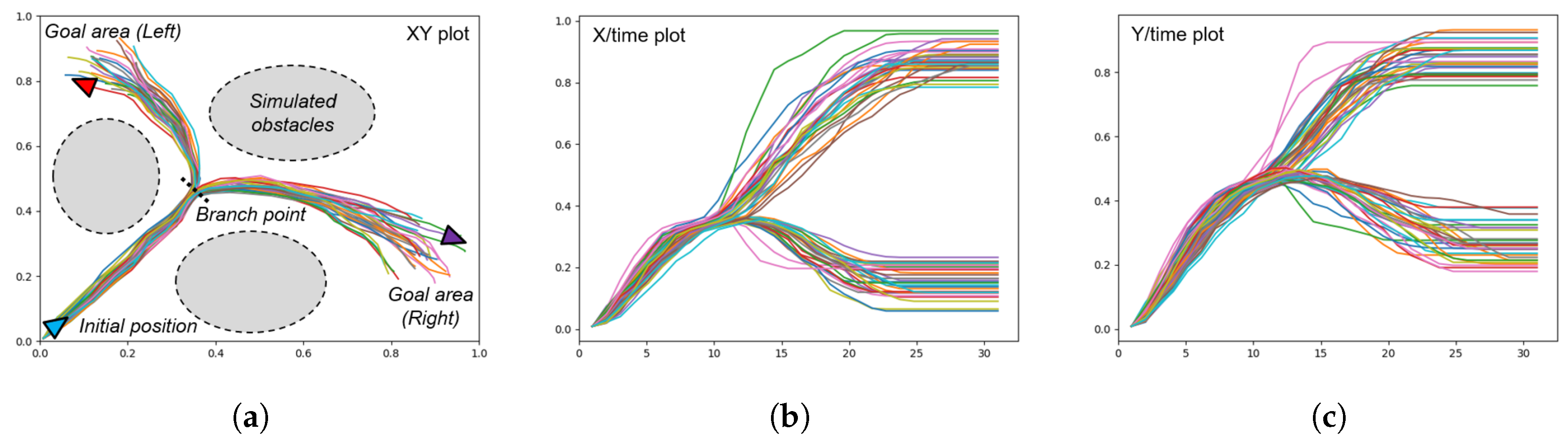
Figure 5.
Plots of the trajectories prepared for a mobile agent generating goal-directed behaviors in 2D space. (a) XY plot showing the initial position of the agent, the branch point, and the two goal areas, (b) the plot of the X position over time, and (c) the plot of the Y position over time. The branch point is visible at around .
Figure 5.
Plots of the trajectories prepared for a mobile agent generating goal-directed behaviors in 2D space. (a) XY plot showing the initial position of the agent, the branch point, and the two goal areas, (b) the plot of the X position over time, and (c) the plot of the Y position over time. The branch point is visible at around .
Figure 6.
Generation using a stochastic initial state (unit Gaussian).
Figure 6.
Generation using a stochastic initial state (unit Gaussian).
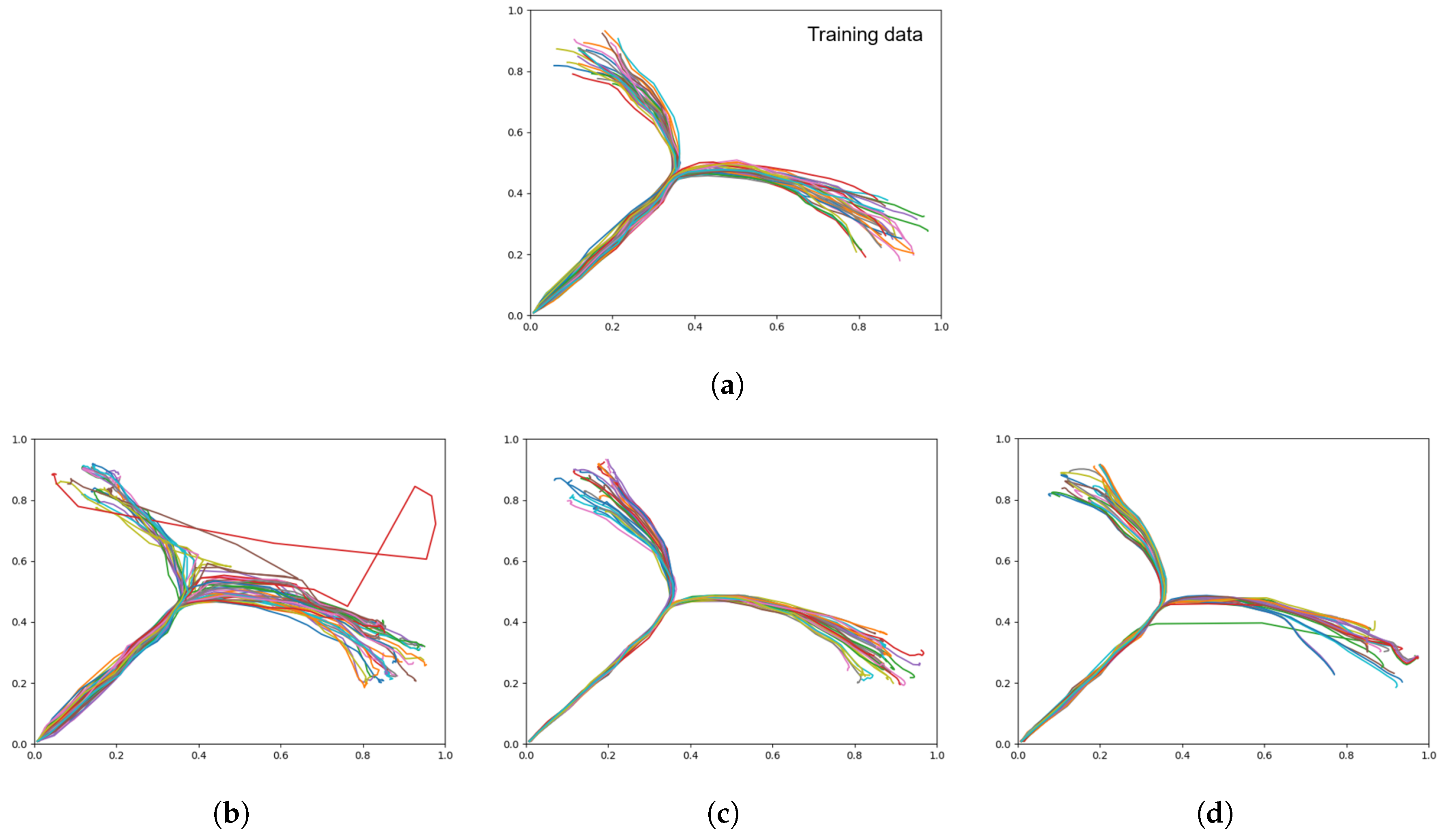
Figure 7.
Trajectory plots showing (a) the training data (ground truth), (b) prior generation with a weak meta-prior, (c) with an intermediate meta-prior, and (d) with a strong meta-prior. Each plot contains 60 trajectories.
Figure 7.
Trajectory plots showing (a) the training data (ground truth), (b) prior generation with a weak meta-prior, (c) with an intermediate meta-prior, and (d) with a strong meta-prior. Each plot contains 60 trajectories.
Figure 8.
Generation using a given posterior adaptation variable .
Figure 8.
Generation using a given posterior adaptation variable .
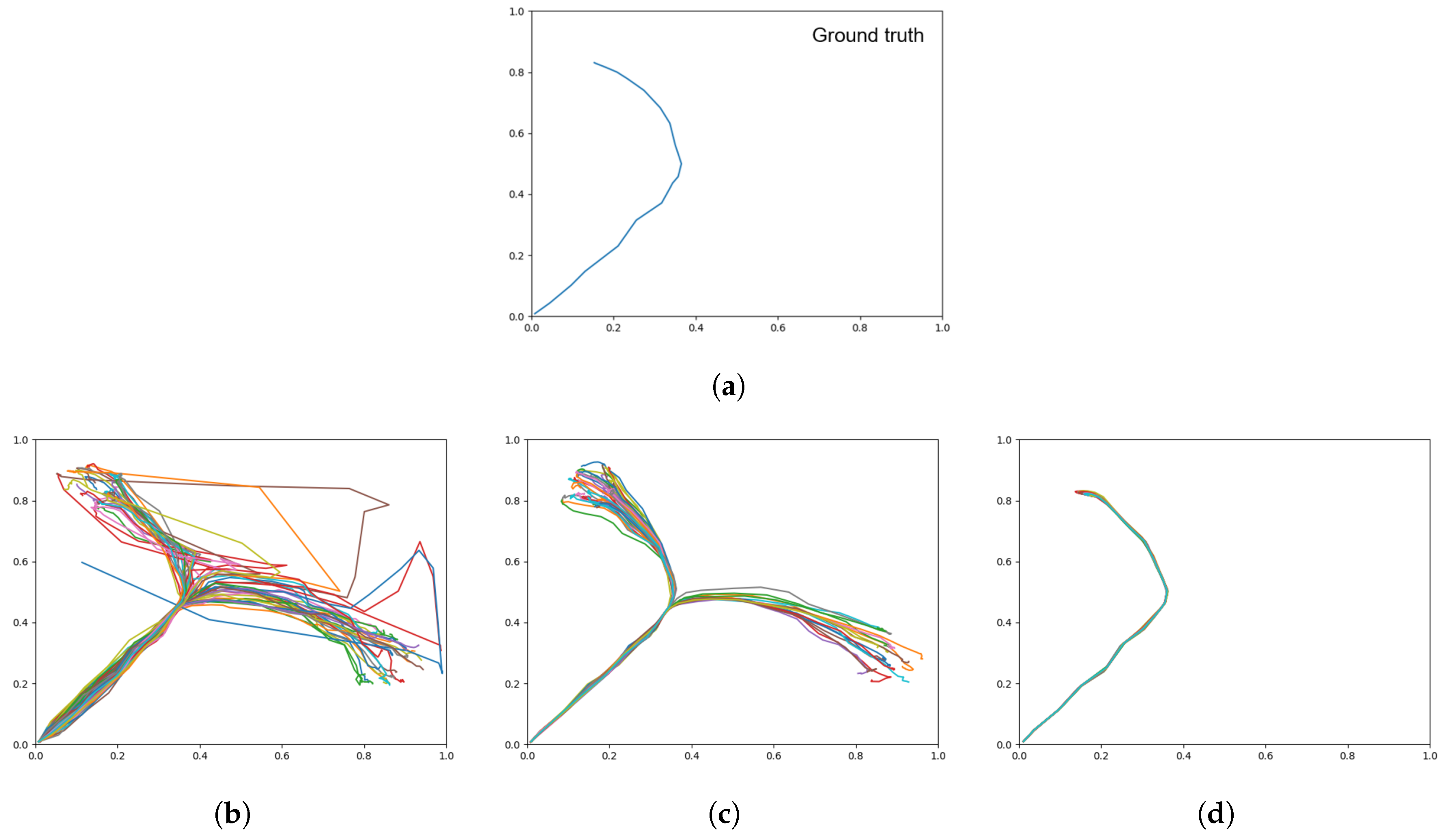
Figure 9.
Trajectory plots showing (a) the target (ground truth), (b) target regeneration with a weak meta-prior, (c) target regeneration with an intermediate meta-prior, and (d) target regeneration with a strong meta-prior. Each plot contains 60 trajectories.
Figure 9.
Trajectory plots showing (a) the target (ground truth), (b) target regeneration with a weak meta-prior, (c) target regeneration with an intermediate meta-prior, and (d) target regeneration with a strong meta-prior. Each plot contains 60 trajectories.
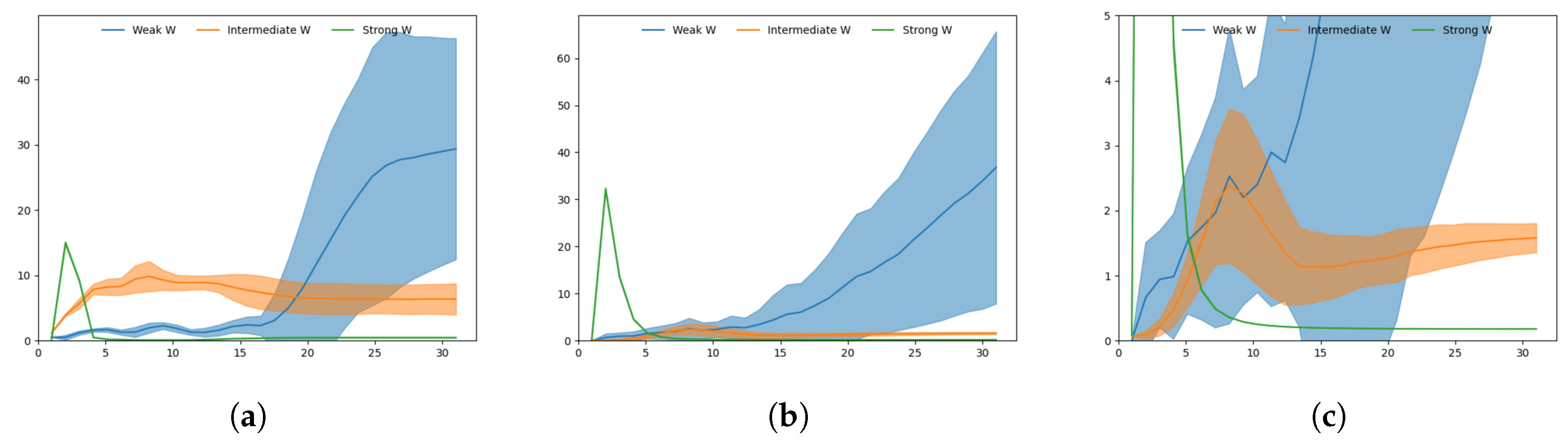
Figure 10.
Plots of Kullback-Leibler divergence (KLD) during target regeneration given a particular adaptation value. (a) Shows KLD for weak, intermediate and strong meta-prior in the bottom layer, (b) shows KLD for weak, intermediate and strong meta-prior in the top layer. (c) Adjusts the scale of (b) so the intermediate meta-prior result can be more clearly seen. The peak in KLD in the intermediate meta-prior network is visible around . The shaded areas indicate the standard deviation of KLD over 60 generated trajectories.
Figure 10.
Plots of Kullback-Leibler divergence (KLD) during target regeneration given a particular adaptation value. (a) Shows KLD for weak, intermediate and strong meta-prior in the bottom layer, (b) shows KLD for weak, intermediate and strong meta-prior in the top layer. (c) Adjusts the scale of (b) so the intermediate meta-prior result can be more clearly seen. The peak in KLD in the intermediate meta-prior network is visible around . The shaded areas indicate the standard deviation of KLD over 60 generated trajectories.
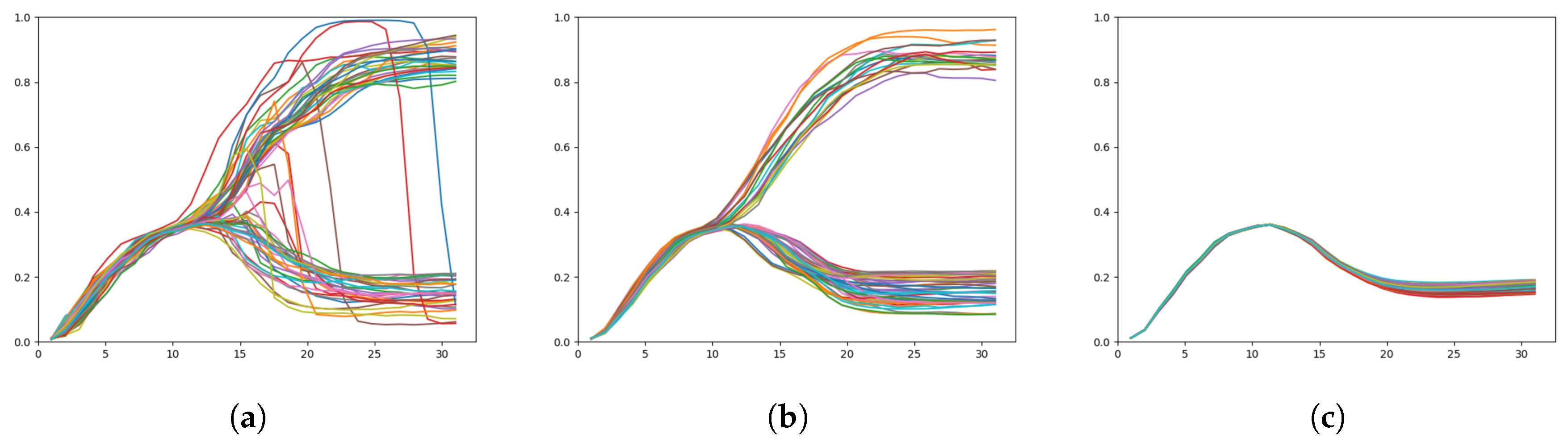
Figure 11.
Plots of the x coordinate over time, target regeneration given a particular adaptation value with (a) a weak meta-prior, (b) an intermediate meta-prior, and (c) a strong meta-prior. The branch point is visible around , except in (c) which does not exhibit any branching behavior.
Figure 11.
Plots of the x coordinate over time, target regeneration given a particular adaptation value with (a) a weak meta-prior, (b) an intermediate meta-prior, and (c) a strong meta-prior. The branch point is visible around , except in (c) which does not exhibit any branching behavior.
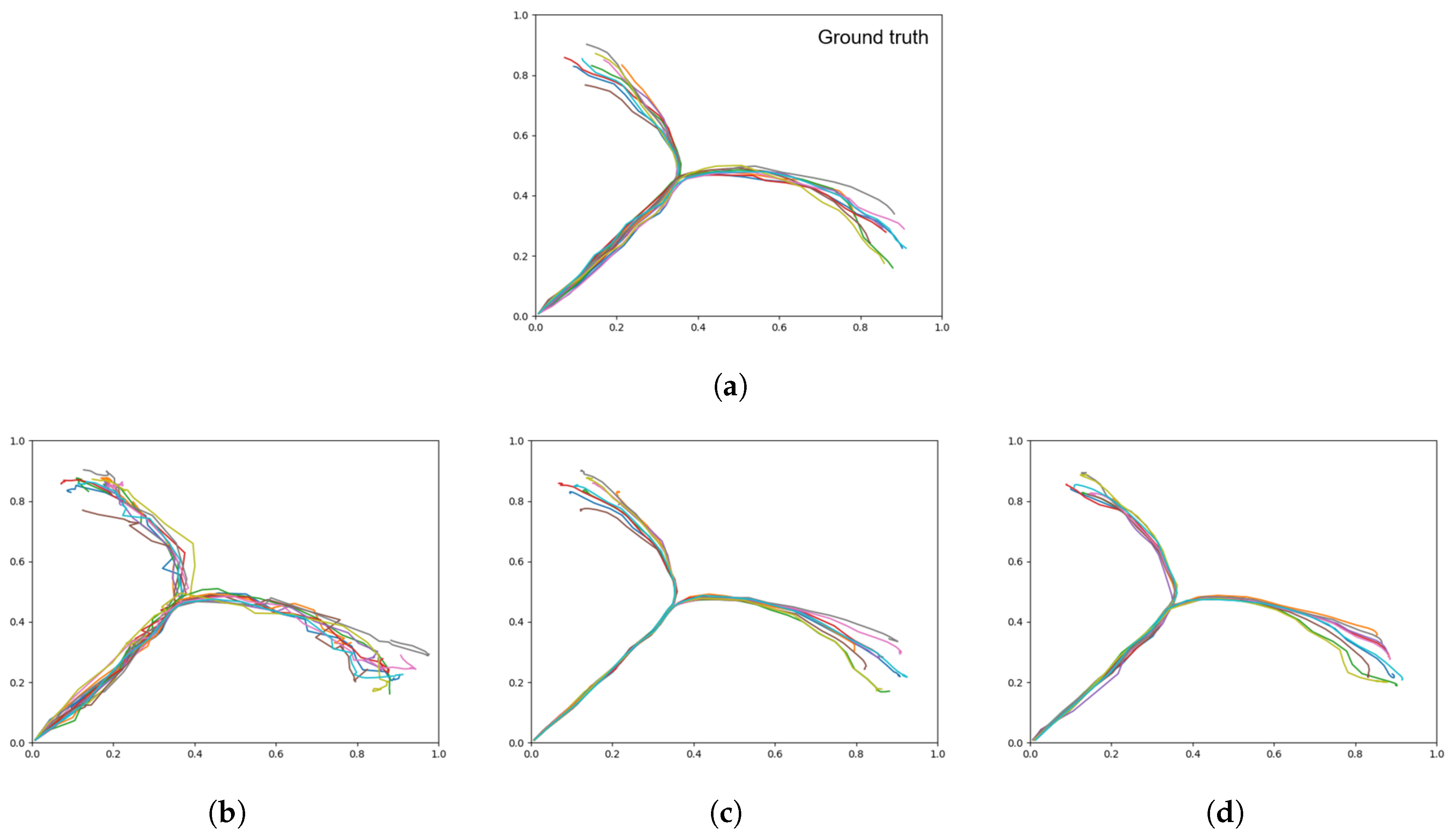
Figure 12.
Plots showing motor plans of the 20 test sequences. (
a) Shows the ground truth for untrained test data set, with the remaining plots generated with a (
b) weak meta-prior, (
c) intermediate meta-prior, and (
d) strong meta-prior as described in
Table 2.
Figure 12.
Plots showing motor plans of the 20 test sequences. (
a) Shows the ground truth for untrained test data set, with the remaining plots generated with a (
b) weak meta-prior, (
c) intermediate meta-prior, and (
d) strong meta-prior as described in
Table 2.
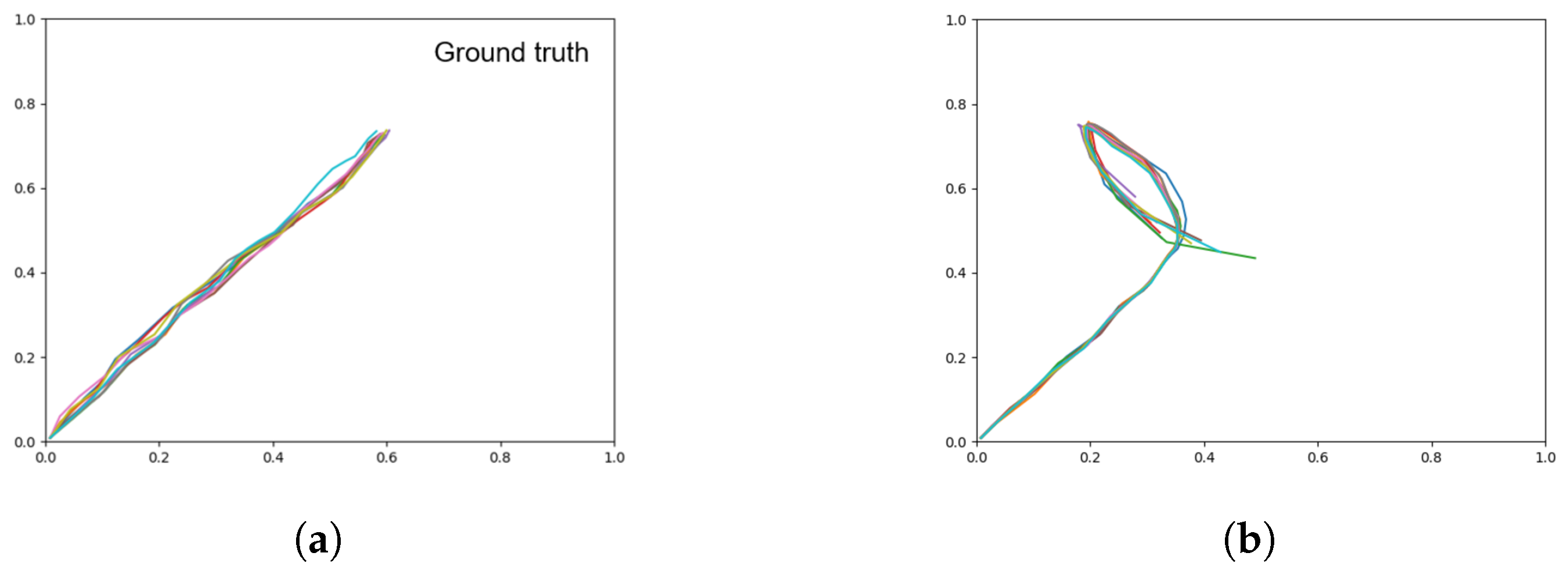
Figure 13.
Plots showing motor plans of the 10 test sequences with goals set in an untrained region. (a) Shows the ground truth test trajectories, and (b) shows the results of plan generation.
Figure 13.
Plots showing motor plans of the 10 test sequences with goals set in an untrained region. (a) Shows the ground truth test trajectories, and (b) shows the results of plan generation.
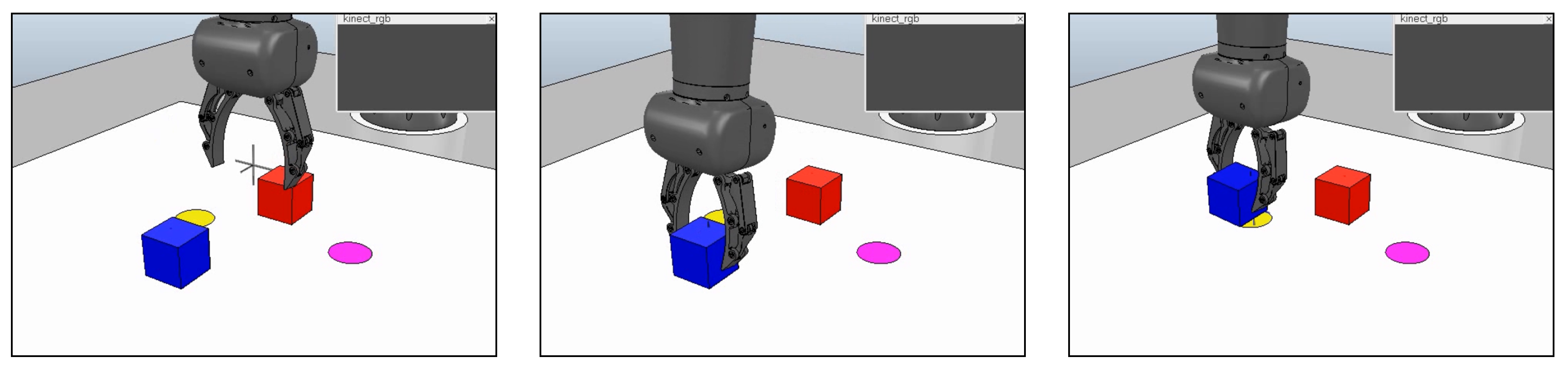
Figure 14.
Simulated robot executing the grasp and place task. In the workspace in front of the robot, there are two graspable blocks and two goal circles. Crosshair markers show the predicted positions of the gripper and the two blocks.
Figure 14.
Simulated robot executing the grasp and place task. In the workspace in front of the robot, there are two graspable blocks and two goal circles. Crosshair markers show the predicted positions of the gripper and the two blocks.
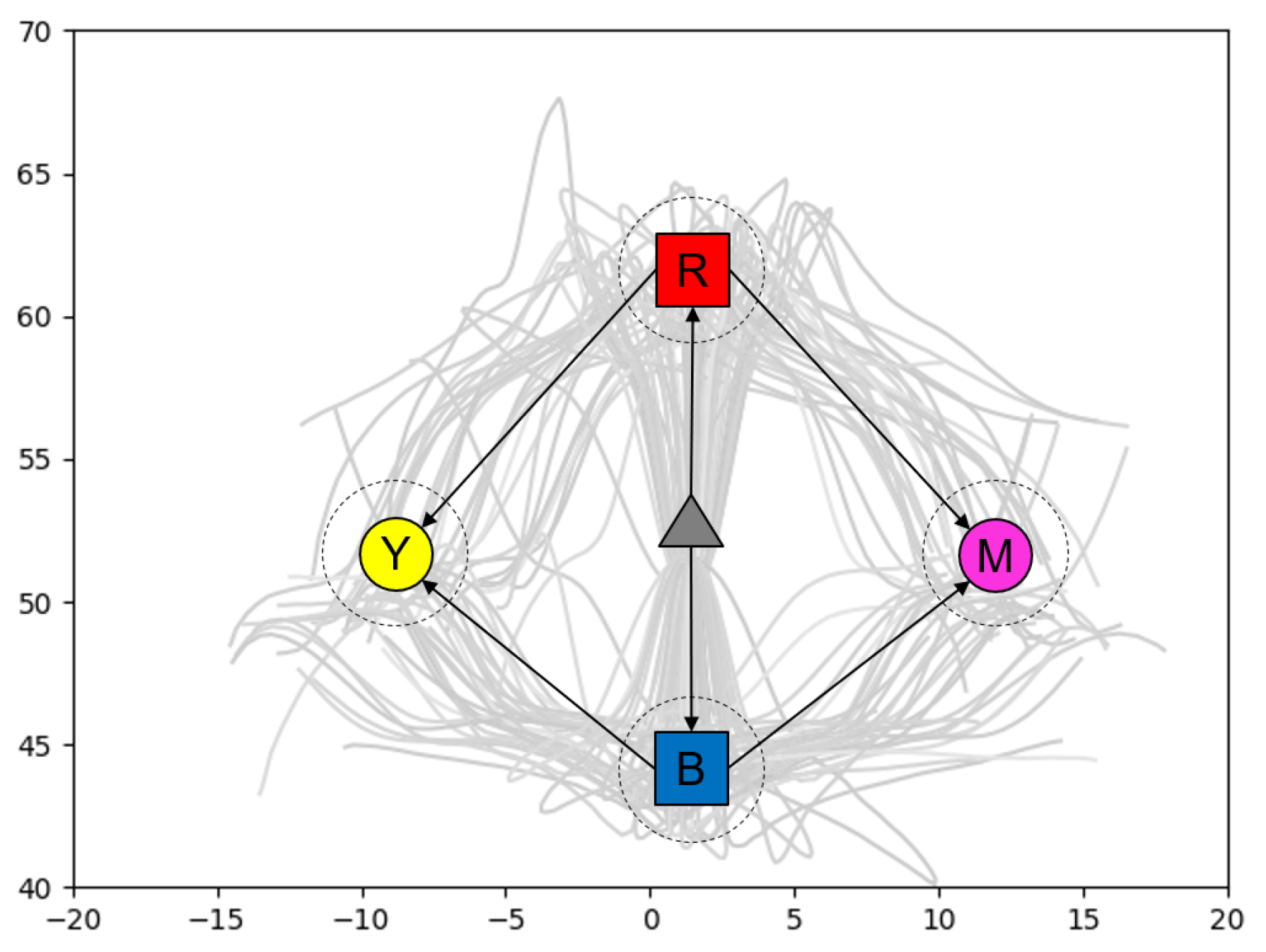
Figure 15.
Trajectories of the gripper in two dimensions, with the mean positions of the blocks and goal circles overlaid. Dashed circles represent the standard deviation of the positions.
Figure 15.
Trajectories of the gripper in two dimensions, with the mean positions of the blocks and goal circles overlaid. Dashed circles represent the standard deviation of the positions.
Figure 16.
Graphical representations of (a) the forward model (FM) and (b) the stochastic initial state (SI) model as implemented in this paper.
Figure 16.
Graphical representations of (a) the forward model (FM) and (b) the stochastic initial state (SI) model as implemented in this paper.
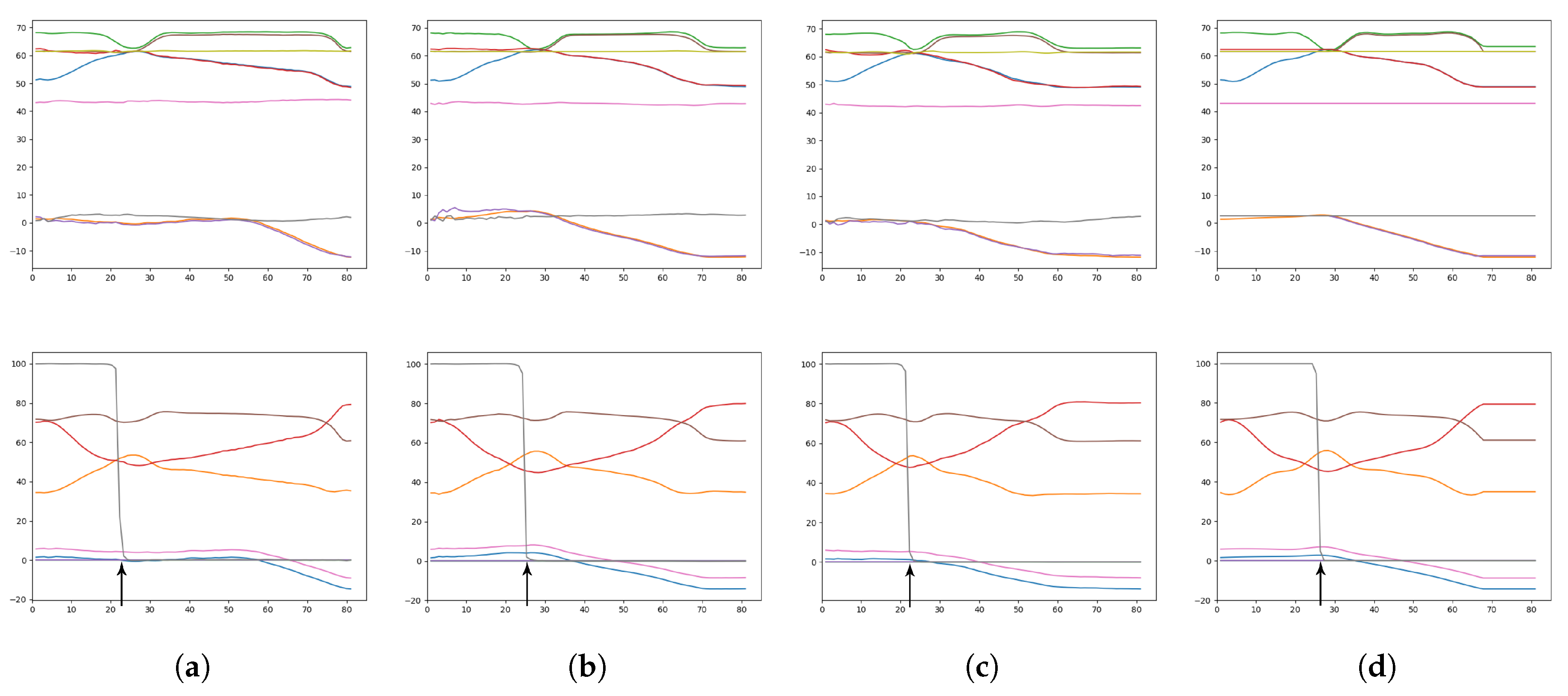
Figure 17.
Plots showing the predicted sensory states (top row) and the motor plans (bottom row) for a given goal. The colored lines within each plot represent a sequence of predictions for one sensory or proprioception dimension. The columns of plots correspond to (a) weak meta-prior, (b) intermediate meta-prior, (c) strong meta-prior, and (d) ground truth. An arrow indicates the grasp point, where the robot attempts to pick up the block. While the exact timestep of the grasp point can vary, if the relationship between the predicted dimensions is not maintained the grasping attempt is more likely to fail.
Figure 17.
Plots showing the predicted sensory states (top row) and the motor plans (bottom row) for a given goal. The colored lines within each plot represent a sequence of predictions for one sensory or proprioception dimension. The columns of plots correspond to (a) weak meta-prior, (b) intermediate meta-prior, (c) strong meta-prior, and (d) ground truth. An arrow indicates the grasp point, where the robot attempts to pick up the block. While the exact timestep of the grasp point can vary, if the relationship between the predicted dimensions is not maintained the grasping attempt is more likely to fail.
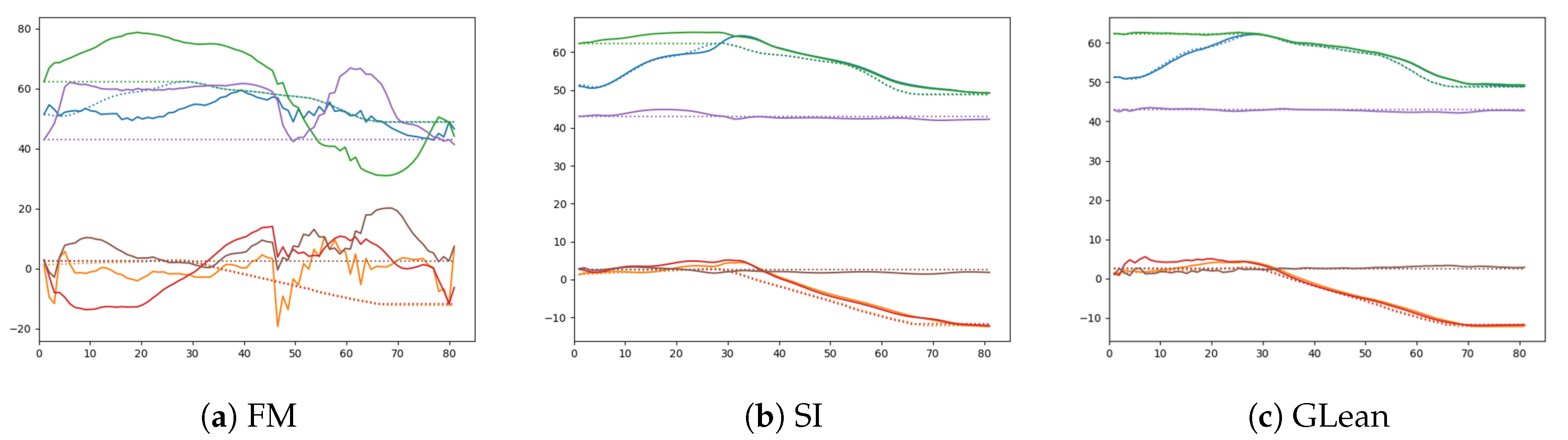
Figure 18.
Comparison between the generated sensory predictions (solid lines) and the ground truth sensory states (dashed lines) for (a) forward model, (b) stochastic initial state, and (c) GLean.
Figure 18.
Comparison between the generated sensory predictions (solid lines) and the ground truth sensory states (dashed lines) for (a) forward model, (b) stochastic initial state, and (c) GLean.
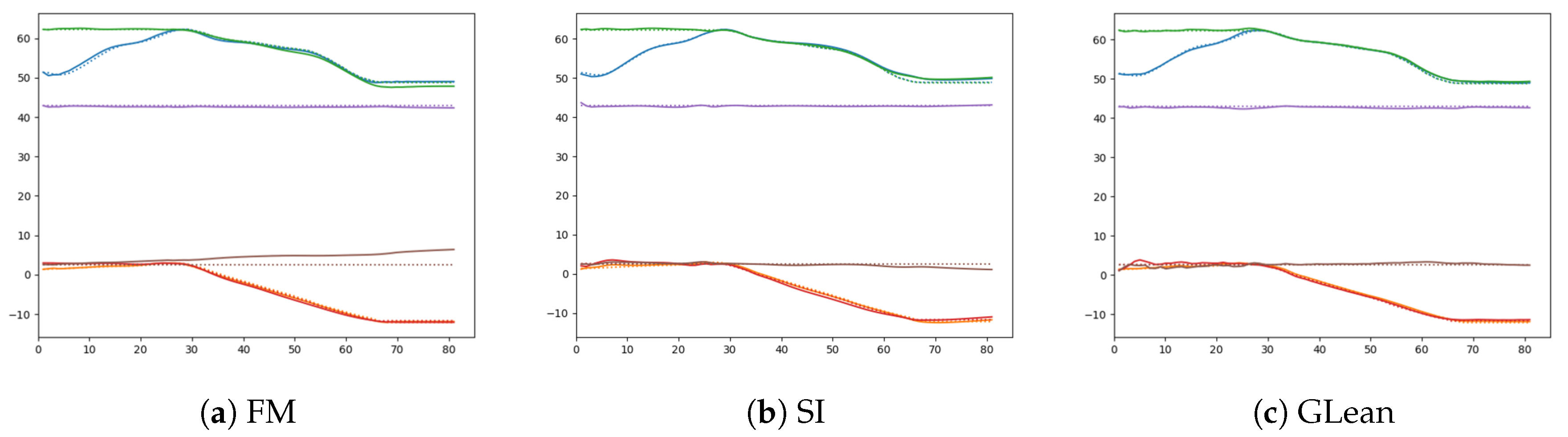
Figure 19.
Comparison of one-step look ahead sensory prediction (solid lines) and the ground truth (dashed lines) among three different models—(a) forward model, (b) stochastic initial state, and (c) GLean.
Figure 19.
Comparison of one-step look ahead sensory prediction (solid lines) and the ground truth (dashed lines) among three different models—(a) forward model, (b) stochastic initial state, and (c) GLean.
Table 1.
PV-RNN parameters for Experiment 1.
Table 1.
PV-RNN parameters for Experiment 1.
| | MTRNN Layer |
|---|
| | 1 | 2 |
|---|
| Neurons | 20 | 10 |
| Z-units | 2 | 1 |
| 4 | 8 |
Table 2.
Meta-prior settings for the 2D experiment.
Table 2.
Meta-prior settings for the 2D experiment.
| | MTRNN Layer |
|---|
| Meta-Prior Setting | 1 | 2 |
|---|
| Weak | 0.00001 | 0.000005 |
| Intermediate | 0.01 | 0.005 |
| Strong | 0.2 | 0.1 |
Table 3.
Distribution of goals reached by networks with different meta-priors, after 60 prior generation sequences.
Table 3.
Distribution of goals reached by networks with different meta-priors, after 60 prior generation sequences.
| Training Meta-Prior | Left Goal % | Right Goal % |
|---|
| Weak | 38.3 | 61.7 |
| Intermediate | 46.7 | 53.3 |
| Strong | 55.0 | 45.0 |
| Ground truth | 50.0 | 50.0 |
Table 4.
Distribution of goals reached by networks with different meta-priors, after 60 target regeneration sequences.
Table 4.
Distribution of goals reached by networks with different meta-priors, after 60 target regeneration sequences.
| Training Meta-Prior | Left Goal % | Right Goal % |
|---|
| Weak | 56.7 | 43.3 |
| Intermediate | 70.0 | 30.0 |
| Strong | 100.0 | 0.0 |
| Target | 100.0 | 0.0 |
Table 5.
Plan generation results on the 20 trajectory test set with varying meta-prior. Best result highlighted in bold.
Table 5.
Plan generation results on the 20 trajectory test set with varying meta-prior. Best result highlighted in bold.
| Meta-Prior | Average | Average RMSE | Average GD |
|---|
| Weak | 159.1 | | |
| Intermediate | 3.36 | | |
| Strong | 0.17 | | |
Table 6.
Network parameters used for the simulated robot experiment for 3 different models—GLean, FM, and SI.
Table 6.
Network parameters used for the simulated robot experiment for 3 different models—GLean, FM, and SI.
| (a) GLean |
| | MTRNN Layer |
| | 1 | 2 | 3 |
| Neurons | 30 | 20 | 10 |
| Z-units | 3 | 2 | 1 |
| 2 | 4 | 8 |
| (b) FM |
| | MTRNN Layer |
| | 1 | 2 | 3 |
| Neurons | 30 | 20 | 10 |
| Z-units | 0 | 0 | 0 |
| 2 | 4 | 8 |
| (c) SI |
| | MTRNN Layer |
| | 1 | 2 | 3 |
| Neurons | 30 | 20 | 10 |
| Z-units | 30 * | 20 * | 10 * |
| 2 | 4 | 8 |
Table 7.
Meta-Prior Settings for the Simulated Robot Experiment.
Table 7.
Meta-Prior Settings for the Simulated Robot Experiment.
| | MTRNN Layer |
|---|
| Meta-Prior Setting | L1 | L2 | L2 |
|---|
| Weak | 0.0004 | 0.0002 | 0.0001 |
| Intermediate | 0.0008 | 0.0004 | 0.0002 |
| Strong | 0.002 | 0.001 | 0.0005 |
Table 8.
GLean generated plans with networks trained with different meta-priors, compared with ground truth. Note that in order for the results in the following tables to be comparable to the previous experiment, the output values were rescaled to . Only the sensory states are compared between generated and ground truth trajectories. Best result highlighted in bold.
Table 8.
GLean generated plans with networks trained with different meta-priors, compared with ground truth. Note that in order for the results in the following tables to be comparable to the previous experiment, the output values were rescaled to . Only the sensory states are compared between generated and ground truth trajectories. Best result highlighted in bold.
| Meta-Prior | Average | Average RMSE | Average GD |
|---|
| Weak | 12.48 | | |
| Intermediate | 4.64 | | |
| Strong | 2.35 | | |
Table 9.
Simulation results of executing GLean generated plans with networks trained with different meta-priors. Best result highlighted in bold.
Table 9.
Simulation results of executing GLean generated plans with networks trained with different meta-priors. Best result highlighted in bold.
| Meta-Prior | Success Rate | Average Error at Goal |
|---|
| Weak | 51.5% | cm |
| Intermediate | 86.0% | cm |
| Strong | 60.5% | cm |
Table 10.
Plan generation results of GLean, FM, and SI. Best result highlighted in bold.
Table 10.
Plan generation results of GLean, FM, and SI. Best result highlighted in bold.
| Model | Average | Average RMSE | Average GD |
|---|
| Forward model | – | | |
| Stochastic initial state | 3.32 | | |
| GLean | 4.64 | | |
Table 11.
Simulation results of executing plans generated by GLean, FM, and SI. Best result highlighted in bold.
Table 11.
Simulation results of executing plans generated by GLean, FM, and SI. Best result highlighted in bold.
| Model | Success Rate | Average Error at Goal |
|---|
| Forward model (FM) | 0.0% | – |
| Stochastic initial state (SI) | 68.0% | cm |
| GLean | 86.0% | cm |
Table 12.
Comparison of average errors in sensory predictions generated by GLean, FM, and SI when provided with the ground truth motor states.
Table 12.
Comparison of average errors in sensory predictions generated by GLean, FM, and SI when provided with the ground truth motor states.
| Model | Average RMSE |
|---|
| Forward model (FM) | 0.0119 |
| Stochastic initial state (SI) | 0.0107 |
| GLean | 0.0086 |