Renormalization Analysis of Topic Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Brief Overview of Topic Models
2.2. Entropic Approach for Determining the Optimal Number of Topics
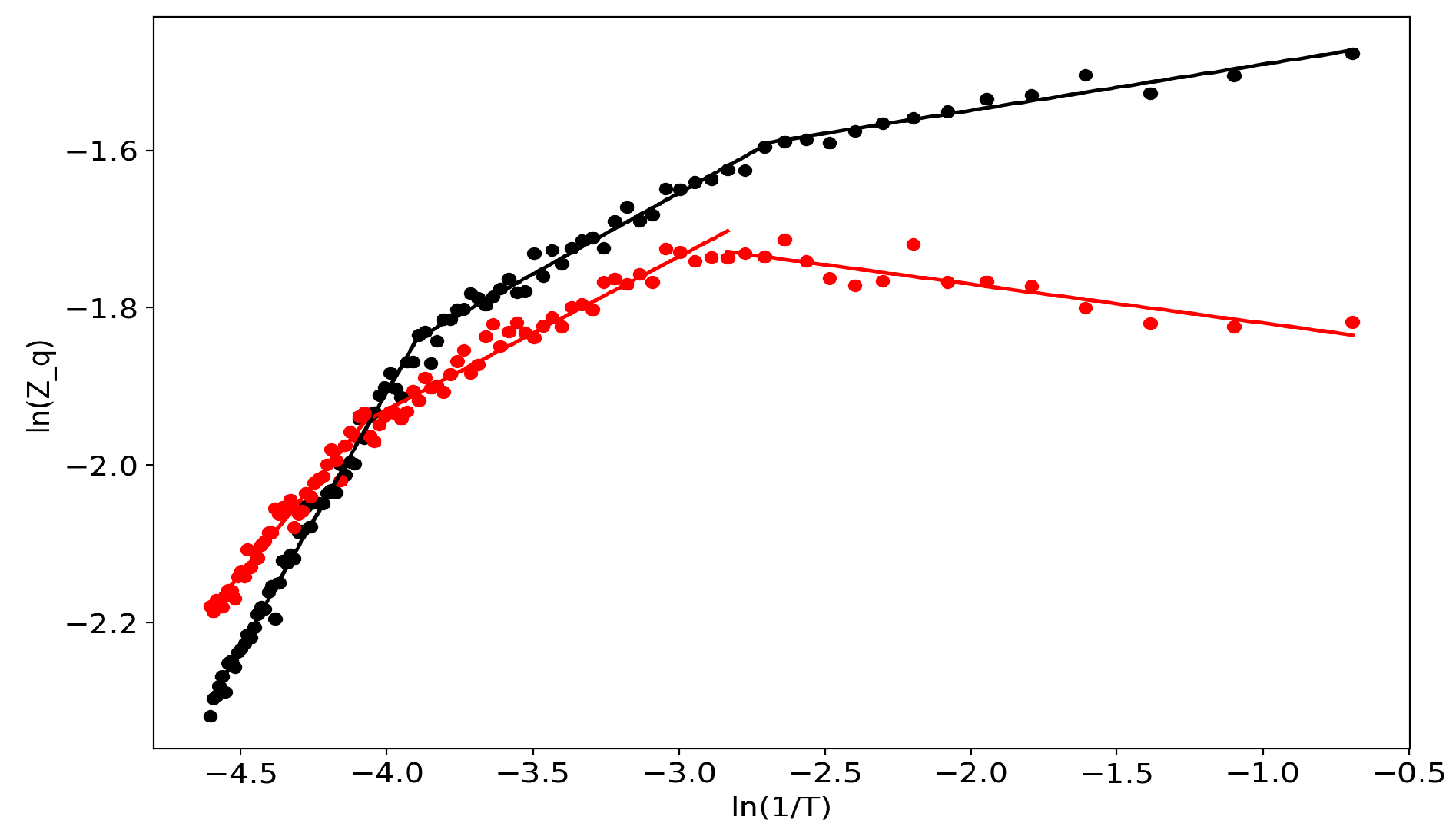
2.3. Self-Similar Behavior of Topic Models
3. Results
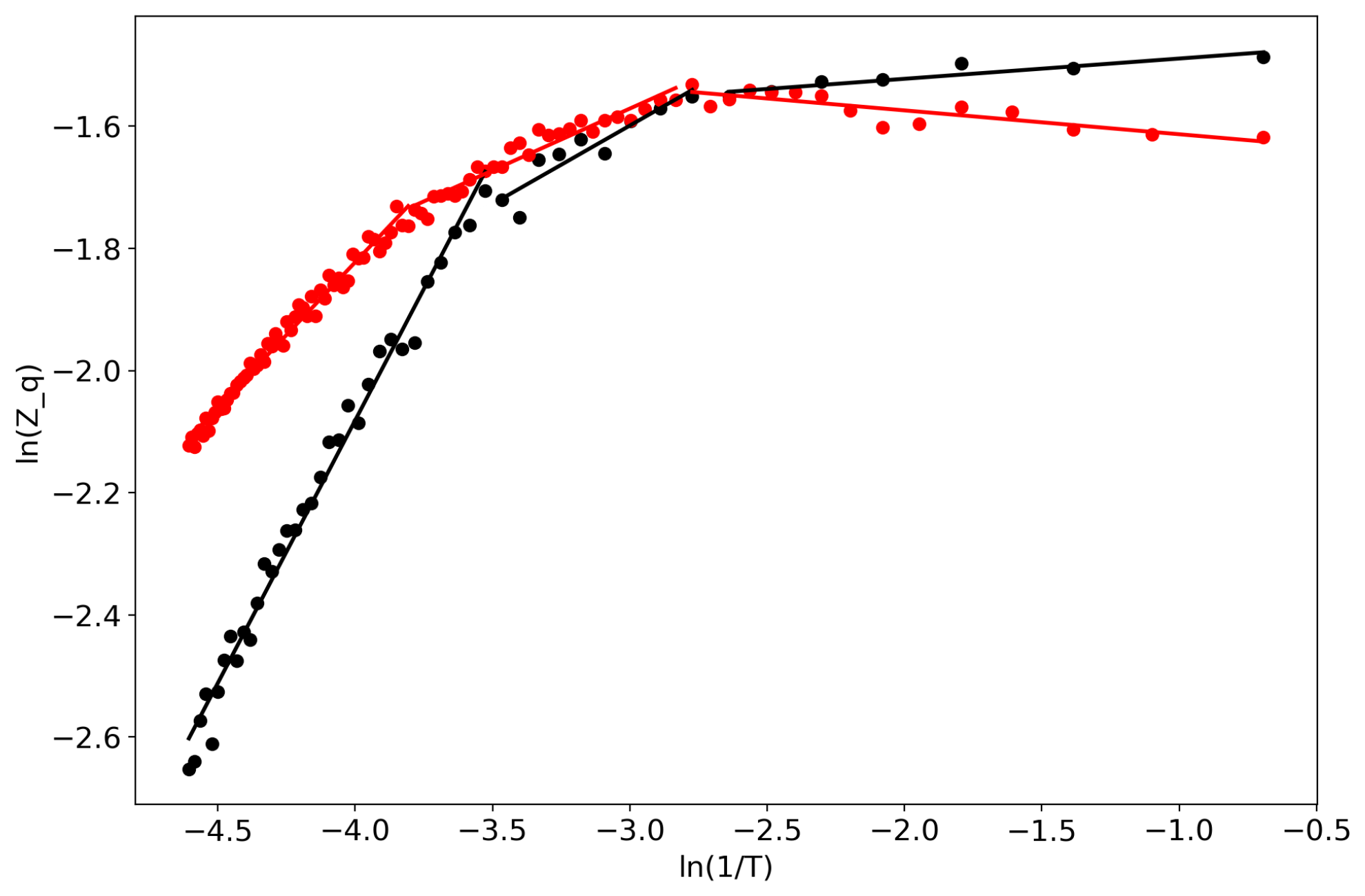
3.1. General Formulation of the Renormalization Approach in Topic Modeling
- Selection of two most similar topics in terms of symmetric Kullback–Leibler (KL) divergence [45]: for topics and , .
- Selection of two topics with the smallest values of local Renyi entropy. Here, local Renyi entropy is according to Equation (5), where only probabilities of words in that topic are considered.
- Selection of two random topics. In this procedure, two integer random numbers are generated in the range that indicate the indexes of the chosen topics, and if they are not equal, then we merge these topics.
3.2. Renormalization for the LDA Model with Variational E–M Algorithm
- We select a pair of topics and using one of the principles described in Section 3.1.
- We merge the topics. Based on Equation (6), we calculate the distribution of a new topic t resulted from merging of and as follows:Furthermore, we should normalize the obtained values of so that it would satisfy . Let us note that Equation (7) represents a linear combination of probability density functions (in particular, probability mass functions) of two topics, where the mixture weights are chosen to resemble in some sense an iteration step of the inference algorithm of the model. However, Equation (7) can not be considered directly as a mixture distribution since it does not sum up to 1. However, after normalization, we obtain, indeed, a probability distribution. Correspondingly, the values of vector should also be recalculated. The hyperparameter of the newly formed topic t is assigned to . Then, vector is normalized so that . At this step, columns and are dropped from matrix and replaced with the single new column . Therefore, the size of matrix becomes equal to .
- We calculate the global Renyi entropy for the new topic solution (matrix ) according to Equation (5). The Renyi entropy calculated in this way is further referred to as global Renyi entropy since it accounts for distributions of all topics.
3.3. Renormalization for the GLDA Model
- We select a pair of topics and using one of the principles described in Section 3.1.
- We merge the chosen topics. In terms of counters, the merging of topics corresponds to a simple summation of the counters. Therefore, the distribution of a new topic t resulted from merging of and can be calculated as follows:It is clear that the distribution of the new topic adds up to one. Note that, at this step, the number of columns in the matrix decreases.
- We calculate the global Renyi entropy for the new topic solution (matrix ) according to Equation (5).
3.4. Renormalization for the pLSA Model
- We select a pair of topics and using one of the principles described in Section 3.1.
- We merge the chosen topics. Due to the simplicity of this model and the absence of hyperparameters, the distribution of a new topic t resulted from merging of and can be calculated as follows:Thus, the merging of the chosen topics corresponds to the summation of the probabilities of words under the selected topics. Then, we normalize the obtained column so that and replace columns , with the single column .
- We calculate the global Renyi entropy for the new topic solution (matrix ) according to Equation (5).
3.5. Data and Computational Experiments
- ‘Lenta’ dataset (available at https://github.com/hse-scila/balanced-lenta-dataset): a set of 8624 news items in the Russian language from Lenta.ru online news agency. The documents of this dataset were assigned to one of ten categories (https://www.kaggle.com/yutkin/corpus-of-russian-news-articles-from-lenta). In total, the dataset contains 23,297 unique words.
- ‘20 Newsgroups’ dataset (available at http://qwone.com/~jason/20Newsgroups/): a well-known set of 15,404 news items in the English language. The number of unique words in the dataset equals to 50,948. The documents of this dataset were assigned to one or more of 20 topic groups, but according to [46], this dataset can be described with 14–20 topics as some of them are in fact very similar.
- ‘French dataset’: a set of 25,000 news items in the French language collected randomly from newspaper "Le Quotidien d’Oran" (http://www.lequotidien-oran.com/). The vocabulary of this dataset contains 18,749 unique words.
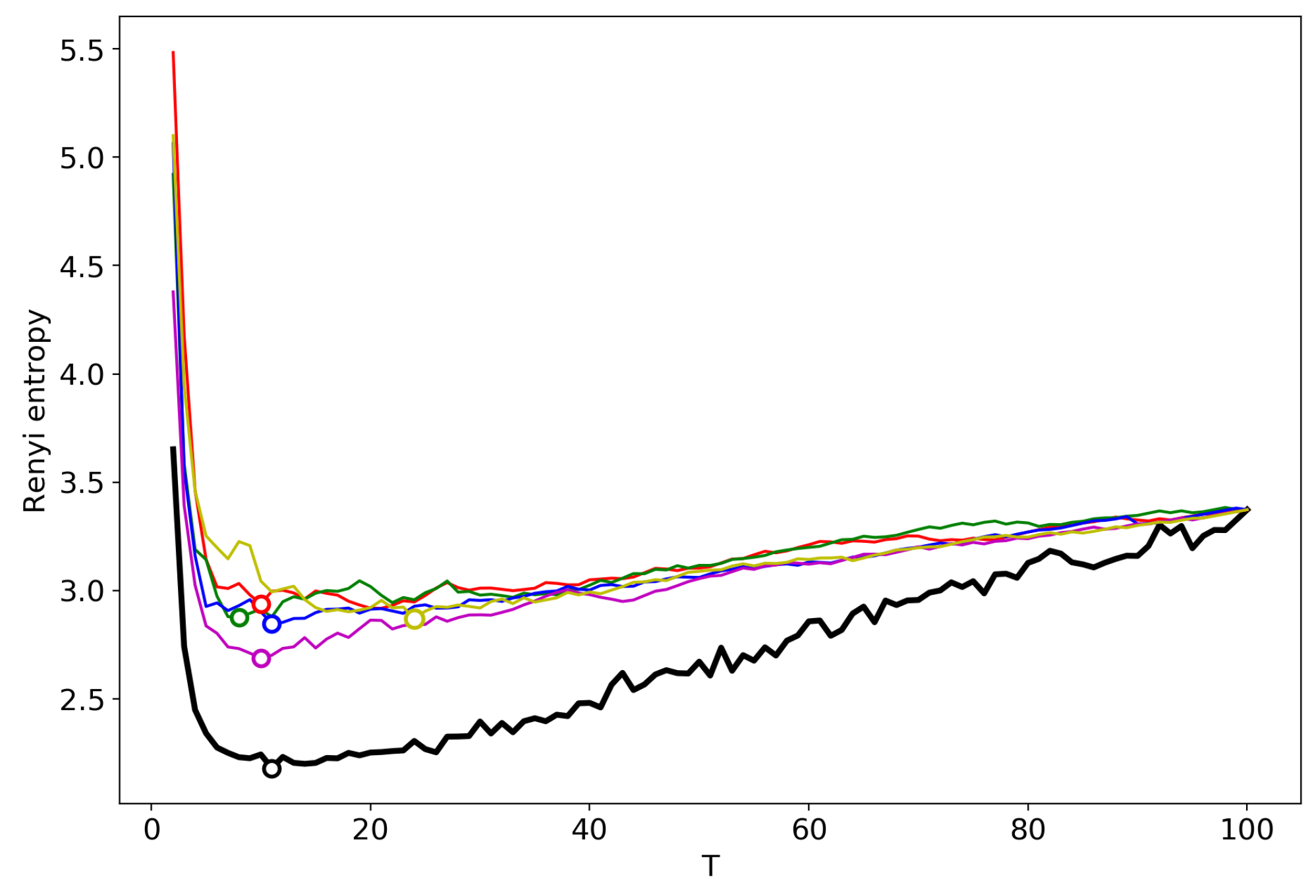
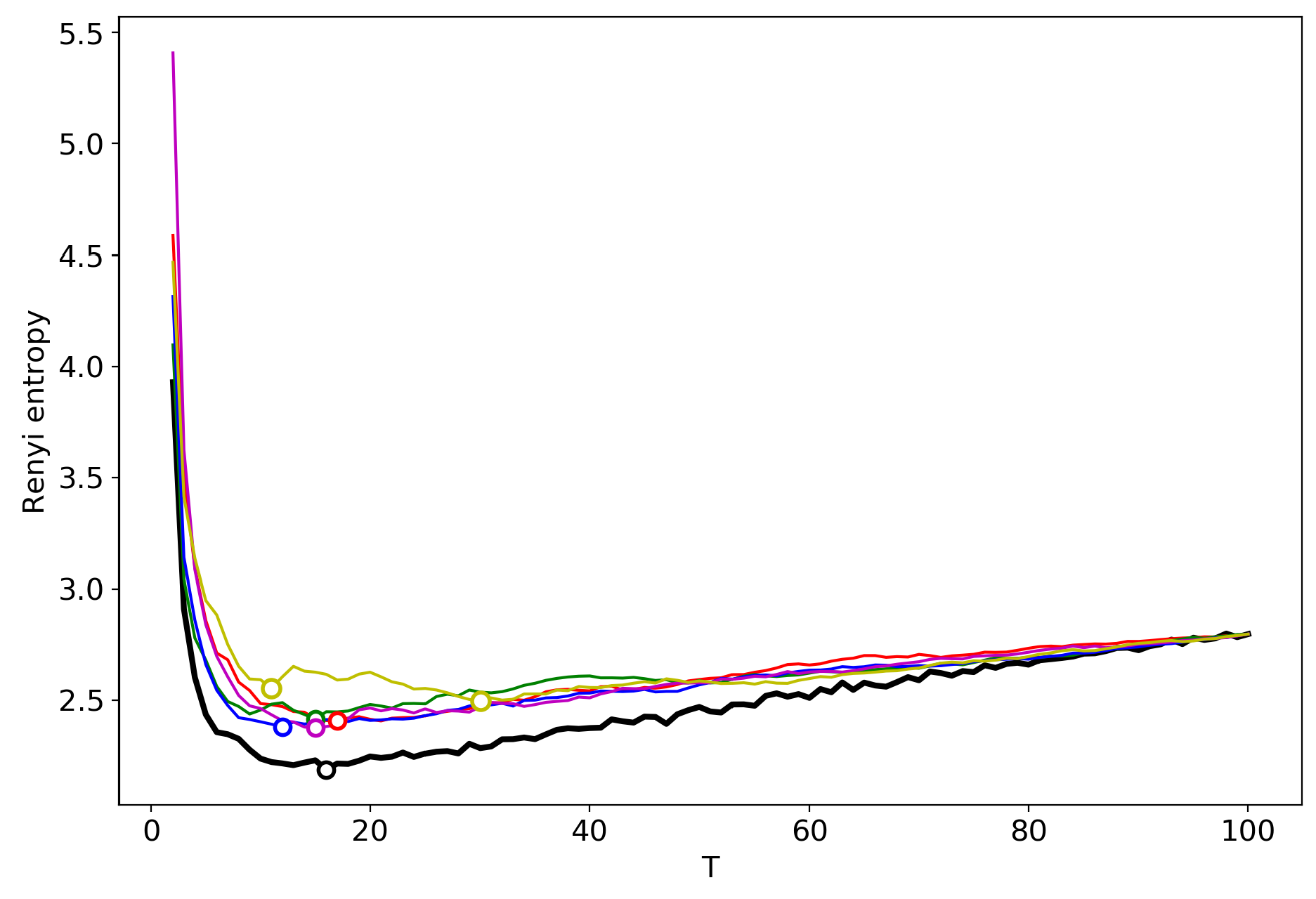
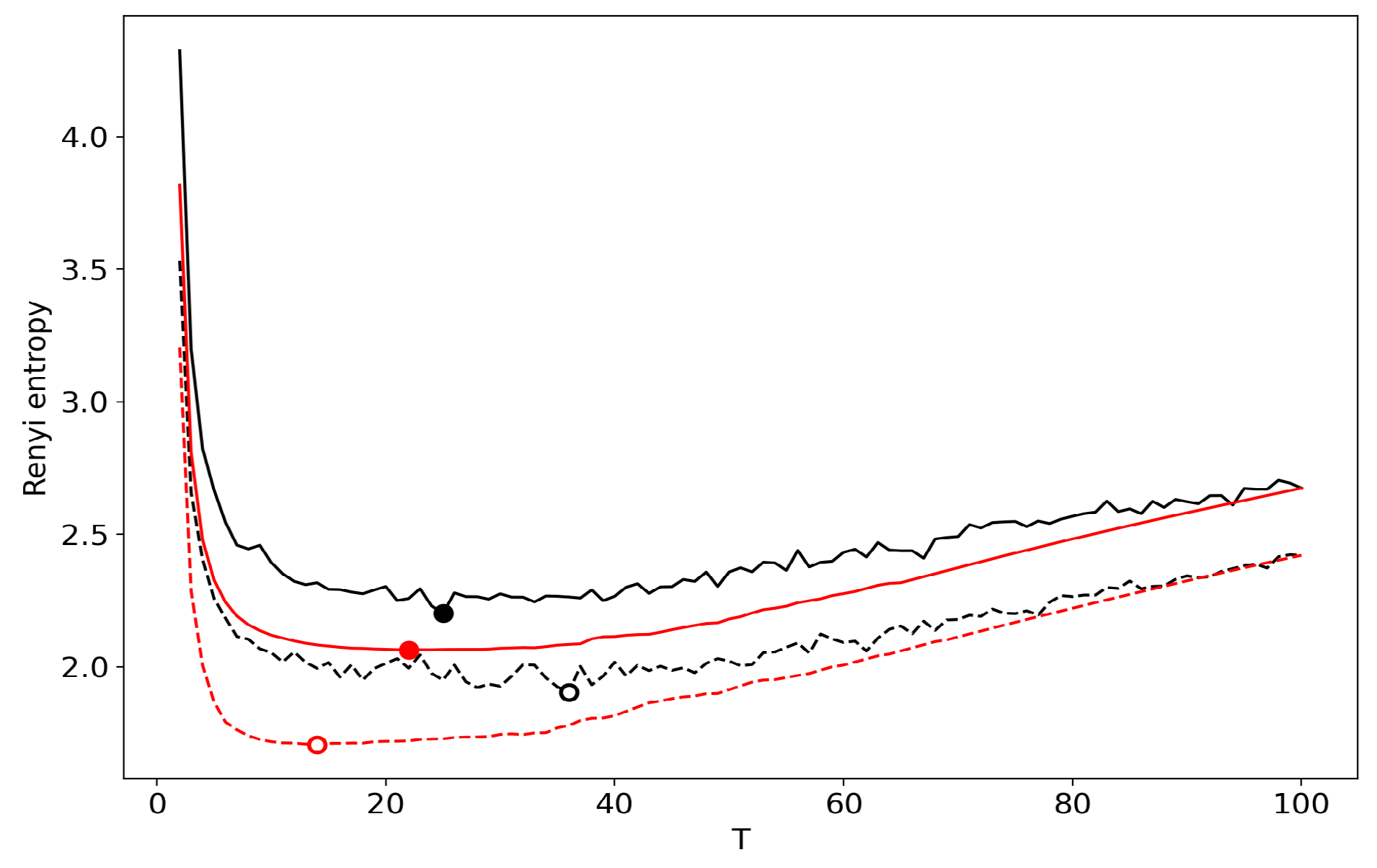
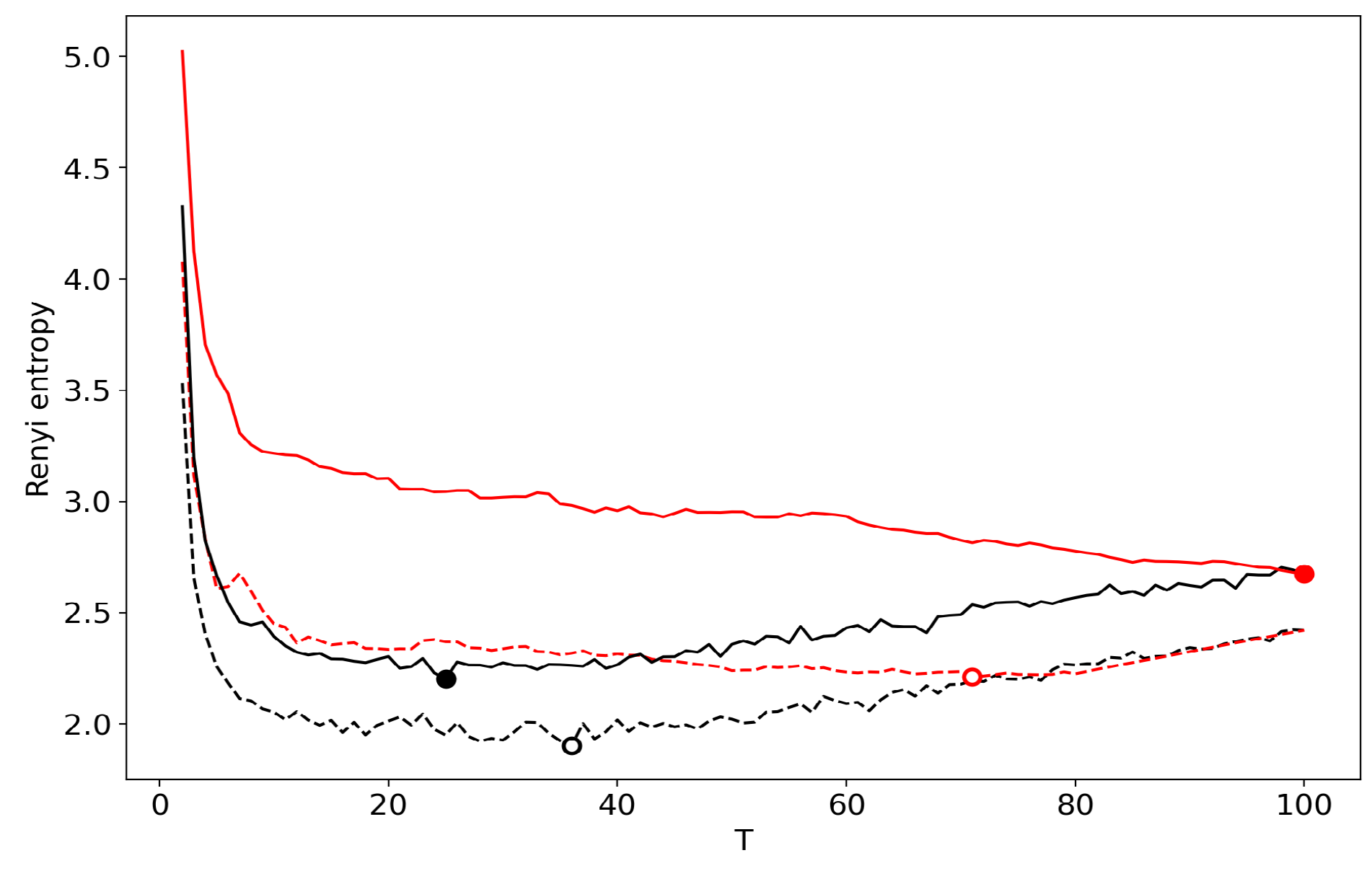
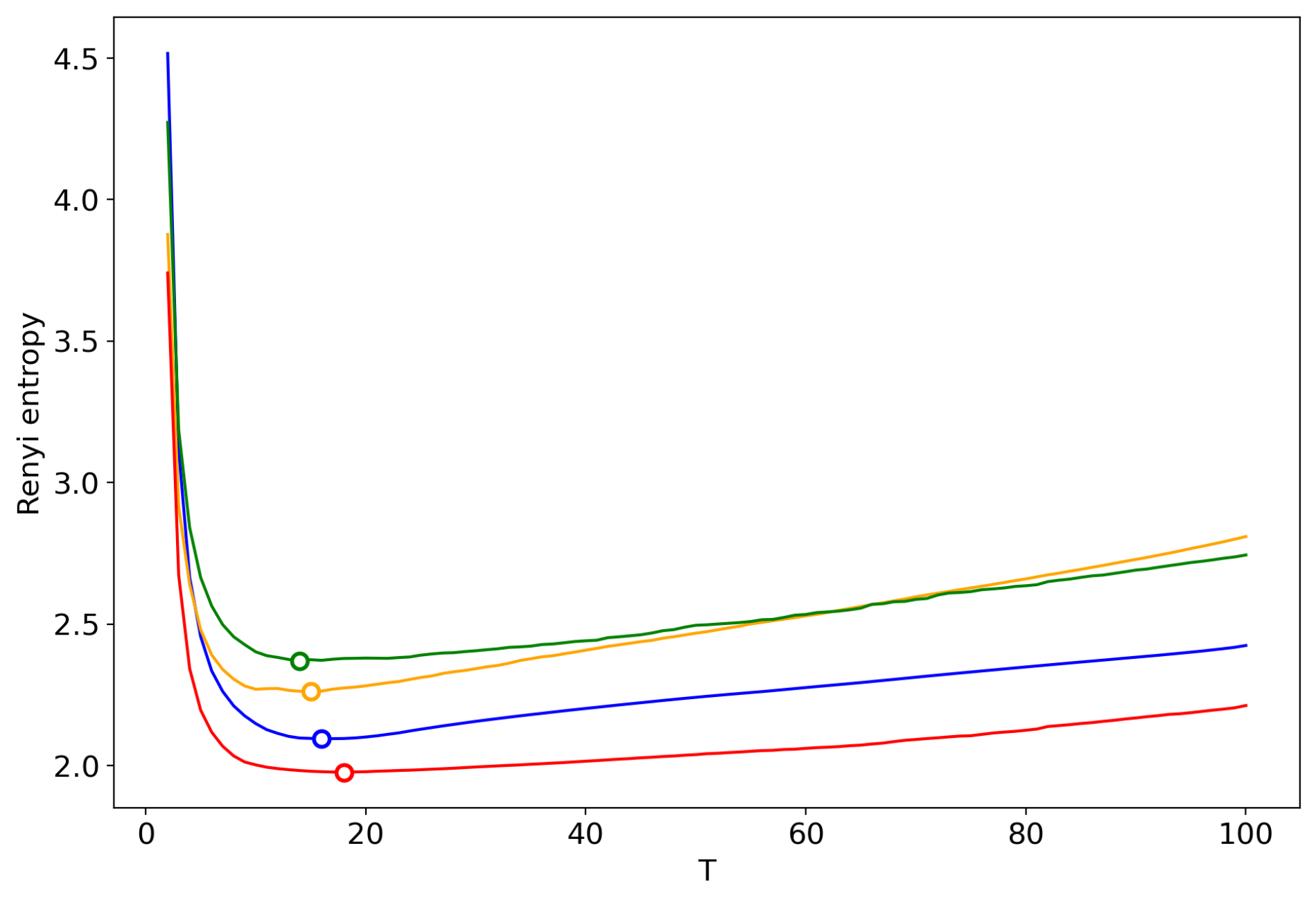
3.6. Results for LDA with a Variational E–M Algorithm
3.7. Results for the GLDA Model
3.8. Results for the pLSA Model
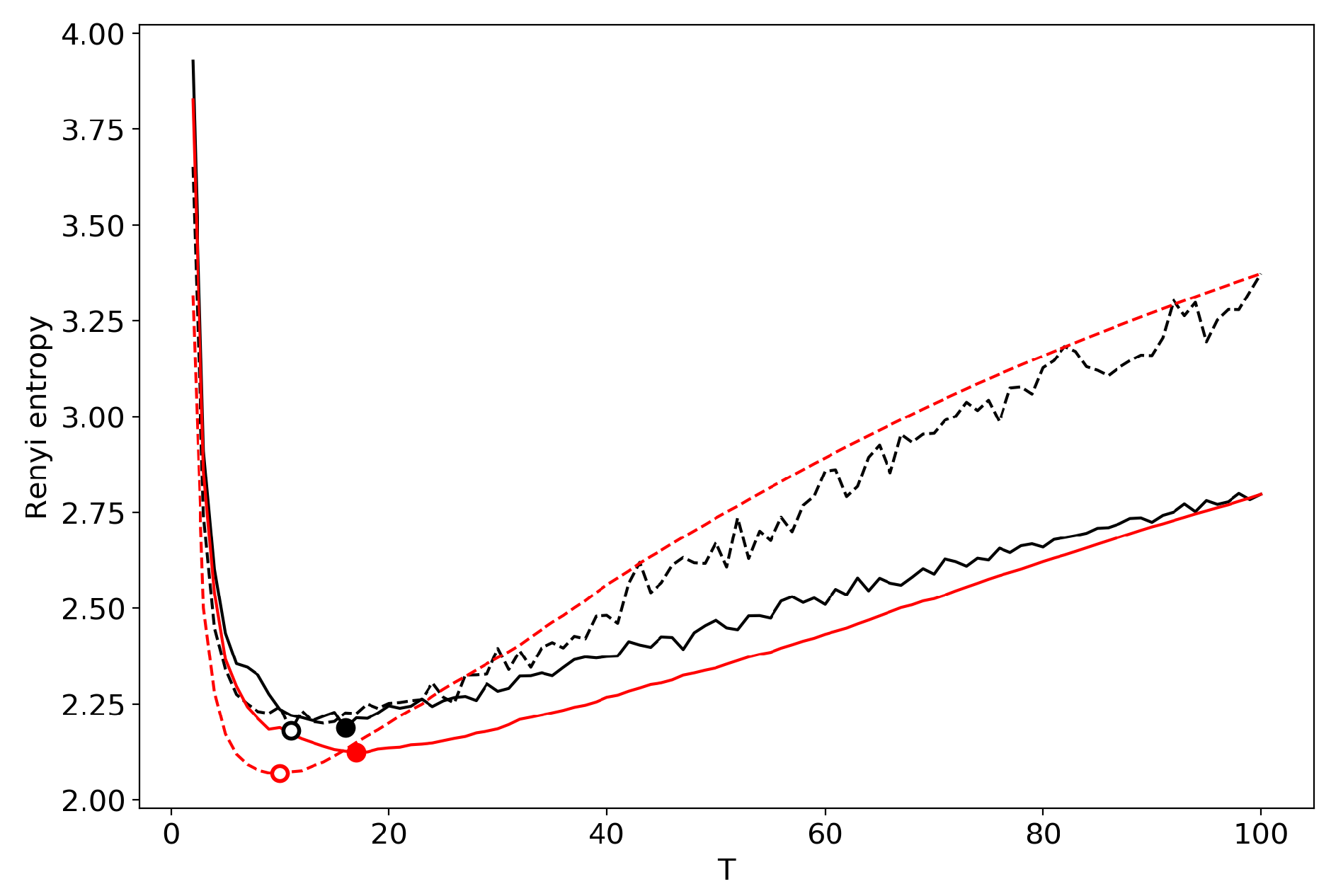
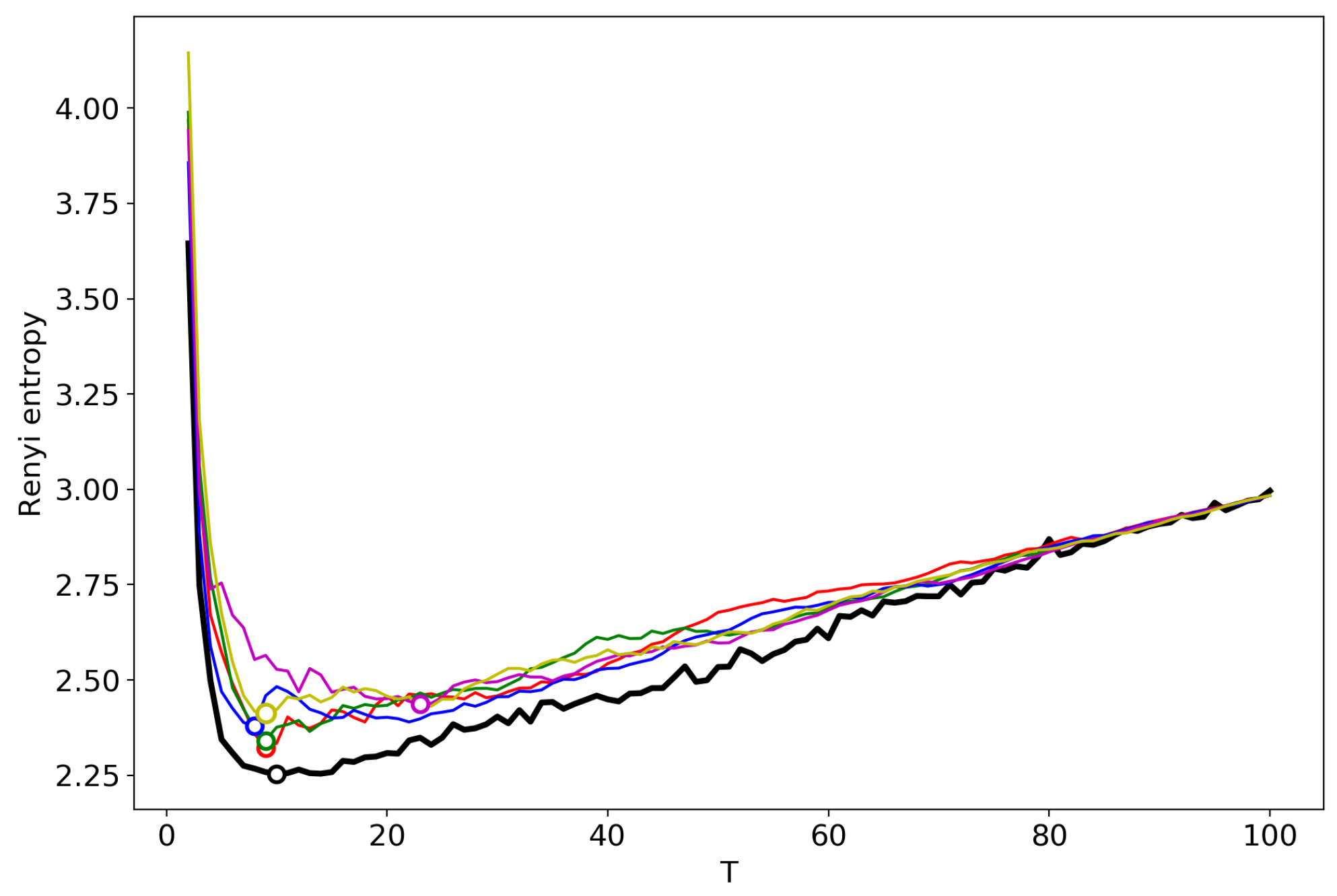
3.9. A Concept of Selecting the Number of Topics for an Unlabeled Dataset
3.10. Computational Speed
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| E–M | Expectation–Maximization |
| GLDA | Granulated Latent Dirichlet Allocation |
| KL | Kullback–Leibler |
| LDA | Latent Dirichlet Allocation |
| pLSA | probabilistic Latent Semantic Analysis |
| TM | Topic Modeling |
| VLDA | Latent Dirichlet Allocation model with variational E–M algorithm |
Appendix A. Description of the Topic Models Used in the Numerical Experiments
Appendix A.1. Probabilistic Latent Semantic Analysis Model
- E-step. Using Bayes’ rule, conditional probabilities are calculated for all and each , [25]:
- M-step. New approximations of , are obtained based on conditional probabilities:
Appendix A.2. Latent Dirichlet Allocation Model with Variational E–M Algorithm
- E-step. Minimizing Kullback–Leibler divergence from p to q by performing the following updates until convergence:where is the digamma function;
- M-step. Using q, re-estimate :where is the number of words in document d, denotes corresponding for document d, is the indicator function that takes value 1 if the condition is true, and 0 otherwise.
Appendix A.3. Latent Dirichlet Allocation Model with Granulated Gibbs Sampling
- Sample a word instance uniformly at random.
- Sample its topic assignment (analogously to [30]) according towhere is the number of words from document d assigned to topic j excluding the current word , is the number of instances of word assigned to topic j excluding the current instance n. Let us denote the obtained value of as z.
- Set for all words such that , where l is a predefined window size.
References
- Roberts, M.; Stewart, B.; Tingley, D. Navigating the local modes of big data: The case of topic models. In Computational Social Science: Discovery and Prediction; Cambridge University Press: New York, NY, USA, 2016. [Google Scholar]
- Newman, D.J.; Block, S. Probabilistic Topic Decomposition of an Eighteenth-Century American Newspaper. J. Am. Soc. Inf. Sci. Technol. 2006, 57, 753–767. [Google Scholar] [CrossRef]
- Boyd-Graber, J.; Hu, Y.; Mimno, D. Applications of Topic Models. Found. Trends Inf. Retr. 2017, 11, 143–296. [Google Scholar] [CrossRef]
- Jockers, M.L. Macroanalysis: Digital Methods and Literary History; University of Illinois Press: Champaign, IL, USA, 2013. [Google Scholar]
- Chernyavsky, I.; Alexandrov, T.; Maass, P.; Nikolenko, S.I. A Two-Step Soft Segmentation Procedure for MALDI Imaging Mass Spectrometry Data. In German Conference on Bioinformatics 2012; OpenAccess Series in Informatics (OASIcs); Böcker, S., Hufsky, F., Scheubert, K., Schleicher, J., Schuster, S., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2012; Volume 26, pp. 39–48. [Google Scholar] [CrossRef]
- Tu, N.A.; Dinh, D.L.; Rasel, M.K.; Lee, Y.K. Topic Modeling and Improvement of Image Representation for Large-Scale Image Retrieval. Inf. Sci. 2016, 366, 99–120. [Google Scholar] [CrossRef]
- Cao, J.; Xia, T.; Li, J.; Zhang, Y.; Tang, S. A Density-Based Method for Adaptive LDA Model Selection. Neurocomputing 2009, 72, 1775–1781. [Google Scholar] [CrossRef]
- Arun, R.; Suresh, V.; Veni Madhavan, C.E.; Narasimha Murthy, M.N. On Finding the Natural Number of Topics with Latent Dirichlet Allocation: Some Observations. In Advances in Knowledge Discovery and Data Mining; Zaki, M.J., Yu, J.X., Ravindran, B., Pudi, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 391–402. [Google Scholar]
- Wallach, H.M.; Mimno, D.; McCallum, A. Rethinking LDA: Why Priors Matter. In Proceedings of the 22Nd International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2009; pp. 1973–1981. [Google Scholar]
- Manning, C.D.; Schütze, H. Foundations of Statistical Natural Language Processing; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Mimno, D.; Wallach, H.M.; Talley, E.; Leenders, M.; McCallum, A. Optimizing Semantic Coherence in Topic Models. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, EMNLP ’11, Edinburgh, UK, 27–31 July 2011; Association for Computational Linguistics: Stroudsburg, PA, USA, 2011; pp. 262–272. [Google Scholar]
- Koltcov, S.; Ignatenko, V.; Koltsova, O. Estimating Topic Modeling Performance with Sharma–Mittal Entropy. Entropy 2019, 21, 660. [Google Scholar] [CrossRef]
- Koltcov, S. Application of Rényi and Tsallis entropies to topic modeling optimization. Phys. A Stat. Mech. Its Appl. 2018, 512, 1192–1204. [Google Scholar] [CrossRef]
- Koltcov, S.N. A thermodynamic approach to selecting a number of clusters based on topic modeling. Tech. Phys. Lett. 2017, 43, 584–586. [Google Scholar] [CrossRef]
- Koltcov, S.; Ignatenko, V.; Boukhers, Z.; Staab, S. Analyzing the Influence of Hyper-parameters and Regularizers of Topic Modeling in Terms of Renyi Entropy. Entropy 2020, 22, 394. [Google Scholar] [CrossRef]
- Ignatenko, V.; Koltcov, S.; Staab, S.; Boukhers, Z. Fractal approach for determining the optimal number of topics in the field of topic modeling. J. Phys. Conf. Ser. 2019, 1163, 012025. [Google Scholar] [CrossRef]
- Koltcov, S.; Ignatenko, V.; Pashakhin, S. Fast tuning of topic models: an application of Rényi entropy and renormalization theory. In Proceedings of the 5th International Electronic Conference on Entropy and Its Applications, Online, 18–30 November 2019. [Google Scholar] [CrossRef]
- Koltsov, S.; Ignatenko, V. Renormalization approach to the task of determining the number of topics in topic modeling. unpublished.
- Kadanoff, L.P. Statistical Physics: Statics, Dynamics and Renormalization; World Scientific: Singapore, 2000. [Google Scholar]
- Wilson, K.G. The renormalization group and critical phenomena. Rev. Mod. Phys. 1983, 55, 583–600. [Google Scholar] [CrossRef]
- Olemskoi, A. SYnergetics of Complex Systems: Phenomenology and Statistical Theory; Krasand: Moscow, Russia, 2009. [Google Scholar]
- Carpinteri, A.C.B. Multifractal nature of concrete fracture surfaces and size effects on nominal fracture energy. Mater. Struct. 1995, 28, 435–443. [Google Scholar] [CrossRef]
- Essam, J.W. Potts models, percolation, and duality. J. Math. Phys. 1979, 20, 1769–1773. [Google Scholar] [CrossRef]
- Hofmann, T. Probabilistic Latent Semantic Indexing. In Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR ’99, Berkeley, CA, USA, 15–19 August 1999; ACM: New York, NY, USA, 1999; pp. 50–57. [Google Scholar] [CrossRef]
- Hofmann, T. Unsupervised Learning by Probabilistic Latent Semantic Analysis. Mach. Learn. 2001, 42, 177–196. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Koltcov, S.; Nikolenko, S.I.; Koltsova, O.; Bodrunova, S. Stable Topic Modeling for Web Science: Granulated LDA. In Proceedings of the 8th ACM Conference on Web Science, WebSci ’16, Hannover, Germany, 22–25 May 2016; pp. 342–343. [Google Scholar] [CrossRef]
- Pitman, J. Sequential constructions of random partitions. In Combinatorial Stochastic Processes: Ecole d’Eté de Probabilités de Saint-Flour XXXII – 2002; Picard, J., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 55–75. [Google Scholar] [CrossRef]
- Griffiths, T.L.; Ghahramani, Z. The Indian Buffet Process: An Introduction and Review. J. Mach. Learn. Res. 2011, 12, 1185–1224. [Google Scholar]
- Griffiths, T.L.; Steyvers, M. Finding scientific topics. Proc. Natl. Acad. Sci. USA 2004, 101, 5228–5235. [Google Scholar] [CrossRef]
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Hierarchical Dirichlet Processes. J. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Sharing Clusters among Related Groups: Hierarchical Dirichlet Processes. In Proceedings of the 17th International Conference on Neural Information Processing Systems, NIPS’04, Vancouver, BC, Canada, 13–18 December 2004; MIT Press: Cambridge, MA, USA, 2004; pp. 1385–1392. [Google Scholar]
- Blei, D.; Griffiths, T.; Jordan, M.; Tenenbaum, J. Hierarchical topic models and the nested Chinese restaurant process. In Proceedings of the 17th Annual Conference on Neural Information Processing Systems, NIPS 2003, Vancouver, BC, Canada, 8–13 December 2013. [Google Scholar]
- Chen, X.; Zhou, M.; Carin, L. The Contextual Focused Topic Model. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’12, Beijing, China, 12–16 August 2012; Association for Computing Machinery: New York, NY, USA, 2012; pp. 96–104. [Google Scholar] [CrossRef]
- Williamson, S.; Wang, C.; Heller, K.A.; Blei, D.M. The IBP Compound Dirichlet Process and Its Application to Focused Topic Modeling. In Proceedings of the 27th International Conference on International Conference on Machine Learning, ICML’10, Haifa, Israel, 21–24 July 2010; Omnipress: Madison, WI, USA, 2010; pp. 1151–1158. [Google Scholar]
- Hjort, N.L.; Holmes, C.; Müller, P.; Walker, S.G. (Eds.) Bayesian Nonparametrics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Rasmussen, C.; Williams, C. Gaussian Processes for Machine Learning; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2006; p. 248. [Google Scholar]
- Gershman, S.J.; Blei, D.M. A tutorial on Bayesian nonparametric models. J. Math. Psychol. 2012, 56, 1–12. [Google Scholar] [CrossRef]
- Tkačik, G.; Mora, T.; Marre, O.; Amodei, D.; Palmer, S.E.; Berry, M.J.; Bialek, W. Thermodynamics and signatures of criticality in a network of neurons. Proc. Natl. Acad. Sci. USA 2015, 112, 11508–11513. [Google Scholar] [CrossRef]
- Beck, C. Generalised information and entropy measures in physics. Contemp. Phys. 2009, 50, 495–510. [Google Scholar] [CrossRef]
- Jizba, P.; Arimitsu, T. The world according to Rényi: thermodynamics of multifractal systems. Ann. Phys. 2004, 312, 17–59. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
- Casini, H.; Medina, R.; Landea, I.S.; Torroba, G. Renyi relative entropies and renormalization group flows. J. High Energy Phys. 2018, 2018, 1–27. [Google Scholar] [CrossRef]
- McComb, W.D. Renormalization Methods: A Guide For Beginners; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Steyvers, M.; Griffiths, T. Probabilistic Topic Models. In Handbook of Latent Semantic Analysis; Landauer, T., Mcnamara, D., Dennis, S., Kintsch, W., Eds.; Lawrence Erlbaum Associates: New York, NY, USA, 2007. [Google Scholar]
- Basu, S.; Davidson, I.; Wagstaff, K. (Eds.) Chapman & Hall/CRC Data Mining and Knowledge Discovery Series, 1st ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2008. [Google Scholar]
- Koltsov, S.; Nikolenko, S.; Koltsova, O.; Filippov, V.; Bodrunova, S. Stable Topic Modeling with Local Density Regularization. In Internet Science: Third International Conference; Springer International Publishing: Cham, Switzerland, 2016; Volume 9934, pp. 176–188. [Google Scholar] [CrossRef]
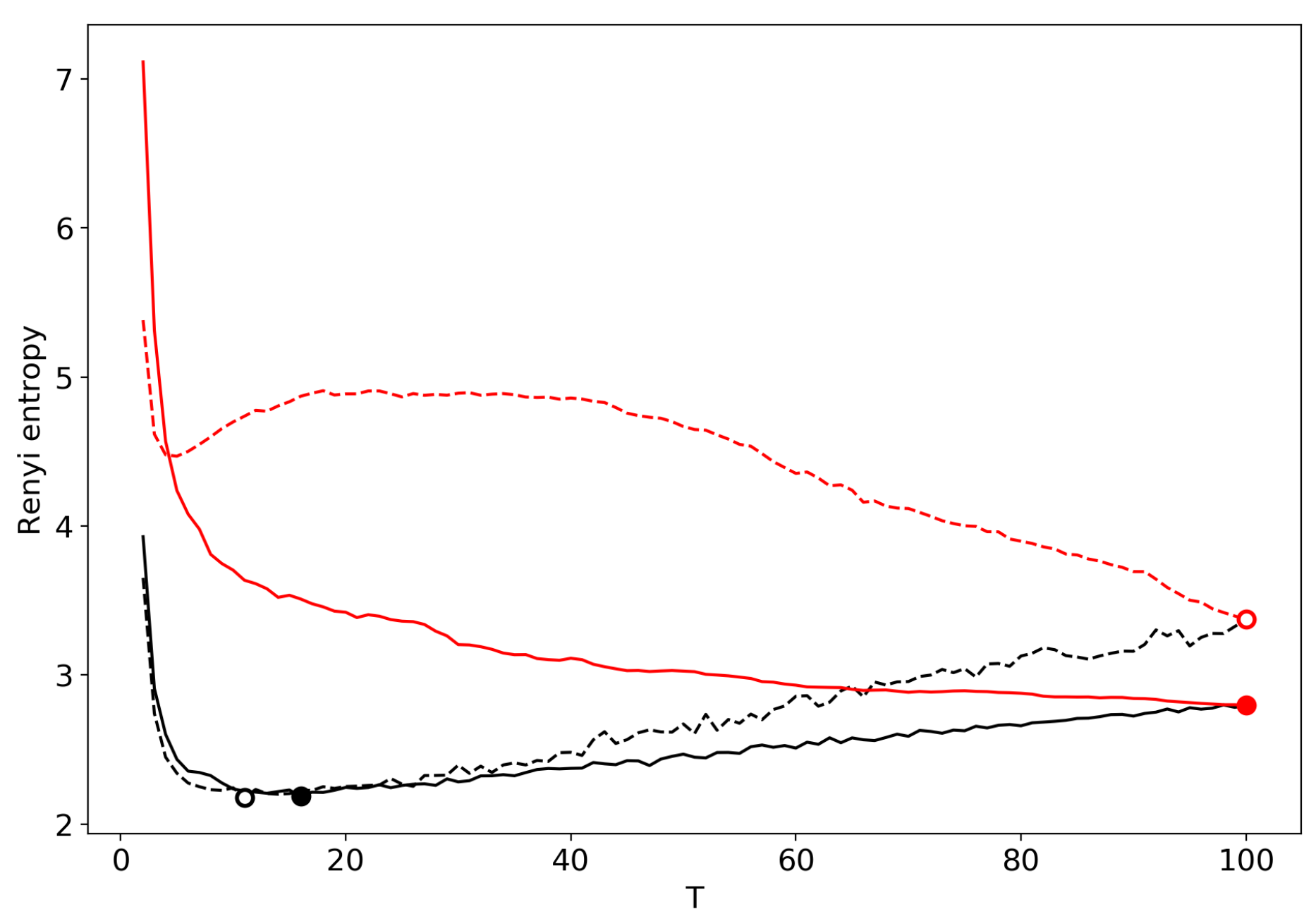
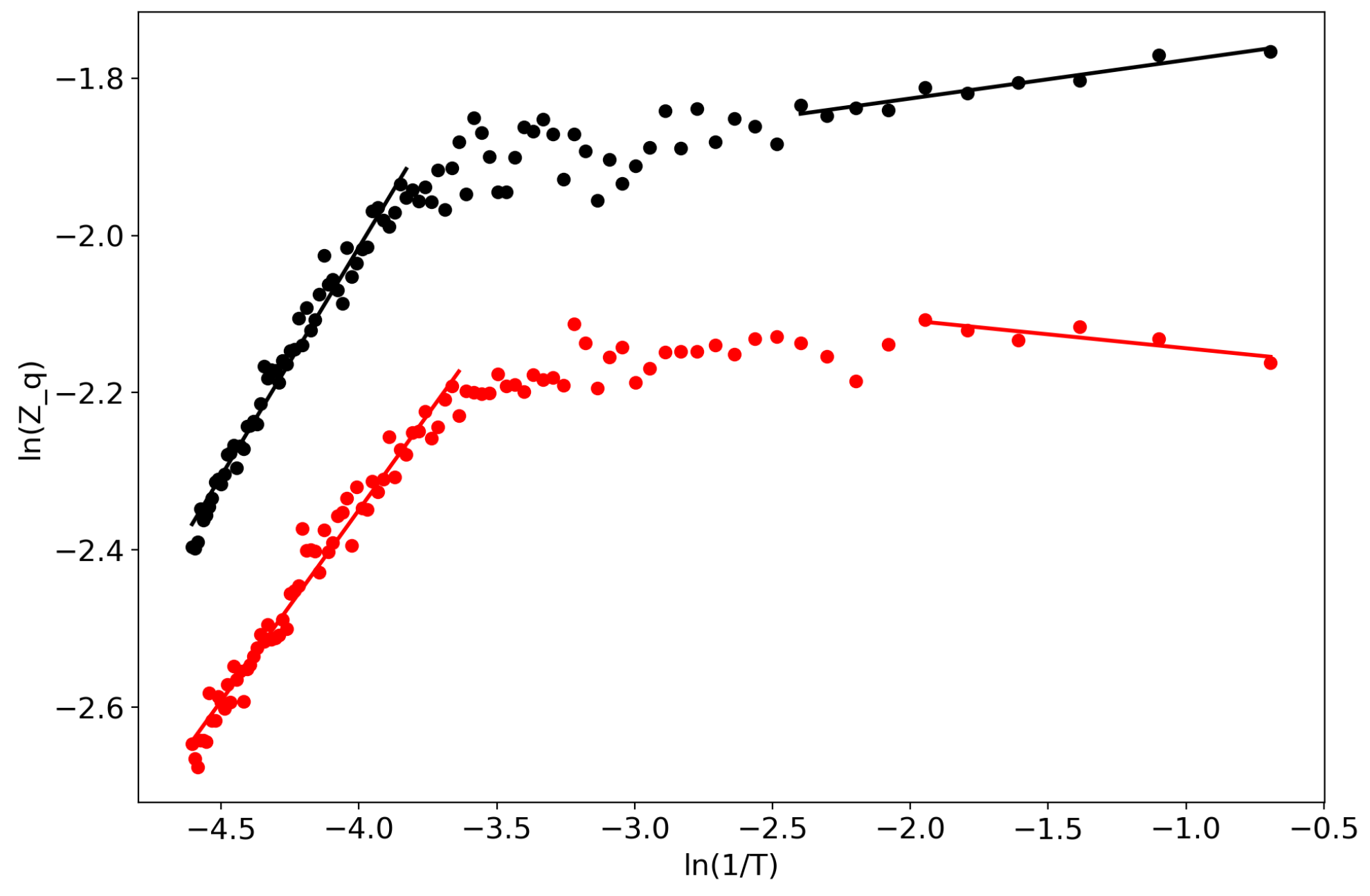
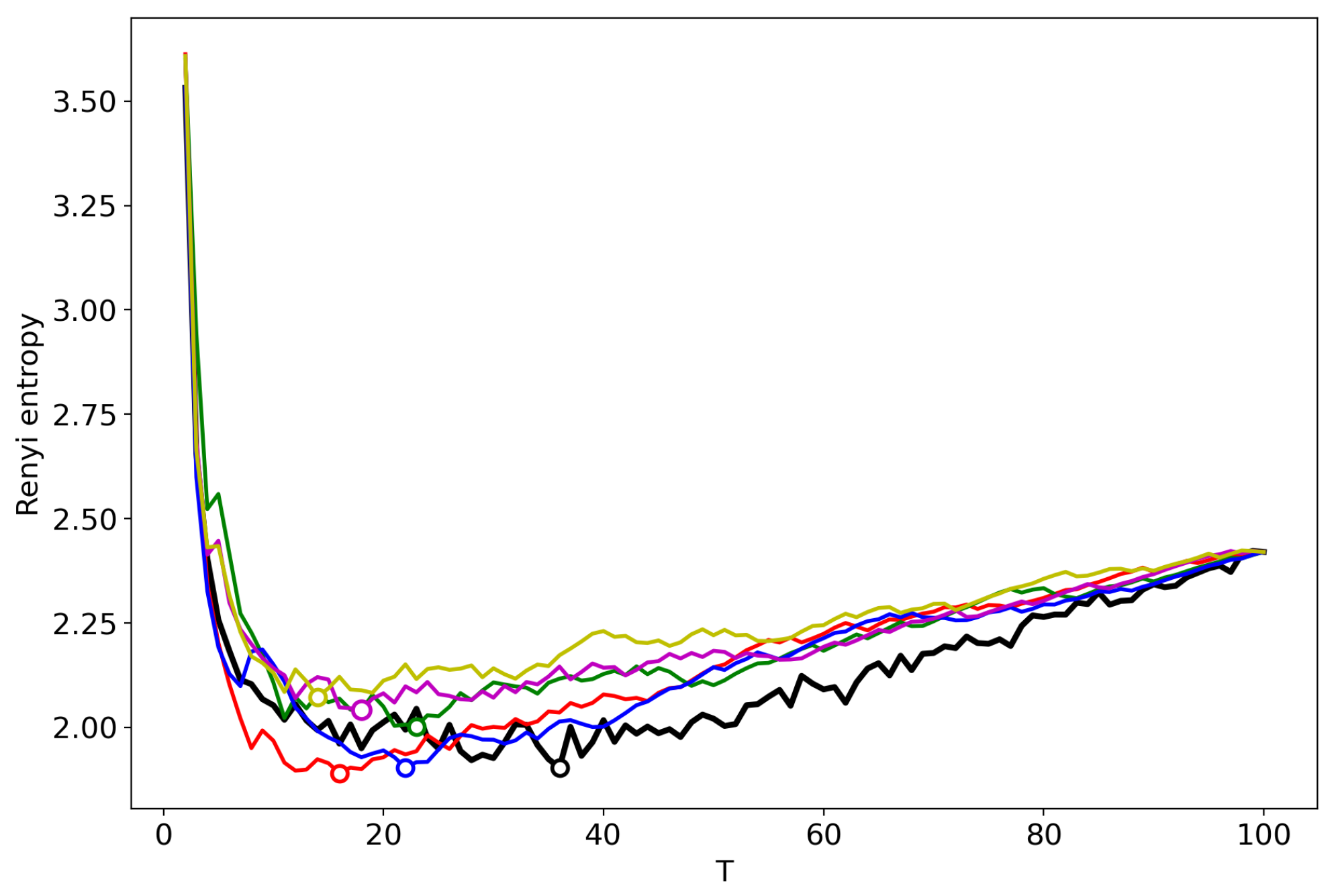
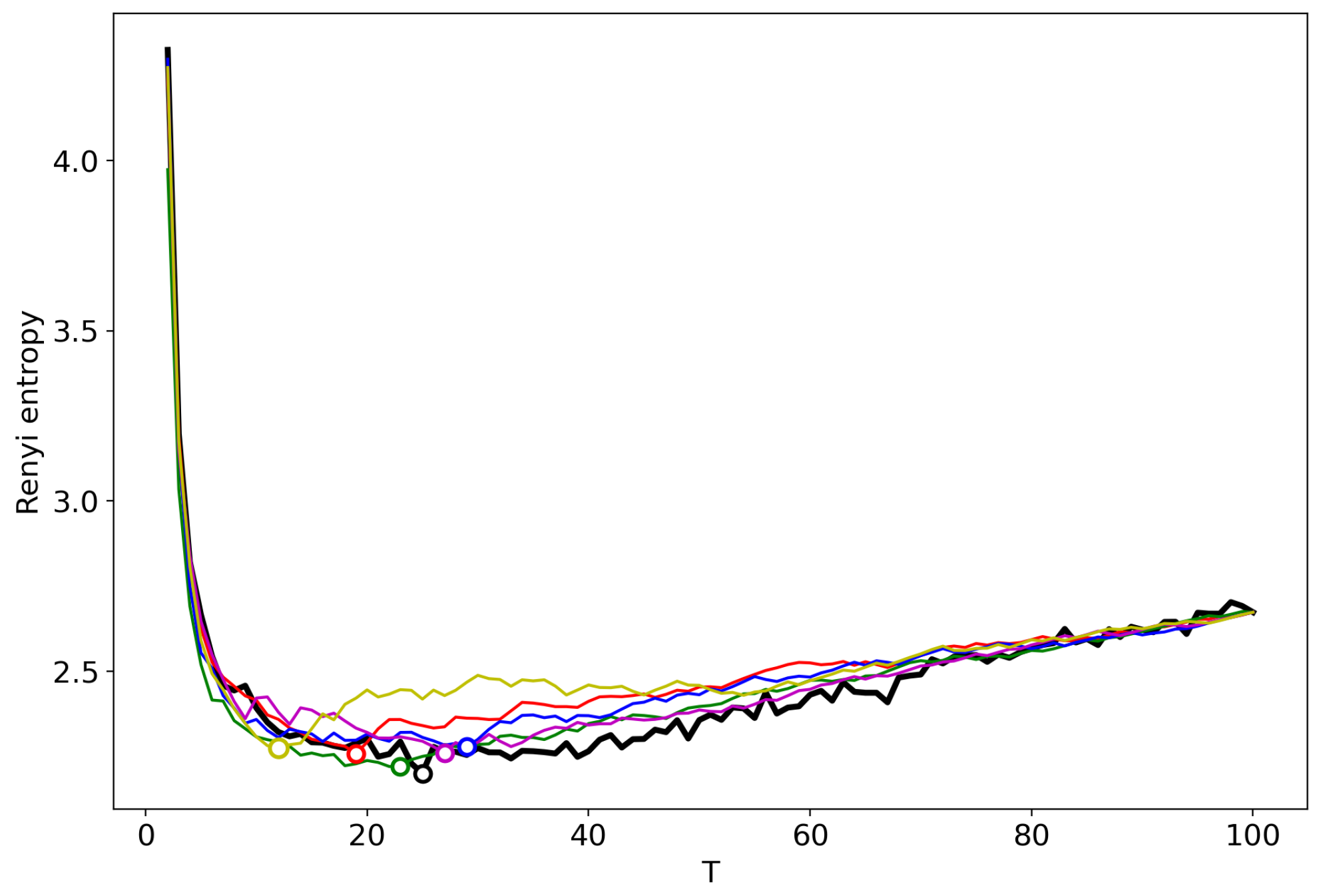
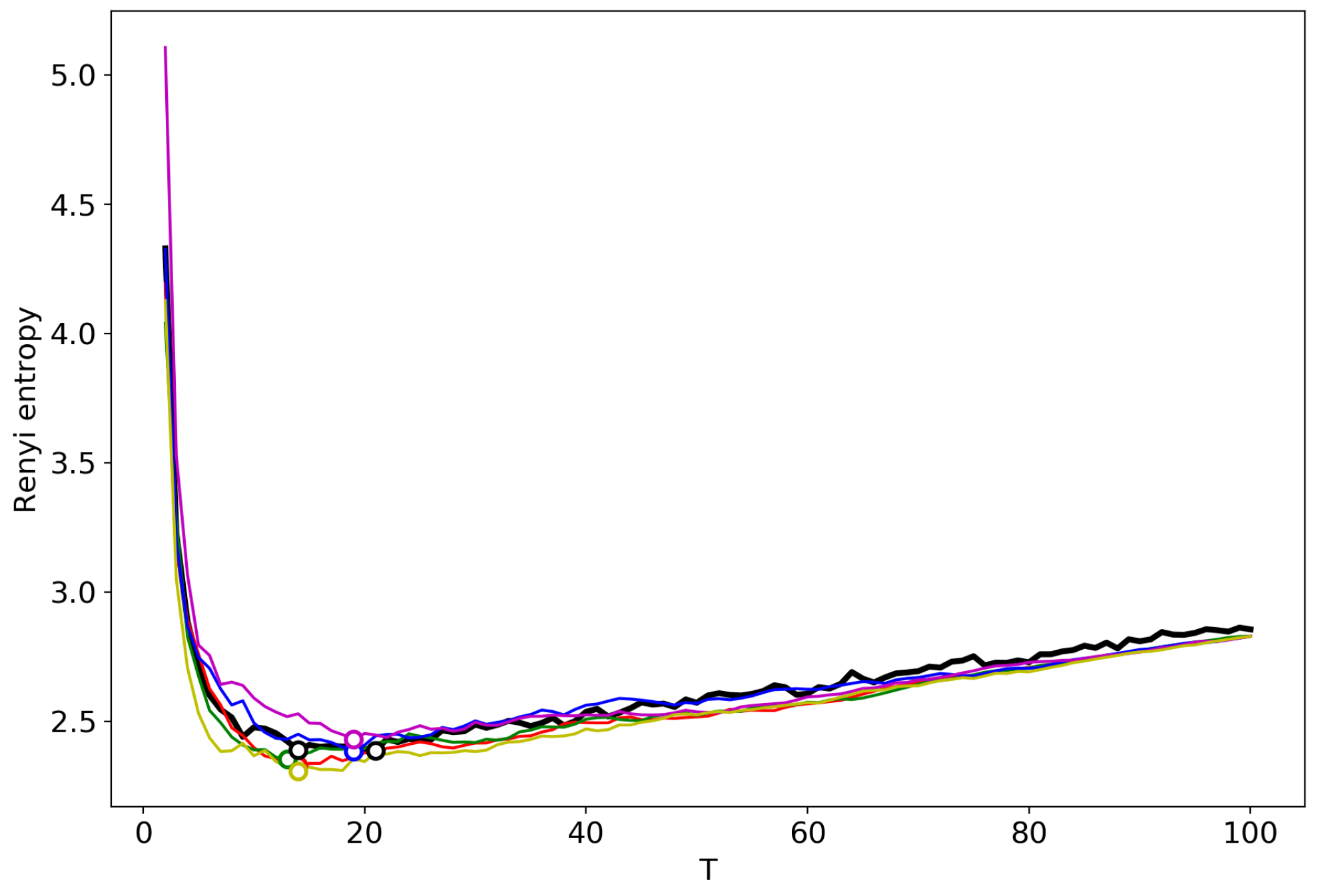
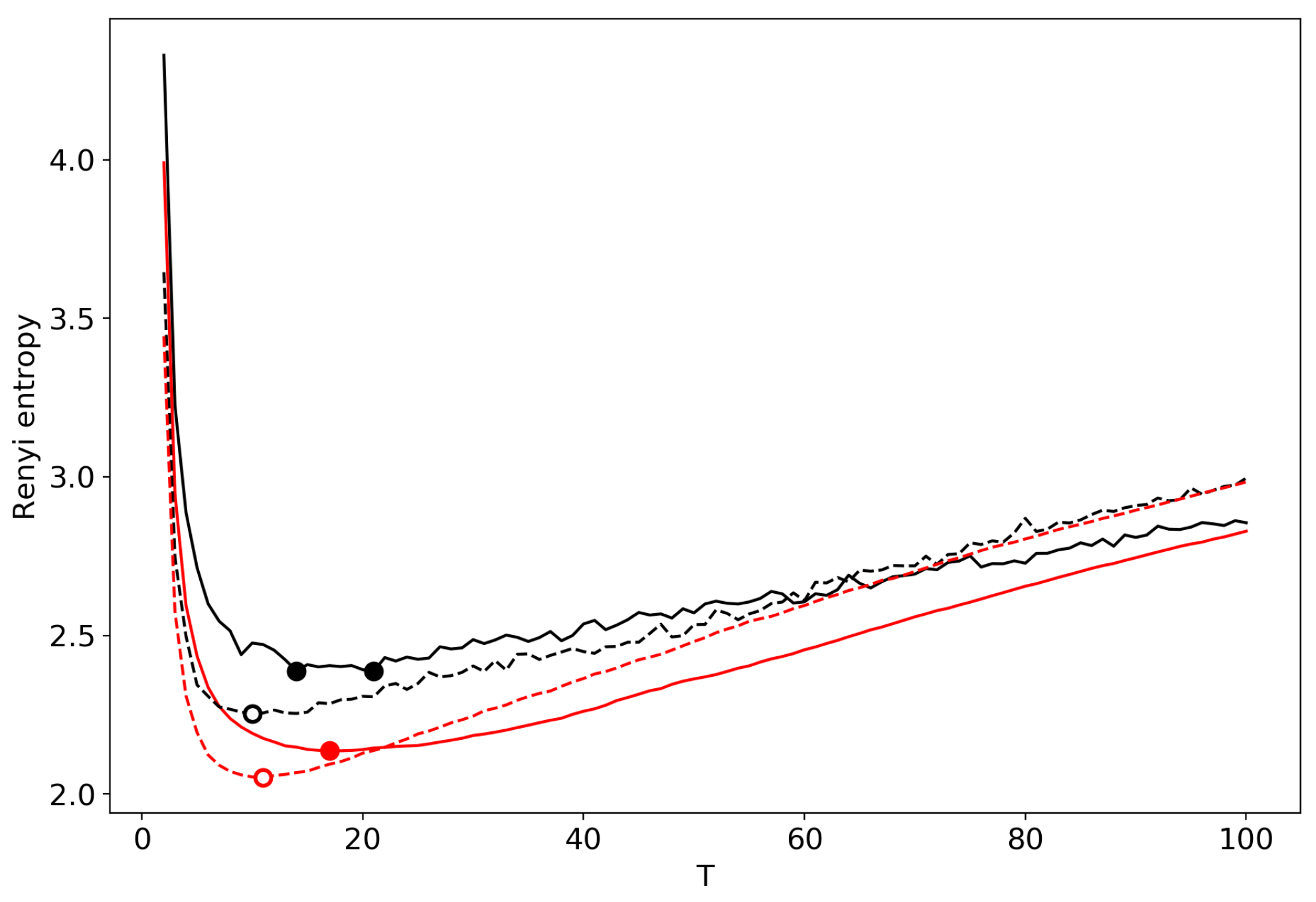
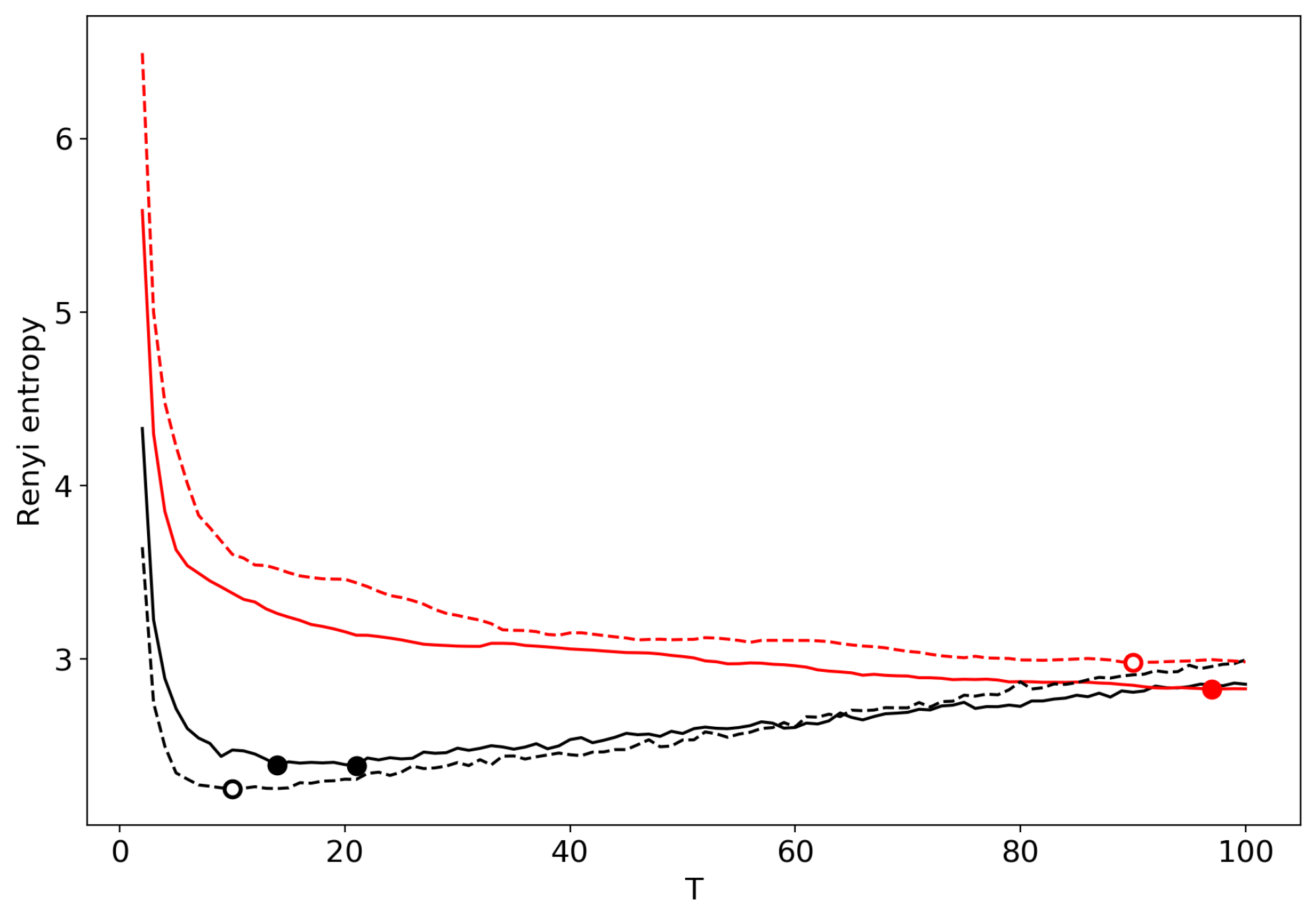
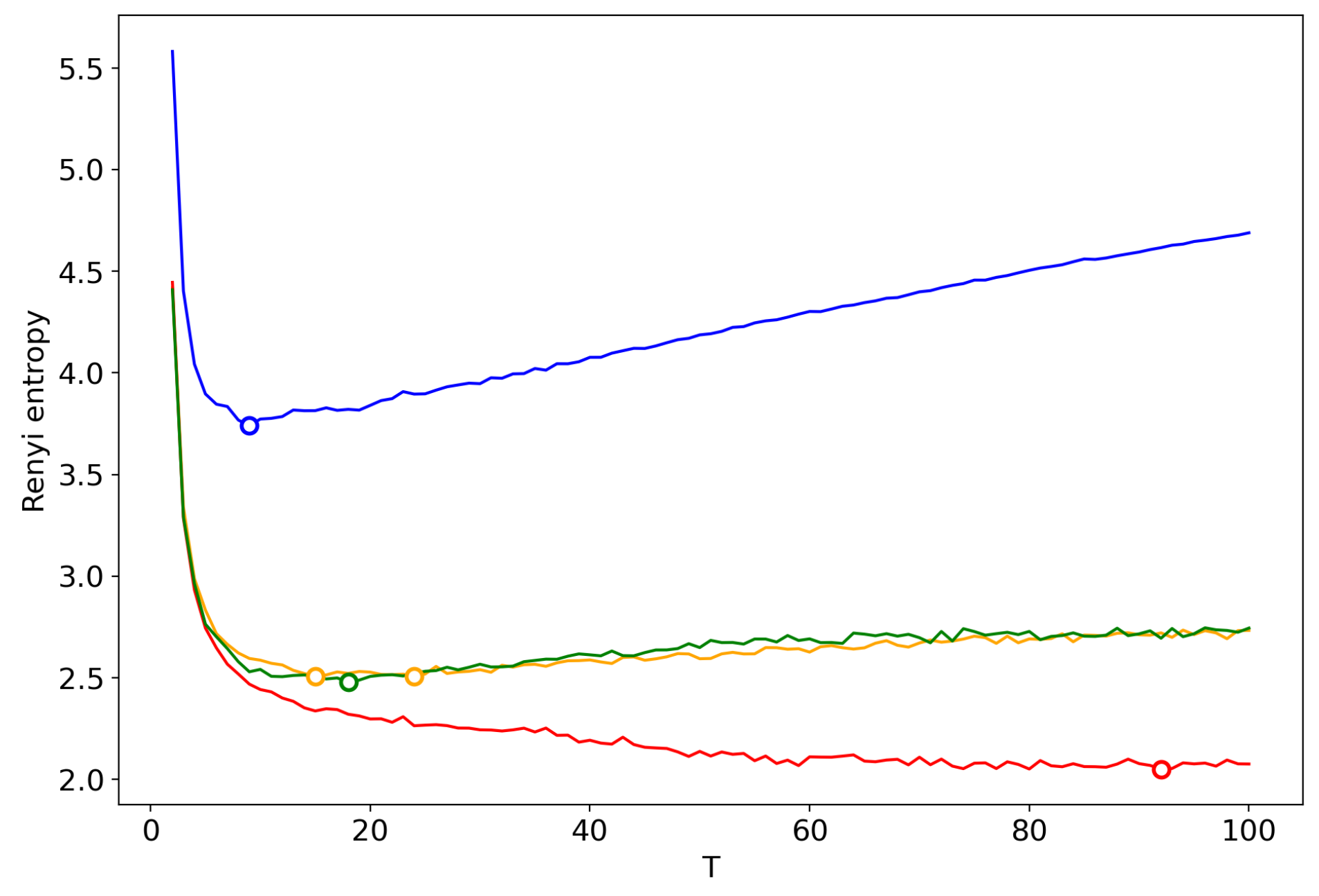
| Dataset | T Search Method | Algorithm | ||
|---|---|---|---|---|
| VLDA | GLDA | pLSA | ||
| Lenta (10 topics) | Successive TM simulations | 11 | 36 | 10 |
| Renormalization (random) | 11 | 18 | 8 | |
| Renormalization (min. Renyi entropy) | 10 | 14 | 11 | |
| Renormalization (min. KL divergence) | 100 | 71 | 90 | |
| 20 Newsgoups (14–20 topics) | Successive TM simulations | 16 | 25 | 14 |
| Renormalization (random) | 15 | 25 | 18 | |
| Renormalization (min. Renyi entropy) | 17 | 22 | 17 | |
| Renormalization (min. KL divergence) | 100 | 100 | 97 | |
| French dataset | Successive TM simulations | 9 | 92 | 15; 24 |
| Renormalization (random) | 93 | 40 | 25 | |
| Renormalization (min. Renyi entropy) | 16 | 18 | 15 | |
| Renormalization (min. KL divergence) | 100 | 100 | 99 | |
| Algorithm | Datase | Successive TM Simulations | Solution on 100 Topics | Renorm. (random) | Renorm. (min. Renyi Entropy) | Renorm. (min. KL Divergence) |
|---|---|---|---|---|---|---|
| pLSA | Lenta | 360 min | 9.2 min | 0.947 min | 0.942 min | 2.31 min |
| pLSA | 20 Newsgroups | 1296 min | 24.3 min | 0.927 min | 0.926 min | 2.347 min |
| pLSA | French dataset | 1109 min | 31 min | 2.5 min | 2.47 min | 6.01 min |
| GLDA | Lenta | 81 min | 0.9 min | 0.042 min | 0.08 min | 3.39 min |
| GLDA | 20 Newsgroups | 281 min | 3.78 min | 0.123 min | 0.197 min | 11.153 min |
| GLDA | French dataset | 2310 min | 8.5 min | 0.1 min | 0.171 min | 9.906 min |
| VLDA | Lenta | 780 min | 25 min | 0.969 min | 1.114 min | 3.951 min |
| VLDA | 20 Newsgroups | 1320 min | 40 min | 2.933 min | 3.035 min | 10.69 min |
| VLDA | French dataset | 2940 min | 73 min | 2.949 min | 3.129 min | 10.71 min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koltcov, S.; Ignatenko, V. Renormalization Analysis of Topic Models. Entropy 2020, 22, 556. https://doi.org/10.3390/e22050556
Koltcov S, Ignatenko V. Renormalization Analysis of Topic Models. Entropy. 2020; 22(5):556. https://doi.org/10.3390/e22050556
Chicago/Turabian StyleKoltcov, Sergei, and Vera Ignatenko. 2020. "Renormalization Analysis of Topic Models" Entropy 22, no. 5: 556. https://doi.org/10.3390/e22050556
APA StyleKoltcov, S., & Ignatenko, V. (2020). Renormalization Analysis of Topic Models. Entropy, 22(5), 556. https://doi.org/10.3390/e22050556





