1. Introduction
The basis of equilibrium thermodynamics relies on the existence of the equilibrium state. The equilibrium state can be characterized by a set of appropriate parameters and some kind of energy-based function of these parameters and internal constraints. The constraints allow comparing this function in the state of equilibrium with states of constrained equilibrium [
1]. For a monoatomic system, the internal energy
is a function of three parameters of state, namely entropy
volume
and the number of particles
which fully characterize all thermodynamics changes that can occur in the system. For an unconstrained isolated system,
is maximized at constant
with respect to all states obtained by internal constraints.
A prerequisite for any system to become non-equilibrium is a continuous energy flow. This macroscopic flow of energy leads to an increase of the system energy up to the point when the energy flow into the system matches exactly the flow out of the system. At this point, the non-equilibrium steady state is reached. Two parameters characterize the NESS: the flow and the internal energy U. We show that , where is the energy at equilibrium. We make three case studies: (i) a system internally heated between two parallel walls of the same temperature; (ii) a heat flow between two parallel plates of different temperature; and (iii) a Poisseulle flow between two parallel plates.
Non-equilibrium states are ubiquitous in nature and truly equilibrium states are exceptions. However, despite many decades of study, we have not reached the same status of understanding of non-equilibrium states as we have for equilibrium ones. There is no systematic approach for dealing with NESS. Attempts to create such approaches include: minimum/maximum entropy production principle [
2], steady state thermodynamics [
3], and driven lattice gas systems [
4]. The heat flowing into the system is recognized as a source of entropy increase in [
5,
6,
7]. In information theoretical techniques and extended thermodynamics, the heat flow appears as a natural thermodynamic variable in non-equilibrium steady states. The entropy of some ideal systems such as ideal gases, photons, phonons, and ideal harmonic chains, among others, in the presence of a heat flow is studied in [
8,
9,
10,
11,
12]. However, the energy that has to be stored in NESS has not been recognized as potentially a function of state, from which in principle we could derive all properties of NESS [
13].
In this paper, we attempt to address the latter issues. In a recent paper, a quantity
is shown to be minimized in steady states for three different systems [
13]. This quantity has the dimension of time. In [
13],
is shown to coincide with the characteristic time scale of the system energy dissipation immediately after the shutdown of external energy flow. The minimization is demonstrated through introducing a constraint into the system and showing that
for the unconstrained system is always less than in the constrained system. In this paper, we analyze energy storage and
in Systems (i)–(iii) defined above (these systems are different from the ones in [
13]) and we arrive at the same conclusions as in [
13]. Moreover, we introduce the embedded energy, which is an analog of the Helmholtz free energy for NESS, and provide its interpretation.
We point out that, in this paper, we extensively use the temperature profile to obtain the stored energy
. The local temperature is defined from the ideal gas law. It would be interesting, however, to consider using effective temperature in non-equilibrium systems and to study their role in energy storage [
14,
15].
2. Models and Results
We consider an ideal gas driven out-of-equilibrium by three different ways of energy delivery that are common in physical realizations. In Case (i) the energy is delivered through a homogeneous energy source, in Case (ii) by an external heat flow, and in Case (iii) by an external matter flow.
In steady states, the local energy does not change in time. Therefore, from local energy conservation, we have
where
is the local energy source at the position
. Here, we assume the Fourier’s law for the local heat flux,
where
k is the heat conductivity and
is the local temperature. We further assume that in the NESS the ideal gas law is fulfilled locally and that the pressure (and hence the energy density) is constant. From these assumptions, we obtain the following relation between the energy density
and the temperature profile,
where
V is the volume of the system and
and
are the energy density and temperature at equilibrium, respectively. In this paper, we denote the corresponding equilibrium value of a variable with a subscript 0. We show the derivation of Equation (
4) in
Appendix A. From
, we define the stored energy as
Without performing work (as is the case for our systems), all out-going energy flow
is in the form of heat, which we denote as
,
where
S is the area through which the heat flows out and
is the unit normal vector. In the steady state, the total energy flow into the system equals the total energy flow out of the system
. In the following, we denote the out-going energy flow in the steady state by
.
By introducing geometrical constraints, the system is partitioned into two subsystems. These constraints do not change the local expressions for
and
. In addition, for each subsystem, definitions of the stored energy
and the out-going heat flow
remain the same. On the other hand, the subsystem energy density depends on the constrain in general. However, in all three cases, the number of particles in each subsystem is kept proportional to the volume of the system, i.e.,
. As a result, the expression of
has the same form as Equation (
4) (see
Appendix A). For the constrained system, we define the stored energy as
and the total out-going heat flow as
. For every case studied in this paper, we compare the ratio
for the constrained system,
with the ratio
(see Equation (
1)) for the unconstrained system.
2.1. Energy Source
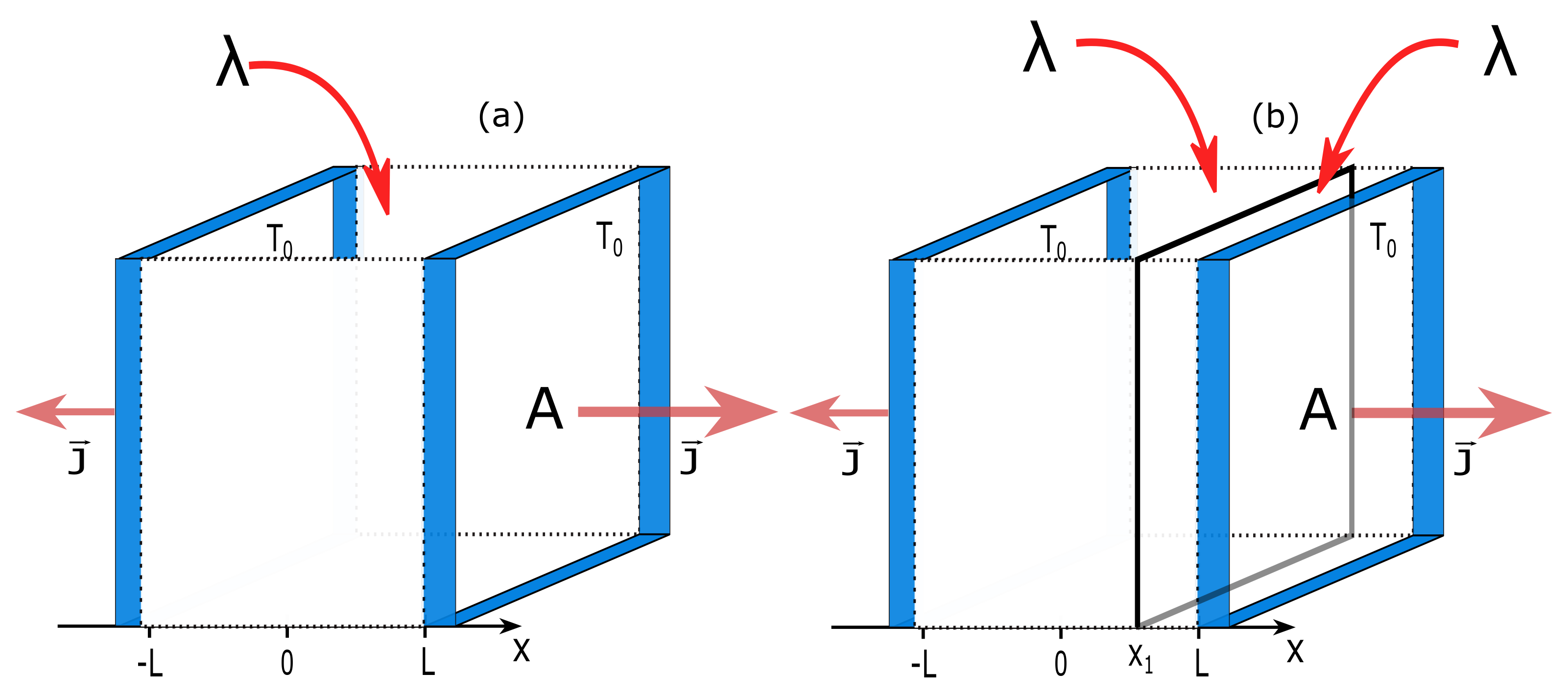
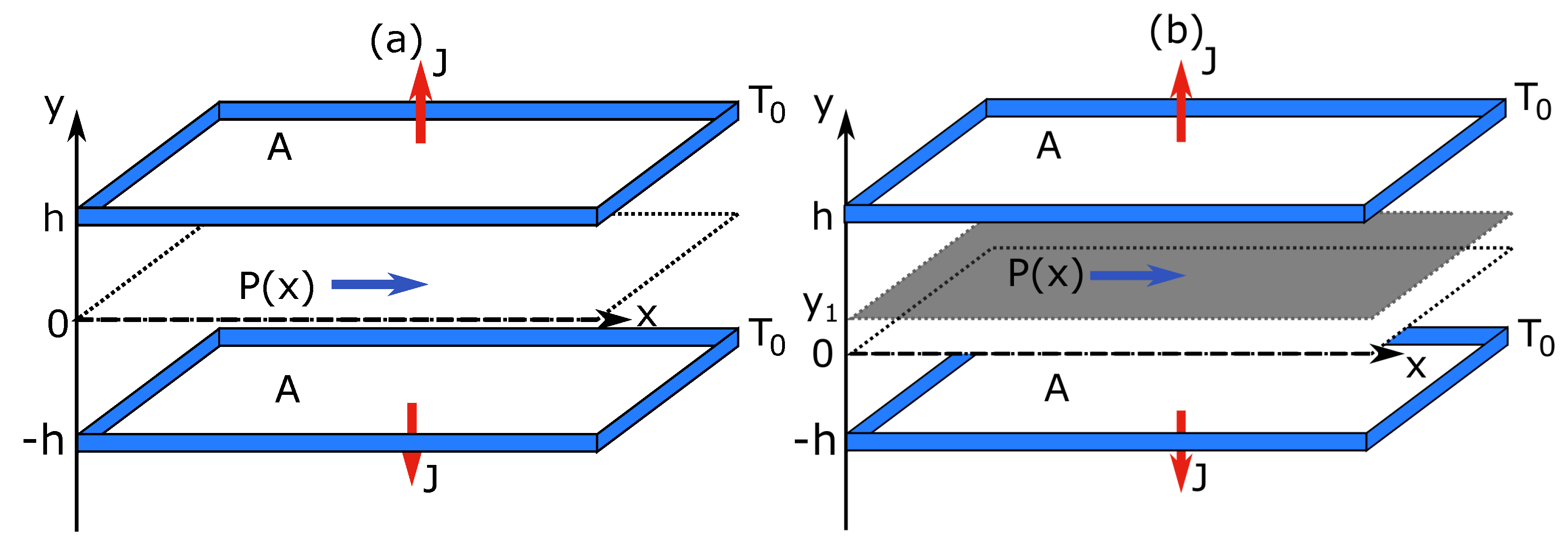
In Case (i), we consider a three-dimensional ideal gas placed between two diathermal walls of area
A (
). The walls are kept at temperature
and are fixed at
. The energy source is distributed homogeneously over the system with
. As internal constraints, we choose a diathermal wall and fix it at
. This wall separates the system into two subsystems 1 and 2 with volumes
and
, respectively. A scheme of the system is shown in
Figure 1.
Consider first the unconstrained system. As the coordinates
y and
z do not influence the temperature profile, it is sufficient to consider
dependence. The temperature profile
is obtained by solving Equation (
2), which now has the form
. Using dimensionless variables
,
and normalizing
x to
, we obtain
Using Equation (
4), we find the energy density to be
As stated above, the out-going heat flow equals the in-coming energy flow,
. Combining with Equation (
10), we find
In the presence of the diathermal wall, the boundary conditions at the constraint are
and
. Solving for the subsystem temperature profile with corresponding boundary conditions, we find that
is not changed by the constraint, i.e.,
, in their respective domains. Therefore, we obtain the energy densities as
As the total energy source does not change, the out-going heat flow is not changed either,
. Together with Equation (
12) and (
13), we have
Now, we compare Equations (
11) and (
14). The relation reduces to
Dividing both sides of Equation (
15) by
gives
where
. For
,
and
. We multiply this by both sides of Equation (
16) and rearrange the terms to obtain
Since
, we have verified for this model
2.2. Heat Flow
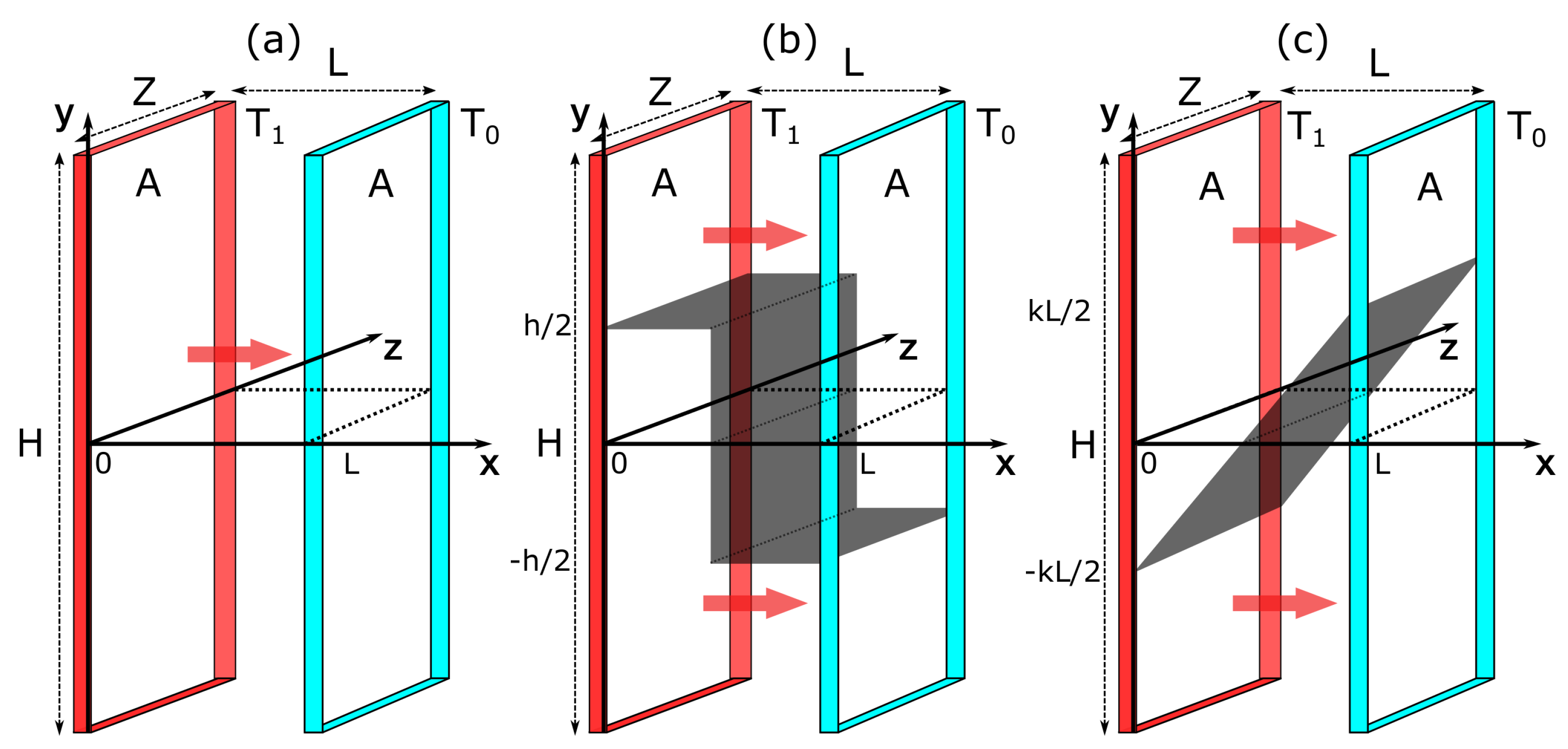
In Case (ii), an ideal gas is in contact with two walls at different temperatures
. The walls are of a large area
(with height
H and width
Z) and are placed at
and
(see
Figure 2). The steady state is driven by a constant heat flow through the system with no bulk energy supply, i.e.,
. For the constraints, we choose an adiabatic wall. We consider two situations. In the first, the wall extends from left to right in a zigzag manner. Its position is given by
where
is the Heaviside function. We refer to this constraint as
vertical (
Figure 2b). In the second, the wall is a straight line with a slope
k, i.e.,
. We refer to this constraint as
linear (
Figure 2c). Both constraints are fixed at
, so that the subsystems are symmetric in shape. Furthermore, they are chosen to ensure a non-zero heat flow in each subsystem. In other words, each subsystem is always in contact with both boundaries.
For the unconstrained case, the temperature profile only depends on
x. Solving Equation (
2) (which is now
) with boundary conditions
and
, we have
The energy density is then
Since we choose
, the heat flow passes through the system from left to right. The unit normal vector of the left (right) boundary is
(
). The local heat flux is
. Hence, the heat flow going through the system can be calculated using either of the following expressions,
which gives,
For the constrained system, the temperature profile depends also on the
y-coordinate. It satisfies the equation
with the following boundary conditions,
At and L, the system is in contact with the plates. This is represented by the Dirichlet boundary conditions. In addition, since the constraint is an adiabatic wall, we have Neumann boundary conditions at . Finally, at the boundaries far away from the constraint, we expect the effect of the constraint to diminish. In other words, at , we assume that the heat fluxes are parallel to the x-axis. To ensure this, we need to set and for .
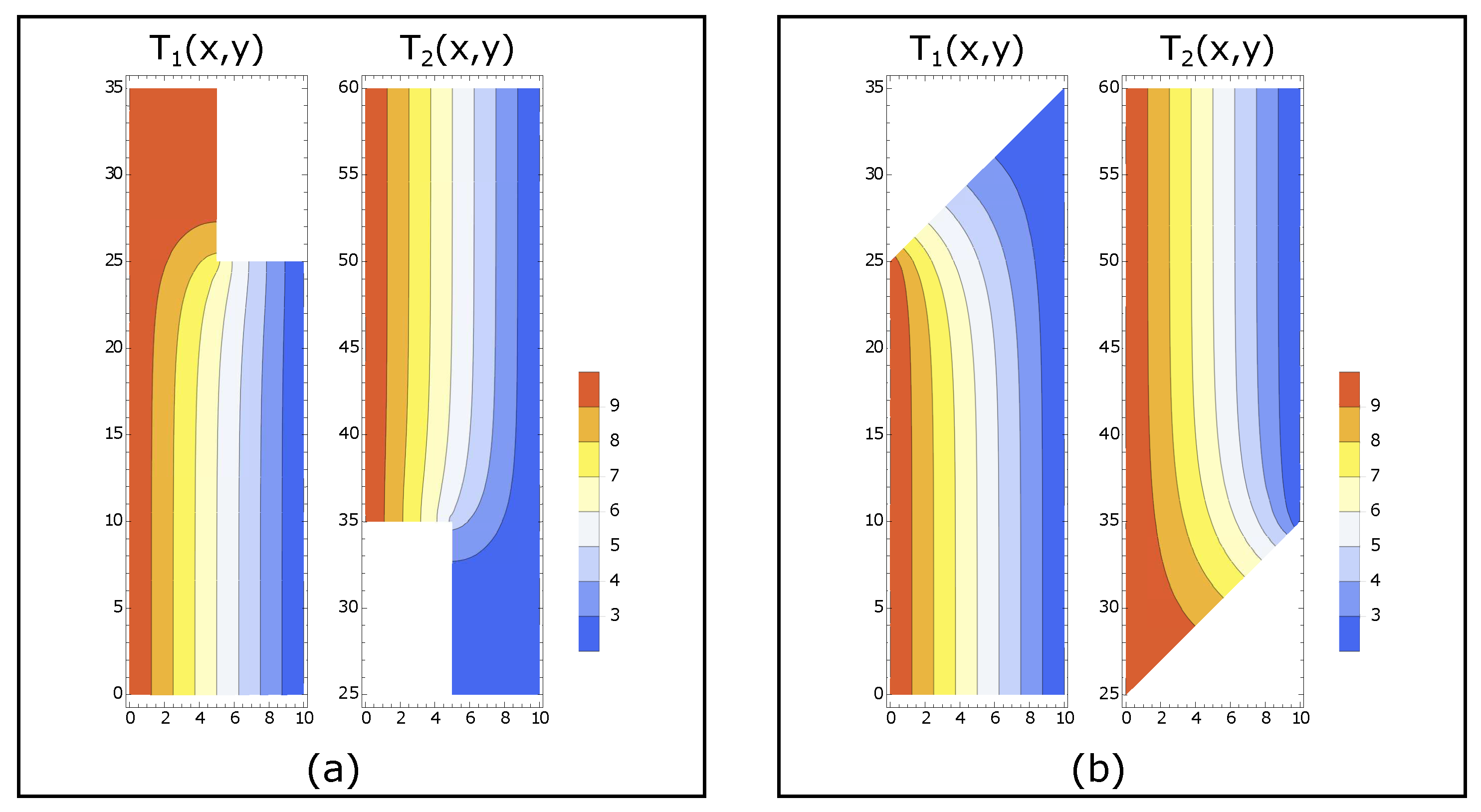
The temperature profiles are obtained numerically using the finite element method. In this method, the system is separated into small domains called
mesh and the function is approximated using polynomials [
16]. Examples of the contour plot of temperature profiles are shown in
Figure 3.
After obtaining temperature profiles, the stored energy density is calculated using Equation (
4). The total heat flow is obtained using either the left or right boundary according to Equation (
21),
where
(
) for the vertical (linear) constraint.
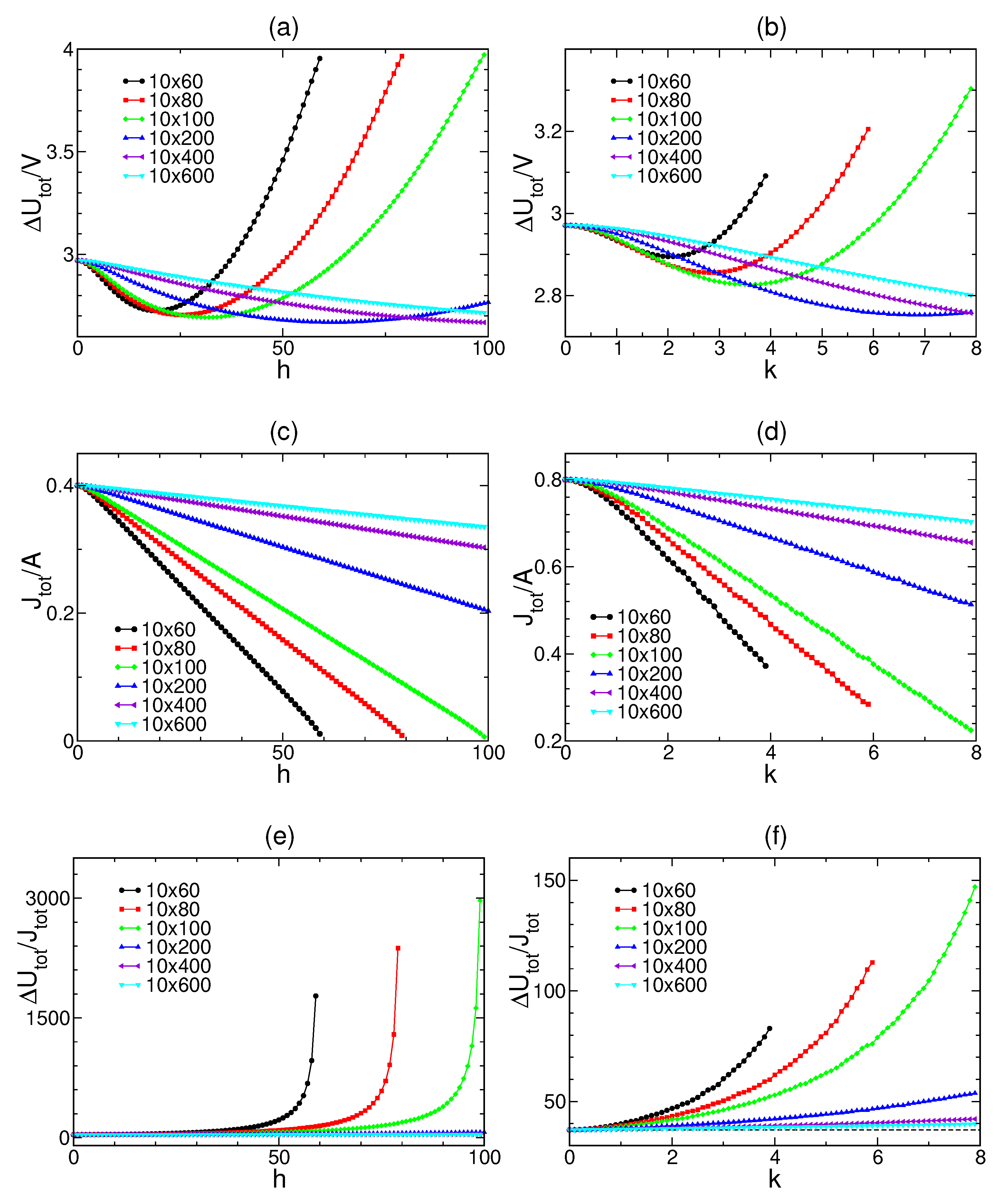
For both constraints, we study
,
and
at different parameters
h and
k with different system sizes (see
Figure 4). In all cases, we find
and
. If
and
, the system is separated into identical subsystems and
. Hence,
for all these systems.
2.3. Matter Flow
In Case (iii), the ideal gas is flowing between two parallel walls located at
(see
Figure 5). The flow is assumed to be laminar and the fluid incompressible. It is driven by a constant pressure gradient along the
x-axis,
. Such a flow is known as the Poiseuille flow [
17]. Both walls are kept at temperature
. An adiabatic slip wall is introduced as the constraint into the system. It is placed at
with
.
In the steady state, the velocity profile and the temperature profile can be obtained from the Navier–Stokes equation. We note that, due to the presence of the external pressure gradient and since the mass density of the incompressible fluid is homogeneous
, the energy density is not constant throughout the system. We first obtain the velocity profile
from
where
is the viscosity. Given the non-slip conditions at the boundaries
, we find
Secondly, from the momentum equation, we obtain the dissipation density function
. The dissipation density function governs the rate at which the mechanical energy of the flow is converted to heat. The out-going heat flow
is given by,
where
A is the area of the plates and
is the volume of the system. Moreover, we assume that the heat transfer obeys the Fourier’s law. From (Equation (
2)),
together with boundary conditions
, we obtain the temperature profile,
Finally, we assume that the internal energy locally obeys the ideal gas law given by Equation (
A4). The total energy of the system consists of the kinetic energy and the internal energy,
where the number density
, with
m the mass of a single atom or molecule. Combining Equations (
27), (
30) and (
31), we obtain
For the constrained system, additional boundary conditions are
,
,
and
. Following the same method, we find the velocity profiles as
and the temperature profiles as
From these equations, we obtain
Comparing
and
, the relation reduces to
Analysis shows that .
2.4. Energy Density as Function of Heat Flow
It is interesting to note that, for all the above studied models, the steady state energy density
is a product of the equilibrium energy density
and a dimensionless function of the heat flow
. For the ideal gas system with a homogeneous energy supply, where
,
can be written as (compare Equation (
10))
Next, for the heat flow model, with
(compare Equation (
22)), the steady state energy density can be expressed as
Lastly, for the matter flow model, with
(compare Equation (
27)), the steady state internal energy density can be expressed as (compare Equation (
31)),
Thus, in all studied steady states, we find .
3. Conclusions
We use the ideal gas model with three different energy delivery methods to test the hypothesis that is minimized in steady states. The results in all models confirm that .
Further, in all studied steady states, we find and therefore is a parameter of NESS. By making a Legendre transform of U with respect to , we get an analog of the Helmholtz free energy for NESS, especially since is the entropy flow leaving the system through the wall at temperature . We introduce a quantity , which we call the embedded energy, since it is the stored energy minus the outflow of energy in the characteristic time . Thus, represents the part of the energy that must stay in the system for all times to keep the outflow of energy, while is the energy that constantly flows through the system in time .