Sentience and the Origins of Consciousness: From Cartesian Duality to Markovian Monism
Abstract
1. Introduction
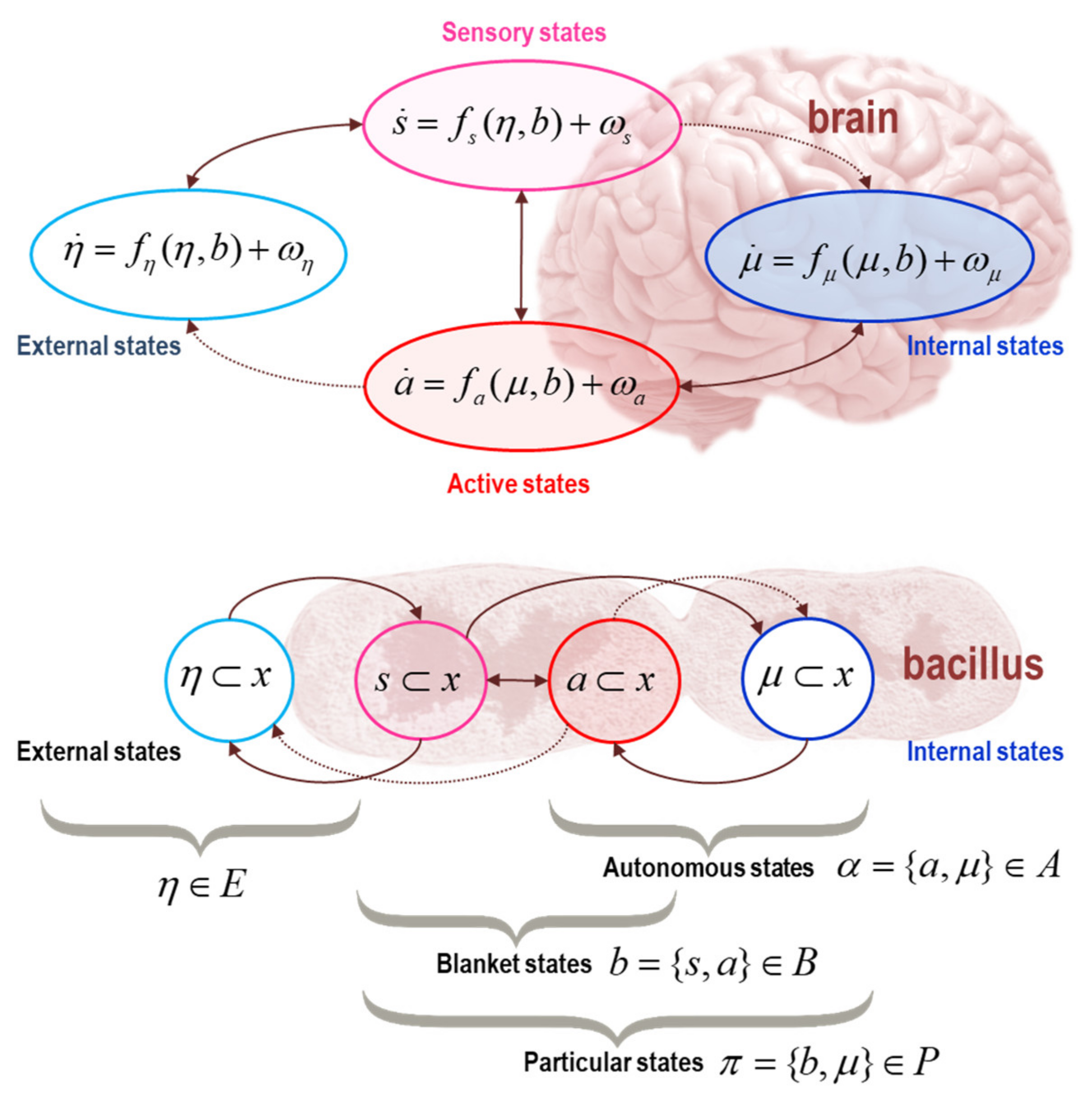
2. Markov Blankets and Self-Organisation
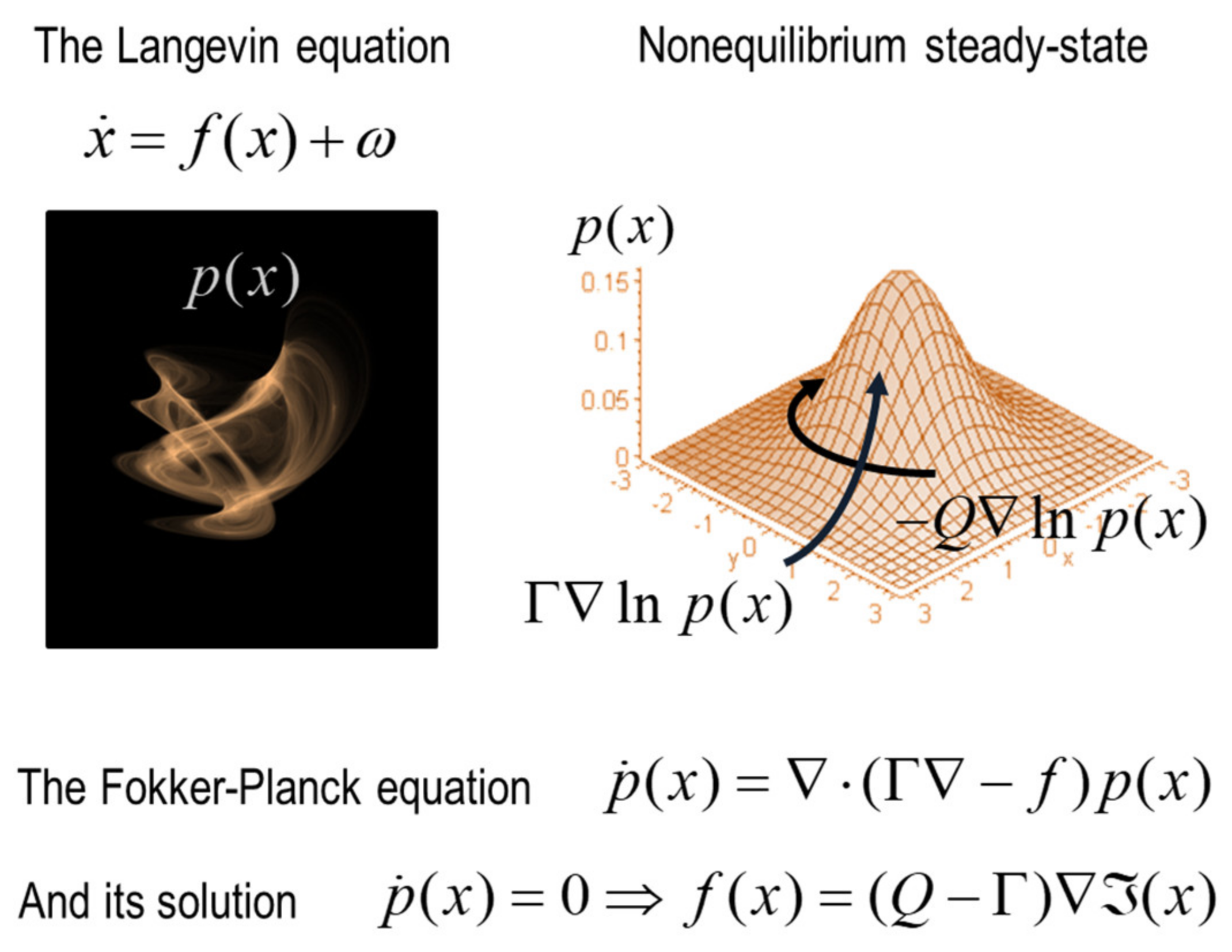
3. The Langevin Formalism and Density Dynamics
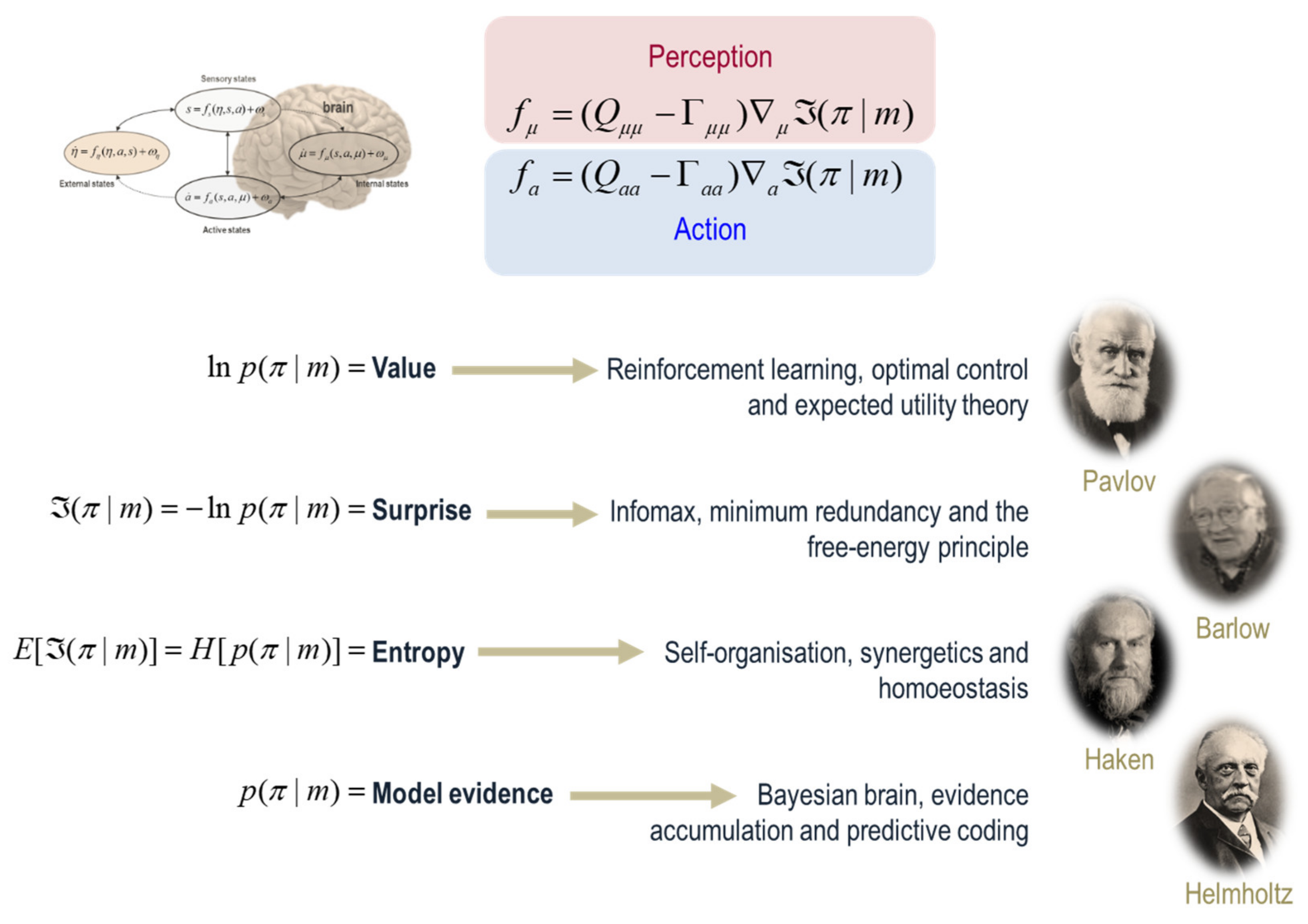
4. Bayesian Mechanics
5. Information Geometry and Beliefs
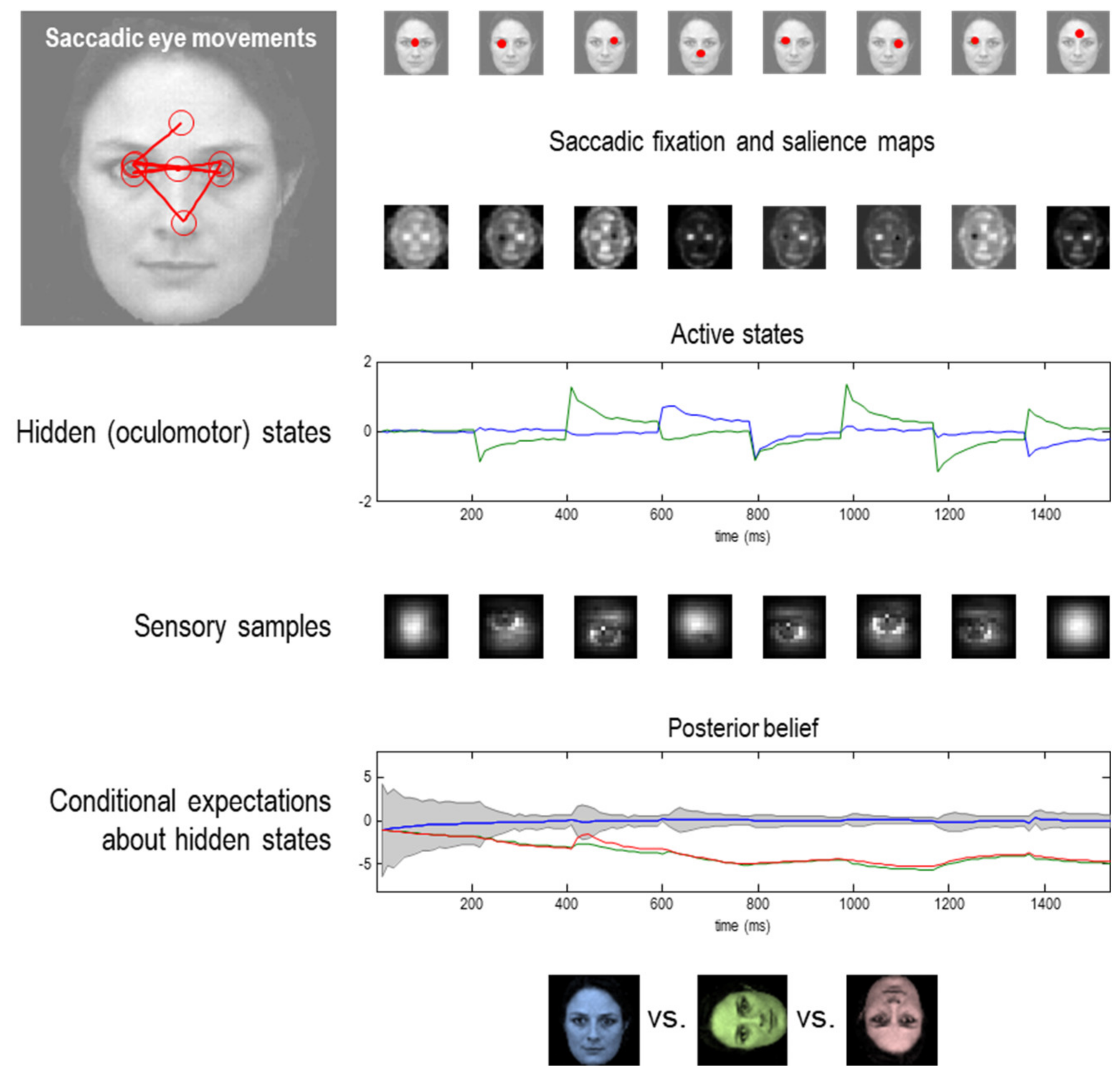
6. A Force to Be Reckoned with
7. Active Inference and the Future
8. Active Inference and the Path Integral Formulation
9. Markovian Monism
10. Markovian Monism as Panprotopsychism?
11. Markovian Monism as Neutral Monism?
12. Markovian Monism as a Dual-Aspect Theory?
13. Markovian Monism as Reductive Materialism
14. Consciousness and Integrated Information
- Intrinsic existence—consciousness exists: each experience is actual and exists from its own intrinsic perspective. This is a necessary consequence of Bayesian mechanics under the free energy principle because the dynamics underlying inference are physically realised and are, by construction, intrinsic in the sense of pertaining to internal states.
- Composition—consciousness is structured: with multiple phenomenal distinctions. Again, this is a necessary aspect of Bayesian mechanics, which is defined in terms of the structure implicit in conditional independencies. Indeed, from a statistical perspective, minimising variational free energy is synonymous with structure learning [59,121,122].
- Information—consciousness is unique: each experience is the particular way it is, thereby differing from other possible experiences (i.e., differentiation). Again, this is a fundament of Bayesian mechanics under the free energy principle; in the sense that any information geometry implies a particular point on a statistical manifold (of internal or intrinsic states) maps to a particular probability or belief state with phenomenal support (i.e., an extrinsic belief distribution over the external states).
- Integration—consciousness is unified: each experience is irreducible to disjoint subsets of phenomenal distinctions (i.e., integration). Again, this is a necessary aspect of the information geometry that underwrites the free energy principle. This follows because for each point on the internal statistical manifold, there is a single probabilistic belief (i.e., variational density). In other words, although this density could be very high dimensional, it is just one probabilistic belief that cannot be dissembled or reduced. Another aspect of the axiom of integration is that “every part of the system has both causes and effects within the rest of the system” ([123], p. 3). This is true for systems possessing a Markov blanket, because the gradient flows of internal states (and associated belief updating) are, by definition, conditionally dependent.
- Exclusion—consciousness is definite: each experience is characterised by what it is (neither less no more than) and flows at the speed it flows (neither faster nor slower). Again, this is a necessary consequence of the density dynamics that underwrites the free energy principle. In other words, flows on the extrinsic (statistical) manifold are unique and entail particular probabilistic beliefs about external states, i.e., precise beliefs about being in a particular (external) state but not another. Furthermore, each probabilistic belief has its own sufficient statistics that exclude the possibility of other sufficient statistics. For example, beliefs about my temperature can be stipulated with an expectation that my temperature is such and such. This precludes the possibility that I expect to my temperature to be anything else. In contrast to the exclusion axiom, however, the existence of a Markov blanket at one spatiotemporal scale does not exclude the existence of (e.g., nested) Markov blankets at other spatiotemporal scales.
15. Information Geometry and Altered States of Consciousness
16. Conclusions
Author Contributions
Funding
Conflicts of Interest
Glossary of Terms and Expressions
| Expression | Description | Units |
| Variables | ||
| Trajectory or path through state space | a.u. (m) | |
| Random fluctuations | a.u. (m) | |
| Markovian partition into external, sensory, active, and internal states | a.u. (m) | |
| Time derivative (Newton notation) | m/s | |
| Autonomous states | a.u. (m) | |
| Blanket states | a.u. (m) | |
| Particular states | a.u. (m) | |
| External states | a.u. (m) | |
| Amplitude (i.e., half the variance) of random fluctuations | J·s/kg | |
| Rate of solenoidal flow | J·s/kg | |
| Mobility coefficient | s/kg | |
| Temperature | K (Kelvin) | |
| Information length | nats | |
| Critical time | s | |
| Fisher (information metric) tensor | a.u. | |
| Functions, functionals and potentials | ||
| The expected flow of states from any point in state space. This is the expected temporal derivative of x, averaging over random fluctuations in the motion of states. | ||
| Expectation or average | ||
| Probability density function parameterised by sufficient statistics λ | ||
| Variational density—an (approximate posterior) density over external states that is parameterised by internal states | ||
| Action: the surprisal of a path, i.e., the path integral of the Lagrangian | ||
| Thermodynamic potential | J or kg m2/s2 | |
| Variational free energy free energy—an upper bound on the surprisal of particular states | nats | |
| Expected free energy free energy—an upper bound on the (classical) action of an autonomous path | nats | |
| Operators | ||
| Differential or gradient operator (on a scalar field) | ||
| Curvature operator (on a scalar field) | ||
| Entropies and potentials | ||
| Surprisal or self-information | nats | |
| Relative entropy or Kullback–Leibler divergence | nats | |
| (arbitrary units (a.u.), e.g., metres (m), radians (rad), etc.). | ||
References
- Friston, K. A free energy principle for a particular physics. arXiv 2019, arXiv:1906.10184. [Google Scholar]
- Pearl, J. Probabilistic Reasoning In Intelligent Systems: Networks of Plausible Inference; Morgan Kaufmann: San Fransisco, CA, USA, 1988. [Google Scholar]
- Parr, T.; Da Costa, L.; Friston, K. Markov blankets, information geometry and stochastic thermodynamics. Philos. Trans. A Math. Phys. Eng. Sci. 2020, 378, 20190159. [Google Scholar] [CrossRef] [PubMed]
- Kirchhoff, M.; Parr, T.; Palacios, E.; Friston, K.; Kiverstein, J. The Markov blankets of life: Autonomy, active inference and the free energy principle. J. R. Soc. Interface 2018, 15. [Google Scholar] [CrossRef] [PubMed]
- Palacios, E.R.; Razi, A.; Parr, T.; Kirchhoff, M.; Friston, K. Biological Self-organisation and Markov blankets. bioRxiv 2017, arXiv:10.1101/227181. [Google Scholar]
- Clark, A. How to Knit Your Own Markov Blanket. In Philosophy and Predictive Processing; Metzinger, T.K., Wiese, W., Eds.; MIND Group: Frankfurt, Germany, 2017. [Google Scholar]
- Friston, K.J.; Kahan, J.; Razi, A.; Stephan, K.E.; Sporns, O. On nodes and modes in resting state fMRI. Neuroimage 2014, 99, 533–547. [Google Scholar] [CrossRef]
- Pellet, J.P.; Elisseeff, A. Using Markov blankets for causal structure learning. J. Mach. Learn. Res. 2008, 9, 1295–1342. [Google Scholar]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef]
- Sekimoto, K. Langevin Equation and Thermodynamics. Prog. Theor. Phys. Suppl. 1998, 130, 17–27. [Google Scholar] [CrossRef]
- Ao, P. Emerging of Stochastic Dynamical Equalities and Steady State Thermodynamics. Commun. Theor. Phys. 2008, 49, 1073–1090. [Google Scholar] [CrossRef]
- Seifert, U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep. Prog. Phys. Phys. Soc. 2012, 75, 126001. [Google Scholar] [CrossRef]
- Crauel, H.; Flandoli, F. Attractors for Random Dynamical-Systems. Probab. Theory Rel. 1994, 100, 365–393. [Google Scholar] [CrossRef]
- Birkhoff, G.D. Dynamical Systems; American Mathematical Society: New York, NY, USA, 1927. [Google Scholar]
- Tribus, M. Thermodynamics and Thermostatics: An Introduction to Energy, Information and States of Matter, with Engineering Applications; D. Van Nostrand Company Inc.: New York, NY, USA, 1961. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. Ser. II 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jones, D.S. Elementary Information Theory; Clarendon Press: Oxford, UK, 1979. [Google Scholar]
- MacKay, D.J.C. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kerr, W.C.; Graham, A.J. Generalized phase space version of Langevin equations and associated Fokker-Planck equations. Eur. Phys. J. B 2000, 15, 305–311. [Google Scholar] [CrossRef]
- Frank, T.D.; Beek, P.J.; Friedrich, R. Fokker-Planck perspective on stochastic delay systems: Exact solutions and data analysis of biological systems. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2003, 68, 021912. [Google Scholar] [CrossRef]
- Frank, T.D. Nonlinear Fokker-Planck Equations: Fundamentals and Applications. Springer Series in Synergetics; Springer: Berlin, Germany, 2004. [Google Scholar]
- Tomé, T. Entropy Production in Nonequilibrium Systems Described by a Fokker-Planck Equation. Braz. J. Phys. 2006, 36, 1285–1289. [Google Scholar] [CrossRef]
- Kim, E.-j. Investigating Information Geometry in Classical and Quantum Systems through Information Length. Entropy 2018, 20, 574. [Google Scholar] [CrossRef]
- Yuan, R.; Ma, Y.; Yuan, B.; Ping, A. Bridging Engineering and Physics: Lyapunov Function as Potential Function. arXiv 2010, arXiv:1012.2721v1. [Google Scholar]
- Friston, K.; Ao, P. Free energy, value, and attractors. Comput. Math. Methods Med. 2012, 2012, 937860. [Google Scholar] [CrossRef]
- Sutton, R.S.; Precup, D.; Singh, S. Between MDPs and semi-MDPs: A framework for temporal abstraction in reinforcement learning. Artif. Intell. 1999, 112, 181–211. [Google Scholar] [CrossRef]
- Kauder, E. Genesis of the Marginal Utility Theory: From Aristotle to the End of the Eighteenth Century. Econ. J. 1953, 63, 638–650. [Google Scholar] [CrossRef]
- Fleming, W.H.; Sheu, S.J. Risk-sensitive control and an optimal investment model II. Ann. Appl. Probab. 2002, 12, 730–767. [Google Scholar] [CrossRef]
- Haken, H. Synergetics: An Introduction. Non-Equilibrium Phase Transition and Self-Selforganisation in Physics, Chemistry and Biology; Springer Verlag: Berlin, Germany, 1983. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Todorov, E.; Jordan, M.I. Optimal feedback control as a theory of motor coordination. Nat. Neurosci. 2002, 5, 1226–1235. [Google Scholar] [CrossRef] [PubMed]
- Kappen, H.J. Path integrals and symmetry breaking for optimal control theory. J. Stat. Mech. Theory Exp. 2005, 11, 11011. [Google Scholar] [CrossRef]
- Barlow, H. Possible principles underlying the transformations of sensory messages. In Sensory Communication; Rosenblith, W., Ed.; MIT Press: Cambridge, MA, USA, 1961; pp. 217–234. [Google Scholar]
- Tschacher, W.; Haken, H. Intentionality in non-equilibrium systems? The functional aspects of self-organised pattern formation. New Ideas Psychol. 2007, 25, 1–15. [Google Scholar] [CrossRef]
- Bernard, C. Lectures on the Phenomena Common to Animals and Plants; Charles C Thomas: Springfield, IL, USA, 1974. [Google Scholar]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Hohwy, J. The Self-Evidencing Brain. Noûs 2016, 50, 259–285. [Google Scholar] [CrossRef]
- Friston, K.; Da Costa, L.; Parr, T. Some interesting observations on the free energy principle. arXiv 2020, arXiv:2002.04501. [Google Scholar]
- Bossaerts, P.; Murawski, C. From behavioural economics to neuroeconomics to decision neuroscience: The ascent of biology in research on human decision making. Curr. Opin. Behav. Sci. 2015, 5, 37–42. [Google Scholar] [CrossRef]
- Linsker, R. Perceptual neural organization: Some approaches based on network models and information theory. Annu. Rev. Neurosci. 1990, 13, 257–281. [Google Scholar] [CrossRef]
- Optican, L.; Richmond, B.J. Temporal encoding of two-dimensional patterns by single units in primate inferior cortex. II Information theoretic analysis. J. Neurophysiol. 1987, 57, 132–146. [Google Scholar] [CrossRef]
- Friston, K.; Kilner, J.; Harrison, L. A free energy principle for the brain. J. Physiol. 2006, 100, 70–87. [Google Scholar] [CrossRef] [PubMed]
- Nicolis, G.; Prigogine, I. Self-Organization in Non-Equilibrium Systems; John Wiley: New York, NY, USA, 1977. [Google Scholar]
- Kauffman, S. The Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Conant, R.C.; Ashby, W.R. Every Good Regulator of a system must be a model of that system. Int. J. Syst. Sci. 1970, 1, 89–97. [Google Scholar] [CrossRef]
- Ashby, W.R. Principles of the self-organizing dynamic system. J. Gen. Psychol. 1947, 37, 125–128. [Google Scholar] [CrossRef] [PubMed]
- MacKay, D.J. Free-energy minimisation algorithm for decoding and cryptoanalysis. Electron. Lett. 1995, 31, 445–447. [Google Scholar] [CrossRef]
- Helmholtz, H. Concerning the perceptions in general. In Treatise on Physiological Optics; Dover: New York, NY, USA, 1962. [Google Scholar]
- Gregory, R.L. Perceptions as hypotheses. Philos. Trans. R. Soc. Lond. B 1980, 290, 181–197. [Google Scholar]
- Dayan, P.; Hinton, G.E.; Neal, R.M.; Zemel, R.S. The Helmholtz machine. Neural Comput. 1995, 7, 889–904. [Google Scholar] [CrossRef]
- Beal, M.J. Variational Algorithms for Approximate Bayesian Inference. Ph.D. Thesis, University College London, London, UK, 2003. [Google Scholar]
- Dauwels, J. On Variational Message Passing on Factor Graphs. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007; pp. 2546–2550. [Google Scholar]
- Suh, S.; Chae, D.H.; Kang, H.G.; Choi, S. Echo-State Conditional Variational Autoencoder for Anomaly Detection. In Proceedings of the 2016 International Joint Conference on Neural Networks, Vancouver, BC, Canada, 24–29 July 2016; pp. 1015–1022. [Google Scholar]
- Roweis, S.; Ghahramani, Z. A unifying review of linear gaussian models. Neural Comput. 1999, 11, 305–345. [Google Scholar] [CrossRef]
- Hinton, G.E.; Zemel, R.S. Autoencoders, minimum description length and Helmholtz free energy. In Proceedings of the 6th International Conference on Neural Information Processing Systems, Denver, CO, USA, November 1994; pp. 3–10. [Google Scholar]
- Ikeda, S.; Tanaka, T.; Amari, S.-I. Stochastic reasoning, free energy, and information geometry. Neural Comput. 2004, 16, 1779–1810. [Google Scholar] [CrossRef]
- Knill, D.C.; Pouget, A. The Bayesian brain: The role of uncertainty in neural coding and computation. Trends Neurosci. 2004, 27, 712–719. [Google Scholar] [CrossRef]
- Yedidia, J.S.; Freeman, T.; Weiss, Y. Constructing free-energy approximations and generalized belief propagation algorithms. IEEE Trans. Inf. Theory 2005, 51, 2282–2312. [Google Scholar] [CrossRef]
- Amari, S. Natural gradient works efficiently in learning. Neural Comput. 1998, 10, 251–276. [Google Scholar] [CrossRef]
- Ay, N. Information Geometry on Complexity and Stochastic Interaction. Entropy 2015, 17, 2432. [Google Scholar] [CrossRef]
- Caticha, A. The basics of information geometry. AIP Conf. Proc. 2015, 1641, 15–26. [Google Scholar] [CrossRef]
- Crooks, G.E. Measuring thermodynamic length. Phys. Rev. Lett. 2007, 99, 100602. [Google Scholar] [CrossRef] [PubMed]
- Herbart, J.F. Lehrbuch zur Psychologie, 2nd ed.; Unzer: Königsberg, Prussia, 1834. [Google Scholar]
- Holmes, Z.; Weidt, S.; Jennings, D.; Anders, J.; Mintert, F. Coherent fluctuation relations: From the abstract to the concrete. Quantum 2019, 3, 124. [Google Scholar] [CrossRef]
- Van Gulick, R. Reduction, Emergence and Other Recent Options on the Mind/Body Problem. A Philosophic Overview. J. Conscious. Stud. 2001, 8, 1–34. [Google Scholar]
- Hobson, J.A.; Friston, K.J. A Response to Our Theatre Critics. J. Conscious. Stud. 2016, 23, 245–254. [Google Scholar]
- Brown, H.; Adams, R.A.; Parees, I.; Edwards, M.; Friston, K. Active inference, sensory attenuation and illusions. Cogn. Process. 2013, 14, 411–427. [Google Scholar] [CrossRef]
- Clark, A. The many faces of precision. Front. Psychol. 2013, 4, 270. [Google Scholar]
- Hohwy, J. The Predictive Mind; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Seth, A. The cybernetic brain: From interoceptive inference to sensorimotor contingencies. In Open MIND; Metzinger, T., Windt, J.M., Eds.; MIND Group: Frankfurt a.M., Germany, 2014. [Google Scholar]
- Hobson, J.A.; Friston, K.J. Waking and dreaming consciousness: Neurobiological and functional considerations. Prog. Neurobiol. 2012, 98, 82–98. [Google Scholar] [CrossRef]
- Friston, K.; Buzsaki, G. The Functional Anatomy of Time: What and When in the Brain. Trends Cogn. Sci. 2016, 20, 500–511. [Google Scholar] [CrossRef] [PubMed]
- Adams, R.A.; Shipp, S.; Friston, K.J. Predictions not commands: Active inference in the motor system. Brain Struct. Funct. 2013, 218, 611–643. [Google Scholar] [CrossRef] [PubMed]
- Ungerleider, L.G.; Haxby, J.V. ‘What’ and ‘where’ in the human brain. Curr. Opin. Neurobiol. 1994, 4, 157–165. [Google Scholar] [CrossRef]
- Shigeno, S.; Andrews, P.L.R.; Ponte, G.; Fiorito, G. Cephalopod Brains: An Overview of Current Knowledge to Facilitate Comparison With Vertebrates. Front. Physiol. 2018, 9, 952. [Google Scholar] [CrossRef]
- Seth, A.K. Interoceptive inference, emotion, and the embodied self. Trends Cogn. Sci. 2013, 17, 565–573. [Google Scholar] [CrossRef]
- Arnold, L. Random Dynamical Systems (Springer Monographs in Mathematics); Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Kleeman, R. A Path Integral Formalism for Non-equilibrium Hamiltonian Statistical Systems. J. Stat. Phys. 2014, 158, 1271–1297. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Pezzulo, G.; Rigoli, F.; Friston, K. Active Inference, homeostatic regulation and adaptive behavioural control. Prog. Neurobiol. 2015, 134, 17–35. [Google Scholar] [CrossRef]
- Sterling, P.; Eyer, J. Allostasis: A new paradigm to explain arousal pathology. In Handbook of Life Stress, Cognition and Health; John Wiley & Sons: Hoboken, NJ, USA, 1988; pp. 629–649. [Google Scholar]
- Balleine, B.W.; Dickinson, A. Goal-directed instrumental action: Contingency and incentive learning and their cortical substrates. Neuropharmacology 1998, 37, 407–419. [Google Scholar] [CrossRef]
- Ramsay, D.S.; Woods, S.C. Clarifying the Roles of Homeostasis and Allostasis in Physiological Regulation. Psychol. Rev. 2014, 121, 225–247. [Google Scholar] [CrossRef]
- Stephan, K.E.; Manjaly, Z.M.; Mathys, C.D.; Weber, L.A.E.; Paliwal, S.; Gard, T.; Tittgemeyer, M.; Fleming, S.M.; Haker, H.; Seth, A.K.; et al. Allostatic Self-efficacy: A Metacognitive Theory of Dyshomeostasis-Induced Fatigue and Depression. Front. Hum. Neurosci. 2016, 10, 550. [Google Scholar] [CrossRef] [PubMed]
- Attias, H. Planning by Probabilistic Inference. In Proceedings of the 9th International Workshop on Artificial Intelligence and Statistics, Key West, FL, USA, 3–6 January 2003. [Google Scholar]
- Toussaint, M.; Storkey, A. Probabilistic inference for solving discrete and continuous state Markov Decision Processes. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 945–952. [Google Scholar]
- Botvinick, M.; Toussaint, M. Planning as inference. Trends Cogn Sci. 2012, 16, 485–488. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Curious model-building control systems. Proc. Int. Jt. Conf. Neural Netw. Singap. 1991, 2, 1458–1463. [Google Scholar]
- Schmidhuber, J. Formal Theory of Creativity, Fun, and Intrinsic Motivation (1990–2010). IEEE Trans. Auton. Ment. Dev. 2010, 2, 230–247. [Google Scholar] [CrossRef]
- Sun, Y.; Gomez, F.; Schmidhuber, J. Planning to Be Surprised: Optimal Bayesian Exploration in Dynamic Environments. In Proceedings of the Artificial General Intelligence: 4th International Conference, AGI 2011, Mountain View, CA, USA, 3–6 August 2011; Schmidhuber, J., Thórisson, K.R., Looks, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 41–51. [Google Scholar]
- Gibson, J.J. The theory of affordances. In Perceiving, Acting, and Knowing: Toward an Ecological Psychology; Erlbaum: Hillsdale, NJ, USA, 1977; pp. 67–82. [Google Scholar]
- Bruineberg, J.; Rietveld, E. Self-organization, free energy minimization, and optimal grip on a field of affordances. Front. Hum. Neurosci. 2014, 8, 599. [Google Scholar] [CrossRef]
- Parr, T.; Friston, K.J. Working memory, attention, and salience in active inference. Sci. Rep. 2017, 7, 14678. [Google Scholar] [CrossRef]
- Friston, K.; Mattout, J.; Kilner, J. Action understanding and active inference. Biol. Cybern. 2011, 104, 137–160. [Google Scholar] [CrossRef]
- Rizzolatti, G.; Craighero, L. The mirror-neuron system. Annu. Rev. Neurosci. 2004, 27, 169–192. [Google Scholar] [CrossRef]
- Kilner, J.M.; Friston, K.J.; Frith, C.D. Predictive coding: An account of the mirror neuron system. Cogn. Process. 2007, 8, 159–166. [Google Scholar] [CrossRef]
- Gallese, V.; Goldman, A. Mirror neurons and the simulation theory of mind-reading. Trends Cogn. Sci. 1998, 2, 493–501. [Google Scholar] [CrossRef]
- Friston, K.; Adams, R.A.; Perrinet, L.; Breakspear, M. Perceptions as hypotheses: Saccades as experiments. Front. Psychol. 2012, 3, 151. [Google Scholar] [CrossRef] [PubMed]
- Dennett, D.C. True believers: The intentional strategy and why it works. In Scientific Explanation: Papers Based on Herbert Spencer Lectures Given in the University of Oxford; Heath, A.F., Ed.; Clarendon Press: Oxford, UK, 1981; pp. 150–167. [Google Scholar]
- Chalmers, D.J. Panpsychism and panprotopsychism. In Consciousness in the Physical World: Perspectives on Russellian Monism; Oxford University Press: New York, NY, USA, 2015; pp. 246–276. [Google Scholar]
- Stubenberg, L. Neutral monism. In The Stanford Encyclopedia of Philosophy; Zalta, E.N., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2018. [Google Scholar]
- Howell, R. The Russellian Monist’s Problems with Mental Causation. Philos. Q. 2015, 65, 22–39. [Google Scholar] [CrossRef]
- Kirchhoff, M.D.; Froese, T. Where There is Life There is Mind: In Support of a Strong Life-Mind Continuity Thesis. Entropy 2017, 19, 169. [Google Scholar] [CrossRef]
- Skrbina, D. Minds, objects, and relations. Toward a dual-aspect ontology. In Mind that Abides. Panpsychism in the New Millenium; Skrbina, D., Ed.; John Benjamins Publishing Company: Amsterdam, The Netherlands; Philadelphia, PA, USA, 2009; pp. 361–397. [Google Scholar]
- Velmans, M. Reflexive Monism. J. Conscious. Stud. 2008, 15, 5–50. [Google Scholar]
- Benovsky, J. Dual-Aspect Monism. Philos. Investig. 2016, 39, 335–352. [Google Scholar] [CrossRef]
- Solms, M.; Friston, K. How and Why Consciousness Arises. Some Considerations from Physics and Physiology. J. Conscious. Stud. 2018, 25, 202–238. [Google Scholar]
- Woodward, J. Mental Causation and Neural Mechanisms. In Being Reduced: New Essays on Reduction, Explanation, and Causation; Hohwy, J., Kallestrup, J., Eds.; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Papineau, D. Causation is Macroscopic but Not Irreducible. In Mental Causation and Ontology; Gibb, S.C., Lowe, E.J., Ingthorsson, R.D., Eds.; Oxford University Press: Oxford, UK, 2013; pp. 126–151. [Google Scholar]
- Mansell, W. Control of perception should be operationalized as a fundamental property of the nervous system. Top. Cogn. Sci. 2011, 3, 257–261. [Google Scholar] [CrossRef]
- Seth, A.K. Inference to the Best Prediction. In Open MIND; Metzinger, T.K., Windt, J.M., Eds.; MIND Group: Frankfurt, Germany, 2015. [Google Scholar]
- Chalmers, D.J. The Meta-Problem of Consciousness. J. Conscious. Stud. 2018, 25, 6–61. [Google Scholar]
- Clark, A.; Friston, K.; Wilkinson, S. Bayesing Qualia. Consciousness as Inference, Not Raw Datum. J. Conscious. Stud. 2019, 26, 19–33. [Google Scholar]
- Schweizer, P. Triviality Arguments Reconsidered. Minds Mach. 2019, 29, 287–308. [Google Scholar] [CrossRef]
- Fodor, J. The mind-body problem. Sci. Am. 1981, 244, 114–123. [Google Scholar] [CrossRef] [PubMed]
- Piccinini, G. Computation without Representation. Philos. Stud. 2006, 137, 205–241. [Google Scholar] [CrossRef]
- Gładziejewski, P. Predictive coding and representationalism. Synthese 2016, 193, 559–582. [Google Scholar] [CrossRef]
- Tononi, G. An information integration theory of consciousness. BMC Neurosci. 2004, 5, 42. [Google Scholar] [CrossRef]
- Tononi, G. Consciousness as Integrated Information: A Provisional Manifesto. Biol. Bull. 2008, 215, 216–242. [Google Scholar] [CrossRef]
- Balduzzi, D.; Tononi, G. Qualia: The Geometry of Integrated Information. PLoS Comput. Biol. 2009, 5, 1–24. [Google Scholar] [CrossRef]
- van Leeuwen, C. Perceptual-learning systems as conservative structures: Is economy an attractor? Psychol. Res. 1990, 52, 145–152. [Google Scholar] [CrossRef]
- Tervo, D.G.; Tenenbaum, J.B.; Gershman, S.J. Toward the neural implementation of structure learning. Curr. Opin. Neurobiol. 2016, 37, 99–105. [Google Scholar] [CrossRef]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef]
- Wiese, W. Toward a Mature Science of Consciousness. Front. Psychol. 2018, 9, 693. [Google Scholar] [CrossRef]
- Wiese, W. Experienced Wholeness. Integrating Insights from Gestalt Theory, Cognitive Neuroscience, and Predictive Processing; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Bayne, T. On the axiomatic foundations of the integrated information theory of consciousness. Neurosci. Conscious. 2018, 2018, niy007. [Google Scholar] [CrossRef] [PubMed]
- Hobson, J.A. REM sleep and dreaming: Towards a theory of protoconsciousness. Nat. Rev. Neurosci. 2009, 10, 803–813. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Dayan, P.; Frey, B.J.; Neal, R.M. The “wake-sleep” algorithm for unsupervised neural networks. Science 1995, 268, 1158–1161. [Google Scholar] [CrossRef] [PubMed]
- Hobson, J.A. Dreaming as Delirium; The MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Hobson, J.A.; Friston, K.J. Consciousness, Dreams, and Inference The Cartesian Theatre Revisited. J. Conscious. Stud. 2014, 21, 6–32. [Google Scholar]
- Friston, K.J.; Lin, M.; Frith, C.D.; Pezzulo, G.; Hobson, J.A.; Ondobaka, S. Active Inference, Curiosity and Insight. Neural Comput. 2017, 29, 2633–2683. [Google Scholar] [CrossRef]
- Metzinger, T. Being No One: The Self-Model Theory of Subjectivity; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Tononi, G.; Cirelli, C. Sleep function and synaptic homeostasis. Sleep Med. Rev. 2006, 10, 49–62. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Flat minima. Neural Comput. 1997, 9, 1–42. [Google Scholar] [CrossRef]
- Gilestro, G.F.; Tononi, G.; Cirelli, C. Widespread changes in synaptic markers as a function of sleep and wakefulness in Drosophila. Science 2009, 324, 109–112. [Google Scholar] [CrossRef]
- Palmer, C.J.; Seth, A.K.; Hohwy, J. The felt presence of other minds: Predictive processing, counterfactual predictions, and mentalising in autism. Conscious. Cogn. 2015, 36, 376–389. [Google Scholar] [CrossRef]
- Kaplan, R.; Friston, K.J. Planning and navigation as active inference. Biol. Cybern. 2018, 112, 323–343. [Google Scholar] [CrossRef]
- Sengupta, B.; Tozzi, A.; Cooray, G.K.; Douglas, P.K.; Friston, K.J. Towards a Neuronal Gauge Theory. PLoS Biol. 2016, 14, e1002400. [Google Scholar] [CrossRef] [PubMed]
- Limanowski, J.; Friston, K. ‘Seeing the Dark’: Grounding Phenomenal Transparency and Opacity in Precision Estimation for Active Inference. Front. Psychol. 2018, 9, 643. [Google Scholar] [CrossRef] [PubMed]
- Fotopoulou, A.; Tsakiris, M. Mentalizing homeostasis: The social origins of interoceptive inference—Replies to Commentaries. Neuropsychoanalysis 2017, 19, 71–76. [Google Scholar] [CrossRef]
- Dehaene, S.; Naccache, L. Towards a cognitive neuroscience of consciousness: Basic evidence and a workspace framework. Cognition 2001, 79, 1–37. [Google Scholar] [CrossRef]
- Cavanna, A.E.; Trimble, M.R. The precuneus: A review of its functional anatomy and behavioural correlates. Brain 2006, 129, 564–583. [Google Scholar] [CrossRef]
- Still, S.; Sivak, D.A.; Bell, A.J.; Crooks, G.E. Thermodynamics of prediction. Phys. Rev. Lett. 2012, 109, 120604. [Google Scholar] [CrossRef]
| 1 | The important point is that such systems can be described ‘as if’ they represent probability distributions. More substantial representationalist accounts can be built on this foundation, see Section 13. |
| 2 | In the sense that anything just is a Markov blanket, the relevant timescale is the duration over which the thing exists. Generally, smaller things last for short periods of time and bigger things last longer. This is a necessary consequence of composing Markov blankets of Markov blankets (i.e., things of things). In terms of sentient systems, the relevant time scale is the time over which a sentient system persists (e.g., the duration of being a sentient person). |
| 3 | In turn, this leads to quantum, statistical and classical mechanics, which can be regarded as special cases of density dynamics under certain assumptions. For example, when the system attains nonequilibrium steady-state, the solution to the density dynamics (i.e., Fokker Planck equation) becomes the solution to the Schrödinger equation that underwrites quantum electrodynamics. When random fluctuations become negligible (in large systems), we move from the dissipative thermodynamics to conservative classical mechanics. A technical treatment along these lines can be found in [1] with worked (numerical) examples. |
| 4 | Technically, Equation (1) only holds on the attracting set. However, this does not mean the dynamics collapse to a single point. The attracting manifold would usually support stochastic chaos and dynamical itinerancy—that may look like a succession of transients. |
| 5 | Note that the attracting set is in play throughout the ‘lifetime’ of any ‘thing’ because, by definition, a ‘thing’ has to be at nonequilibrium steady-state. This follows because the Markov blanket is a partition of states at nonequilibrium steady-state. |
| 6 | Note that as in (2) and
denote antisymmetric and leading diagonal matrices, respectively. |
| 7 | In itself, this is remarkable, in the sense that it captures the essence of many descriptions of adaptive behaviour, ranging from expected utility theory in economics [26,27,28] through to synergetics and self-organisation [21,29]. See Figure 3. To see how these descriptions follow from the gradient flows in (3), we only have to note that the mechanics of internal and active states can be regarded as perception and action, where both are in the service of minimising a particular surprisal. This surprisal can be regarded as a cost function from the point of view of engineering and behavioural psychology [30,31,32]. From the perspective of information theory, surprisal corresponds to self-information, leading to notions such as the principle of minimum redundancy or maximum efficiency [33]. The average value of surprisal is entropy [17]. This means that anything that exists will—appear to—minimise the entropy of its particular states over time [29,34]. In other words, it will appear to resist the second law of thermodynamics (which is again remarkable, because we are dealing with open systems that are far from equilibrium). From the point of view of a physiologist, this is nothing more than a generalised homoeostasis [35]. Finally, from the point of view of a statistician, the negative surprisal would look exactly the same as Bayesian model evidence [36]. |
| 8 | Note that in going from Equation (3) to the equations in Figure 3, we have assumed that the solenoidal coupling (Q) has a block diagonal form. In other words, we are ignoring the solenoidal coupling between internal and active states [9]. The interesting relationship between conditional independence and solenoidal coupling is pursued in a forthcoming submission to Entropy [38]. |
| 9 | could also be defined as the expected value of which will we approximated by ensemble averages of internal states. |
| 10 | This functional can be expressed in several forms; namely, an expected energy minus the entropy of the variational density, which is equivalent to the self-information associated with particular states (i.e., surprisal) plus the KL divergence between the variational and posterior density (i.e., bound). In turn, this can be decomposed into the negative log likelihood of particular states (i.e., accuracy) and the KL divergence between posterior and prior densities (i.e., complexity). In short, variational free energy constitutes a Lyapunov function for the expected flow of autonomous states. Variational free energy, like particular surprisal, depends on, and only on, particular states. Without going into technical details, it is sufficient to note that working with the variational free energy resolves many analytic and computational problems of working with surprisal per se; especially, if we want to interpret perception in terms of approximate Bayesian inference. It is perhaps sufficient to note that this variational free energy underlies nearly every statistical procedure in the physical and data sciences [51,52,53,54,55,56]. For example, it is the (negative) evidence lower bound used in state of the art (variational autoencoder) deep learning [53,55]. In summary, the variational free energy is always implicitly or explicitly under the hood of any inference process, ranging from simple analyses of variance through to the Bayesian brain [57]. |
| 11 | For example, if I set off in a straight line and travelled 40,075 km, I will have moved exactly no distance, because I would have circumnavigated the globe. |
| 12 | The notion of a metric is very general; in the sense that any metric space is defined by the way that it is measured. In the special case of a statistical manifold, the metric is supplied by the way in which probability densities change as we move over the manifold. In this instance, the metric is the Fisher information. Technically, the Fisher information metric can be thought of as an infinitesimal form of the relative entropy (i.e., the Kullback-Leibler divergence between the densities encoded by two infinitesimally close points on the manifold). Specifically, it is the Hessian of the divergence. Heuristically, this means the Fisher information metric scores the number of distinguishable probability densities encountered when moving from one point on the manifold to another. |
| 13 | In turn, this flow will, in a well-defined metric sense, cause movement in a belief space. This is just a statement of the way things must be—if things exist. Having said this, one is perfectly entitled to describe this sort of sentient dynamics (i.e., the Bayesian mechanics) as being caused by the same forces or gradients that constitute the (Fisher information) metric in (6). This is nothing more than a formal restatement of Johann Friedrich Herbart’s “mechanics of the mind”; according to which conscious representations behave like counteracting forces [63]. |
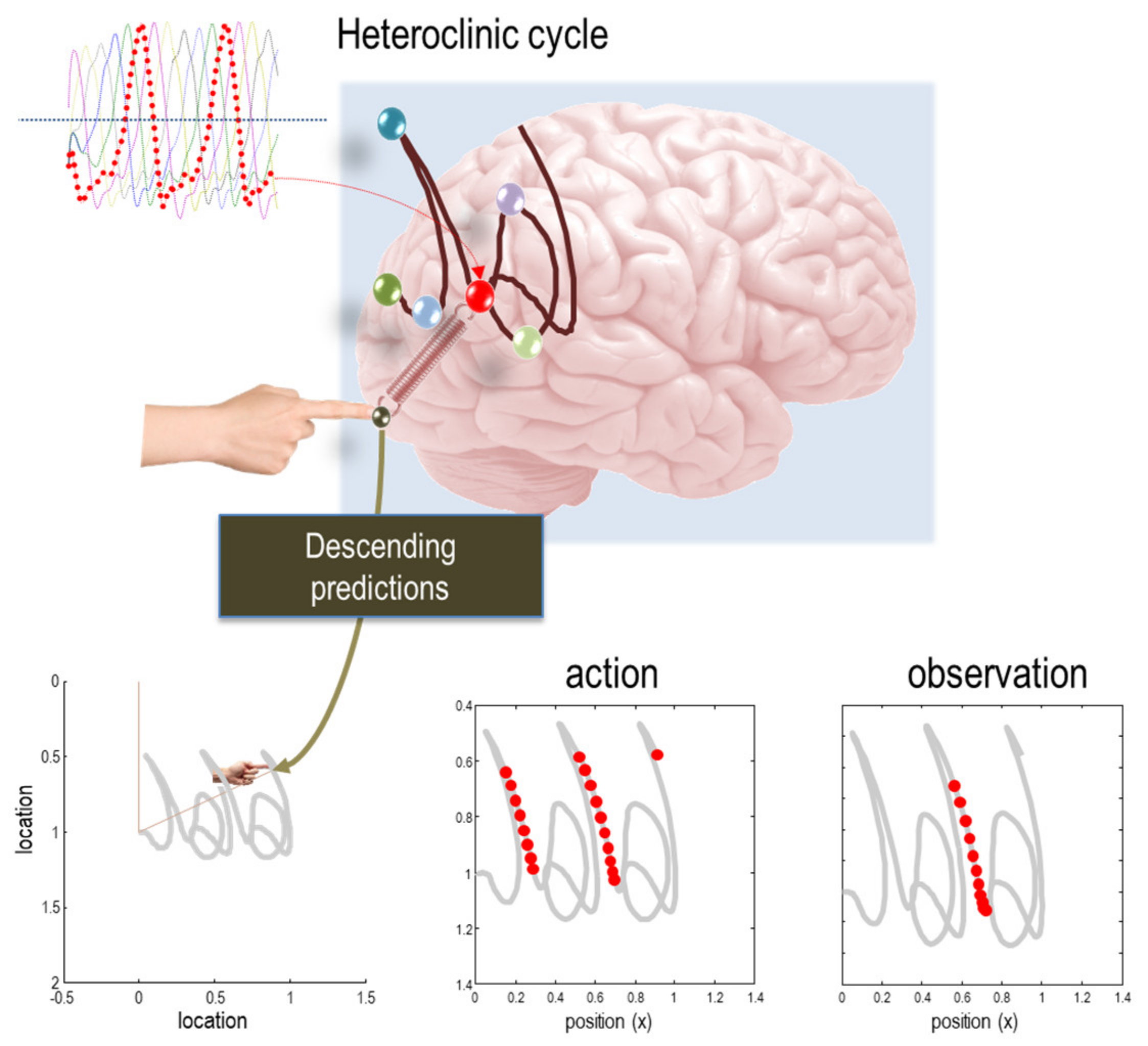
| 14 | An intuition here, can be built by considering what you will be doing in a few minutes, as opposed to next year. The difference between the probability over different ‘states of being’ between the present and in 2 min time is much greater than the corresponding differences between this time next year and this time next year, plus two min. |
| 15 | Another way of thinking about the distinction between the intrinsic and extrinsic information geometries is that the implicit probability distributions are over internal and external states, respectively. This means the intrinsic geometry describes the probabilistic behaviour of internal states, while the extrinsic geometry describes the Bayesian beliefs encoded by internal states about external states. |
| 16 | This is also how the following statement could be interpreted: “We are dualists only in asserting that, while the brain is material, the mind is immaterial” [66]. Technically, the link between the intrinsic and extrinsic information geometries follows because any change in internal states implies a conjugate movement on both statistical manifolds. However, these manifolds are formally different: one is a manifold containing parameters of beliefs about external states, while the other is a manifold containing parameters of the probability density over (future) internal states; namely, time (or appropriate statistical parameter apt for describing thermodynamics). |
| 17 | There are many interesting issues here. For example, it means that the intrinsic anatomy and dynamics (i.e., physiology) of internal states must, in some way, recapitulate the dynamical or causal structure of the outside world [71,72,73]. There are many examples of this. One celebrated example is the segregation of the brain into ventral (‘what’) and dorsal (‘where’) streams [74] that may reflect the statistical independence between ‘what’ and ‘where’. For example, knowing what something is does not, on average, tell me where it is. Another interesting example is that it should be possible to discern the physical structure of systemic states by looking at the brain of any creature. For example, if I looked at my brain, I would immediately guess that my embodied world had a bilateral symmetry, while if I looked at the brain of an octopus, I might guess that it’s embodied world had a rotational symmetry [75]. These examples emphasise the ‘body as world’ in a non-radical enactive or embodied sense [76]. This begs the question of how the generative model—said to be entailed by internal states—shapes perception and, crucially, action. |
| 18 | Note that time here does not refer to clock or universal time, it is the time since an initial (i.e., known) state at any point in a systems history. This enables the itinerancy of nonequilibrium steady-state dynamics to be associated with the number of probabilistic configurations a system will pass through, over time, when prepared in some initial state. |
| 19 | For a recent response to the meta-problem, see [113]. The authors identify three features that are central for conscious systems: (1) depth (including temporal depth); (2) responsiveness to “interoceptive information concerning the agent’s own bodily states and self-predicted patterns of future reaction”; (3) “the capacity to keep inferred, highly certain mid-level sensory re-codings fixed while imaginatively varying top-level beliefs.” ([113], p. 31). Note that these are all gradual features, in line with the view that consciousness is a vague concept. |
| 20 | Note that this treatment departs from the classical conception of computation, according to which there is “no computation without representation” [115]. According to many proponents of this view, representation is prior to computation. In other words, a physical system only performs a computation if it has genuine representational states. Mechanistic conceptions of computation and representation reject this view. Accordingly, physical systems can perform computations without representation (see [116].). |
| 21 | Of course, functionalism itself is ontologically neutral, in that it identifies mental states with functional states that could be realised by different substrates. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Friston, K.J.; Wiese, W.; Hobson, J.A. Sentience and the Origins of Consciousness: From Cartesian Duality to Markovian Monism. Entropy 2020, 22, 516. https://doi.org/10.3390/e22050516
Friston KJ, Wiese W, Hobson JA. Sentience and the Origins of Consciousness: From Cartesian Duality to Markovian Monism. Entropy. 2020; 22(5):516. https://doi.org/10.3390/e22050516
Chicago/Turabian StyleFriston, Karl J., Wanja Wiese, and J. Allan Hobson. 2020. "Sentience and the Origins of Consciousness: From Cartesian Duality to Markovian Monism" Entropy 22, no. 5: 516. https://doi.org/10.3390/e22050516
APA StyleFriston, K. J., Wiese, W., & Hobson, J. A. (2020). Sentience and the Origins of Consciousness: From Cartesian Duality to Markovian Monism. Entropy, 22(5), 516. https://doi.org/10.3390/e22050516




