Fact, Fiction, and Fitness
Abstract
1. Introduction
[Psychophysics] anticipates the discovery of general laws relating the sensations to physical attributes. That is, the measured sensations are expected to correspond systematically to the physical quantities that give rise to them.
Here “objective” means independent of any observer or observation: an “objective aspect of the visual world,” is a structure or state of the OIW. The philosopher Jerry Fodor was adamant that [20]:Definitely do compute explicit properties of the real visible surfaces out there, and one interesting aspect of the evolution of visual systems is the gradual movement toward the difficult task of representing progressively more objective aspects of the visual world.
Fodor is here using “true” in the sense of correspondence referred to above. The cognitive scientist Zygmunt Pizlo concurs that [21]:There is nothing in the ’evolutionary,’ or the ’biological’ or the ’scientific’ worldview that shows, or even suggests, that the proper function of cognition is other than the fixation of true beliefs.
Veridicality is an essential characteristic of perception and cognition. It is absolutely essential. Perception and cognition without veridicality would be like physics without the conservation laws.
OK, so (radical) embodied cognitive scientists can be realists. That is, they can believe that there is an animal-independent world, and that some of our perceptions and thoughts get it right.
2. Natural Selection
Similarly, the psychologist Roger Shepard proposes that evolution shaped our senses to internalize various regularities of the external world. In his article “Perceptual-cognitive universals as reflections of the world” he claims [29]:Our sensory systems are organized to give us a detailed and accurate view of reality, exactly as we would expect if truth about the outside world helps us to navigate it more effectively.
It is worth noting here that the assumption of an OIW underlies all of these statements.Natural selection has ensured that (under favorable viewing conditions) we generally perceive the transformation that an external object is actually undergoing in the external world, however simple or complex, rigid or nonrigid.
Looked at from an evolutionary point of view, the principal function of nervous systems is [...] to get the body parts where they should be in order that the organism may survive [...] Truth, whatever that is, definitely takes the hindmost.
Later he concedes, however, that “we do have some reliable notions about the distribution of middle-sized objects around us” [32]. It is now widely understood that the primary selective forces in human evolution, at any rate, are social [33]. The “world” to which human perceptions are adapted is, therefore, not just the presumed OIW, but is also a world of other experiencing organisms. While the social character of the human world is often explicitly acknowledged (e.g., by Trivers [28]), the OIW is still regarded as the “ground truth” by theorists of veridical perception.Our minds evolved by natural selection to solve problems that were life-and-death matters to our ancestors, not to commune with correctness.
3. Evolutionary Games
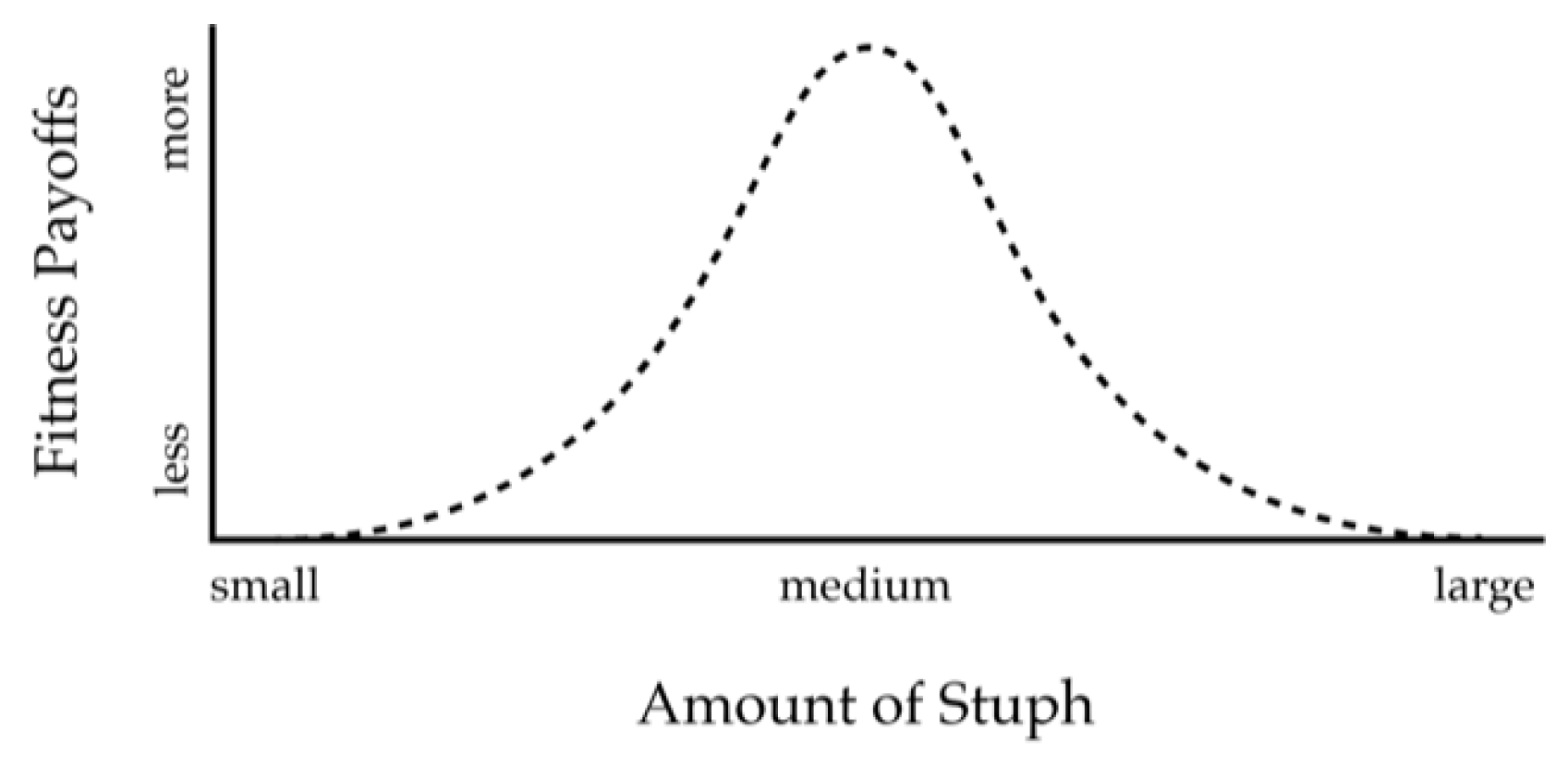
4. Four Theorems
3D symmetrical shapes of objects allow us not only to perceive the shapes, themselves, veridically, but also to perceive the sizes, positions, orientations and distances among the objects veridically.
5. Discussion: Does Natural Selection Favor Veridical Perceptions?
- We use the counting measure to prove that the probabilities of homomorphisms are zero. One might argue that this is the wrong measure. The main reason for using counting measure is that it is the canonical unbiased measure on finite sets of payoff functions. Proposing any specific biased measure would need careful explanation of why the logic of natural selection dictates this specific biased measure. We believe, however, that this burden cannot be met.
- The conclusions of our proofs are immune to the objection, “You cannot say whether something is veridical or not without first knowing what it is saying.” This objection assumes a representational account of perception, which is not required by our proof. Moreover, this objection is false on its face: an error-correcting code detects that a message received is not a veridical copy of the message sent, without knowing what the message is saying.
- One might wonder whether the theory of evolution can be an impartial arbiter in the debate over whether natural selection entails veridical perceptions. After all, does the theory itself not simply assume the veridicality of certain perceptions, such as organisms, species, physical resources, and (using some laboratory assay) DNA? How could the theory conclude against veridicality without refuting itself? This quandary has a simple solution, however. There is an algorithmic core to evolution by natural selection—variation, selection, and retention—which requires no commitment to DNA, organisms, and other such claims about the structure of the world. This algorithm, popularized as “Universal Darwinism,” applies to the evolution of organisms, but it has been speculated that it even applies to the evolution of art, music, memes, language, and social institutions [46,47].
- Our argument is based on evolution by natural selection. One can object that evolution is affected by many other factors—including genetic drift, pleiotropy, linkage, and constraints from physics and biochemistry—and that natural selection plays a relatively minor role.However, the standard evolutionary argument for veridical perceptions is that accurate perceptions are fitter, which is an argument from natural selection. To our knowledge, there are no arguments for veridical perception based on genetic drift, pleiotropy, linkage, or constraints from physics and biochemistry. Such arguments seem unlikely. It is hard to imagine how neutral drift, for instance, could favor veridical perceptions.
- Our argument focuses on just four structures: total orders, symmetric groups, cyclic groups, and measurable structures. There are, of course, many other structures relevant to perception, such as topologies, metrics, and partial orders. These structures also need to be studied, to see whether they are preserved by payoff functions. Ideally, one can hope for a general theorem, perhaps using category theory, that specifies all structures that are not preserved and thus not veridically perceived.
- One might object that many payoff functions are close to being homomorphisms of the structures of the world in, say, the sense of a norm, and thus that natural selection will shape perceptions to be close to veridical, if not precisely veridical. We reply that they will also be close to being homomorphisms of countless other structures that are not in the world, and thus that natural selection will equally shape perceptions to be close to countless non-veridical structures. There is no argument here for natural selection favoring perceptions that are close to veridical rather than close to countless non-veridical possibilities.
6. Conclusions
These brilliantly colored and kinetic visions…are immediate and vivid…I work using just one ’sense trigger,’ such as sound…listening to only one selection of music at a time, played over and over again until the painting or sculpture is finished. A work need not be completed in one day provided I listen exactly to the same music when I return to work.
Evolution is likely not done with the perceptual interface of Homo sapiens. It is still tinkering. Here we see the data structures of physical objects given novel use in hearing and taste. This application is clearly not veridical. Ball bearings are not a veridical presentation of Karo syrup; ivy is not a veridical presentation of angostura bitters. The physical objects that we normally see when we open our eyes are, no less than these synesthetic objects, non-veridical data structures. They are just satisficing solutions to the problem of compressing and presenting fitness information for action, planning, and reasoning.When I taste something with an intense flavor, the feeling sweeps down my arm into my fingertips. I feel it—its weight, its texture, whether it’s warm or cold, everything. I feel it like I’m actually grasping something. Of course, there’s nothing really there. But it’s not an illusion because I feel it.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OIW | Observer-independent physical world |
| ITP | Interface theory of perception |
Appendix A. Proofs
Appendix A.1. Definitions
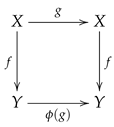
Appendix A.2. Total Orders Theorem: Counting Functions that are Monotonic, i.e., First-Order Homomorphisms Preserving (or Reversing) Order
Appendix A.3. Permutation Groups Theorem: Counting Functions Preserving Symmetry under the Symmetric Group S n
Appendix A.4. Cyclic Groups Theorem: Counting Functions Preserving Cyclicity on a Finite Group; or Periodic Functions on a Lattice
Appendix A.5. Measurable Structure Theorem: Counting Measurable Functions, that is, (Backward) Homomorphisms Preserving Algebra or Partition Structure
- 1.
- The collection of subsets in the partition corresponding to the algebra on W will be termed the base of the algebra and will be written as .
- 2.
- The order of an algebra is the number of sets constituting its base. For example, the order of the trivial algebra is 1, and the order of the discrete algebra is the size of the underlying set.
- 3.
- The characteristic of an algebra is the multiset giving the sizes of each of the elements of the base: we say that the characteristic is if there are subsets of size . Thus , where n is the size of W. (In other words, the characteristic of an algebra is a partition, in the usual sense, of the number n. Saying that two algebras have the same characteristic is an equivalence relation on the collection of algebras: either algebra can be obtained from the other by a simple renumbering, or permutation, of the set W.)
- If at least one of a and b belong to multi-element sets of , we can perform a basic move, as above, to bring them into the same basic set of the new algebra .
- If both of a and b belong to singleton sets of , then because of the non-discreteness, there is another base set C with 2 or more elements. Pick an element . Make these elements companions by performing three basic moves in sequence, as follows:Of course, is not empty, so these moves preserve the order of the new algebra.
- (i)
- . Then for and , where consists of the remaining elements of W: i.e., .
- (ii)
- . Then for and .
References
- Koenderink, J.J.; van Doorn, A.J.; Kappers, A.M.; Lappin, J.S. Large-scale visual frontoparallels under full-cue conditions. Perception 2002, 31, 1467–1475. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J.; Kappers, A.M.; Doumen, M.J.A.; Todd, J.T. Exocentric pointing in depth. Vis. Res. 2008, 48, 716–723. [Google Scholar] [CrossRef] [PubMed]
- Koenderink, J.J.; Albertazzi, L.; van Doorn, A.J.; van Ee, R.; van de Grind, W.A.; Kappers, A.M.L.; Lappin, J.S.; Norman, J.F.; Stihn Oomes, A.H.; te Pas, S.P.; et al. Does monocular visual space contain planes? Acta Psychol. 2010, 134, 40–47. [Google Scholar] [CrossRef] [PubMed]
- Masrour, F. The geometry of visual space and the nature of visual experience. Philos. Stud. 2015, 172, 1813–1832. [Google Scholar] [CrossRef]
- Koenderink, J.J. Color in the Wild; De Clootrans Press: Utrecht, The Netherlands, 2018; Available online: http://www.gestaltrevision.be/pdfs/koenderink/ColourInTheWild.pdf (accessed on 26 April 2020).
- Logvinenko, A.D. The geometric structure of color. J. Vis. 2015, 15, 16. [Google Scholar] [CrossRef]
- Hoffman, D.D. Visual Intelligence: How We Create What We See; W.W. Norton: New York, NY, USA, 1998. [Google Scholar]
- Koenderink, J.J. Solid Shape; MIT Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Koenderink, J.J. About Shape; De Clootrans Press: Utrecht, The Netherlands, 2016; Available online: http://www.gestaltrevision.be/pdfs/koenderink/ShapeTutorial.pdf (accessed on 1 February 2020).
- Luce, R.D.; Krumhansl, C.L. Measurement, scaling, and psychophysics. In Stevens’ Handbook of Experimental Psychology: Perception and Motivation; Learning and Cognition; Atkinson, R.C., Herrnstein, R.J., Lindzey, G., Luce, R.D., Eds.; John Wiley & Sons: Oxford, UK, 1988; pp. 3–74. [Google Scholar]
- Luce, R.D. A psychophysical theory of intensity proportions, joint presentations, and matches. Psychol. Rev. 2002, 109, 520–532. [Google Scholar] [CrossRef]
- Steingrimsson, R.; Luce, R.D. Empirical evaluation of a model of global psychophysical judgments: III. A form for the psychophysical function and intensity filtering. J. Math. Psychol. 2006, 50, 15–29. [Google Scholar] [CrossRef]
- Pais, A. Einstein and the quantum theory. Rev. Mod. Phys. 1979, 51, 863–914. [Google Scholar] [CrossRef]
- David, M. The correspondence theory of truth. In Stanford Encyclopedia of Philosophy (Fall 2016); Zalta, E., Ed.; Metaphysics Research Lab, Stanford University: Stanford, CA, USA, 2016; Available online: https://plato.stanford.edu/entries/truth-correspondence (accessed on 26 April 2020).
- Adelson, E.H.; Pentland, A. The perception of shading and reflectance. In Perception as Bayesian Inference; Knill, D.C., Richards, W., Eds.; Cambridge University Press: Cambridge, UK, 1996; pp. 409–423. [Google Scholar]
- Pizlo, Z. Perception viewed as an inverse problem. Vis. Res. 2001, 41, 3145–3161. [Google Scholar] [CrossRef]
- Hoffman, D.D.; Singh, M. Computational Evolutionary Perception. Perception 2012, 41, 1073–1091. [Google Scholar] [CrossRef]
- Hoffman, D.D.; Singh, M.; Prakash, C. The Interface Theory of Perception. Psychon. Bull. Rev. 2015, 22, 1480–1506. [Google Scholar] [CrossRef] [PubMed]
- Marr, D. Vision; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Fodor, J.A. The Mind Doesn’t Work That Way: The Scope and Limits of Computational Psychology; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Pizlo, Z.; Li, Y.; Sawada, T.; Steinman, R.M. Making a Machine That Sees Like Us; Oxford University Press: New York, NY, USA, 2014. [Google Scholar]
- Chemero, A. Radical Embodied Cognitive Science; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Noë, A.; O’Regan, J.K. On the brain-basis of visual consciousness: A sensorimotor account. In Vision and Mind: Selected Readings in the Philosophy of Perception; Noë, A., Thompson, E., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 567–598. [Google Scholar]
- Smith, J.M.; Szathmáry, E. The Major Transitions in Evolution. Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Michod, R.E. Darwinian Dynamics; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Hoffman, D.D. The interface theory of perception. In Object Categorization: Computer and Human Vision Perspectives; Dickinson, S., Tarr, M., Leonardis, A., Schiele, B., Eds.; Cambridge University Press: New York, NY, USA, 2009; pp. 148–165. [Google Scholar]
- Palmer, S. Vision Science: Photons to Phenomenology; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Trivers, R.L. The Folly of Fools: The Logic of Deceit and Self-Deception in Human Life; Basic Books: New York, NY, USA, 2011. [Google Scholar]
- Shepard, R. Perceptual-cognitive universals as reflections of the world. Behav. Brain Sci. 2001, 24, 581–601. [Google Scholar] [CrossRef] [PubMed]
- Churchland, P. Epistemology in the age of neuroscience. J. Philos. 1987, 84, 544–555. [Google Scholar] [CrossRef]
- Pinker, S. How the Mind Works; W.W. Norton: New York, NY, USA, 1999. [Google Scholar]
- Pinker, S. So how does the mind work? Mind Lang. 2005, 20, 1–24. [Google Scholar] [CrossRef]
- Dunbar, R.I.M.; Shultz, S. Evolution in the social brain. Science 2007, 317, 1344–1347. [Google Scholar] [CrossRef]
- Nowak, M. Evolutionary Dynamics: Exploring the Equations of Life; Harvard University Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems. An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Prentner, R.; Fields, C. Using AI Methods to Evaluate a Minimal Model for Perception. Open Philos. 2019, 2, 503–524. [Google Scholar] [CrossRef]
- Gould, J. The Structure of Evolutionary Theory; Belknap Press: Cambridge, MA, USA, 2002. [Google Scholar]
- Mayr, E. Animal Species and Evolution; Belknap Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Smith, J.M. Evolution and the Theory of Games; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Singh, M.; Hoffman, D.D. Natural selection and Shape perception. In Shape Perception in Human and Computer Vision: An Interdisciplinary Perspective; Dickinson, S., Pizlo, Z., Eds.; Springer: London, UK, 2013; pp. 171–185. [Google Scholar]
- Mark, J.T.; Marion, B.B.; Hoffman, D.D. Natural selection and veridical perceptions. J. Theor. Biol. 2010, 266, 504–515. [Google Scholar] [CrossRef]
- Hoffman, D.D. The Case against Reality: Why Evolution Hid the Truth from Our Eyes; W.W. Norton: New York, NY, USA, 2019. [Google Scholar]
- Pizlo, Z. Philosophizing cannot substitute for experimentation: Comment on Hoffman, Singh & Prakash. Psychon. Bull. Rev. 2015, 22, 1546–1547. [Google Scholar]
- Reis, C.; Rankin, S.A. Abstract Algebra: Introduction to Groups, Rings and Fields with Applications, 2nd ed.; World Scientific: Singapore, 2017. [Google Scholar]
- Diaz-Vargas, J.; Vargas de los Santos, G. The number of homomorphisms from Zn to Zm. Abstraction Appl. 2015, 13, 1–3. [Google Scholar]
- Dawkins, R. Universal Darwinism. In Evolution from Molecules to Man; Bemdall, D.S., Ed.; Cambridge University Press: Cambridge, UK, 1983. [Google Scholar]
- Dennett, D.C. Darwin’s Dangerous Idea; Touchstone Press: New York, NY, USA, 2005. [Google Scholar]
- Koenderink, J.J. Vision as a user interface. In Proceedings of the Human Vision and Electronic Imaging XVI, San Francisco, CA, USA, 24–27 January 2011. [Google Scholar] [CrossRef]
- Koenderink, J.J. World, environment, umwelt, and inner-world: A biological perspective on visual awareness. In Proceedings of the Human Vision and Electronic Imaging XVIII, San Francisco, CA, USA, 4–7 February 2013. [Google Scholar] [CrossRef]
- Pflüger, L.S.; Oberzaucher, E.; Katina, S.; Holzleitner, I.J.; Grammer, K. Cues to fertility: Perceived attractiveness and facial shape predict reproductive success. Evol. Hum. Behav. 2018, 33, 708–714. [Google Scholar] [CrossRef]
- Cytowic, R.E.; Eagleman, D.M. Wednesday is Indigo Blue: Discovering the Brain of Synesthesia; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Cytowic, R.E. The Man Who Tasted Shapes; MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Robbins, H. A Remark on Stirling’s Formula. Am. Math. Mon. 1955, 62, 26–29. [Google Scholar] [CrossRef]
- Rotman, J. Galois Theory; Springer: New York, NY, USA, 1998. [Google Scholar]
- Morandi, P. Automorphisms of Sn and of An; Lecture notes; New Mexico State University: Las Cruces, NM, USA; Available online: https://wordpress.nmsu.edu/pamorand/mathematical-notes/ (accessed on 27 April 2020).

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prakash, C.; Fields, C.; Hoffman, D.D.; Prentner, R.; Singh, M. Fact, Fiction, and Fitness. Entropy 2020, 22, 514. https://doi.org/10.3390/e22050514
Prakash C, Fields C, Hoffman DD, Prentner R, Singh M. Fact, Fiction, and Fitness. Entropy. 2020; 22(5):514. https://doi.org/10.3390/e22050514
Chicago/Turabian StylePrakash, Chetan, Chris Fields, Donald D. Hoffman, Robert Prentner, and Manish Singh. 2020. "Fact, Fiction, and Fitness" Entropy 22, no. 5: 514. https://doi.org/10.3390/e22050514
APA StylePrakash, C., Fields, C., Hoffman, D. D., Prentner, R., & Singh, M. (2020). Fact, Fiction, and Fitness. Entropy, 22(5), 514. https://doi.org/10.3390/e22050514