Characterization of Marangoni Forced Convection in Casson Nanoliquid Flow with Joule Heating and Irreversibility
Abstract
1. Introduction
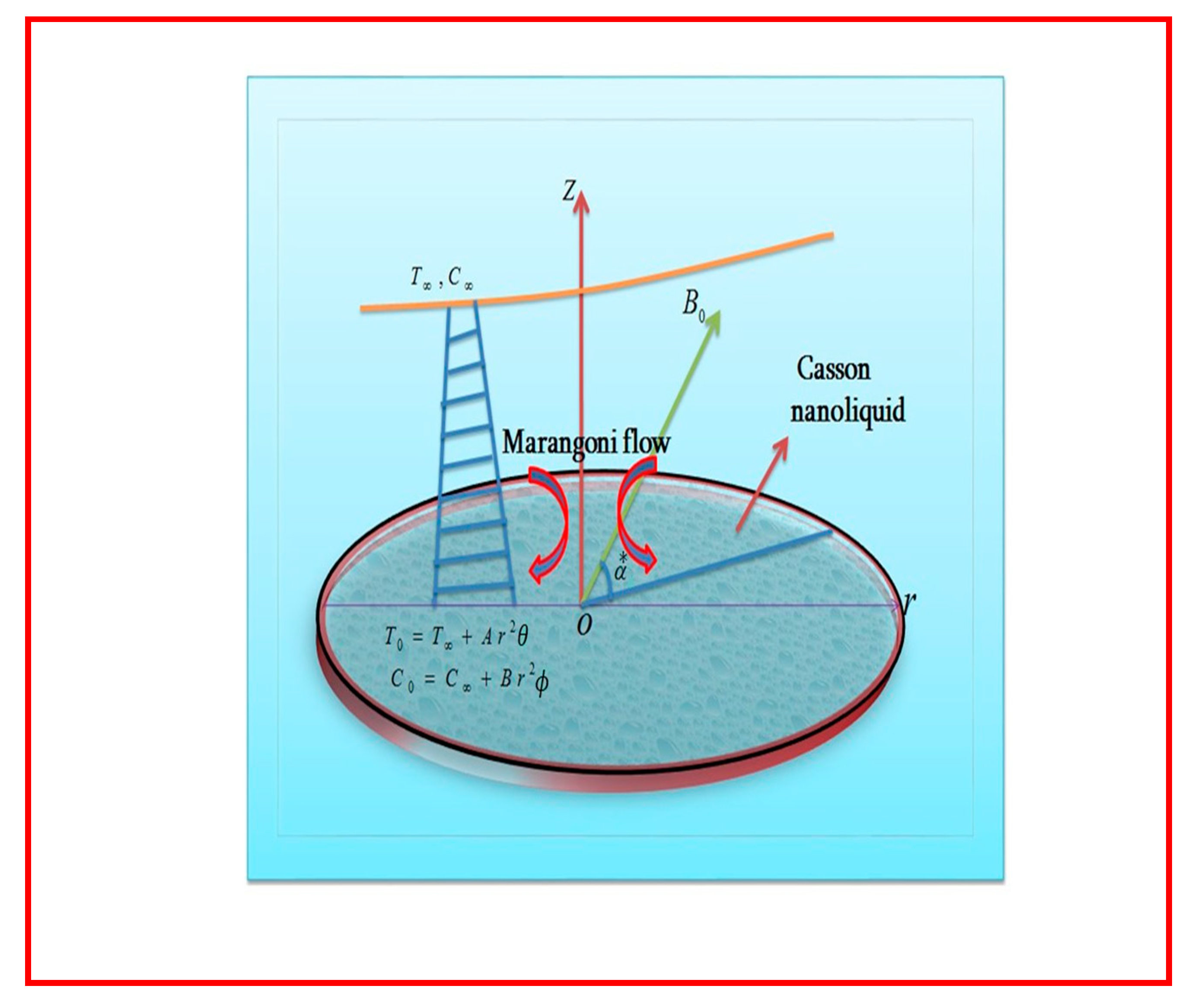
2. Statement of Problem
3. Entropy Modeling
4. Bejan Number
5. Physical Quantities
5.1. Nusselt Number
5.2. Sherwood Number
6. Solution Methodology
7. Validation of Result
8. Discussion
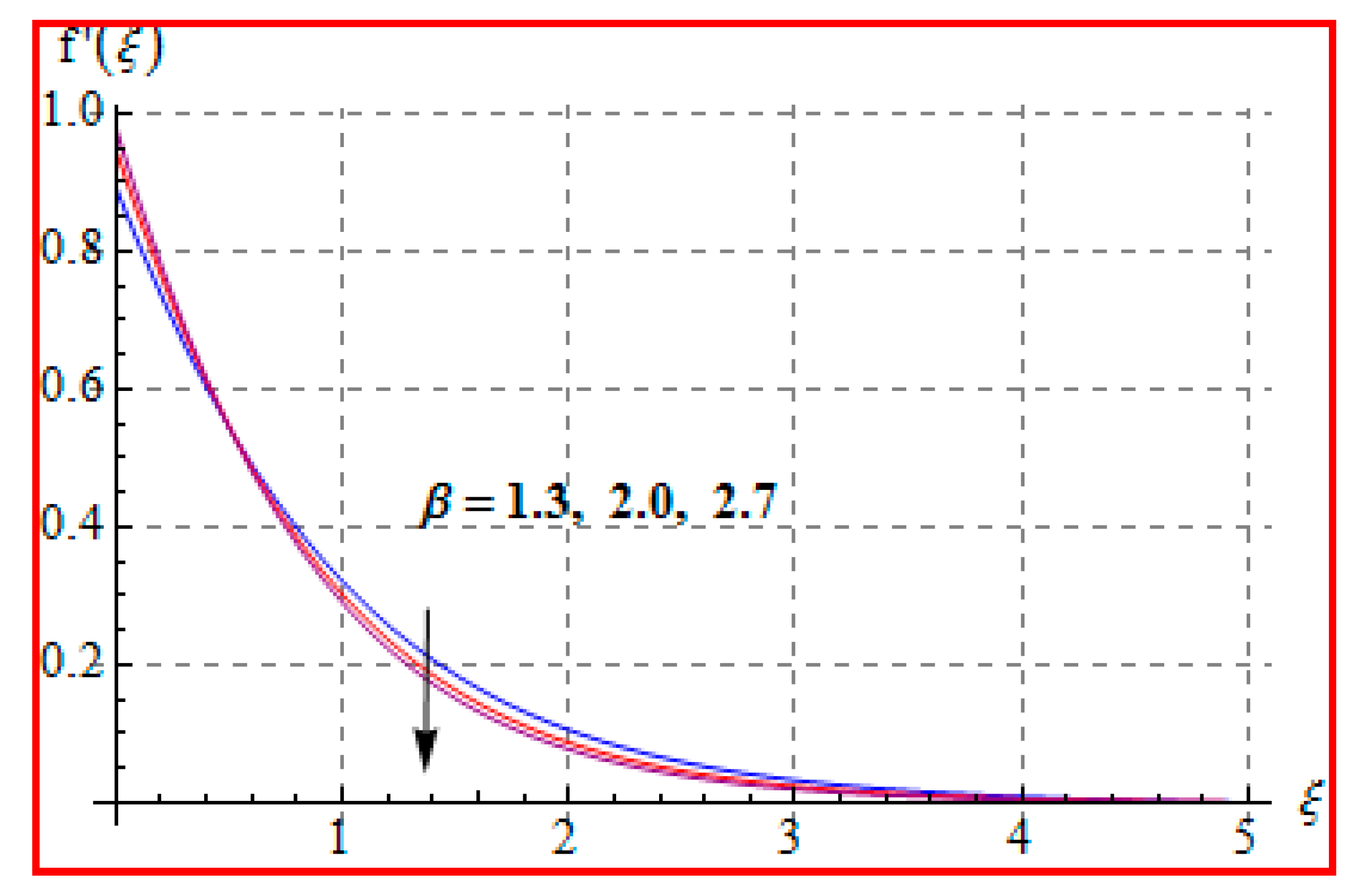
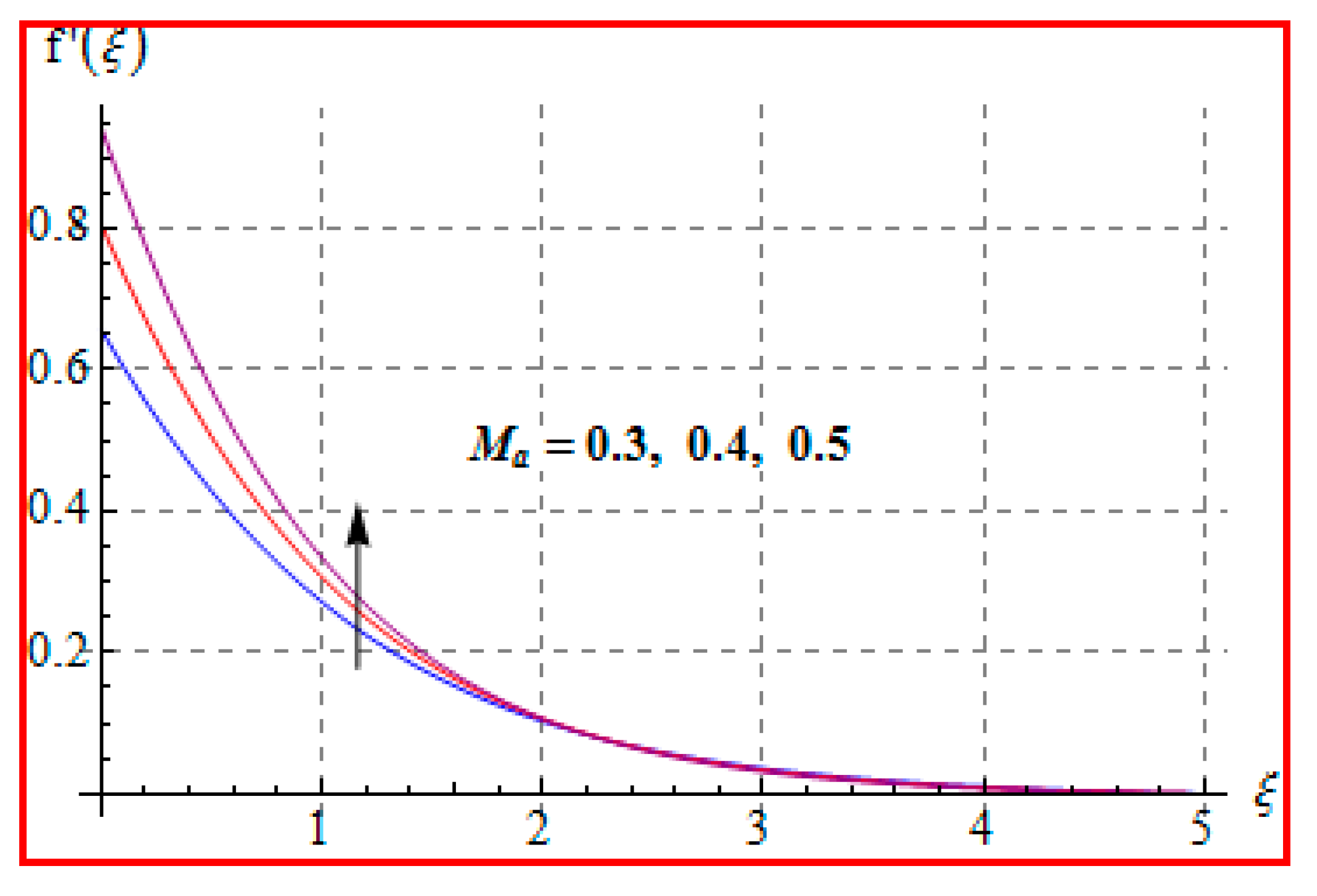
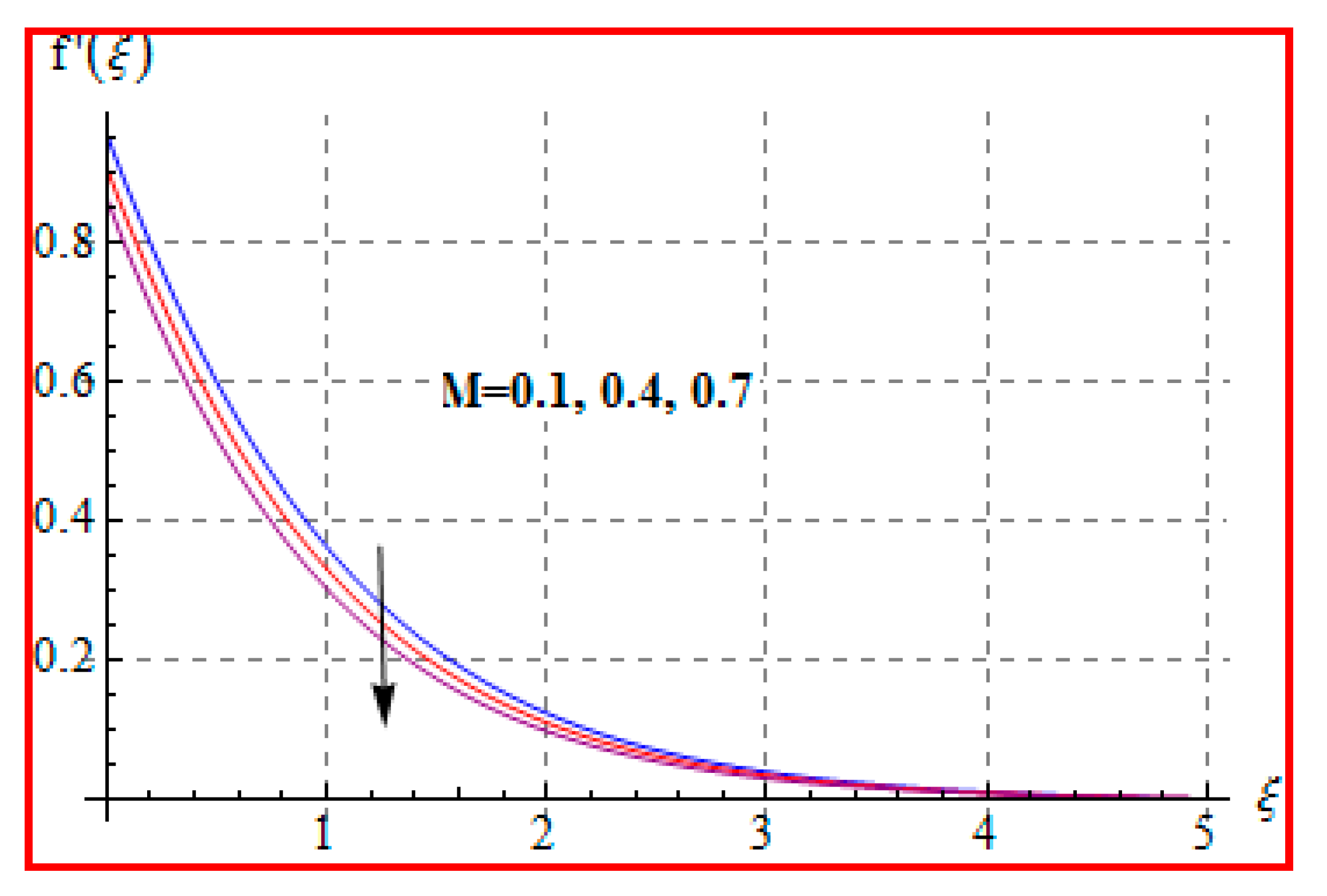
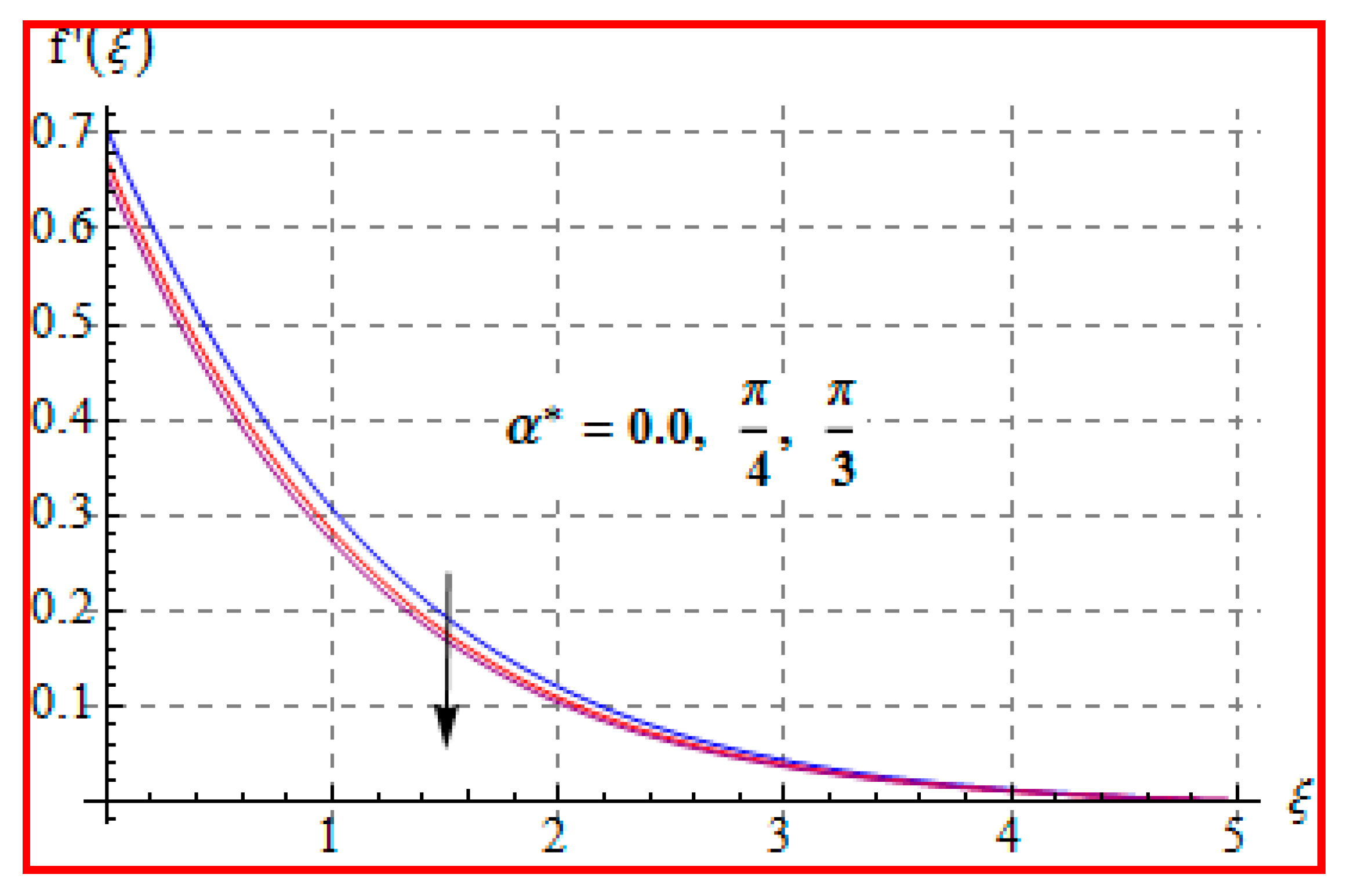
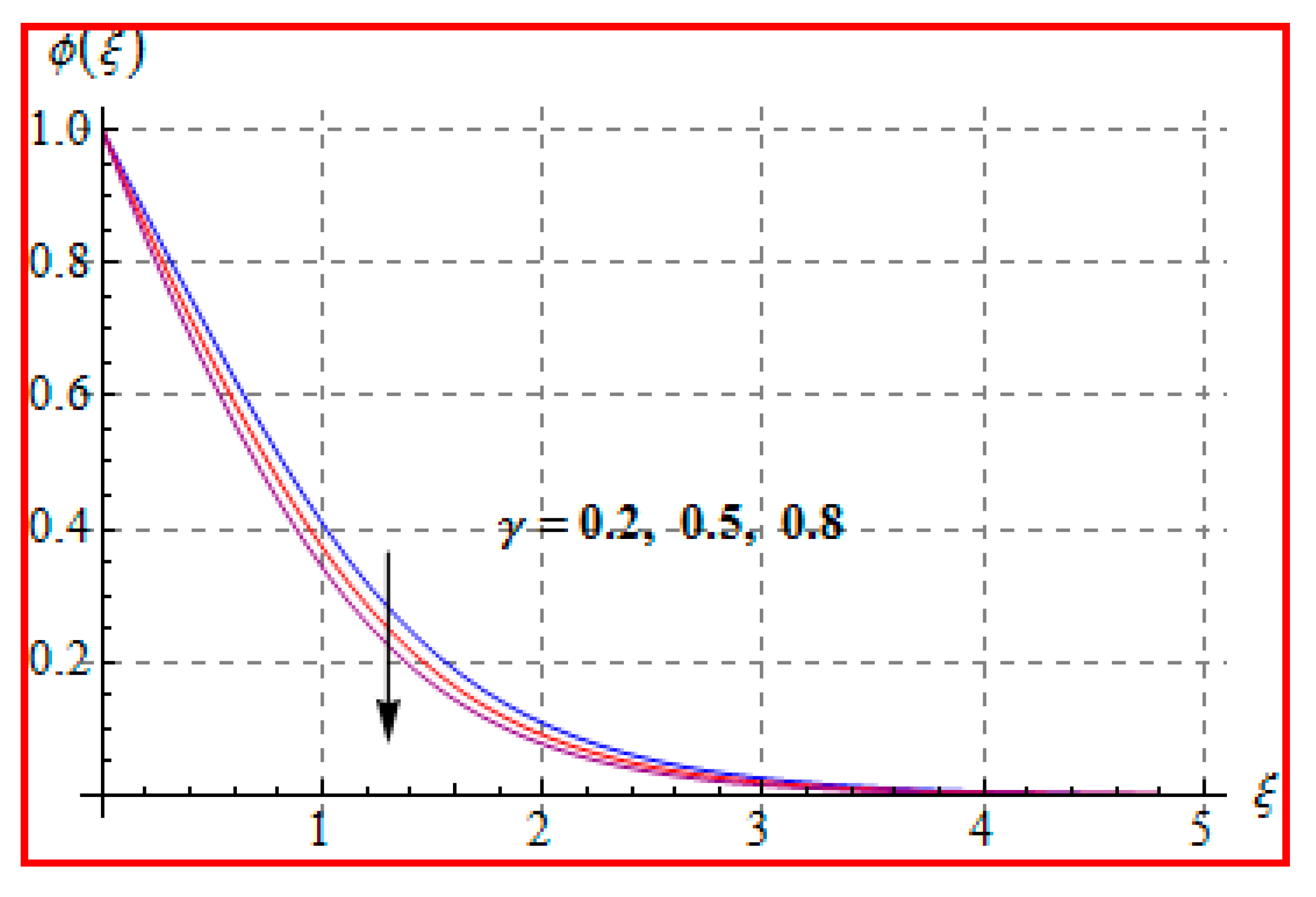
8.1. Velocity
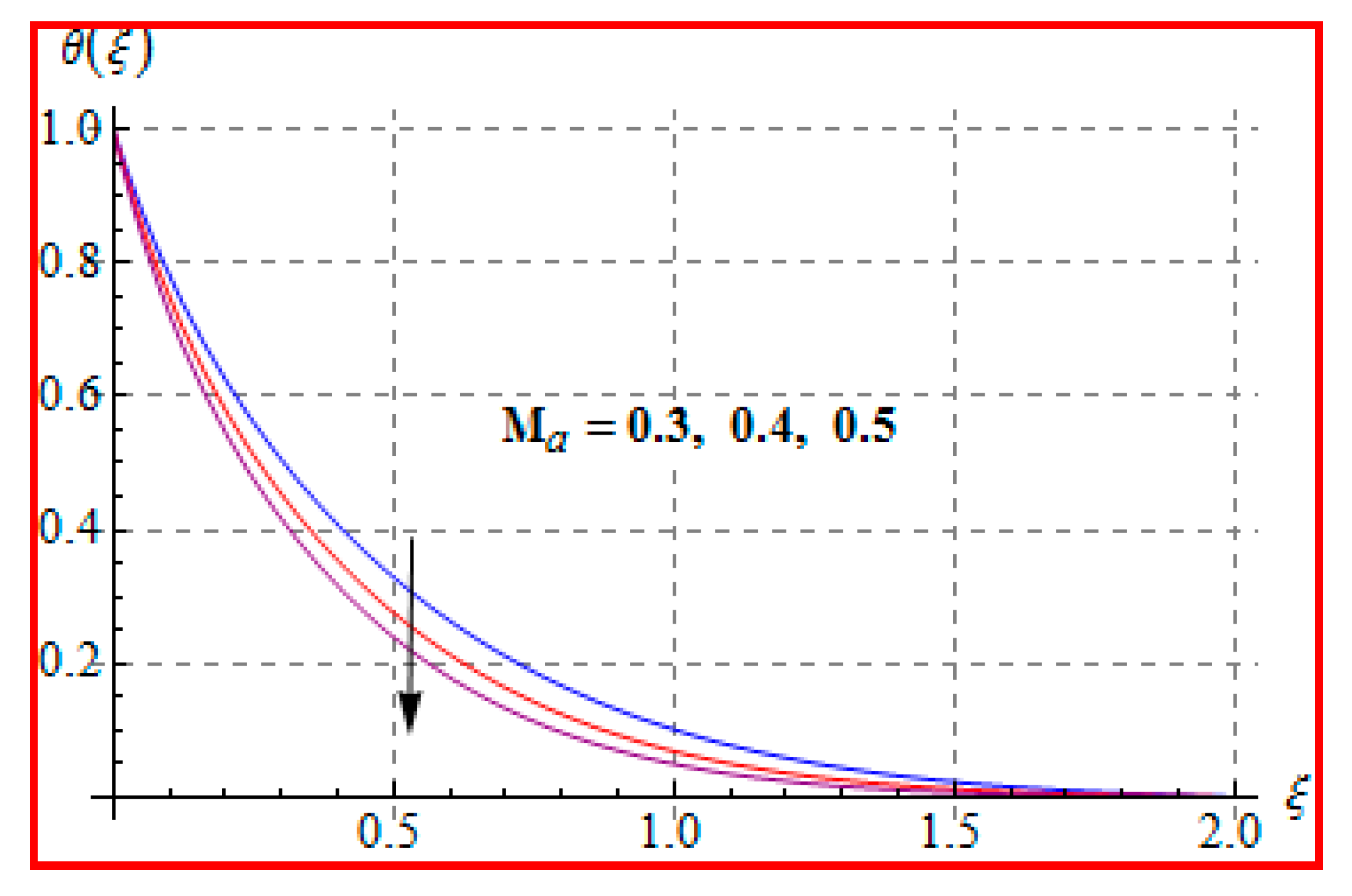
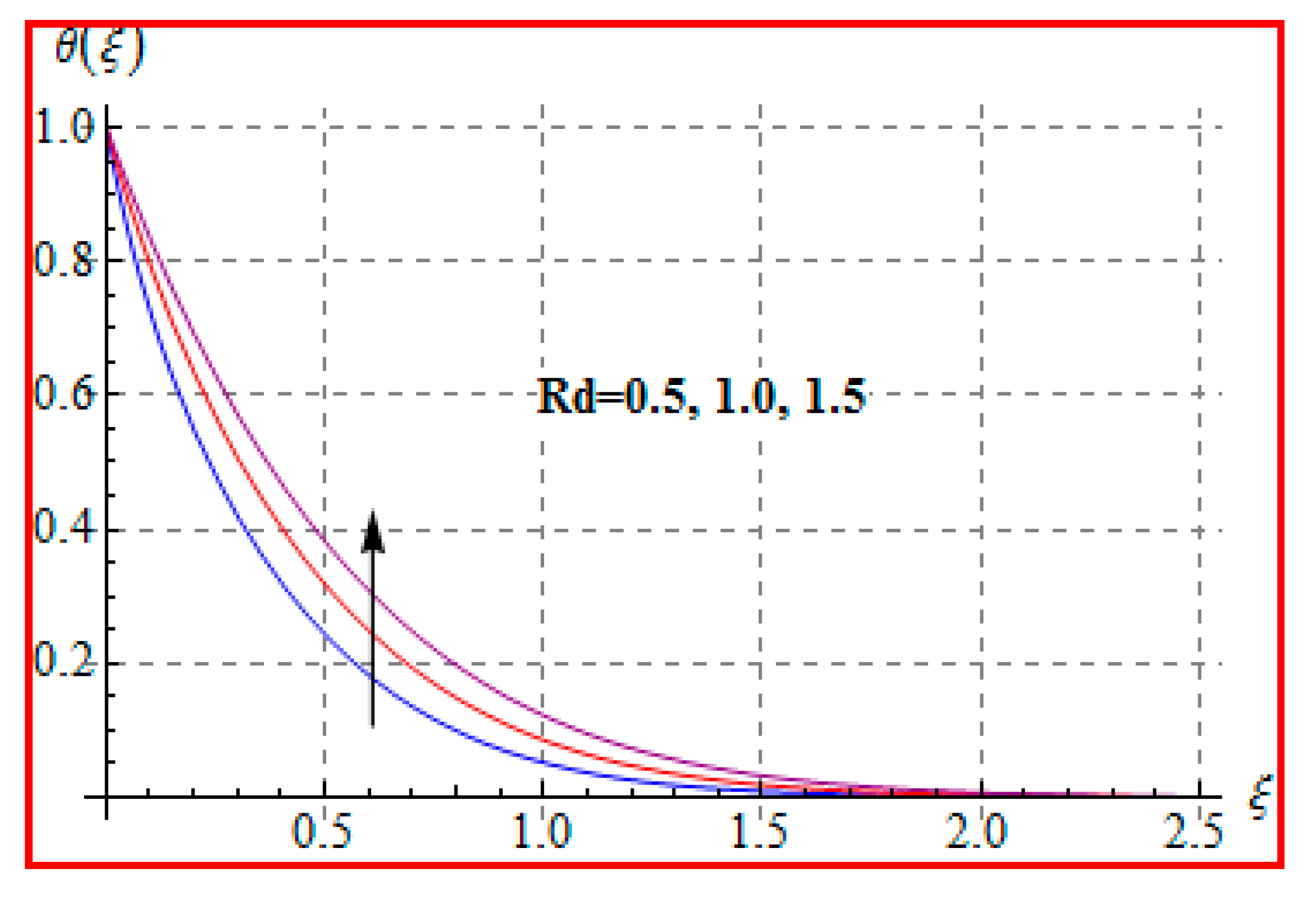
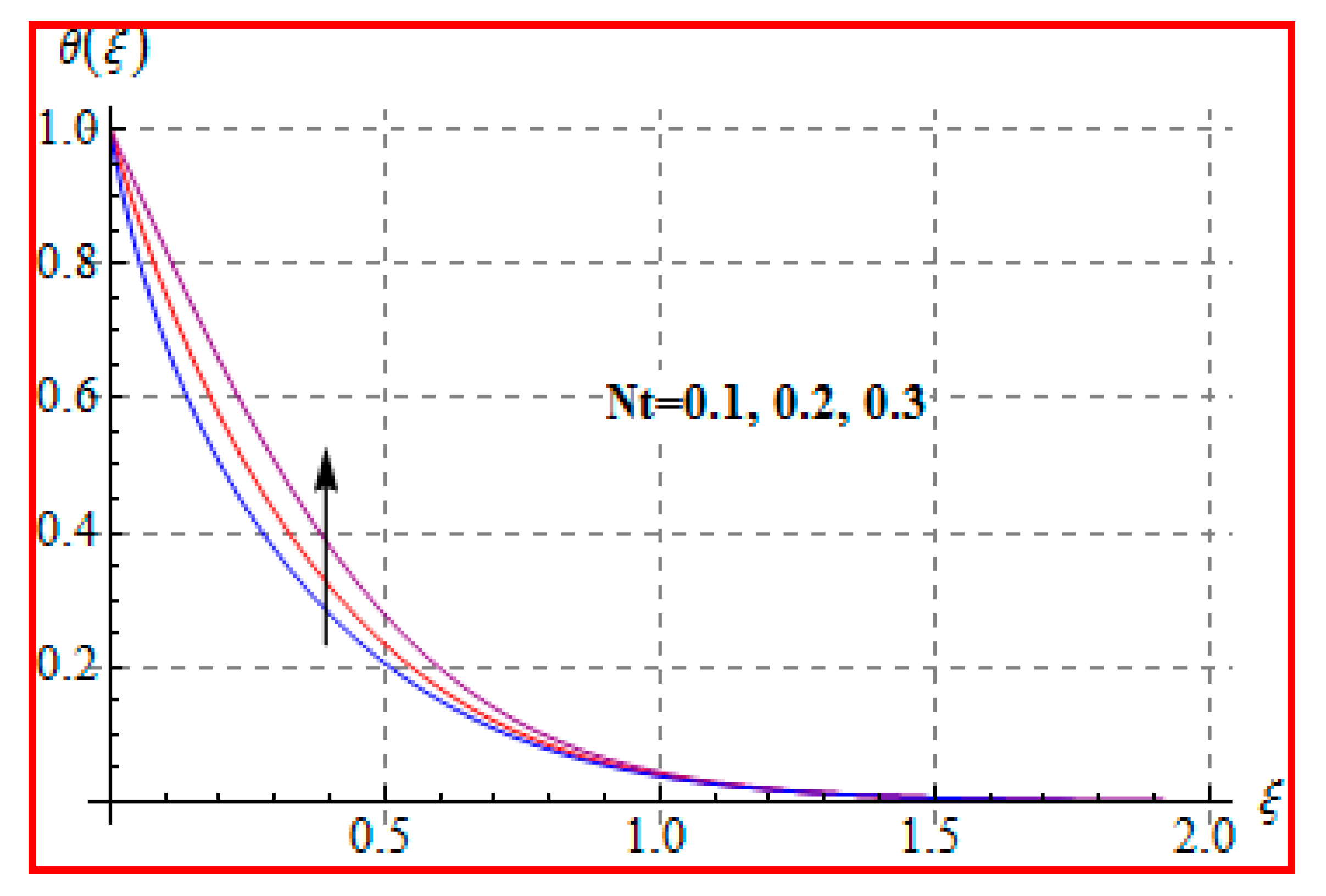
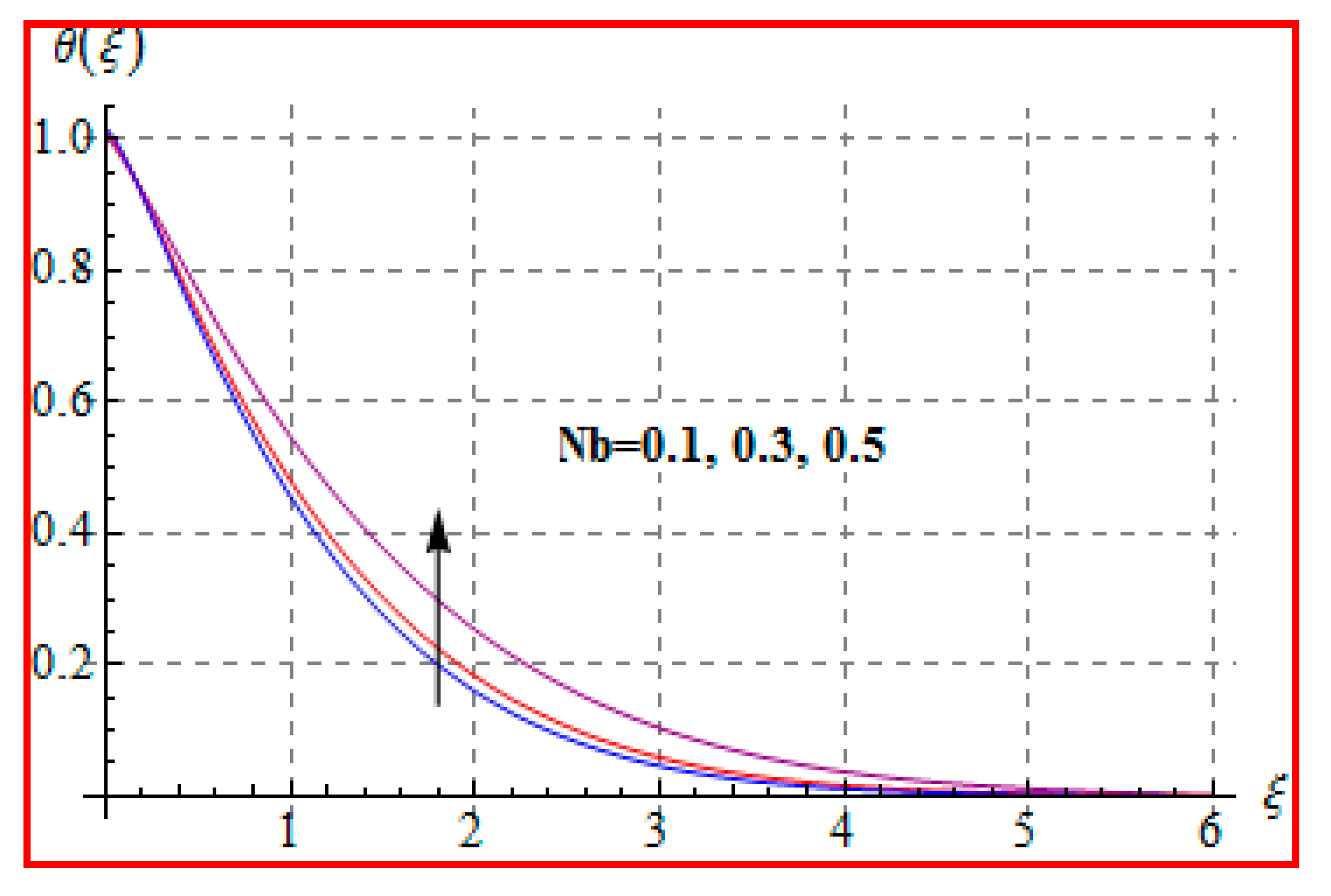
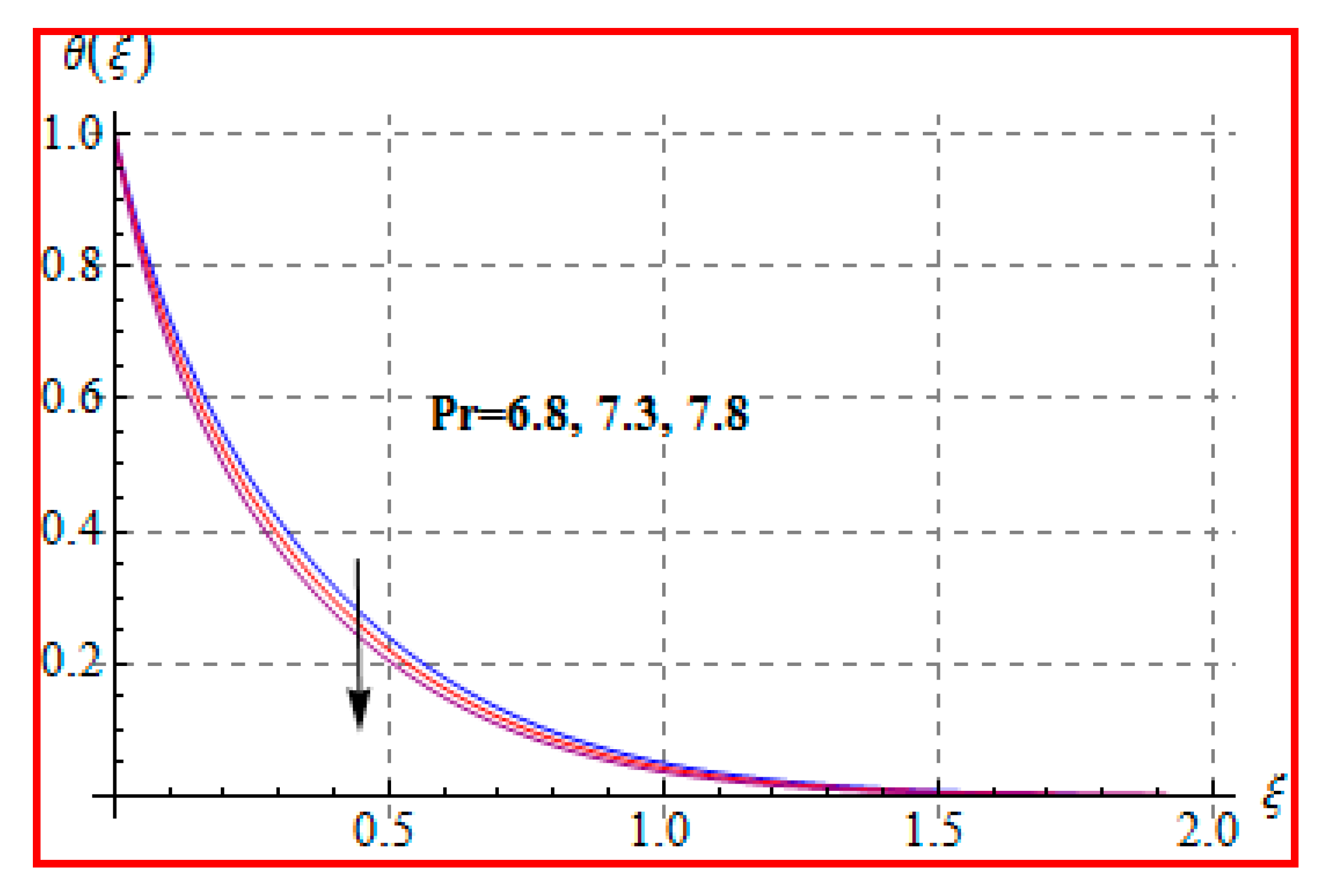
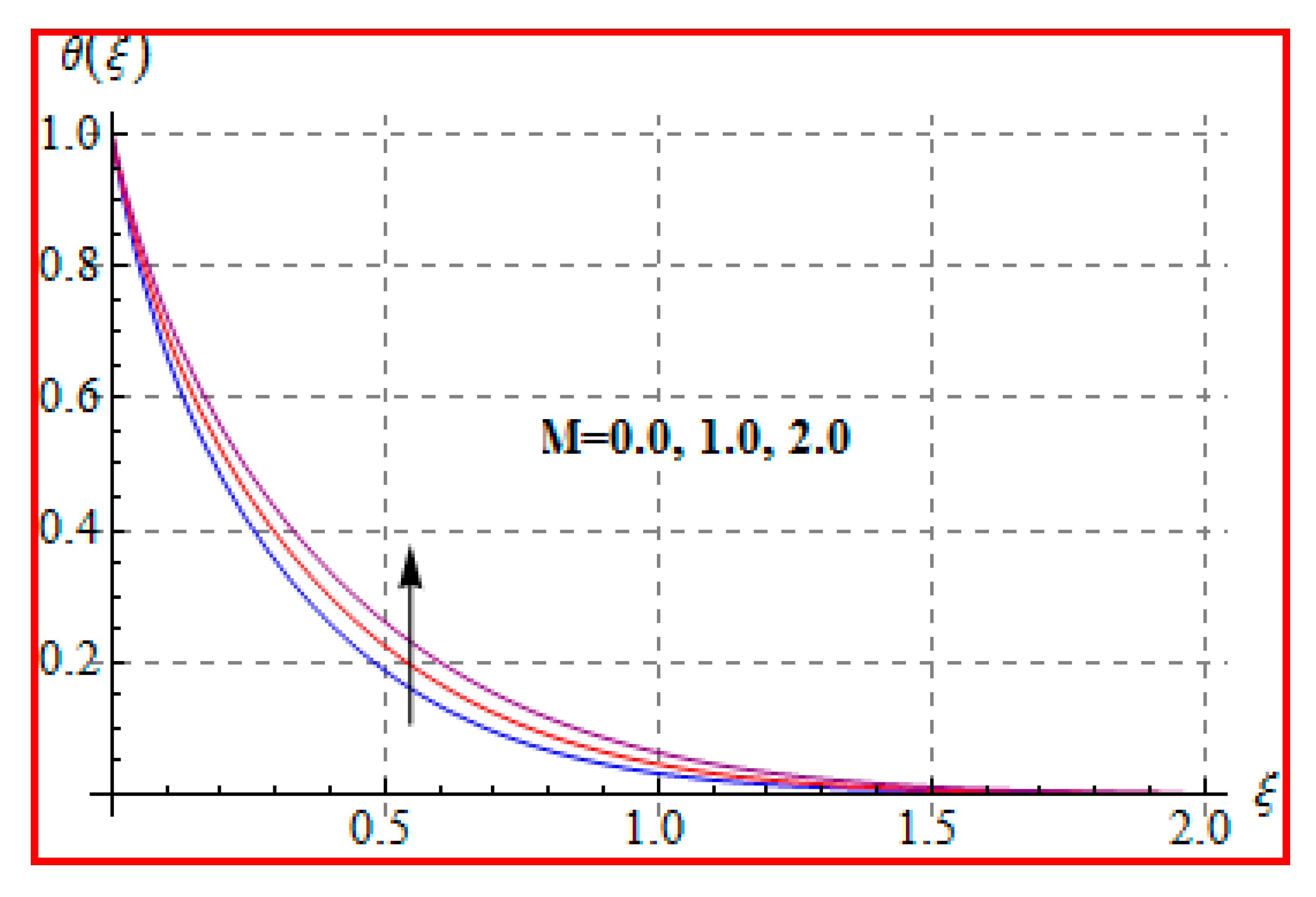
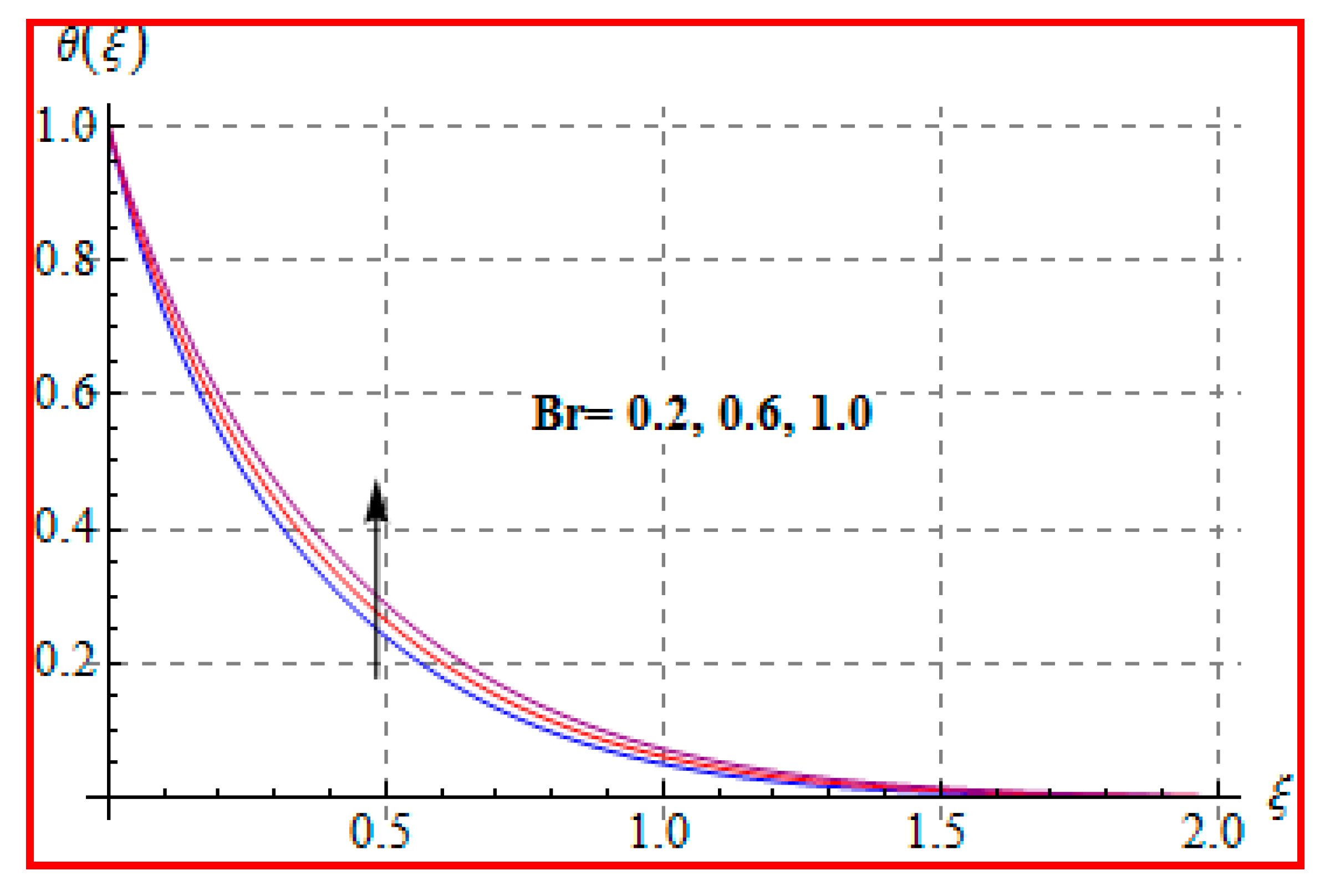
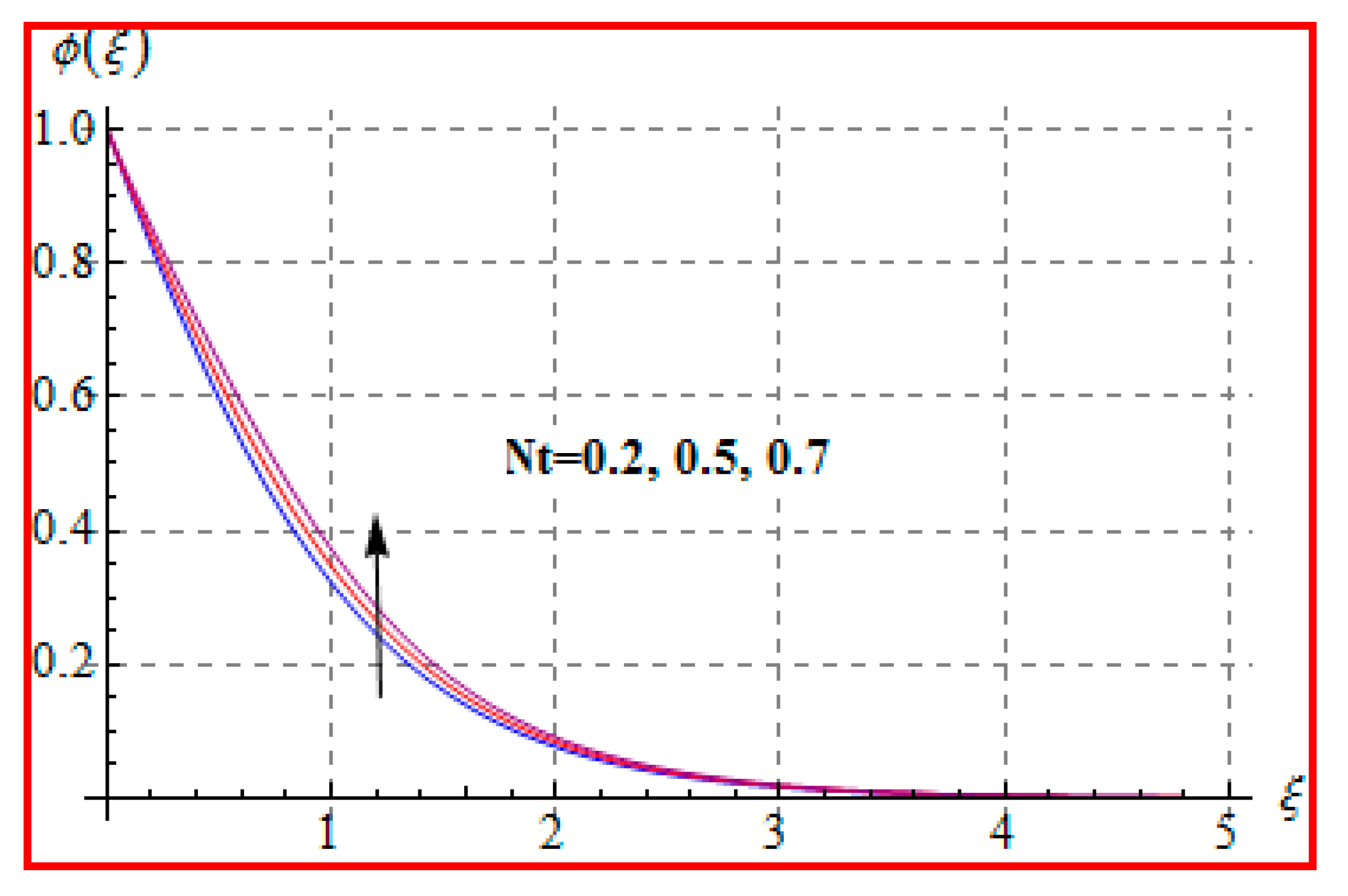
8.2. Temperature
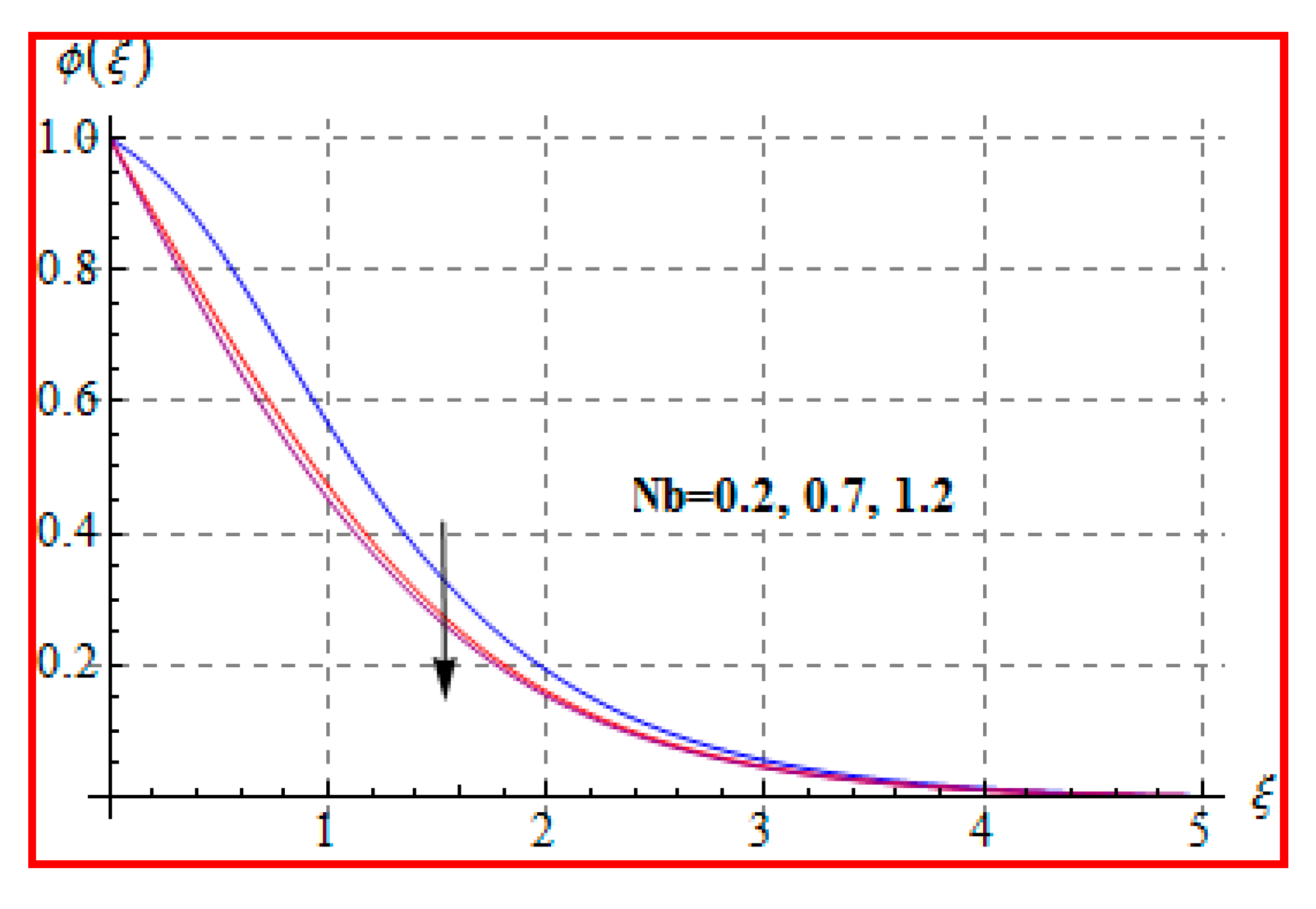
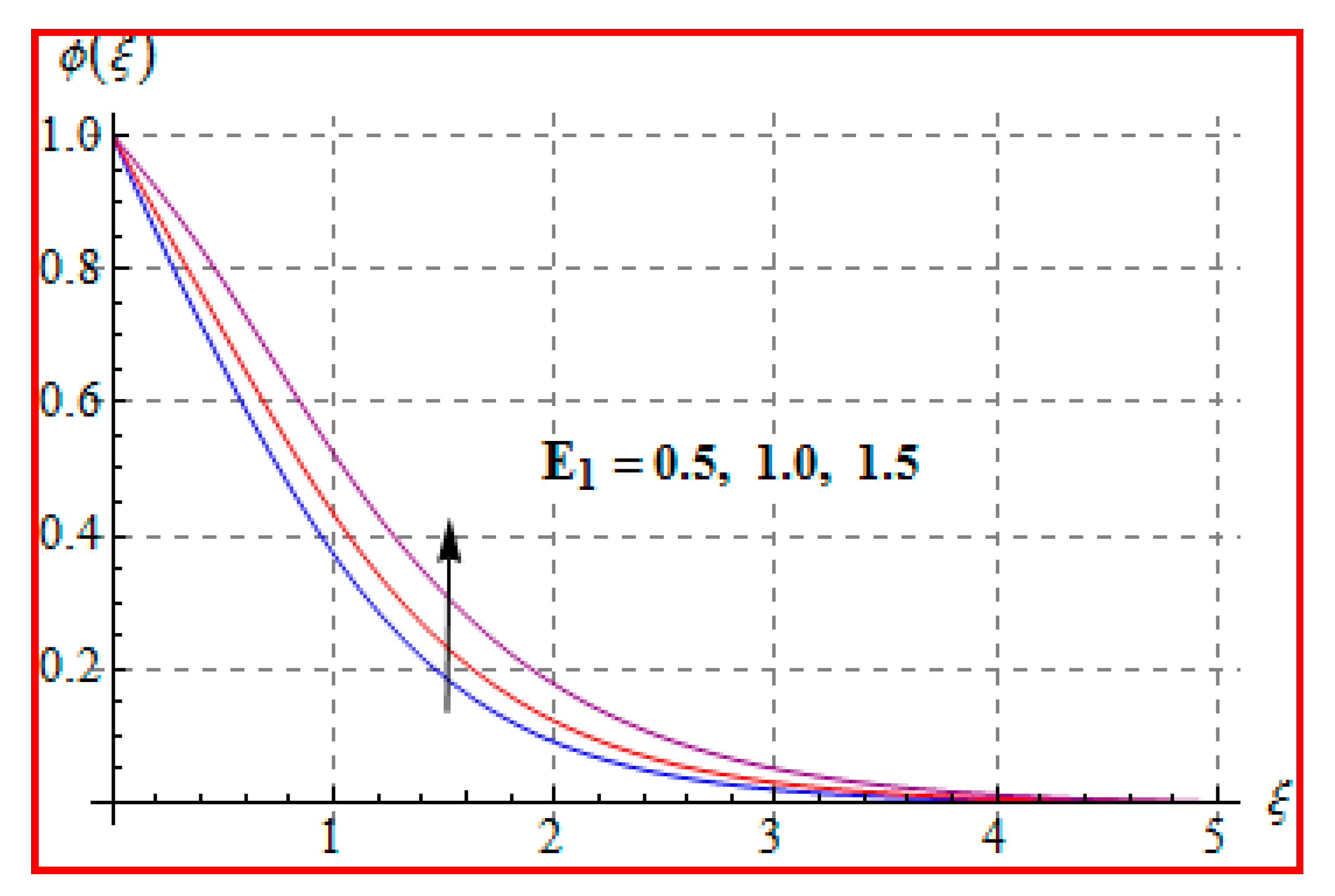
8.3. Concentration
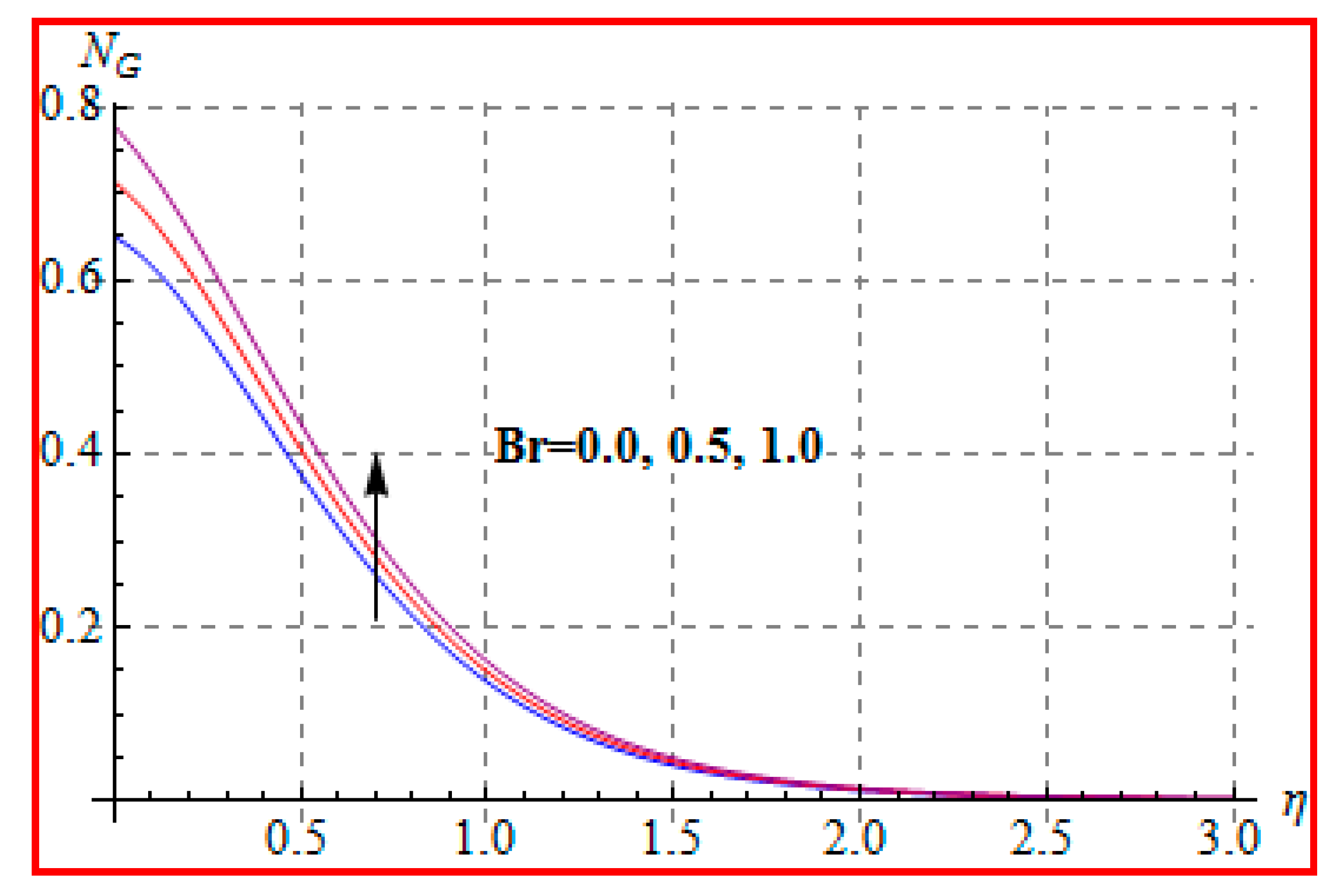
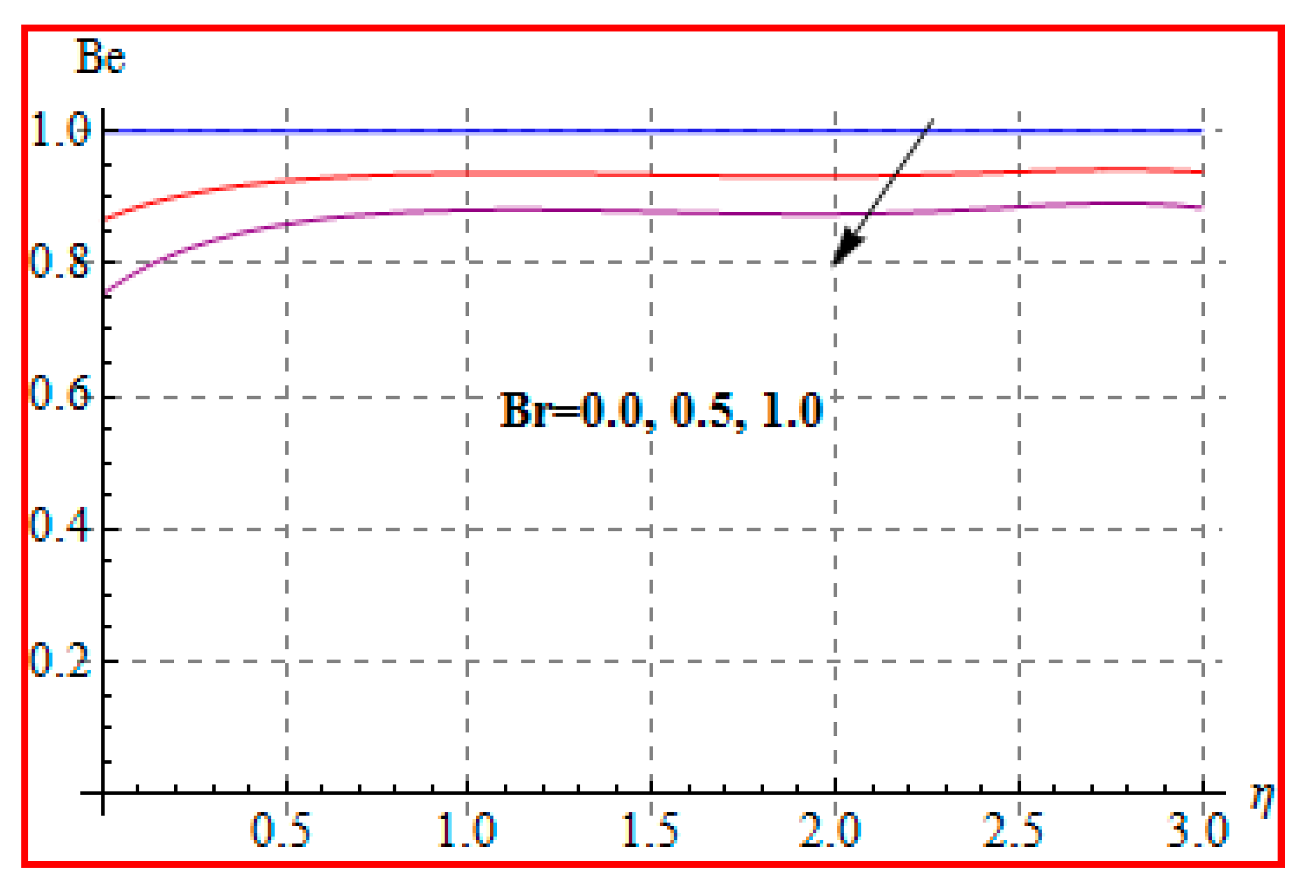
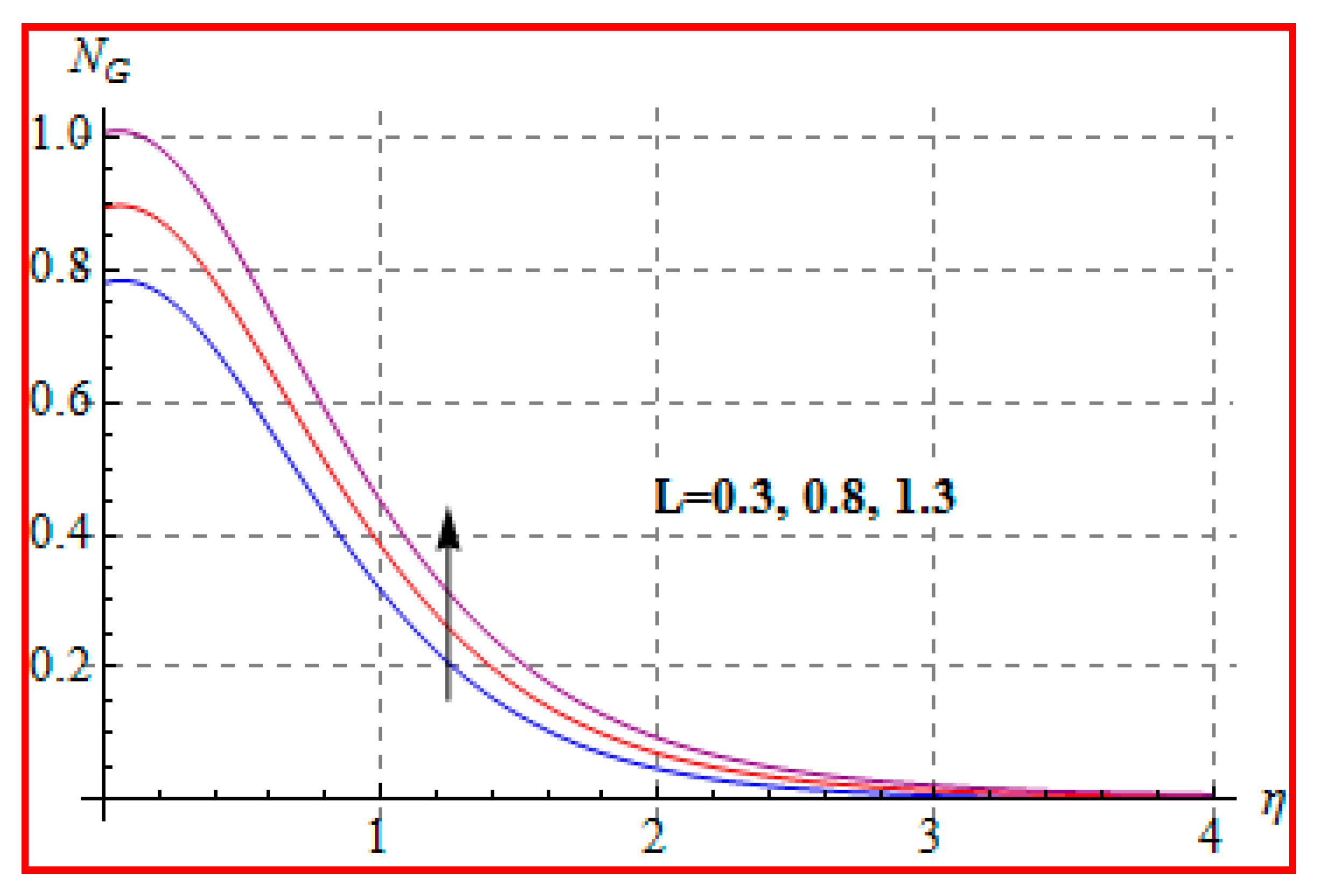
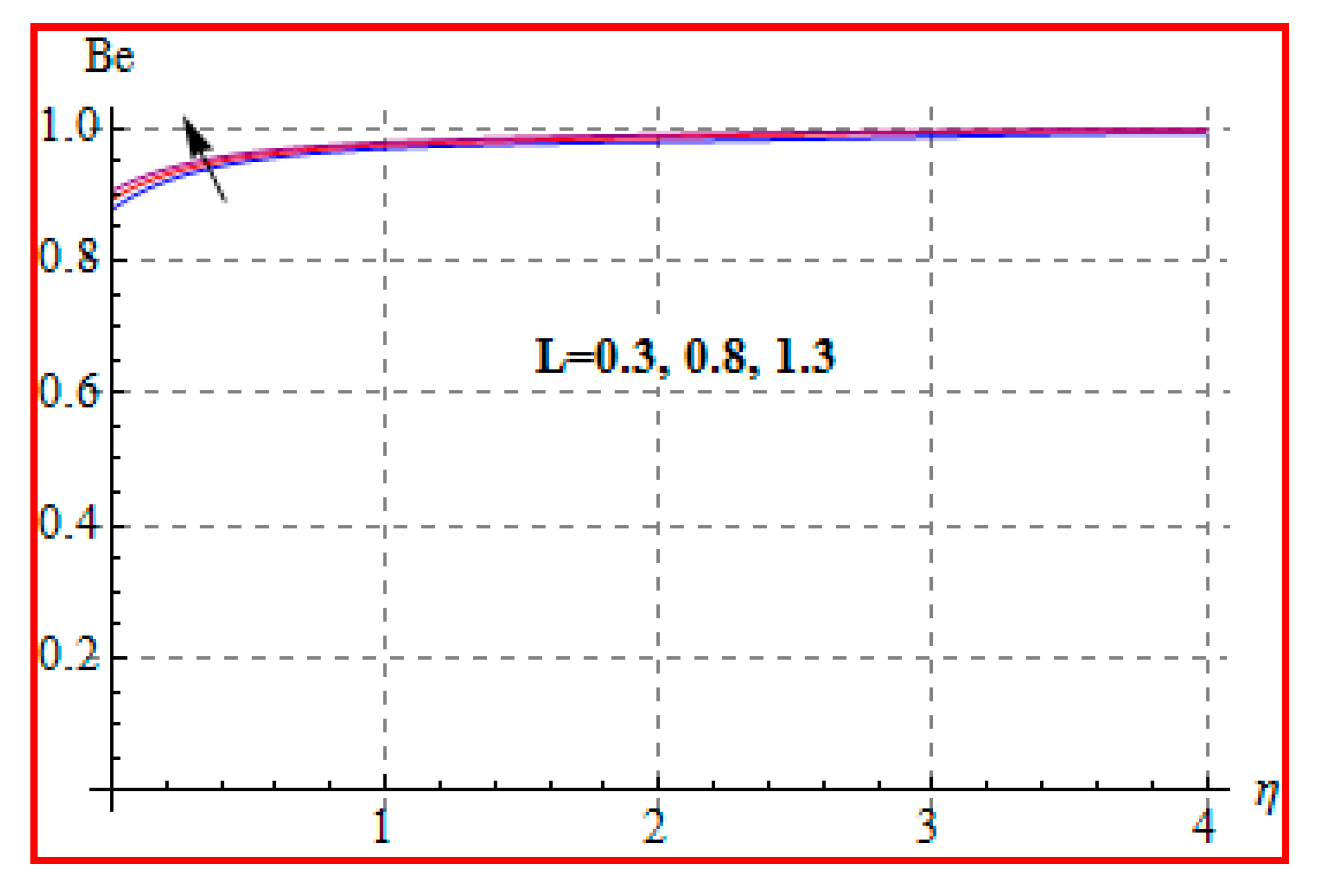
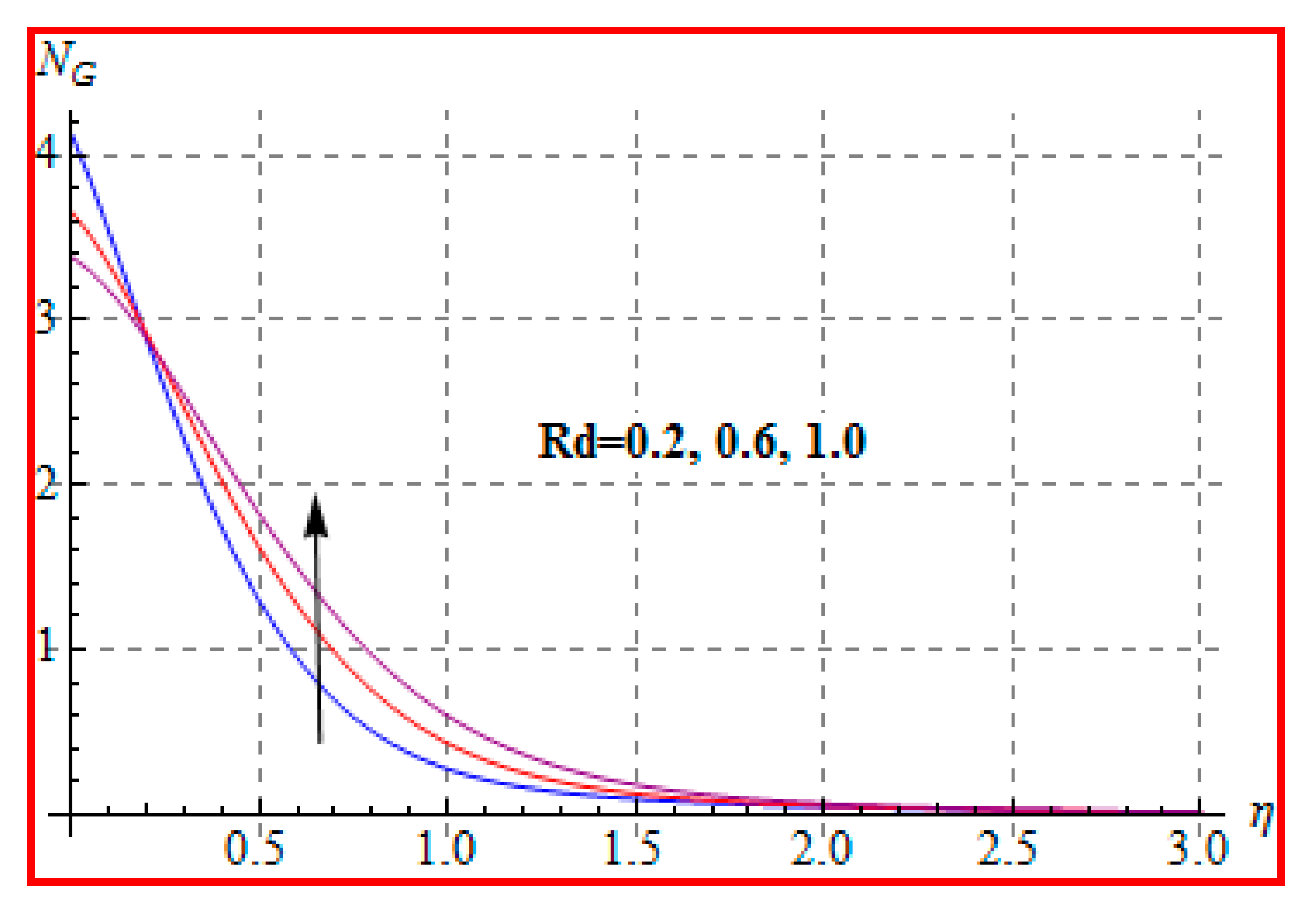
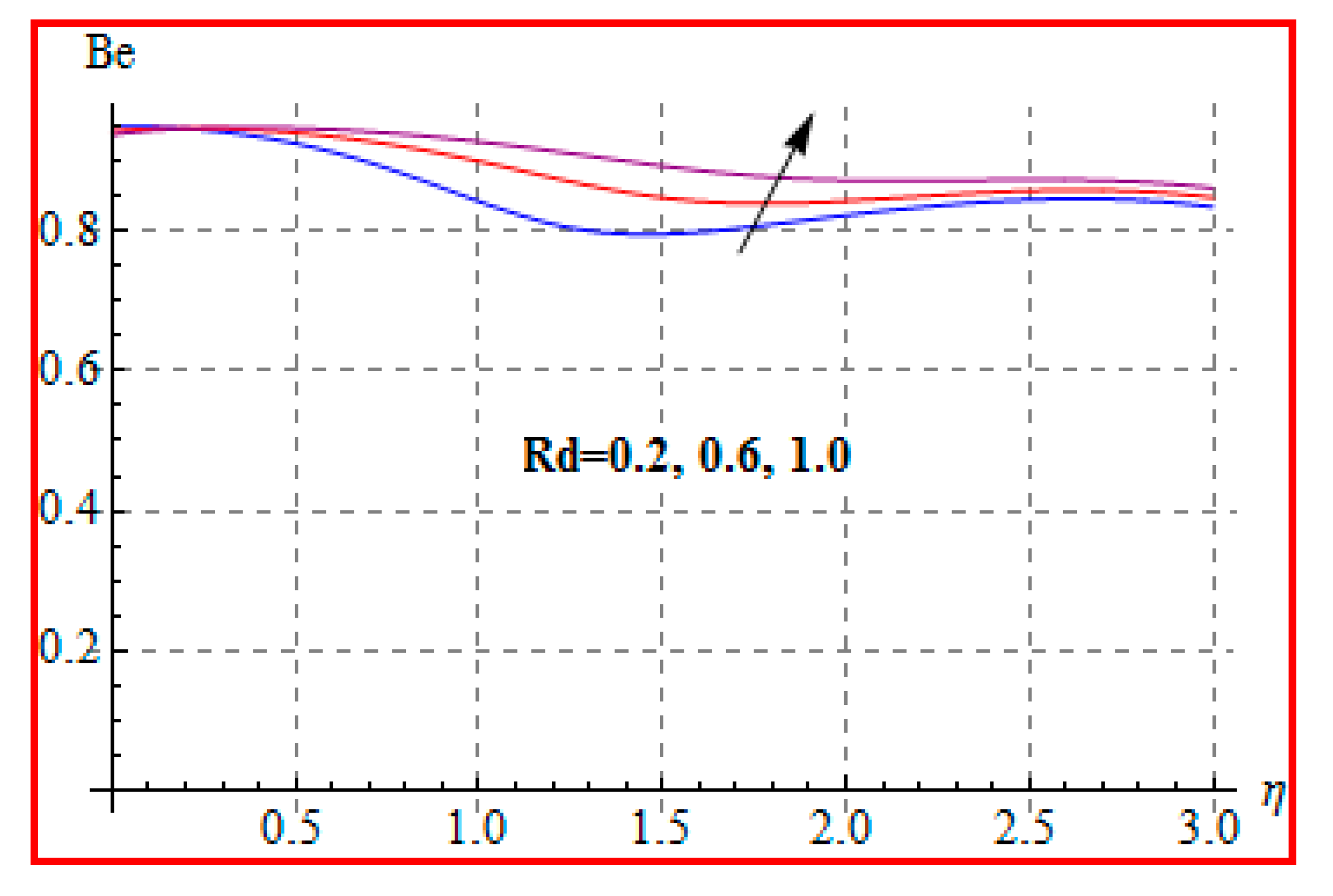
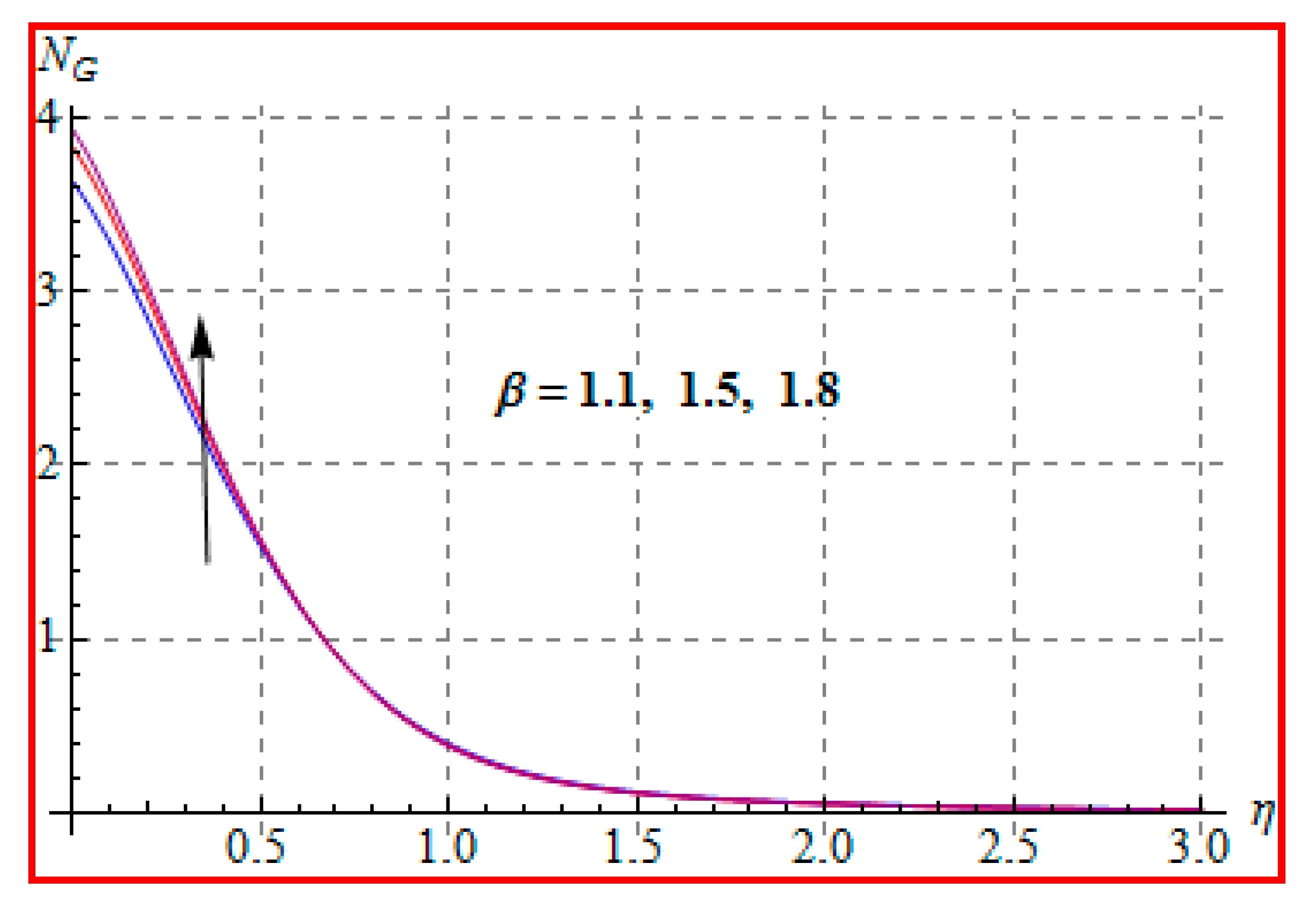
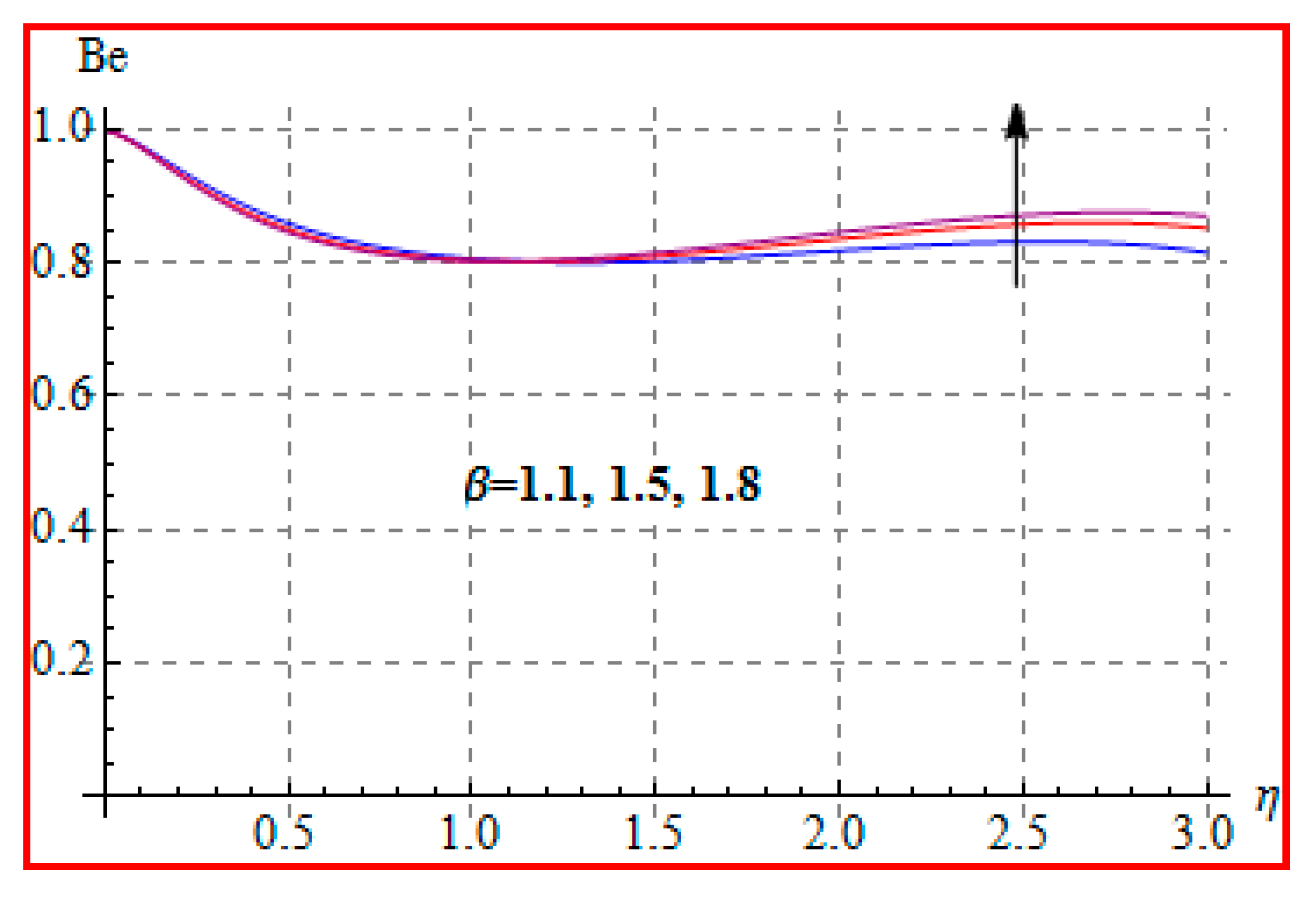
8.4. Entropy Optimization and Bejan Number
8.5. Engineering Quantities
8.5.1. Nusselt Number
8.5.2. Sherwood Number
9. Conclusions
- There is a reduction in velocity for a higher Casson fluid parameter and magnetic field. However, the scenario is different for velocity through the Marangoni number.
- Temperature is enhanced for both thermophoresis and Brownian motion parameters.
- An increasing trend of temperature is noticed for a higher Marangoni number, radiation and magnetic field, and Brinkman number.
- Prandtl number reduces the temperature.
- Concentration for Lewis and Marangoni numbers is opposite to that of the activation energy variable.
- Reverse behavior of Brownian motion and thermophoresis for concentration is noted.
- Bejan number for radiation and Brinkman number have opposite outcomes.
- A qualitative, similar effect of entropy generation and Bejan number is noted with respect to the diffusion parameter.
- Sherwood number for Brownian motion and Lewis number is opposite when compared with the thermophoresis parameter.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shafiq, A.; Zari, I.; Rasool, G.; Tlili, I.; Khan, T.S. On the MHD Casson axisymmetric Marangoni forced convective flow of nanofluids. Mathematics 2019, 7, 1087. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Marangoni effect in second grade forced convective flow of water based nanofluid. J. Adv. Nanotechnol. 2019, 1, 50. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Yasmeen, T. Impact of Marangoni convection in the flow of carbon--water nanofluid with thermal radiation. Int. J. Heat Mass Tranf. 2017, 106, 810–815. [Google Scholar] [CrossRef]
- Imai, Y.; Yamamoto, T.; Sekimoto, A.; Okano, Y.; Sato, R.; Shigeta, Y. Numerical investigation of the nano-scale solutal Marangoni convections. J. Taiwan Inst. Chem. Eng. 2019, 98, 20–26. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, L.; Zhang, X. MHD Marangoni boundary layer flow and heat transfer of pseudo-plastic nanofluids over a porous medium with a modified model. Mech. Time-Depend Mater. 2015, 19, 519–536. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesh, B.J.; Shashikumar, N.S.; Hayat, T.; Alsaedi, A. Marangoni convection in Casson liquid flow due to an infinite disk with exponential space dependent heat source and cross-diffusion effects. Result Phys. 2018, 9, 78–85. [Google Scholar] [CrossRef]
- Wang, L.; Horiuchi, T.; Sekimoto, A.; Okano, Y.; Ujihara, T.; Dost, S. Three-dimensional numerical analysis of Marangoni convection occurring during the growth process of SiC by the RF-TSSG method. J. Cryst. Growth. 2019, 520, 72–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, L. Similarity solutions of Marangoni convection boundary layer flow with gravity and external pressure. Chin. J. Chem. Eng. 2014, 22, 365–369. [Google Scholar] [CrossRef]
- Bestman, A.R. Natural convection boundary layer with suction and mass transfer in a porous medium. Int. J. Energy Res. 1990, 14, 389–396. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.A.; Khan, M.I.; Alsaedi, A. Theoretical investigation of Ree-Eyring nanofluid flow with entropy optimization and Arrhenius activation energy between two rotating disks. Comp. Method. Prog. Biomed. 2019, 177, 57–68. [Google Scholar] [CrossRef]
- Hamid, A.; Hashim; Khan, M. Impacts of binary chemical reaction with activation energy on unsteady flow of magneto-Williamson nanofluid. J. Mol. Liq. 2018, 262, 435–442. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A. Activation energy impact in nonlinear radiative stagnation point flow of Cross nanofluid. Int. Commun. Heat Mass Transf. 2018, 91, 216–224. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Ellahi, R. Analysis of activation energy in Couette-Poiseuille flow of nanofluid in the presence of chemical reaction and convective boundary conditions. Results Phys. 2018, 8, 502–512. [Google Scholar] [CrossRef]
- Khan, M.I.; Alsaedi, A.; Qayyum, S.; Hayat, T.; Khan, M.I. Entropy generation optimization in flow of Prandtl—Eyring nanofluid with binary chemical reaction and Arrhenius activation energy. Colloids Surf. A Physicochem. Eng. Asp. 2019, 570, 117–126. [Google Scholar] [CrossRef]
- Kumar, R.V.M.S.S.K.; Kumar, G.V.; Raju, C.S.K.; Shehzad, S.A.; Varma, S.V.K. Analysis of Arrhenius activation energy in magnetohydrodynamic Carreau fluid flow through improved theory of heat diffusion and binary chemical reaction. J. Phys. Commun. 2018, 2, 035004. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Khan, M.I.; Alsaedi, A.; Khan, T.A. Entropy generation in radiative motion of tangent hyperbolic nanofluid in presence of activation energy and nonlinear mixed convection. Phy. Lett. A. 2018, 382, 2017–2026. [Google Scholar] [CrossRef]
- Dhlamini, M.; Kameswaran, P.K.; Sibanda, P.; Motsaa, S.; Mondal, H. Activation energy and binary chemical reaction effects in mixed convective nanofluid flow with convective boundary conditions. J. Comput. Des. Eng. 2019, 6, 149–158. [Google Scholar] [CrossRef]
- Shevchuk, I.V. Convective Heat and Mass Transfer in Rotating Disk Systems; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Shevchuk, I.V. Modelling of Convective Heat and Mass Transfer in Rotating Flows; Springer International Publishing: Basel, Switzerland, 2016. [Google Scholar]
- Qian, W.; Lin, Y.; Hui, X. Effect of heat and mass transfer on the instability of an annular liquid sheet. Int. J. Heat Mass Tranf. 2019, 143, 118499. [Google Scholar] [CrossRef]
- Su, Y.; Ng, T.; Davidson, J.H. Three dimensional mesoscopic scale simulations of buoyancy driven flow and heat mass transfer through randomly packed fiber boards. Int. J. Heat Mass Tranf. 2019, 143, 118522. [Google Scholar] [CrossRef]
- Jia, B.; Yang, L.; Xie, L.; Fua, Q.; Cui, X. Linear stability of confined swirling annular liquid layers in the presence of gas velocity oscillations with heat and mass transfer. Int. J. Heat Mass Tranf. 2019, 138, 117–125. [Google Scholar] [CrossRef]
- Bouzgarrou, F.; Askri, F.; Mellouli, S.; Algarni, S. Numerical investigation of heat and mass transfer within different configurations of LaNi5-H2; reactor using the unstructured Lattice Boltzmann Method. Int. J. Hydrogen Energy 2019, 44, 31216–31229. [Google Scholar] [CrossRef]
- Sudarsan, P.; Sreedevi, R.P.; Chamkha, A.J. Magnetohydrodynamic (MHD) boundary layer heat and mass transfer characteristics of nanofluid over a vertical cone under convective boundary condition. Propul. Power Res. 2018, 7, 308–319. [Google Scholar]
- Bejan, A. A study of entropy generation in fundamentsl convective heat transfer. J. Heat Tranf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Bejan, A.; Dincer, I.; Lorente, S.; Miguel, A.F.; Reis, A.H. Porous and Complex Flow Structures in Modern Technologies; Springer: New York, NY, USA, 2004. [Google Scholar]
- Bejan, A. Entropy Generation Minimization; CRC Press: New York, NY, USA, 1996. [Google Scholar]
- Bejan, A. Second law analysis in heat transfer. Energy Int. J. 1980, 5, 721–732. [Google Scholar] [CrossRef]
- Gibanov, N.S.; Sheremet, M.A.; Oztop, H.F.; A-Salem, K. MHD natural convection and entropy generation in an open cavity having different horizontal porous blocks saturated with a ferrofluid. J. Magn. Magn. Mater. 2018, 452, 193–204. [Google Scholar] [CrossRef]
- Saleem, M.; Hossain, M.A.; Mahmud, S.; Pop, I. Entropy generation in Marangoni convection flow of heated fluid in an open ended cavity. Int. J. Heat Mass Tranf. 2011, 54, 4473–4484. [Google Scholar] [CrossRef]
- Khan, S.A.; Saeed, T.; Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A. Entropy optimized CNTs based Darcy-Forchheimer nanomaterial flow between two stretchable rotating disks. Int. J. Hydrogen Energy 2019, 44, 31579–31592. [Google Scholar] [CrossRef]
- Zhuang, Y.J.; Zhu, Q.Y. Analysis of entropy generation in combined buoyancy-Marangoni convection of power-law nanofluids in 3D heterogeneous porous media. Int. J. Heat Mass Tranf. 2018, 118, 686–707. [Google Scholar] [CrossRef]
- Khatami, S.; Rahbar, N. An analytical study of entropy generation in rectangular natural convective porous fins. Ther. Sci. Eng. Prog. 2019, 11, 142–149. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Alsaedi, A. Entropy generation minimization and statistical declaration with probable error for skin friction coefficient and Nusselt number. Chin. J. Phys. 2018, 56, 1525–1546. [Google Scholar] [CrossRef]
- Sithole, H.; Mondal, H.; Sibanda, P. Entropy generation in a second grade magnetohydrodynamic nanofluid flow over a convectively heated stretching sheet with nonlinear thermal radiation and viscous dissipation. Result. Phys. 2018, 9, 1077–1085. [Google Scholar] [CrossRef]
- Olanrewaju, M.A.; Gbadeyan, J.A.; Idowu, A.S. Flow and heat transfer analysis of a second grade fluid with Newtonian heating in the presence of elastic deformation in a porous medium. Pac. J. Sci. Technol. 2016, 17, 30–48. [Google Scholar]
- Aziz, A.; Alsaedi, A.; Muhammad, A.T.; Hayat, T. Numerical study for heat generation/absorption in flow of nanofluid by a rotating disk. Results Phys. 2018, 8, 785–792. [Google Scholar] [CrossRef]


| PR. | SITHOLE ET AL. [35] | OLANREWAJU ET AL. [36] | PRESENT RESULT |
|---|---|---|---|
| 0.5 | 0.21441547 | 0.214368 | 0.214363 |
| 0.7 | 0.24976956 | 0.250142 | 0.250139 |
| 1.0 | 0.28782508 | 0.289161 | 0.289142 |
| 2.0 | 0.35519994 | 0.356176 | 0.356145 |
| 0.0 | 0.5 | 0.4 | 0.5 | 1.00091 |
| 0.2 | 0.983521 | |||
| 0.4 | 0.974563 | |||
| 0.3 | 0.1 | 0.4 | 0.5 | 0.895316 |
| 0.6 | 0.934756 | |||
| 1.0 | 0.979105 | |||
| 0.3 | 0.5 | 0.2 | 0.5 | 0.99962 |
| 0.5 | 0.998332 | |||
| 0.8 | 0.997925 | |||
| 0.3 | 0.5 | 0.4 | 0.5 | 0.978231 |
| 1.0 | 0.989432 | |||
| 1.5 | 0.994214 |
| 0.3 | 0.2 | 0.5 | 0.503491 |
| 0.6 | 0.615362 | ||
| 0.9 | 0.676212 | ||
| 0.2 | 0.2 | 0.5 | 0.514252 |
| 0.5 | 0.374541 | ||
| 0.8 | 0.234561 | ||
| 0.2 | 0.2 | 0.5 | 0.534567 |
| 1.0 | 0.697349 | ||
| 1.5 | 0.816734 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadiq, M.A.; Hayat, T. Characterization of Marangoni Forced Convection in Casson Nanoliquid Flow with Joule Heating and Irreversibility. Entropy 2020, 22, 433. https://doi.org/10.3390/e22040433
Sadiq MA, Hayat T. Characterization of Marangoni Forced Convection in Casson Nanoliquid Flow with Joule Heating and Irreversibility. Entropy. 2020; 22(4):433. https://doi.org/10.3390/e22040433
Chicago/Turabian StyleSadiq, Muhammad Adil, and Tasawar Hayat. 2020. "Characterization of Marangoni Forced Convection in Casson Nanoliquid Flow with Joule Heating and Irreversibility" Entropy 22, no. 4: 433. https://doi.org/10.3390/e22040433
APA StyleSadiq, M. A., & Hayat, T. (2020). Characterization of Marangoni Forced Convection in Casson Nanoliquid Flow with Joule Heating and Irreversibility. Entropy, 22(4), 433. https://doi.org/10.3390/e22040433





