A Bi-Invariant Statistical Model Parametrized by Mean and Covariance on Rigid Motions
Abstract
1. Introduction
2. Euclidean Groups
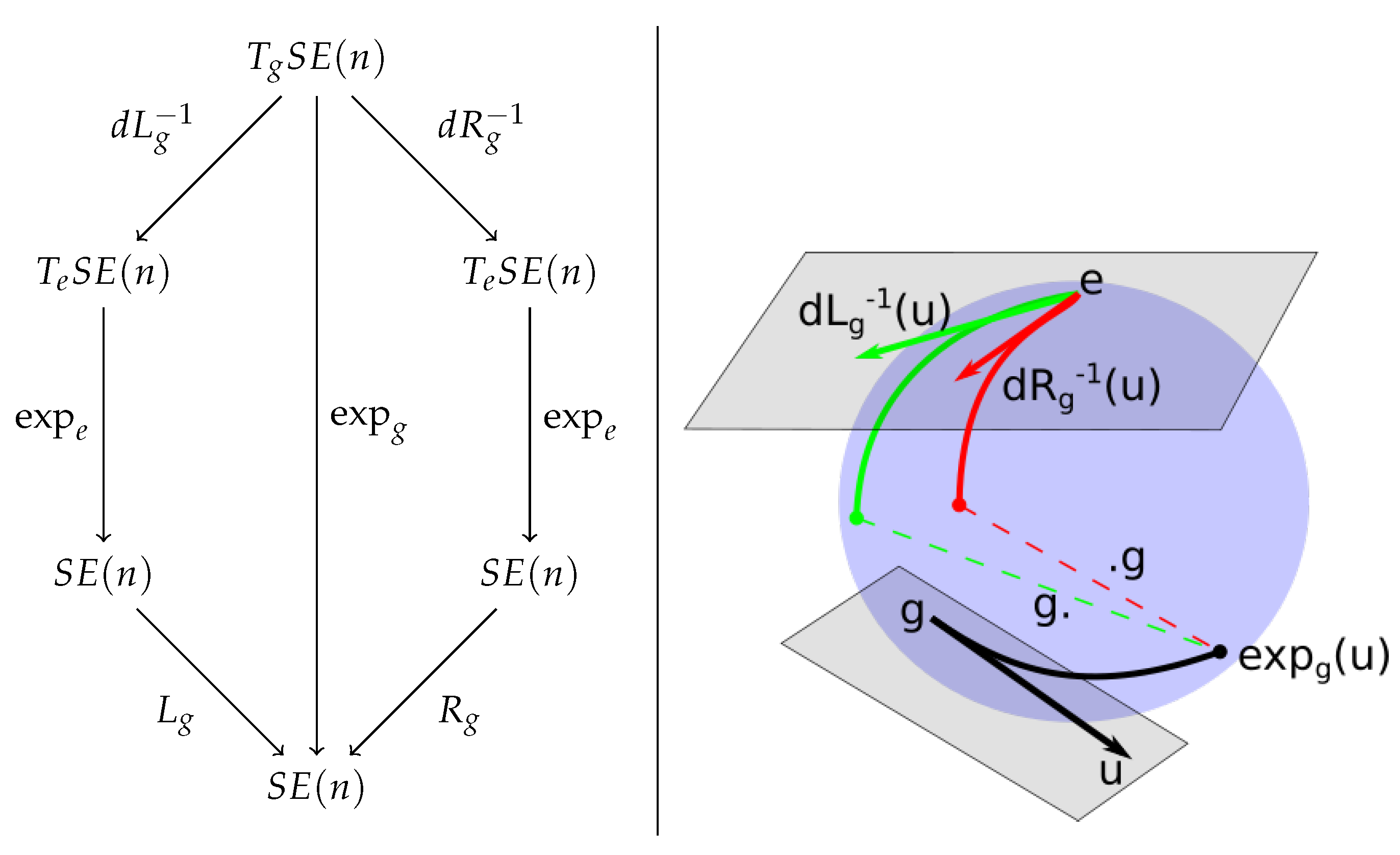
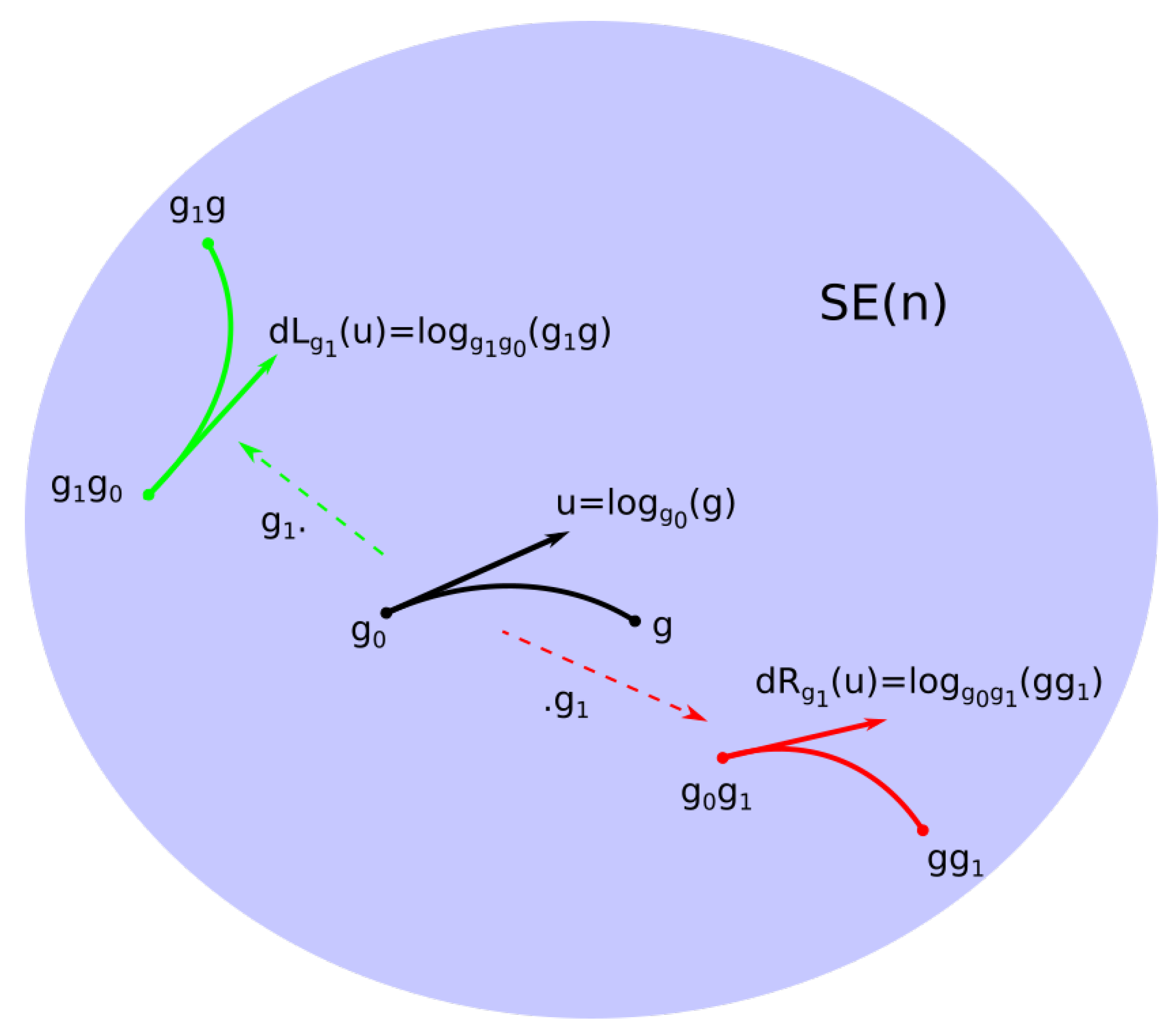
3. Bi-Invariant Local Linearizations
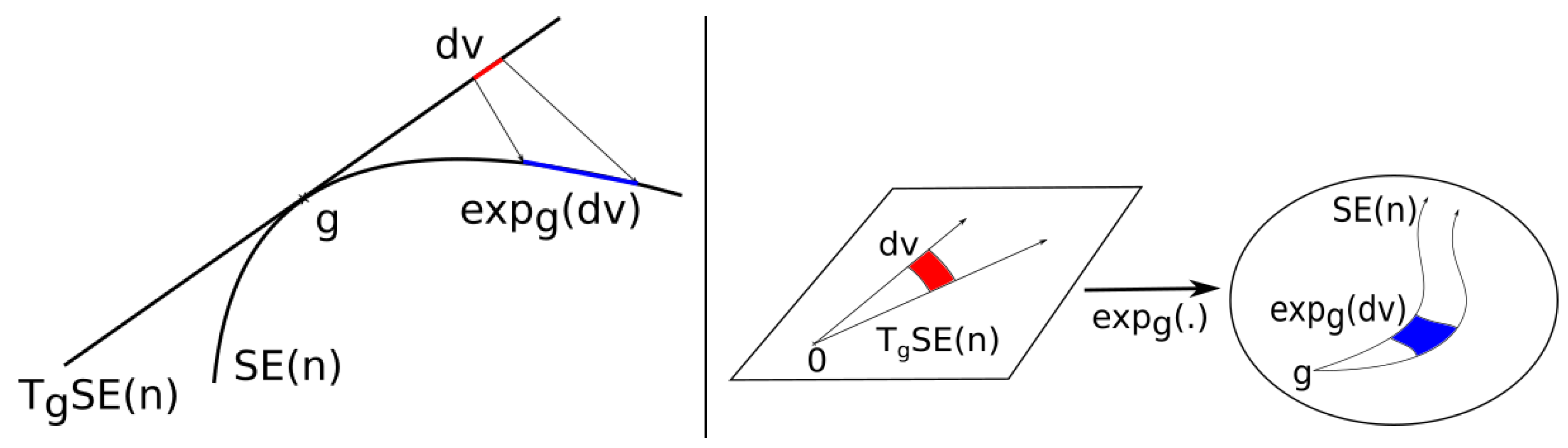
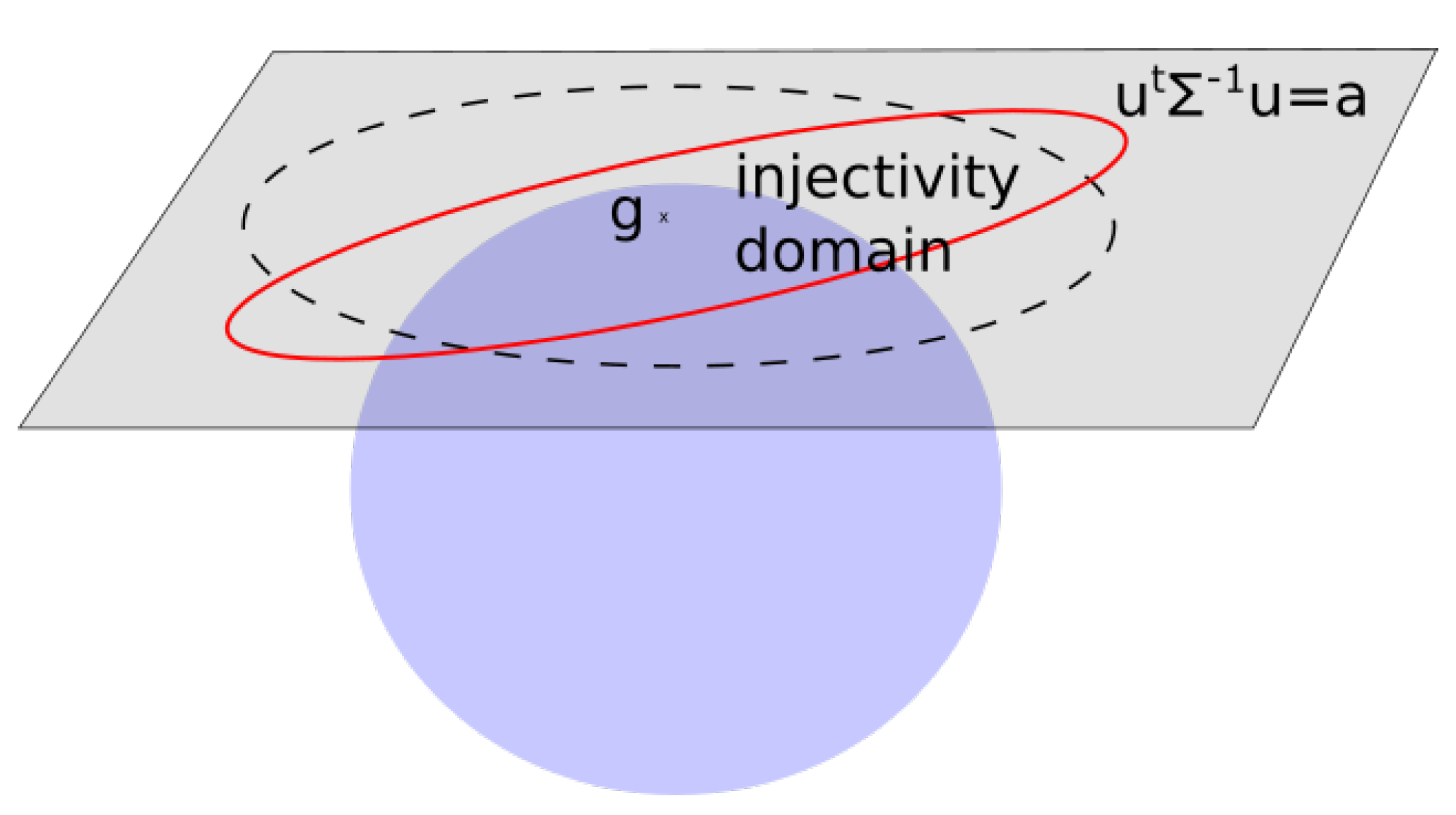
3.1. The Exponential at Point G
| , |
3.2. Jacobian Determinant of the Exponential
4. First and Second Moments of a Distribution on a Lie Group
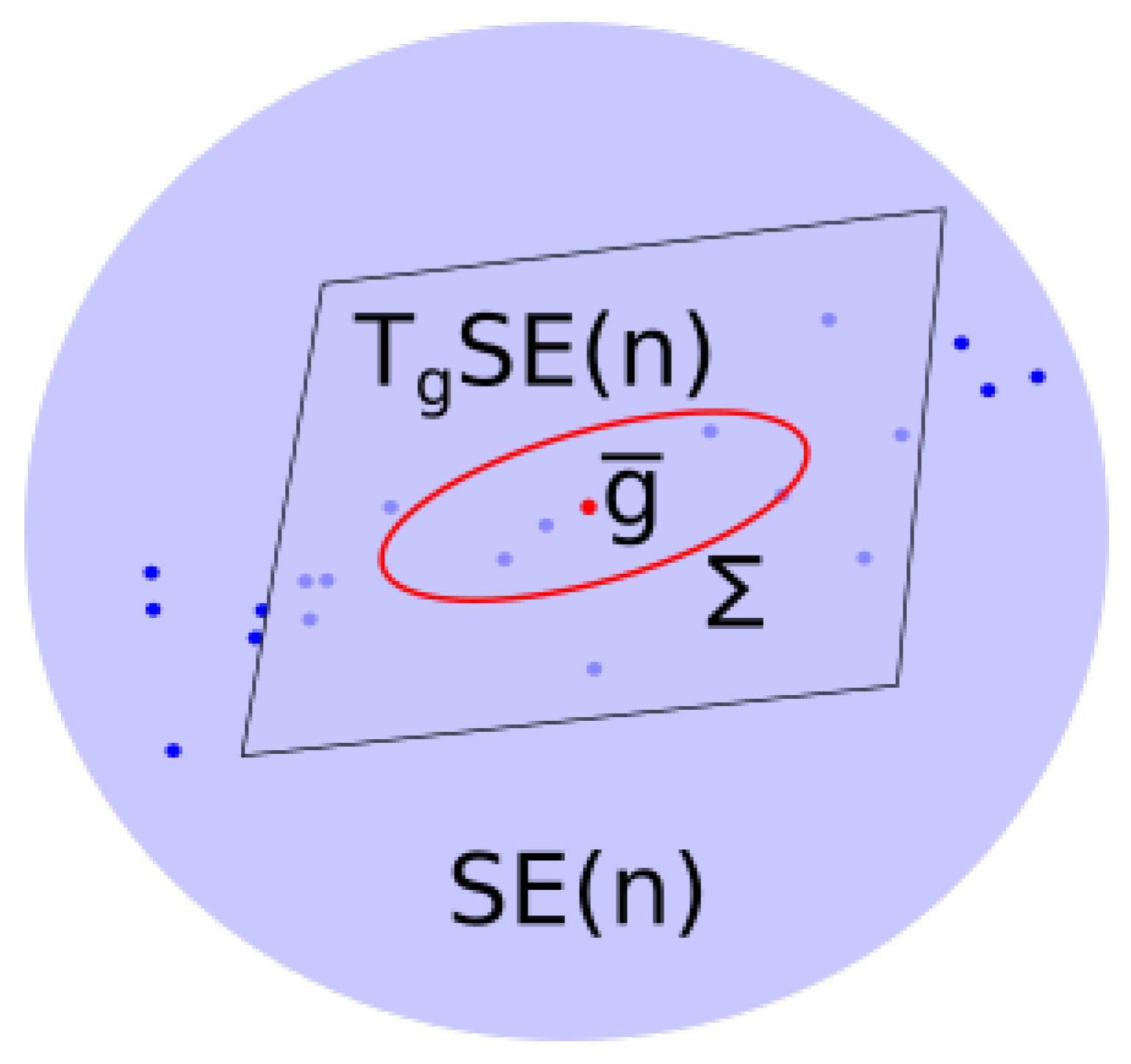
4.1. Bi-Invariant Means
4.2. Covariance in a Vector Space
4.3. Covariance of a Distribution on
5. Statistical Models for Bi-Invariant Statistics
5.1. The Model
- (i)
- (ii)
- (iii)
- .
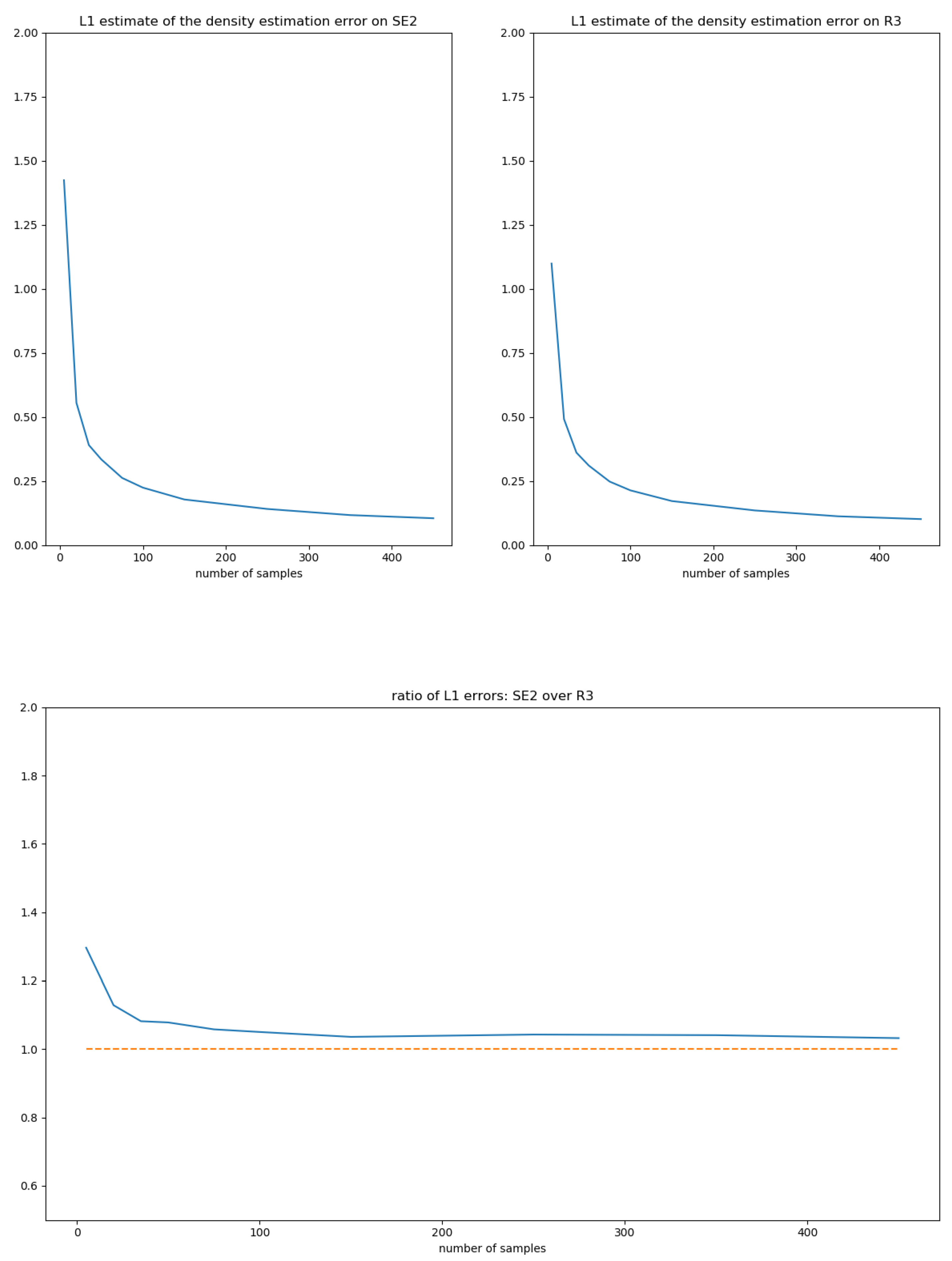
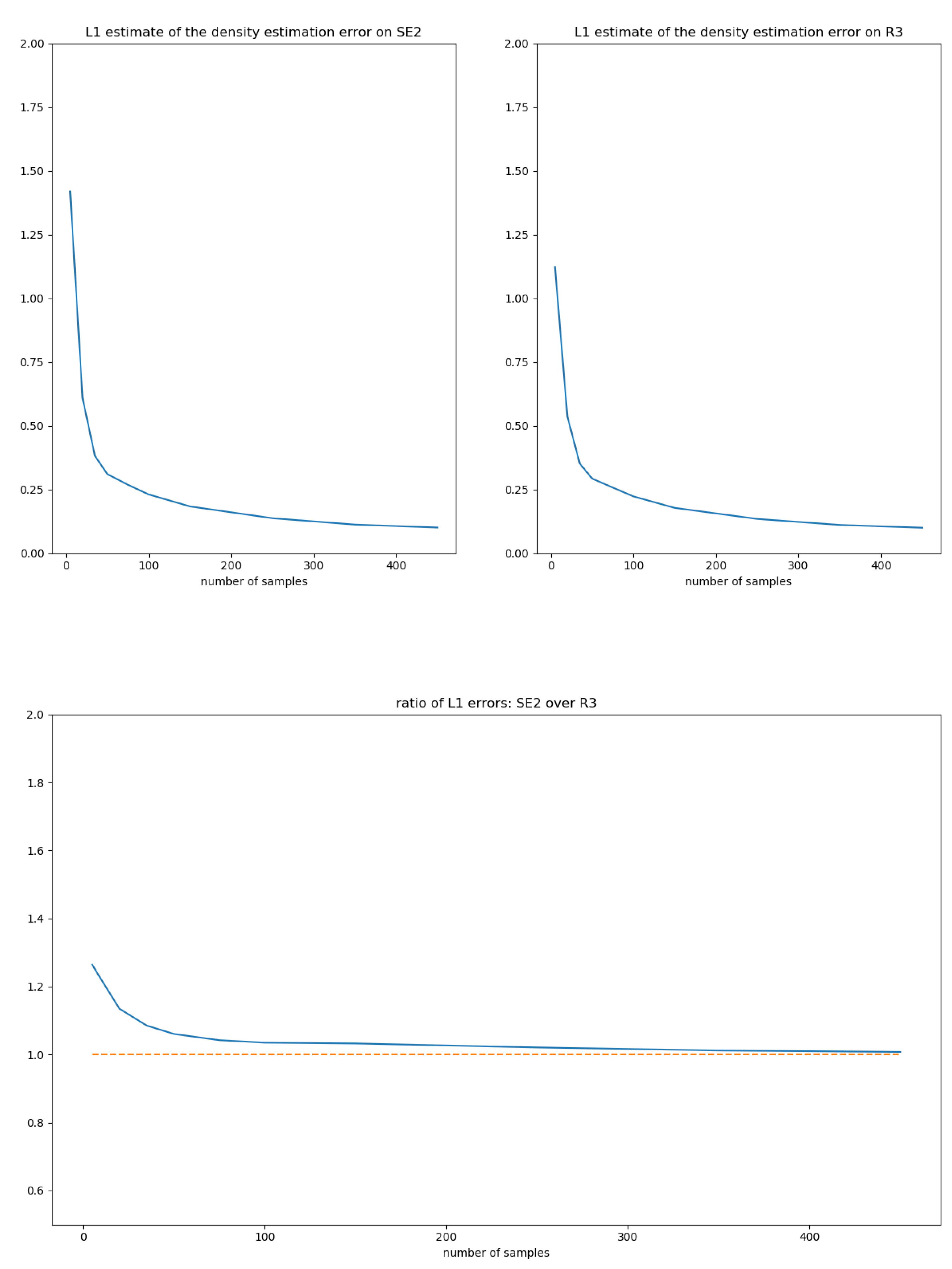
5.2. Sampling Distributions of
5.3. Evaluation of the Convergence of the Moment-Matching Estimator
6. Conclusion and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Eigenvalues of adA
References
- Chevallier, E. Towards Parametric Bi-Invariant Density Estimation on SE (2). In Proceedings of International Conference on Geometric Science of Information; Springer: Cham, Switzerland, 2019; pp. 695–702. [Google Scholar]
- Pennec, X.; Arsigny, V. Exponential barycenters of the canonical Cartan connection and invariant means on Lie groups. In Matrix Information Geometry; Springer: Berlin/Heidelberg, Germany, 2013; pp. 123–166. [Google Scholar]
- Émery, M.; Mokobodzki, G. Sur le barycentre d’une probabilité dans une variété. In Séminaire de probabilités XXV; Springer: Berlin/Heidelberg, Germany, 1991; pp. 220–233. [Google Scholar]
- Pennec, X. Intrinsic statistics on Riemannian manifolds: Basic tools for geometric measurements. J. Math. Imaging Vis. 2006, 25, 127. [Google Scholar] [CrossRef]
- Chevallier, E.; Forget, T.; Barbaresco, F.; Angulo, J. Kernel density estimation on the siegel space with an application to radar processing. Entropy 2016, 18, 396. [Google Scholar] [CrossRef]
- Chevallier, E. A family of anisotropic distributions on the hyperbolic plane. In Proceedings of International Conference on Geometric Science of Information; Nielsen, F., Barbaresco, F., Eds.; Springer: Cham, Switzerland, 2017; pp. 717–724. [Google Scholar]
- Chevallier, E.; Kalunga, E.; Angulo, J. Kernel density estimation on spaces of Gaussian distributions and symmetric positive definite matrices. SIAM J. Imaging Sci. 2017, 10, 191–215. [Google Scholar] [CrossRef]
- Falorsi, L.; de Haan, P.; Davidson, T.R.; De Cao, N.; Weiler, M.; Forré, P.; Cohen, T.S. Explorations in homeomorphic variational auto-encoding. arXiv 2018, arXiv:1807.04689. [Google Scholar]
- Forster, C.; Carlone, L.; Dellaert, F.; Scaramuzza, D. On-Manifold Preintegration for Real-Time Visual–Inertial Odometry. IEEE Trans. Robot. 2016, 33, 1–21. [Google Scholar] [CrossRef]
- Grattarola, D.; Livi, L.; Alippi, C. Adversarial autoencoders with constant-curvature latent manifolds. Appl. Soft Comput. 2019, 81, 105511. [Google Scholar] [CrossRef]
- Pelletier, B. Kernel density estimation on Riemannian manifolds. Stat. Probab. Lett. 2005, 73, 297–304. [Google Scholar] [CrossRef]
- Barfoot, T.D.; Furgale, P.T. Associating uncertainty with three-dimensional poses for use in estimation problems. IEEE Trans. Rob. 2014, 30, 679–693. [Google Scholar] [CrossRef]
- Lesosky, M.; Kim, P.T.; Kribs, D.W. Regularized deconvolution on the 2D-Euclidean motion group. Inverse Prob. 2008, 24, 055017. [Google Scholar] [CrossRef]
- Hendriks, H. Nonparametric estimation of a probability density on a Riemannian manifold using Fourier expansions. Ann. Stat. 1990, 18, 832–849. [Google Scholar] [CrossRef]
- Huckemann, S.; Kim, P.; Koo, J.; Munk, A. Mobius deconvolution on the hyperbolic plane with application to impedance density estimation. Ann. Stat. 2010, 38, 2465–2498. [Google Scholar] [CrossRef]
- Kim, P.; Richards, D. Deconvolution density estimation on the space of positive definite symmetric matrices. In Nonparametric Statistics and Mixture Models: A Festschrift in Honor of Thomas P. Hettmansperger; World Scientific Publishing: Singapore, 2008; pp. 147–168. [Google Scholar]
- Sola, J.; Deray, J.; Atchuthan, D. A micro Lie theory for state estimation in robotics. arXiv 2018, arXiv:1812.01537. [Google Scholar]
- Eade, E. Lie groups for 2d and 3d transformations. Available online: http://ethaneade.com/lie.pdf (accessed on 10 April 2020).
- Eade, E. Lie Groups for Computer Vision; Cambridge Univ. Press: Cambridge, UK, 2014. [Google Scholar]
- Eade, E. Derivative of the Exponential Map. Available online: http://ethaneade.com/lie.pdf (accessed on 10 April 2020).
- Cartan, É. On the geometry of the group-manifold of simple and semi-groups. Proc. Akad. Wetensch. 1926, 29, 803–815. [Google Scholar]
- Lorenzi, M.; Pennec, X. Geodesics, parallel transport & one-parameter subgroups for diffeomorphic image registration. Int. J. Comput. Vision 2013, 105, 111–127. [Google Scholar]
- Postnikov, M.M. Geometry VI: Riemannian Geometry; Encyclopedia of mathematical science; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Rossmann, W. Lie Groups: An Introduction Through Linear Groups; Oxford University Press on Demand: Oxford, UK, 2006; Volume 5. [Google Scholar]
- Helgason, S. Differential Geometry, Lie Groups, and Symmetric Spaces; Academic Press: Cambridge, MA, USA, 1979. [Google Scholar]
- Pennec, X. Bi-invariant means on Lie groups with Cartan-Schouten connections. In Proceedings of International Conference on Geometric Science of Information (GSI 2013); Springer: Berlin/Heidelberg, Germany, 2013; pp. 59–67. [Google Scholar]
- Arsigny, V.; Pennec, X.; Ayache, N. Bi-invariant Means in Lie Groups. Application to Left-invariant Polyaffine Transformations. Available online: https://hal.inria.fr/inria-00071383/ (accessed on 9 April 2020).
- Sommer, S.; Lauze, F.; Hauberg, S.; Nielsen, M. Manifold valued statistics, exact principal geodesic analysis and the effect of linear approximations. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 43–56. [Google Scholar]
- Miolane, N.; Le Brigant, A.; Mathe, J.; Hou, B.; Guigui, N.; Thanwerdas, Y.; Heyder, S.; Peltre, O.; Koep, N.; Zaatiti, H.; et al. Geomstats: A Python Package for Riemannian Geometry in Machine Learning. 2020. Available online: https://hal.inria.fr/hal-02536154/file/main.pdf (accessed on 8 April 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chevallier, E.; Guigui, N. A Bi-Invariant Statistical Model Parametrized by Mean and Covariance on Rigid Motions. Entropy 2020, 22, 432. https://doi.org/10.3390/e22040432
Chevallier E, Guigui N. A Bi-Invariant Statistical Model Parametrized by Mean and Covariance on Rigid Motions. Entropy. 2020; 22(4):432. https://doi.org/10.3390/e22040432
Chicago/Turabian StyleChevallier, Emmanuel, and Nicolas Guigui. 2020. "A Bi-Invariant Statistical Model Parametrized by Mean and Covariance on Rigid Motions" Entropy 22, no. 4: 432. https://doi.org/10.3390/e22040432
APA StyleChevallier, E., & Guigui, N. (2020). A Bi-Invariant Statistical Model Parametrized by Mean and Covariance on Rigid Motions. Entropy, 22(4), 432. https://doi.org/10.3390/e22040432



