Radiative MHD Nanofluid Flow over a Moving Thin Needle with Entropy Generation in a Porous Medium with Dust Particles and Hall Current
Abstract
1. Introduction
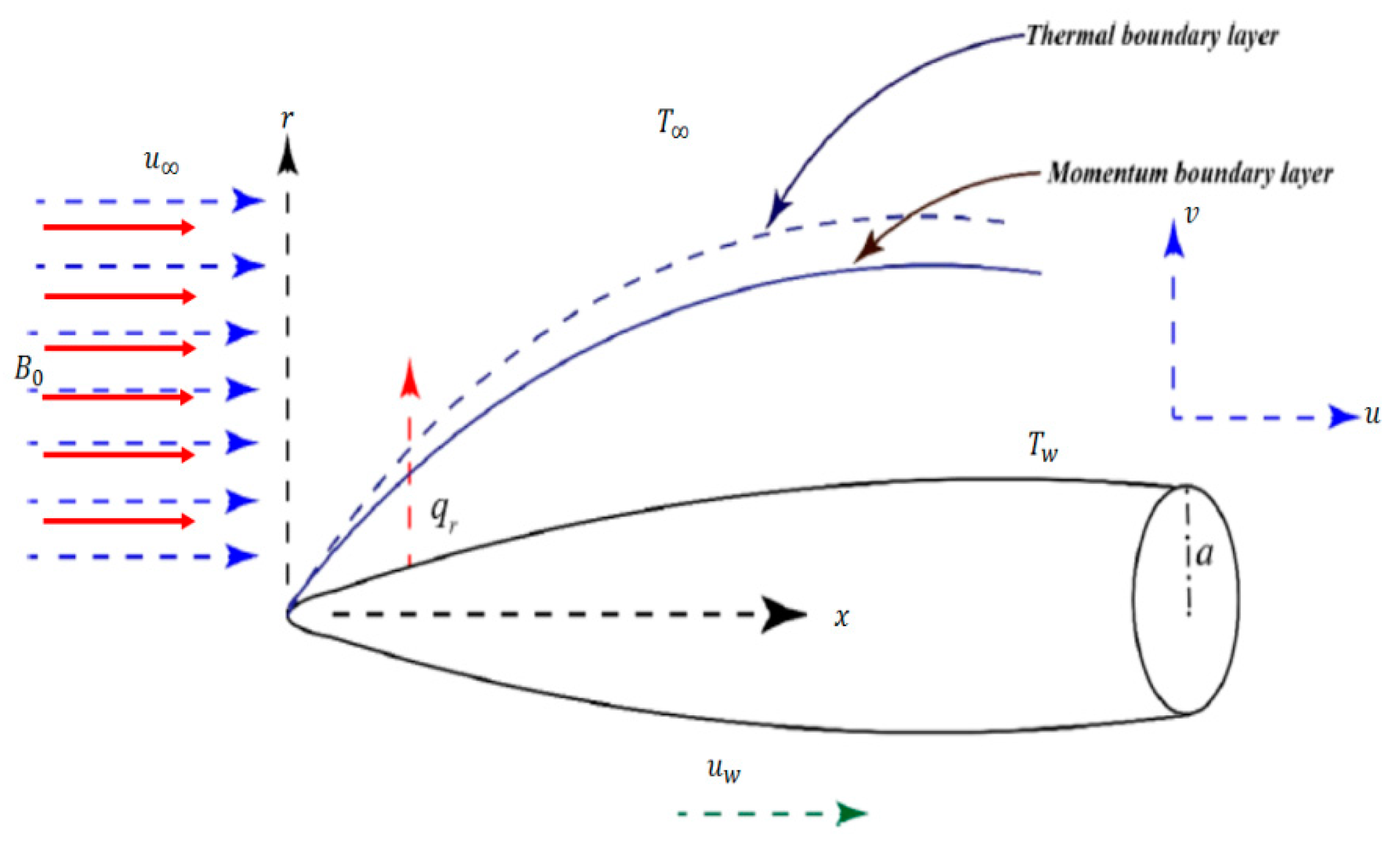
2. Mathematical Modeling
- Continuity equation:Fluid phase
- Momentum equation:Fluid phase
- Continuity equation:Particle phase
- Momentum equation:Particle phase
- Energy equation:Fluid phase
- Energy equation:Particle phase
3. Similarity Transformation
- Momentum equation:Fluid phase
- Momentum equation:Particle phase
- Energy equation:Fluid phase
- Energy equation:Particle phaseassociated with boundary conditions
4. Nusselt Number and Skin Friction Coefficient
5. Entropy Generation
6. Numerical Scheme
7. Results and Discussion
8. Final Remarks
- ⮚
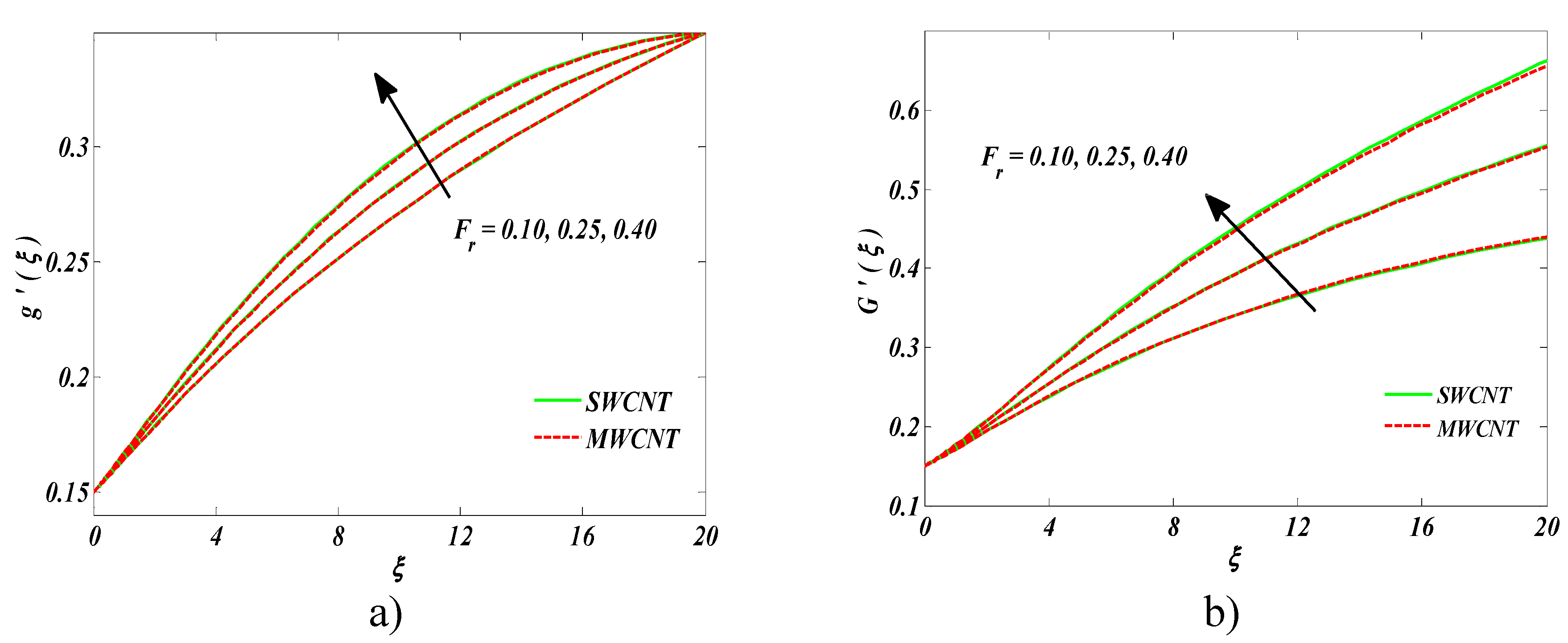
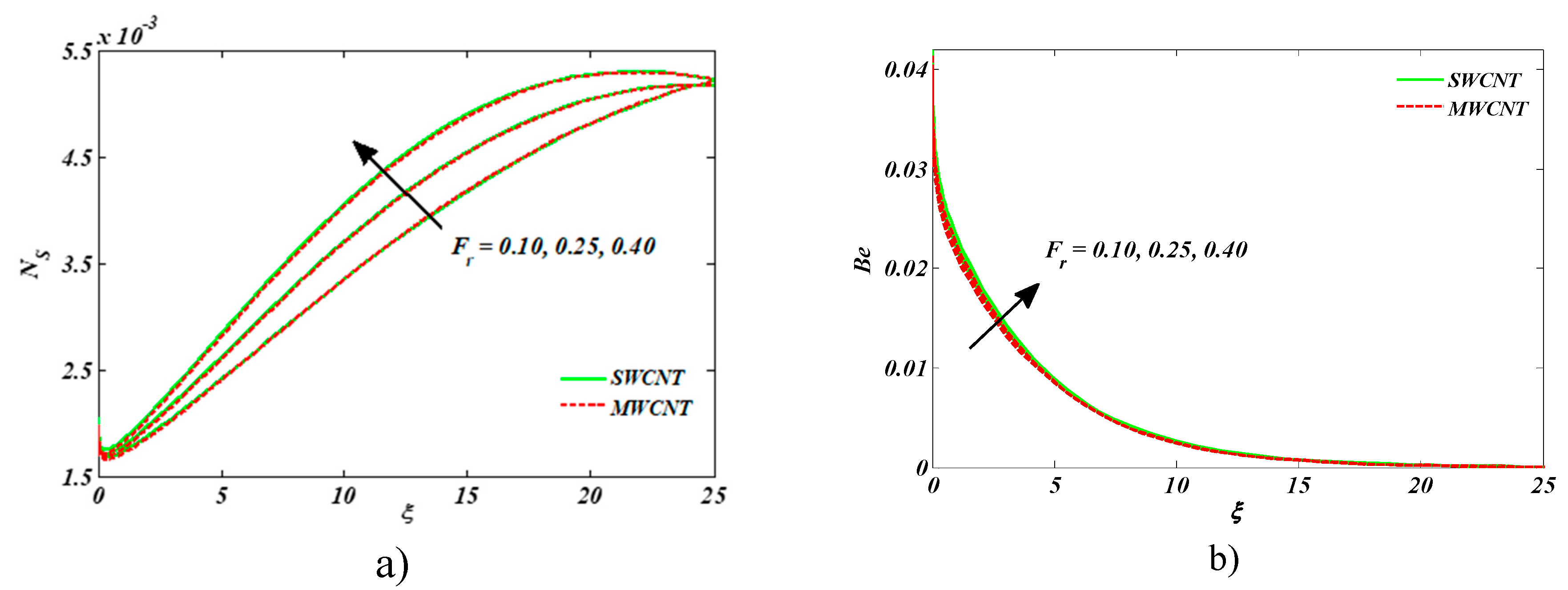
- Bejan number increased for larger values of Darcy–Forchheimer number.
- ⮚
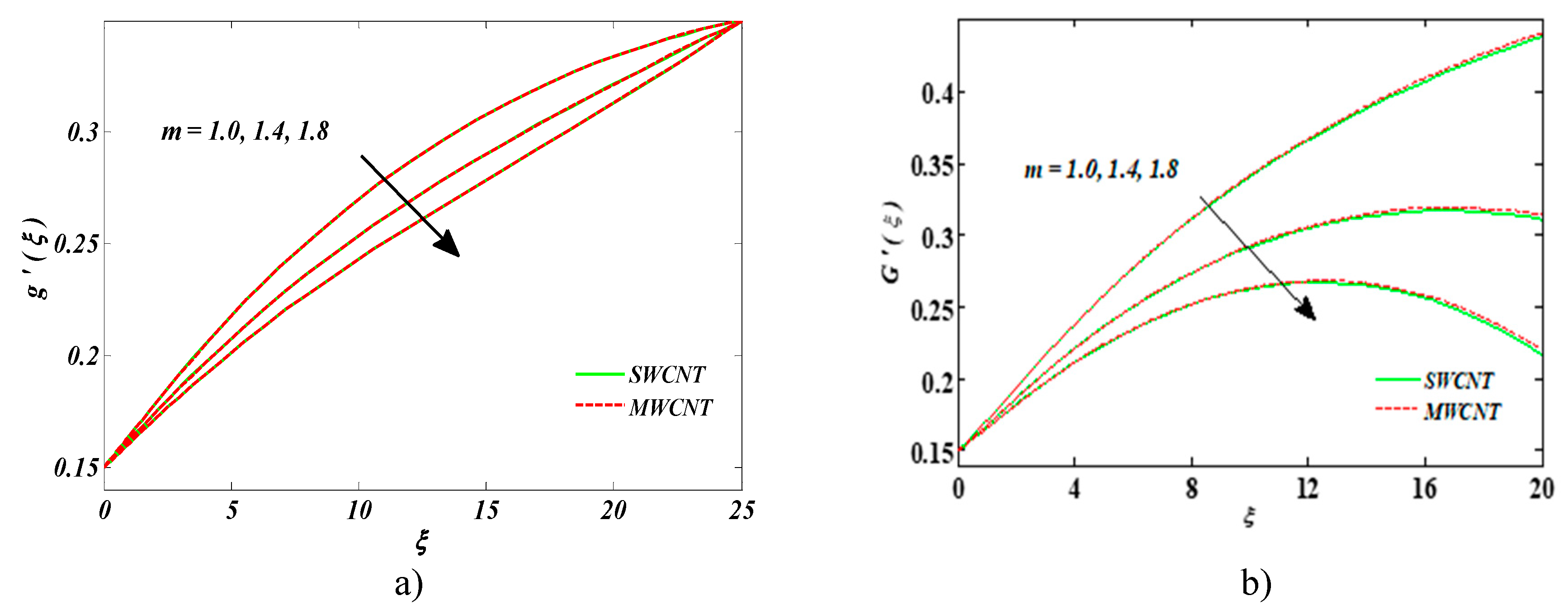
- Velocity was on the decline once the size of the needle and Darcy–Forchheimer parameter’s values were enhanced.
- ⮚
- Higher estimates of Hall current parameter escalated the velocity profiles for both CNTs.
- ⮚
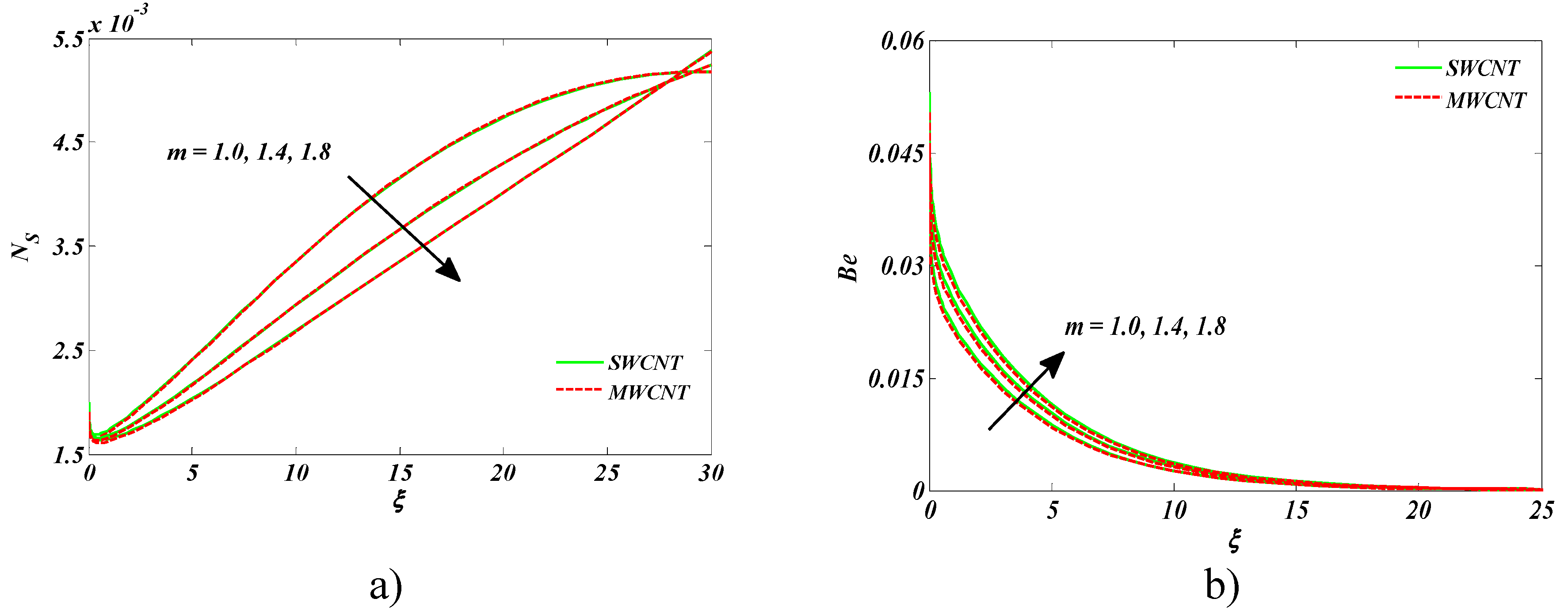
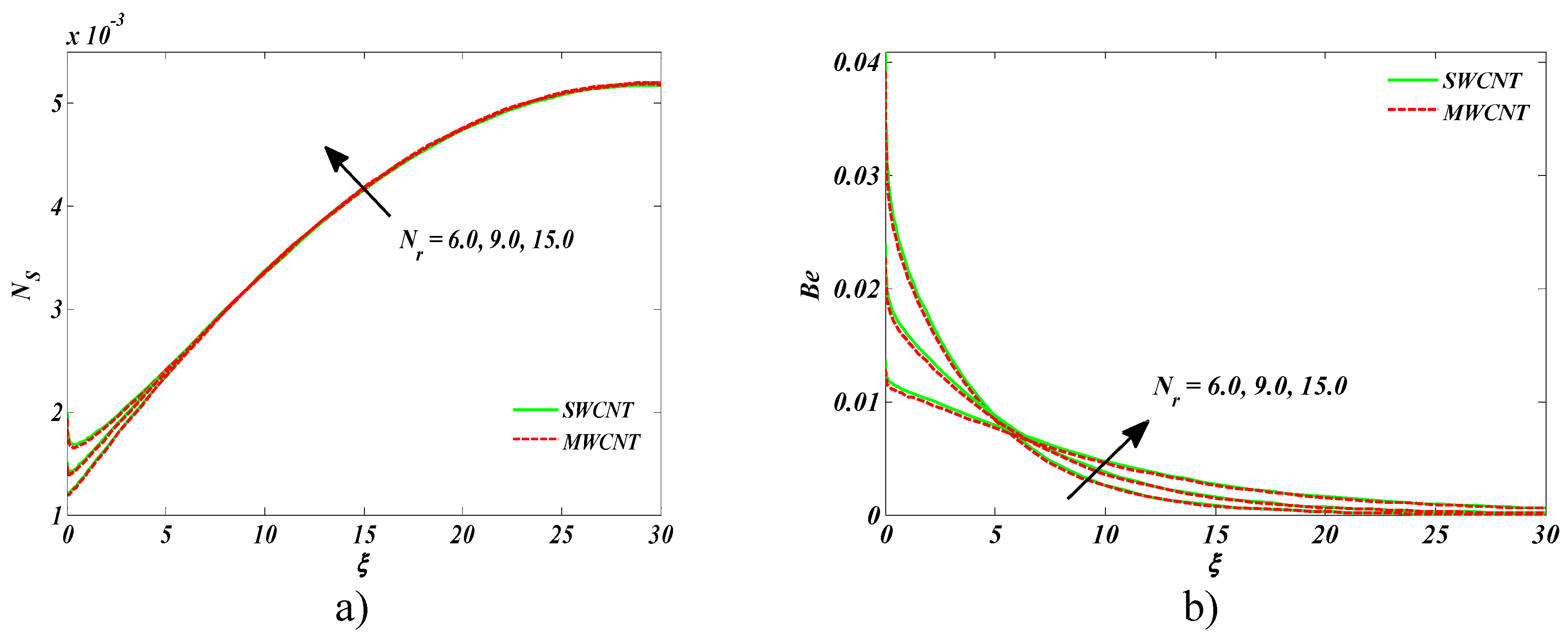
- An upsurge in entropy generation and the Bejan number was witnessed versus the radiation parameter.
- ⮚
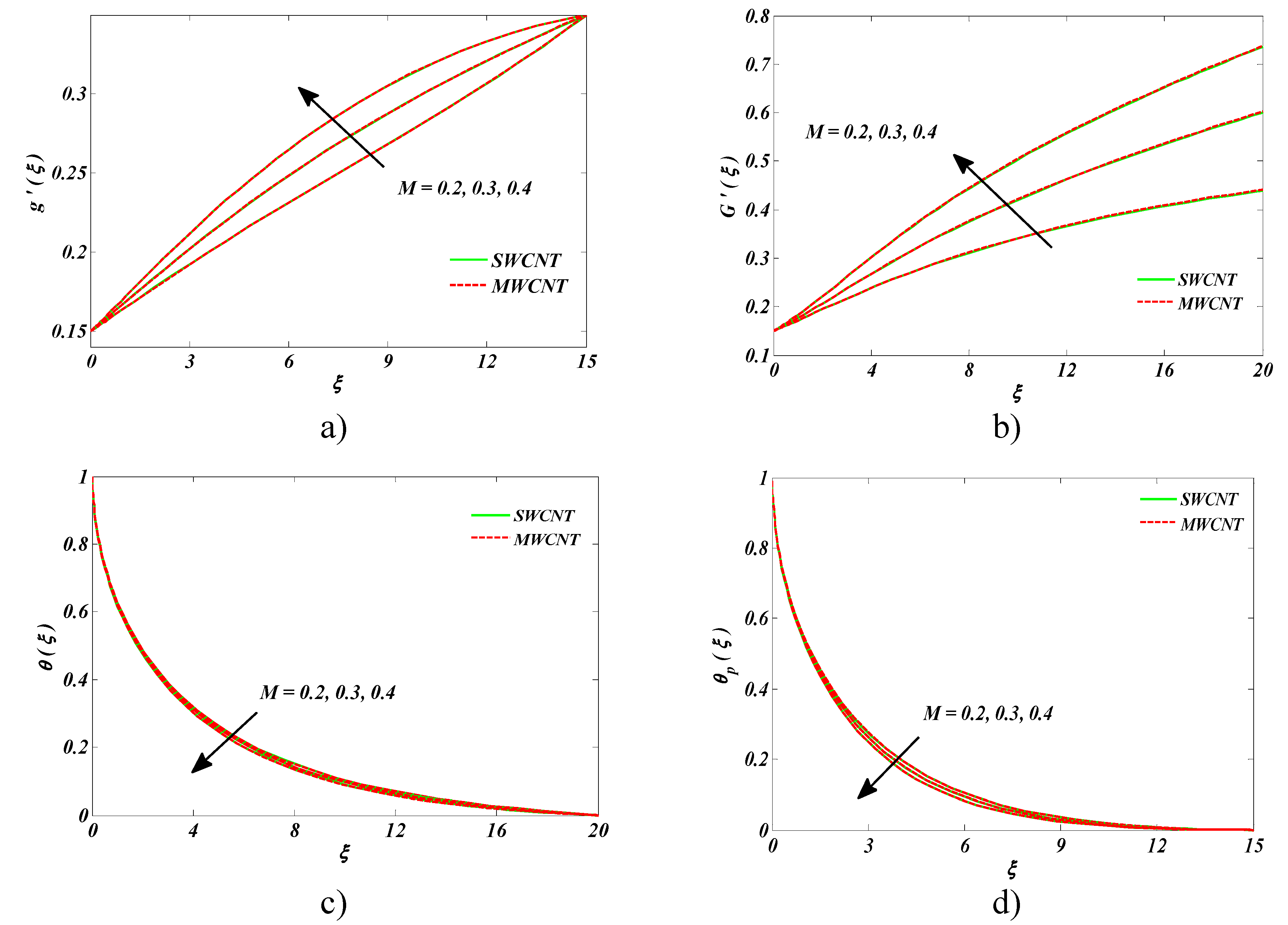
- Sturdier magnetic field diminished the velocity of the fluid.
- ⮚
- Skin friction coefficient declined for growing estimates of dust particles’ mass concentration.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Coordinate measured in radial direction | |
| Velocity components along and directions | |
| Effective dynamic viscosity of nanofluid | |
| Density of nanofluid | |
| Kinematic viscosity of nanofluid | |
| Darcy-permeability of the porous medium | |
| Drag coefficient | |
| Volume fraction of dust particles | |
| Stokes resistance | |
| Number density of dust particles | |
| Electric conductivity | |
| Applied magnetic field | |
| Hall parameter | |
| md | Mass concentration of the dust particles |
| knf | Effective thermal conductivity of the nanofluid |
| (ρCp)nf | Effective heat capacitance of the nanofluid |
| N1 | Density of the particle phase |
| τv | Relaxation time of dust particles |
| τT | Thermal equilibrium time |
| τw | Shear stress at the surface |
| Entropy generation rate per unit volume | |
| Velocity components of particle phase in x and r directions | |
| Specific heat of the dust particles | |
| Velocity of the moving needle | |
| Velocity outside the boundary layer | |
| Dimensional temperature of the nanofluid | |
| Temperature of the dust particle | |
| Constant surface temperature of the thin needle | |
| Ambient temperature | |
| Porosity parameter | |
| Forchheimer parameter | |
| Dust particles mass concentration | |
| Fluid particle interaction parameter for velocity | |
| Magnetic field parameter | |
| Prandtl number | |
| Nonlinear radiation parameter | |
| Temperature ratio parameter | |
| Eckert number | |
| Fluid particle interaction parameter for temperature | |
| Ratio of specific heat | |
| Surface heat flux | |
| Entropy generation number |
References
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Rehman, A.U.; Mehmood, R.; Nadeem, S. Entropy analysis of radioactive rotating nanofluid with thermal slip. Appl. Therm. Eng. 2017, 112, 832–840. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, T.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Lu, D.; Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. A Thin Film Flow of Nanofluid Comprising Carbon Nanotubes Influenced by Cattaneo-Christov Heat Flux and Entropy Generation. Coatings 2019, 9, 296. [Google Scholar] [CrossRef]
- Hassan, M.; Mohyud-Din, S.T.; Ramzan, M. Study of heat transfer and entropy generation in ferrofluid under low oscillating magnetic field. Indian J. Phys. 2019, 93, 749–758. [Google Scholar] [CrossRef]
- Suleman, M.; Ramzan, M.; Zulfiqar, M.; Bilal, M.; Shafee, A.; Chung, J.D.; Lu, D.; Farooq, U. Entropy analysis of 3D non-Newtonian MHD nanofluid flow with nonlinear thermal radiation past over exponential stretched surface. Entropy 2018, 20, 930. [Google Scholar] [CrossRef]
- Ramzan, M.; Sheikholeslami, M.; Chung, J.D.; Shafee, A. Melting heat transfer and entropy optimization owing to carbon nanotubes suspended Casson nanoliquid flow past a swirling cylinder-A numerical treatment. AIP Adv. 2018, 8, 115130. [Google Scholar] [CrossRef]
- Li, Z.; Hedayat, M.; Sheikholeslami, M.; Shafee, A.; Zrelli, H.; Tlili, I.; Nguyen, T.K. Numerical simulation for entropy generation and hydrothermal performance of nanomaterial inside a porous cavity using Fe3O4 nanoparticles. Phys. A 2019, 524, 272–288. [Google Scholar] [CrossRef]
- Khan, M.I.; Shah, F.; Hayat, T.; Alsaedi, A. Transportation of CNTs based nanomaterial flow confined between two coaxially rotating disks with entropy generation. Phys. A 2019, 527, 121154. [Google Scholar] [CrossRef]
- Abbas, S.Z.; Khan, W.A.; Sun, H.; Ali, M.; Irfan, M.; Shahzed, M.; Sultan, F. Mathematical modeling and analysis of Cross nanofluid flow subjected to entropy generation. Appl. Nanosci. 2019, 1–2. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56. [Google Scholar] [CrossRef]
- Bethune, D.S.; Kiang, C.H.; De Vries, M.S.; Gorman, G.; Savoy, R.; Vazquez, J.; Beyers, R. Cobalt-catalysed growth of carbon nanotubes with single-atomic-layer walls. Nature 1993, 363, 605. [Google Scholar] [CrossRef]
- Baughman, R.H.; Zakhidov, A.A.; De Heer, W.A. Carbon nanotubes--the route toward applications. Science 2002, 297, 787–792. [Google Scholar] [CrossRef] [PubMed]
- Dresselhaus, M.S.; Dresselhaus, G.; Eklund, P.C. Science of Fullerenes and Carbon Nanotubes: Their Properties and Applications; ACADEMIC PRESS: New Yourk, NY, USA, 1996. [Google Scholar]
- De Volder, M.F.; Tawfick, S.H.; Baughman, R.H.; Hart, A.J. Carbon nanotubes: Present and future commercial applications. Science 2013, 339, 535–539. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica 2013, 48, 275–285. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab: Du Page County, IL, USA, 1995. [Google Scholar]
- Eastman, J.A.; Choi, U.S.; Li, S.; Thompson, L.J.; Lee, S. Enhanced thermal conductivity through the development of nanofluids. MRS Online Proc. Libr. Arch. 1996. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, S.R.; Choi, S.U.; Eastman, J.A. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S.A. Numerical analysis of Fe3O4–H2O nanofluid flow in permeable media under the effect of external magnetic source. Int. J. Heat Mass Transf. 2018, 118, 182–192. [Google Scholar] [CrossRef]
- Khan, M.I.; Kumar, A.; Hayat, T.; Waqas, M.; Singh, R. Entropy generation in flow of Carreau nanofluid. J. Mol. Liq. 2019, 278, 677–687. [Google Scholar] [CrossRef]
- Sheikholeslami, M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Method Appl. M 2019, 344, 319–333. [Google Scholar] [CrossRef]
- Khan, W.A.; Sultan, F.; Ali, M.; Shahzad, M.; Khan, M.; Irfan, M. Consequences of activation energy and binary chemical reaction for 3D flow of Cross-nanofluid with radiative heat transfer. J. Braz. Soc. Mech. Sci. 2019, 41, 4. [Google Scholar] [CrossRef]
- Hosseini, S.R.; Sheikholeslami, M. Investigation of the nanofluid convective flow and entropy generation within a microchannel heat sink involving magnetic field. Powder Technol. 2019, 351, 195–202. [Google Scholar] [CrossRef]
- Ahmed, J.; Khan, M.; Ahmad, L. MHD swirling flow and heat transfer in Maxwell fluid driven by two coaxially rotating disks with variable thermal conductivity. Chin. J. Phys. 2019, 60, 22–34. [Google Scholar] [CrossRef]
- Cheng, B.; Yang, S.; Liu, H.; Zhang, L.; Wang, F. Investigation of the interaction between carbon nanotube tip and silicon sample through molecular dynamic simulation. Chin. J. Phys. 2019, 60, 407–415. [Google Scholar] [CrossRef]
- Talla, J.A.; Alsalieby, A.F. Effect of uniaxial tensile strength on the electrical properties of doped carbon nanotubes: Density functional theory. Chin. J. Phys. 2019, 59, 418–425. [Google Scholar] [CrossRef]
- Bilal, M.; Ramzan, M. Hall current effect on unsteady rotational flow of carbon nanotubes with dust particles and nonlinear thermal radiation in Darcy–Forchheimer porous media. J. Therm. Anal. Calorim. 2019, 138, 3127–3137. [Google Scholar] [CrossRef]
- Nadeem, S.; Abbas, N.; Elmasry, Y.; Malik, M.Y. Numerical analysis of water based CNTs flow of micropolar fluid through rotating frame. Comput. Methods Programs Biomed. 2020, 186, 105194. [Google Scholar] [CrossRef]
- Ibrahim, M.; Khan, M.I. Mathematical modeling and analysis of SWCNT-Water and MWCNT-Water flow over a stretchable sheet. Comput. Methods Programs Biomed. 2019, 187, 105222. [Google Scholar] [CrossRef]
- Shahzadi, I.; Sadaf, H.; Nadeem, S.; Saleem, A. Bio-mathematical analysis for the peristaltic flow of single wall carbon nanotubes under the impact of variable viscosity and wall properties. Comput. Methods Programs Biomed. 2017, 139, 137–147. [Google Scholar] [CrossRef]
- Maleki, R.; Afrouzi, H.H.; Hosseini, M.; Toghraie, D.; Piranfar, A.; Rostami, S. pH-sensitive loading/releasing of doxorubicin using single-walled carbon nanotube and multi-walled carbon nanotube: A molecular dynamics study. Comput. Methods Programs Biomed. 2020, 186, 105210. [Google Scholar] [CrossRef]
- Zheng, S.; Liang, W.; Chu, H.; Zhou, H. Effects of radiation reabsorption of C1-C6 hydrocarbon flames at normal and elevated pressures. Fuel 2020, 266, 117061. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Waqas, M.; Khan, M.I.; Alsaedi, A. Entropy generation minimization and binary chemical reaction with Arrhenius activation energy in MHD radiative flow of nanomaterial. J. Mol. Liq. 2018, 259, 274–283. [Google Scholar] [CrossRef]
- Ramzan, M.; Mohammad, M.; Howari, F.; Chung, J.D. Entropy analysis of carbon nanotubes based nanofluid flow past a vertical cone with thermal radiation. Entropy 2019, 21, 642. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Behnoush, R.; Milad, D.; Ahmad, S.; Zhixiong, Li.; Truong, K.N. Application of nano-refrigerant for boiling heat transfer enhancement employing an experimental study. Int. J. Heat Mass Transfer. 2019, 141, 974–980. [Google Scholar] [CrossRef]
- Ramzan, M.; Riasat, S.; Kadry, S.; Long, C.; Nam, Y.; Lu, D. Numerical simulation of 3D condensation nanofluid film flow with Carbon nanotubes on an inclined rotating disk. Appl. Sci. 2020, 10, 168. [Google Scholar] [CrossRef]
- Ramzan, M.; Mohammad, M.; Howari, F. Magnetized suspended carbon nanotubes based nanofluid flow with bio-convection and entropy generation past a vertical cone. Sci. Rep. 2019, 9, 1–5. [Google Scholar] [CrossRef]
- Karvelas, E.; Liosis, C.; Benos, L.; Karakasidis, T.; Sarris, I. Micromixing efficiency of particles in heavy metal removal processes under various inlet conditions. Water. 2019, 11, 1135. [Google Scholar] [CrossRef]
- Fragkou, A.D.; Karakasidis, T.E.; Sarris, I.E. Recurrence quantification analysis of MHD turbulent channel flow. Phys. A Stat. Mech. Appl. 2019, 531, 121741. [Google Scholar] [CrossRef]
- Chen, J.L.; Smith, T.N. Forced convection heat transfer from nonisothermal thin needles. J. Heat Transf. 1978, 100, 358–362. [Google Scholar] [CrossRef]
- Afridi, M.I.; Tlili, I.; Qasim, M.; Khan, I. Nonlinear Rosseland thermal radiation and energy dissipation effects on entropy generation in CNTs suspended nanofluids flow over a thin needle. Bound Value Probl. 2018, 2018, 148. [Google Scholar] [CrossRef]
- Sulochana, C.; Prakash, J.; Sandeep, N. Unsteady MHD flow of a dusty nanofluid past a vertical stretching surface with non-uniform heat source/sink. Int. J. Sci. Eng. 2016, 10, 1–9. [Google Scholar]
- Raju, C.S.; Saleem, S.; Al-Qarni, M.M.; Upadhya, S.M. Unsteady nonlinear convection on Eyring–Powell radiated flow with suspended graphene and dust particles. Microsyst. Technol. 2019, 25, 1321–1331. [Google Scholar] [CrossRef]
- Xue, Q.Z. Model for thermal conductivity of carbon nanotube-based composites. Phys. B 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Boundary layer flow over a continuously moving thin needle in a parallel free stream. Chin. Phys. Lett. 2007, 24, 2895. [Google Scholar] [CrossRef]



| Properties | Nano-Fluid |
|---|---|
| Density | |
| Heat capacity | |
| Viscosity | |
| Thermal conductivity |
| Thermo-Physical Properties | H2O | SWCNT | MWCNT |
|---|---|---|---|
| Cp (j/kg)K | 425 | 796 | |
| ρ (kg/m3) | 997.1 | 2600 | 1600 |
| k (W/mK) | 0.613 | 6600 | 3000 |
| Prandtl number (Pr) |
| Ishak et al. [47] | Chen and Smith [42] | M. Idrees Afridi et al. [43] | Present Results | |
|---|---|---|---|---|
| 0.1 | 1.2888 | 1.28881 | 1.28881 | 1.28508 |
| 0.01 | 8.4924 | 8.49244 | 8.49233 | 8.4878 |
| 0.001 | 62.1637 | 62.16372 | 62.16370 | 62.1594 |
| Skin Friction Coefficient | |||||||
|---|---|---|---|---|---|---|---|
| SWCNT | MWCNT | ||||||
| 0.001 | 0.00184647 | 0.00184157 | |||||
| 0.01 | 0.00583012 | 0.00581468 | |||||
| 0.2 | 0.02591430 | 0.02584880 | |||||
| 0.1 | 0.00583012 | 0.00581468 | |||||
| 2.0 | 0.00583276 | 0.00581722 | |||||
| 3.5 | 0.00583491 | 0.00581927 | |||||
| 0.10 | 0.00583012 | 0.00581468 | |||||
| 0.25 | 0.00644651 | 0.00640784 | |||||
| 0.4 | 0.00706302 | 0.00700110 | |||||
| 1.0 | 0.00583012 | 0.00581468 | |||||
| 2.0 | 0.00582586 | 0.00581043 | |||||
| 3.0 | 0.00582165 | 0.00580623 | |||||
| 0.2 | 0.00583012 | 0.00581468 | |||||
| 0.3 | 0.00711701 | 0.00710157 | |||||
| 0.4 | 0.00840431 | 0.00838888 | |||||
| 1.0 | 0.00583012 | 0.00581468 | |||||
| 1.4 | 0.00499559 | 0.00498015 | |||||
| 1.8 | 0.00447082 | 0.00445537 | |||||
| Nusselt Number | |||||||
|---|---|---|---|---|---|---|---|
| SWCNT | MWCNT | ||||||
| 0.10 | 1.10739 | 1.05489 | |||||
| 0.25 | 1.12048 | 1.06695 | |||||
| 0.40 | 1.13570 | 1.08087 | |||||
| 1.0 | 1.10739 | 1.05489 | |||||
| 2.0 | 1.28855 | 1.22836 | |||||
| 3.0 | 1.44647 | 1.37965 | |||||
| 0.3 | 1.12089 | 1.06788 | |||||
| 0.5 | 1.10739 | 1.05489 | |||||
| 0.9 | 1.09958 | 1.04738 | |||||
| 1.0 | 1.10739 | 1.05489 | |||||
| 1.4 | 1.09857 | 1.04640 | |||||
| 1.8 | 1.09329 | 1.04131 | |||||
| 6.0 | 1.10739 | 1.05489 | |||||
| 9.0 | 0.80951 | 0.77264 | |||||
| 15.0 | 0.59158 | 0.56589 | |||||
| 1.1 | 1.10739 | 1.05489 | |||||
| 1.4 | 0.80635 | 0.77013 | |||||
| 1.7 | 0.71356 | 0.68292 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tlili, I.; Ramzan, M.; Kadry, S.; Kim, H.-W.; Nam, Y. Radiative MHD Nanofluid Flow over a Moving Thin Needle with Entropy Generation in a Porous Medium with Dust Particles and Hall Current. Entropy 2020, 22, 354. https://doi.org/10.3390/e22030354
Tlili I, Ramzan M, Kadry S, Kim H-W, Nam Y. Radiative MHD Nanofluid Flow over a Moving Thin Needle with Entropy Generation in a Porous Medium with Dust Particles and Hall Current. Entropy. 2020; 22(3):354. https://doi.org/10.3390/e22030354
Chicago/Turabian StyleTlili, Iskander, Muhammad Ramzan, Seifedine Kadry, Hyun-Woo Kim, and Yunyoung Nam. 2020. "Radiative MHD Nanofluid Flow over a Moving Thin Needle with Entropy Generation in a Porous Medium with Dust Particles and Hall Current" Entropy 22, no. 3: 354. https://doi.org/10.3390/e22030354
APA StyleTlili, I., Ramzan, M., Kadry, S., Kim, H.-W., & Nam, Y. (2020). Radiative MHD Nanofluid Flow over a Moving Thin Needle with Entropy Generation in a Porous Medium with Dust Particles and Hall Current. Entropy, 22(3), 354. https://doi.org/10.3390/e22030354








