The Establishment and Dynamic Properties of a New 4D Hyperchaotic System with Its Application and Statistical Tests in Gray Images
Abstract
1. Introduction
2. A New Hyperchaotic System
3. Analysis of Dynamic Properties
3.1. Subsection Equilibrium Curve
3.2. Judgment of Local Stability
3.3. Poincare Section Diagram
3.4. Periodic Attractor
3.5. Quasi-Periodic Attractors
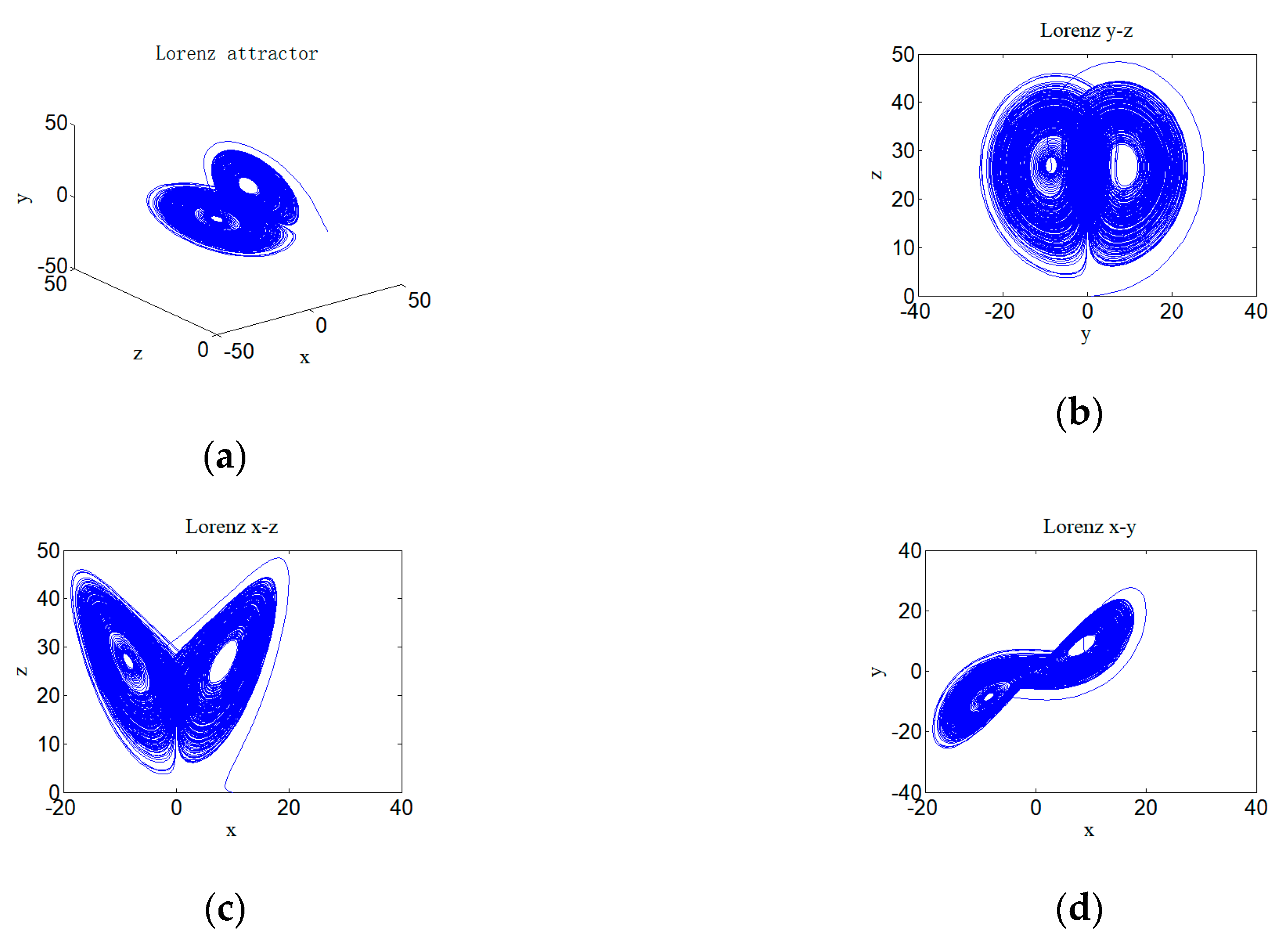
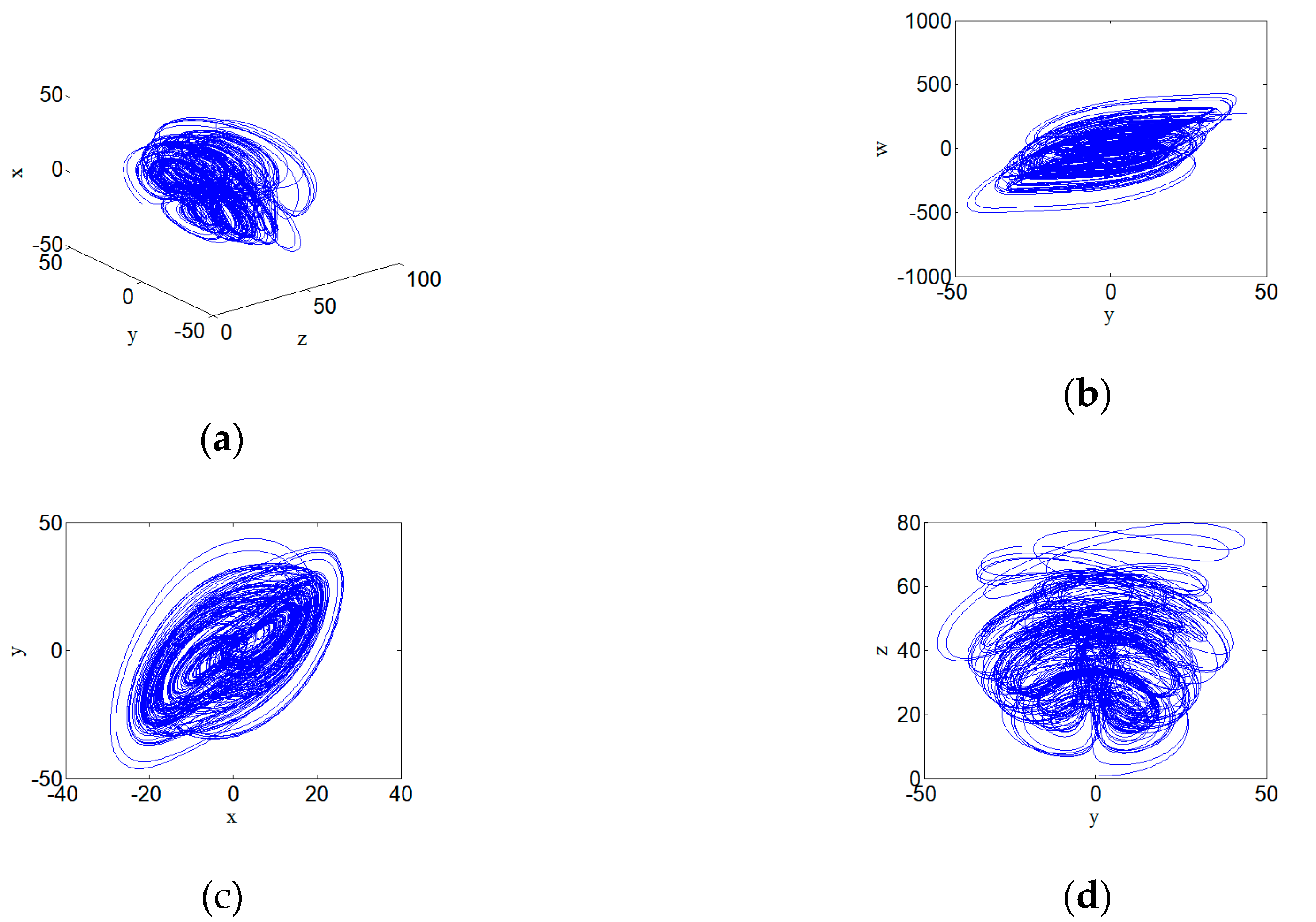
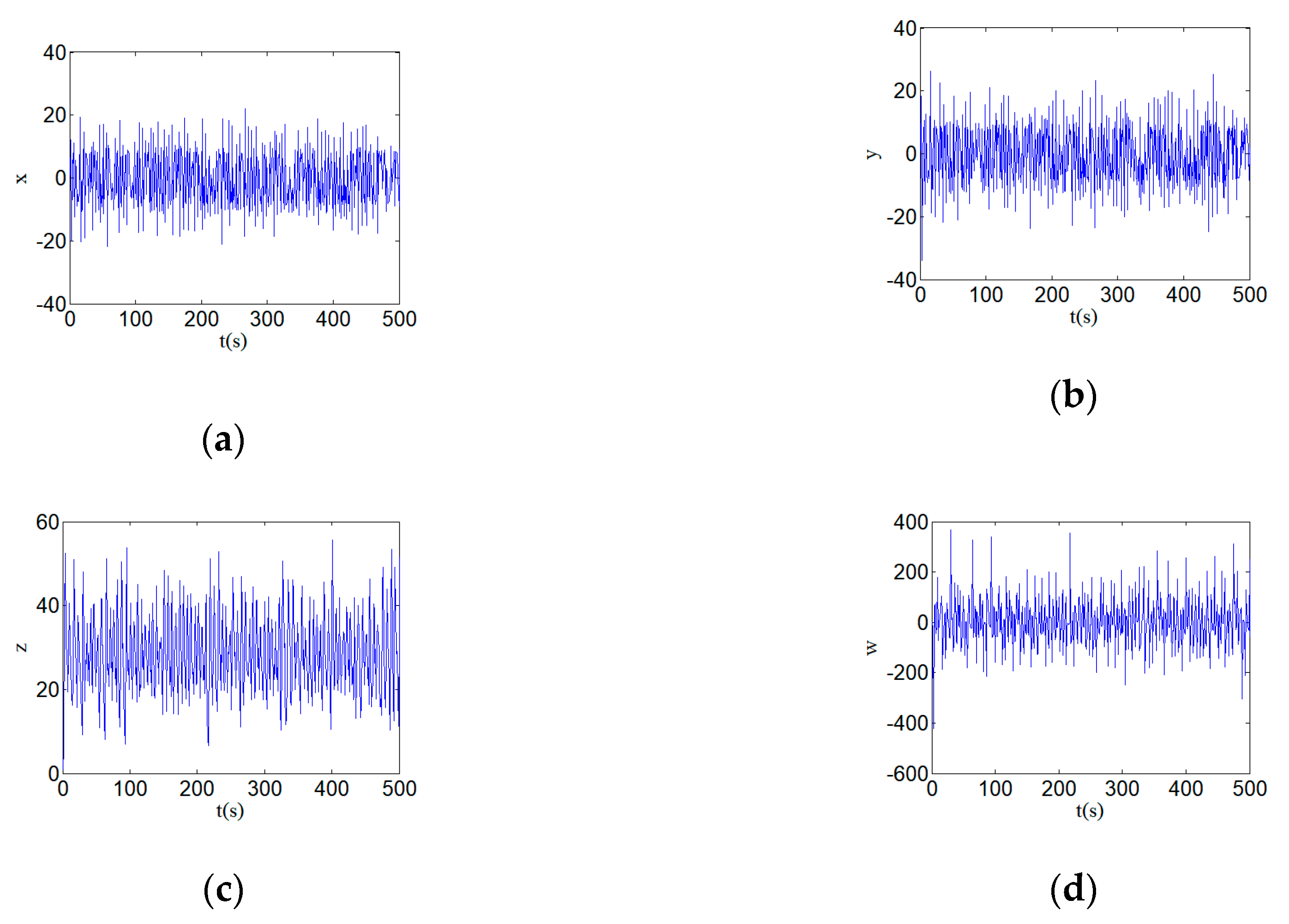
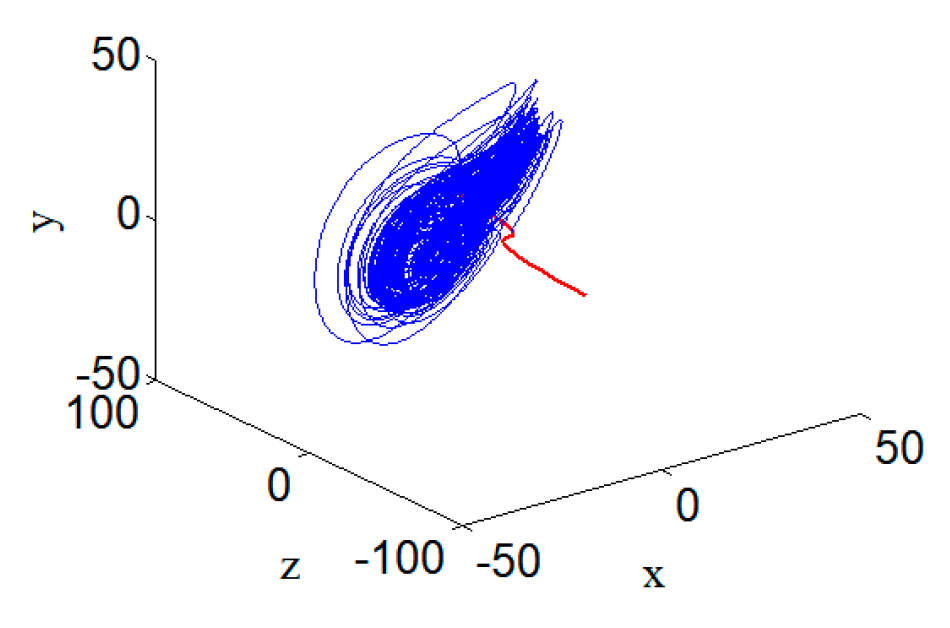
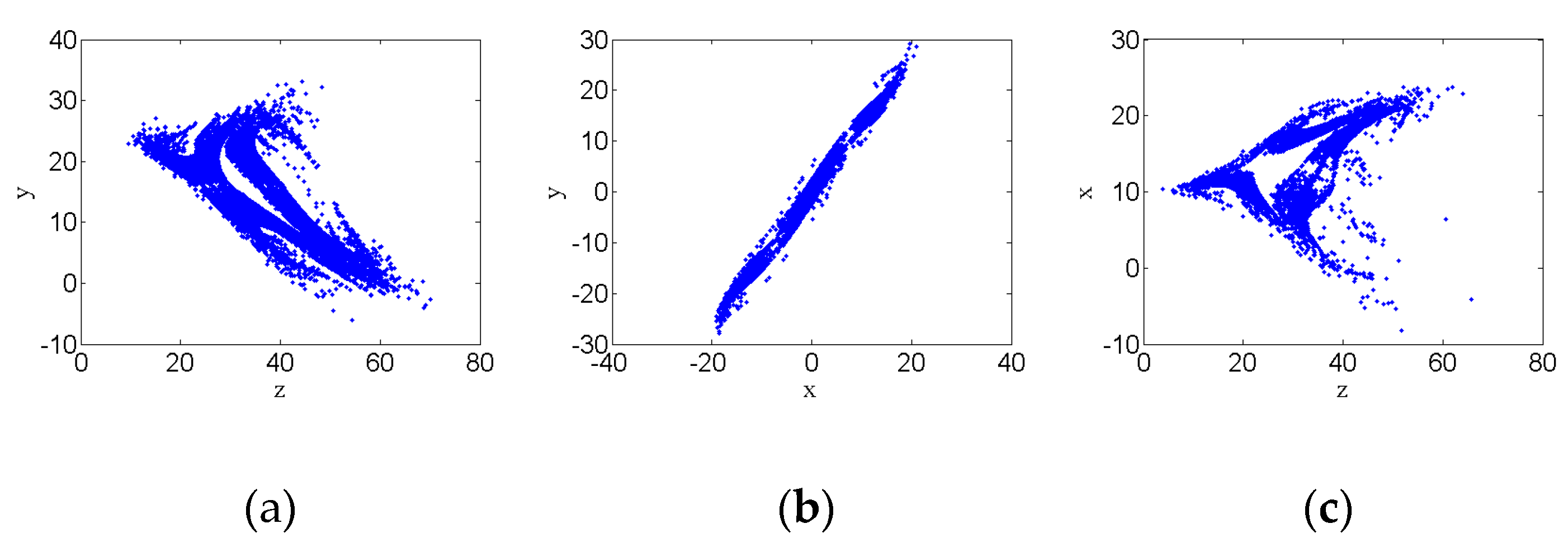
3.6. Chaotic Attractor
3.7. Bifurcation and Lyapunov Exponent
4. Normalization and Quantization
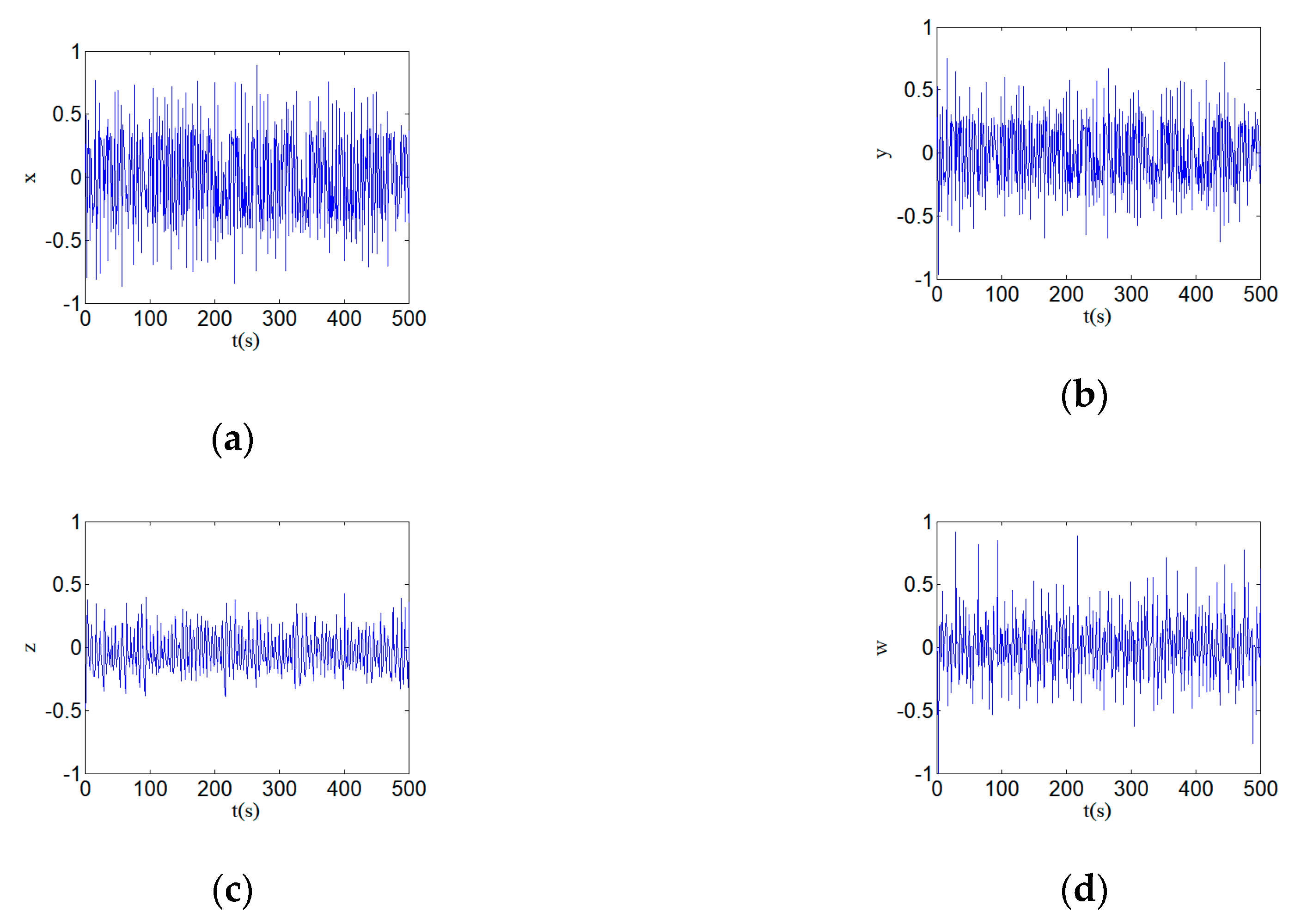
4.1. Normalization Treatment
4.2. Quantization
4.3. NIST Test
4.4. Permutation Entropy
4.5. Approximate Entropy
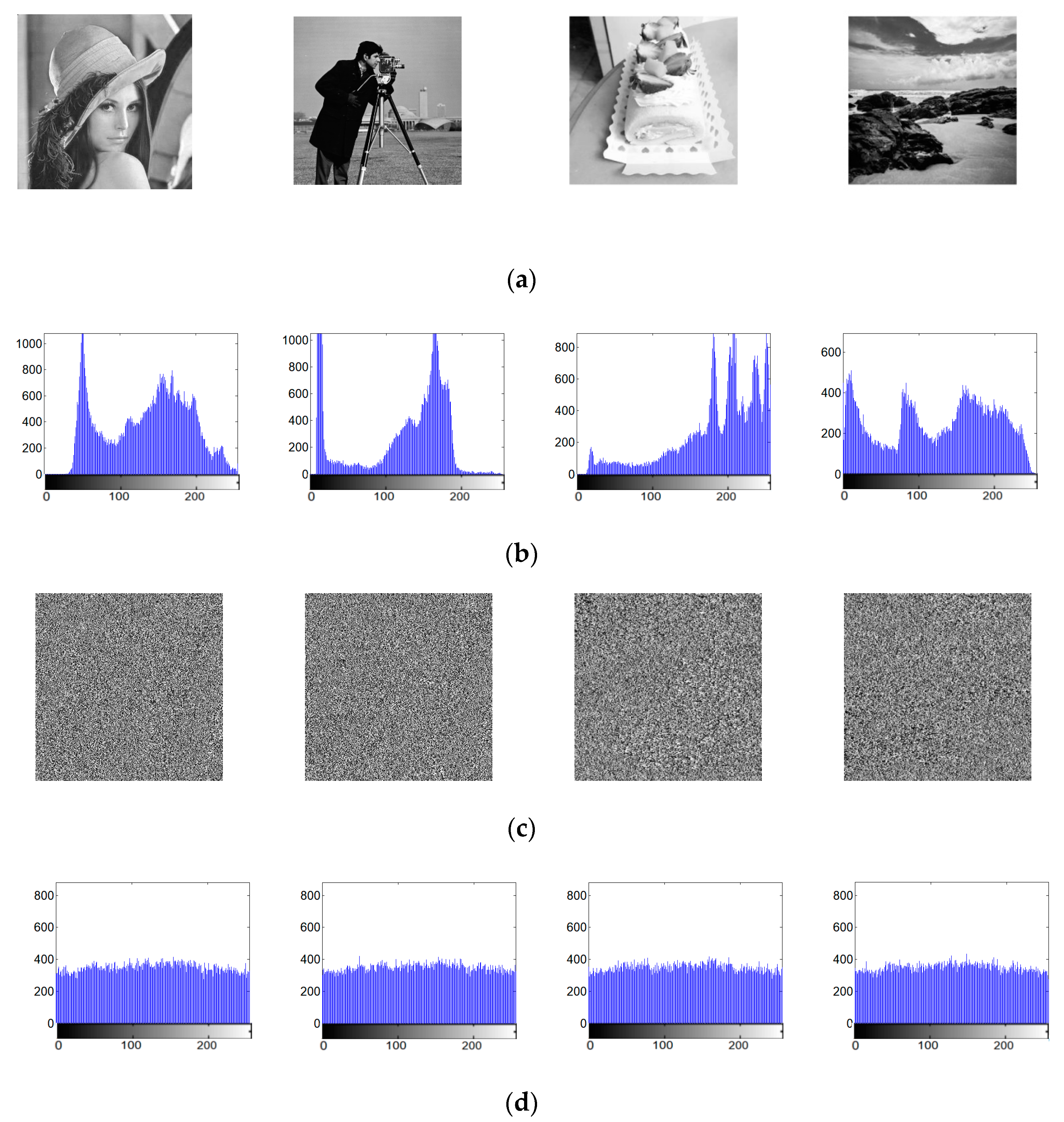
5. Application in Image Encryption
5.1. Image Encryption Scheme
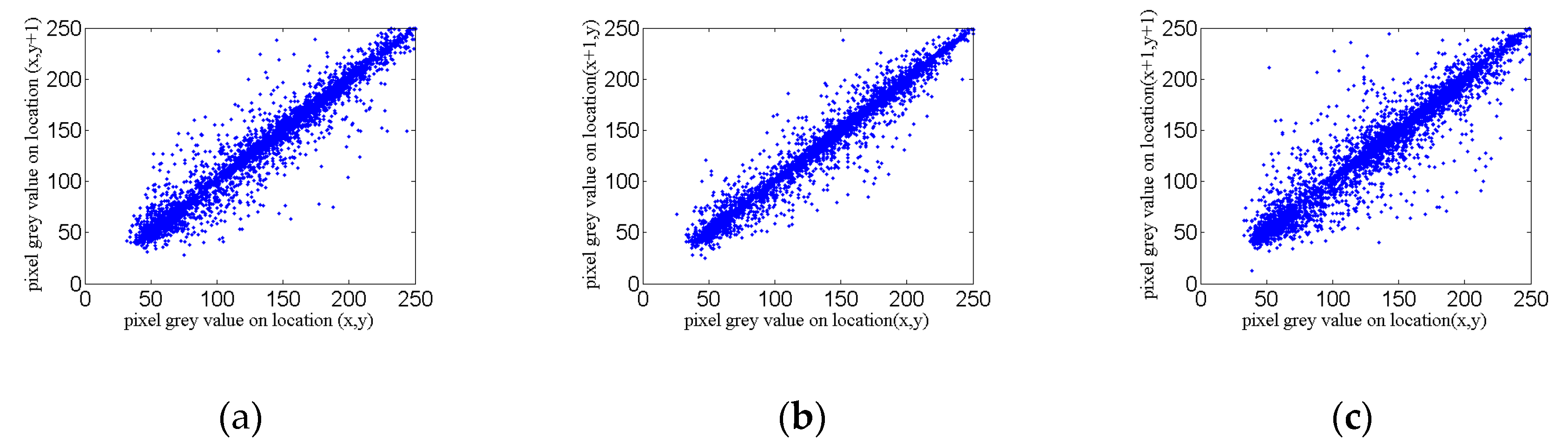
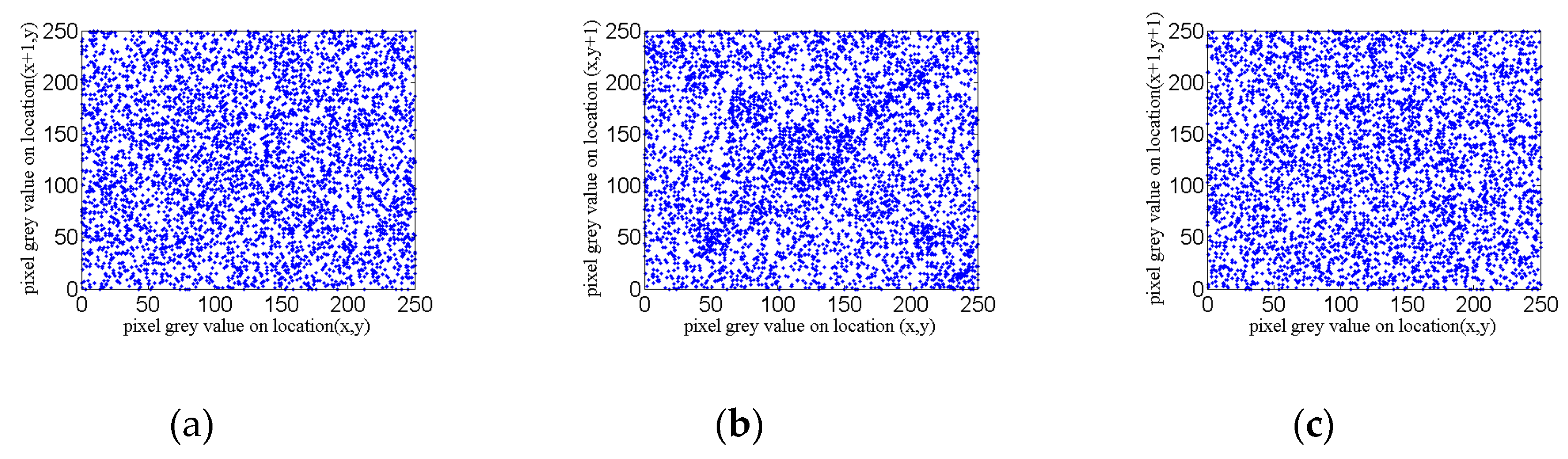
5.2. Correlation Coefficient Analysis
5.3. The Information Entropy
5.4. Analysis of Differential Attack
5.5. Analysis of Plaintext Attack and Ciphertext Attack
5.6. Analysis of Noise Attack
5.7. Analysis of Exhaustive Attack
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lorenz, E.N. Deterministic non-periodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Li, X.; Xie, Z.; Wu, J.; Li, T. Image Encryption Based on Dynamic Filtering and Bit Cuboid Operations. Complexity 2019, 2019, 7485621. [Google Scholar] [CrossRef]
- Wang, X.; Gao, S. Image encryption algorithm for synchronously updating Boolean networks based on matrix semi-tensor product theory. Inf. Sci. 2020, 507, 16–36. [Google Scholar] [CrossRef]
- Wang, X.; Feng, L.; Zhao, H. Fast image encryption algorithm based on parallel computing system. Inf. Sci. 2019, 486, 340–358. [Google Scholar] [CrossRef]
- Ai, B.-Q.; Wang, X.-J.; Liu, G.-T.; Liu, L.-G. Correlated noise in a logistic growth model. Phys. Rev. E 2003, 67, 022903. [Google Scholar] [CrossRef]
- Wang, L.Y.; Cheng, H. Pseudo-Random Number Generator Based on Logistic Chaotic System. Entropy 2019, 21, 960. [Google Scholar] [CrossRef]
- Rubens, R. Quantum-chaotic key distribution in optical networks: From secrecy to implementation with logistic map. Quantum Inf. Process. 2018, 17, 329. [Google Scholar]
- Sheela, S.J. Image encryption based on modified Henon map using hybrid chaotic shift transform. Multimed. Tools. Appl. 2018, 77, 25223–25251. [Google Scholar] [CrossRef]
- Roy, A. Audio signal encryption using chaotic Henon map and lifting wavelet transforms. Eur. Phys. J. 2017, 132, 524. [Google Scholar] [CrossRef]
- Balibrea-Iniesta, F.; Lopesino, C.; Wiggins, S.; Mancho, A.M. Chaotic Dynamics in Nonautonomous Maps: Application to the Nonautonomous Henon Map. Int. J. Bifurcat. Chaos 2015, 25, 1550172. [Google Scholar] [CrossRef]
- Jamal, R.K. Secure Communication Coupled Laser Based on Chaotic Rossler Circuits, Nonlinear Optics. Quantum Optics 2019, 51, 79–91. [Google Scholar]
- Girdhar, A. A RGB image encryption technique using Lorenz and Rossler chaotic system on DNA sequences. Multimed Tools Appl. 2018, 77, 27017–27039. [Google Scholar] [CrossRef]
- Mandal, M.K. Symmetric key image encryption using chaotic Rossler system. Secur. Commun. Netw. 2014, 7, 2145–2152. [Google Scholar] [CrossRef]
- Mishra, J. Modified Chua chaotic attractor with differential operators with non-singular kernels. Chaos Solitons Fractals 2019, 125, 64–72. [Google Scholar] [CrossRef]
- Freud, S. On the Influence of the Coupling Strength among Chua’s Circuits on the Structure of Their Hyper-Chaotic Attractors. Int. J. Bifurcat. Chaos 2016, 26, 1650115. [Google Scholar] [CrossRef]
- Korneta, W.; Garcia-Moreno, E.; Sena, A.L. Noise activated dc signal sensor based on chaotic Chua circuit. Commun. Nonlinear Sci. Numer. Simul. 2015, 24, 145–152. [Google Scholar] [CrossRef]
- Sathiyamurthi, P.; Ramakrishnan, S. Testing and Analysis of Chen Chaotic Mapping for Speech Cryptography. J. Test. Eval. 2019, 47, 3028–3040. [Google Scholar] [CrossRef]
- Huang, X.; Liu, L.F.; Li, X.J.; Yu, M.R.; Wu, Z.J. A New Pseudorandom Bit Generator Based on Mixing Three-Dimensional Chen Chaotic System with a Chaotic Tactics. Complexity 2019, 2019, 6567198. [Google Scholar] [CrossRef]
- Ozkaynak, F.; Celik, V.; Ozer, A.B. A new S-box construction method based on the fractional-order chaotic Chen system. Signal Image Video P 2017, 11, 659–664. [Google Scholar] [CrossRef]
- Liu, L.C.; Du, C.H.; Zhang, X.F.; Li, J.; Shi, S.S. Dynamics and Entropy Analysis for a New 4-D Hyperchaotic System with Coexisting Hidden Attractors. Entropy 2019, 21, 287. [Google Scholar] [CrossRef]
- Ma, J.; Chen, Z.; Wang, Z.; Zhang, Q. A four-wing hyper-chaotic attractor generated from a 4-D memristive system with a line equilibrium. Nonlinear Dyn. 2015, 81, 1275–1288. [Google Scholar] [CrossRef]
- Singh, J.P.; Roy, B.K.; Jafari, S. New family of 4-D hyperchaotic and chaotic systems with quadric surfaces of equilibria. Chaos Solitons Fractals 2018, 106, 243–257. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Analysis, adaptive control and synchronization of a novel 4-D hyperchaotic hyperjerk system via backstepping control method. Arch. Control.Sci. 2016, 26, 311–338. [Google Scholar] [CrossRef]
- Koyuncu, I.; Alcin, M.; Tuna, M.; Pehlivan, I.; Varan, M.; Vaidyanathan, S. Real-time high-speed 5-D hyperchaotic Lorenz system on FPGA. Int. J. Comput. Appl. Technol. 2019, 61, 152–165. [Google Scholar]
- Bonyah, E. Chaos in a 5-D hyperchaotic system with four wings in the light of non-local and non-singular fractional derivatives. Chaos Solitons Fractals 2018, 116, 316–331. [Google Scholar] [CrossRef]
- Zhang, L.M.; Sun, K.H.; He, S.B.; Wang, H.H.; Xu, Y.X. Solution and dynamics of a fractional-order 5-D hyperchaotic system with four wings. Eur. Phys. J. Plus 2017, 132, 31. [Google Scholar] [CrossRef]
- Vaidyanathan, S.; Volos, C.; Pham, V.T. Hyperchaos, adaptive control and synchronization of a novel 5-D hyperchaotic system with three positive Lyapunov exponents and its SPICE implementation. Arch. Control Sci. 2014, 24, 409–446. [Google Scholar] [CrossRef]
- Hu, Z.Y.; Chan, C.K. A 7-D Hyperchaotic System-Based Encryption Scheme for Secure Fast-OFDM-PON. J. Lightwave. Technol. 2018, 36, 3373–3381. [Google Scholar] [CrossRef]
- Liu, J.; Tong, X.J.; Wang, Z.; Ma, J.; Yi, L.T. An Improved Rao-Nam Cryptosystem Based on Fractional Order Hyperchaotic System and EDF-QC-LDPC. Int. J. Bifurcat. Chaos 2019, 29, 1950122. [Google Scholar] [CrossRef]
- Lassoued, A.; Boubaker, O. Dynamic Analysis and Circuit Design of a Novel Hyperchaotic System with Fractional-Order Terms. Complexity 2019, 2019, 1564573. [Google Scholar] [CrossRef]
- Boraha, M.; Roy, B.K. Design of fractional-order hyperchaotic systems with maximum number of positive Lyapunov exponents and their antisynchronisation using adaptive control. Int. J. Control 2018, 91, 2615–2630. [Google Scholar] [CrossRef]
- Goufo, E.F.D. On chaotic models with hidden attractors in fractional calculus above power law. Chaos Solitons Fractals 2019, 127, 24–30. [Google Scholar] [CrossRef]
- Bayani, A.; Rajagopal, K.; Khalaf, A.J.M.; Jafari, S.; Leutcho, G.D.; Kengne, J. Dynamical analysis of a new multistable chaotic system with hidden attractor: Antimonotonicity, coexisting multiple attractors, and offset boosting. Phys. Lett. A 2019, 383, 1450–1456. [Google Scholar] [CrossRef]
- Pham, V.T.; Volos, C.; Jafari, S.; Kapitaniak, T. A Novel Cubic-Equilibrium Chaotic System with Coexisting Hidden Attractors: Analysis, and Circuit Implementation. J. Circuit Syst. Comp. 2018, 27, 1850066. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, G.S.; Bao, H. Bursting oscillations and coexisting attractors in a simple memristor-capacitor-based chaotic circuit. Nonlinear. Dyn. 2019, 97, 1477–1494. [Google Scholar] [CrossRef]
- Lai, Q.; Nestor, T.; Kengne, J.; Zhao, X.W. Coexisting attractors and circuit implementation of a new 4D chaotic system with two equilibria. Chaos Solitons Fractals 2018, 107, 92–102. [Google Scholar] [CrossRef]
- Li, T.; Yang, M.; Wu, J.; Jing, X. A Novel Image Encryption Algorithm Based on a Fractional-Order Hyperchaotic System and DNA Computing. Complexity 2017, 2017, 9010251. [Google Scholar] [CrossRef]
- Li, T.; Shi, J.; Li, X.; Wu, J.; Pan, F. Image Encryption Based on Pixel-Level Diffusion with Dynamic Filtering and DNA-Level Permutation with 3D Latin Cubes. Entropy 2019, 21, 319. [Google Scholar] [CrossRef]
- Molteni, F.; Kucharski, F. A heuristic dynamical model of the North Atlantic Oscillation with a Lorenz-type chaotic attractor. Clim. Dyn. 2019, 52, 6173–6193. [Google Scholar] [CrossRef]
- Mallory, K.; van Gorder, R.A. Competitive Modes for the Detection of Chaotic Parameter Regimes in the General Chaotic Bilinear System of Lorenz Type. Int. J. Bifurcat. Chaos 2015, 25, 1530012. [Google Scholar] [CrossRef]
- Yan, W.H.; Ding, Q. A New Matrix Projective Synchronization and Its Application in Secure Communication. IEEE Access 2019, 7, 112977–112984. [Google Scholar] [CrossRef]
- Ding, L.N.; Liu, C.Y.; Zhang, Y.P. A New Lightweight Stream Cipher Based on Chaos. Symmetry 2019, 11, 853. [Google Scholar] [CrossRef]
- Garcia-Bosque, M.; Diez-Senorans, G.; Perez-Resa, A. A 1 Gbps Chaos-Based Stream Cipher Implemented in 0.18 mu m CMOS Technology. Electronics 2019, 8, 623. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Wu, J.; Xie, Z.; Shi, J. Joint image compression and encryption based on sparse Bayesian learning and bit-level 3D Arnold cat maps. PLoS ONE 2019, 14, e0224382. [Google Scholar] [CrossRef] [PubMed]
- Ping, P.; Xu, F.; Mao, Y.C.; Wang, Z.J. Designing permutation-substitution image encryption networks with Henon map. Neurocomputing 2018, 283, 53–63. [Google Scholar] [CrossRef]
- Ye, G.D.; Huang, X.L. An efficient symmetric image encryption algorithm based on an intertwining logistic map. Neurocomputing 2017, 251, 45–53. [Google Scholar] [CrossRef]
- Haroun, M.F.; Gulliver, T.A. Real-time image encryption using a low-complexity discrete 3D dual chaotic cipher. Nonlinear Dyn. 2015, 82, 1523–1535. [Google Scholar] [CrossRef]
- Wu, J.; Shi, J.; Li, T. A Novel Image Encryption Approach Based on a Hyperchaotic System, Pixel-Level Filtering with Variable Kernels, and DNA-Level Diffusion. Entropy 2020, 22, 5. [Google Scholar] [CrossRef]
- Wang, X.; Gao, S. Application of matrix semi-tensor product in chaotic image encryption. J. Frankin. Inst. 2019, 18, 11638–11667. [Google Scholar] [CrossRef]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Miles, S.; Barker, E. A statistical test suite for random and pseudorandom number generators for cryptographic applications. Appl. Phys. Lett. 2015, 22, 1645–1776. [Google Scholar]
- Zhu, C.; Hu, Y.; Sun, K. New image encryption algorithm based on hyperchaotic system and ciphertext diffusion in crisscross pattern. J. Electron. Inf. Technol. 2012, 34, 1735–1743. [Google Scholar] [CrossRef]
- Fan, C.L.; Ding, Q. A Novel Image Encryption Scheme Based on Self-Synchronous Chaotic Stream Cipher and Wavelet Transform. Entropy 2018, 20, 445. [Google Scholar] [CrossRef]
- Li, P.; Xu, J.; Mou, J.; Yang, F.F. Fractional-order 4D hyperchaotic memristive system and application in color image encryption. EURASIP J. Image 2019, 2019, 22. [Google Scholar] [CrossRef]
- Chai, X.; Gan, Z.; Lu, Y.; Chen, Y.; Han, D. A novel image encryption algorithm based on the chaotic system and DNA computing. Int. J. Mod. Phys. C 2017, 28, 1750069. [Google Scholar] [CrossRef]
- Zhan, K.; Wei, D.; Shi, J.; Yu, J. Cross-utilizing hyperchaotic and DNA sequences for image encryption. J. Electron. Imaging 2017, 26, 013021. [Google Scholar] [CrossRef]

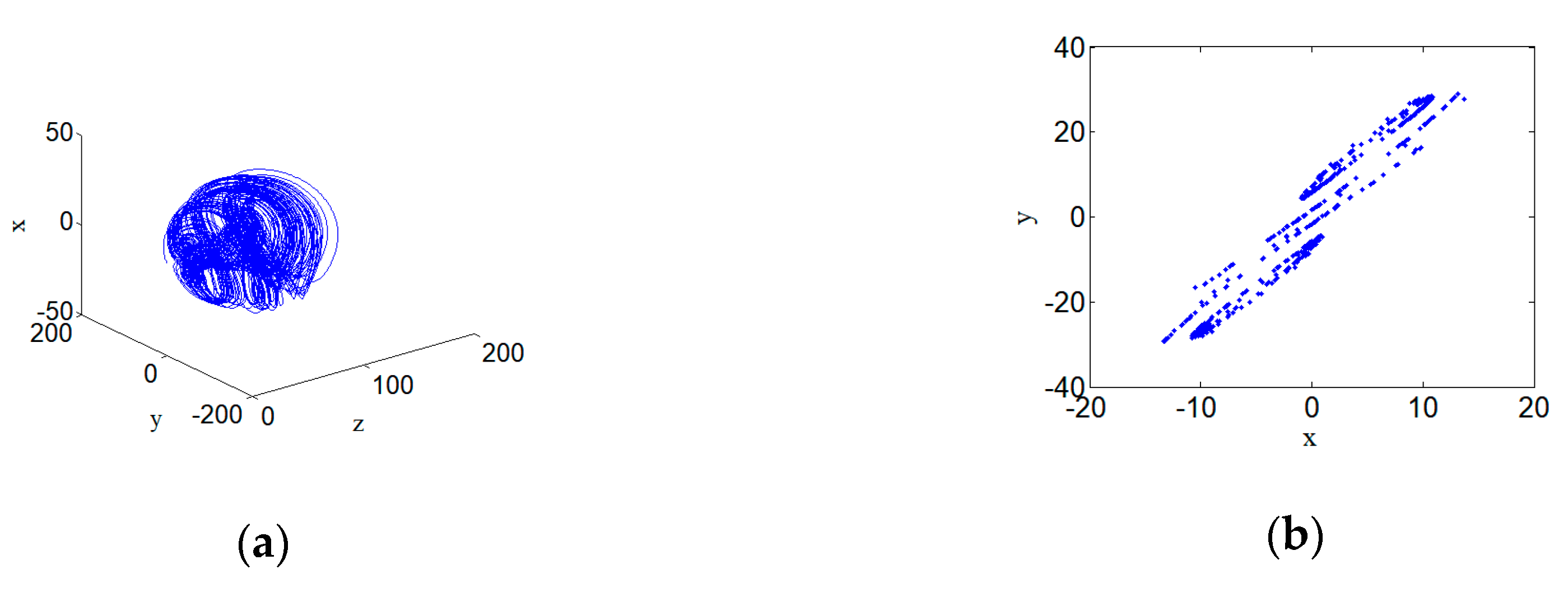






| Test | Result | ||||
|---|---|---|---|---|---|
| Frequency Test | 0.110561 | 0.251486 | 0.528546 | 0.228145 | Success |
| Frequency Test within a Block | 0.835247 | 0.142578 | 0.512879 | 0.627428 | Success |
| Runs Test | 0.759814 | 0.521473 | 0.715854 | 0.452842 | Success |
| Test for the Longest Run of Ones in a Block | 0.214189 | 0.204144 | 0.158728 | 0.157569 | Success |
| Binary Matrix Rank Test | 0.352471 | 0.521632 | 0.428745 | 0.638175 | Success |
| Discrete Fourier Transform Test | 0.644782 | 0.472575 | 0.284784 | 0.258741 | Success |
| Non-Overlapping Template Matching Test | 0.652417 | 0.418622 | 0.157525 | 0.784452 | Success |
| Overlapping Template Matching Test | 0.524718 | 0.514832 | 0.527865 | 0.518653 | Success |
| Maurer’s “Universal Statistical” Test | 0.195748 | 0.147258 | 0.285954 | 0.287695 | Success |
| Linear Complexity Test | 0.652149 | 0.625411 | 0.528765 | 0.318528 | Success |
| Serial Test | 0.058472 | 0.052148 | 0.078458 | 0.052145 | Success |
| Approximation Entropy Test | 0.024187 | 0.021458 | 0.025481 | 0.011285 | Success |
| Cumulative Sums Test | 0.421863 | 0.565281 | 0.627854 | 0.458654 | Success |
| Random Excursions Test | 0.524862 | 0.442389 | 0.458745 | 0.514865 | Success |
| Random Excursions Variant Test | 0.352874 | 0.328489 | 0.257841 | 0.258145 | Success |
| Time Series | m | τ | PE |
|---|---|---|---|
| 3 | 1 | 0.6201 | |
| 3 | 1 | 0.6548 | |
| 3 | 1 | 0.5724 | |
| 3 | 1 | 0.6017 |
| Time Series | m | ApEn | ||
|---|---|---|---|---|
| 2 | 0.1172 | 2048 | 0.7824 | |
| 2 | 0.1036 | 2048 | 0.7653 | |
| 2 | 0.1284 | 2048 | 0.7906 | |
| 2 | 0.1165 | 2048 | 0.7819 |
| Direction | Horizontal | Vertical | Diagonal |
|---|---|---|---|
| Lena image before encryption | 0.9842 | 0.6160 | 0.1969 |
| Lena image after encryption | 0.0043 | −0.0230 | −0.0027 |
| [2] before encryption | 0.9144 | 0.9545 | 0.9562 |
| [2] after encryption | −0.0014 | 0.0028 | 0.0080 |
| [38] before encryption | 0.9254 | 0.9438 | 0.9325 |
| [38] after encryption | 0.0045 | 0.0012 | 0.0001 |
| [45] before encryption | 0.9577 | 0.9440 | 0.9126 |
| [45] after encryption | −0.0082 | 0.0027 | 0.0030 |
| [51] before encryption | 0.9249 | 0.9593 | 0.9026 |
| [51] after encryption | −0.0042 | −0.0011 | 0.0029 |
| Image | InEn |
|---|---|
| Lena image | 7.9978 |
| [38] | 7.9971 |
| [52] | 7.9965 |
| [53] | 7.9971 |
| [54] | 7.9851 |
| Image | NPCR | UACI% |
| Lena image | 0.9961 | 33.42 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, L.; Ding, Q. The Establishment and Dynamic Properties of a New 4D Hyperchaotic System with Its Application and Statistical Tests in Gray Images. Entropy 2020, 22, 310. https://doi.org/10.3390/e22030310
Ding L, Ding Q. The Establishment and Dynamic Properties of a New 4D Hyperchaotic System with Its Application and Statistical Tests in Gray Images. Entropy. 2020; 22(3):310. https://doi.org/10.3390/e22030310
Chicago/Turabian StyleDing, Lina, and Qun Ding. 2020. "The Establishment and Dynamic Properties of a New 4D Hyperchaotic System with Its Application and Statistical Tests in Gray Images" Entropy 22, no. 3: 310. https://doi.org/10.3390/e22030310
APA StyleDing, L., & Ding, Q. (2020). The Establishment and Dynamic Properties of a New 4D Hyperchaotic System with Its Application and Statistical Tests in Gray Images. Entropy, 22(3), 310. https://doi.org/10.3390/e22030310





