1. Introduction
We developed the BiEntropy function [
1] as a means of comparing the relative order and disorder of the digits of binary strings of arbitrary length.
We originally tested the algorithm in the fields of Prime Number Theory, Human Vision, Cryptography, Random Number Generation, and Quantitative Finance. As a by-product of our work with prime numbers, we derived two very short corollaries which reaffirmed the irrationality of the prime constant [
2].
We subsequently used BiEntropy to identify a significant difference between the alternating and non-alternating knots of 9 and 10 crossings [
3] in the simple cubic lattice. Our work has been cited in the fields of cryptography, internet information processing, mobile computing, and random number generation [
4,
5,
6,
7,
8]. Most recently, BiEntropy has been re-implemented, re-tested, and made publicly available on GitHub [
9]. It has been prominently cited in a related US Government patent [
10].
Despite this background of activity on the use and application of BiEntropy in diverse areas, including in particular prime number theory, we have failed until now to conduct the simplest of tests to ascertain if there was any relationship between BiEntropy and primality. The historical importance and deep roots of the problem of primality in mathematics finally caused us to commence our investigation. There is an extensive literature on prime number theory. Resources such as [
11,
12,
13,
14,
15] and the references therein provide a useful background.
In this paper, we empirically investigate the relationship between BiEntropy and primality in the 8 and 32 bit binary strings. We then develop the TriEntropy function and investigate its relationship with primality within the 9 trit trinary strings. We briefly investigate the relationship between BiEntropy and TriEntropy. We conclude with a discussion of the theoretical basis behind this work and demonstrate how it generalises to all natural numbers.
All of the investigative, experimental, and computational work in this paper was performed within the Microsoft Excel spreadsheet environment [
16]. This gave us great flexibility in the creative process, high development productivity, and notable computational and graphical functionality. These attributes have already been observed [
17,
18] and may facilitate the accessibility and furtherance of this work, especially within the educational domain [
19,
20].
The layout of this paper reflects the order in which the experimental and theoretical work took place, except that work on the Fermat and Mersenne primes was moved to
Appendix B. We provide online a complete set of spreadsheets used to perform the computations and graphics within this paper. Details regarding access to these spreadsheets is given in the
Supplementary Materials section.
2. BiEntropy
The BiEntropy algorithm uses a weighted average of the Shannon entropies [
21] of a string and all but the last binary derivative [
22] of the string.
2.1. Shannon Entropy
Shannon’s Entropy of a binary string
s =
s1, …,
sn where P(
sI = 1) =
p (and 0 log
2 0 is defined to be 0) is:
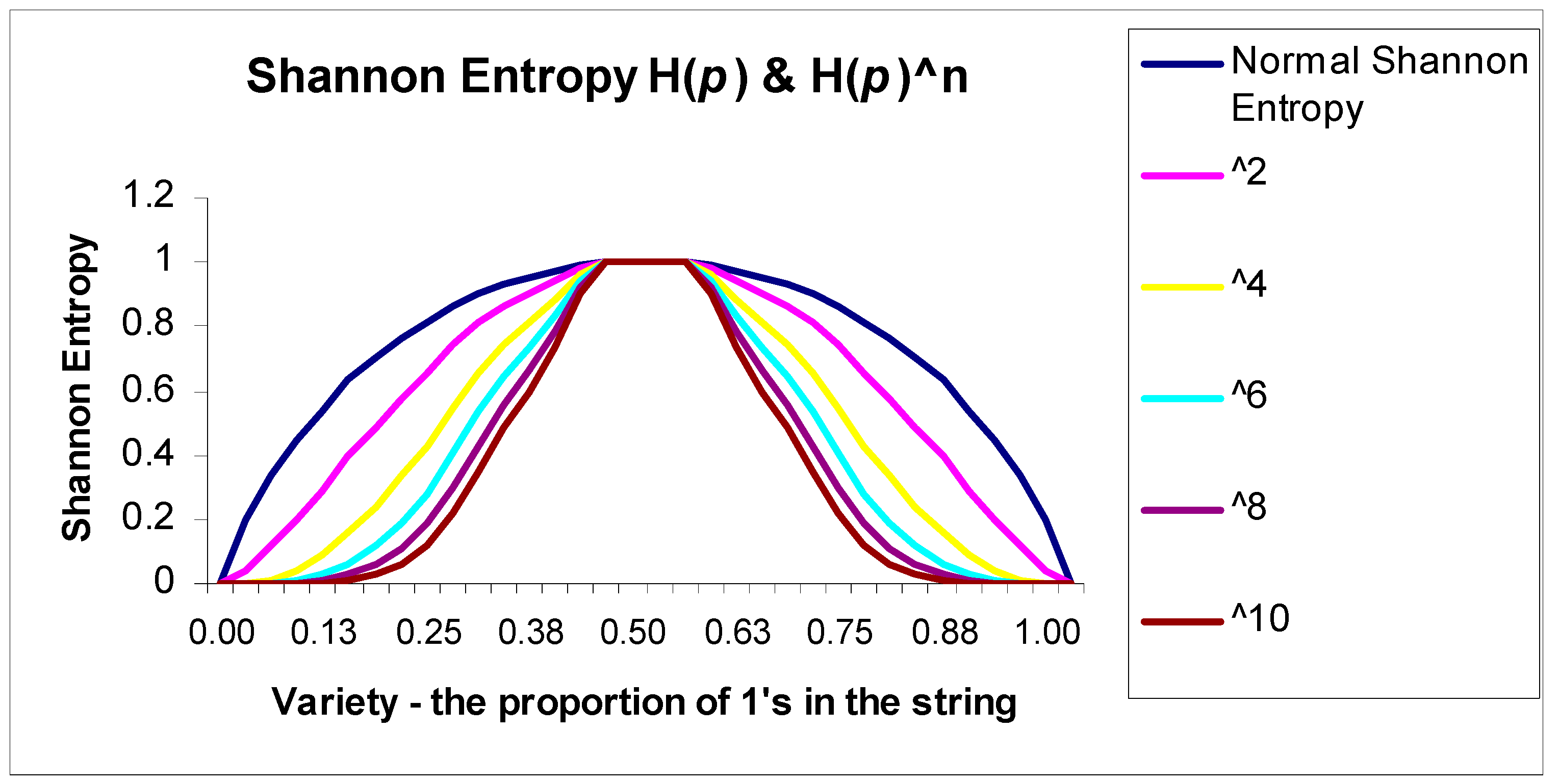
For perfectly ordered strings which are all 1’s or all 0’s, i.e., p = 0 or p = 1, H(p) returns 0. Where p = 0.5, H(p) returns 1, reflecting maximum variety. However, for a string such as 01010101, where also p = 0.5, H(p) also returns 1, ignoring completely the periodic nature of the string.
We can discover the periodicity of a binary string by using the binary derivatives of the string.
2.2. Binary Derivatives and Periodicity
The first binary derivative of s, d1(s), is the binary string of length n − 1 formed by XORing adjacent pairs of digits. We refer to the kth derivative of s, dk(s) as the binary derivative of dk−1(s). There are n − 1 binary derivatives of s. p(k) is the proportion of 1’s in dk.
Almost fifty years ago, Nathanson [
22], following the work of Goka [
23], defined the notions of period and eventual period within arbitrary binary strings and outlined the related properties of binary strings and their derivatives both individually and collectively. Amongst a number of useful results, we find that a binary string is periodic with period 2
m for some
m ≥ 0 if and only if
dk= 0 for some
k ≥ 1.
2.3. BiEntropy Definition
BiEntropy, or BiEn for short, is a weighted average of the Shannon entropies of the string and the first
n − 2 binary derivatives of the string. There are numerous ways of weighting the Shannon entropies. In this series of experiments, we weight the Shannon entropies using powers of two:
The final derivative dn−1 is not used, as there is no variation in the contribution to the total entropy in either of its two binary states. The highest weight is assigned to the highest derivative dn−2.
2.4. BiEntropy Properties
BiEntropy provides a number between 0 and 1 inclusive which indicates the relative order and disorder of the digits of a binary string of length n > 1. The shortest perfectly ordered strings are 00 and 11 which have a BiEntropy of 0. The only perfectly disordered strings are 01 and 10, which have a BiEntropy of 1. An ordered (i.e., periodic) string such as 01010101, for example, has a low BiEntropy of 0.01. A disordered string such as 10000110 has a high BiEntropy of, e.g., 0.95.
3. BiEntropy and Primality of the Natural Numbers < 256
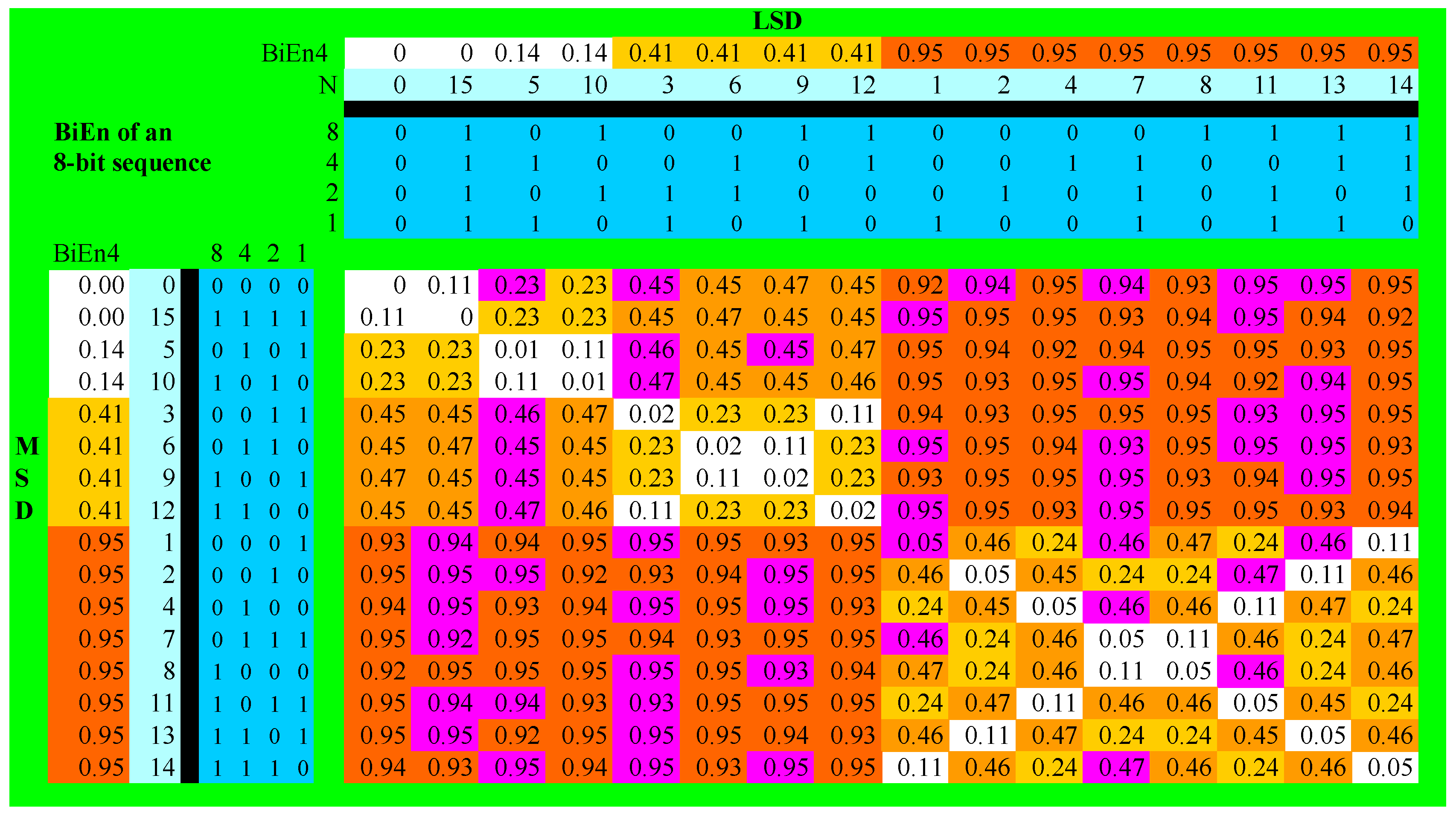
We show in
Figure 1 below the BiEntropy of the natural numbers < 256. The rows correspond to the most significant digits, and the columns to the least significant digits of their binary representations. The rows and columns are ordered by the 4 bit BiEntropy of the most and least significant digits, respectively. BiEntropy is colour coded with white < 0.15, yellow < 0.25, orange <0.5, and red < 1.0. Note the symmetry of the diagram about the diagonal. The primes are coloured purple. For example, 5 = 00000101 has an 8-bit BiEntropy of 0.23 and would be coloured yellow given the symmetry but is coded purple because it is (a Fermat) prime. The Fermat Prime 17 = 00010001 has a low BiEntropy of 0.05 due to the periodic nature of its digits. It would be coloured white but is coloured purple because of its primality. Furthermore, 127 = 01111111 has a BiEntropy of 0.92 and would be coloured red, however it is not only prime, but is a Mersenne Prime and is coloured purple. Note that 0 and 1 are simply “not prime”.
It is easy to see that most of the primes lie in the red quadrants, with only one prime (a Fermat prime) on the white diagonal. Note that the primality of the natural numbers < 256 has a variance with the natural symmetry of BiEntropy, as depicted in
Figure 1.
The differences between the four prime proportions of
Table 1 below are significant at
p < 0.01. We have thus discovered a segmentation of the primes based upon BiEntropy, or more generally, the binary derivative. Looking for 8 bit primes in the red segment is approximately nine times more productive than looking in the white or yellow segments.
We show in
Table 2 below the clear distinction between the BiEntropies of the primes, the non-primes, and the composite odd numbers at
p < 0.0001 for the natural numbers < 256. The BiEntropy of the four Mersenne primes < 256 and the 33 twin primes < 256 is similar to the BiEntropy of all the Primes < 256. Thus, the number of the primes and the composite odds < 256 is 129, which includes the even prime.
If we sort the natural numbers < 256 by their BiEntropies and group them into eight segments as in
Table 3, differences in prime density between the lowest and highest BiEntropy segment becomes markedly higher.
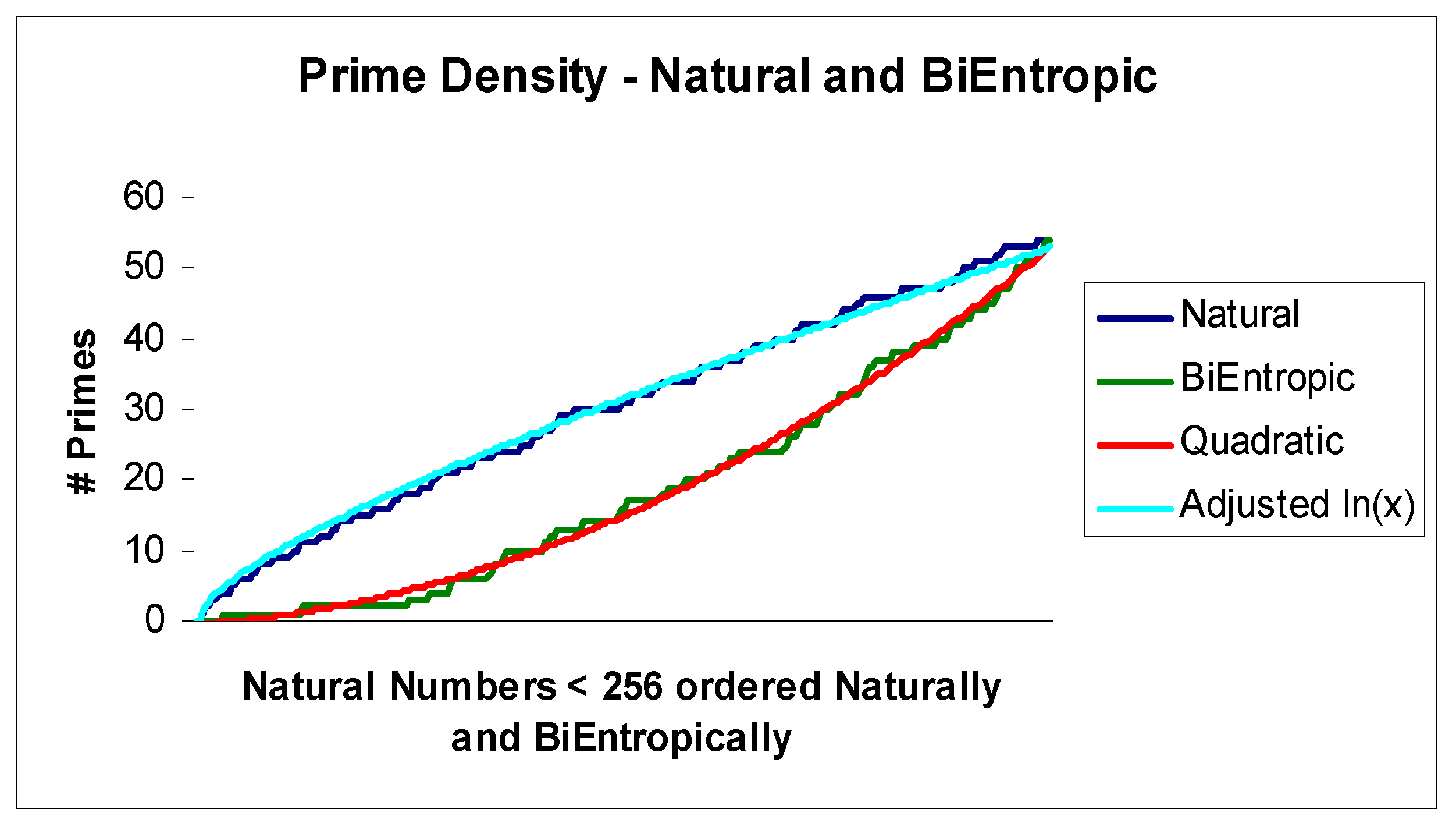
Prime density π(x), the number of primes less than or equal to x, is approximately x/ln (x) due to the Prime Number Theorems of Jacques Hadamard and Charles de la Vallée Poussin in 1896. BiEntropy appears to modify the prime density to O(x2) for very small integers. Using BiEntropy or other prime density functions we can therefore usefully speak of q(x, y, i) which is the number of primes in the ith y sized ordered interval < x. Thus q(256, 32, 8) is 14, as above. Naturally, π(256) = q(256, 256, 1) = 54.
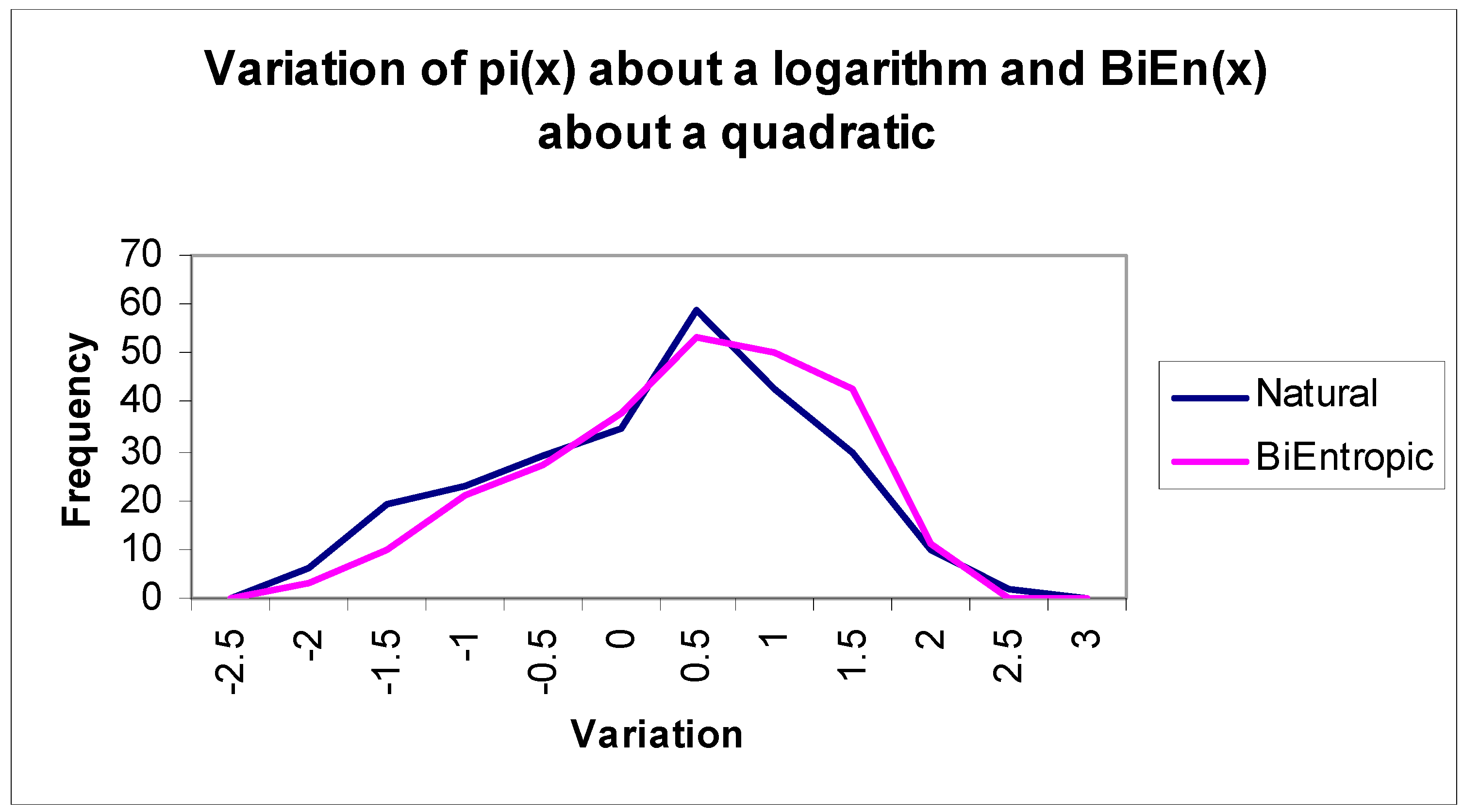
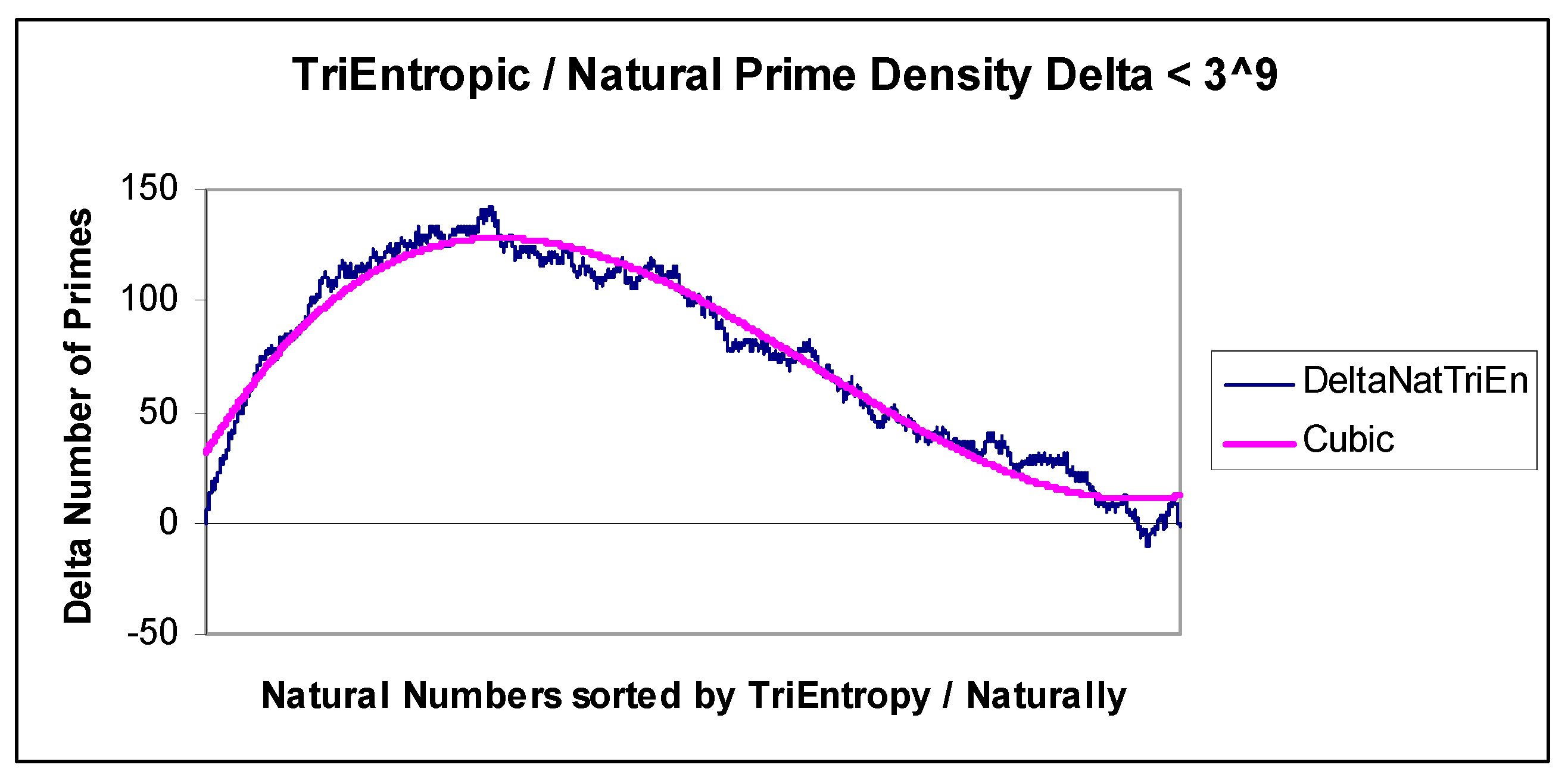
Finally, we depict the continuous relationship between BiEntropy and primality graphically in
Figure 2, which reveals an almost deterministic relationship. We fit the related natural logarithm and quadratic curves and show the associated errors in
Figure 3. We have adjusted the Natural Logarithm curve so that Log(256) matches π(256), which Li(
x) does in the limit. Note that BiEntropy is a weighted average of the Shannon entropies of a binary string and the first
n − 2 binary derivatives of the string. No (explicit) trial division has taken place in order to calculate BiEntropy. The number of primes < 256 = 54, and total BiEntropy for the primes < 256 = 42.64.
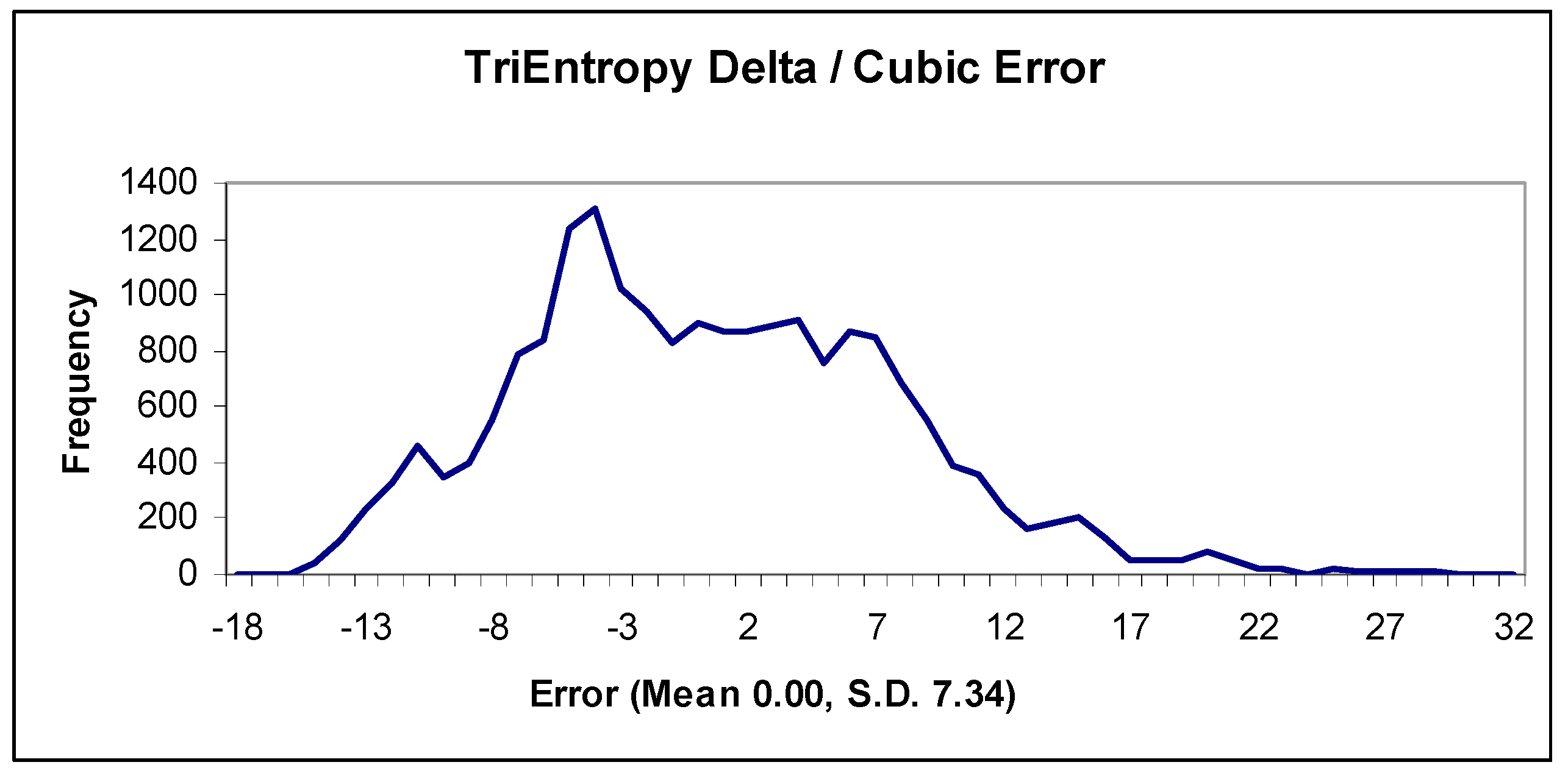
The means of
Figure 3 are coincident due to the small multiplicative adjustment we made. The standard deviations of the errors are almost identical, at 0.93 for the natural logarithm and 0.98 for the quadratic. Thus, the actual error in the BiEntropic prime density for integers
x < 256 is < √
x log(
x) and is evidently Gaussian. As we will see, the error converges to 0 as
x→ ∞.
6. Interaction between BiEntropy and TriEntropy
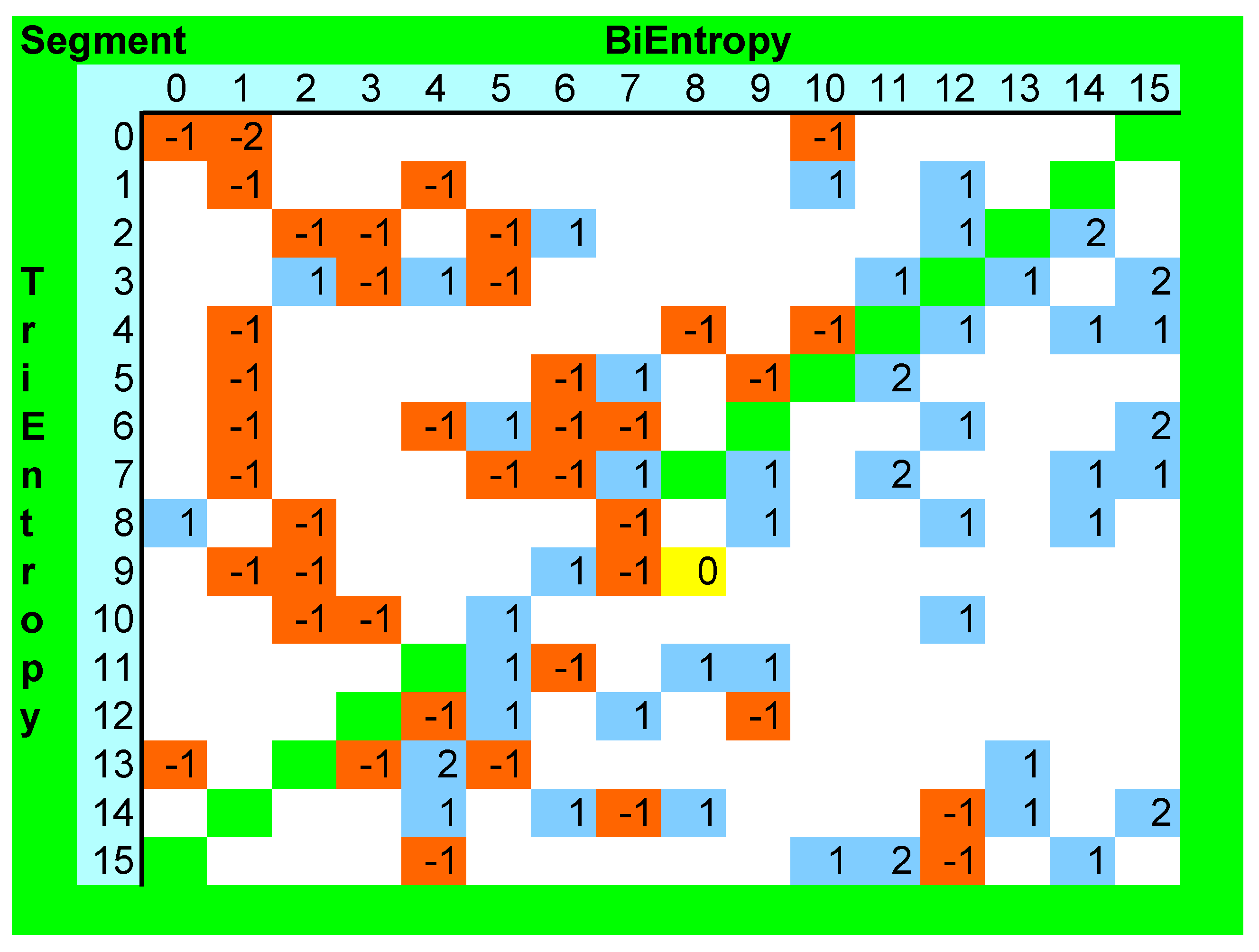
We investigated the interaction between BiEntropy and TriEntropy in the natural numbers < 256. We did this by allocating two segment numbers between 0 and 15 inclusive to each natural number depending upon the BiEntropy and TriEntropy. The 16 natural numbers with the lowest BiEntropy were allocated to BiEntropy segment 0 and the 16 natural numbers with the highest BiEntropy were allocated to BiEntropy Segment 15, etc., and similarly for TriEntropy. We show in
Figure 10 below, a diagram of the frequency of occurrence of the primes in blue and numbers divisible by six in red arranged by BiEntropic segment number on the
x axis and by TriEntropic segment number on the
y axis. The primes are coded as positive numbers and the numbers divisible by six are coded as negative numbers. There was one collision in segment 8–9 corresponding to the numbers 42 and 103 which is coded yellow.
Although the data volume is small, we expect from our earlier experiments that increasing BiEntropy and increasing TriEntropy will disclose more primes and fewer composites. This is what appears to be the case. Ignoring the bottom left to top right diagonal, primes are relatively absent from the top left triangle (11/120 versus 40/120,
p< 0.0001) and numbers divisible by six are relatively absent from the bottom right triangle (11/120 versus 30/120,
p< 0.002), which corresponds to prior expectation. There was only one segment collision, whereas eight might have been expected (54 * 42/256) if the distribution of primes and numbers divisible by six was uniform across all the BiEntropic and TriEntropic segments. Note that the 202 non-primes are uniformly distributed across
Figure 10, which information is not shown for brevity, but is available in the
Supplementary Materials.
8. Discussion
Thus, the principal reason why BiEntropy and TriEntropy have any relationship with primality is the simple fact that, except for the Fermat numbers (and e.g., 23 = 11
22), periodic and
n-periodic numbers cannot be prime in any base. Hence, the main diagonal of
Figure 1 (for all
x, and in all bases) is almost devoid of primes and there are no primes on the cross diagonals. Ignoring the Fermat primes, 32/256 = 12.5% of natural numbers < 256 cannot be prime due to the periodicity or
n-periodicity within seven of their last eight binary derivatives.
If a binary string is periodic, one, and then all the further derivatives, fall to 0 [
22]. BiEntropy picks this up, as the Shannon entropy is 0. Symmetrically, if a derivative is all 1’s, it will also have a 0 Shannon entropy and will (unless it is the last used derivative) become all 0’s in the next derivative. The earlier that periodicity is observed (i.e., for shorter periods), the lower the weighted total becomes, as all the higher weights are 0. Non-periodic strings are otherwise ranked accordingly, with those strings with the most derivatives at or close to
p = 0.5, gaining the highest BiEntropy. BiEntropy is the Hamming distance for primality. Except in certain circumstances (e.g.,
s = 00000001), the bits of a binary derivative are undecidable. Determination of the bits of a binary derivative is a simple variation of the halting problem—if the last binary derivative is 1, the routine halts else it does not halt.
Whilst a string is periodic if and only if one of its derivatives is all 0’s [
22], the reverse does not apply, hence primality is stochastic. Davies et al. [
26] proved that if the bits of a string occur with a probability of 0.5, the bits of the derivatives also occur with a probability of 0.5, and the binary derivatives are independent. Hence, the error between a quadratic and the BiEntropic prime density, which is a quadratic function of the probability of occurrence of each bit of the derivative, is Gaussian due to the central limit theorem. Note that the number of binary derivatives for any
x is finite.
By a simple induction, every binary number is the binary derivative of a number one bit longer, and its bits occur with a probability of 0.5. Its bits are proven [
26] independent of its earlier derivatives. Hence, the primes are Gaussian, as the probability of occurrence of each of their bits is undifferentiated from every other binary number and every other binary derivative.
BiEntropic prime density is quadratic because BiEntropy is quadratic. For example, in the 8 bit version of BiEntropy, the probability of an arbitrary string not being prime because the string is all 1’s, or the probability that a binary derivative is 0, is:
i.e., there is only one 8 bit string (
s =
d0) that is all 0’s, whereas the last used derivative
d6 of length 2 is all 0’s on 64 occasions and
d5 of length 3 is all 0’s on 32 occasions. BiEntropy measures exactly the probability that a binary string cannot be prime or may be prime with a precision given by the number of bits in
d0. TriEntropy is cubic for similar reasons.
The relationship between BiEntropy and primality generalises for all x for the simple reason that all x ≥ 256 (for example) eventually end up as an 8 bit (for example) string by virtue of successive binary differentiation. Determination of many of the mathematical and statistical properties of all x can be obtained inductively by observation of properties in the last m binary derivatives, which is easy to do when m is small.
Thus, there exists a set of constants
ak,
bk, and
ck, such that
And another (similar) set of constants
uk,
vk, and
wk, such that
For each ak, bk, ck and uk, vk, and wk, there exists a set of (m2 − m)/2 binary derivatives from which the distribution of primes is derived with known probabilities and calculable or estimable variance. The variance in natural prime density is constrained by the variance in the BiEntropic prime densities for all xk < x because the same data—the natural numbers—is Gaussian distributed about two differing central measures—a quadratic and a logarithmic integrand.
Therefore, in the limit, the BiEntropic/Quadratic and Logarithmic Integrand/Natural error distributions are coincident with near identical error distributions, which we illustrated empirically in
Figure 3. Furthermore, as
x→∞, and since the number of bits in the binary derivatives = (
m2 −
m)/2, where
m = log
2(
x), the variance in the error between the BiEntropic and Quadratic prime densities is
O(log(
x)/
x) due to the central limit theorem. Hence, the error between the Logarithmic Integrand and the natural prime densities rapidly tends to 0.
which is clearly distinctive from the von Koch [
27] bound for proof of the Riemann Hypothesis.
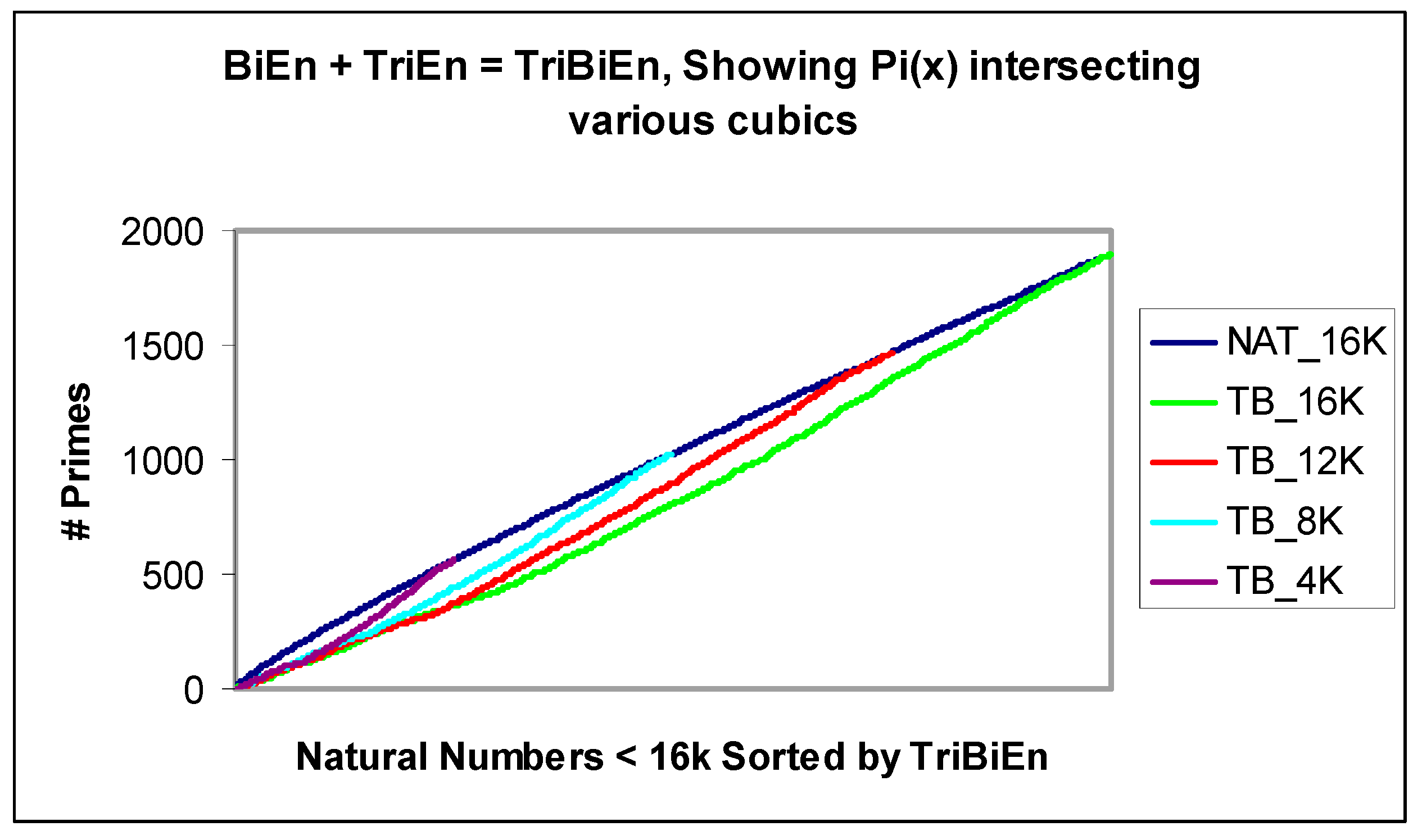
A similar set of cubic constants apply for TriEntropy and the arithmetic addition of BiEntropy and TriEntropy, which we shall denote TriBiEntropy. We illustrate the cubics of TriBiEntropy intersecting
π(
x) for various
x in
Figure 11.
9. Conclusions
We have shown a clear empirical link between BiEntropy and primality for the natural numbers < 28. We have repeated this analysis statistically for the natural numbers < 232 and found similar results, including the prime density remaining O(x2). We developed a related TriEntropy function and showed that TriEntropy changes prime density to O(x3) for the natural numbers < 39. In addition, TriEntropy has addressed a natural weakness in the detection of periods of length 3, or multiples thereof, in the BiEntropy function.
Since BiEntropy and TriEntropy are simply measures of the order and disorder (i.e., the periodicity) of a string, the implication is that prime numbers expressed in binary or trinary have more disordered representations. The reverse implication is that composites have more ordered representations. This result has been suggested in earlier work in algorithmic information theory.
We have shown how to increase the sensitivity of BiEntropy by increasing the exponent of the Shannon entropy within the BiEntropy calculation. We have demonstrated a significant link between BiEntropy and TriEntropy in the natural numbers < 28 and the practicality of combining BiEntropy and TriEntropy via arithmetic addition. We have given a brief outline of the theoretical underpinnings behind this initial experimental work and shown how it generalises for all the natural numbers.
We have shown how the variance of the error between π(x) and Li (x) tends to 0 due to the Gaussian constraints on the variance of π(x) imposed by the binary derivative. These are much tighter constraints than the bound proven by Von Koch in 1901 as being equivalent to proof of the Riemann Hypothesis.
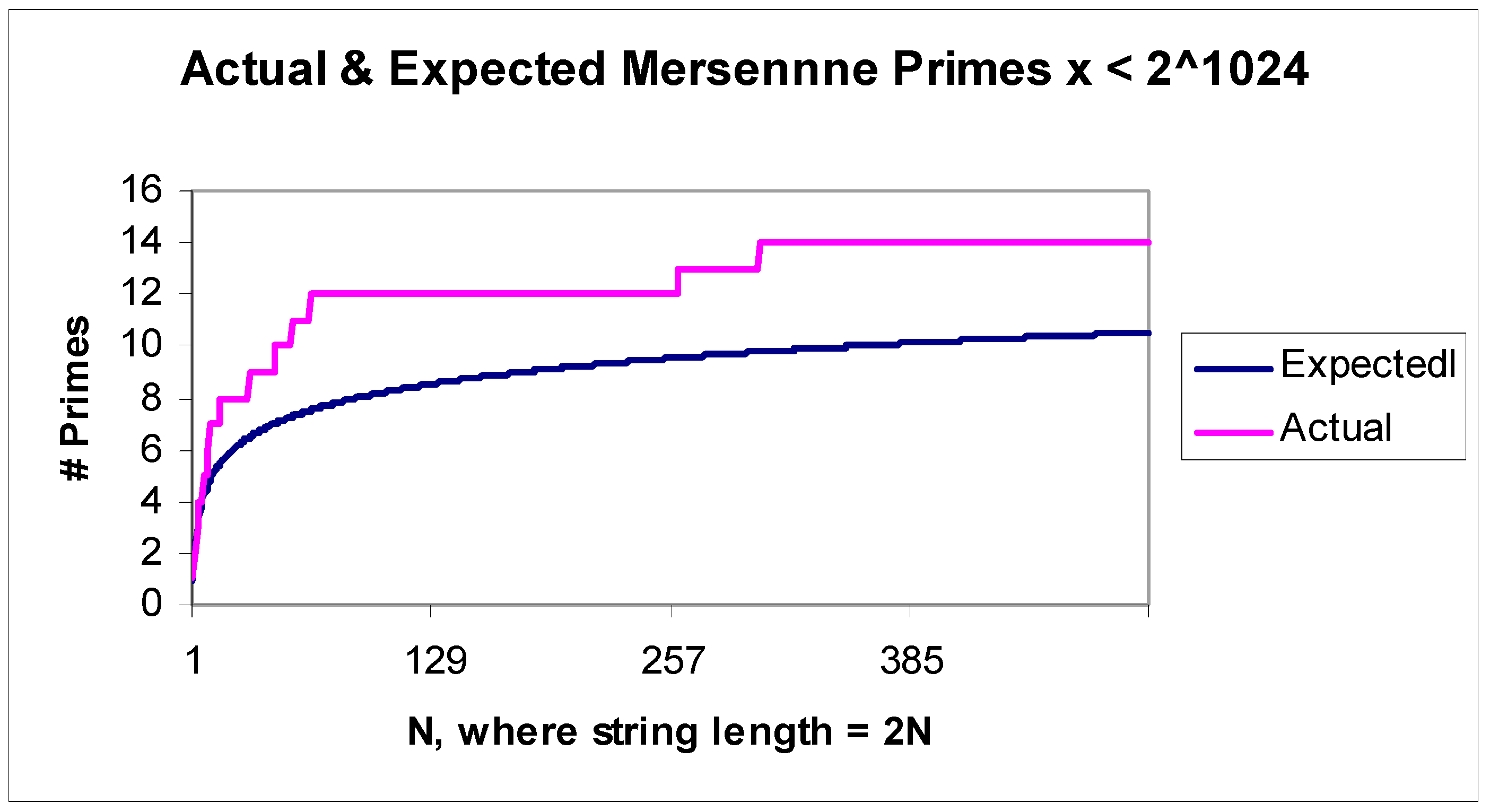
We have provided, in
Appendix B, easily derived absolutely convergent asymptotes for the numbers of Fermat and Mersenne primes.
Finally, since the distribution of primes is Gaussian due to the binary derivative, this implies that the twin primes conjecture is true.