Blind Mesh Assessment Based on Graph Spectral Entropy and Spatial Features
Abstract
1. Introduction
- (1)
- Most of the existing 3D MQA methods are not blind. We propose a new BMQA method based on Graph Spectral Entropy and spatial features, referred to as BMQA-GSES. New features in the graph spectral domain and spatial domain are defined and extracted for BMQA. The graph spectral features of 3D mesh can reveal the underlying shape information, while the spatial features of the 3D mesh can simulate the external information of the 3D mesh that can be directly perceived by human eyes.
- (2)
- Inspired by GSP, the Gaussian curvature signal is transformed from the spatial domain to the graph spectral domain by GFT in the proposed method. In addition, the signal smoothness and information entropy of amplitude features under different frequency components are then extracted in the graph spectral domain as underlying shape features of 3D mesh.
- (3)
- Considering that the concavity, convexity and the structural information of the distorted 3D mesh will change, four spatial features are combined on the base of extracting the graph spectral features.
2. Motivation
3. The Proposed BMQA-GSES Method
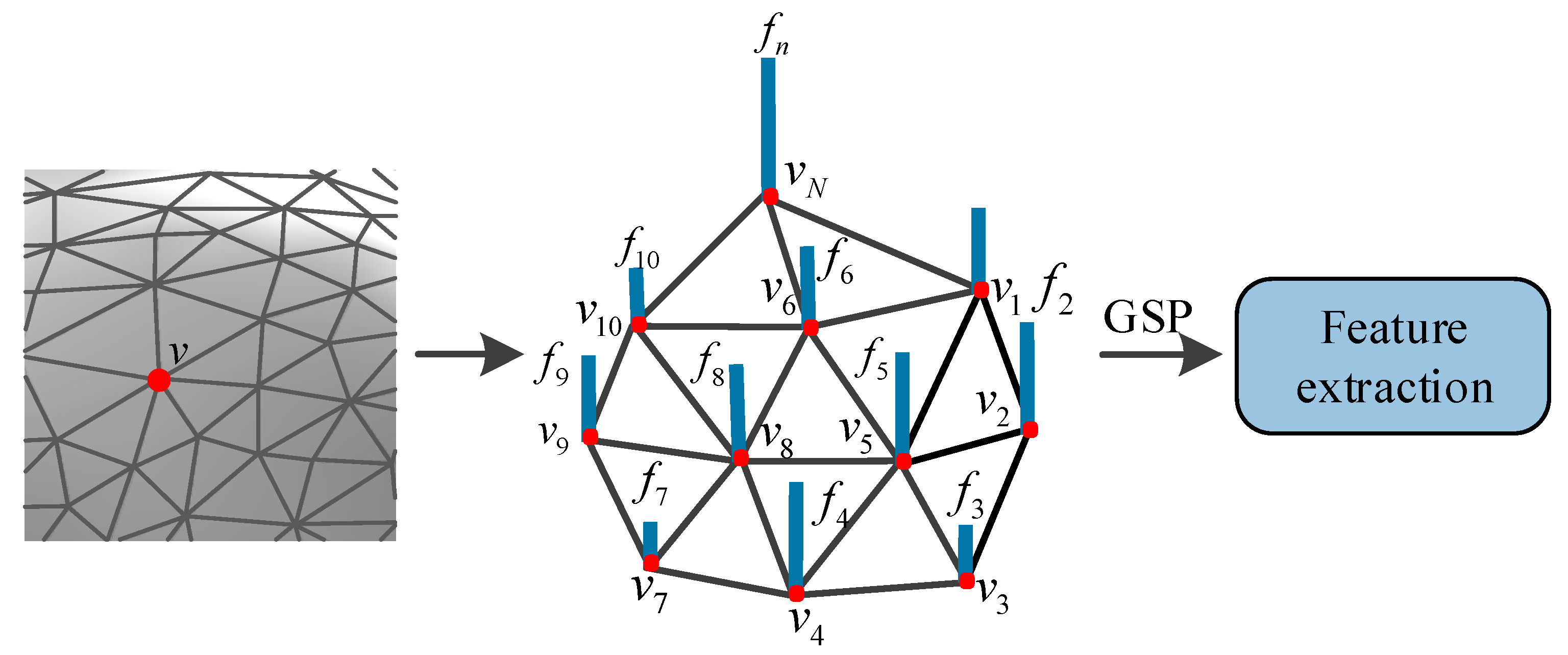
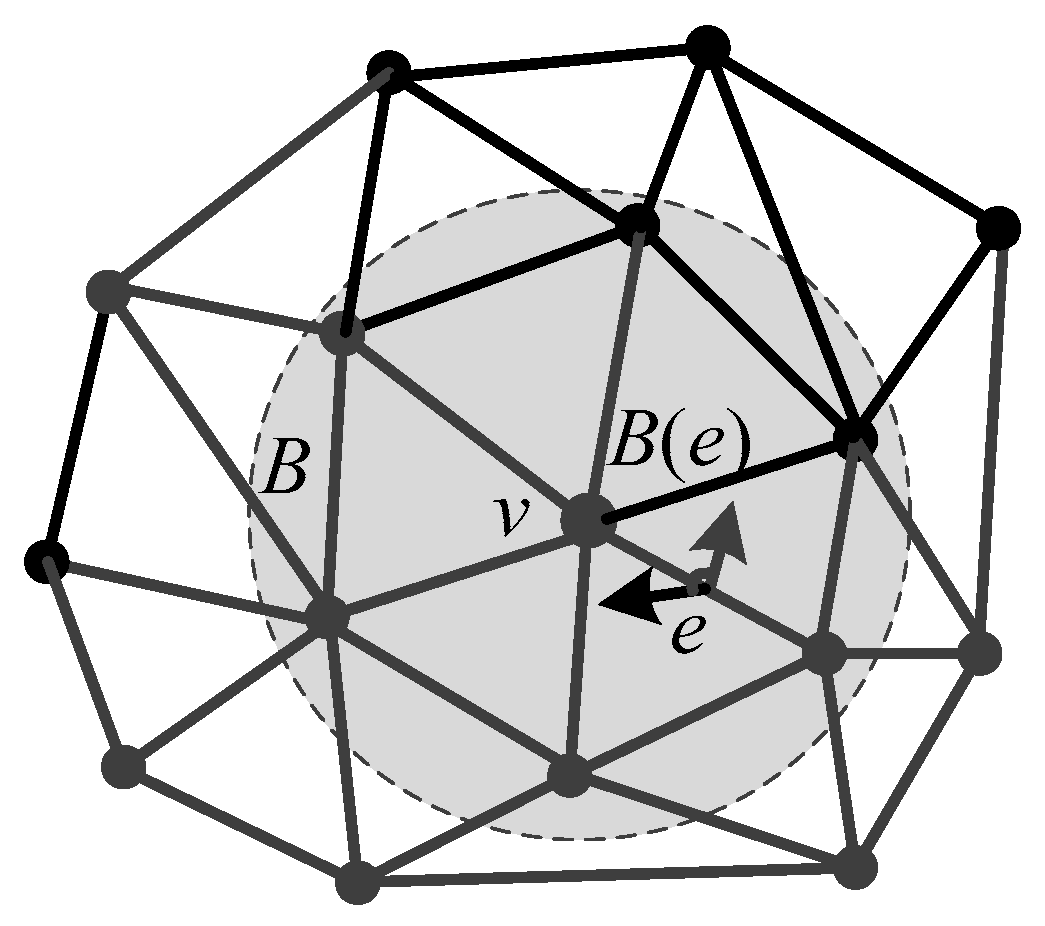
3.1. Graph Spectral Features Analysis
- (1)
- The Gaussian curvature on each vertex of the 3D mesh is firstly calculated, denoted as signal ;
- (2)
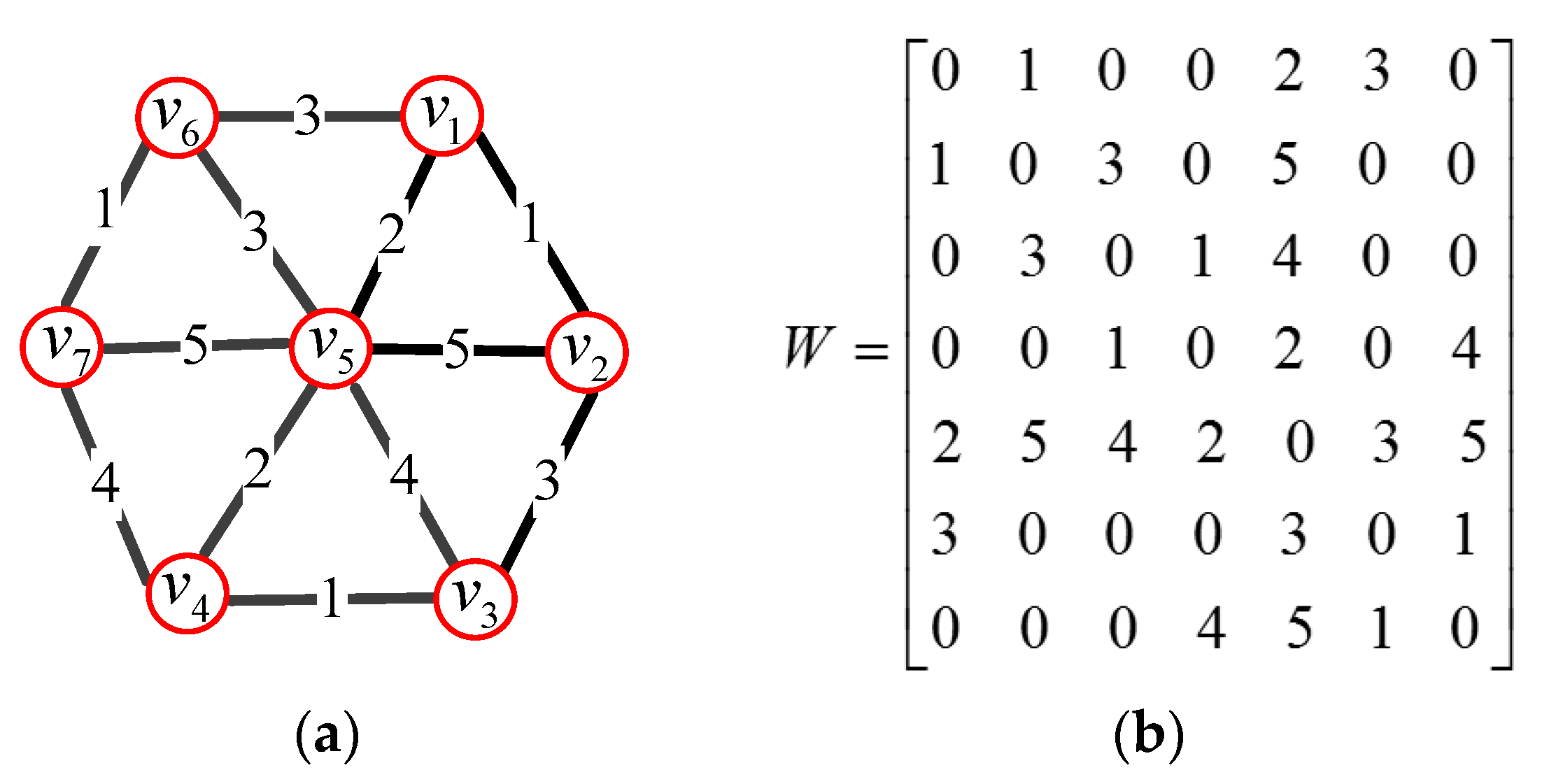
- The weighted graph G = {v,ε,W} is then used to represent 3D mesh, where v represents vertices of 3D mesh, ε represents edges of 3D mesh, and W is weighted adjacency matrix of 3D mesh;
- (3)
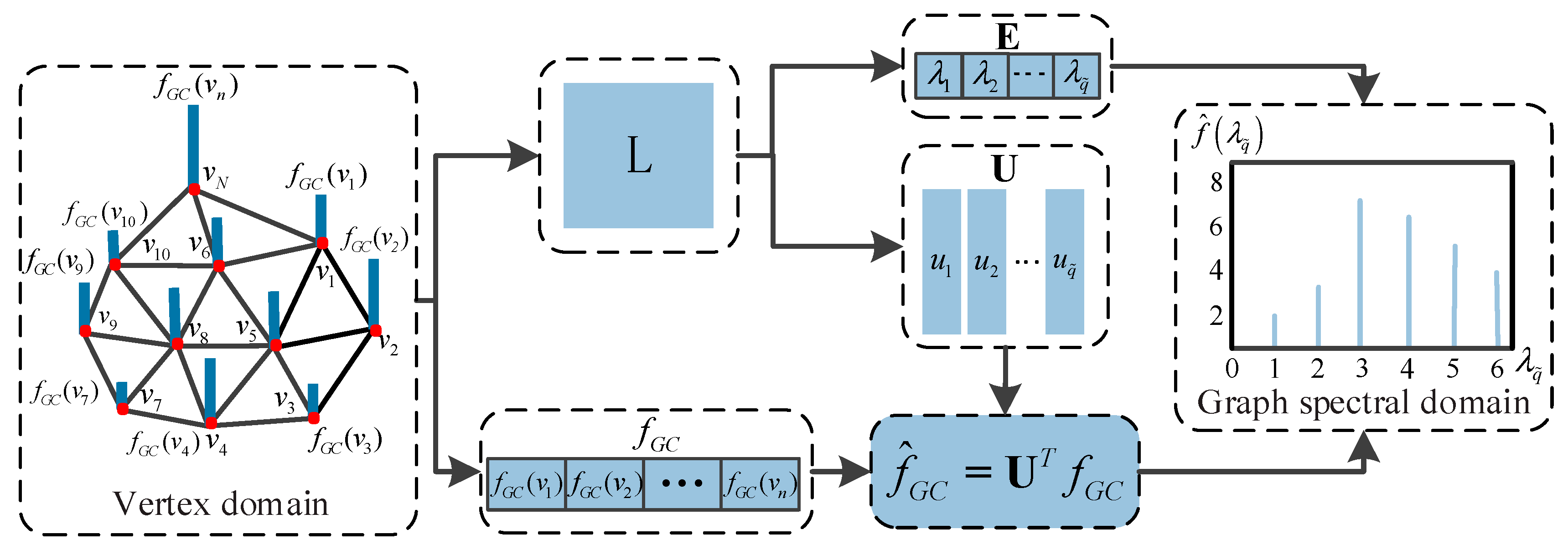
- The graph Laplacian matrix L can be calculated from (6) and (7). The graph Laplacian matrix is sparse and has very large dimensions because the 3D mesh is composed of a lot of vertices. Therefore, the Lanczos method is used to calculate the eigenvectors U and eigenvalues E of the sparse matrix L;
- (4)
- The Gaussian curvature signal is transformed by GFT based on the obtained eigenvector U, i.e., (9). Since there is a one-to-one correspondence between the eigenvalues and the eigenvectors, the corresponding amplitude of each eigenvalue can be obtained. The eigenvalues of the GFT replace the concept of frequency in the classical Fourier transform, so the eigenvalues and the corresponding amplitudes constitute the graph spectrum of 3D mesh.
- (5)
- The information entropy of amplitudes under different frequency components is extracted to describe the characteristics of 3D mesh in the graph spectral domain.
3.2. Spatial Features Analysis
3.2.1. Concave and Convex Feature Analyses
3.2.2. Structural Feature Analyses
3.3. Pooling Strategy
4. Experimental Results and Discussion
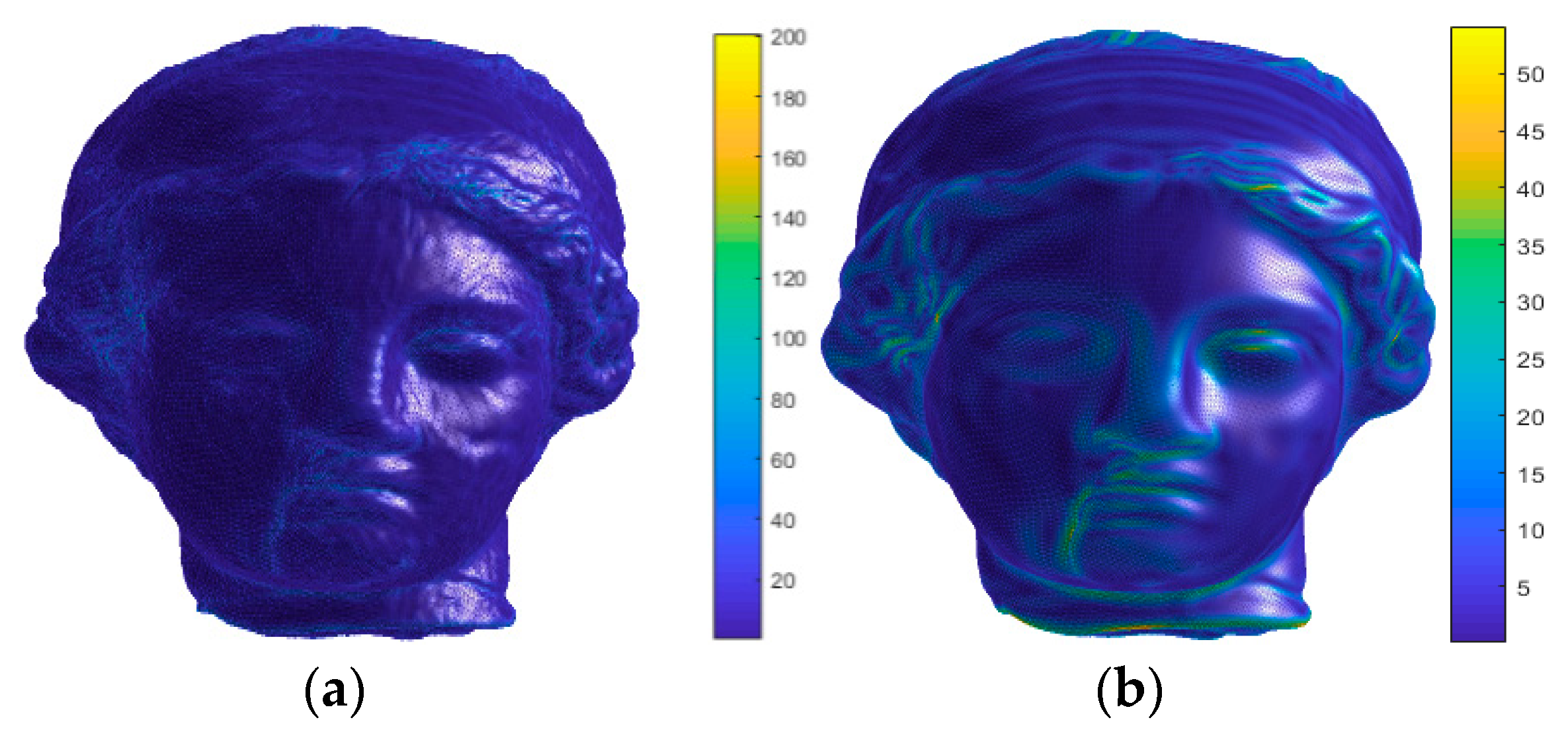
4.1. Graph Spectral and Spatial Features Analysis
4.2. Overall Performance Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lalos, A.S.; Vlachos, E.; Arvanitis, G.; Moustakas, K.; Berberidis, K. Signal Processing on Static and Dynamic 3D Meshes: Sparse Representations and Applications. IEEE Access 2019, 7, 15779–15803. [Google Scholar] [CrossRef]
- Abdallah, E.E.; Ben Hamza, A.; Bhattacharya, P. Watermarking 3D models using spectral mesh compression. Signal Image Video Process. 2009, 3, 375–389. [Google Scholar] [CrossRef]
- Abdallah, E.E.; Ben Hamza, A.; Bhattacharya, P. Spectral graph-Theoretic approach to 3D mesh watermarking. Proc. Graph. Interface 2007, 327–334. [Google Scholar] [CrossRef]
- Abouelaziz, I.; El Hassouni, M.; Cherifi, H. Blind 3D mesh visual quality assessment using support vector regression. Multimed. Tools Appl. 2018, 77, 24365–24386. [Google Scholar] [CrossRef]
- Guo, J.; Vidal, V.; Cheng, I.; Basu, A.; Baskurt, A. Subjective and Objective Visual Quality Assessment of Textured 3D Meshes. ACM Trans. Appl. Percept. 2017, 14. [Google Scholar] [CrossRef]
- Aspert, N.; Santa-Cruz, D.; Ebrahimi, T. Mesh: Measuring errors between surfaces using the Hausdorff distance. IEEE Int. Conf. Multimed. Expo. 2002, 1, 705–708. [Google Scholar]
- Karni, Z.; Gotsman, C. Spectral compression of mesh geometry. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA , 23–28 July 2000; pp. 279–286. [Google Scholar]
- Sorkine, O.; Cohenor, D.; Toledo, S. High-Pass quantization for mesh encoding. In Proceedings of the Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Aachen, Germany, 23–25 June 2003; pp. 42–51. [Google Scholar]
- Corsini, M.; Gelasca, E.D.; Ebrahimi, T.; Barni, M. Watermarked 3-D mesh quality assessment. IEEE Trans. Multimed. 2007, 9, 247–256. [Google Scholar] [CrossRef]
- Gelasca, E.D.; Ebrahimi, T.; Corsini, M.; Barni, M. Objective evaluation of the perceptual quality of 3D watermarking. In Proceedings of the IEEE International Conference on Image Processing, Quebec City, QC, Canada, 27–30 September 2015; pp. 241–244. [Google Scholar]
- Lavoué, G.; Gelasca, E.D.; Dupont, F.; Baskurt, A.; Ebrahimi, T. Perceptually driven 3D distance metrics with application to watermarking. Proc. SPIE-Int. Soc. Opt. Eng. 2006. [Google Scholar] [CrossRef]
- Lavoué, G.; Corsini, M. A comparison of perceptually-Based metrics for objective evaluation of geometry processing. IEEE Trans. Multimed. 2010, 12, 636–649. [Google Scholar] [CrossRef]
- Váša, L.; Jan, R. Dihedral angle mesh error: A fast perception correlated distortion measure for fixed connectivity triangle meshes. Comput. Graph. Forum 2012, 31, 1715–1724. [Google Scholar] [CrossRef]
- Wang, K.; Torkhani, F.; Montanvert, A. A fast roughness-Based approach to the assessment of 3D mesh visual quality. Comput. Graph. 2012, 36, 808–818. [Google Scholar] [CrossRef]
- Abouelaziz, I.; Omari, M.; Hassouni, M.E.; Cherifi, H. Reduced Reference 3D Mesh Quality Assessment Based on Statistical Models. In Proceedings of the 11th International Conference on Signal-Image Technology and Internet-Based Systems (SITIS), Bangkok, Thailand, 23–27 November 2015; pp. 170–177. [Google Scholar]
- Abouelaziz, I.; Hassouni, M.E.; Cherifi, H. No-Reference 3D mesh quality assessment based on dihedral angles model and support vector regression. In Proceedings of the International Conference on Image and Signal Processing, Trois-Rivières, QC, Canada, 30 May –1 June 2016; pp. 369–377. [Google Scholar]
- Abouelaziz, I.; Hassouni, M.E.; Cherifi, H. A convolutional neural network framework for blind mesh visual quality assessment. In Proceedings of the IEEE International Conference on Image Processing, Beijing, China, 17–20 September 2017; pp. 755–759. [Google Scholar]
- Abouelaziz, I.; Chetouani, A.; Hassouni, M.E.; Cherifi, H. Mesh visual quality assessment Metrics: A Comparison Study. In Proceedings of the 13th International Conference on Signal-Image Technology and Internet-Based Systems (SITIS), Jaipur, India, 4–7 Decenber 2017; pp. 283–288. [Google Scholar]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-Dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Teke, O.; Vaidyanathan, P.P. Uncertainty Principles and Sparse Eigenvectors of graphs. IEEE Trans. Signal Process. 2017, 65, 5406–5420. [Google Scholar] [CrossRef]
- Masoumi, M.; Li, C.; Ben Hamza, A. A spectral graph wavelet approach for nonrigid 3D shape retrieval. Pattern Recognit. Lett. 2016, 83, 339–348. [Google Scholar] [CrossRef]
- Masoumi, M.; Ben Hamza, A. A Spectral shape classification: A deep learning approach. J. Vis. Commun. Image Represent. 2017, 43, 198–211. [Google Scholar] [CrossRef]
- Tseng, C.C.; Lee, S.L.; Su, R.H. A missing temperature data estimation method using graph Fourier transform. In Proceedings of the IEEE International Conference on Consumer Electronics-TW, Taipei, Taiwan, 12–14 June 2017; pp. 87–88. [Google Scholar]
- Sardellitti, S.; Barbarossa, S.; Lorenzo, P.D. On the Graph Fourier Transform for Directed Graphs. IEEE J. Sel. Top. Signal Process. 2017, 11, 796–811. [Google Scholar] [CrossRef]
- Sandryhaila, A.; Moura, J.M.F. Discrete Signal Processing on Graphs. IEEE Trans. Signal Process. 2013, 61, 1644–1656. [Google Scholar] [CrossRef]
- Dong, L.; Fang, Y.; Lin, W.; Seah, H.S. Perceptual Quality Assessment for 3D Triangle Mesh Based on Curvature. IEEE Trans. Multimed. 2015, 17, 2174–2184. [Google Scholar] [CrossRef]
- Jiao, X.; Wu, T.; Qin, X. Mesh segmentation by combining mesh saliency with spectral clustering. J. Comput. Appl. Math. 2017, 329, 134–146. [Google Scholar] [CrossRef]
- Martínez-Martínez, C.T.; Méndez-Bermúdez, J.A. Information Entropy of Tight-Binding Random Networks with Losses and Gain: Scaling and Universality. Entropy 2019, 21, 86. [Google Scholar] [CrossRef]
- Liu, J.; Xu, M.; Xu, X.; Haung, Y. Nonreference Image Quality Evaluation Algorithm Based on Wavelet Convolutional Neural Network and Information Entropy. Entropy 2019, 21, 1070. [Google Scholar] [CrossRef]
- Cohen-Steiner, D.; Morvan, J.M. Restricted Delaunay triangulations and normal cycle. In Proceedings of the 19th annual symposium on Computational geometry (SCG ‘03), San Diego, CA, USA, 8–10 June 2003; pp. 312–321. [Google Scholar]
- Peiand, S.; Chen, L. Image Quality Assessment Using Human Visual DOG Model Fused with Random Forest. IEEE Trans. Image Process. 2015, 24, 3282–3292. [Google Scholar]
- ITU-T P.1401. Methods, Metrics and Procedures for Statistical Evaluation, Qualification and Comparison of Objective Quality Prediction Models; International Telecommunication Union: Geneva, Switzerland, 2012. [Google Scholar]


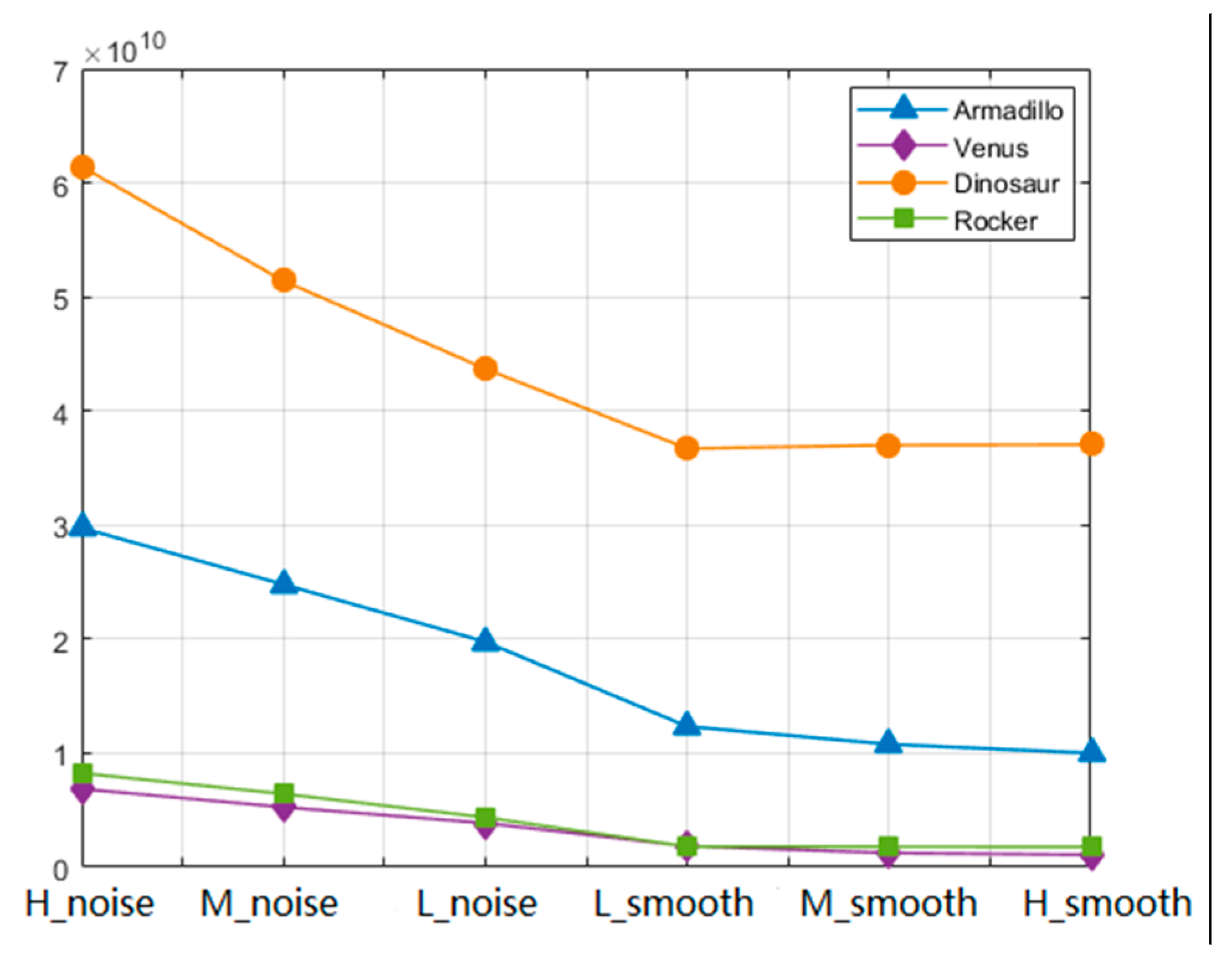





| Noise | Smooth | |||||
|---|---|---|---|---|---|---|
| Level | Low | Medium | High | Low | Medium | High |
| Armadillo | −0.2032 | −0.1828 | −0.1616 | −0.2480 | −0.2678 | −0.2798 |
| Venus | −0.1742 | −0.1505 | −0.1318 | −0.2292 | −0.2505 | −0.2594 |
| Dinosaur | −0.2655 | −0.2456 | −0.2233 | −0.2813 | −0.2815 | −0.2836 |
| Rocker | −0.0691 | −0.0656 | −0.0622 | −0.0837 | −0.0859 | −0.0878 |
| Feature Types | Features | Armadillo | Venus | Dinosaur | Rocker | Whole Database | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| rp | rs | rp | rs | rp | rs | rp | rs | rp | rs | ||
| Graph spectral domain | FS | 98.2 | 80.0 | 89.2 | 73.8 | 94.9 | 80.0 | 97.3 | 94.9 | 79.4 | 52.6 |
| FAM | 97.0 | 80.0 | 90.8 | 80.0 | 71.9 | 40.0 | 98.3 | 80.0 | 94.8 | 62.4 | |
| Spatial domain | FSI | 90.7 | 40.0 | 96.5 | 80.0 | 90.6 | 73.8 | 96.4 | 94.9 | 40.4 | 23.1 |
| FC | 98.1 | 80.0 | 95.2 | 80.1 | 96.7 | 80.0 | 97.5 | 80.0 | 83.9 | 57.3 | |
| FDA | 98.6 | 80.0 | 98.5 | 80.0 | 98.1 | 75.5 | 93.5 | 94.8 | 84.9 | 87.0 | |
| FA | 96.5 | 79.9 | 94.5 | 79.9 | 98.2 | 80.0 | 96.9 | 80.1 | 82.2 | 86.6 | |
| All | 98.7 | 80.0 | 98.8 | 80.1 | 99.2 | 80.4 | 99.5 | 99.9 | 90.5 | 87.9 | |
| Type | Method | Principle |
|---|---|---|
| FR | HD [6] | Hausdorff distance |
| GL2 [8] | vertex coordinate positions and the Geometrical Laplacian operator | |
| MSDM [11] | Local curvature, Contrast, and Structure | |
| MSDM2 [12] | Multiscale mesh structural distortion | |
| DAME [13] | Dihedral angles | |
| RR | 3DWPM1 [9] | Global roughness |
| 3DWPM2 [10] | Global roughness | |
| FMPD [14] | Local roughness analysis and global roughness computation | |
| KLD Gamma [15] | Dihedral angles and statistical Gamma distributionmodel | |
| KLD Weibull [15] | Dihedral angles and statistical Weibull distribution model | |
| NR | NR-SVR [16] | Dihedral angles, visual masking modulation and parameters estimation |
| The proposed | Graph spectral features and spatial features |
| Type | Method | Armadillo | Venus | Dinosaur | Rocker | Whole Database | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| rp | rs | rp | rs | rp | rs | rp | rs | rp | rs | ||
| FR | HD [6] | 30.2 | 69.5 | 0.8 | 1.6 | 22.6 | 30.9 | 5.5 | 18.1 | 11.4 | 13.8 |
| GL2 [8] | 55.5 | 77.8 | 77.6 | 91.0 | 12.5 | 30.6 | 17.1 | 29.0 | 42.4 | 39.3 | |
| MSDM [11] | 70.0 | 84.8 | 72.3 | 87.6 | 56.8 | 73.0 | 75.0 | 89.8 | 75.0 | 73.9 | |
| MSDM2 [12] | 85.3 | 81.6 | 87.5 | 89.3 | 85.7 | 85.9 | 87.2 | 89.6 | 81.4 | 80.4 | |
| DAME [13] | 76.3 | 60.3 | 83.9 | 91.0 | 88.9 | 92.8 | 80.1 | 85.0 | 75.2 | 76.6 | |
| RR | 3DWPM1 [9] | 35.7 | 65.8 | 46.6 | 71.6 | 35.7 | 62.7 | 53.2 | 87.5 | 61.8 | 69.3 |
| 3DWPM2 [10] | 43.1 | 74.1 | 16.4 | 34.8 | 19.9 | 52.4 | 29.9 | 37.8 | 49.6 | 49.0 | |
| FMPD [14] | 83.2 | 75.4 | 83.9 | 87.5 | 88.9 | 89.6 | 84.7 | 88.8 | 83.5 | 81.9 | |
| KLD Gamma [15] | 77.7 | 71.1 | 83.4 | 88.6 | 70.6 | 67.9 | 57.5 | 78.7 | 74.0 | 71.6 | |
| KLD Weibull [15] | 77.2 | 67.5 | 75.4 | 86.1 | 70.6 | 71.3 | 70.4 | 77.0 | 74.1 | 71.7 | |
| NR | NR-SVR [16] | 91.5 | 76.8 | 88.6 | 85.7 | 84.1 | 78.6 | 86.6 | 86.2 | 87.8 | 81.5 |
| The proposed | 98.7 | 80.0 | 98.8 | 80.1 | 99.2 | 80.4 | 99.5 | 99.9 | 90.5 | 87.9 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Yu, M.; Chen, K.; Jiang, G.; Chen, F.; Peng, Z. Blind Mesh Assessment Based on Graph Spectral Entropy and Spatial Features. Entropy 2020, 22, 190. https://doi.org/10.3390/e22020190
Lin Y, Yu M, Chen K, Jiang G, Chen F, Peng Z. Blind Mesh Assessment Based on Graph Spectral Entropy and Spatial Features. Entropy. 2020; 22(2):190. https://doi.org/10.3390/e22020190
Chicago/Turabian StyleLin, Yaoyao, Mei Yu, Ken Chen, Gangyi Jiang, Fen Chen, and Zongju Peng. 2020. "Blind Mesh Assessment Based on Graph Spectral Entropy and Spatial Features" Entropy 22, no. 2: 190. https://doi.org/10.3390/e22020190
APA StyleLin, Y., Yu, M., Chen, K., Jiang, G., Chen, F., & Peng, Z. (2020). Blind Mesh Assessment Based on Graph Spectral Entropy and Spatial Features. Entropy, 22(2), 190. https://doi.org/10.3390/e22020190





