Multipartite Entanglement Generation in a Structured Environment
Abstract
1. Introduction
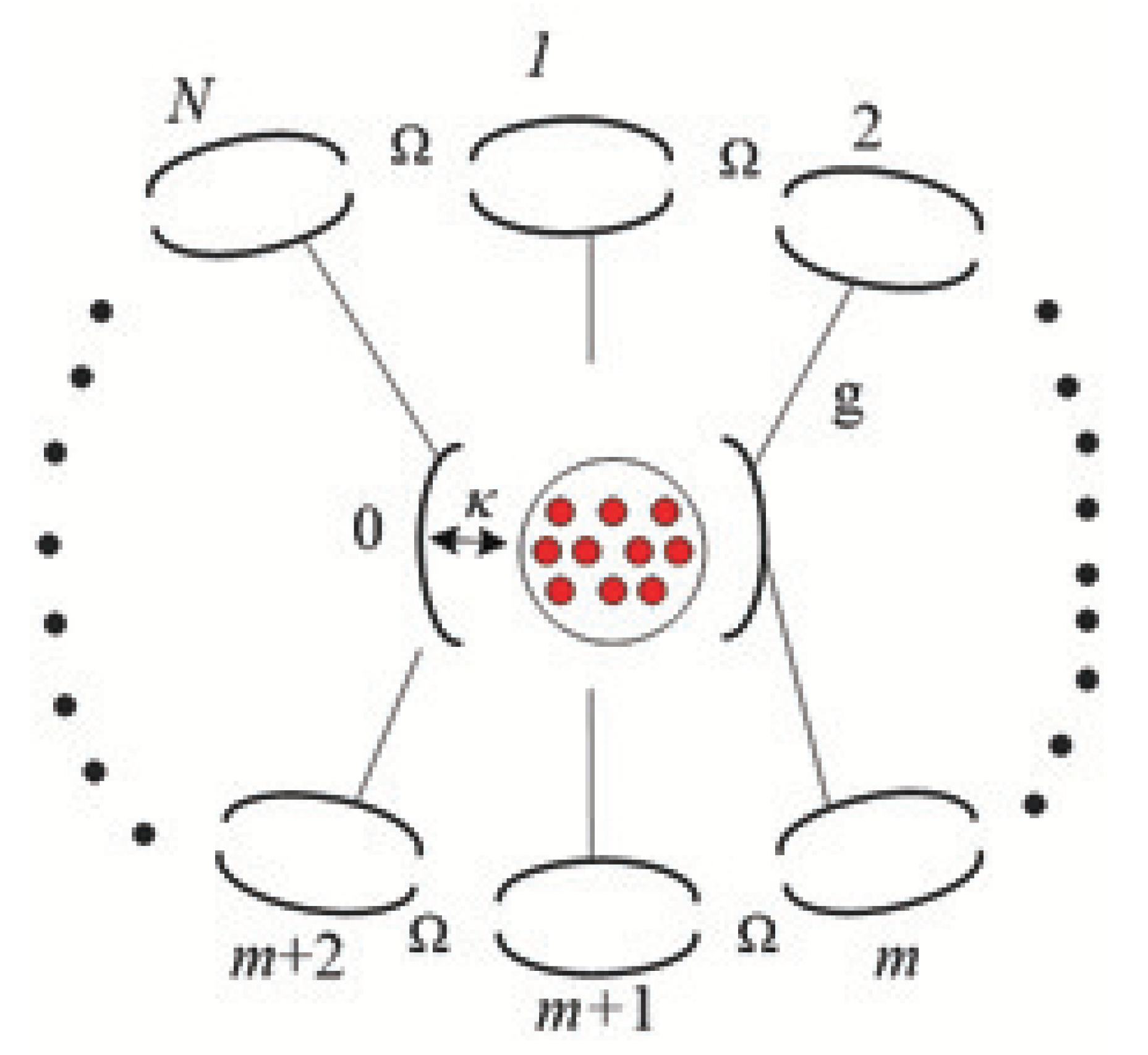
2. Hamiltonian of Our Model
3. Time Evolution of Quantum States
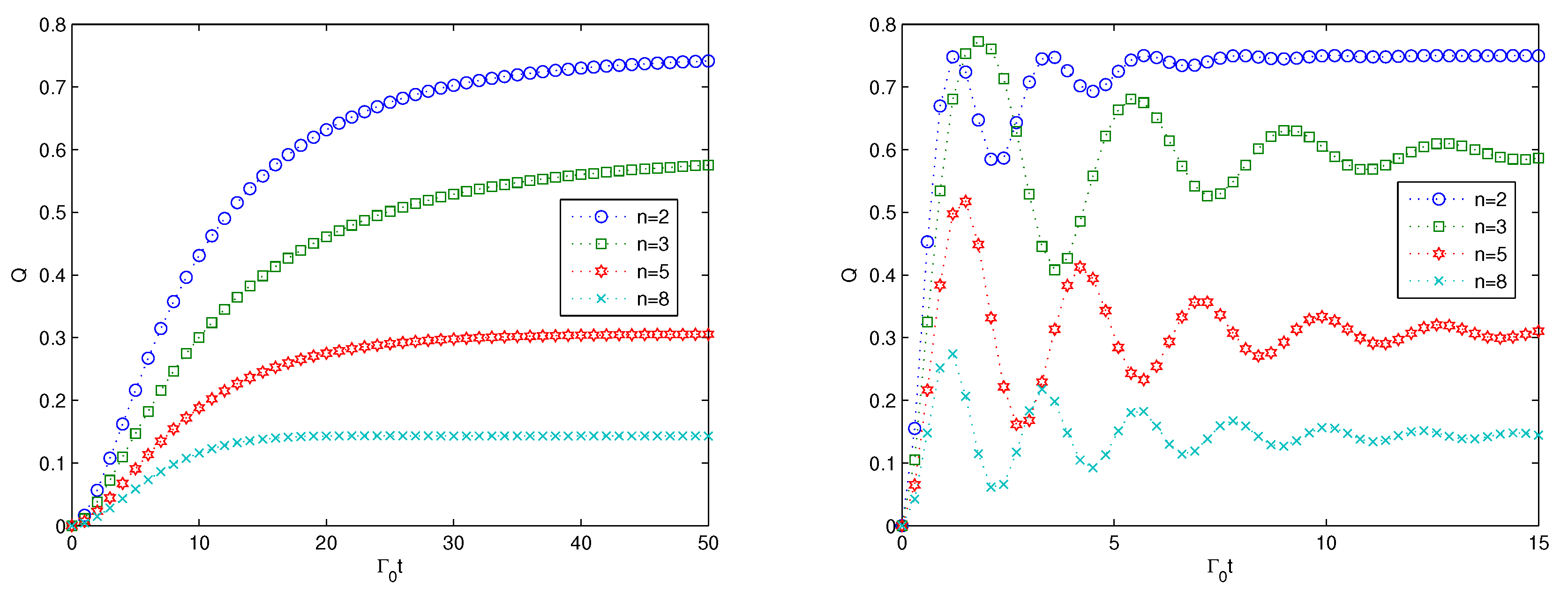
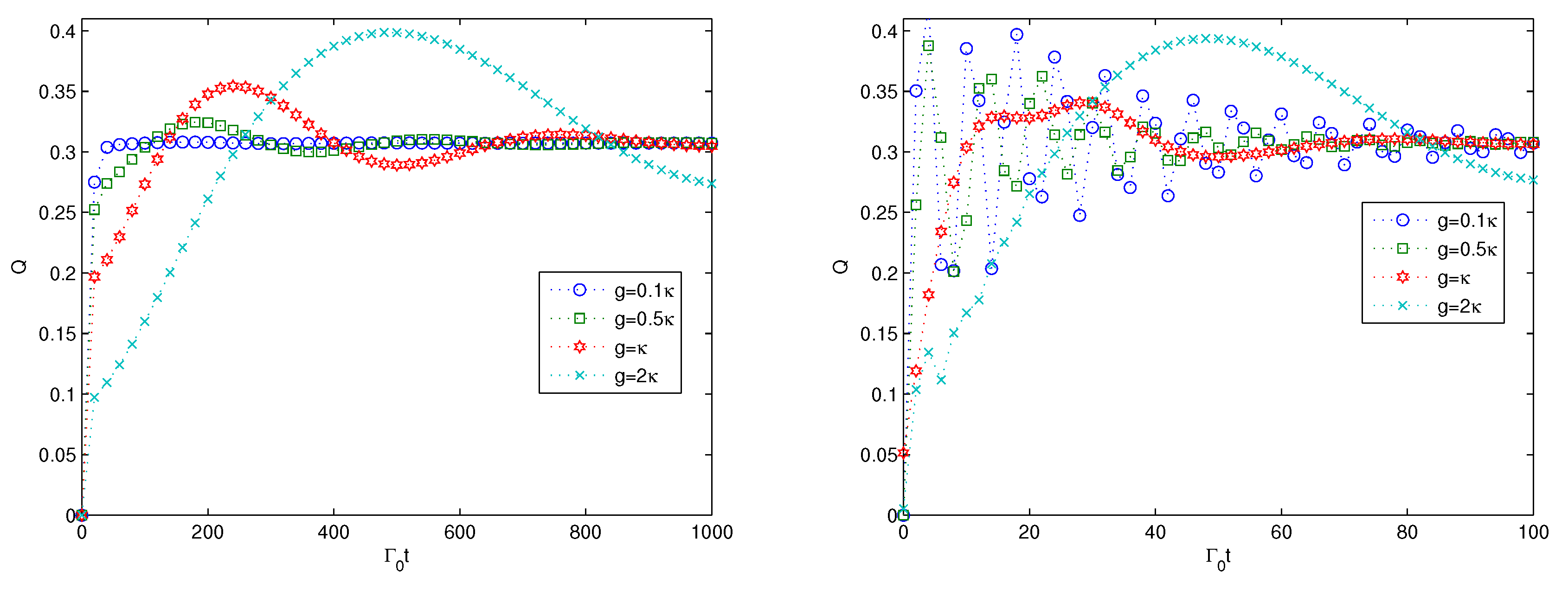
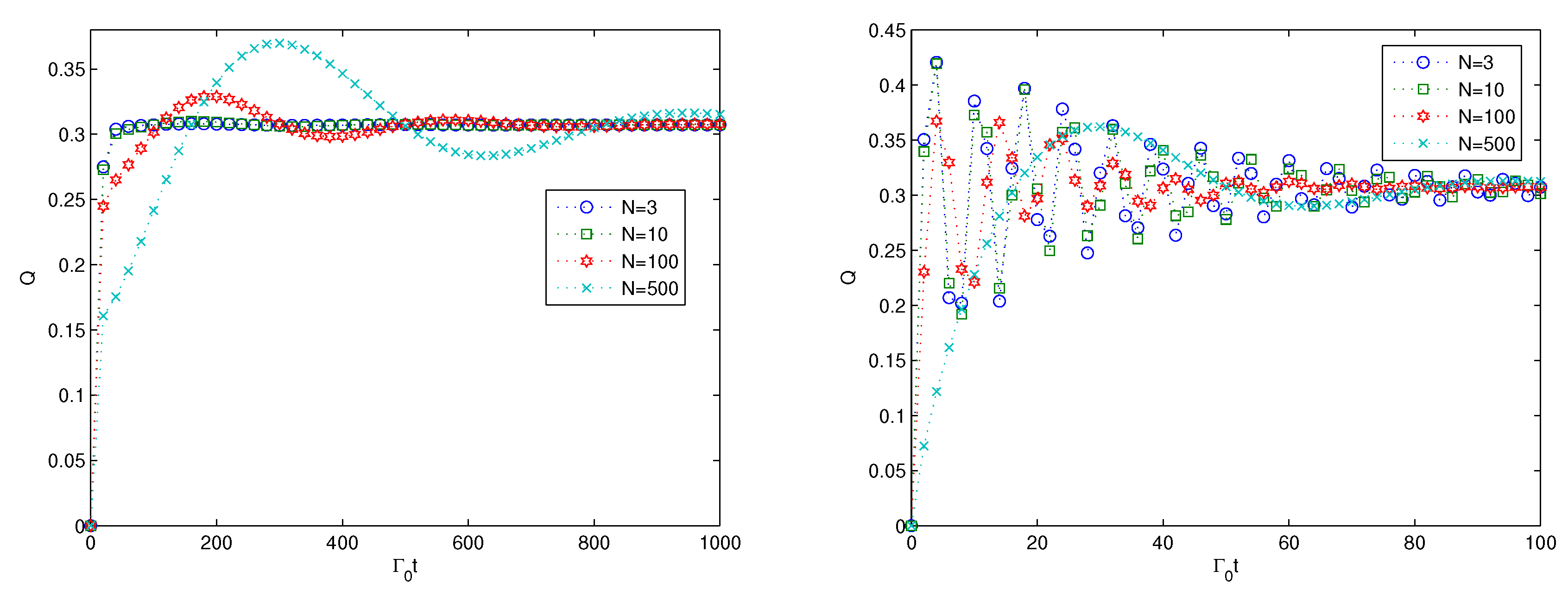
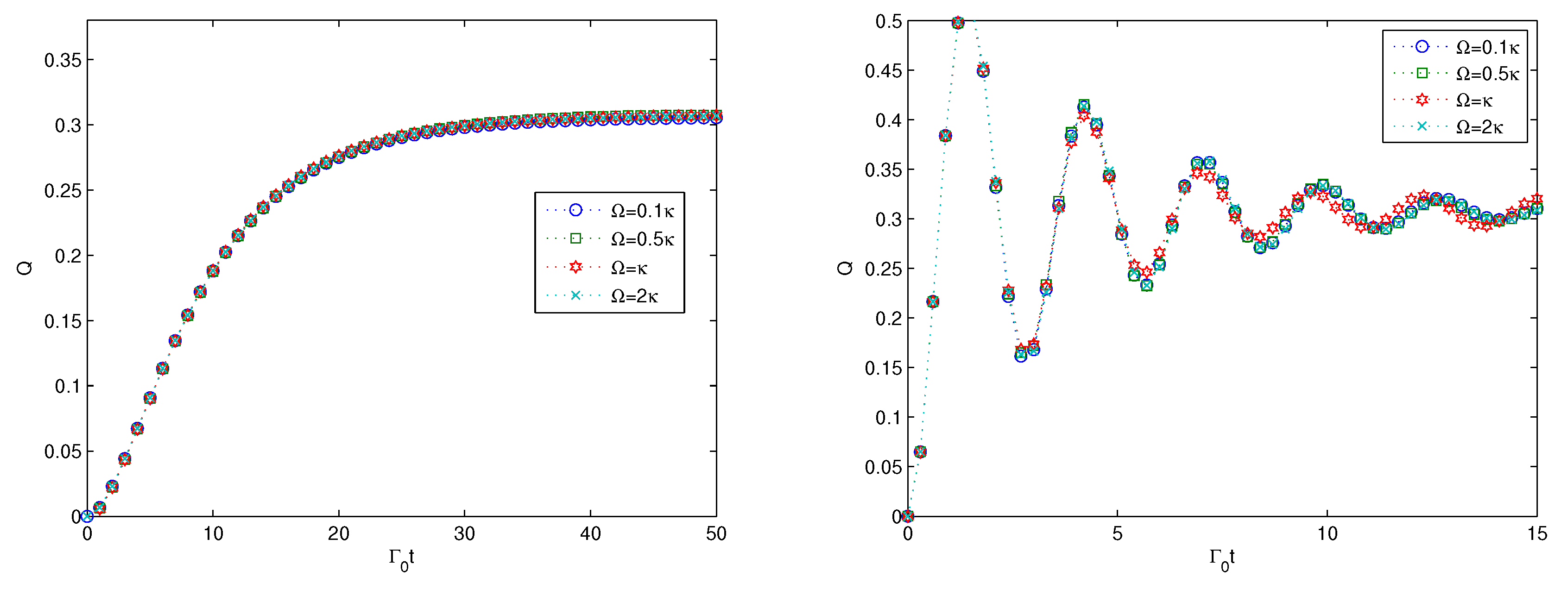
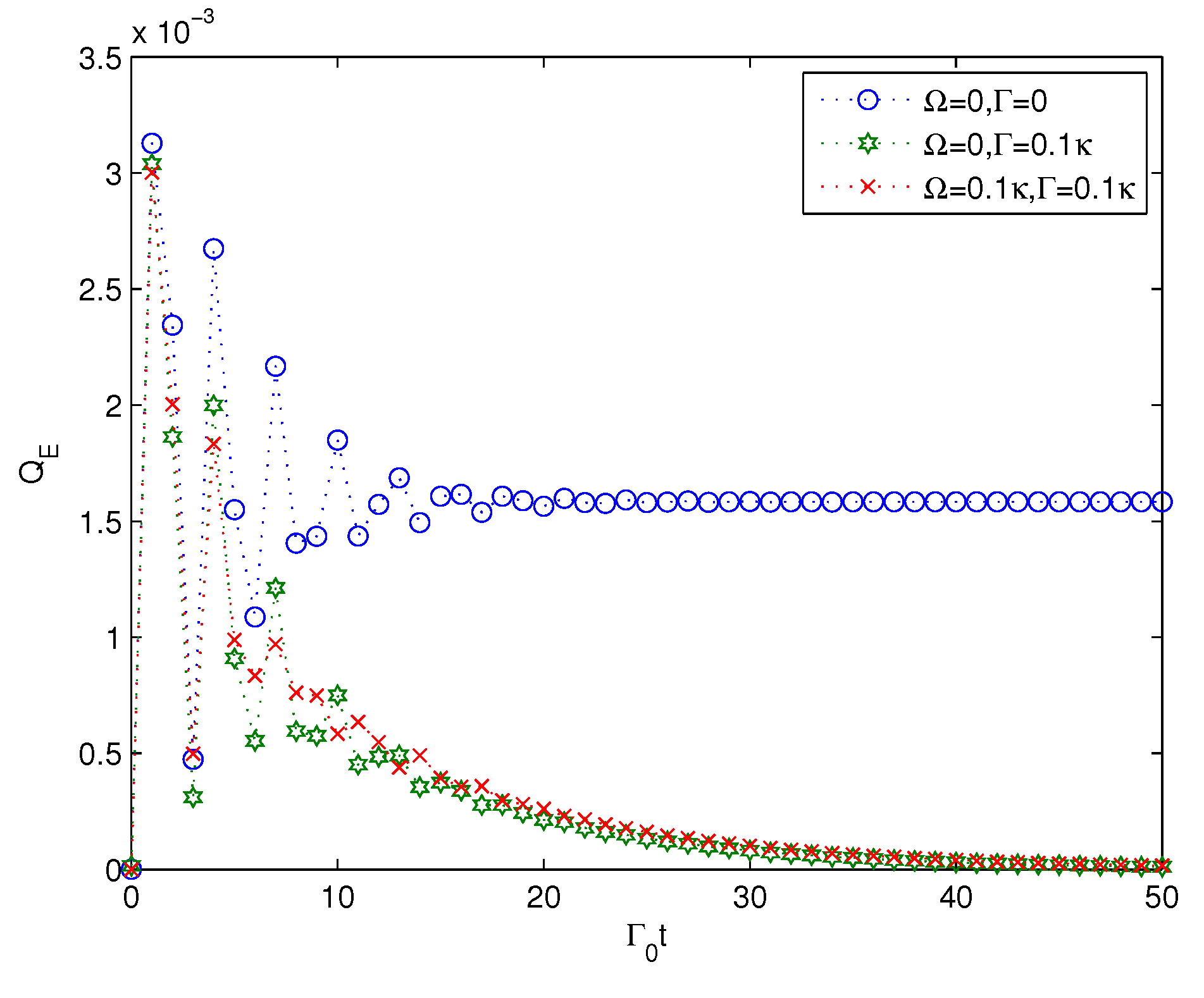
4. Multipartite Entanglement Generation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ekert, A.K. Quantum cryptography based on Bells theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef] [PubMed]
- Vedral, V.; Plenio, M.B.; Rippin, M.A.; Knight, P.L. Quantifying entanglement. Phys. Rev. Lett. 1997, 78, 2275. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bennett, C.H.; DiVincenzo, D.P. Quantum information and computation. Nature 2000, 404, 247. [Google Scholar] [CrossRef]
- Simon, C.; Pan, J.W. Polarization entanglement purification using spatial entanglement. Phys. Rev. Lett. 2002, 89, 257901. [Google Scholar] [CrossRef]
- Gingrich, R.M.; Adami, C. Quantum entanglement of moving bodies. Phys. Rev. Lett. 2002, 89, 270402. [Google Scholar] [CrossRef]
- Carvalho, A.R.; Mintert, F.; Buchleitner, A. Decoherence and multipartite entanglement. Phys. Rev. Lett. 2004, 93, 230501. [Google Scholar] [CrossRef]
- Yeo, Y.; Chua, W.K. Teleportation and dense coding with genuine multipartite entanglement. Phys. Rev. Lett. 2006, 96, 060502. [Google Scholar] [CrossRef]
- Boixo, S.; Monras, A. Operational interpretation for global multipartite entanglement. Phys. Rev. Lett. 2008, 100, 100503. [Google Scholar] [CrossRef]
- Yang, D.; Eisert, J. Entanglement combing. Phys. Rev. Lett. 2009, 103, 220501. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Facchi, P.; Marzolino, U.; Parisi, G.; Pascazio, S.; Scardicchio, A. Phase transitions of bipartite entanglement. Phys. Rev. Lett. 2008, 101, 050502. [Google Scholar] [CrossRef]
- Kaneda, F.; Shimizu, R.; Ishizaka, S.; Mitsumori, Y.; Kosaka, H.; Edamatsu, K. Experimental activation of bound entanglement. Phys. Rev. Lett. 2012, 109, 040501. [Google Scholar] [CrossRef]
- Pan, J.W.; Chen, Z.B.; Lu, C.Y.; Weinfurter, H.; Zeilinger, A.; Żukowski, M. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 2012, 84, 777. [Google Scholar] [CrossRef]
- Carnio, E.G.; Buchleitner, A.; Gessner, M. Robust asymptotic entanglement under multipartite collective dephasing. Phys. Rev. Lett. 2015, 115, 010404. [Google Scholar] [CrossRef]
- Su, X.; Tian, C.; Deng, X.; Li, Q.; Xie, C.; Peng, K. Quantum entanglement wwapping between two multipartite entangled states. Phys. Rev. Lett. 2016, 117, 240503. [Google Scholar] [CrossRef]
- Vedral, V. Quantum entanglement. Nat. Phys. 2014, 10, 256. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehne, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419. [Google Scholar] [CrossRef]
- Franco, R.L.; Compagno, G. Quantum entanglement of identical particles by standard information-theoretic notions. Sci. Rep. 2016, 6, 20603. [Google Scholar] [CrossRef]
- Franco, R.L.; Compagno, G. Indistinguishability of elementary systems as a resource for quantum information processing. Phys. Rev. Lett. 2018, 120, 240403. [Google Scholar] [CrossRef]
- Cai, Y.; Roslund, J.; Ferrini, G.; Arzani, F.; Xu, X.; Fabre, C.; Treps, N. Multimode entanglement in reconfigurable graph states using optical frequency combs. Nat. Commun. 2017, 8, 15645. [Google Scholar] [CrossRef]
- Eberly, J.H.; Yu, T. The end of an entanglement. Science 2007, 316, 555. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Sudden death of entanglement. Science 2009, 323, 598. [Google Scholar] [CrossRef]
- Mortezapour, A.; Borji, M.A.; Franco, R.L. Protecting entanglement by adjusting the velocities of moving qubits inside non-Markovian environments. Laser Phys. Lett. 2017, 14, 055201. [Google Scholar] [CrossRef]
- Franco, R.L.; DArrigo, A.; Falci, G.; Compagno, G.; Paladino, E. Preserving entanglement and nonlocality in solid-state qubits by dynamical decoupling. Phys. Rev. B 2014, 90, 054304. [Google Scholar] [CrossRef]
- Plenio, M.B.; Kirmani, S. An introduction to entanglement measures. Quantum Inf. Comput. 2007, 7, 1. [Google Scholar]
- Aolita, L.; Melo, F.D.; Davidovich, L. Open-system dynamics of entanglement: a key issues review. Rep. Prog. Phys. 2015, 78, 042001. [Google Scholar] [CrossRef]
- Lai, A.C.; Pedicini, M.; Rognone, S. Quantum entanglement and the Bell matrix. Quantum Inform. Process. 2016, 15, 2393. [Google Scholar] [CrossRef]
- DArrigo, A.; Benenti, G.; Franco, R.L.; Falci, G.; Paladino, E. Hidden entanglement, system-environment information flow and non-Markovianity. Int. J. Quantum Inform. 2014, 12, 1461005. [Google Scholar] [CrossRef]
- Dijkstra, A.G.; Tanimura, Y. Non-Markovian entanglement eynamics in the presence of system-bath coherence. Phys. Rev. Lett. 2010, 104, 250401. [Google Scholar] [CrossRef]
- Mortezapour, A.; Franco, R.L. Protecting quantum resources via frequency modulation of qubits in leaky cavities. Sci. Rep. 2018, 8, 14304. [Google Scholar] [CrossRef] [PubMed]
- Dehghani, A.; Mojaveri, B.; Bahrbeig, R.J.; Nosrati, F.; Franco, R.L. Entanglement transfer in a noisy cavity network with parity-deformed fields. J. Opt. Soc. Am. B 2019, 36, 1858. [Google Scholar] [CrossRef]
- Tasgin, M.E. Many-particle entanglement criterion for superradiantlike states. Phys. Rev. Lett. 2017, 119, 033601. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Zeng, Y.; Fan, H.; You, J.Q.; Nori, F. Characterization of topological states via dual multipartite entanglement. Phys. Rev. Lett. 2018, 120, 250501. [Google Scholar] [CrossRef]
- Wang, X.L.; Luo, Y.H.; Huang, H.L.; Chen, M.C.; Su, Z.E.; Liu, C.; Chen, C.; Li, W.; Fang, Y.Q.; Jiang, X.; et al. 18-qubit entanglement with six Photons’ three degrees of freedom. Phys. Rev. Lett. 2018, 120, 260502. [Google Scholar] [CrossRef]
- Wang, X.; Feng, M.; Sanders, B.C. Multipartite entangled states in coupled quantum dots and cavity QED. Phys. Rev. A 2003, 67, 022302. [Google Scholar] [CrossRef]
- Brubß, D.; Datta, N.; Ekert, A.; Kwek, L.C.; Macchiavello, C. Multipartite entanglement in quantum spin chains. Phys. Rev. A 2005, 72, 014301. [Google Scholar] [CrossRef]
- Weinstein, Y.S.; Hellberg, C.S. Matrix-element distributions as a signature of entanglement generation. Phys. Rev. A 2005, 72, 022331. [Google Scholar] [CrossRef]
- Migliore, R.; Yuasa, K.; Nakazato, H.; Messina, A. Generation of multipartite entangled states in Josephson architectures. Phys. Rev. B 2006, 74, 104503. [Google Scholar] [CrossRef]
- Ferraro, A.; Paris, M.G.A. Multimode entanglement and telecloning in a noisy environment. Phys. Rev. A 2005, 72, 032312. [Google Scholar] [CrossRef]
- Franco, C.D.; Paternostro, M.; Tsomokos, D.I.; Huelga, S.F. Control-limited perfect state transfer, quantum stochastic resonance, and many-body entangling gate in imperfect qubit registers. Phys. Rev. A 2008, 77, 062337. [Google Scholar] [CrossRef]
- Mariantoni, M.; Deppe, F.; Marx, A.; Gross, R.; Wilhelm, F.K.; Solano, E. Two-resonator circuit quantum electrodynamics: A superconducting quantum switch. Phys. Rev. B 2008, 78, 104508. [Google Scholar] [CrossRef]
- Chiuri, A.; Vallone, G.; Bruno, N.; Macchiavello, C.; Bru, D.; Mataloni, P. Hyperentangled mixed phased Dicke states: optical design and detection. Phys. Rev. Lett. 2010, 105, 250501. [Google Scholar] [CrossRef]
- Hovhannisyan, K.V.; Perarnau-Llobet, M.; Huber, M.; Acin, A. Entanglement generation is not necessary for optimal work extraction. Phys. Rev. Lett. 2013, 111, 240401. [Google Scholar] [CrossRef]
- Elliott, T.J.; Kozlowski, W.; Caballero-Benitez, S.F.; Mekhov, I.B. Multipartite entangled spatial modes of ultracold atoms generated and controlled by quantum measurement. Phys. Rev. Lett. 2015, 114, 113604. [Google Scholar] [CrossRef]
- Kaufmann, H.; Ruster, T.; Schmiegelow, C.T.; Luda, M.A.; Kaushal, V.; Schulz, J.; von Lindenfels, D.; Schmidt-Kaler, F.; Poschinger, U.G. Scalable creation of long-Lived multipartite entanglement. Phys. Rev. Lett. 2017, 119, 150503. [Google Scholar] [CrossRef]
- Kasture, S. Scalable approach to generation of large symmetric Dicke states. Phys. Rev. A 2018, 97, 043862. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715. [Google Scholar] [CrossRef]
- Plenio, M.B.; Huelga, S.F. Entangled light from white noise. Phys. Rev. Lett. 2002, 88, 197901. [Google Scholar] [CrossRef]
- Mancini, S.; Wang, J. Towards feedback control of entanglement. Eur. Phys. J. D 2005, 32, 257. [Google Scholar] [CrossRef]
- Angelakis, D.G.; Bose, S.; Mancini, S. Steady-state entanglement between hybrid light-matter qubits. Euro. phys. Lett. 2009, 85, 20007. [Google Scholar] [CrossRef]
- Krauter, H.; Muschik, C.A.; Jensen, K.; Wasilewski, W.; Petersen, J.M.; Cirac, J.I.; Polzik, E.S. Entanglement generated by dissipation and steady state entanglement of two macroscopic objects. Phys. Rev. Lett. 2011, 107, 080503. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Nourmandipour, A.; Tavassoly, M.K. Dynamics and protecting of entanglement in two-level systems interacting with a dissipative cavity: The Gardiner–Collett approach. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 165502. [Google Scholar] [CrossRef][Green Version]
- Memarzadeh, L.; Mancini, S. Entanglement dynamics for qubits dissipating into a common environment. Phys. Rev. A 2013, 87, 032303. [Google Scholar] [CrossRef]
- Memarzadeh, L.; Mancini, S. Stationary entanglement achievable by environment-induced chain links. Phys. Rev. A 2011, 83, 042329. [Google Scholar] [CrossRef]
- Nourmandipour, A.; Tavassoly, M.K.; Rafiee, M. Dynamics and protection of entanglement in n-qubit systems within Markovian and non-Markovian environments. Phys. Rev. A 2016, 93, 022327. [Google Scholar] [CrossRef]
- Hu, B.L.; Paz, J.P.; Zhang, Y. Quantum Brownian motion in a general environment: Exact master equation with nonlocal dissipation and colored noise. Phys. Rev. D 1992, 45, 2843. [Google Scholar] [CrossRef]
- Strunz, W.T.; Yu, T. Convolutionless Non-Markovian master equations and quantum trajectories: Brownian motion. Phys. Rev. A 2004, 69, 052115. [Google Scholar] [CrossRef]
- Vacchini, B.; Breuer, H.P. Exact master equations for the non-Markovian decay of a qubit. Phys. Rev. A 2010, 81, 042103. [Google Scholar] [CrossRef]
- Zhang, W.M.; Lo, P.Y.; Xiong, H.N.; Tu, W.M.Y.; Nori, F. General Non-Markovian Dynamics of Open Quantum Systems. Phys. Rev. Lett. 2012, 109, 170402. [Google Scholar] [CrossRef]
- Wolf, M.M.; Eisert, J.; Cubitt, T.S.; Cirac, J.I. Assessing non-Markovian quantum dynamics. Phys. Rev. Lett. 2008, 101, 150402. [Google Scholar] [CrossRef] [PubMed]
- Wilson, J.H.; Fregoso, B.M.; Galitski, V.M. Entanglement dynamics in a non-Markovian environment: An exactly solvable model. Phys. Rev. B 2012, 85, 174304. [Google Scholar] [CrossRef]
- Li, C.F.; Wang, H.T.; Yuan, H.Y.; Ge, R.C.; Guo, G.C. Non-Markovian Dynamics of Quantum and Classical Correlations in the Presence of System-Bath Coherence. Chin. Phys. Lett. 2011, 28, 120302. [Google Scholar] [CrossRef][Green Version]
- Ma, T.; Chen, Y.; Chen, T.; Hedemann, S.R.; Yu, T. Crossover between non-Markovian and Markovian dynamics induced by a hierarchical environment. Phys. Rev. A 2014, 90, 042108. [Google Scholar] [CrossRef]
- Sanz, A.S.; Elran, Y.; Brumer, P. Temperature crossover of decoherence rates in chaotic and regular bath dynamics. Phys. Rev. E 2012, 85, 036218. [Google Scholar] [CrossRef]
- Xu, K.; Han, W.; Zhang, Y.J.; Xia, Y.J.; Fan, H. Environment-assisted non-Markovian speedup dynamics control. Ann. Phys. 2018, 388, 1. [Google Scholar] [CrossRef]
- Wang, D.; Huang, A.J.; Hoehn, R.D.; Ming, F.; Sun, W.Y.; Shi, J.D.; Ye, L.; Kais, S. Entropic uncertainty relations for Markovian and non-Markovian processes under a structured bosonic reservoir. Sci. Rep. 2017, 7, 1066. [Google Scholar] [CrossRef]
- Shen, H.Z.; Li, D.X.; Su, S.L.; Zhou, Y.H.; Yi, X.X. Exact non-Markovian dynamics of qubits coupled to two interacting environments. Phys. Rev. A 2017, 96, 033805. [Google Scholar] [CrossRef]
- Campbell, S.; Ciccarello, F.; Palma, G.M.; Vacchini, B. System-environment correlations and Markovian embedding of quantum non-Markovian dynamics. Phys. Rev. A 2018, 98, 012142. [Google Scholar] [CrossRef]
- Xu, K.; Han, W.; Zhang, Y.J.; Xia, Y.J.; Fan, H. Hierarchical-environment-assisted non-Markovian speedup dynamics control. Phys. Rev. A 2018, 98, 022114. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J.; Vacchini, B. Non-Markovian dynamics in open quantum systems. Rev. Mod. Phy. 2016, 88, 021002. [Google Scholar] [CrossRef]
- Franco, R.L.; Bellomo, B.; Maniscalco, S.; Compagno, G. Dynamics of quantum correlations in two-qubit systems within non-Markovian environments. Int. J. Mod. Phys. B 2013, 27, 1345053. [Google Scholar] [CrossRef]
- Xu, J.S.; Sun, K.; Li, C.F.; Xu, X.Y.; Guo, G.C.; Andersson, E.; Franco, R.L.; Compagno, G. Experimental recovery of quantum correlations in absence of system-environment back-action. Nat. Commun. 2013, 4, 2851. [Google Scholar] [CrossRef] [PubMed]
- Orieux, A.; DArrigo, A.; Ferranti, G.; Franco, R.L.; Benenti, G.; Paladino, E.; Falci, G.; Sciarrino, F.; Mataloni, P. Experimental on-demand recovery of entanglement by local operations within non-Markovian dynamics. Sci. Rep. 2015, 5, 8575. [Google Scholar] [CrossRef]
- Darrigo, A.; Franco, R.L.; Benenti, G.; Paladino, E.; Falci, G. Recovering entanglement by local operations. Ann. Phys. 2014, 350, 211. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J.; Franco, R.L. Cavity-based architecture to preserve quantum coherence and entanglement. Sci. Rep. 2015, 5, 13843. [Google Scholar] [CrossRef]
- Mortezapour, A.; Naeimi, G.; Franco, R.L. Coherence and entanglement dynamics of vibrating qubits. Optics Commun. 2018, 424, 26. [Google Scholar] [CrossRef]
- Mirkin, N.; Poggi, P.; Wisniacki, D. Entangling protocols due to non-Markovian dynamics. Phys. Rev. A 2019, 99, 020301. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef]
- Franco, R.L.; Compagno, G. Overview on the Phenomenon of Two-Qubit Entanglement Revivals in Classical Environments. In Lectures on General Quantum Correlations and their Applications, Quantum Science and Technology; Fanchini, F., Soares-Pinto, D., Adesso, G., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Madsen, K.H.; Ates, S.; Lund-Hansen, T.; Loffler, A.; Reitzenstein, S.; Forchel, A.; Lodahl, P. Observation of non-Markovian dynamics of a single quantum dot in a micropillar cavity. Phys. Rev. Lett. 2011, 106, 233601. [Google Scholar] [CrossRef]
- Laine, E.-M.; Piilo, J.; Breuer, H.-P. Measure for the non-Markovianity of quantum processes. Phys. Rev. A 2010, 81, 062115. [Google Scholar] [CrossRef]
- Lambert, N.; Emary, C.; Brandes, T. Entanglement and entropy in a spin-boson quantum phase transition. Phys. Rev. A 2005, 71, 053804. [Google Scholar] [CrossRef]
- Emary, C. A bipartite class of entanglement monotones for N-qubit pure states. J. Phys. A 2004, 37, 8293. [Google Scholar] [CrossRef]
- Imoto, N.; Haus, H.A.; Yamamoto, Y. Quantum nondemolition measurement of the photon number via the optical Kerr effect. Phys. Rev. A 1985, 32, 2287. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Muller, M.; Schindler, P.; Nigg, D.; Monz, T.; Chwalla, M.; Hennrich, M.; Roos, C.F.; Zoller, P.; Blatt, R. An open-system quantum simulator with trapped ions. Nature 2011, 470, 486. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Ma, X.S.; Cheng, M.-T. Multipartite Entanglement Generation in a Structured Environment. Entropy 2020, 22, 191. https://doi.org/10.3390/e22020191
Wang S, Ma XS, Cheng M-T. Multipartite Entanglement Generation in a Structured Environment. Entropy. 2020; 22(2):191. https://doi.org/10.3390/e22020191
Chicago/Turabian StyleWang, Shijiao, Xiao San Ma, and Mu-Tian Cheng. 2020. "Multipartite Entanglement Generation in a Structured Environment" Entropy 22, no. 2: 191. https://doi.org/10.3390/e22020191
APA StyleWang, S., Ma, X. S., & Cheng, M.-T. (2020). Multipartite Entanglement Generation in a Structured Environment. Entropy, 22(2), 191. https://doi.org/10.3390/e22020191



