A Novel Comprehensive Evaluation Method for Estimating the Bank Profile Shape and Dimensions of Stable Channels Using the Maximum Entropy Principle
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
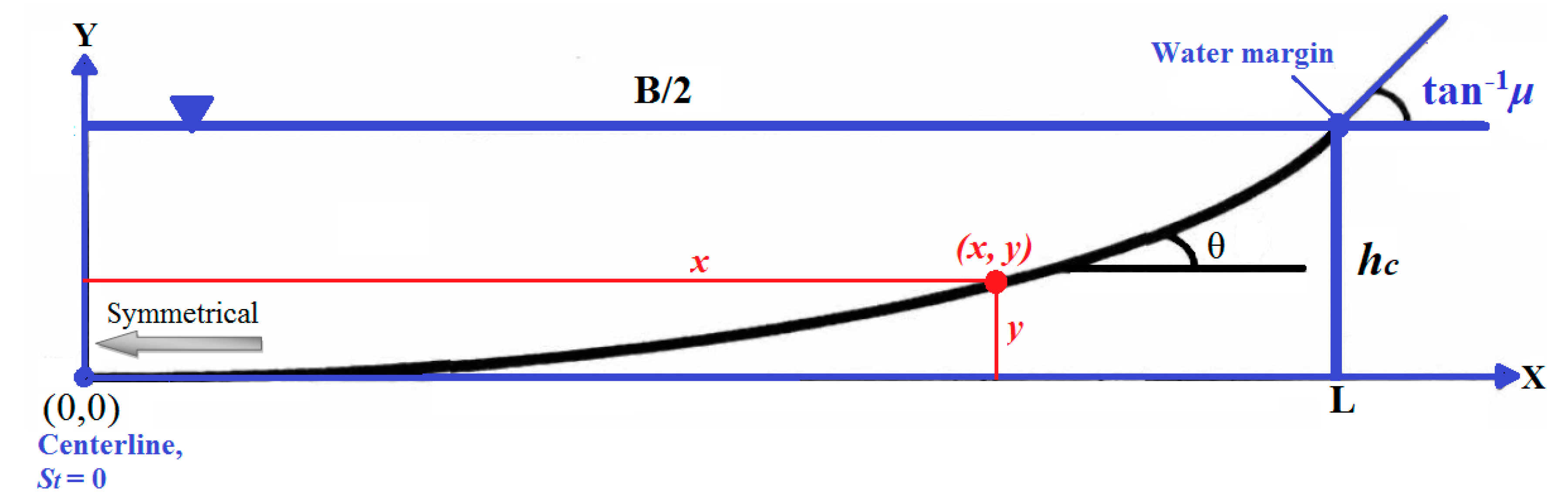
3.1. Maximum Entropy Principle in Estimating the Transverse Slope of Stable Banks
3.2. Calculating μ
3.3. Entropy-Based Design Model of Threshold Channels (EDMTC)
3.4. Experimental Data
3.5. Used Data in Modeling
- Ikeda (1981) → one run as S3 (8 samples)
- Diplas (1990) → one run as S4 (25 samples)
- Babaeyan (1996) → one run as S5 (8 samples)
- Macky (1999) → one run as S6 (101 samples)
- Hassanzadeh et al. (2014) → two runs as S7 (33 samples) and S8 (38 samples)
- and Khodashenas (2016) → four runs as S9 (44 samples), S10 (33 samples), S11 (57 samples) and S12 (20 samples)
3.6. Evaluation of Model Efficiency
4. Results
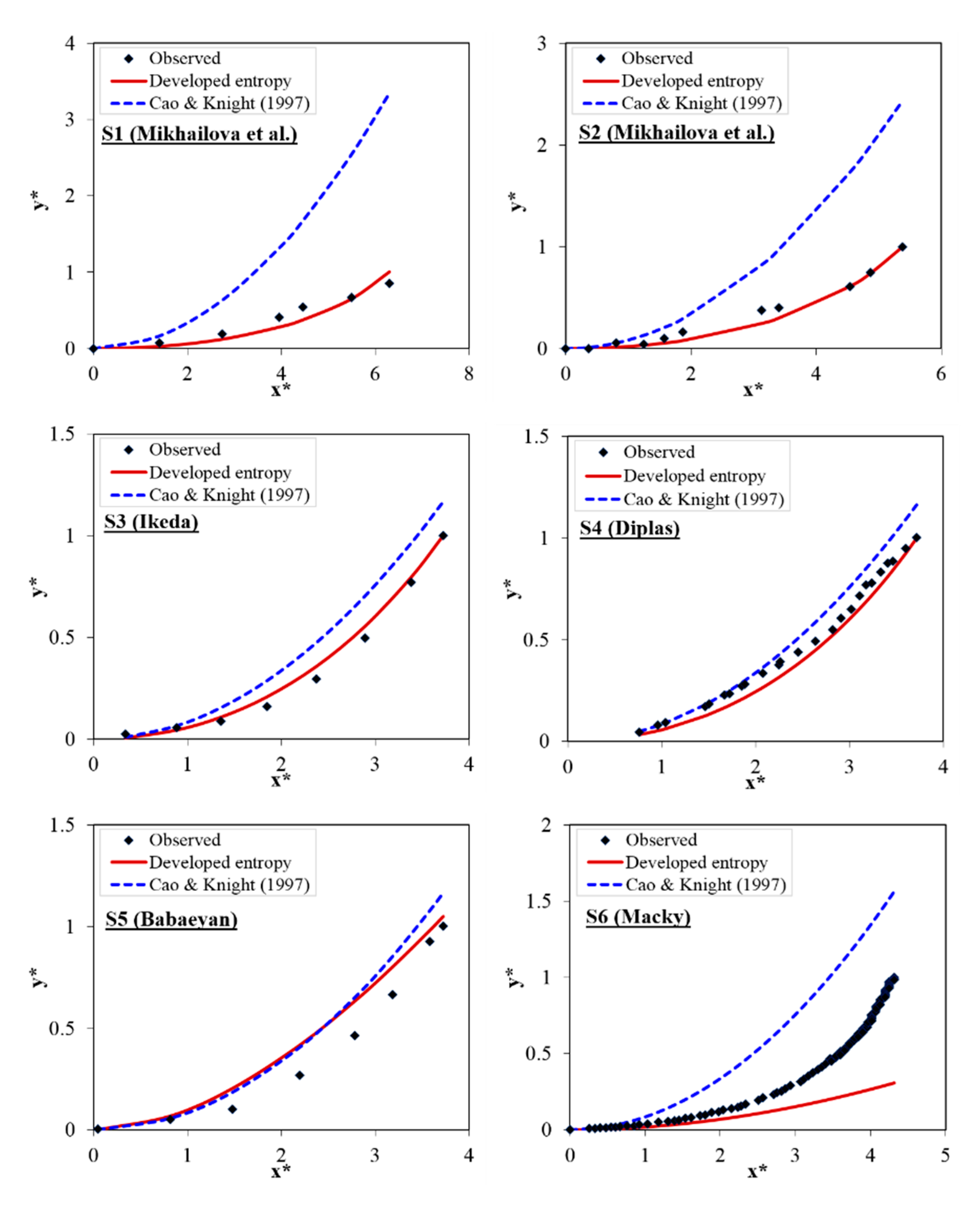
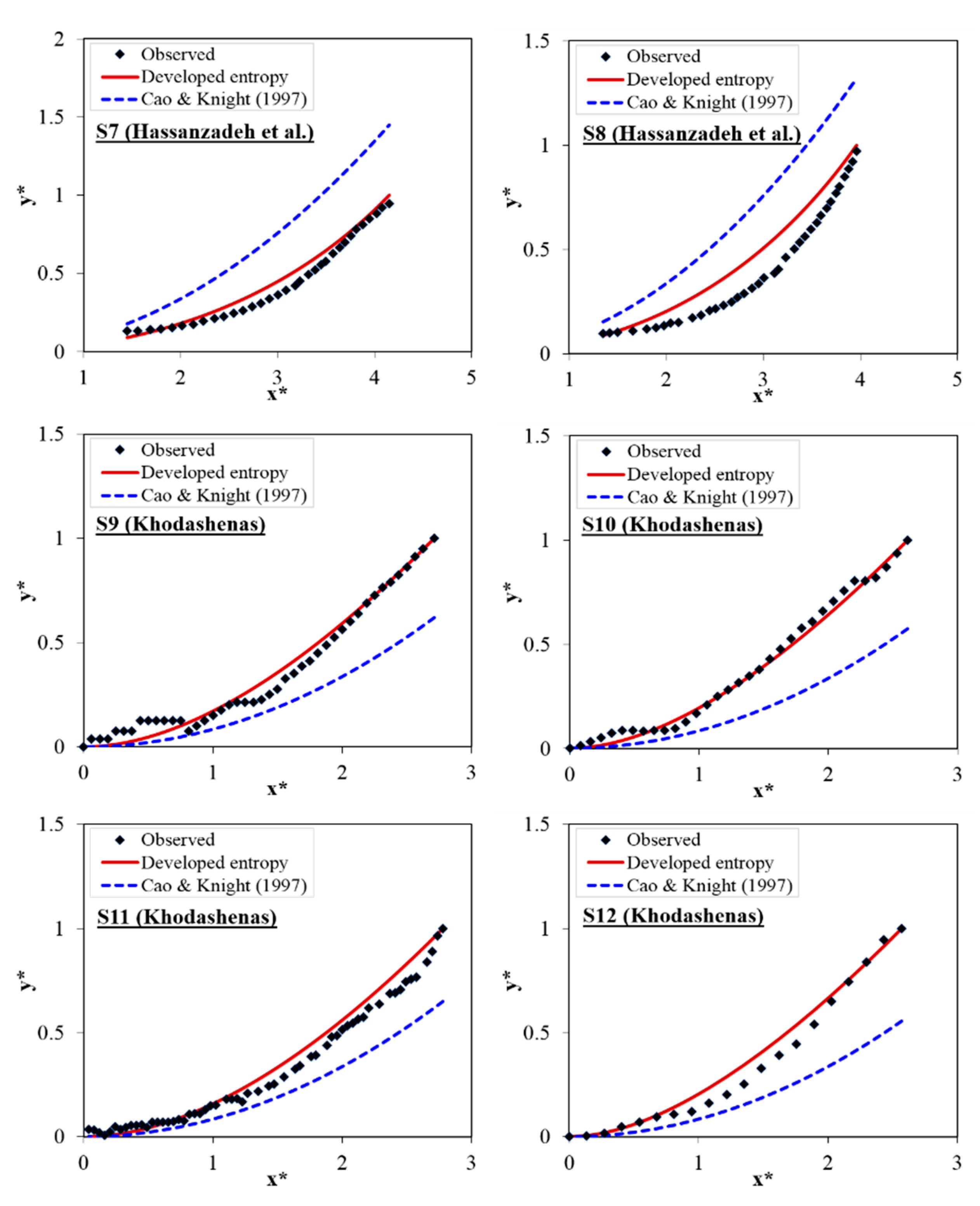
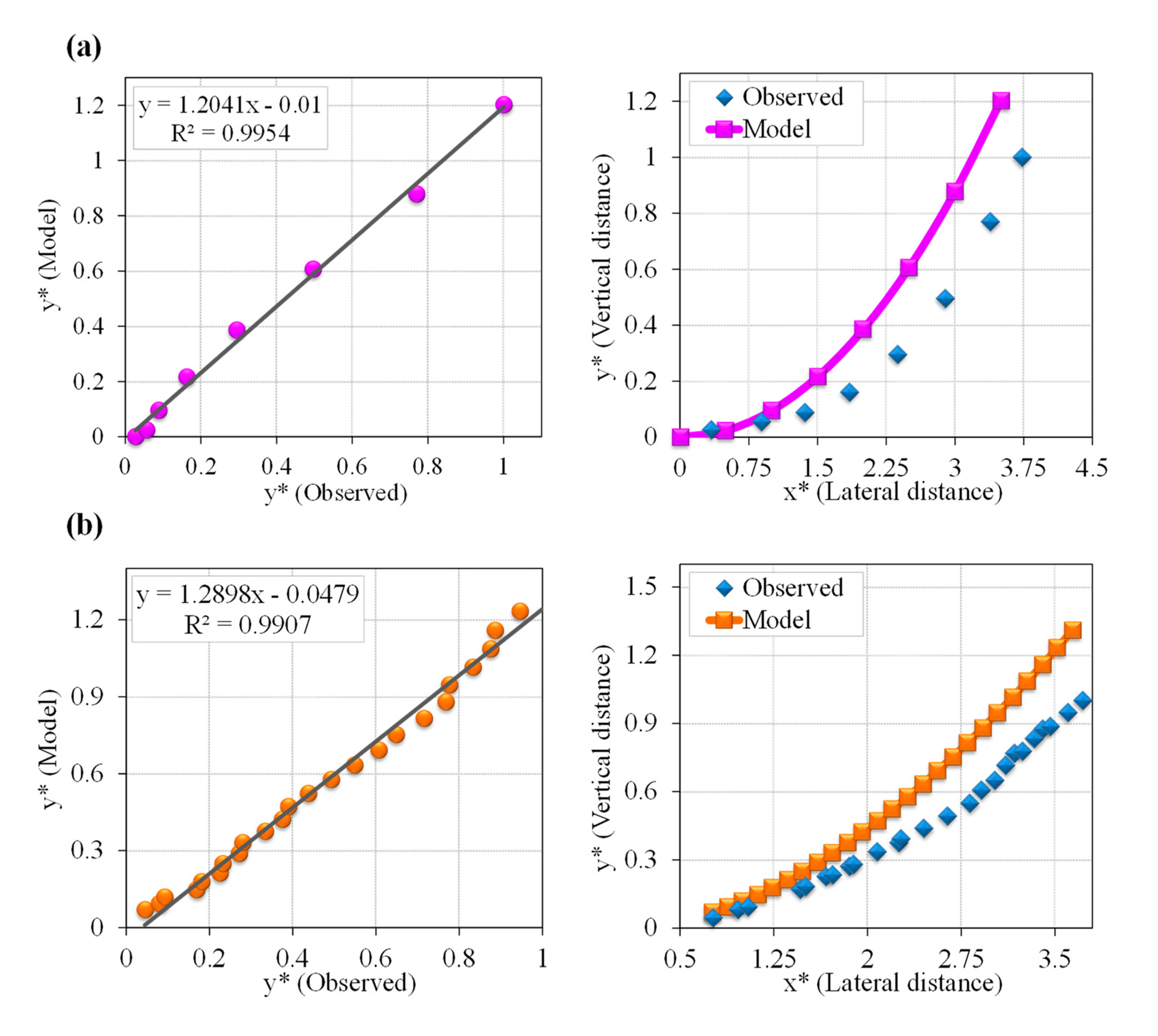
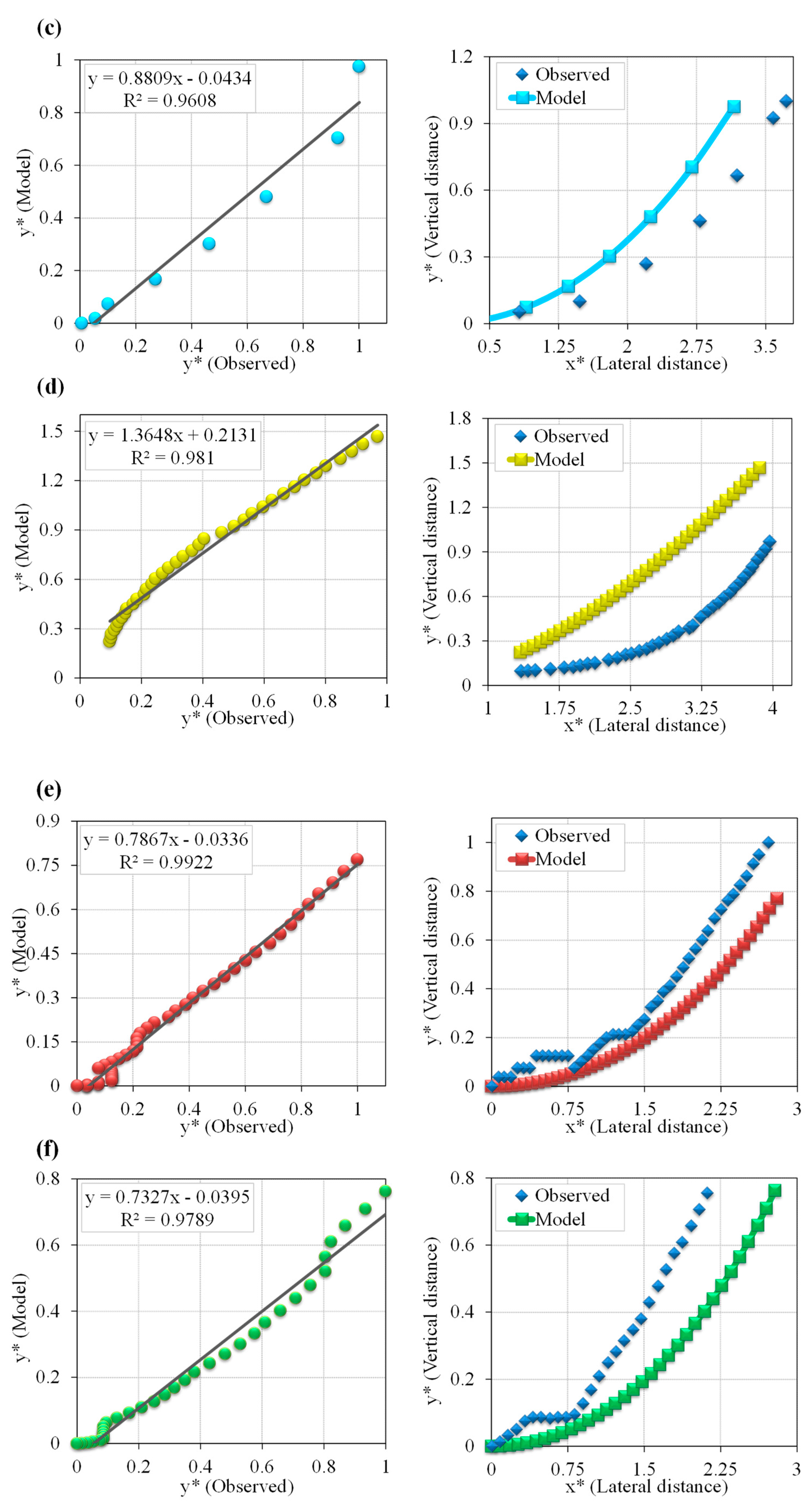
4.1. Entropy Model in Predicting Bank Profile Shapes
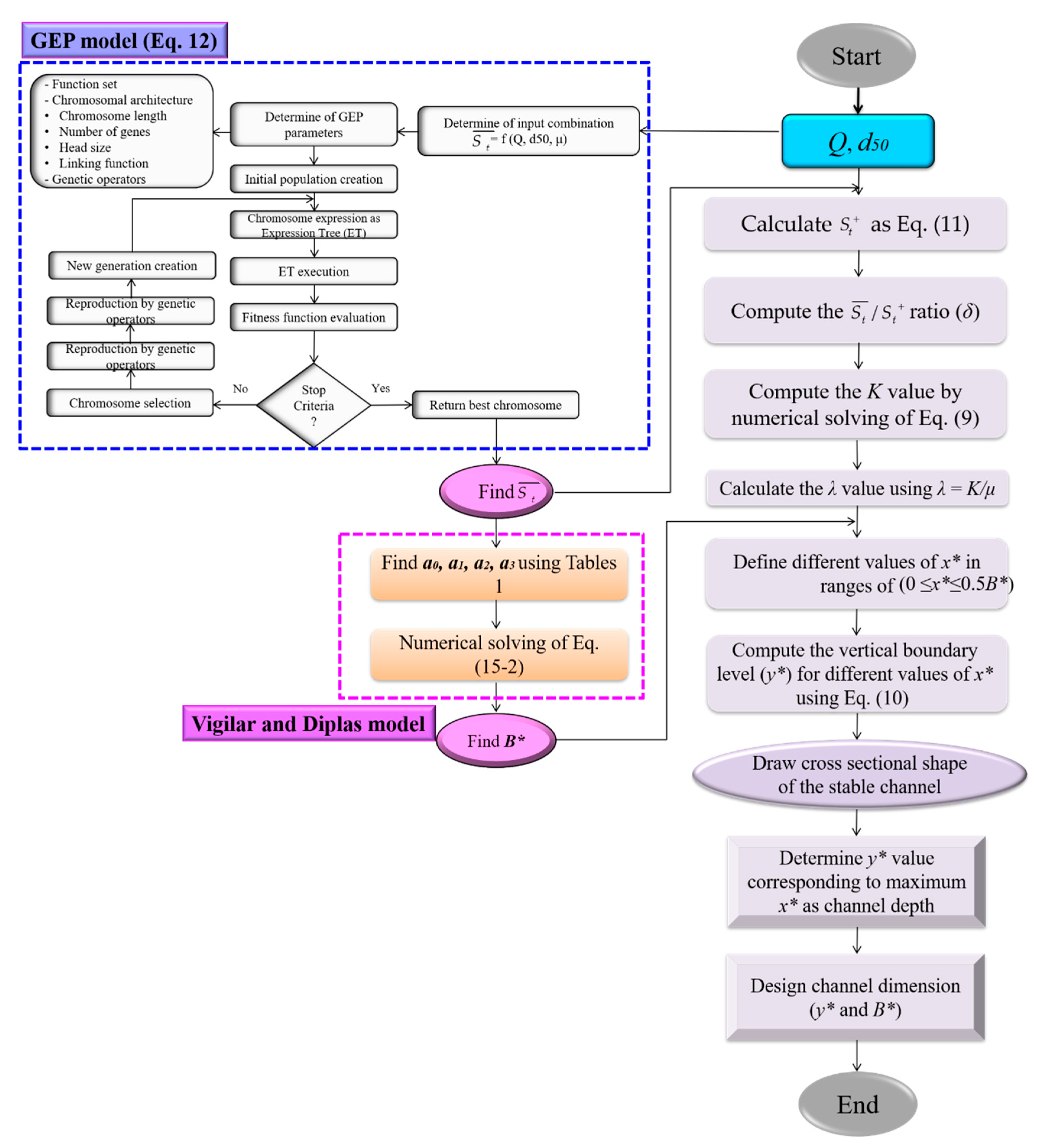
4.2. Presenting the Entropy-Based Design Model of Threshold Channels (EDMTC)
Evaluation of EDMTC Performance
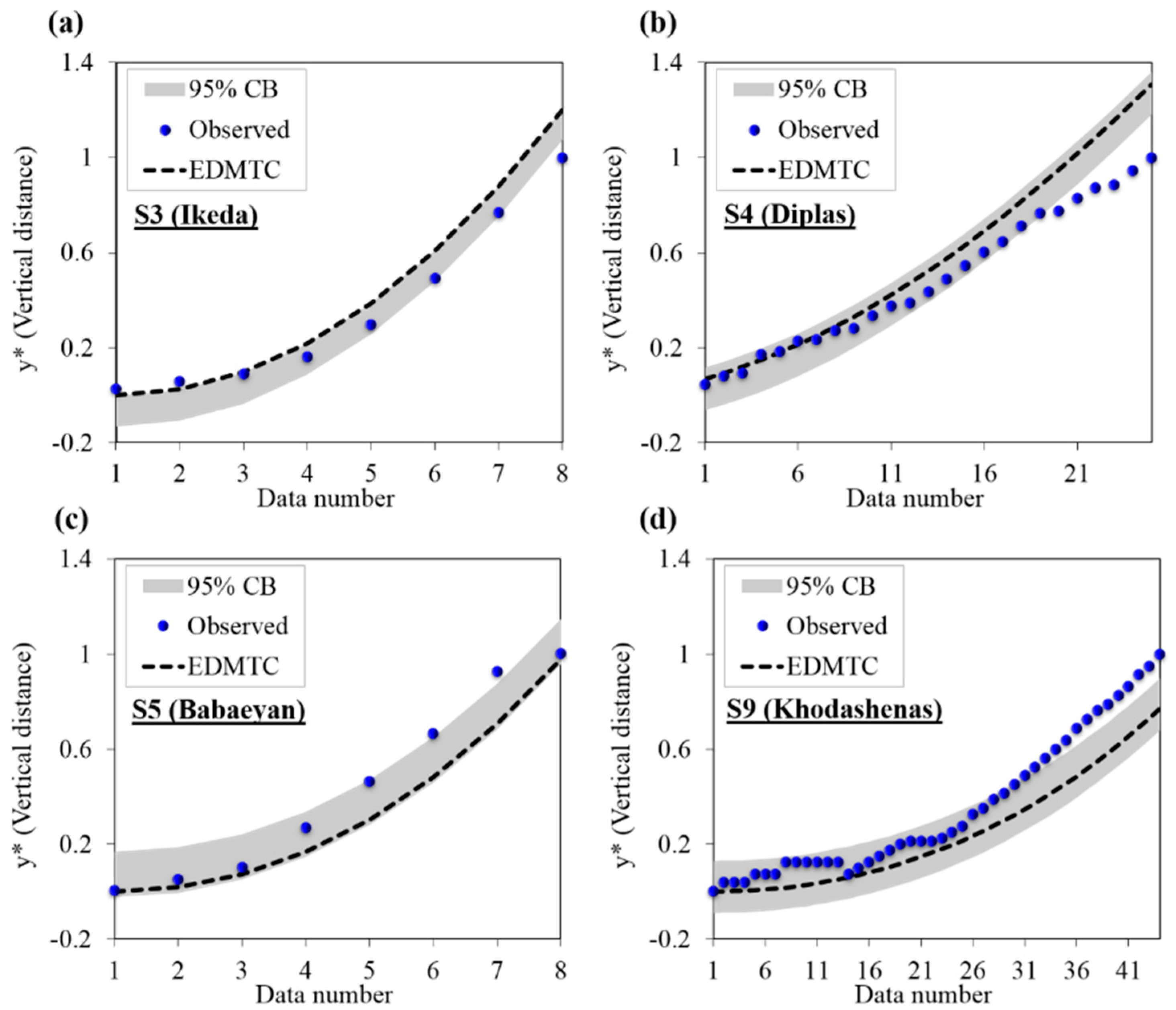
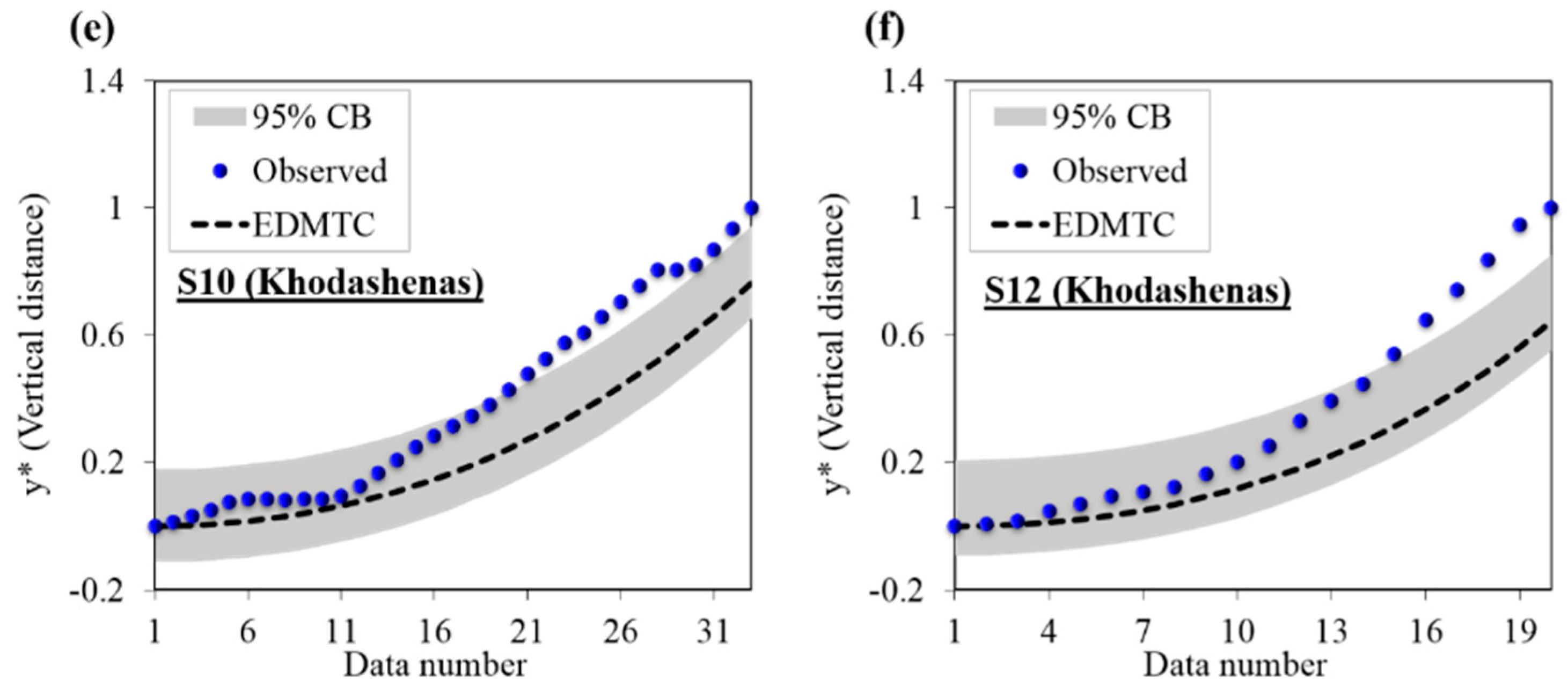
4.3. Uncertainty Analysis of the Proposed EDMTC and GEP Model
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Julien, P.Y.; Wargadalam, J. Alluvial Channel Geometry: Theory and Applications. J. Hydraul. Eng. 1995, 121, 312–325. [Google Scholar] [CrossRef]
- Parker, G. Self-formed straight rivers with equilibrium banks and mobile bed. Part 1. The sand-silt river. J. Fluid Mech. 1978, 89, 109–125. [Google Scholar] [CrossRef]
- Wolman, M.G.; Brush, L.M. Factors Controlling the Size and Shape of Stream Channels in Coarse Noncohesive Sands; US Government Printing Office: Washington, DC, USA, 1961.
- Glover, R.E.; Florey, Q.L. Stable Channel Profiles; Lab. Rep. 325Hydraul; U.S. Bureau of Reclamation: Washington, DC, USA, 1951.
- Lane, E.W. Progress report on studies on the design of stable channels by the Bureau of Reclamation. Proc. Am. Soc. Civ. Eng. ASCE 1953, 79, 1–31. [Google Scholar]
- Parker, G. Self-formed straight rivers with equilibrium banks and mobile bed, Part 2. The gravel river. J. Fluid Mech. 1978, 89, 127–146. [Google Scholar] [CrossRef]
- Babaeyan-Koopaei, K. A Study of Straight Stable Channels and Their Interactions with Bridge Structures. Ph.D. Thesis, University of Newcastle Upon Tyne, Newcastle Upon Tyne, UK, 1996. [Google Scholar]
- Hey, R.D.; Heritage, G.L. Dimensional and dimensionless regime equations for gravel-bed rivers. In International Conference on River Regime; Hydraulics Research Limited; Wiley: Wallingford, UK, 1988; pp. 1–8. [Google Scholar]
- Lawrence, S.D. Fluvial Hydraulics; Oxford University Press: Oxford, UK, 2009; pp. 92–111. [Google Scholar]
- Gholami, A.; Bonakdari, H.; Mohammadian, M.; Zaji, A.H.; Gharabaghi, B. Assessment of geomorphological bank evolution of the alluvial threshold rivers based on entropy concept parameters. Hydrol. Sci. J. 2019, 64, 856–872. [Google Scholar] [CrossRef]
- Vigilar, G.; Diplas, P. Stable channels with mobile bed: Model verification and graphical solution. J. Hydraul. Eng. Asce 1998, 124, 1097–1108. [Google Scholar] [CrossRef]
- Afzalimehr, H.; Abdolhosseini, M.; Singh, V.P. Hydraulic geometry relations for stable channel design. J. Hydrol. Eng. 2010, 15, 859–864. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Shaghaghi, S.; Khoshbin, F. Developing an expert group method of data handling system for predicting the geometry of a stable channel with a gravel bed. Earth Surf. Process. Landf. 2017, 42, 1460–1471. [Google Scholar] [CrossRef]
- Hey, R.D.; Thorne, C.R. Stable channels with mobile gravel beds. J. Hydraul. Eng. 1986, 112, 671–689. [Google Scholar] [CrossRef]
- Bonakdari, H.; Gholami, A.; Gharabaghi, B. Modelling Stable Alluvial River Profiles Using Back Propagation-Based Multilayer Neural Networks. In Proceedings of the Intelligent Computing-Proceedings of the Computing Conference, London, UK, 16–17 July 2019; Springer: Cham, Switzerland, 2019; pp. 607–624. [Google Scholar]
- Métivier, F.; Lajeunesse, E.; Devauchelle, O. Laboratory rivers: Lacey’s law, threshold theory, and channel stability. Earth Surf. Dyn. 2017, 5, 187. [Google Scholar] [CrossRef]
- Bonakdari, H.; Gholami, A.; Sattar, A.M.; Gharabaghi, B. Development of robust evolutionary polynomial regression network in the estimation of stable alluvial channel dimensions. Geomorphology 2020, 350, 106895. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Khodashenas, S.R. Reliability and sensitivity analysis of robust learning machine in prediction of bank profile morphology of threshold sand rivers. Measurement 2020, 153, 107411. [Google Scholar] [CrossRef]
- Singh, V.P. Entropy Theory in Hydraulic Engineering: An Introduction; American Society of Civil Engineers: Reston, VA, USA, 2014. [Google Scholar]
- Ikeda, S. Self-formed straight channels in sandy beds. J. Hydraul. Div. Asce 1981, 107, 389–406. [Google Scholar]
- Diplas, P. Characteristics of self-formed straight channels. J. Hydraul. Eng. ASCE 1990, 116, 707–728. [Google Scholar] [CrossRef]
- Pizzuto, J.E. Numerical simulation of gravel river widening. Water Resour. Res. 1990, 26, 1971–1980. [Google Scholar] [CrossRef]
- Diplas, P.; Vigilar, G. Hydraulic geometry of threshold channels. J. Hydraul. Eng. Asce 1992, 118, 597–614. [Google Scholar] [CrossRef]
- Vigilar, G.; Diplas, P. Design of a threshold channel. In Hydraulic Engineering: Saving a Threatened Resource—In Search of Solutions; ASCE: Reston, VA, USA, 1992; pp. 729–734. [Google Scholar]
- Vigilar, G.; Diplas, P. Stable channels with mobile bed: Formulation and numerical solution. J. Hydraul. Eng. Asce 1997, 123, 189–199. [Google Scholar] [CrossRef]
- Dey, S. Bank profile of threshold channels: A simplified approach. J. Irrig. Drain. Eng. Asce 2001, 127, 184–187. [Google Scholar] [CrossRef]
- Yu, G.; Knight, D.W. Geometry of self-formed straight threshold channels in uniform material. In Water Maritime and Energy, Proceedings of the Institute of Civil Engineering, London, UK; Institute of Civil Engineering: London, UK, 14 September 1998; Volume 130, pp. 31–41. [Google Scholar]
- Cao, S.; Knight, D.W. Entropy-based design approach of threshold alluvial channels. J. Hydraul. Res. 1997, 35, 505–524. [Google Scholar] [CrossRef]
- Chow, V.D. Open Channel Hydraulics; McGraw-Hill: New York, NY, USA, 1959; pp. 20–21. [Google Scholar]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Mohammadian, M.; Gharabaghi, B.; Khodashenas, S.R. Uncertainty Analysis of Intelligent Model of Hybrid Genetic Algorithm and Particle Swarm Optimization with ANFIS to Predict Threshold Bank Profile Shape Based on Digital Laser Approach Sensing. Measurement 2018, 121, 294–303. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Gharabaghi, B.; Khodashenas, S.R.; Talesh, S.H.A.; Jamali, A.A. Methodological approach of predicting threshold channel bank profile by multi-objective evolutionary optimization of ANFIS. Eng. Geol. 2018, 239, 298–309. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Talesh, S.H.A.; Khodashenas, S.R.; Jamali, A. Analyzing bank profile shape of alluvial stable channels using robust optimization and evolutionary ANFIS methods. Appl. Water Sci. 2019, 9, 40. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zeynoddin, M.; Ebtehaj, I.; Gharabaghi, B.; Khodashenas, S.R. Reliable method of determining stable threshold channel shape using experimental and gene expression programming techniques. Neural Comput. Appl. 2019, 31, 5799–5817. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Samui, P.; Mohammadian, M.; Gharabaghi, B. Predicting stable alluvial channel profiles using emotional artificial neural networks. Appl. Soft Comput. 2019, 78, 420–437. [Google Scholar] [CrossRef]
- Deng, Z.Q.; Singh, V.P. Mechanism and conditions for change in channel pattern. J. Hydraul. Res. 1999, 37, 465–478. [Google Scholar] [CrossRef]
- Liang, J.H.; Ghidaoui, M.S.; Deng, J.Q.; Gray, W.G. A Boltzmann-based finite volume algorithm for surface water flows on cells of arbitrary shapes. J. Hydraul. Res. 2007, 45, 147–164. [Google Scholar] [CrossRef]
- Eskov, V.M.; Eskov, V.V.; Vochmina, Y.V.; Gorbunov, D.V.; Ilyashenko, L.K. Shannon entropy in the research on stationary regimes and the evolution of complexity. Mosc. Univ. Phys. Bull. 2017, 72, 309–317. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, D.; Yang, H.; Sivapalan, M. Unifying catchment water balance models for different time scales through the maximum entropy production principle. Water Resour. Res. 2016, 52, 7503–7512. [Google Scholar] [CrossRef]
- Chiu, C.L. Entropy and probability concepts in hydraulics. J. Hydraul. Eng. 1987, 113, 583–599. [Google Scholar] [CrossRef]
- Araujo, J.C.D.; Chaudhry, F.H. Experimental evaluation of 2-D entropy model for open-channel flow. J. Hydraul. Eng. 1998, 124, 1064–1067. [Google Scholar] [CrossRef]
- Bonakdari, H. Establishment of relationship between mean and maximum velocities in narrow sewers. J. Environ. Manag. 2012, 113, 474–480. [Google Scholar] [CrossRef]
- Bonakdari, H.; Sheikh, Z.; Tooshmalani, M. Comparison between Shannon and Tsallis entropies for prediction of shear stress distribution in open channels. Stoch. Environ. Res. Risk Assess. 2015, 29, 1–11. [Google Scholar] [CrossRef]
- Chiu, C.L.; Said, C.A.A. Maximum and mean velocities and entropy in open-channel flow. J. Hydraul. Eng. 1995, 121, 26–35. [Google Scholar] [CrossRef]
- Chiu, C.L.; Chen, Y.C. An efficient method of discharge estimation based on probability concept. J. Hydraul. Res. 2003, 41, 589–596. [Google Scholar] [CrossRef]
- Cui, H.; Singh, V.P. Application of minimum relative entropy theory for streamflow forecasting. Stoch. Environ. Res. Risk Assess. 2017, 31, 587–608. [Google Scholar] [CrossRef]
- Kazemian-Kale-Kale, A.; Bonakdari, H.; Gholami, A.; Khozani, Z.S.; Akhtari, A.A.; Gharabaghi, B. Uncertainty analysis of shear stress estimation in circular channels by Tsallis entropy. Phys. A Stat. Mech. Its Appl. 2018, 510, 558–576. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zaji, A.H.; Akhtari, A.A. Simulation of open channel bend characteristics using computational fluid dynamics and artificial neural networks. Eng. Appl. Comput. Fluid Mech. 2015, 9, 355–369. [Google Scholar] [CrossRef]
- Marini, G.; De Martino, G.; Fontana, N.; Fiorentino, M.; Singh, V.P. Entropy approach for 2D velocity distribution in open-channel flow. J. Hydraul. Res. 2011, 49, 784–790. [Google Scholar] [CrossRef]
- Moramarco, T.; Saltalippi, C.; Singh, P. Estimation of mean velocity in natural channels based on Chiu’s velocity distribution equation. J. Hydrol. Eng. 2004, 9, 42–50. [Google Scholar] [CrossRef]
- Singh, V.P.; Luo, H. Entropy theory for distribution of one-dimensional velocity in open channels. J. Hydrol. Eng. 2011, 16, 725–735. [Google Scholar] [CrossRef]
- Singh, V.P.; Cui, H. Suspended sediment concentration distribution using Tsallis entropy. Phys. A Stat. Mech. Its Appl. 2014, 414, 31–42. [Google Scholar] [CrossRef]
- Sterling, M.; Knight, D.W. An attempt at using the entropy approach to predict the transverse distribution of boundary shear stress in open channel flow. Stochastic Environ. Res. Risk Assess. 2002, 16, 127–142. [Google Scholar] [CrossRef]
- Choo, Y.M.; Yun, G.S.; Choo, T.H.; Kwon, Y.B.; Sim, S.Y. Study of shear stress in laminar pipe flow using entropy concept. Environ. Earth Sci. 2017, 76, 616. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Mohammadian, M. Enhanced formulation of the probability principle based on maximum entropy to design the bank profile of channels in geomorphic threshold. Stoch. Environ. Res. Risk Assess. 2019, 33, 1013–1034. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Mohammadian, A. A method based on the Tsallis entropy for characterizing threshold channel bank profiles. Phys. A Stat. Mech. Its Appl. 2019, 526, 121089. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics I. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Barbe, D.E.; Cruise, J.F.; Singh, V.P. Solution of three constraint entropy-based velocity distribution. J. Hydraul. Eng. 1991, 117, 1389–1396. [Google Scholar] [CrossRef]
- Cao, S.; Chang, H.H. Entropy as a probability concept in energy-gradient distribution. In Proceedings of the National Conference Hydraulic Engineering, Colorado Springs, CO, USA, 8–12 August 1988; ASCE: New York, NY, USA, 1988; pp. 1013–1018. [Google Scholar]
- Pipes, L.A. Applied Mathematics for Engineering and Physicists; McGraw-Hill: London, UK, 1970. [Google Scholar]
- Van Burkalow, A. Angle of repose and angle of sliding friction: An experimental study. Geol. Soc. Am. Bull. 1945, 56, 669–707. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Sattar, A.; Bonakdari, H.; Zaji, A.H. Prediction of scour depth around bridge piers using self-adaptive extreme learning machine. J. Hydroinform. 2017, 19, 207–224. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zaji, A.H.; Akhtari, A.A.; Khodashenas, S.R. Predicting the Velocity Field in a 90° Open Channel Bend Using a Gene Expression Programming Model. Flow Meas. Instrum. 2015, 46, 189–192. [Google Scholar] [CrossRef]
- Mikhailova, N.A.; Shevchenko, O.B.; Selyametov, M.M. Laboratory of Investigation of the formation of stable channels. Hydro Tech. Constr. 1980, 14, 714–722. [Google Scholar] [CrossRef]
- Macky, G.H. Large flume experiments on the stable straight gravel bed channel. Water Resour. Res. 1999, 35, 2601–2603. [Google Scholar] [CrossRef]
- Hassanzadeh, Y.; Majdzadeh, T.M.R.; Imanshoar, F.; Jafari, A. Validation of river bank profiles in sand-bed rivers. J. Civ. Environ. Eng. 2014, 43, 59–68. [Google Scholar]
- Khodashenas, S.R. Threshold gravel channels bank profile: A comparison among 13 models. Int. J. River Basin Manag. 2016, 14, 337–344. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zaji, A.H.; Michelson, D.G.; Akhtari, A.A. Improving the performance of multi-layer perceptron and radial basis function models with a decision tree model to predict flow variables in a sharp 90 bend. Appl. Soft Comput. 2016, 48, 563–583. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Akhtari, A.A. Developing finite volume method (FVM) in numerical simulation of flow pattern in 60 open channel bend. J. Appl. Res. Water Wastewater 2016, 3, 193–200. [Google Scholar]
- Gholami, A.; Bonakdari, H.; Ebtehaj, I.; Akhtari, A.A. Design of an adaptive neuro-fuzzy computing technique for predicting flow variables in a 90° sharp bend. J. Hydroinform. 2017, 19, 572–585. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zaji, A.H.; Fenjan, S.A.; Akhtari, A.A. New radial basis function network method based on decision trees to predict flow variables in a curved channel. Neural Comput. Appl. 2018, 30, 2771–2785. [Google Scholar] [CrossRef]
- Harman, C.; Stewardson, M.; DeRose, R. Variability and uncertainty in reach bankfull hydraulic geometry. J. Hydrol. 2008, 351, 13–25. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H. No-deposition sediment transport in sewers using of gene expression programming. Soft Comput. Civ. Eng. 2017, 1, 29–53. [Google Scholar]
- Newcombe, R.G. Two-sided confidence intervals for the single proportion: Comparison of seven methods. Stat. Med. 1998, 17, 857–872. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zaji, A.H.; Akhtari, A.A. A comparison of artificial intelligence-based classification techniques in predicting flow variables in sharp curved channels. Eng. Comput. 2020, 36, 295–324. [Google Scholar] [CrossRef]
- Gholami, A.; Bonakdari, H.; Zaji, A.H.; Akhtari, A.A. An efficient classified radial basis neural network for prediction of flow variables in sharp open-channel bends. Appl. Water Sci. 2019, 9, 145. [Google Scholar] [CrossRef]
- Gholami, A.; Akhtari, A.A.; Minatour, Y.; Bonakdari, H.; Javadi, A.A. Experimental and numerical study on velocity fields and water surface profile in a strongly-curved 90 open channel bend. Eng. Appl. Comput. Fluid Mech. 2014, 8, 447–461. [Google Scholar] [CrossRef]
- Berry, G.; Armitage, P. Mid-P confidence intervals: A brief review. J. R. Stat. Soc. Ser. D (Stat.) 1995, 44, 417–423. [Google Scholar] [CrossRef]
- Cox, D.R.; Hinkley, D.V. Theoretical Statistics; Chapman and Hall: London, UK, 1974. [Google Scholar]
| a0 | a1 | a2 | a3 | δ*cr |
|---|---|---|---|---|
| μ = 0.4 | ||||
| 1.0001 | −0.0135 | −0.0411 | 0 | 0.93 |
| 1.0004 | −0.0236 | −0.0412 | 0 | 0.935 |
| 1.0008 | −0.0307 | −0.0412 | 0 | 0.94 |
| 1.0009 | −0.0342 | −0.0413 | 0 | 0.945 |
| μ = 0.55 | ||||
| 1.0003 | −0.018 | −0.0503 | −0.0029 | 0.9 |
| 1.0006 | −0.0299 | −0.0527 | −0.0027 | 0.905 |
| 1.0008 | −0.0366 | −0.0547 | −0.0025 | 0.91 |
| 1.001 | −0.0416 | −0.0565 | −0.0022 | 0.915 |
| 1.0011 | −0.0463 | −0.0586 | −0.0019 | 0.921 |
| μ= 0.65 | ||||
| 1.0006 | −0.0278 | −0.0543 | −0.006 | 0.885 |
| 1.001 | −0.0444 | −0.06 | −0.0054 | 0.895 |
| 1.0013 | −0.0529 | −0.0647 | −0.0048 | 0.905 |
| 1.0041 | −0.0556 | −0.0665 | −0.0045 | 0.909 |
| μ= 0.76 | ||||
| 1.0009 | −0.0365 | −0.0544 | −0.0105 | 0.87 |
| 1.0014 | −0.0531 | -0.061 | −0.0101 | 0.88 |
| 1.0017 | −0.0621 | −0.0662 | −0.0095 | 0.89 |
| 1.0018 | −0.0662 | −0.0701 | −0.009 | 0.897 |
| μ= 0.84 | ||||
| 1.0011 | −0.0418 | −0.0516 | −0.0146 | 0.86 |
| 1.0016 | −0.0594 | −0.059 | −0.0143 | 0.87 |
| 1.002 | −0.0697 | −0.0634 | −0.0141 | 0.88 |
| 1.0021 | −0.0742 | −0.0708 | −0.013 | 0.89 |
| μ= 1.0 | ||||
| 1.0016 | −0.0571 | −0.0466 | −0.0233 | 0.845 |
| 1.0022 | −0.0738 | −0.0531 | −0.0237 | 0.855 |
| 1.0025 | −0.0828 | −0.0589 | −0.0236 | 0.865 |
| 1.0028 | −0.0884 | −0.0656 | −0.023 | 0.875 |
| 1.0028 | −0.0892 | −0.0683 | −0.0226 | 0.878 |
| Researchers | Runs. No. | No. of Series | d50 [mm] | Discharge (Q) [L/s] | Water Surface Half-Width (B/2) [cm] | Central Water Depth (hc) [cm] |
|---|---|---|---|---|---|---|
| Mikhailova et al. [65] | 2 | S1 | 0.2 | 65 | 112 | 10.4 |
| S2 | 0.2 | 69 | 132.5 | 14.4 | ||
| Ikeda [20] | 1 | S3 | 1.3 | 16.28 | 24.8 | 3.54 |
| Diplas [21] | 1 | S4 | 1.9 | 12.526 | 33 | 3.85 |
| Babaeyan [7] | 1 | S5 | 1 | 2.5 | 52.6 | 2.63 |
| Macky [66] (Field data) | 1 | S6 | 3.42 | 64.3 | 127 | 3.7 |
| Hassanzadeh et al. [67] | 2 | S7 | 1.2 | 11.09 | 32 | 8.6 |
| S8 | 1.6 | 20.07 | 40.6 | 10.9 | ||
| Khodashenas [68] | 4 | S9 | 0.53 | 6.2 | 21.7 | 8 |
| S10 | 0.53 | 2.57 | 16 | 6.3 | ||
| S11 | 0.53 | 2.18 | 17 | 6.12 | ||
| S12 | 0.53 | 1.157 | 9.5 | 3.7 |
| MARE | RMSE | Bias | R2 | λ | |||||
|---|---|---|---|---|---|---|---|---|---|
| Data Series | DEM | CKM | DEM | CKM | DEM | CKM | DEM | CKM | DEM |
| S1 | 0.254 | 1.95 | 0.103 | 1.31 | −0.04 | 0.99 | 0.93 | 0.981 | −5.56 |
| S2 | 0.86 | 3.95 | 0.057 | 0.7 | −0.036 | 0.47 | 0.98 | 0.988 | −4.26 |
| S3 | 0.228 | 0.47 | 0.037 | 0.141 | 0.022 | 0.116 | 0.99 | 0.981 | −1.62 |
| S4 | 0.15 | 0.11 | 0.053 | 0.08 | −0.05 | 0.064 | 0.99 | 0.997 | −1.75 |
| S5 | 0.43 | 0.42 | 0.1 | 0.135 | −0.08 | 0.114 | 0.99 | 0.988 | 2.11 |
| S6 | 0.58 | 1.03 | 0.38 | 0.5 | −0.31 | 0.45 | 0.96 | 0.957 | 1.5 |
| S7 | 0.147 | 0.86 | 0.056 | 0.37 | 0.045 | 0.35 | 0.98 | 0.966 | −2.46 |
| S8 | 0.315 | 0.99 | 0.109 | 0.34 | 0.098 | 0.32 | 0.97 | 0.95 | −2.2 |
| S9 | 0.26 | 0.50 | 0.044 | 0.184 | 0.008 | −0.148 | 0.98 | 0.989 | 1.72 |
| S10 | 0.18 | 0.56 | 0.028 | 0.24 | −0.01 | −0.192 | 0.99 | 0.987 | 2.2 |
| S11 | 0.23 | 0.46 | 0.05 | 0.14 | 0.03 | −0.108 | 0.99 | 0.996 | 1.4 |
| S12 | 0.17 | 0.47 | 0.05 | 0.22 | 0.03 | −0.16 | 0.985 | 0.996 | 2.4 |
| Averaged | 0.317 | 0.981 | 0.08 | 0.363 | −0.02 | 0.189 | 0.978 | 0.981 | - |
| Dataset | R2 | MARE | RMSE | MAE | Bias |
|---|---|---|---|---|---|
| Ikeda [20] (S3) | 0.995 | 0.357 | 0.098 | 0.078 | 0.064 |
| Diplas [21] (S4) | 0.991 | 0.186 | 0.132 | 0.097 | 0.094 |
| Babaeyan [7] (One set) (S5) | 0.961 | 0.400 | 0.124 | 0.095 | −0.095 |
| Macky [66] (S6) | 0.942 | 0.568 | 0.556 | 0.381 | 0.380 |
| Hassanzadeh et al. [67] (S7) | 0.986 | 1.164 | 0.456 | 0.436 | 0.436 |
| Hassanzadeh et al. [67] (S8) | 0.981 | 1.146 | 0.380 | 0.364 | 0.364 |
| Khodashenas [68] (S9) | 0.992 | 0.426 | 0.127 | 0.109 | −0.109 |
| Khodashenas [68] (S10) | 0.979 | 0.473 | 0.169 | 0.143 | −0.143 |
| Khodashenas [68] (S11) | 0.994 | 0.361 | 0.096 | 0.076 | −0.076 |
| Khodashenas [68] (S12) | 0.995 | 0.475 | 0.193 | 0.147 | −0.147 |
| Average | 0.9816 | 0.5556 | 0.2331 | 0.1926 | 0.0768 |
| Model | Datasets | Sample Number | MPE | WUB | CB | ||
|---|---|---|---|---|---|---|---|
| EDMTC | Ikeda [20] (S3) | 8 | 0.08 | −0.064 | ±0.07 | 0.065 | −0.13 to 0.00 |
| Diplas [21] (S4) | 25 | 0.09 | −0.094 | ±0.04 | 0.09 | −0.13 to −0.05 | |
| Babaeyan [7] (S5) | 8 | 0.08 | 0.095 | ±0.075 | 0.095 | +0.02 to +0.17 | |
| Khodashenas [68] (S9) | 44 | 0.07 | 0.109 | ±0.02 | 0.11 | +0.09 to +0.13 | |
| Khodashenas [68] (S10) | 33 | 0.09 | 0.143 | ±0.035 | 0.145 | +0.11 to +0.18 | |
| Khodashenas [68] (S12) | 20 | 0.13 | 0.147 | ±0.06 | 0.15 | +0.09 to +0.21 | |
| All datasets | 266 | 0.33 | −0.14 | ±0.04 | 0.14 | −0.18 to −0.10 | |
| GEP, Equation (12) | All datasets | 20 | 0.02 | -0.009 | ±0.01 | ±0.01 | −0.02 to 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonakdari, H.; Gholami, A.; Mosavi, A.; Kazemian-Kale-Kale, A.; Ebtehaj, I.; Azimi, A.H. A Novel Comprehensive Evaluation Method for Estimating the Bank Profile Shape and Dimensions of Stable Channels Using the Maximum Entropy Principle. Entropy 2020, 22, 1218. https://doi.org/10.3390/e22111218
Bonakdari H, Gholami A, Mosavi A, Kazemian-Kale-Kale A, Ebtehaj I, Azimi AH. A Novel Comprehensive Evaluation Method for Estimating the Bank Profile Shape and Dimensions of Stable Channels Using the Maximum Entropy Principle. Entropy. 2020; 22(11):1218. https://doi.org/10.3390/e22111218
Chicago/Turabian StyleBonakdari, Hossein, Azadeh Gholami, Amir Mosavi, Amin Kazemian-Kale-Kale, Isa Ebtehaj, and Amir Hossein Azimi. 2020. "A Novel Comprehensive Evaluation Method for Estimating the Bank Profile Shape and Dimensions of Stable Channels Using the Maximum Entropy Principle" Entropy 22, no. 11: 1218. https://doi.org/10.3390/e22111218
APA StyleBonakdari, H., Gholami, A., Mosavi, A., Kazemian-Kale-Kale, A., Ebtehaj, I., & Azimi, A. H. (2020). A Novel Comprehensive Evaluation Method for Estimating the Bank Profile Shape and Dimensions of Stable Channels Using the Maximum Entropy Principle. Entropy, 22(11), 1218. https://doi.org/10.3390/e22111218









