Time Series Complexities and Their Relationship to Forecasting Performance
Abstract
1. Introduction
2. Materials
2.1. Synthetic Time Series
2.1.1. Sine Waves TS
2.1.2. Logistic Map TS
2.1.3. GRATIS TS
2.2. M4 Competition TS
3. Methods
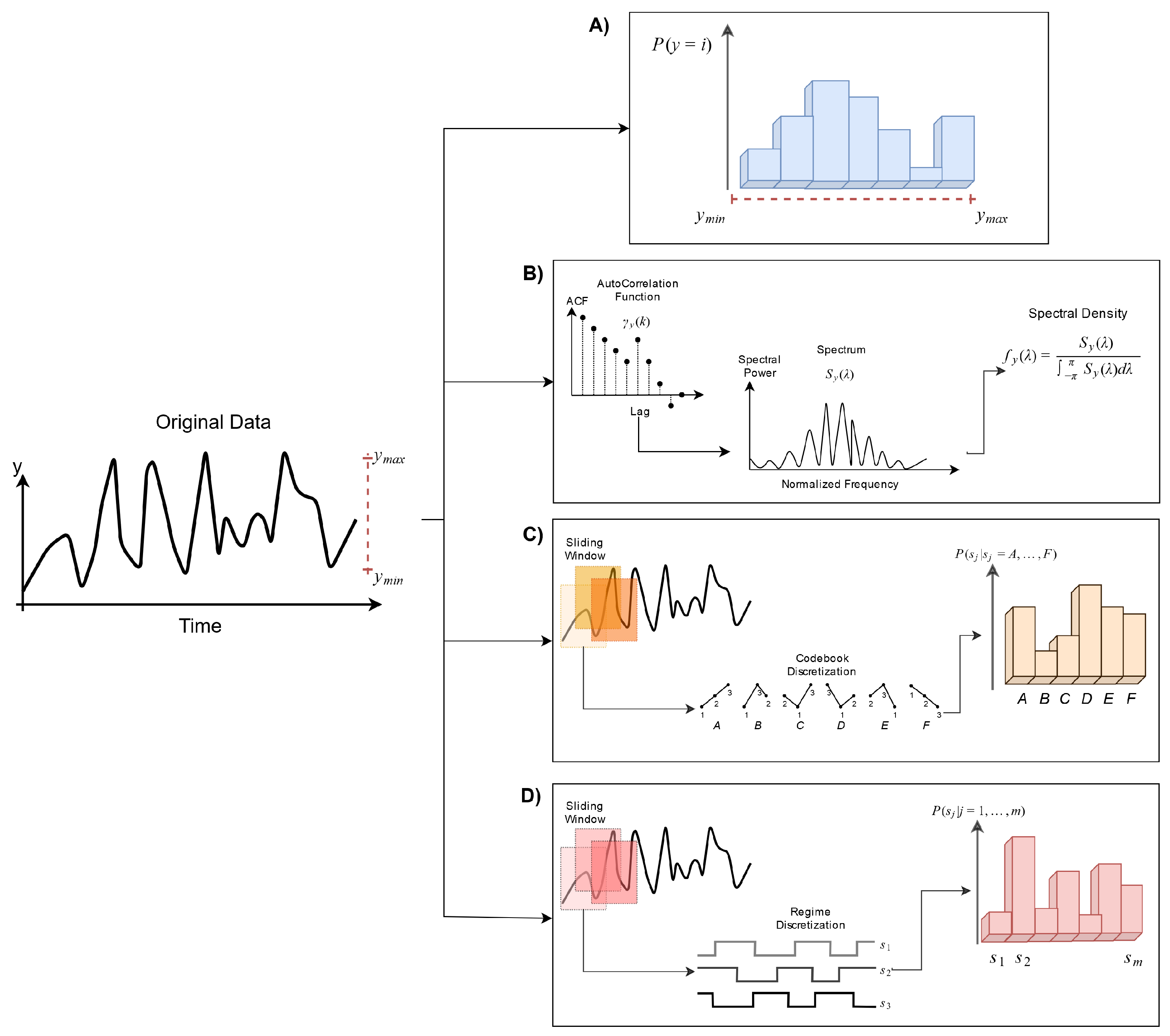
3.1. A Background on Entropies
3.1.1. Spectral Entropy
3.1.2. Permutation Entropy
3.1.3. 2-Regimes Entropy
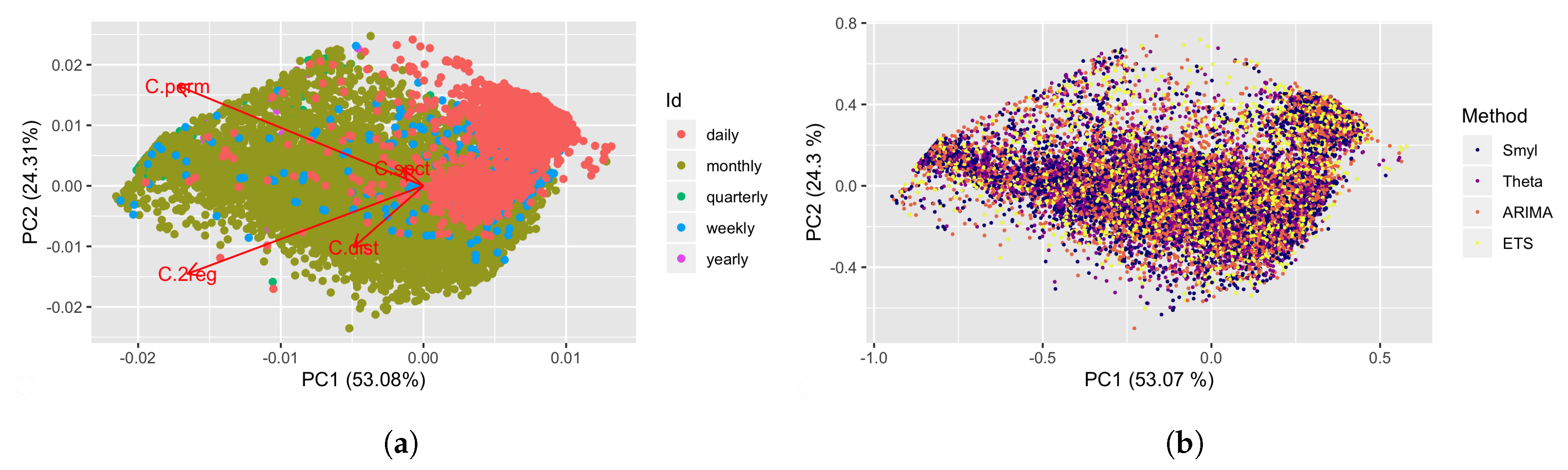
3.2. ESC and the Complexity Feature Space
3.3. Forecasting Methods: Smyl, Theta, ARIMA and ETS
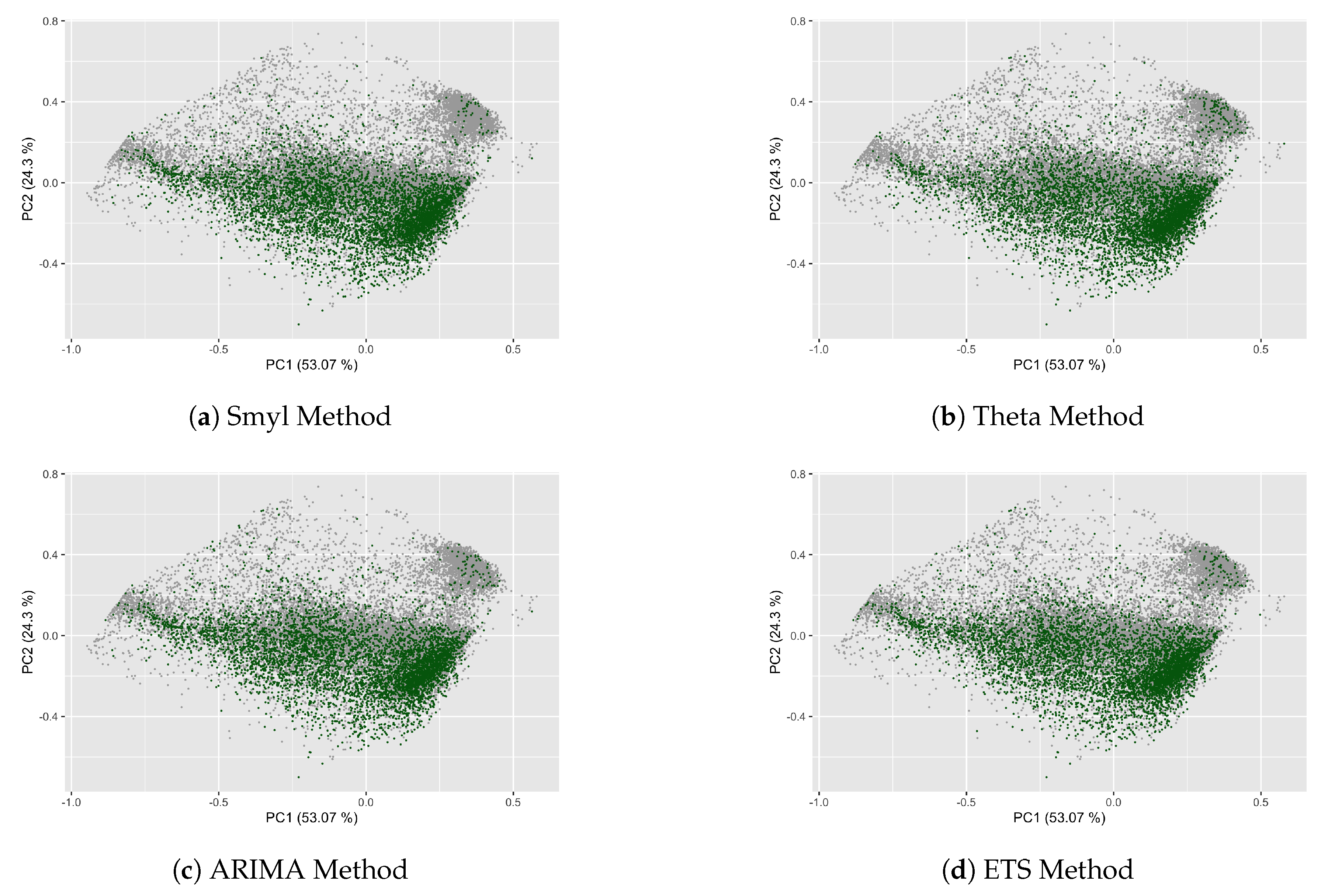
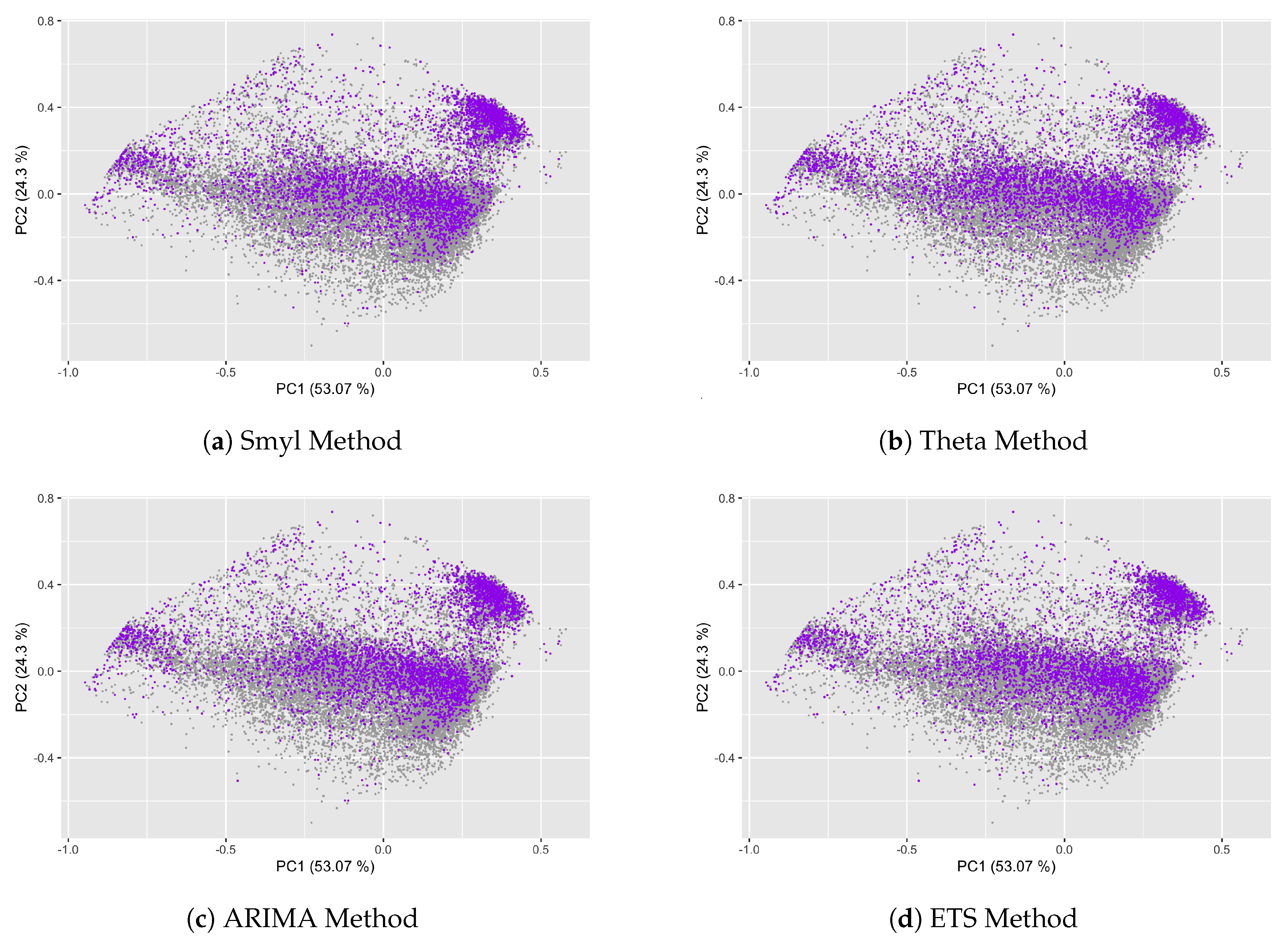
- Smyl: This is a hybrid method that combines exponential smoothing (ES) with recurrent neural network (RNN); this method is called ES-RNN [9] and is the winning method for M4 Competition.
- Theta: was one of winning methods on M3, the previous competition, and in the past was indicated to be a variant of the classical exponential smoothing method [10].
- ARIMA (Autoregressive Integrated Moving Average): It is one of the most widely used by the Box & Jenkings methodology [41], mainly applied for nonlinear patterns in TS.
- ETS (exponential smoothing state space [13]): This method is especially used in forecasting for TS that presents trends and seasonality.
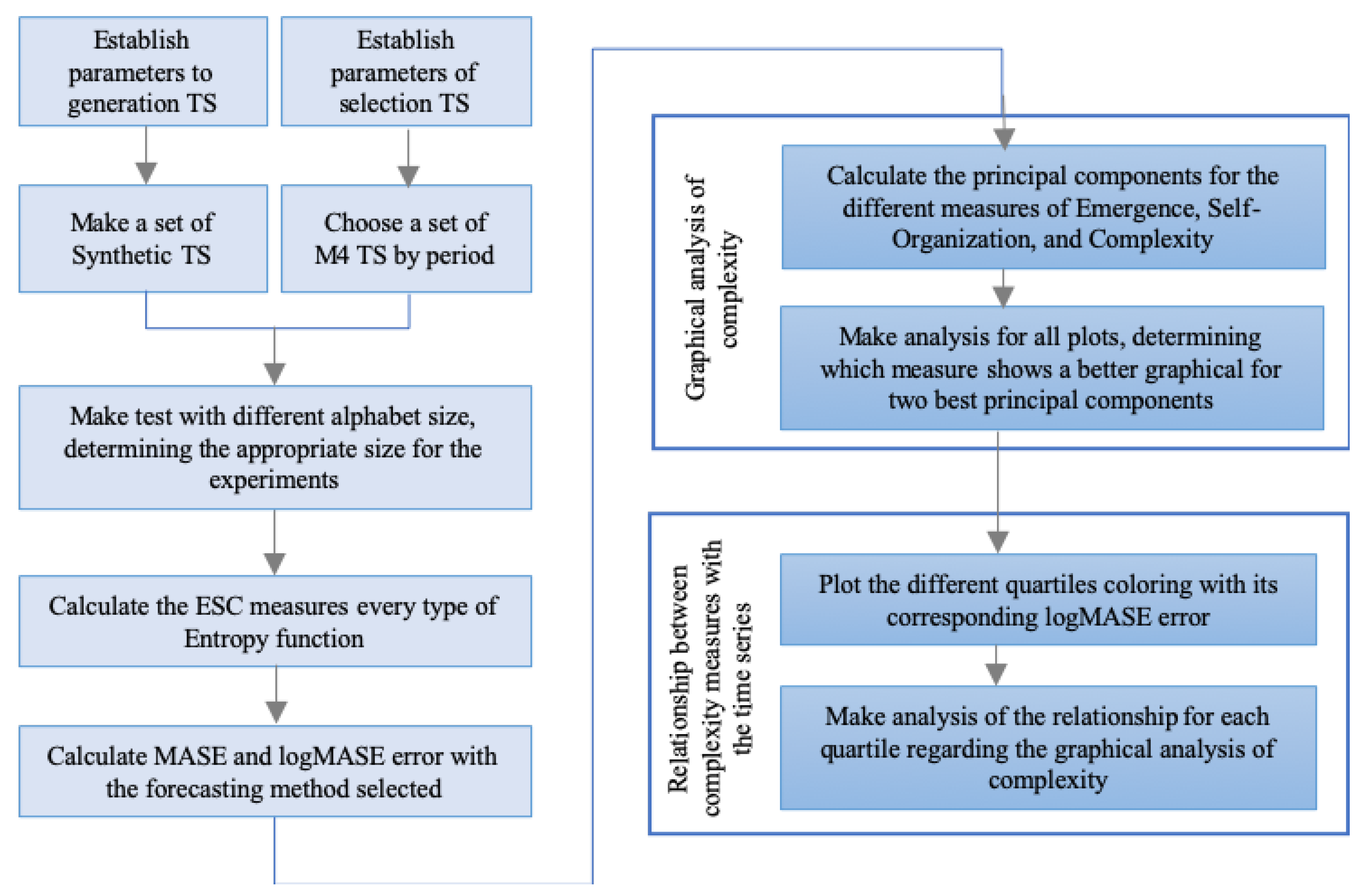
3.4. Analyzing the Forecasting Performance in the CFS
Parameters Settings
4. Results
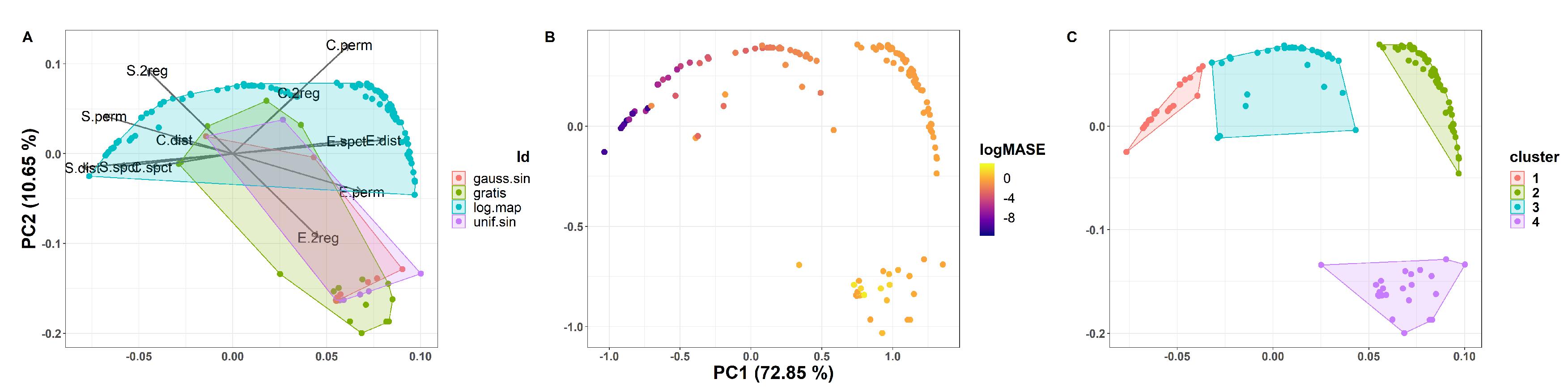
4.1. Complexities and Forecastability of the Synthetic TS
4.1.1. The Logistic Map
4.1.2. The CFS of All Synthetic Data
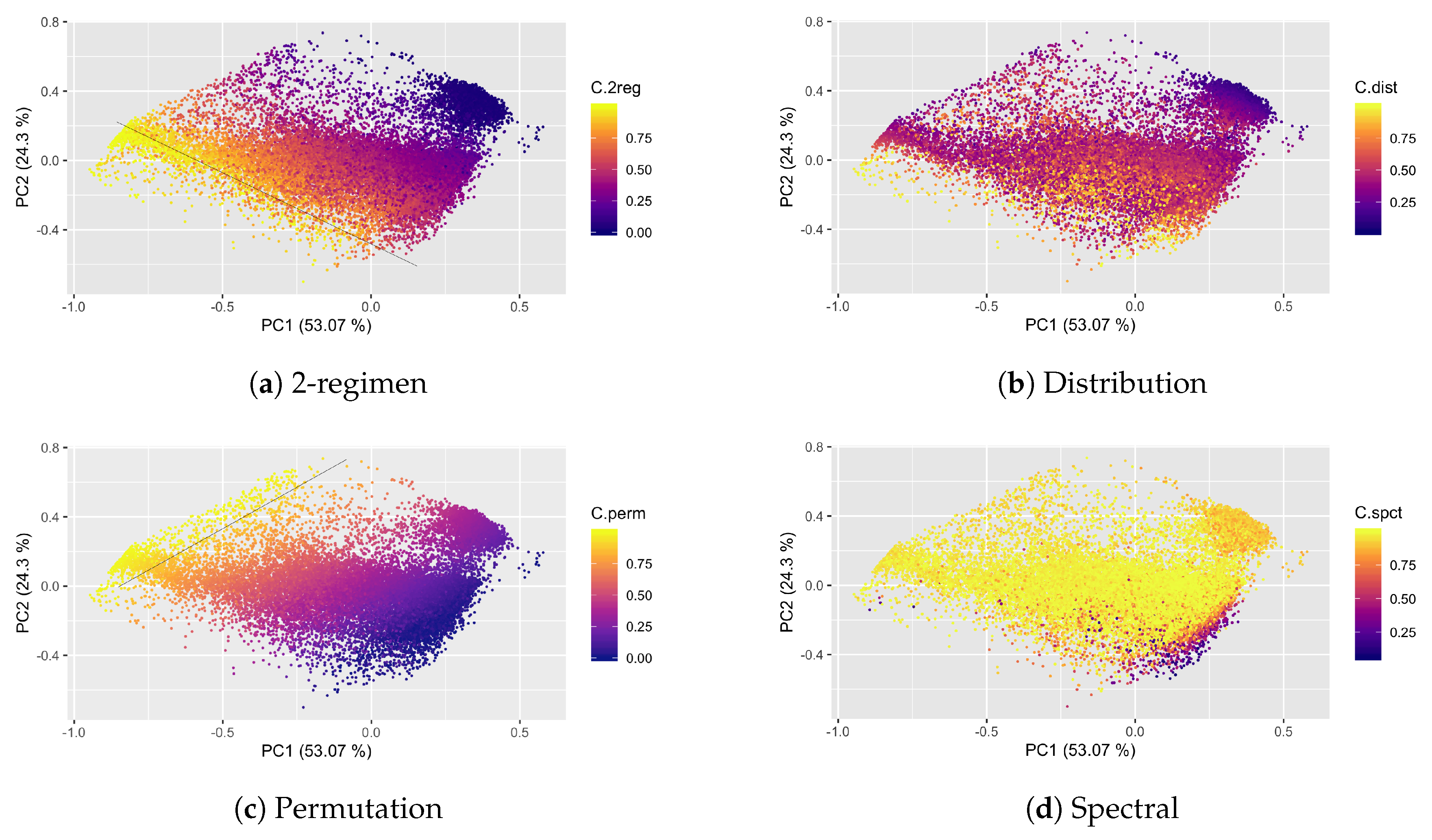
4.2. Complexities and Forecastability of the M4 Competition TS
4.3. Regression Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Chichester, UK, 2008; p. 469. [Google Scholar]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. Predicting/hypothesizing the findings of the M4 Competition. Int. J. Forecast. 2019, 36, 29–36. [Google Scholar] [CrossRef]
- Wang, X.; Smith, K.; Hyndman, R. Characteristic-based clustering for time series data. Data Min. Knowl. Discov. 2006, 13, 335–364. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W.; Blahut, R.E. The mathematical theory of communication. Urbana Univ. Ill. Press 1949, 117, 379–423. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Jauregui, M.; Zunino, L.; Lenzi, E.K. Characterizing time series via complexity-entropy curves. Phys. Rev. E 2017, 95. [Google Scholar] [CrossRef] [PubMed]
- Mortoza, L.P.; Piqueira, J.R. Measuring complexity in Brazilian economic crises. PLoS ONE 2017, 12, e0173280. [Google Scholar] [CrossRef] [PubMed]
- Mikhailovsky, G.E.; Levich, A.P. Entropy, information and complexity or which aims the arrow of time? Entropy 2015, 17, 4863–4890. [Google Scholar] [CrossRef]
- Santamaría-bonfil, G. A Package for Measuring emergence, Self-organization, and Complexity Based on Shannon entropy. Front. Robot. AI 2017, 4, 10. [Google Scholar] [CrossRef]
- Smyl, S. A hybrid method of exponential smoothing and recurrent neural networks for time series forecasting. Int. J. Forecast. 2020, 36, 75–85. [Google Scholar] [CrossRef]
- Assimakopoulos, V.; Nikolopoulos, K. The theta model: A decomposition approach to forecasting. Int. J. Forecast. 2000, 16, 521–530. [Google Scholar] [CrossRef]
- Brockwell, P.; Davis, R. Introduction to Time Series and Forecasting; Springer: Berlin/Heidelberger, Germany, 2002; p. 437. [Google Scholar]
- De Gooijer, J.G.; Hyndman, R.J.; Gooijer, J.G.D.; Hyndman, R.J. 25 Years of Time Series Forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B.; Snyder, R.D.; Grose, S. A state space framework for automatic forecasting using exponential smoothing methods. Int. J. Forecast. 2002, 18, 439–454. [Google Scholar] [CrossRef]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: 100,000 time series and 61 forecasting methods. Int. J. Forecast. 2020, 36, 54–74. [Google Scholar] [CrossRef]
- Kang, Y.; Hyndman, R.J.; Li, F. GRATIS: GeneRAting TIme Series with diverse and controllable characteristics. arXiv 2019, arXiv:stat.ML/1903.02787. [Google Scholar]
- Makridakis, S.; Spiliotis, E.; Assimakopoulos, V. The M4 Competition: Results, findings, conclusion and way forward The M4 Competition: Results, findings, conclusion and way forward. Int. J. Forecast. 2018, 34. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Kang, Y.; Hyndman, R.J.; Smith-Miles, K. Visualising forecasting algorithm performance using time series instance spaces. Int. J. Forecast. 2017, 33, 345–358. [Google Scholar] [CrossRef]
- Brida, J.G.; Punzo, L.F. Symbolic time series analysis and dynamic regimes. Struct. Chang. Econ. Dyn. 2003, 14, 159–183. [Google Scholar] [CrossRef]
- Amigó, J.M.; Keller, K.; Unakafova, V.A. Ordinal symbolic analysis and its application to biomedical recordings. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373. [Google Scholar] [CrossRef]
- Pennekamp, F.; Iles, A.C.; Garland, J.; Brennan, G.; Brose, U.; Gaedke, U.; Jacob, U.; Kratina, P.; Matthews, B.; Munch, S.; et al. The intrinsic predictability of ecological time series and its potential to guide forecasting. Ecol. Monogr. 2019, 89. [Google Scholar] [CrossRef]
- Verdú, S. Empirical Estimation of Information Measures: A Literature Guide. Entropy 2019, 21, 720. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Goerg, G. Forecastable Component Analysis. In Proceedings of the 30th International Conference on Machine Learning (ICML-13), Atlanta, GA, USA, 16–21 June 2013; Volume 28, pp. 64–72. [Google Scholar]
- Zenil, H.; Kiani, N.A.; Tegnér, J. Low-algorithmic-complexity entropy-deceiving graphs. Phys. Rev. E 2017, 96, 012308. [Google Scholar] [CrossRef] [PubMed]
- Balzter, H.; Tate, N.J.; Kaduk, J.; Harper, D.; Page, S.; Morrison, R.; Muskulus, M.; Jones, P. Multi-scale entropy analysis as a method for time-series analysis of climate data. Climate 2015, 3, 227–240. [Google Scholar] [CrossRef]
- Haken, H.; Portugali, J. Information and Self-Organization. Entropy 2017, 19, 18. [Google Scholar] [CrossRef]
- Riedl, M.; Müller, A.; Wessel, N. Practical considerations of permutation entropy: A tutorial review. Eur. Phys. J. Spec. Top. 2013, 222, 249–262. [Google Scholar] [CrossRef]
- Gershenson, C.; Fernández, N. Complexity and information: Measuring emergence, self-organization, and homeostasis at multiple scales. Complexity 2012, 18, 29–44. [Google Scholar] [CrossRef]
- Atmanspacher, H. On macrostates in complex multi-scale systems. Entropy 2016, 18, 426. [Google Scholar] [CrossRef]
- Zunino, L.; Olivares, F.; Bariviera, A.F.; Rosso, O.A. A simple and fast representation space for classifying complex time series. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2017, 381, 1021–1028. [Google Scholar] [CrossRef]
- López-Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321–326. [Google Scholar] [CrossRef]
- Piryatinska, A.; Darkhovsky, B.; Kaplan, A. Binary classification of multichannel-EEG records based on the ϵ-complexity of continuous vector functions. Comput. Methods Programs Biomed. 2017, 152, 131–139. [Google Scholar] [CrossRef]
- Amigó, J.M. The equality of Kolmogorov-Sinai entropy and metric permutation entropy generalized. Phys. D Nonlinear Phenom. 2012, 241, 789–793. [Google Scholar] [CrossRef]
- Brandmaier, A.M. pdc: An R Package for Complexity-Based Clustering of Time Series. J. Stat. Softw. 2015, 67, 1–23. [Google Scholar] [CrossRef]
- Alcaraz, R. Symbolic entropy analysis and its applications. Entropy 2018, 20, 568. [Google Scholar] [CrossRef]
- Lizier, J.T. JIDT: An Information-Theoretic Toolkit for Studying the Dynamics of Complex Systems. Front. Robot. AI 2014. [Google Scholar] [CrossRef]
- Fernández, N.; Aguilar, J.; Piña-García, C.; Gershenson, C. Complexity of lakes in a latitudinal gradient. Ecol. Complex. 2017, 31, 1–20. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis Forecasting and Control; John Wiley & Sons: Chichester, UK, 2015. [Google Scholar]
- Contreras-Reyes, J.E.; Canales, T.M.; Rojas, P.M. Influence of climate variability on anchovy reproductive timing off northern Chile. J. Mar. Syst. 2016, 164, 67–75. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. B (Methodol.) 1964. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic time series forecasting: The forecast package for R. J. Stat. Softw. 2008. [Google Scholar] [CrossRef]
- Cao, L. Practical method for determining the minimum embedding dimension of a scalar time series. Phys. D Nonlinear Phenom. 1997, 110, 43–50. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]

| Selected Series | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Frequency | Demographic | Finance | Industry | Macro | Micro | Other | Total | Size | % |
| Yearly | 1088 | 6519 | 3716 | 3903 | 6538 | 1236 | 23,000 | 56 | 0.24% |
| Quarterly | 1858 | 5305 | 4637 | 5315 | 6020 | 865 | 24,000 | 256 | 1.07% |
| Monthly | 5728 | 10,987 | 10,017 | 10,016 | 10,975 | 277 | 48,000 | 18,406 | 38.35% |
| Weekly | 24 | 164 | 6 | 41 | 112 | 12 | 359 | 293 | 81.62% |
| Daily | 10 | 1559 | 422 | 127 | 1476 | 633 | 4227 | 3599 | 85.14% |
| Hourly | 0 | 0 | 0 | 0 | 0 | 414 | 414 | 0 | 0.00% |
| Total | 8708 | 24,534 | 18,798 | 19,402 | 25,121 | 3437 | 100,000 | 22,610 | 22.61% |
| 49 | 52 | 53 | 61 | 71 | 67 | 72 | 52 | 48 | … | 54 |
| – | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | … | 1 |
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| C.2reg | −0.6768 | −0.5947 | 0.4336 | 0.0142 |
| C.dist | −0.2003 | −0.4150 | −0.8776 | −0.1323 |
| C.perm | −0.7057 | 0.6777 | −0.1757 | 0.1086 |
| C.spct | −0.0607 | 0.1219 | 0.1047 | −0.9851 |
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| Standard deviation | 0.2923 | 0.1978 | 0.1592 | 0.1052 |
| Proportion of Variance | 0.5308 | 0.2431 | 0.1574 | 0.0687 |
| Cumulative Proportion | 0.5308 | 0.7739 | 0.9313 | 1.0000 |
| Yearly | Quarterly | Monthly | Weekly | Daily | |
|---|---|---|---|---|---|
| MSE | 115.0187 | 6.8431 | 21.1561 | 4.3047 | 56.2699 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ponce-Flores, M.; Frausto-Solís, J.; Santamaría-Bonfil, G.; Pérez-Ortega, J.; González-Barbosa, J.J. Time Series Complexities and Their Relationship to Forecasting Performance. Entropy 2020, 22, 89. https://doi.org/10.3390/e22010089
Ponce-Flores M, Frausto-Solís J, Santamaría-Bonfil G, Pérez-Ortega J, González-Barbosa JJ. Time Series Complexities and Their Relationship to Forecasting Performance. Entropy. 2020; 22(1):89. https://doi.org/10.3390/e22010089
Chicago/Turabian StylePonce-Flores, Mirna, Juan Frausto-Solís, Guillermo Santamaría-Bonfil, Joaquín Pérez-Ortega, and Juan J. González-Barbosa. 2020. "Time Series Complexities and Their Relationship to Forecasting Performance" Entropy 22, no. 1: 89. https://doi.org/10.3390/e22010089
APA StylePonce-Flores, M., Frausto-Solís, J., Santamaría-Bonfil, G., Pérez-Ortega, J., & González-Barbosa, J. J. (2020). Time Series Complexities and Their Relationship to Forecasting Performance. Entropy, 22(1), 89. https://doi.org/10.3390/e22010089







