Quantifying the Variability in Resting-State Networks
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methodology
3. Results
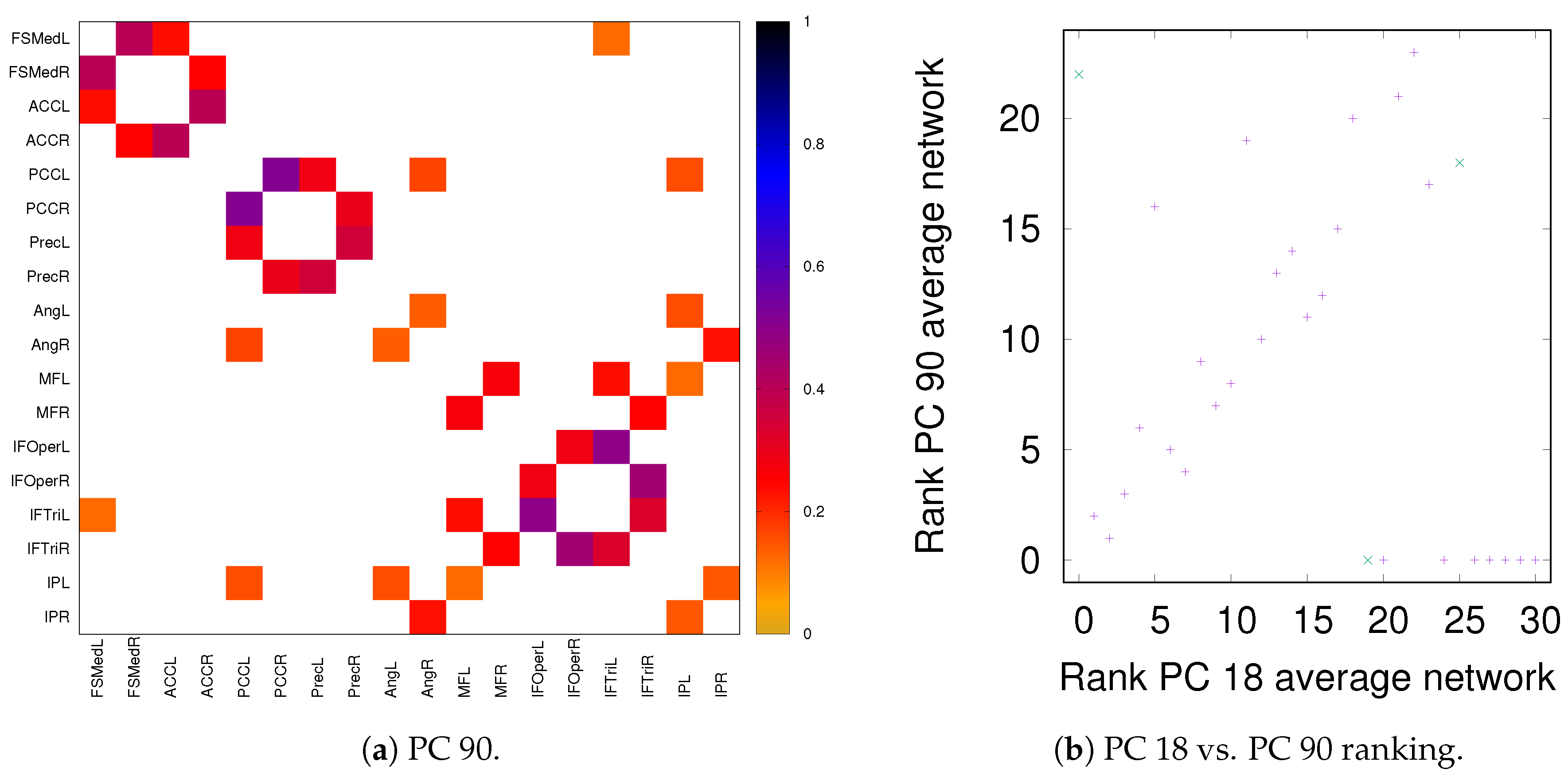
3.1. Robustness in the Inferred Rank Order: Existence of a Well-Defined Backbone
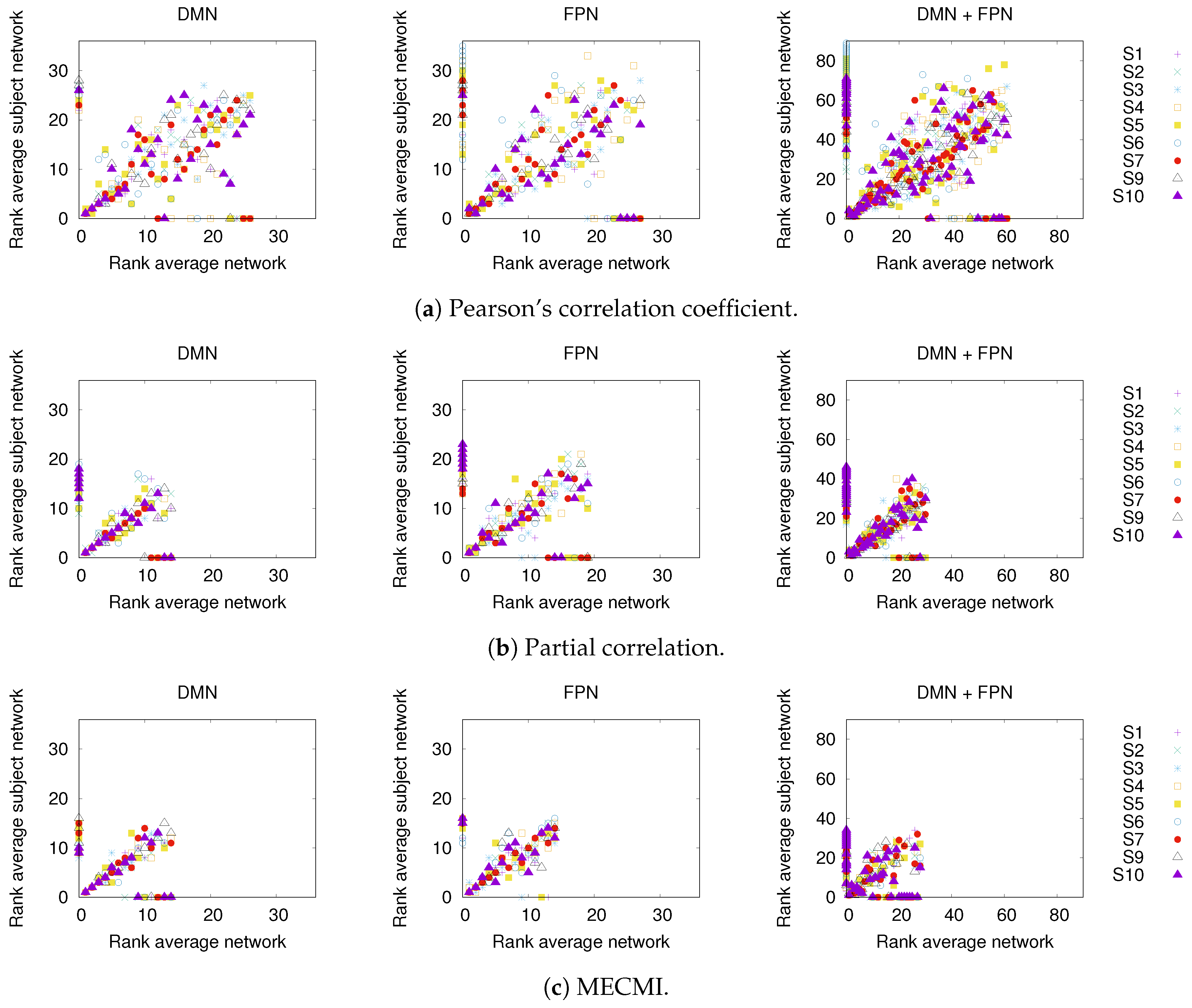
3.1.1. Group Average vs. Individual Subjects
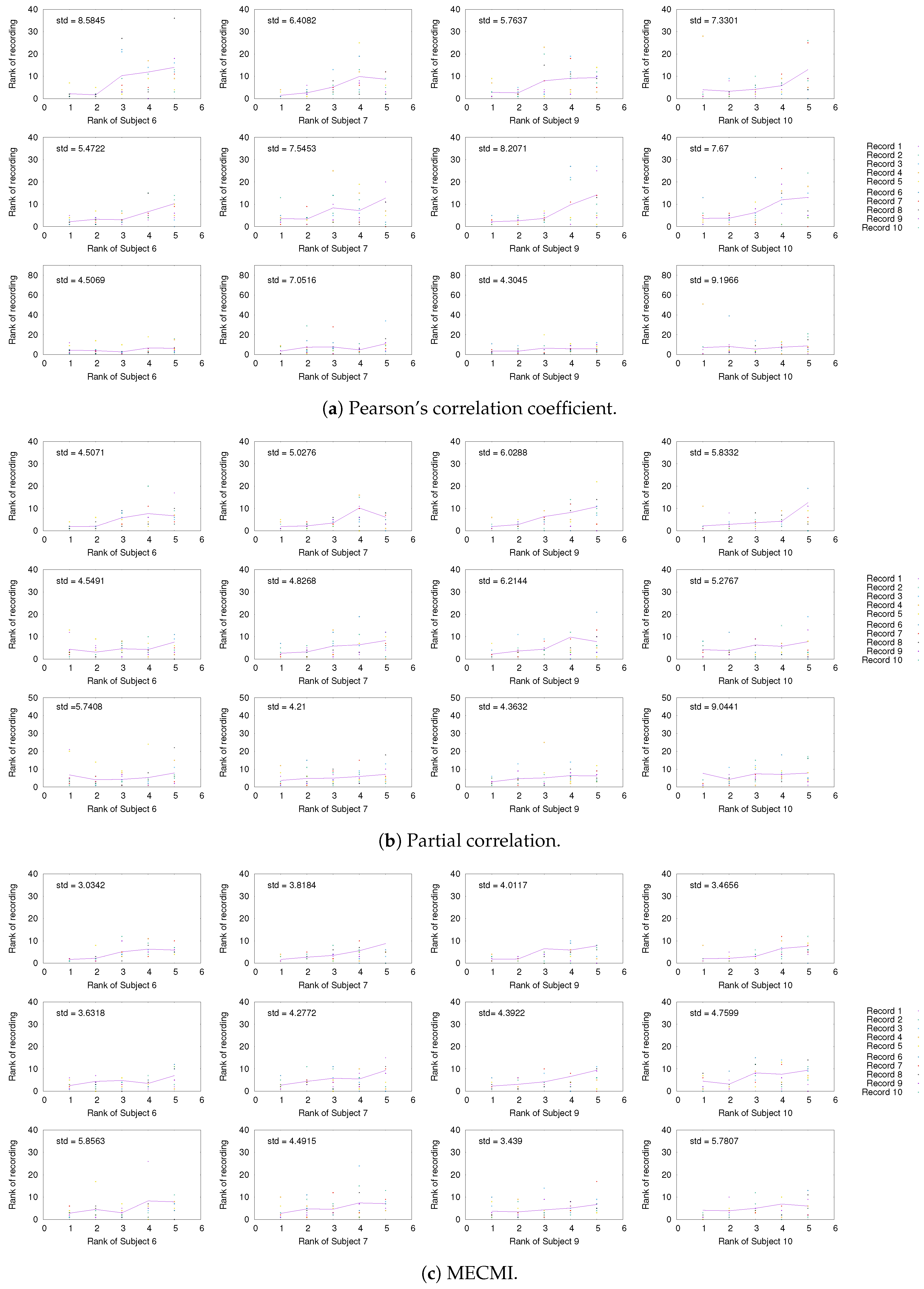
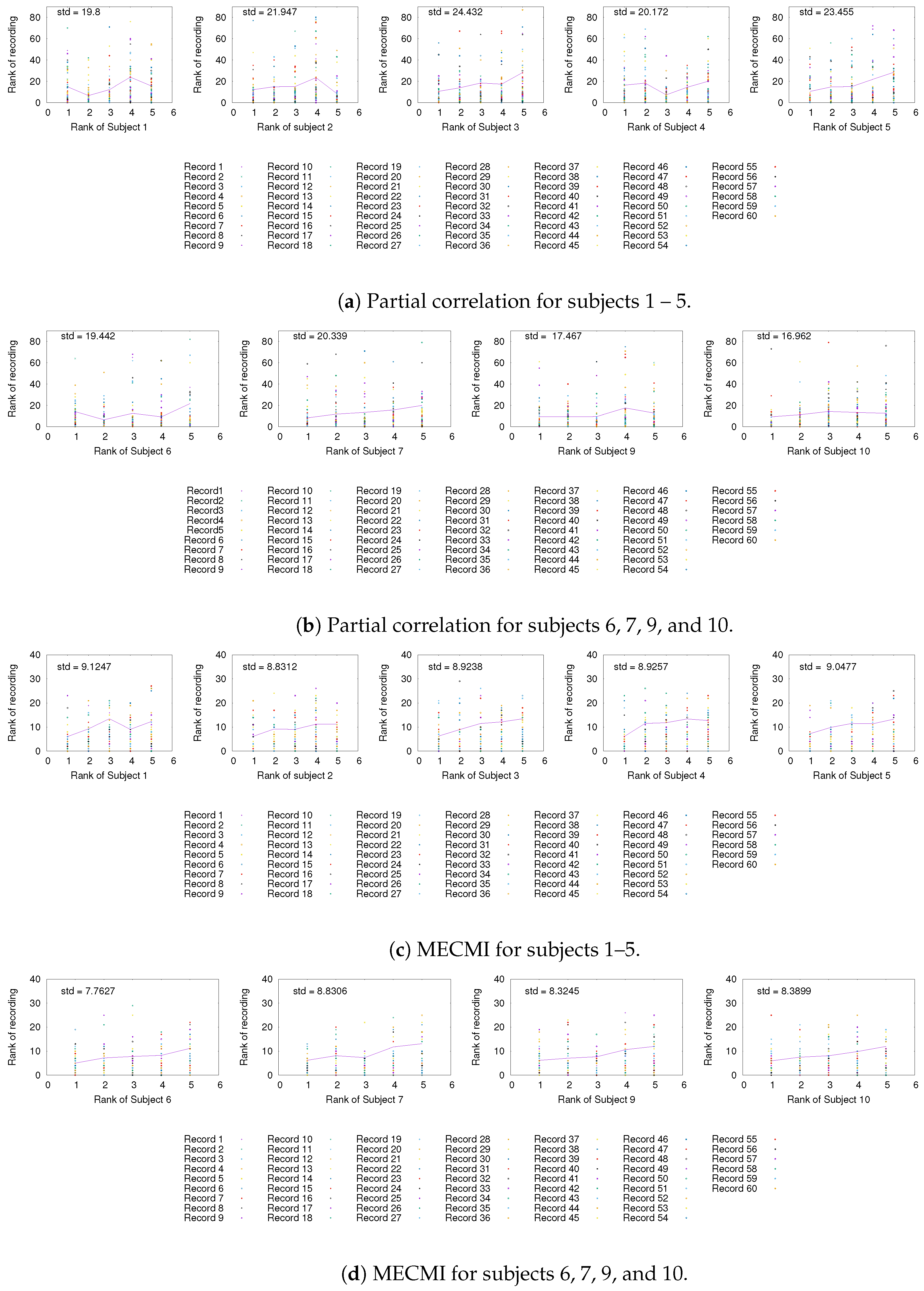
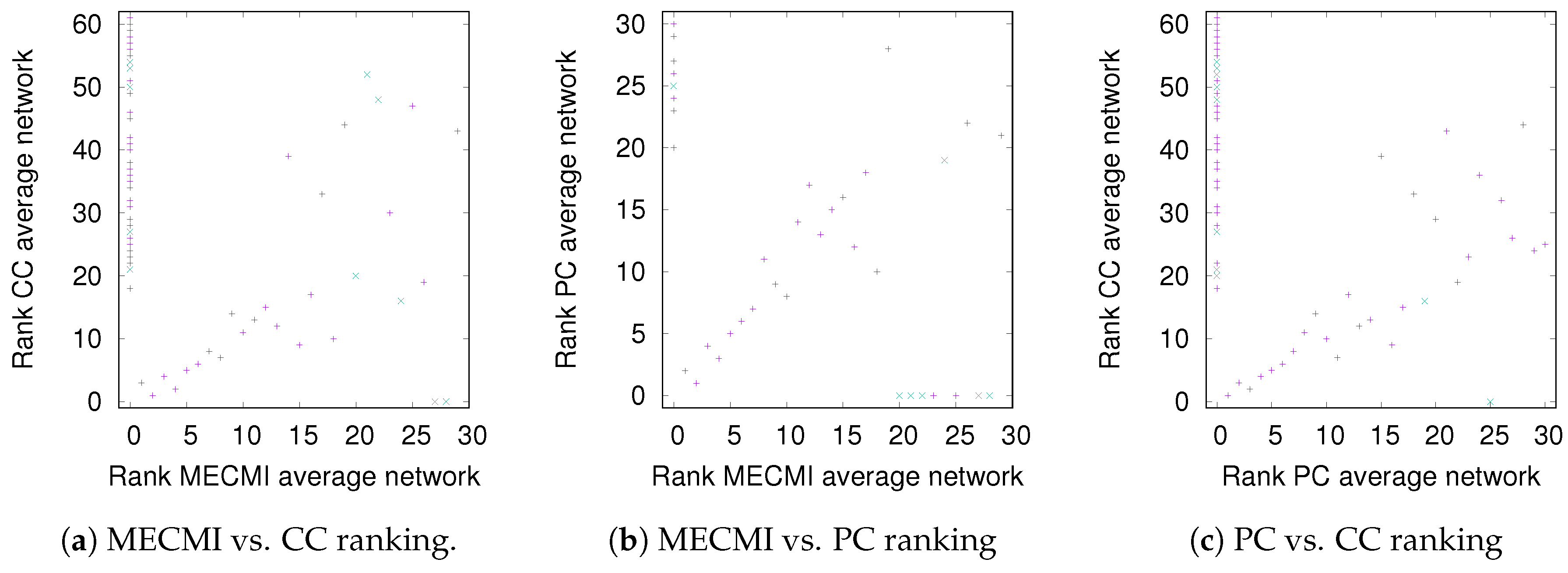
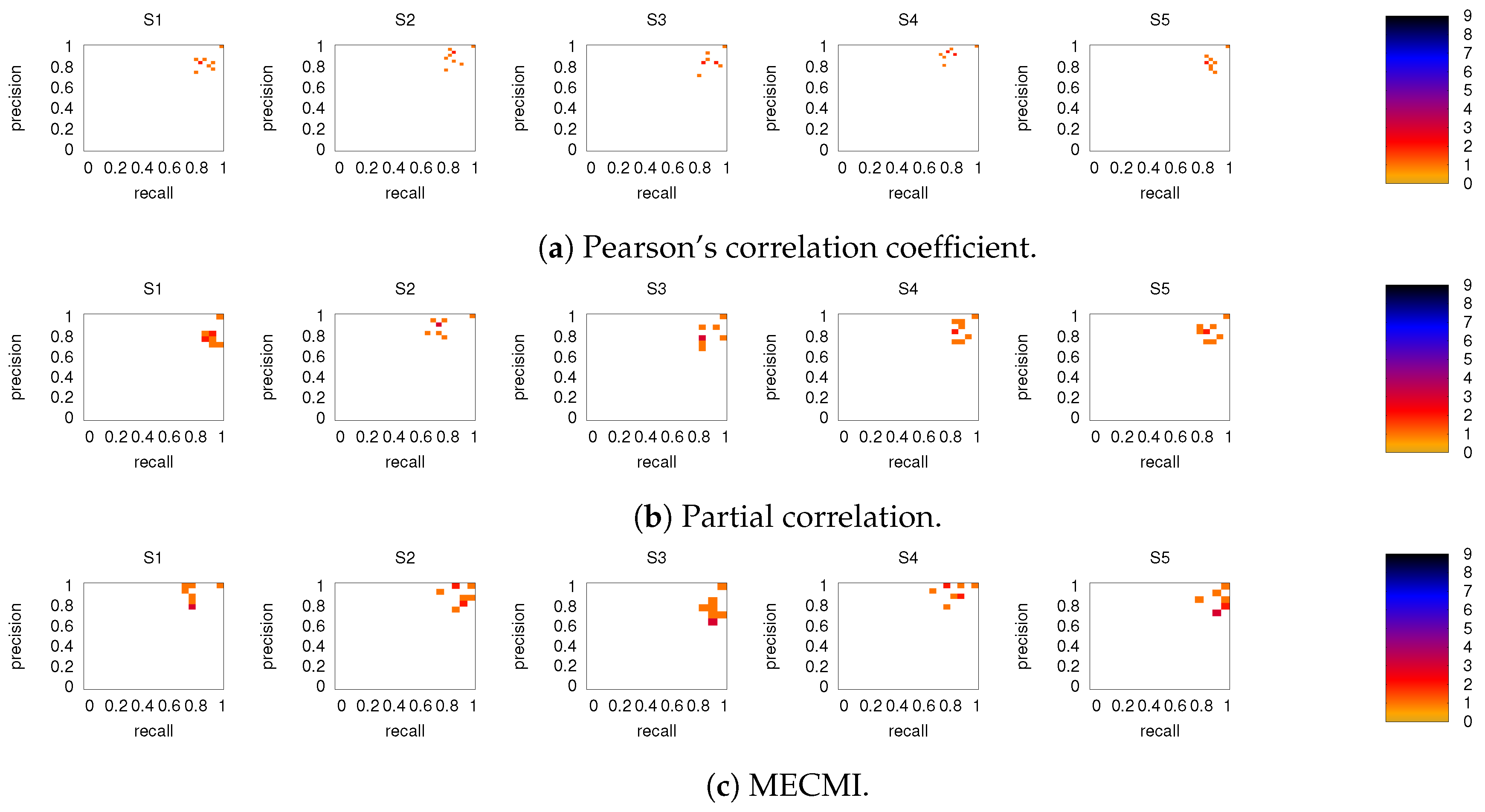
3.1.2. Robustness across Similarity Measures
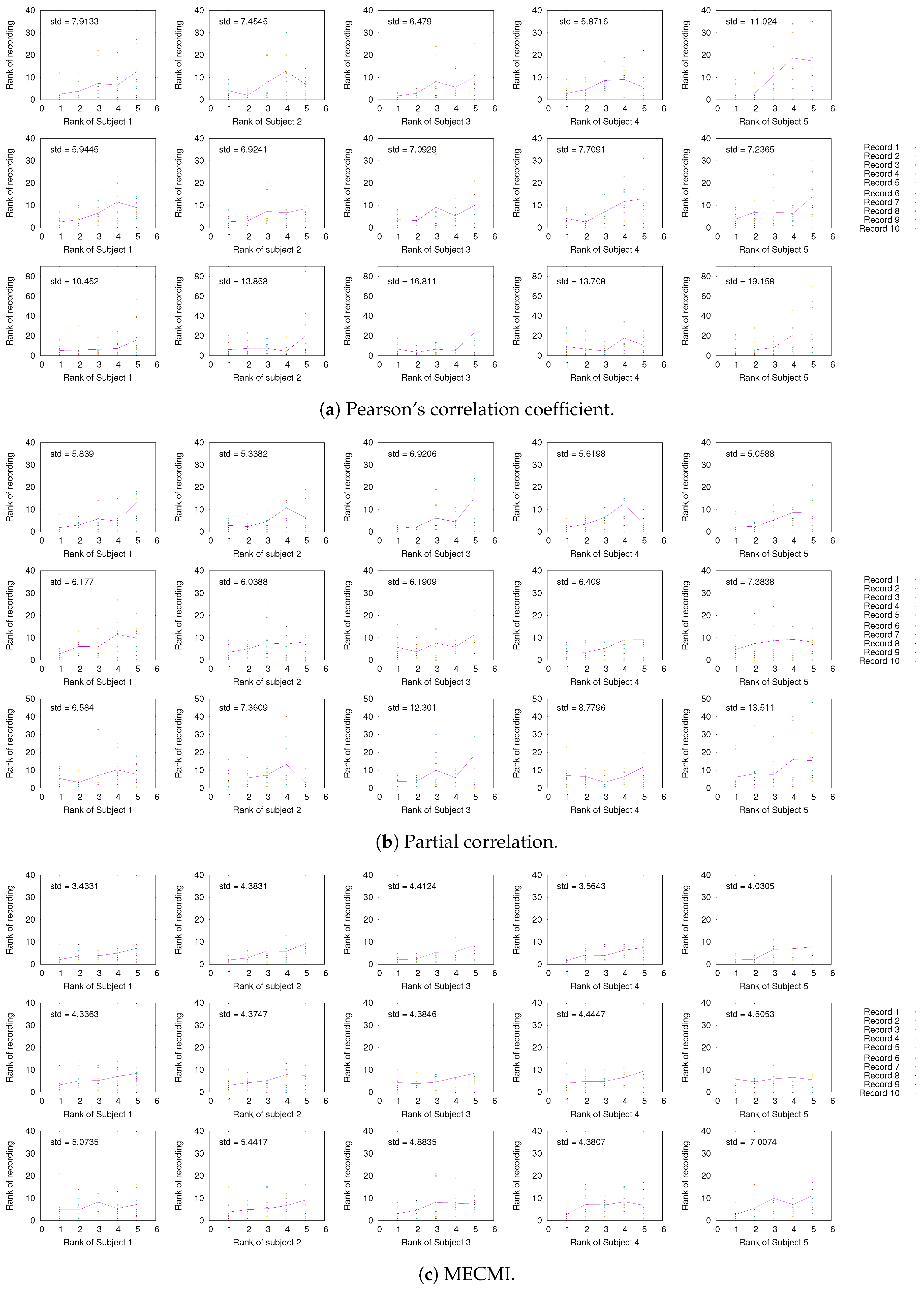
3.1.3. Detection of the Backbone in Individual Recordings
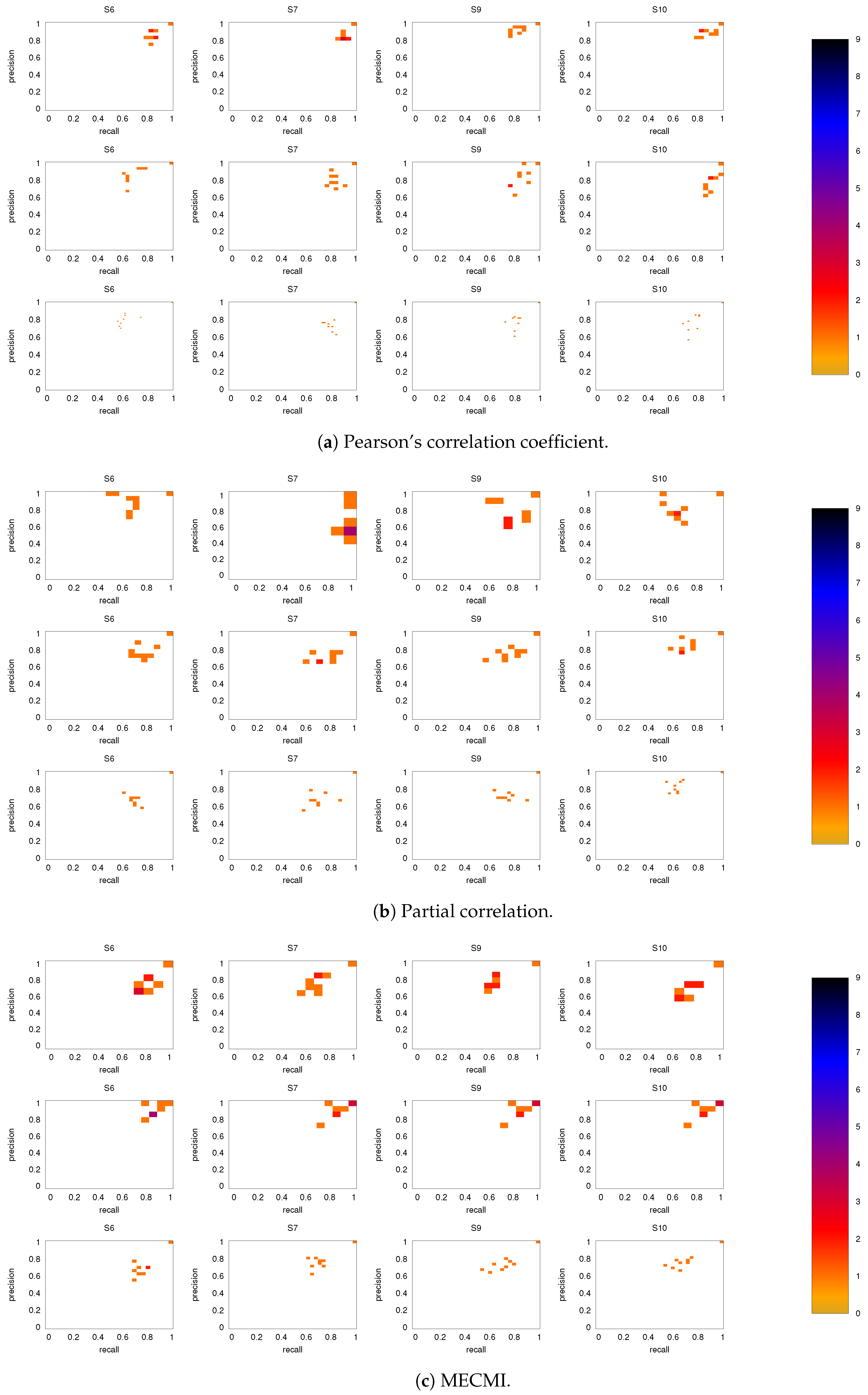
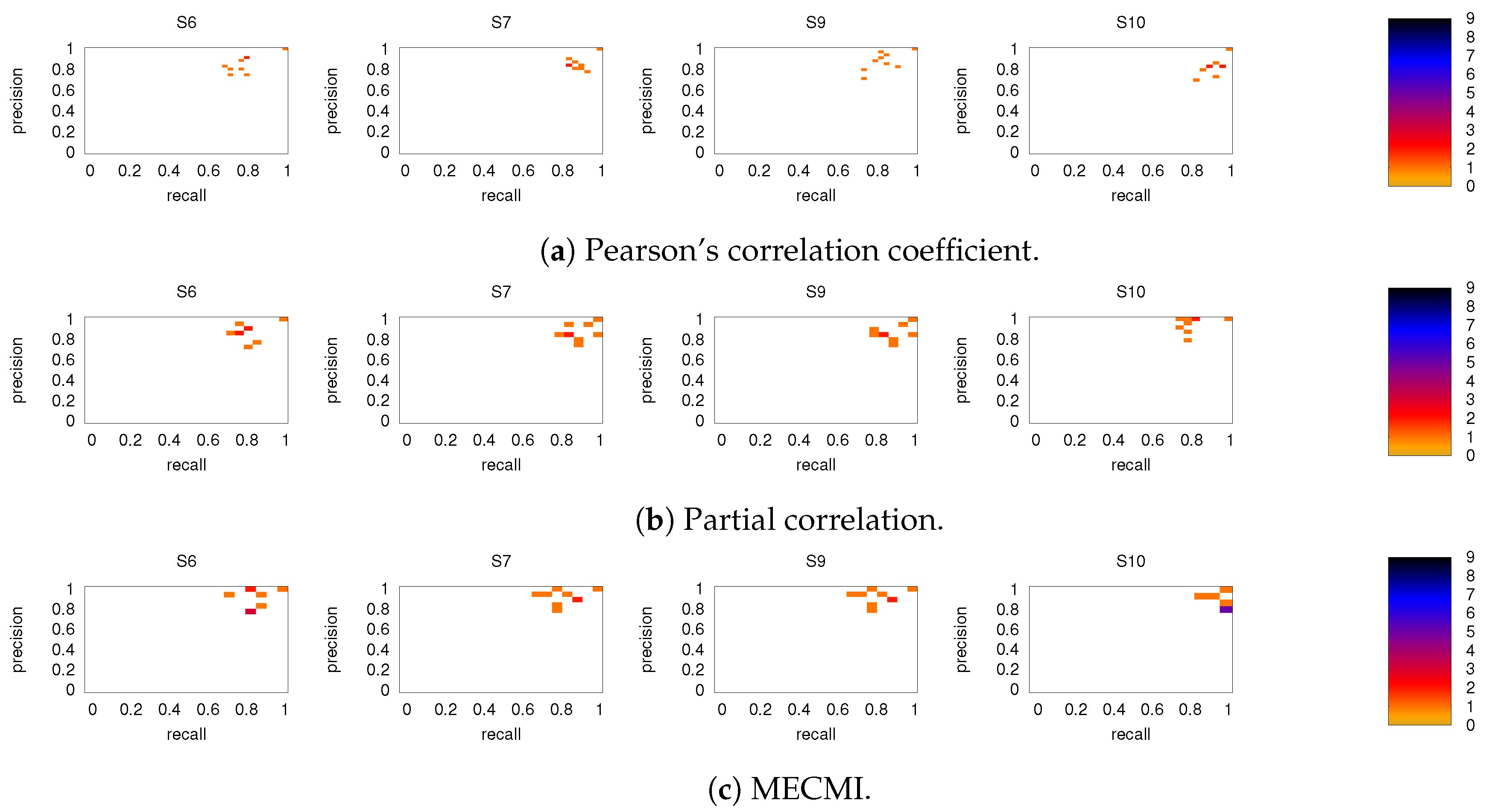
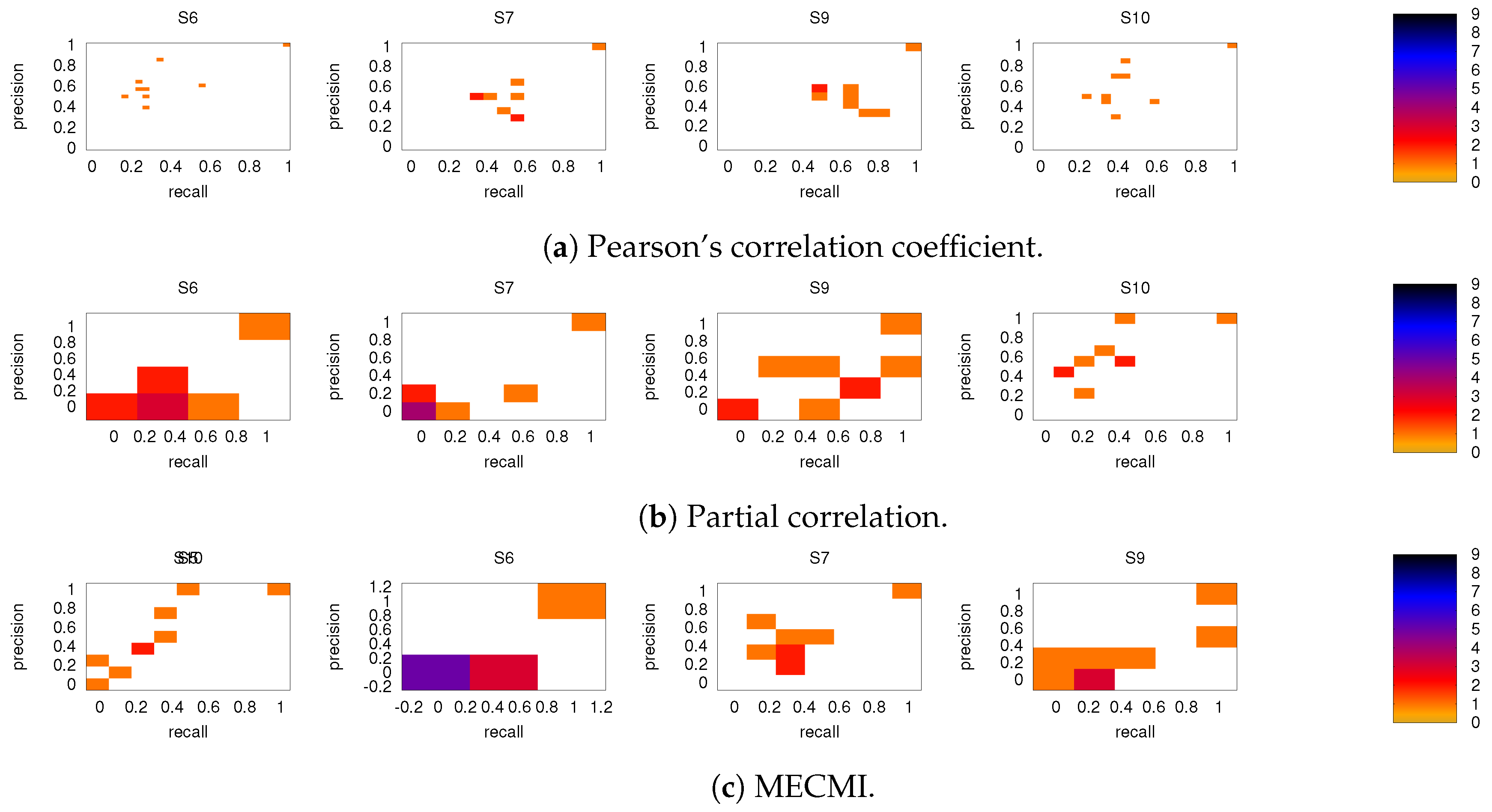
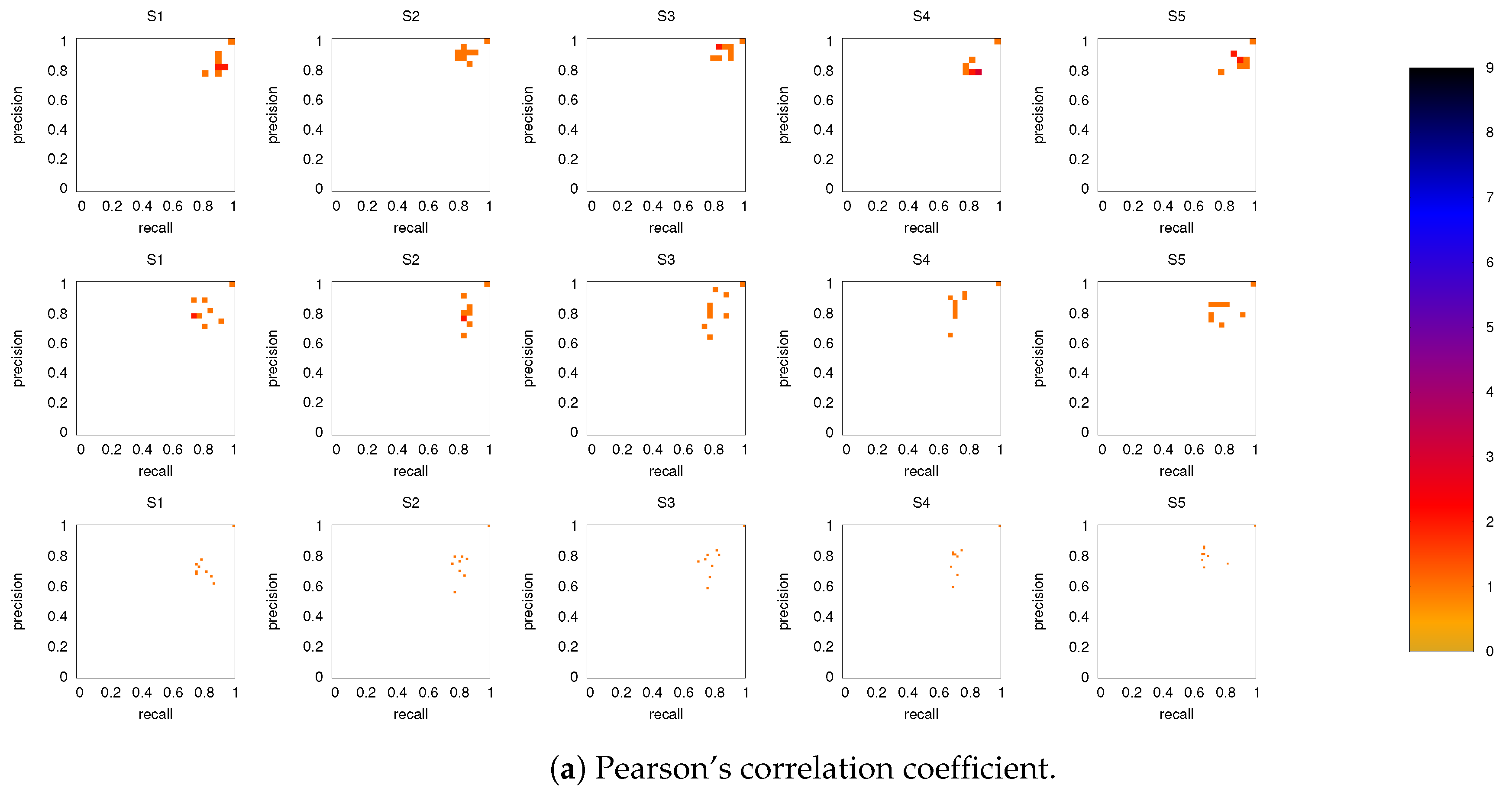
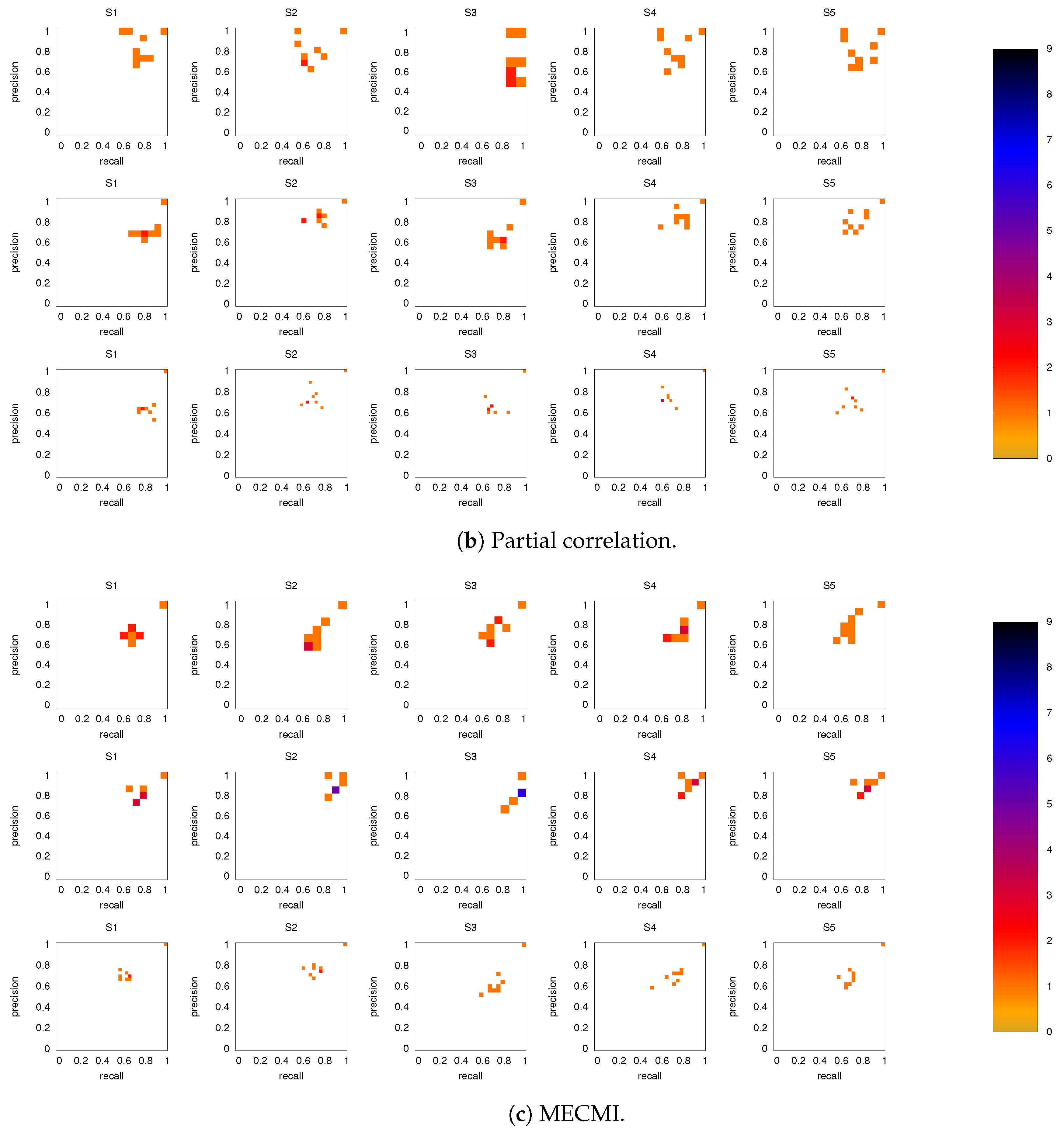
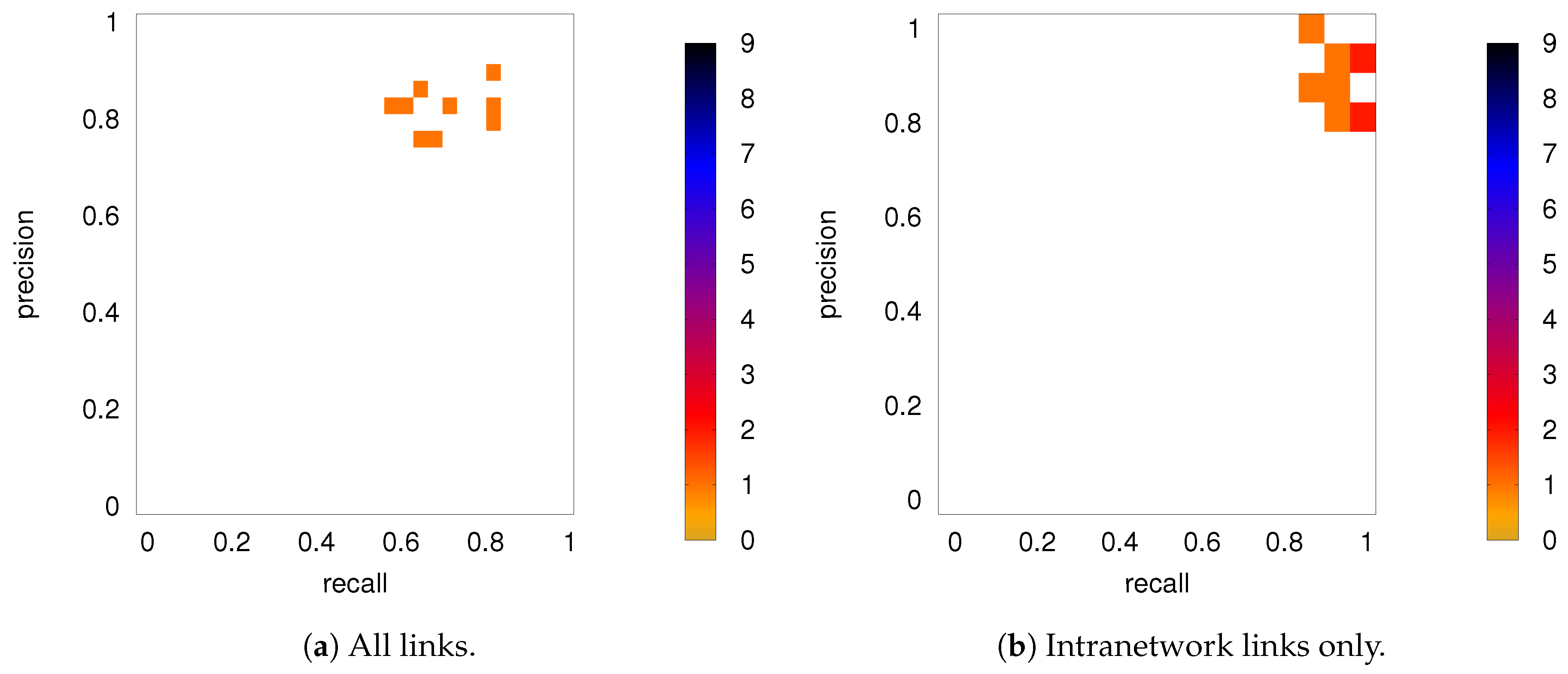
3.2. Precision-Recall Analysis: Robustness of the Network Links
3.2.1. Robustness across Similarity Measures
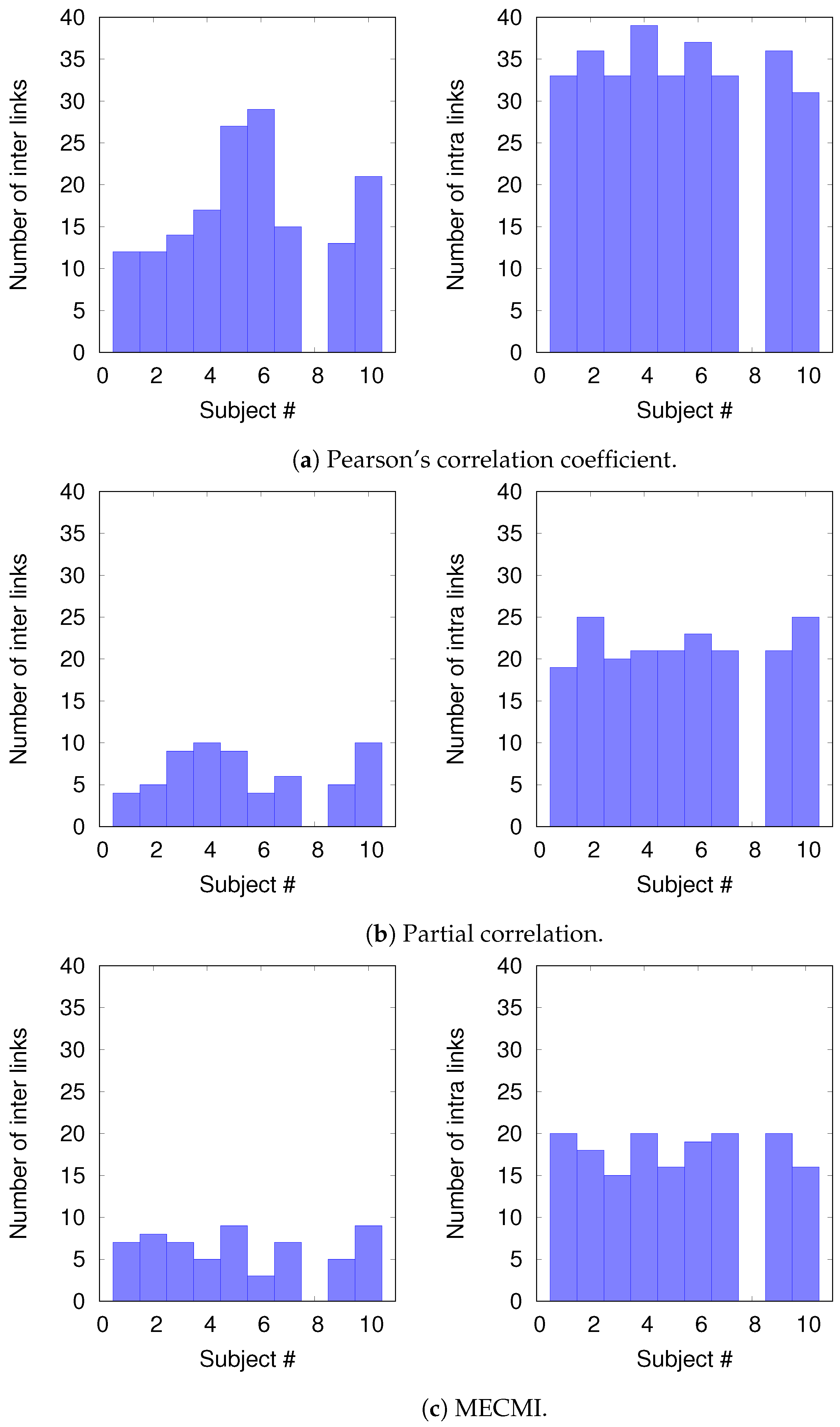
3.2.2. Robustness: Intranetwork Links vs. Internetwork Links
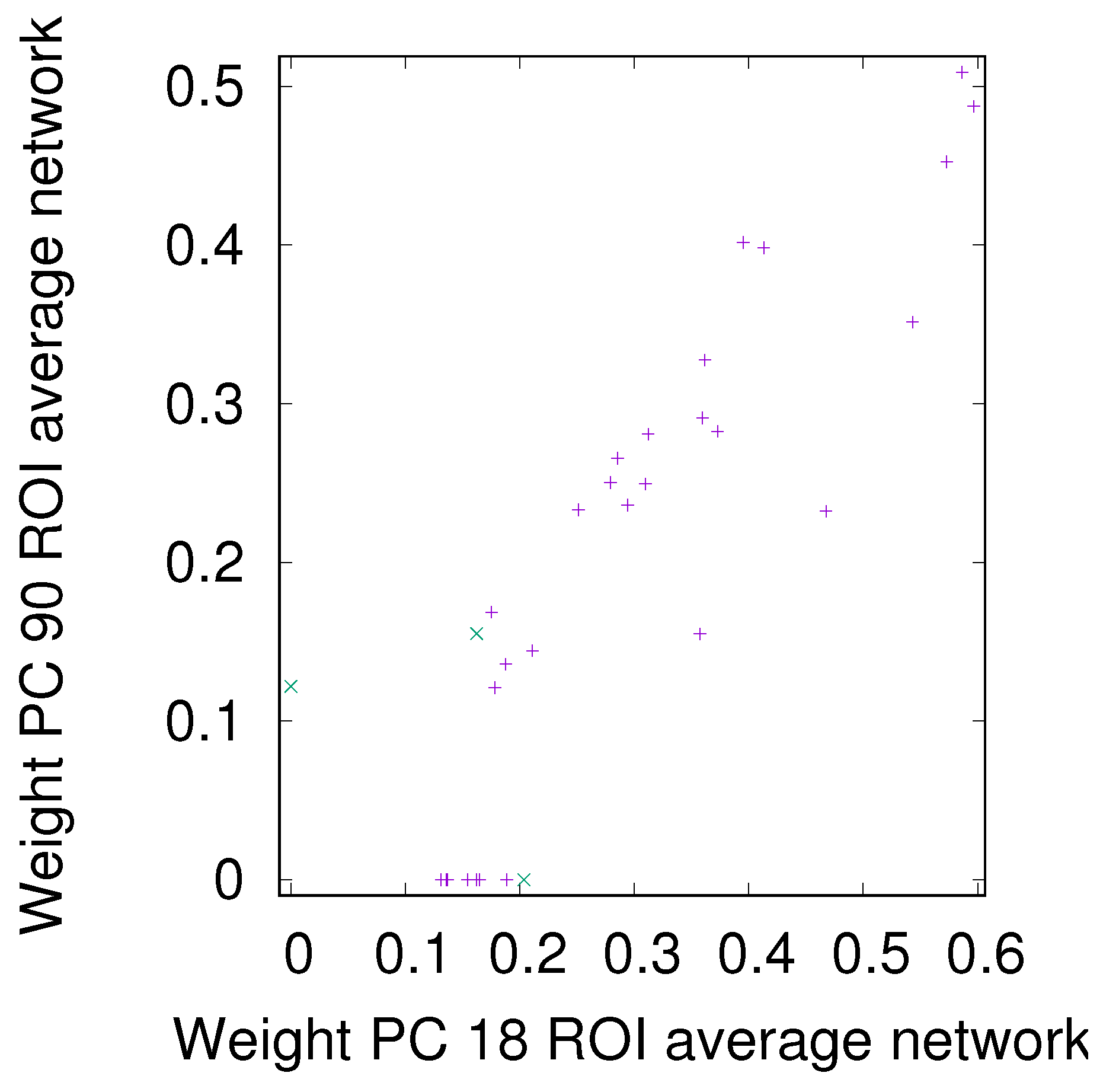
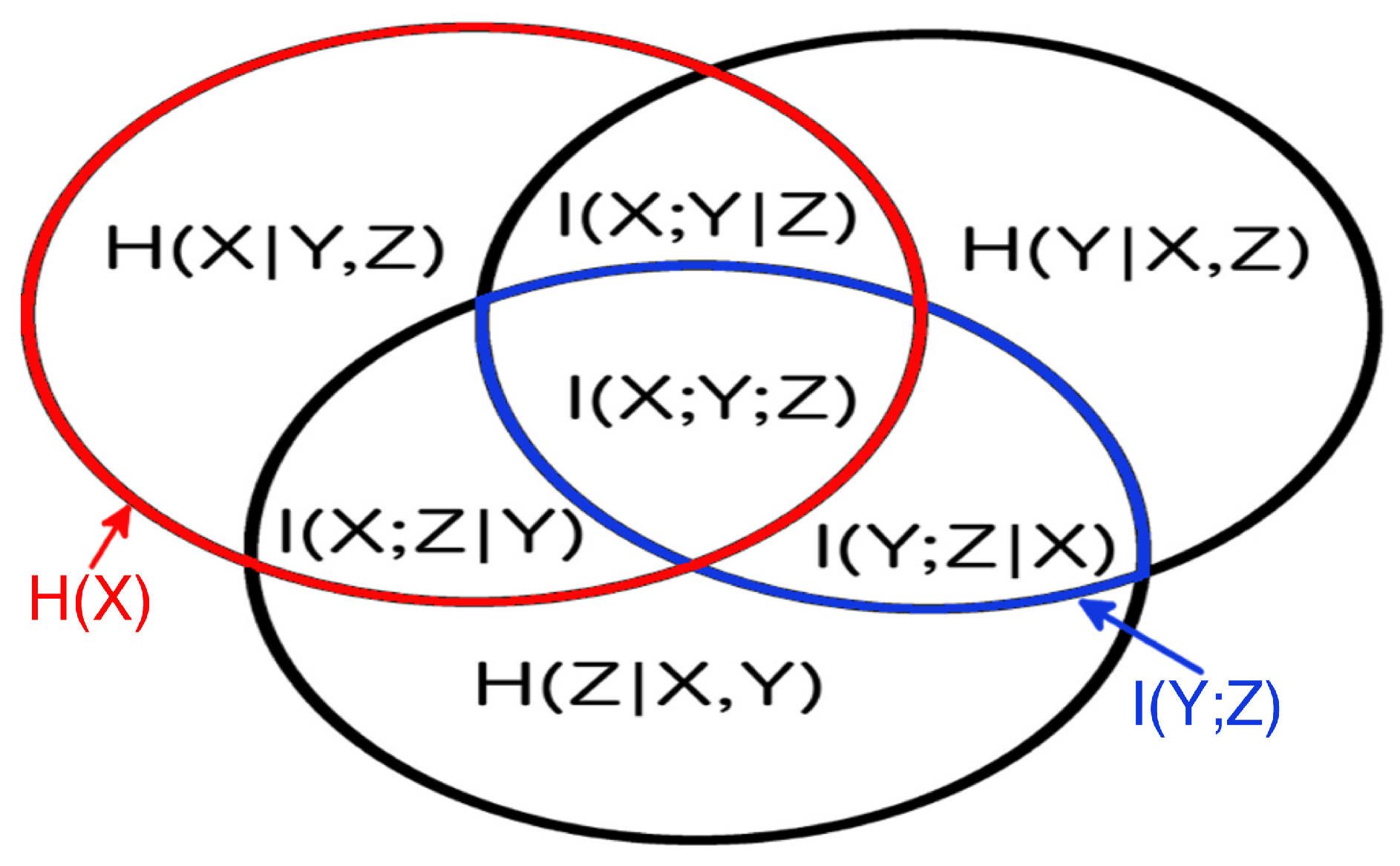
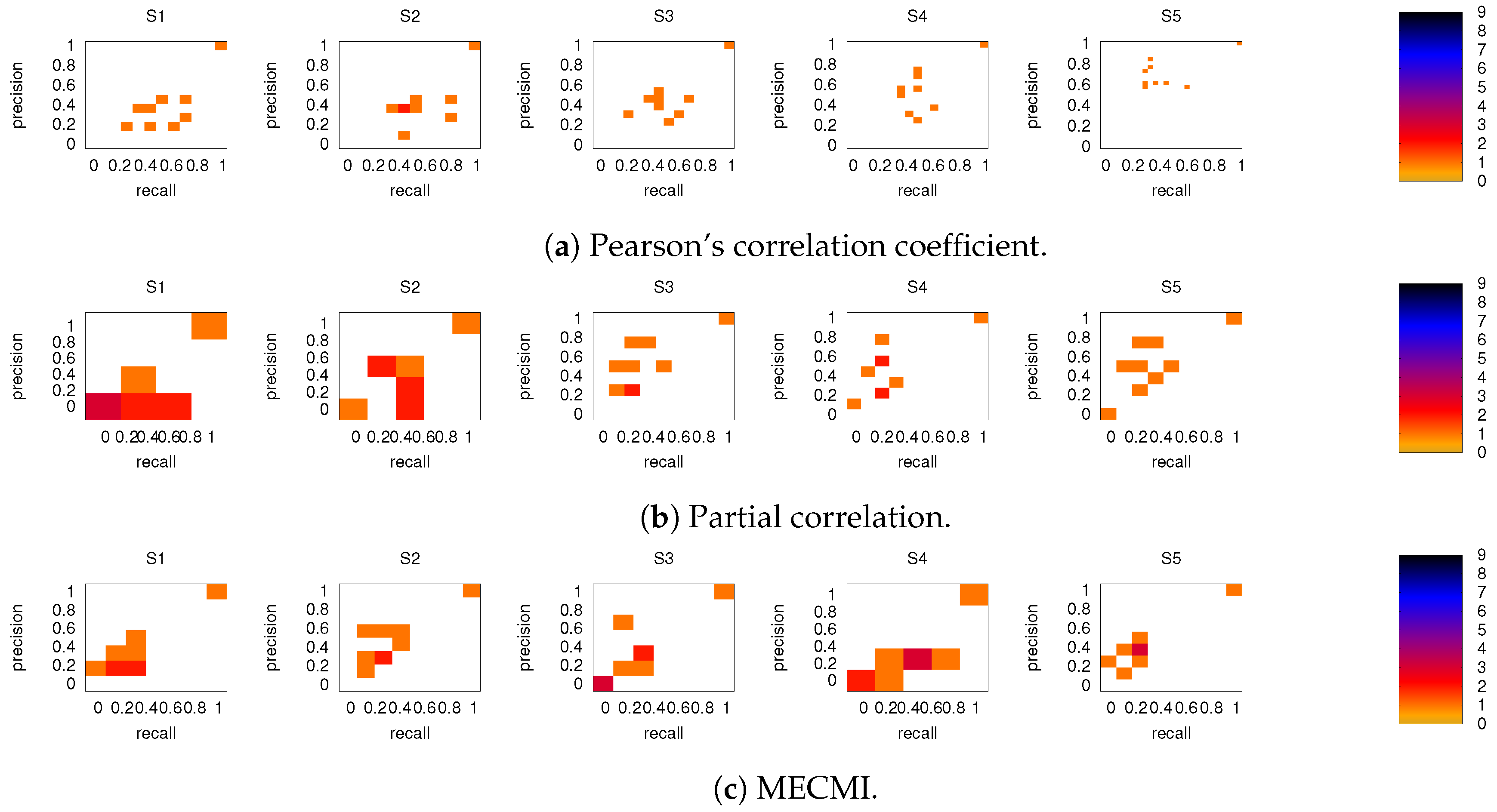
3.3. Partial Analysis: Local vs. Global Conditioning
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bassett, D.S.; Sporns, O. Network neuroscience. Nat. Neurosci. 2017, 20, 353–364. [Google Scholar] [CrossRef]
- Hastings, H.M.; Davidsen, J.; Leung, H. Challenges in the analysis of complex systems: Introduction and overview. Eur. Phys. J. Spec. Top. 2017, 226, 3185–3197. [Google Scholar] [CrossRef]
- Bassett, D.S.; Zurn, P.; Gold, J.I. On the nature and use of models in network neuroscience. Nat. Rev. Neurosci. 2018, 19, 566–578. [Google Scholar] [CrossRef] [PubMed]
- Power, J.D.; Schlaggar, B.L.; Petersen, S.E. Primer Studying Brain Organization via Spontaneous fMRI Signal. Neuron 2014, 84, 681–696. [Google Scholar] [CrossRef] [PubMed]
- Bullmore, E.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186. [Google Scholar] [CrossRef] [PubMed]
- Hlinka, J.; Paluš, M.; Vejmelka, M.; Mantini, D.; Corbetta, M. Functional connectivity in resting-state fMRI: Is linear correlation sufficient? NeuroImage 2011, 54, 2218–2225. [Google Scholar] [CrossRef]
- Friston, K.J. Functional and effective connectivity in neuroimaging: A synthesis. Hum. Brain Mapp. 1994, 2, 56–78. [Google Scholar] [CrossRef]
- Hlinka, J.; Hartman, D.; Paluš, M. Small-world topology of functional connectivity in randomly connected dynamical systems. Chaos 2012, 22. [Google Scholar] [CrossRef]
- Hlinka, J.; Hartman, D.; Jajcay, N.; Tomeček, D.; Tintěra, J.; Paluš, M. Small-world bias of correlation networks: From brain to climate. Chaos 2017, 27, 035812. [Google Scholar] [CrossRef]
- Sporns, O.; Betzel, R.F. Modular Brain Networks. Annu. Rev. Psychol. 2016, 67, 613–640. [Google Scholar] [CrossRef]
- Bray, S.; Arnold, A.E.; Levy, R.M.; Iaria, G. Spatial and temporal functional connectivity changes between resting and attentive states. Hum. Brain Mapp. 2015, 36, 549–565. [Google Scholar] [CrossRef] [PubMed]
- Calhoun, V.D.; Adal, T. Multisubject Independent Component Analysis of fMRI: A Decade of Intrinsic Networks, Default Mode, and Neurodiagnostic Discovery. IEEE Rev. Biomed. Eng. 2012, 5, 60–73. [Google Scholar] [CrossRef]
- Shen, H.; Xu, H.; Wang, L.; Lei, Y.; Yang, L.; Zhang, P.; Qin, J.; Zeng, L.; Zhou, Z.; Yang, Z.; et al. Making Group Inferences Using Sparse Representation of Resting-State Functional MRI Data With Application to Sleep Deprivation. Hum. Brain Mapp. 2017, 38, 4671–4689. [Google Scholar] [CrossRef] [PubMed]
- Ray, K.L.; Lesh, T.A.; Howell, A.M.; Salo, T.P.; Ragland, J.D.; MacDonald, A.W.; Gold, J.M.; Silverstein, S.M.; Barch, D.M.; Carter, C.S. Functional network changes and cognitive control in schizophrenia. Neuroimage Clin. 2017, 15, 161–170. [Google Scholar] [CrossRef] [PubMed]
- Zanchi, D.; Montandon, M.L.; Sinanaj, I.; Rodriguez, C.; Depoorter, A.; Herrmann, F.R.; Borgwardt, S.; Giannakopoulos, P.; Haller, S. Decreased fronto-parietal and increased default mode network activation is associated with subtle cognitive deficits in elderly controls. NeuroSignals 2018, 25, 127–138. [Google Scholar] [CrossRef]
- Mohan, A.; Roberto, A.J.; Mohan, A.; Lorenzo, A.; Jones, K.; Carney, M.J.; Liogier-Weyback, L.; Hwang, S.; Lapidus, K.A. The significance of the Default Mode Network (DMN) in neurological and neuropsychiatric disorders: A review. Yale J. Biol. Med. 2016, 89, 49–57. [Google Scholar]
- He, Y.; Wang, J.; Wang, L.; Chen, Z.J.; Yan, C.; Yang, H.; Tang, H.; Zhu, C.; Gong, Q.; Zang, Y.; et al. Uncovering intrinsic modular organization of spontaneous brain activity in humans. PLoS ONE 2009, 4, 23–25. [Google Scholar] [CrossRef]
- Dosenbach, N.U.F.; Fair, D.A.; Miezin, F.M.; Cohen, A.L.; Wenger, K.K.; Dosenbach, R.A.T.; Fox, M.D.; Snyder, A.Z.; Vincent, J.L.; Raichle, M.E.; et al. Distinct brain networks for adaptive and stable task control in humans. Proc. Natl. Acad. Sci. USA 2007, 104, 11073–11078. [Google Scholar] [CrossRef]
- Damoiseaux, J.S.; Rombouts, S.A.R.B.; Barkhof, F.; Scheltens, P.; Stam, C.J.; Smith, S.M.; Beckmann, C.F. Consistent resting-state networks across healthy subjects. Proc. Natl. Acad. Sci. USA 2006, 103, 13848–13853. [Google Scholar] [CrossRef]
- Dubois, J.; Adolphs, R. Building a Science of Individual Differences from fMRI. Trends Cogn. Sci. 2016, 20, 425–443. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.S.; Ferguson, M.A.; Lopez-Larson, M.; Yurgelun-Todd, D. Reproducibility of single-subject functional connectivity measurements. Am. J. Neuroradiol. 2011, 32, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Gordon, E.M.; Laumann, T.O.; Gilmore, A.W.; Newbold, D.J.; Greene, D.J.; Berg, J.J.; Ortega, M.; Hoyt-Drazen, C.; Gratton, C.; Sun, H.; et al. Precision Functional Mapping of Individual Human Brains. Neuron 2017, 95, 791–807. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zuo, X.; He, Y. Graph-based network analysis of resting-state functional MRI. Front. Syst. Neurosci. 2010, 4, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Bassett, D.S.; Meyer-Lindenberg, A.; Achard, S.; Duke, T.; Bullmore, E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proc. Natl. Acad. Sci. USA 2006, 103, 19518–19523. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Wang, J.; Yan, C.; Shu, N.; Xu, K.; Gong, G.; He, Y. Effects of different correlation metrics and preprocessing factors on small-world brain functional networks: A resting-state functional MRI study. PLoS ONE 2012, 7. [Google Scholar] [CrossRef]
- Watanabe, T.; Hirose, S.; Wada, H.; Imai, Y.; Machida, T.; Shirouzu, I.; Konishi, S.; Miyashita, Y.; Masuda, N. A pairwise maximum entropy model accurately describes resting-state human brain networks. Nat. Commun. 2013, 4, 1370. [Google Scholar] [CrossRef]
- Ferrarini, L.; Veer, I.M.; Baerends, E.; Tol, V.; Renken, R.J.; Wee, N.J.A.V.D.; Zitman, F.G.; Veltman, D.J.; Penninx, B.W.J.H.; Buchem, M.A.V.; et al. Hierarchical functional modularity in the resting-state human brain. Hum. Brain Mapp. 2009, 30, 2220–2231. [Google Scholar] [CrossRef]
- Martin, E.A.; Hlinka, J.; Davidsen, J. Pairwise network information and nonlinear correlations. Phys. Rev. E 2016, 94, 1–2. [Google Scholar] [CrossRef]
- Martin, E.A.; Hlinka, J.; Meinke, A.; Děchtěrenko, F.; Tintěra, J.; Oliver, I.; Davidsen, J. Network Inference and Maximum Entropy Estimation on Information Diagrams. Sci. Rep. 2017, 7, 1–15. [Google Scholar] [CrossRef]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazoyer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage 2002, 15, 273–289. [Google Scholar] [CrossRef] [PubMed]
- Whitfield-Gabrieli, S.; Nieto-Castanon, A. Conn: A functional connectivity toolbox for correlated and anticorrelated brain networks. Brain Connect. 2012, 2, 125–141. [Google Scholar] [CrossRef] [PubMed]
- Behzadi, Y.; Restom, K.; Liau, J.; Liu, T.T. A component based noise correction method (CompCor) for BOLD and perfusion based fMRI. NeuroImage 2007, 37, 90–101. [Google Scholar] [CrossRef] [PubMed]
- Chai, X.J.; Castañón, A.N.; Ongür, D.; Whitfield-Gabrieli, S. Anticorrelations in resting state networks without global signal regression. NeuroImage 2012, 59, 1420–1428. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D 2000, 142, 346. [Google Scholar] [CrossRef]
- Salvador, R.; Suckling, J.; Coleman, M.R.; Pickard, J.D.; Menon, D.; Bullmore, E. Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb. Cortex 2005, 15, 1332–2342. [Google Scholar] [CrossRef]
- Yeung, R.W. Information Theory and Network Coding; Springer: New York, NY, USA, 2008. [Google Scholar]
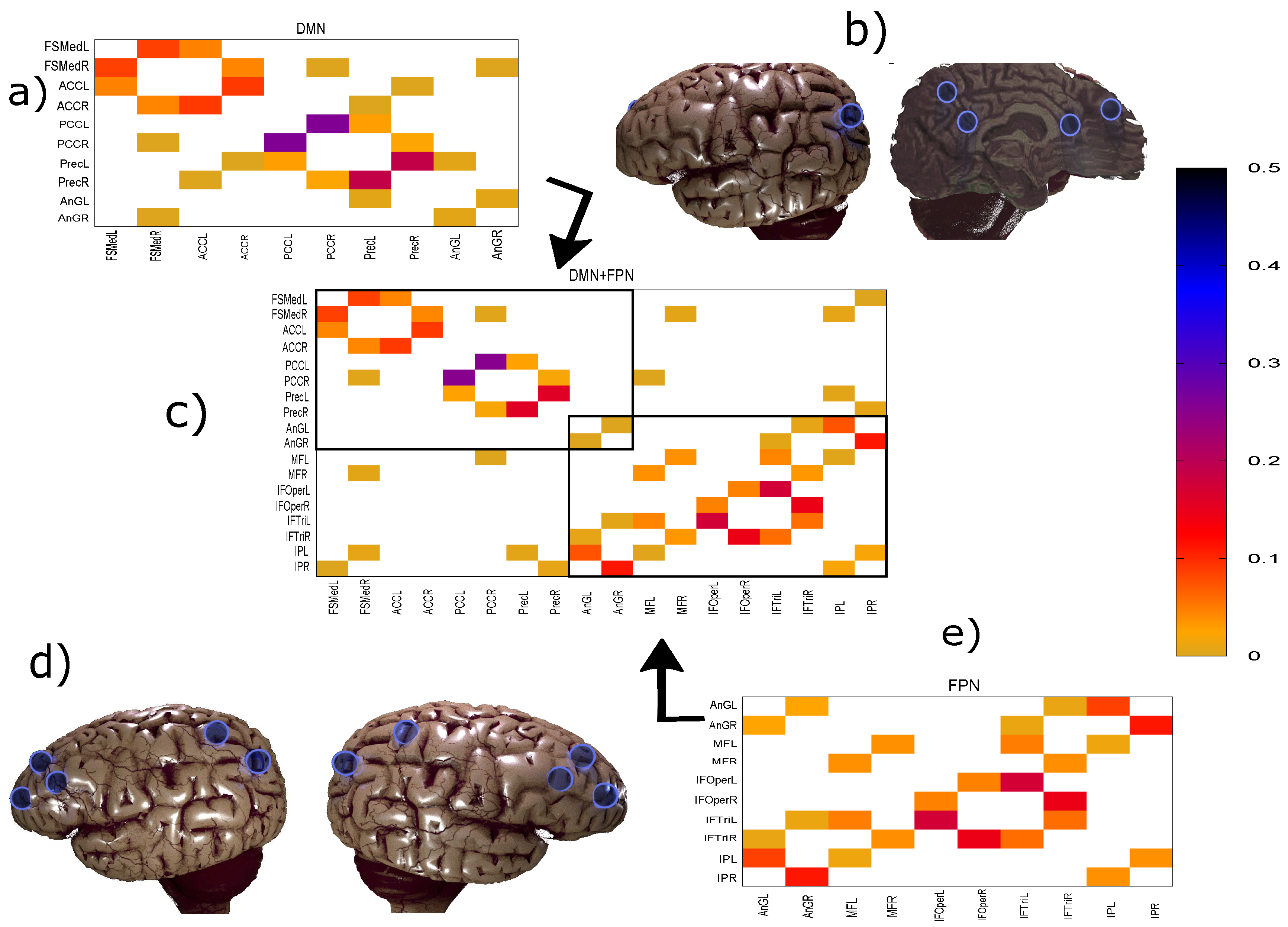
| DMN Regions | FPN Regions |
|---|---|
| Frontal Superior Medial L | Frontal Middle L |
| Frontal Superior Medial R | Frontal Middle R |
| Cingulum Anterior L | Frontal Inferior Opercularis L |
| Cingulum Anterior R | Frontal Inferior Opercularis R |
| Cingulum Posterior L | Frontal Inferior Triangular L |
| Cingulum Posterior R | Frontal Inferior Triangular R |
| Angular L | Parietal Inferior L |
| Angular R | Parietal Inferior R |
| Precuneus L | Angular L |
| Precuneus R | Angular R |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliver, I.; Hlinka, J.; Kopal, J.; Davidsen, J. Quantifying the Variability in Resting-State Networks. Entropy 2019, 21, 882. https://doi.org/10.3390/e21090882
Oliver I, Hlinka J, Kopal J, Davidsen J. Quantifying the Variability in Resting-State Networks. Entropy. 2019; 21(9):882. https://doi.org/10.3390/e21090882
Chicago/Turabian StyleOliver, Isaura, Jaroslav Hlinka, Jakub Kopal, and Jörn Davidsen. 2019. "Quantifying the Variability in Resting-State Networks" Entropy 21, no. 9: 882. https://doi.org/10.3390/e21090882
APA StyleOliver, I., Hlinka, J., Kopal, J., & Davidsen, J. (2019). Quantifying the Variability in Resting-State Networks. Entropy, 21(9), 882. https://doi.org/10.3390/e21090882





