The Poincaré-Shannon Machine: Statistical Physics and Machine Learning Aspects of Information Cohomology
Abstract
:| 1 Introduction | 3 |
| 1.1 Observable Physics of Information | 3 |
| 1.2 Statistical Interpretation: Hierarchical Independences and Dependences Structures | 3 |
| 1.3 Statistical Physics Interpretation: K-Body Interacting Systems | 4 |
| 1.4 Machine Learning Interpretation: Topological Deep Learning | 5 |
| 2 Information Cohomology | 6 |
| 2.1 A Long March through Information Topology | 6 |
| 2.2 Information Functions (Definitions) | 7 |
| 2.3 Information Structures and Coboundaries | 10 |
| 2.3.1 First Degree () | 12 |
| 2.3.2 Second Degree () | 12 |
| 2.3.3 Third Degree () | 12 |
| 2.3.4 Higher Degrees | 13 |
| 3 Simplicial Information Cohomology | 13 |
| 3.1 Simplicial Substructures of Information | 13 |
| 3.2 Topological Self and Free Energy of K-Body Interacting System-Poincaré-Shannon Machine | 14 |
| 3.3 k-Entropy and k-Information Landscapes | 18 |
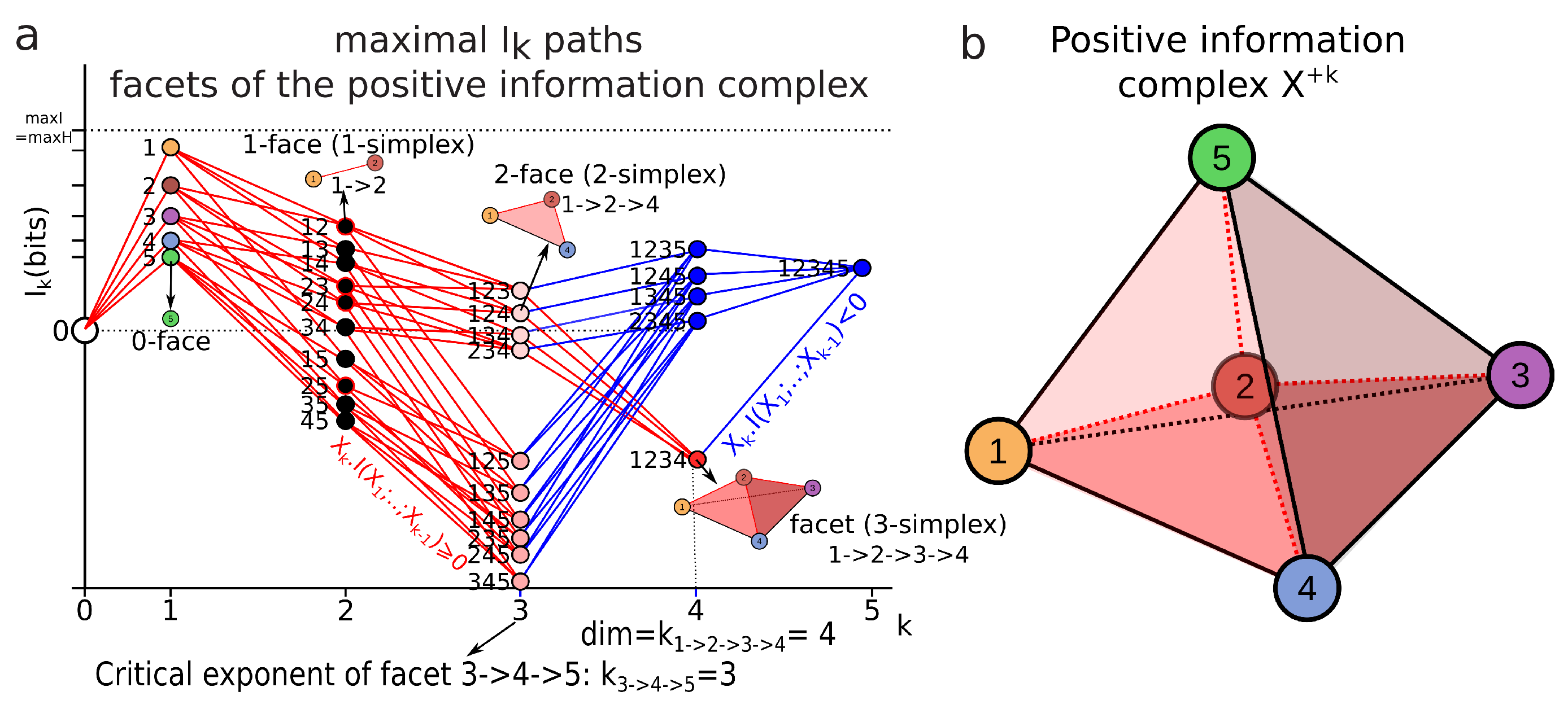
| 3.4 Information Paths and Minimum Free Energy Complex | 19 |
| 3.4.1 Information Paths (Definition) | 19 |
| 3.4.2 Derivatives, Inequalities and Conditional Mutual-Information Negativity | 20 |
| 3.4.3 Information Paths Are Random Processes: Topological Second Law of Thermodynamics and Entropy Rate | 21 |
| 3.4.4 Local Minima and Critical Dimension | 23 |
| 3.4.5 Sum over Paths and Mean Information Path | 24 |
| 3.4.6 Minimum Free Energy Complex | 25 |
| 4 Discussion | 27 |
| 4.1 Statistical Physics | 27 |
| 4.1.1 Statistical Physics without Statistical Limit? Complexity through Finite Dimensional Non-Extensivity | 27 |
| 4.1.2 Naive Estimations Let the Data Speak | 28 |
| 4.1.3 Discrete Informational Analog of Renormalization Methods: No Mean-Field Assumptions Let the Objects Differentiate | 29 |
| 4.1.4 Combinatorial, Infinite, Continuous and Quantum Generalizations | 29 |
| 4.2 Data Science | 29 |
| 4.2.1 Topological Data Analysis | 29 |
| 4.2.2 Unsupervised and Supervised Deep Homological Learning | 30 |
| 4.2.3 Epigenetic Topological Learning—Biological Diversity | 31 |
| 5 Conclusions | 32 |
| References | 33 |
“Now what is science? ...it is before all a classification, a manner of bringing together facts which appearances separate, though they are bound together by some natural and hidden kinship. Science, in other words, is a system of relations. ...it is in relations alone that objectivity must be sought. ...it is relations alone which can be regarded as objective. External objects... are really objects and not fleeting and fugitive appearances, because they are not only groups of sensations, but groups cemented by a constant bond. It is this bond, and this bond alone, which is the object in itself, and this bond is a relation.”H. Poincaré
1. Introduction
1.1. Observable Physics of Information
1.2. Statistical Interpretation: Hierarchical Independences and Dependences Structures
1.3. Statistical Physics Interpretation: K-Body Interacting Systems
1.4. Machine Learning Interpretation: Topological Deep Learning
2. Information Cohomology
2.1. A Long March through Information Topology
2.2. Information Functions (Definitions)
- The Shannon-Gibbs entropy of a single variable is defined by [71]:where denotes the alphabet of .
- The relative entropy or Kullback-Liebler divergence, which was also called “discrimination information” by Kullback [90], is defined for two probability mass functions and by:where is the cross-entropy and the Shannon entropy. It hence generates minus entropy as a special case, taking the deterministic constant probability . With the convention , is always positive or null.
- The joint entropy is defined for any joint product of k random variables and for a probability joint distribution by [71]:where denotes the alphabet of .
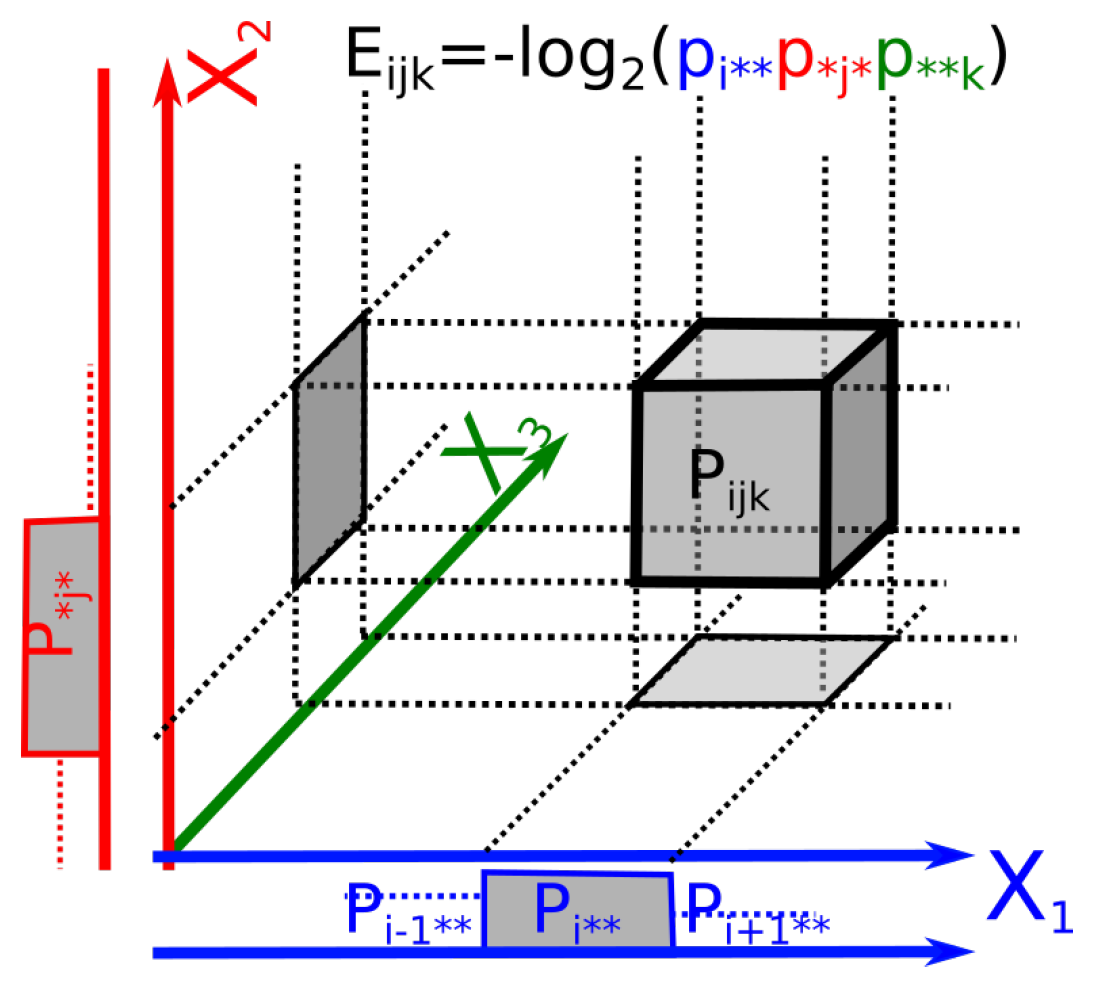
- The mutual information of two variables is defined as [71]:and it can be generalized to k-mutual information (also called co-information) using the alternated sums given by Equation (17), as originally defined by McGill [93] and Hu Kuo Ting [91], giving:For example, the 3-mutual information is the function:For , can be negative [91].
- The total correlation introduced by Watanabe [94] called integration by Tononi and Edelman [95] or multi-information by Studený and Vejnarova [96] and Margolin and colleagues [97], which we denote , is defined by:For two variables, the total correlation is equal to the mutual information (). The total correlation has the favorable property of being a relative entropy 2 between marginal and joint-variable and hence of being always non-negative.
- The conditional entropy of knowing (or given) is defined as [71]:Conditional joint-entropy, or , is defined analogously by replacing the marginal probabilities by the joint probabilities.
- The conditional mutual information of two variables knowing a third is defined as [71]:Conditional mutual information generates all the preceding information functions as subcases, as shown by Yeung [92]. We have the theorem: if , then it gives the mutual information; if , it gives conditional entropy; and if both conditions are satisfied, it gives entropy. Notably, we have .
- if and only if (in short: ),
- if and only if (in short: ),
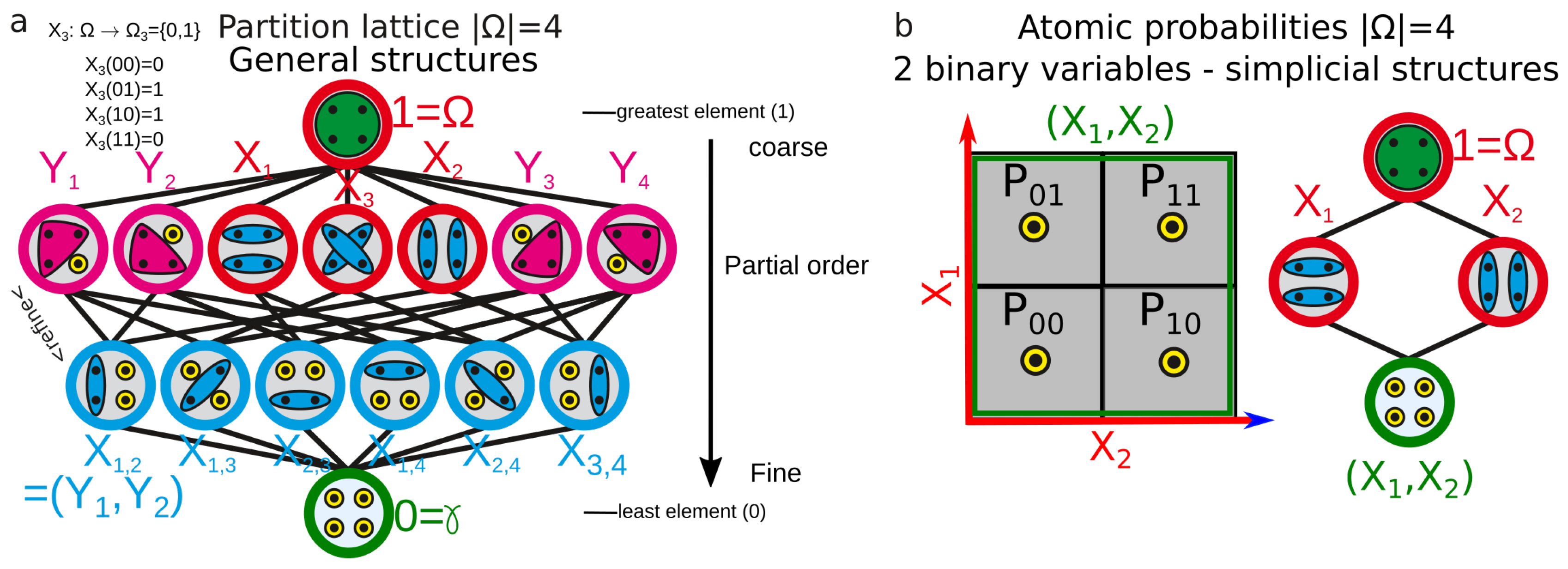
2.3. Information Structures and Coboundaries
- The left action Hochschild-information coboundary and cohomology (with trivial right action):This coboundary, with a trivial right action, is the usual coboundary of Galois cohomology ([103], p. 2) and in general it is the coboundary of homological algebra obtained by Cartan and Eilenberg [104] and MacLane [105] (non-homogenous bar complex).
- The “topological-trivial” Hochschild-information coboundary and cohomology: consider a trivial left action in the preceding setting (e.g., ). It is the subset of the preceding case, which is invariant under the action of conditioning. We obtain the topological coboundary [1]:
- The symmetric Hochschild-information coboundary and cohomology: as introduced by Gerstenhaber and Shack [22], Kassel [102] (p. 13) and Weibel [101] (chap. 9), we consider a symmetric (left and right) action of conditioning, that is, . The left action module is essentially the same as considering a symmetric action bimodule [22,101,102]. We hence obtain the following symmetric coboundary :
2.3.1. First Degree ()
- The left 1-co-boundary is . The 1-cocycle condition gives , which is the chain rule of information shown in Equation (10). Then, following Kendall [106] and Lee [107], it is possible to recover the functional equation of information and to characterize uniquely—up to the arbitrary multiplicative constant k—the entropy (Equation (1)) as the first class of cohomology [1,18]. This main theorem allows us to obtain the other information functions in what follows. Marcolli and Thorngren [20] and the group of Leinster, Fritz and Baez [81,82] independently obtained an analog result using a measure-preserving function and a characteristic one Witt construction, respectively. In these various theoretical settings, this result extends to relative entropy [1,20,82] and Tsallis entropies [18,20].
- The topological 1-coboundary is , which corresponds to the definition of mutual information and hence is a topological 1-coboundary.
- The symmetric 1-coboundary is , which corresponds to the negative of the pairwise mutual information and hence is a symmetric 1-coboundary. Moreover, the 1-cocycle condition characterizes functions satisfying , which corresponds to the information pseudo-metric discovered by Shannon [23], Rajski [24], Zurek [25] and Bennett [26] and has further been applied for hierarchical clustering and finding categories in data by Kraskov and Grassberger [27]: . Therefore, up to an arbitrary scalar multiplicative constant k, the information pseudo-metric is the first class of symmetric cohomology. This pseudo-metric is represented in Figure 3. It generalizes to pseudo k-volumes that we define by (particularly interesting symmetric nonnegative functions computed by the provided software).
2.3.2. Second Degree ()
- The left 2-co-boundary is , which corresponds to minus the 3-mutual information and hence is the left 2-coboundary.
- The topological 2-coboundary is , which corresponds in information to and hence the topological 2-coboundary is always null-trivial.
- The symmetric 2-coboundary is , which corresponds in information to and hence the symmetric 2-coboundary is always null-trivial.
2.3.3. Third Degree ()
- The left 3-co-boundary is , which corresponds in information to and hence the left 3-coboundary is always null-trivial.
- The topological 3-coboundary is , which corresponds in information to and hence is a topological 3-coboundary.
- The symmetric 3-coboundary is , which corresponds in information to and hence is a symmetric 3-coboundary.
2.3.4. Higher Degrees
- For even degrees : we have , and then with boundary terms. In conclusion, we have:
- For odd degrees : and then with boundary terms. In conclusion, we have:
3. Simplicial Information Cohomology
3.1. Simplicial Substructures of Information
3.2. Topological Self and Free Energy of K-Body Interacting System-Poincaré-Shannon Machine
Topological Self and Free Energy of K-Body Interacting Systems
3.3. k-Entropy and k-Information Landscapes
3.4. Information Paths and Minimum Free Energy Complex
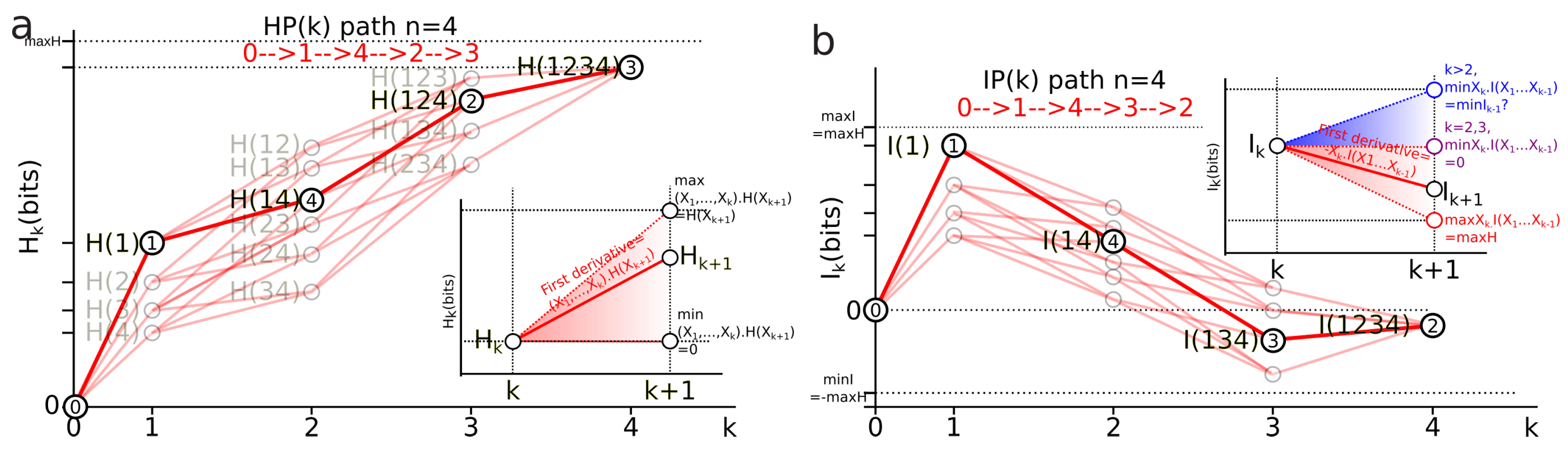
3.4.1. Information Paths (Definition)
3.4.2. Derivatives, Inequalities and Conditional Mutual-Information Negativity
Derivatives of information paths:
Bounds of the derivatives and information inequalities
- For , the conditional information is the conditional entropy and has the same usual bounds .
- For the conditional mutual information is always positive or null and hence ([92], p. 26, the opposite of Theorem 2.40, p. 30), whereas the higher limit is given by ([34] th. 2.17), with equality iff and are conditionally independent given and implying that the slope from to increases in the landscape.
- For , can be negative as a consequence of the preceding inequalities. In terms of information landscape this negativity means that the slope is positive, hence that the information path has crossed a critical point—a minimum. As expressed by Theorem due to Matsuda [34], iff . The minima correspond to zeros of conditional information (conditional independence) and hence detect cocycles in the data. The results on information inequalities define as “Shannonian” [133,134,135] the set of inequalities that are obtained from conditional information positivity () by linear combination, which forms a convex “positive” cone after closure. “Non-Shannonian” inequalities could also be exhibited [133,134], hence defining a new convex cone that includes and is strictly larger than the Shannonian set. Following Yeung’s nomenclature and to underline the relation with his work, we call the positive conditional mutual-information cone (the surface colored in red in Figure 4b) the “Shannonian” cone and the negative conditional mutual-information cone (the surface colored in blue in Figure 4b) the “non-Shannonian” cone.
3.4.3. Information Paths Are Random Processes: Topological Second Law of Thermodynamics and Entropy Rate
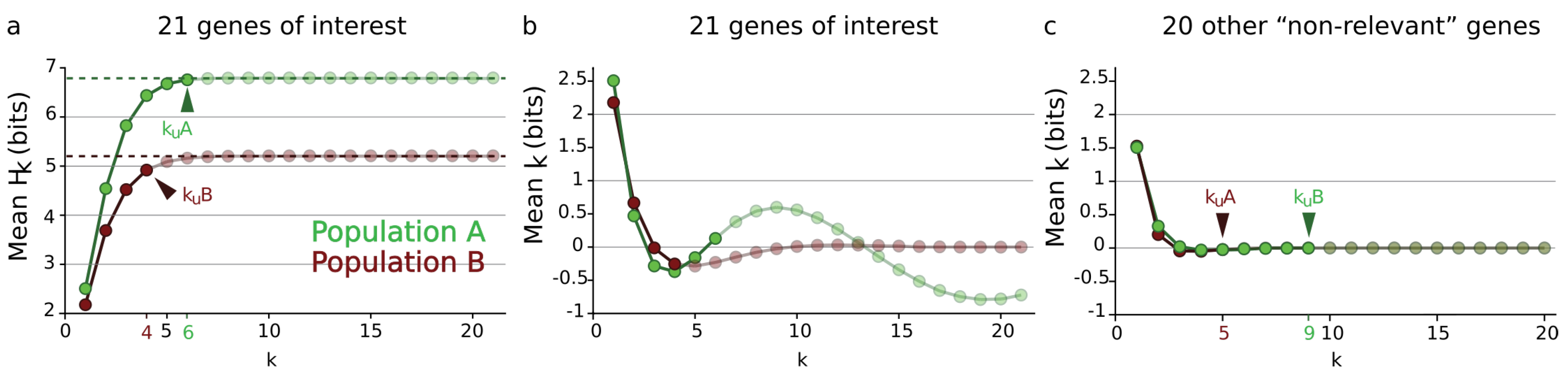
3.4.4. Local Minima and Critical Dimension
3.4.5. Sum over Paths and Mean Information Path
3.4.6. Minimum Free Energy Complex
4. Discussion
4.1. Statistical Physics
4.1.1. Statistical Physics without Statistical Limit? Complexity through Finite Dimensional Non-Extensivity
4.1.2. Naive Estimations Let the Data Speak
4.1.3. Discrete Informational Analog of Renormalization Methods: No Mean-Field Assumptions Let the Objects Differentiate
4.1.4. Combinatorial, Infinite, Continuous and Quantum Generalizations
4.2. Data Science
4.2.1. Topological Data Analysis
4.2.2. Unsupervised and Supervised Deep Homological Learning
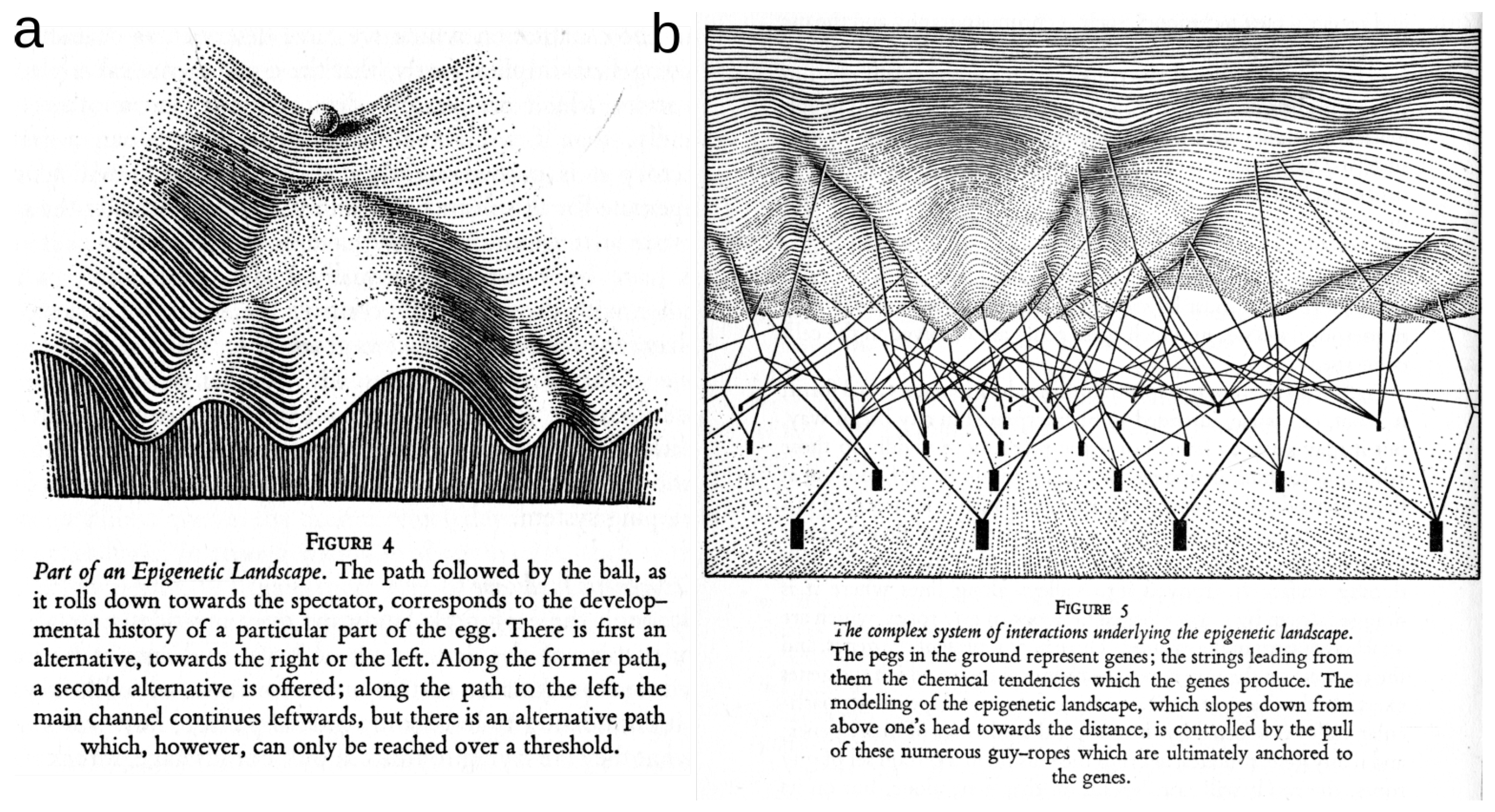
4.2.3. Epigenetic Topological Learning—Biological Diversity
5. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| iid | Independent identically distributed |
| Multivariate k-joint Entropy | |
| Multivariate k-mutual information | |
| Multivariate k-total-correlation or k-multi-information |
References
- Baudot, P.; Bennequin, D. The Homological Nature of Entropy. Entropy 2015, 17, 3253–3318. [Google Scholar] [CrossRef]
- Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, J.C. Topological Information Data Analysis. Entropy 2019, in press. [Google Scholar] [CrossRef]
- Tapia, M.; Baudot, P.; Formizano-Tréziny, C.; Dufour, M.; Temporal, S.; Lasserre, M.; Marquèze-Pouey, B.; Gabert, J.; Kobayashi, K.; Goaillard, J.M. Neurotransmitter identity and electrophysiological phenotype are genetically coupled in midbrain dopaminergic neurons. Sci. Rep. 2018, 8, 13637. [Google Scholar] [CrossRef] [PubMed]
- Mézard, M. Passing Messages Between Disciplines. Science 2003, 301, 1686. [Google Scholar] [CrossRef] [PubMed]
- Caramello, O. The unification of Mathematics via Topos Theory. arXiv 2010, arXiv:1006.3930. Available online: https://arxiv.org/abs/1006.3930 (accessed on 4 September 2019).
- Doering, A.; Isham, C. Classical and quantum probabilities as truth values. J. Math. Phys. 2012, 53, 032101. [Google Scholar] [CrossRef]
- Doering, A.; Isham, C. A Topos Foundation for Theories of Physics: I. Formal Languages for Physics. J. Math. Phys. 2008, 49, 053515. [Google Scholar] [CrossRef]
- Brillouin, L. Science and Information Theory; Academic Press: Cambridge, MA, USA, 1956. [Google Scholar]
- Jaynes, E. Information Theory and Statistical Mechanics II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–191. [Google Scholar] [CrossRef]
- Penrose, R. Angular Momentum: An Approach to Combinatorial Space-Time. In Quantum Theory and Beyondum; Cambridge University Press: Cambridge, UK, 1971; pp. 151–180. [Google Scholar]
- Wheeler, J. Information, Physics, Quantum: The Search for Links. In Complexity, Entropy, and the Physics of Information; Zureked, W.H., Ed.; CRC Press: New York, NY, USA, 1990. [Google Scholar]
- Bennett, C. Notes on Landauer’s principle, Reversible Computation and Maxwell’s Demon. Stud. Hist. Philos. Mod. Phys. 2003, 34, 501–510. [Google Scholar] [CrossRef]
- Wheeler, J.A. Physics and Austerity, Law Without Law; Numéro 122 de Pamhlets on Physics; Center for Theoretical Physics, University of Texas: Austin, TX, USA, 1982. [Google Scholar]
- Born, M. The Statistical Interpretation of Quantum Mechanics. Nobel Lecture. 1954. Available online: https://www.nobelprize.org/prizes/physics/1954/born/lecture/ (accessed on 4 September 2019).
- Baudot, P. Natural Computation: Much Ado about Nothing? An Intracellular Study of Visual Coding in Natural Condition. Ph.D. Thesis, Universit’e Pierre et Marie Curie-Paris VI, Paris, France, September 2006. [Google Scholar]
- Vigneaux, J. The Structure of Information: From Probability to Homology. arXiv 2017, arXiv:1709.07807. Available online: https://arxiv.org/abs/1709.07807 (accessed on 4 September 2019).
- Vigneaux, J. Topology of Statistical Systems. A Cohomological Approach to Information Theory. Ph.D. Thesis, Paris 7 Diderot University, Paris, France, June 2019. [Google Scholar]
- Marcolli, M.; Thorngren, R. Thermodynamic Semirings. arXiv 2011, arXiv:10.4171/JNCG/159. Available online: https://arxiv.org/abs/1108.2874 (accessed on 4 September 2019). [CrossRef]
- Maniero, T. Homological Tools for the Quantum Mechanic. arXiv 2019, arXiv:1901.02011. Available online: https://arxiv.org/abs/1901.02011 (accessed on 4 September 2019).
- Gerstenhaber, M.; Schack, S. A hodge-type decomposition for commutative algebra cohomology. J. Pure Appl. Algebr. 1987, 48, 229–247. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C. The lattice theory of information. In Transactions of the IRE Professional Group on Information Theory; IEEE: Piscataway, NJ, USA, 1953; Volume 1, pp. 105–107. [Google Scholar]
- Rajski, C. A metric space of discrete probability distributions. Inform. Control 1961, 4, 371–377. [Google Scholar] [CrossRef] [Green Version]
- Zurek, W. Thermodynamic cost of computation, algorithmic complexity and the information metric. Nature 1989, 341, 119–125. [Google Scholar] [CrossRef]
- Bennett, C.H.; Gács, P.; Li, M.; Vitányi, P.M.; Zurek, W.H. Information distance. IEEE Trans. Inf. Theory 1998, 44, 1407–1423. [Google Scholar] [CrossRef] [Green Version]
- Kraskov, A.; Grassberger, P. MIC: Mutual Information Based Hierarchical Clustering. In Information Theory and Statistical Learning; Springer: Boston, MA, USA, 2009; pp. 101–123. [Google Scholar]
- Crutchfield, J.P. Information and its metric. In Nonlinear Structures in Physical Systems; Springer: New York, NY, USA, 1990; pp. 119–130. [Google Scholar]
- Wu, F. The Potts model. Rev. Mod. Phys. 1982, 54, 235–268. [Google Scholar] [CrossRef]
- Turban, L. One-dimensional Ising model with multispin interactions. J. Phys. A-Math. Theor. 2016, 49, 355002. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W. Nobel Lecture: Electronic structure of matter—Wave functions and density functionals. Rev. Mod. Phys. 1999, 71, 1253. [Google Scholar] [CrossRef]
- Baez, J.; Pollard, S. Relative Entropy in Biological Systems. Entropy 2016, 18, 46. [Google Scholar] [CrossRef]
- Brenner, N.; Strong, S.P.; Koberle, R.; Bialek, W.; de Ruyter van Steveninck, R.R. Synergy in a neural code. Neural Comput. 2000, 12, 1531–1552. [Google Scholar] [CrossRef] [PubMed]
- Matsuda, H. Information theoretic characterization of frustrated systems. Physica A 2001, 294, 180–190. [Google Scholar] [CrossRef]
- Dunkel, J.; Hilbert, S. Phase transitions in small systems: Microcanonical vs. canonical ensembles. Physica A 2006, 370, 390–406. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.; Thomas, J. Elements of Information Theory; John Wiley & Sons: Chichester, UK, 1991. [Google Scholar]
- Noether, E. Invariant Variation Problems. Transport Theor. Stat. 1971, 1, 186–207. [Google Scholar] [CrossRef]
- Mansfield, E.L. Noether’s Theorem for Smooth, Difference and Finite Element Systems. In Foundations of Computational Mathematics, Santander; Cambridge University Press: Cambridge, UK, 2005; pp. 230–257. [Google Scholar]
- Baez, J.; Fong, B. A Noether theorem for Markov processes. J. Math. Phys. 2013, 54, 013301. [Google Scholar] [CrossRef] [Green Version]
- Neuenschwander, D. Noether’s theorem and discrete symmetries. Am. J. Phys. 1995, 63, 489. [Google Scholar] [CrossRef]
- Kadanoff, L.P. Phase Transitions: Scaling, Universality and Renormalization. Phase Transitions Dirac V2.4. 2010. Available online: https://jfi.uchicago.edu/~leop/TALKS/Phase 20TransitionsV2.4Dirac.pdf (accessed on 4 September 2019).
- Wilson, K.G.; Kogut, J. The renormalization group and the epsilon expansion. Phys. Rep. 1974, 12, 75–200. [Google Scholar] [CrossRef]
- Zinn-Justin, J. Phase Transitions and Renormalization Group; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Feynman, R. QED. The Strange Theory of Light and Matter; Princeton University Press: Princeton, NJ, USA, 1985. [Google Scholar]
- Dirac, P. Directions in Physics; John Wiley & Sons: Chichester, UK, 1978. [Google Scholar]
- Van der Waals, J.D. Over de Continuiteit van den Gas- en Vloeistoftoestand; Luitingh-Sijthoff: Amsterdam, The Netherlands, 1873. [Google Scholar]
- Maxwell, J. Van der Waals on the Continuity of the Gaseous and Liquid States. Nature 1874, 10, 407. [Google Scholar]
- Maxwell, J. On the dynamical evidence of the molecular constitution of bodies. Nature 1875, 1, 357–359. [Google Scholar] [CrossRef]
- Ellerman, D. An introduction to partition logic. Log. J. IGPL 2014, 22, 94–125. [Google Scholar] [CrossRef]
- Ellerman, D. The logic of partitions: introduction to the dual of the logic of subsets. In The Review of Symbolic Logic; Cambridge University Press: Cambridge, UK, 2010; Volume 3, pp. 287–350. [Google Scholar]
- James, R.; Crutchfield, J. Multivariate Dependence beyond Shannon Information. Entropy 2017, 19, 531. [Google Scholar] [CrossRef]
- Foster, D.; Foster, J.; Paczuski, M.; Grassberger, F. Communities, clustering phase transitions, and hysteresis: Pitfalls in constructing network ensembles. Phys. Rev. E 2010, 81, 046115. [Google Scholar] [CrossRef] [Green Version]
- Lum, P.; Singh, G.; Lehman, A.; Ishkanov, T.; Vejdemo-Johansson, M.; Alagappan, M.; Carlsson, J.; Carlsson, G. Extracting insights from the shape of complex data using topology. Sci. Rep. 2013, 3, 1236. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Epstein, C.; Carlsson, G.; Edelsbrunner, H. Topological data analysis. Inverse Probl. 2011, 27, 120201. [Google Scholar]
- Carlsson, G. Topology and data. Bull. Am. Math. Soc. 2009, 46, 255–308. [Google Scholar] [CrossRef] [Green Version]
- Niyogi, P.; Smale, S.; Weinberger, S. A Topological View of Unsupervised Learning from Noisy Data. SIAM J. Comput. 2011, 20, 646–663. [Google Scholar] [CrossRef]
- Buchet, M.; Chazal, F.; Oudot, S.; Sheehy, D. Efficient and Robust Persistent Homology for Measures. Comput. Geom. 2016, 58, 70–96. [Google Scholar] [CrossRef]
- Chintakunta, H.; Gentimis, T.; Gonzalez-Diaz, R.; Jimenez, M.J.; Krim, H. An entropy-based persistence barcode. Pattern Recognit. 2015, 48, 391–401. [Google Scholar] [CrossRef]
- Merelli, E.; Rucco, M.; Sloot, P.; Tesei, L. Topological Characterization of Complex Systems: Using Persistent Entropy. Entropy 2015, 17, 6872–6892. [Google Scholar] [CrossRef] [Green Version]
- Tadic, B.; Andjelkovic, M.; Suvakov, M. The influence of architecture of nanoparticle networks on collective charge transport revealed by the fractal time series and topology of phase space manifolds. J. Coupled Syst. Multiscale Dyn. 2016, 4, 30–42. [Google Scholar] [CrossRef]
- Maletic, S.; Rajkovic, M. Combinatorial Laplacian and entropy of simplicial complexes associated with complex networks. Eur. Phys. J. 2012, 212, 77–97. [Google Scholar] [CrossRef]
- Maletic, S.; Zhao, Y. Multilevel Integration Entropies: The Case of Reconstruction of Structural Quasi-Stability in Building Complex Datasets. Entropy 2017, 19, 172. [Google Scholar] [CrossRef]
- Baudot, P.; Bernardi, M. Information Cohomology Methods for Learning the Statistical Structures of Data. DS3 Data Science, Ecole Polytechnique. 2019. Available online: https://www.ds3-datascience-polytechnique.fr/wp-content/uploads/2019/06/DS3-426_2019_v2.pdf (accessed on 4 September 2019).
- Hopfield, J. Neural Networks and Physical Systems with Emergent Collective Computational Abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Ackley, D.; Hinton, G.; Sejnowski, T.J. A Learning Algorithm for Boltzmann Machines. Cogn. Sci. 1985, 9, 147–169. [Google Scholar] [CrossRef]
- Dayan, P.; Hinton, G.; Neal, R.; Zemel, R. The Helmholtz Machine. Neural Comput. 1995, 7, 889–904. [Google Scholar] [CrossRef]
- Baudot, P. Elements of Consciousness and Cognition. Biology, Mathematic, Physics and Panpsychism: An Information Topology Perspective. arXiv 2018, arXiv:1807.04520. Available online: https://arxiv.org/abs/1807.04520 (accessed on 4 September 2019).
- Port, A.; Gheorghita, I.; Guth, D.; Clark, J.; Liang, C.; Dasu, S.; Marcolli, M. Persistent Topology of Syntax. In Mathematics in Computer Science; Springer: Berlin/Heidelberger, Germany, 2018; Volume 1, pp. 33–50. [Google Scholar]
- Marr, D. Vision; MIT Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Poincare, H. Analysis Situs. Journal de l’École Polytechnique 1895, 1, 1–121. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Labs Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Andre, Y. Symétries I. Idées Galoisiennes; Chap 4 of Leçons de Mathématiques Contemporaines à l’IRCAM, Master; cel-01359200; IRCAM: Paris, France, 2009; Available online: https://cel.archives-ouvertes.fr/cel-01359200 (accessed on 5 september 2019).
- Andre, Y. Ambiguity theory, old and new. arXiv 2008, arXiv:0805.2568. Available online: https://arxiv.org/abs/0805.2568 (accessed on 4 September 2019).
- Yeung, R. On Entropy, Information Inequalities, and Groups. In Communications, Information and Network Security; Springer: Boston, MA, USA, 2003; Volume 712, pp. 333–359. [Google Scholar]
- Cathelineau, J. Sur l’homologie de sl2 a coefficients dans l’action adjointe. Math. Scand. 1988, 63, 51–86. [Google Scholar] [CrossRef]
- Kontsevitch, M. The 11/2 Logarithm. 1995; Unpublished work. [Google Scholar]
- Elbaz-Vincent, P.; Gangl, H. On poly(ana)logs I. Compos. Math. 2002, 130, 161–214. [Google Scholar] [CrossRef]
- Elbaz-Vincent, P.; Gangl, H. Finite polylogarithms, their multiple analogues and the Shannon entropy. In International Conference on Geometric Science of Information; Springer: Berlin/Heidelberger, Germany, 2015. [Google Scholar]
- Connes, A.; Consani, C. Characteristic 1, entropy and the absolute point. In Noncommutative Geometry, Arithmetic, and Related Topics; JHU Press: Baltimore, MD, USA, 2009. [Google Scholar]
- Marcolli, M.; Tedeschi, R. Entropy algebras and Birkhoff factorization. J. Geom. Phys. 2018, 97, 243–265. [Google Scholar] [CrossRef]
- Baez, J.; Fritz, T.; Leinster, T. A Characterization of Entropy in Terms of Information Loss. Entropy 2011, 13, 1945–1957. [Google Scholar] [CrossRef]
- Baez, J.C.; Fritz, T. A Bayesian characterization of relative entropy. Theory Appl. Categ. 2014, 29, 422–456. [Google Scholar]
- Boyom, M. Foliations-Webs-Hessian Geometry-Information Geometry-Entropy and Cohomology. Entropy 2016, 18, 433. [Google Scholar] [CrossRef]
- Drummond-Cole, G.; Park, J.S.; Terilla, J. Homotopy probability theory I. J. Homotopy Relat. Struct. 2015, 10, 425–435. [Google Scholar] [CrossRef]
- Drummond-Cole, G.; Park, J.S.; Terilla, J. Homotopy probabilty Theory II. J. Homotopy Relat. Struct. 2015, 10, 623–635. [Google Scholar] [CrossRef]
- Park, J.S. Homotopy Theory of Probability Spaces I: Classical independence and homotopy Lie algebras. aiXiv 2015, arXiv:1510.08289. Available online: https://arxiv.org/abs/1510.08289 (accessed on 4 September 2019).
- Beilinson, A.; Goncharov, A.; Schechtman, V.; Varchenko, A. Aomoto dilogarithms, mixed Hodge structures and motivic cohomology of pairs of triangles on the plane. In The Grothendieck Festschrift; Birkhäuser: Boston, MA, USA, 1990; Volume 1, pp. 135–172. [Google Scholar]
- Aomoto, K. Addition theorem of Abel type for Hyper-logarithms. Nagoya Math. J. 1982, 88, 55–71. [Google Scholar] [CrossRef]
- Goncharov, A. Regulators; Springer: Berlin/Heidelberger, Germany, 2005; pp. 297–324. [Google Scholar]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Hu, K.T. On the Amount of Information. Theory Probab. Appl. 1962, 7, 439–447. [Google Scholar]
- Yeung, R. Information Theory and Network Coding; Springer: Berlin/Heidelberger, Germany, 2007. [Google Scholar]
- McGill, W. Multivariate information transmission. Psychometrika 1954, 19, 97–116. [Google Scholar] [CrossRef]
- Watanabe, S. Information theoretical analysis of multivariate correlation. IBM J. Res. Dev. 1960, 4, 66–81. [Google Scholar] [CrossRef]
- Tononi, G.; Edelman, G. Consciousness and Complexity. Science 1998, 282, 1846–1851. [Google Scholar] [CrossRef]
- Studeny, M.; Vejnarova, J. The multiinformation function as a tool for measuring stochastic dependence. In Learning in Graphical Models; MIT Press: Cambridge, MA, USA, 1999; pp. 261–296. [Google Scholar]
- Margolin, A.; Wang, K.; Califano, A.; Nemenman, I. Multivariate dependence and genetic networks inference. IET Syst. Biol. 2010, 4, 428–440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Andrews, G. The Theory of Partitions; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Fresse, B. Koszul duality of operads and homology of partitionn posets. Contemp. Math. Am. Math. Soc. 2004, 346, 115–215. [Google Scholar]
- Hochschild, G. On the cohomology groups of an associative algebra. Ann. Math. 1945, 46, 58–67. [Google Scholar] [CrossRef]
- Weibel, C. An Introduction to Homological Algebra; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Kassel, C. Homology and Cohomology of Associative Algebras—A Concise Introduction to Cyclic Homology. Advanced Course on Non-Commutative Geometry. 2004. Available online: https://cel.archives-ouvertes.fr/cel-00119891/ (accessed on 4 September 2019).
- Tate, J. Galois Cohomology; Springer Science & Business Media: Berlin/Heidelberger, Germany, 1991. [Google Scholar]
- Cartan, H.; Eilenberg, S. Homological Algebra; Princeton University Press: Princeton, NJ, USA, 1956. [Google Scholar]
- Mac Lane, S. Homology; Springer Science & Business Media: Berlin/Heidelberger, Germany, 1975. [Google Scholar]
- Kendall, D. Functional Equations in Information Theory. Probab. Theory Relat. Field 1964, 2, 225–229. [Google Scholar] [CrossRef]
- Lee, P. On the Axioms of Information Theory. Ann. Math. Stat. 1964, 35, 415–418. [Google Scholar] [CrossRef]
- Baudot, P.; Tapia, M.; Goaillard, J. Topological Information Data Analysis: Poincare-Shannon Machine and Statistical Physic of Finite Heterogeneous Systems. Preprints 2018040157. 2018. Available online: https://www.preprints.org/manuscript/201804.0157/v1 (accessed on 5 September 2019).
- Lamarche-Perrin, R.; Demazeau, Y.; Vincent, J. The Best-partitions Problem: How to Build Meaningful Aggregations? In Proceedings of the 2013 IEEE/WIC/ACM International Joint Conferences on Web Intelligence (WI) and Intelligent Agent Technologies (IAT), Atlanta, GA, USA, 17–20 November 2013; 2013; p. 18. [Google Scholar]
- Pudlák, P.; Tůma, J. Every finite lattice can be embedded in a finite partition lattice. Algebra Univ. 1980, 10, 74–95. [Google Scholar] [CrossRef]
- Gerstenhaber, M.; Schack, S. Simplicial cohomology is Hochschild Cohomology. J. Pure Appl. Algebr. 1983, 30, 143–156. [Google Scholar] [CrossRef]
- Steenrod, N. Products of Cocycles and Extensions of Mapping. Ann. Math. 1947, 48, 290–320. [Google Scholar] [CrossRef]
- Atiyah, M. Topological quantum field theory. Publ. Math. IHÉS 1988, 68, 175–186. [Google Scholar] [CrossRef]
- Witten, E. Topological Quantum Field Theory. Commun. Math. Phys. 1988, 117, 353–386. [Google Scholar] [CrossRef]
- Schwarz, A. Topological Quantum Field Theory. arXiv 2000, arXiv:hep-th/0011260v1. Available online: https://arxiv.org/abs/hep-th/0011260 (accessed on 4 September 2019).
- Reshef, D.; Reshef, Y.; Finucane, H.; Grossman, S.; McVean, G.; Turnbaugh, P.; Lander, E.; Mitzenmacher, M.; Sabeti, P. Detecting Novel Associations in Large Data Sets. Science 2011, 334, 1518. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Wheeler, J. Information, Physics, quantum: The search for the links. In Proceedings of the 3rd International Symposium on Foundations of Quantum Mechanics, Tokyo, Japan, 28–31 August 1989; pp. 354–368. [Google Scholar]
- Von Bahr, B. On the central limit theorem in Rk. Ark. Mat. 1967, 7, 61–69. [Google Scholar] [CrossRef]
- Ebrahimi, N.; Soofi, E.; Soyer, R. Multivariate maximum entropy identification, transformation, and dependence. J. Multivar. Anal. 2008, 99, 1217–1231. [Google Scholar] [CrossRef] [Green Version]
- Conrad, K. Probability distributions and maximum entropy. Entropy 2005, 6, 10. [Google Scholar]
- Adami, C.; Cerf, N. Prolegomena to a non-equilibrium quantum statistical mechanics. Chaos Solition Fract. 1999, 10, 1637–1650. [Google Scholar]
- Kapranov, M. Thermodynamics and the moment map. arXiv 2011, arXiv:1108.3472. Available online: https://arxiv.org/pdf/1108.3472.pdf (accessed on 4 September 2019).
- Erdos, P. On the distribution function of additive functions. Ann. Math. 1946, 47, 1–20. [Google Scholar] [CrossRef]
- Aczel, J.; Daroczy, Z. On Measures of Information and Their Characterizations; Academic Press: Cambridge, MA, USA, 1975. [Google Scholar]
- Lifshitz, E.M.; Landau, L.D. Statistical Physics (Course of Theoretical Physics, Volume 5); Butterworth-Heinemann: Oxford, UK, 1969. [Google Scholar]
- Han, T.S. Linear dependence structure of the entropy space. Inf. Control 1975, 29, 337–368. [Google Scholar] [CrossRef] [Green Version]
- Bjorner, A. Continuous partition lattice. Proc. Natl. Acad. Sci. USA 1987, 84, 6327–6329. [Google Scholar] [CrossRef] [Green Version]
- Postnikov, A. Permutohedra, Associahedra, and Beyond. Int. Math. Res. Not. 2009, 2009, 1026–1106. [Google Scholar] [CrossRef] [Green Version]
- Matus, F. Conditional probabilities and permutahedron. In Annales de l’Institut Henri Poincare (B) Probability and Statistics; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Yeung, R. Facets of entropy. In Communications in Information and Systems; International Press of Boston: Somerville, MA, USA, 2015; Volume 15, pp. 87–117. [Google Scholar]
- Yeung, R. A framework for linear information inequalities. IEEE Trans. Inf. Theory 1997, 43, 1924–1934. [Google Scholar] [CrossRef] [Green Version]
- Zang, Z.; Yeung, R.W. On Characterization of Entropy Function via Information Inequalities. IEEE Trans. Inf. Theory 1997, 44, 1440–1452. [Google Scholar] [CrossRef]
- Matúš, F. Infinitely Many Information Inequalities. ISIT 2007, 41–47. [Google Scholar] [CrossRef]
- Takacs, D. Stochastic Processes Problems and Solutions; John Wiley & Sons: Chichester, UK, 1960. [Google Scholar]
- Bourbaki, N. Theory of Sets-Elements of Mathematic; Addison Wesley: Boston, MA, USA, 1968. [Google Scholar]
- Brillouin, L. Scientific Uncertainty, and Information; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Griffiths, R. Consistent Histories and the Interpretation of Quantum Mechanics. J. Stat. Phys. 1984, 35, 219. [Google Scholar] [CrossRef]
- Omnes, R. Logical reformulation of quantum mechanics I. Foundations. J. Stat. Phys. 1988, 53, 893–932. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Hartle, J. Quantum mechanics in the light of quantum cosmology. In Complexity, Entropy, and the Physics of Information; Zurek, W., Ed.; Addison-Wesley: Boston, MA, USA, 1990; pp. 425–458. [Google Scholar]
- Lieb, E.H.; Yngvason, J. A Guide to Entropy and the Second Law of Thermodynamics. In Statistical Mechanics; Springer: Berlin/Heidelberger, Germany, 1998; Volume 45, pp. 571–581. [Google Scholar]
- Feynman, R. Space-Time Approach to Non-Relativistic Quantum Mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef] [Green Version]
- Merkh, T.; Montufar, G. Factorized Mutual Information Maximization. arXiv 2019, arXiv:1906.05460. Available online: https://arxiv.org/abs/1906.05460 (accessed on 4 September 2019).
- Weiss, P. L’hypothèse du champ moléculaire et la propriété ferromagnétique. J. Phys. Theor. Appl. 1907, 6, 661–690. [Google Scholar] [CrossRef]
- Parsegian, V. Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Xie, Z.; Chen, J.; Yu, J.; Kong, X.; Normand, B.; Xiang, T. Tensor Renormalization of Quantum Many-Body Systems Using Projected Entangled Simplex States. Phys. Rev. X 2014, 4, 011025. [Google Scholar] [CrossRef] [Green Version]
- Hà, H.T.; Van Tuyl, A. Resolutions of square-free monomial ideals via facet ideals: A survey. arXiv 2006, arXiv:math/0604301. Available online: https://arxiv.org/abs/math/0604301 (accessed on 4 September 2019).
- Newman, M.E.J. Complex Systems: A Survey. arXiv 2011, arXiv:1112.1440v1. Available online: http://arxiv.org/abs/1112.1440v1 (accessed on 4 September 2019).
- Mezard, M.; Montanari, A. Information, Physics, and Computation; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Vannimenus, J.; Toulouse, G. Theory of the frustration effect. II. Ising spins on a square lattice. J. Phys. Condens. Matter 1977, 10, 115. [Google Scholar] [CrossRef]
- Rovelli, C. Notes for a brief history of quantum gravity. arXiv 2008, arXiv:gr-qc/0006061v3. Available online: https://arxiv.org/pdf/gr-qc/0006061.pdf (accessed on 4 September 2019).
- Sorkin, R. Finitary Substitute for Continuous Topology. Int. J. Theor. Phys. 1991, 30, 923–947. [Google Scholar] [CrossRef]
- Strong, S.P.; Van Steveninck, R.D.R.; Bialek, W.; Koberle, R. On the application of information theory to neural spike trains. In Proceedings of the Pacific Symposium on Biocomputing, Maui, HI, USA, 4–9 January 1998; pp. 621–632. [Google Scholar]
- Niven, R. Non-asymptotic thermodynamic ensembles. EPL 2009, 86, 1–6. [Google Scholar] [CrossRef]
- Niven, R. Combinatorial entropies and statistics. Eur. Phys. J. 2009, 70, 49–63. [Google Scholar] [CrossRef]
- Niven, R. Exact Maxwell–Boltzmann, Bose–Einstein and Fermi–Dirac statistics. Phys. Lett. A 2005, 342, 286–293. [Google Scholar] [CrossRef]
- Grassberger, P. Toward a quantitative theory of self-generated complexity. Int. J. Theor. Phys. 1986, 25, 907–938. [Google Scholar] [CrossRef]
- Bialek, W.; Nemenman, I.; Tishby, N. Complexity through nonextensivity. Physica A 2001, 302, 89–99. [Google Scholar] [CrossRef] [Green Version]
- Tsallis, C. Entropic Nonextensivity: A possible measure of Complexity. Chaos Solition Fract. 2002, 13, 371–391. [Google Scholar] [CrossRef]
- Ritort, F. Nonequilibrium fluctuations in small systems: From physics to biology. Adv. Chem. Phys. 2008, 137, 31–123. [Google Scholar]
- Artin, M.; Grothendieck, A.; Verdier, J. Theorie des Topos et Cohomologie Etale des Schemas—(SGA 4) Vol I, II, III; Springer: Berlin/Heidelberger, Germany, 1972. [Google Scholar]
- Kolmogorov, A.N. Grundbegriffe der Wahrscheinlichkeitsrechnung; Springer: Berlin/Heidelberger, Germany, 1933. [Google Scholar]
- Tkacik, G.; Marre, O.; Amodei, D.; Schneidman, E.; Bialek, W.; Berry, M.N. Searching for collective behavior in a large network of sensory neurons. PLoS Comput. Biol. 2014, 10, e1003408. [Google Scholar] [CrossRef] [PubMed]
- Vigneaux, J. Information theory with finite vector spaces. IEEE Trans. Inf. Theory 2019, 99, 1. [Google Scholar] [CrossRef]
- Wada, T.; Suyari, H. The k-Generalizations of Stirling Approximation and Multinominal Coefficients. Entropy 2013, 15, 5144–5153. [Google Scholar] [CrossRef]
- Cerf, N.; Adami, C. Negative entropy and information in quantum mechanic. Phys. Rev. Lett. 1997, 79, 5194. [Google Scholar] [CrossRef]
- Cerf, N.; Adami, C. Entropic Bell Inequalities. Phys. Rev. A 1997, 55, 3371. [Google Scholar] [CrossRef]
- Oudot, S. Persistence Theory: From Quiver Representations to Data Analysis; American Mathematical Society: Providence, RI, USA, 2015; Volume 209. [Google Scholar]
- Schneider, G. Two visual systems. Science 1969, 163, 895–902. [Google Scholar] [CrossRef] [PubMed]
- Goodale, M.; Milner, A. Separate visual pathways for perception and action. Trends Neurosci. 1992, 15, 20–25. [Google Scholar] [CrossRef]
- Kelley, H. Gradient theory of optimal flight paths. ARS 1960, 30, 947–954. [Google Scholar] [CrossRef]
- Dreyfus, S. The numerical solution of variational problems. J. Math. Anal. Appl. 1962, 5, 30–45. [Google Scholar] [CrossRef] [Green Version]
- Rumelhart, D.; Hinton, G.; Williams, R. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Montufar, G.; Morton, J. Discrete Restricted Boltzmann Machines. J. Mach. Learn. Res. 2015, 21, 653–672. [Google Scholar]
- Amari, S. Neural learning in structured parameter spaces—Natural Riemannian gradient. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 127–133. [Google Scholar]
- Martens, J. New Insights and Perspectives on the Natural Gradient Method. arXiv 2017, arXiv:1412.1193. Available online: https://arxiv.org/abs/1412.1193 (accessed on 4 September 2019).
- Bengtsson, I.; Zyczkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Pascanu, R.; Bengio, Y. Revisiting Natural Gradient for Deep Networks. arXiv 2014, arXiv:1301.3584. Available online: https://arxiv.org/abs/1301.3584 (accessed on 4 September 2019).
- Waddington, C.H. The Strategy of the Genes; Routledge: Abingdon-on-Thames, UK, 1957. [Google Scholar]
- Teschendorff, A.; Enver, T. Single-cell entropy for accurate estimation of differentiation potency from a cell’s transcriptome. Nat. Commun. 2017, 8, 15599. [Google Scholar] [CrossRef]
- Jin, S.; MacLean, A.; Peng, T.; Nie, Q. scEpath: Energy landscape-based inference of transition probabilities and cellular trajectories from single-cell transcriptomic data. Bioinformatics 2018, 34, 2077–2086. [Google Scholar] [CrossRef] [PubMed]
- Thom, R. Stabilite struturelle et morphogenese. Poetics 1974, 3, 7–19. [Google Scholar] [CrossRef]
- Linsker, R. Self-organization in a perceptual network. Computer 1988, 21, 105–117. [Google Scholar] [CrossRef]
- Nadal, J.P.; Parga, N. Sensory coding: information maximization and redundancy reduction. In Proceedings of the Neuronal Information Processing, Cargèse, France, 30 June–12 July 1997; World Scientific: Singapore, 1999; Volume 7, pp. 164–171. [Google Scholar]
- Bell, A.J.; Sejnowski, T. An information maximisation approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Glazier, J.; Izaguirre, J.; Alber, M. A parallel implementation of the Cellular Potts Model for simulation of cell-based morphogenesis. Comput. Phys. Commun. 2007, 176, 670–681. [Google Scholar] [CrossRef] [Green Version]
- Galvan, A. Neural plasticity of development and learning. Hum. Brain Mapp. 2010, 31, 879–890. [Google Scholar] [CrossRef]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baudot, P. The Poincaré-Shannon Machine: Statistical Physics and Machine Learning Aspects of Information Cohomology. Entropy 2019, 21, 881. https://doi.org/10.3390/e21090881
Baudot P. The Poincaré-Shannon Machine: Statistical Physics and Machine Learning Aspects of Information Cohomology. Entropy. 2019; 21(9):881. https://doi.org/10.3390/e21090881
Chicago/Turabian StyleBaudot, Pierre. 2019. "The Poincaré-Shannon Machine: Statistical Physics and Machine Learning Aspects of Information Cohomology" Entropy 21, no. 9: 881. https://doi.org/10.3390/e21090881
APA StyleBaudot, P. (2019). The Poincaré-Shannon Machine: Statistical Physics and Machine Learning Aspects of Information Cohomology. Entropy, 21(9), 881. https://doi.org/10.3390/e21090881



