Darcy–Forchheimer MHD Couple Stress 3D Nanofluid over an Exponentially Stretching Sheet through Cattaneo–Christov Convective Heat Flux with Zero Nanoparticles Mass Flux Conditions
Abstract
:1. Introduction
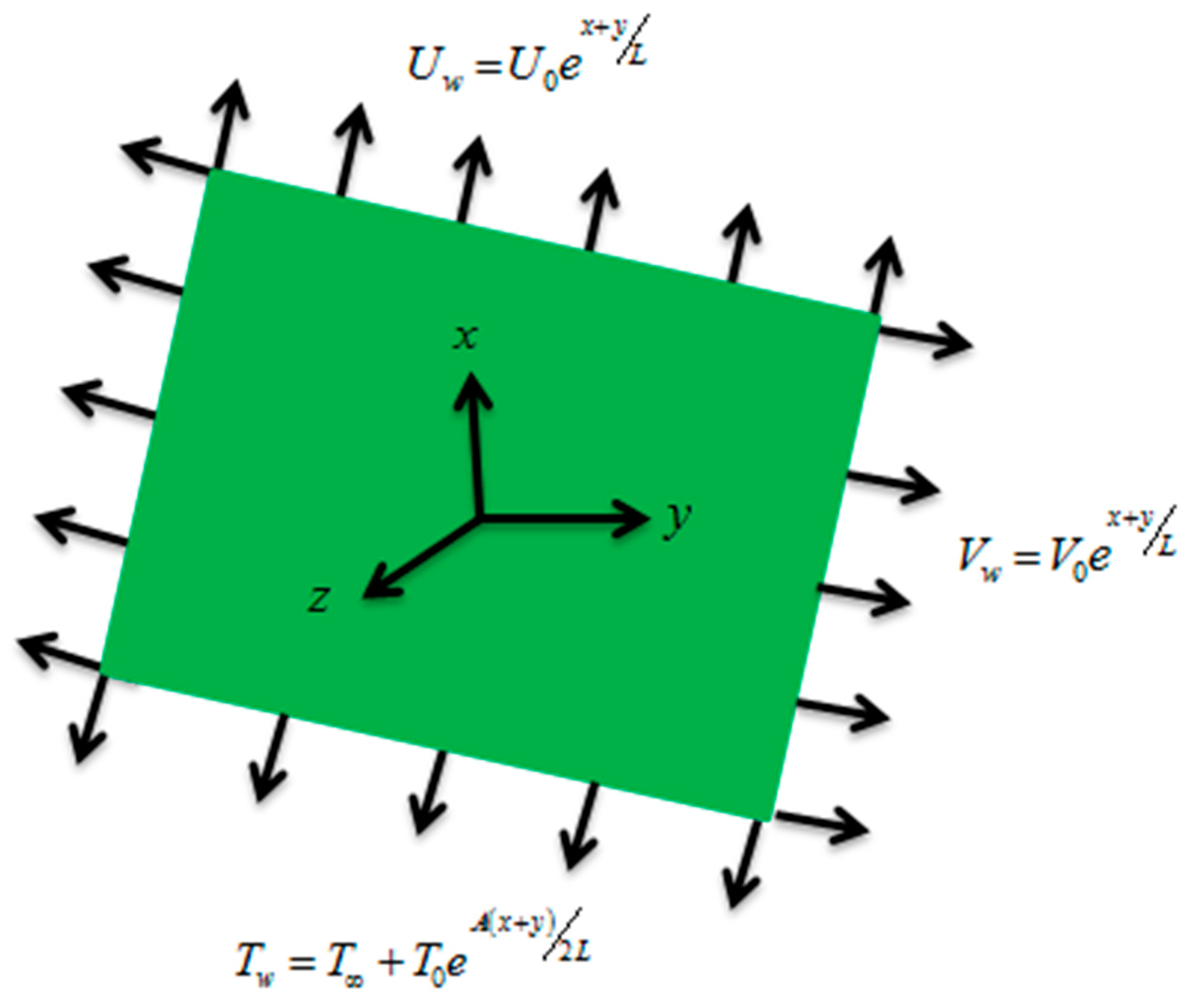
2. Problem Formulation
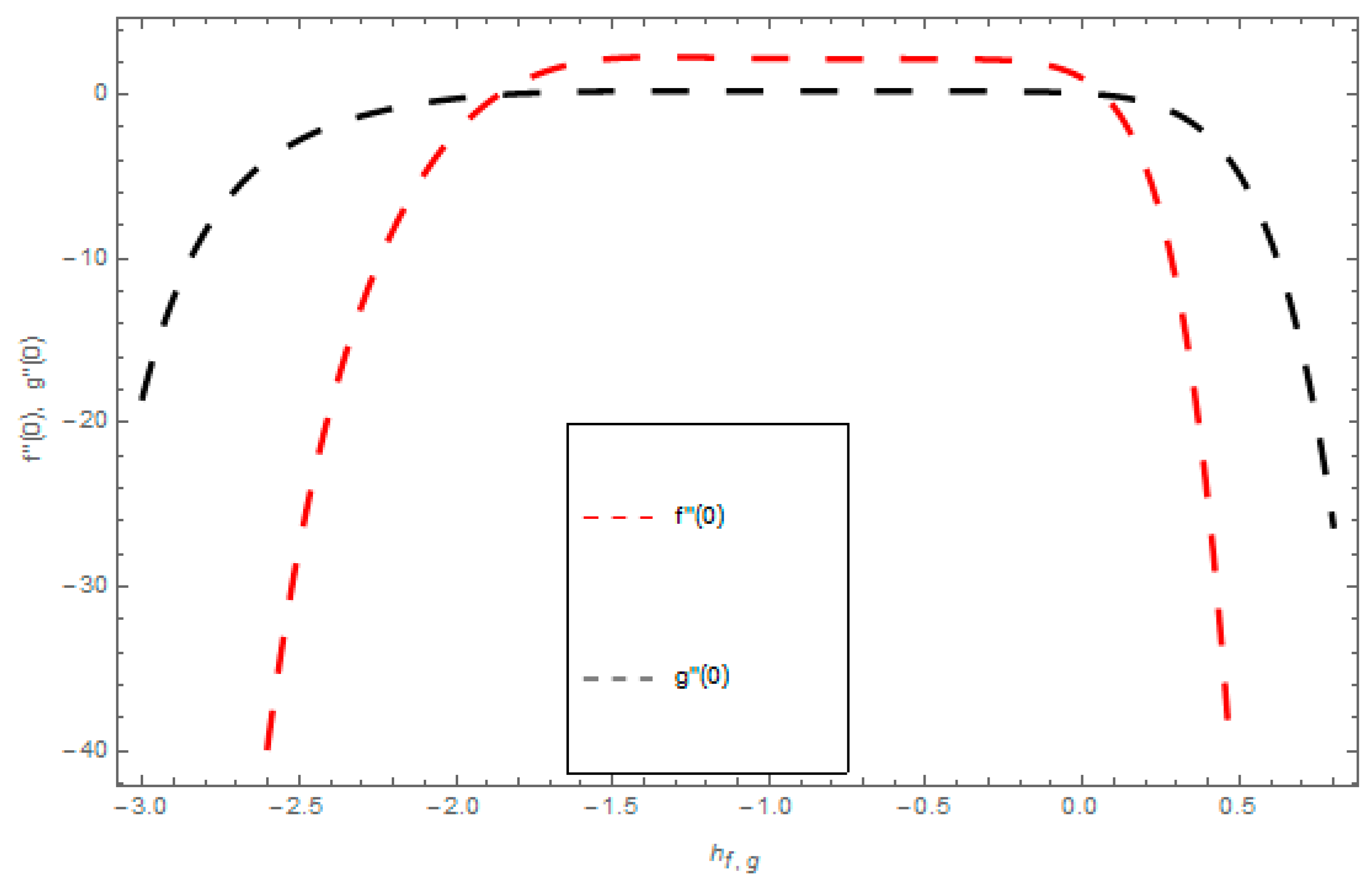
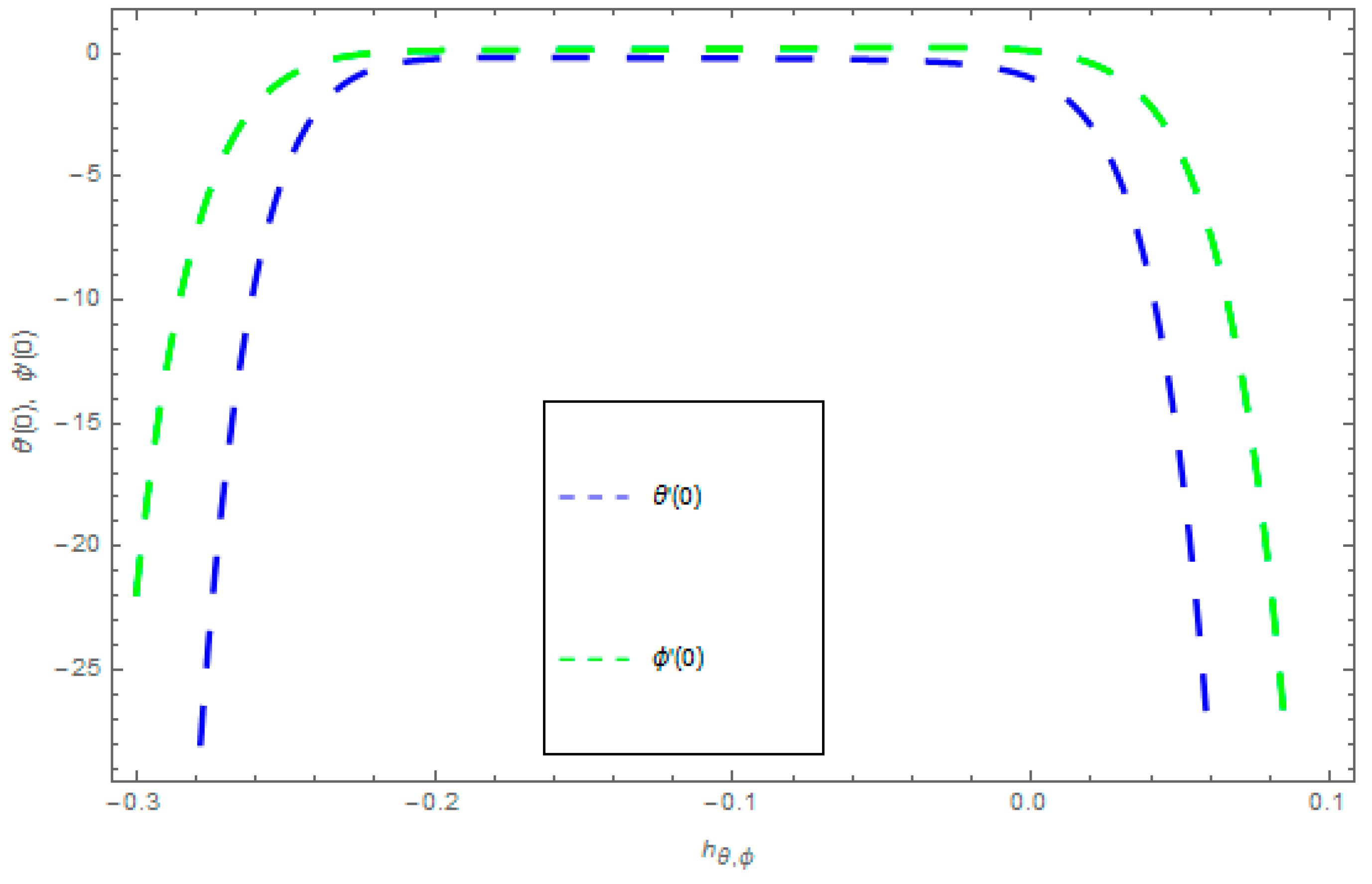
3. Solution by HAM
4. HAM Convergence
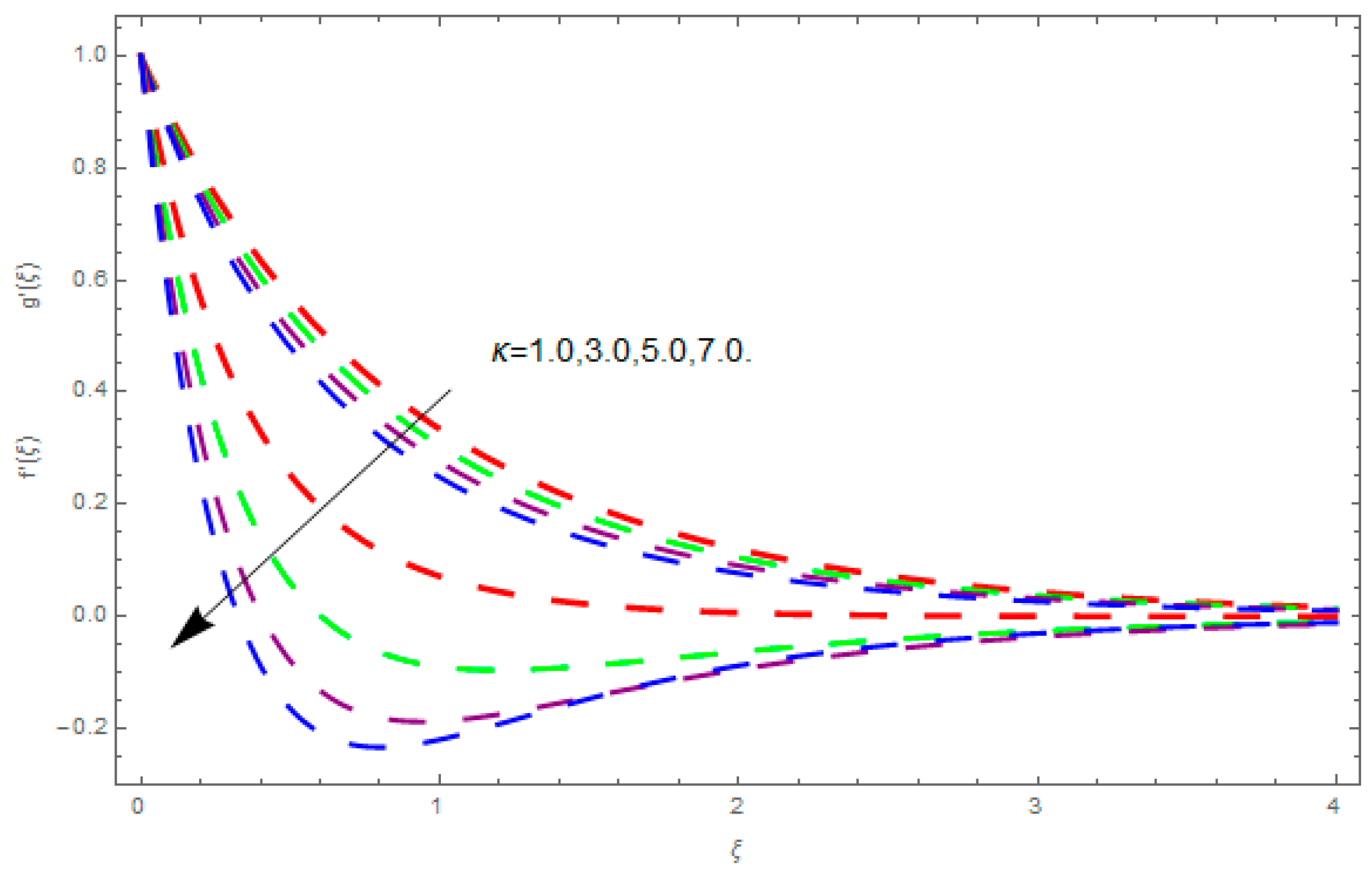
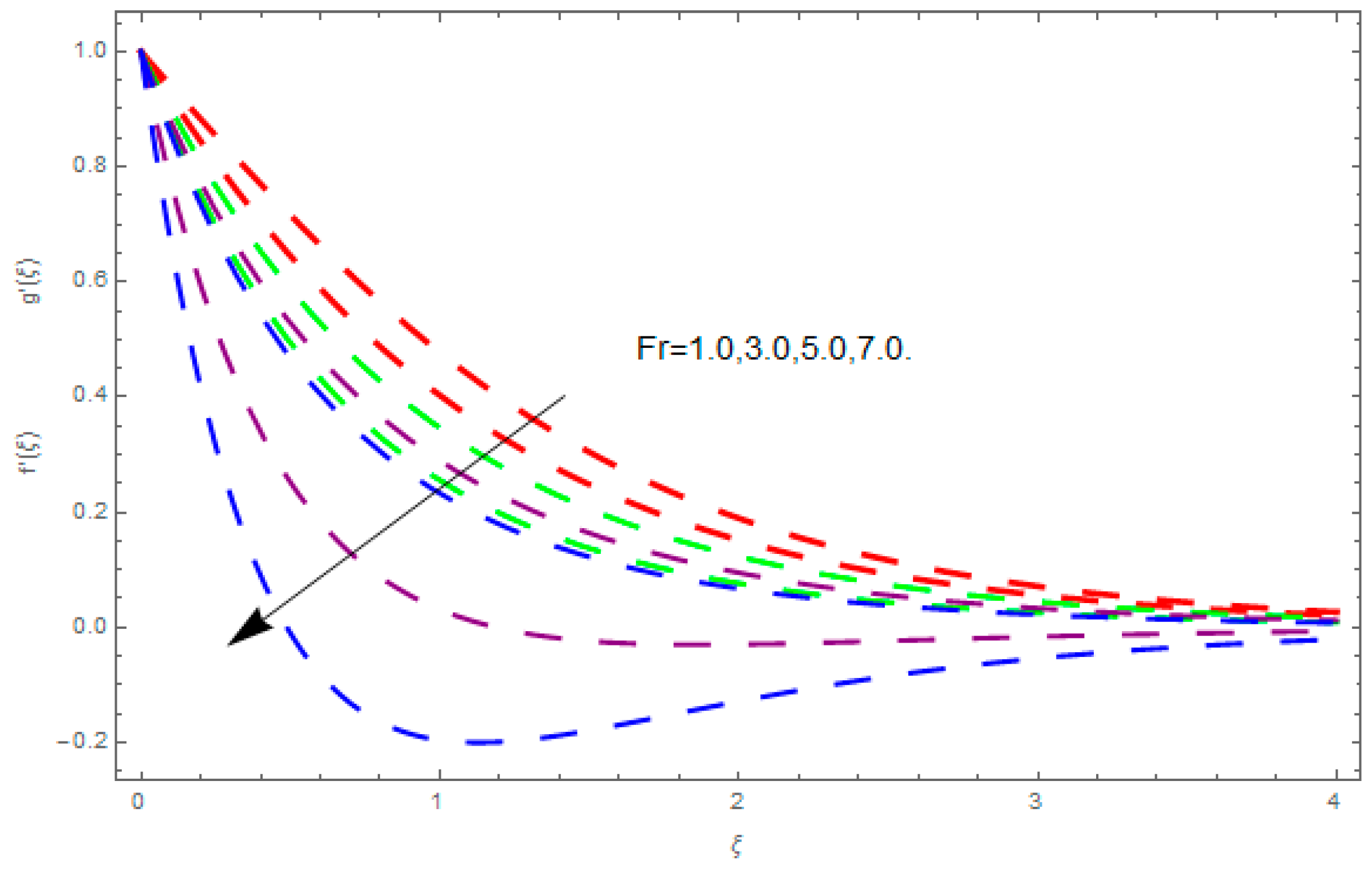
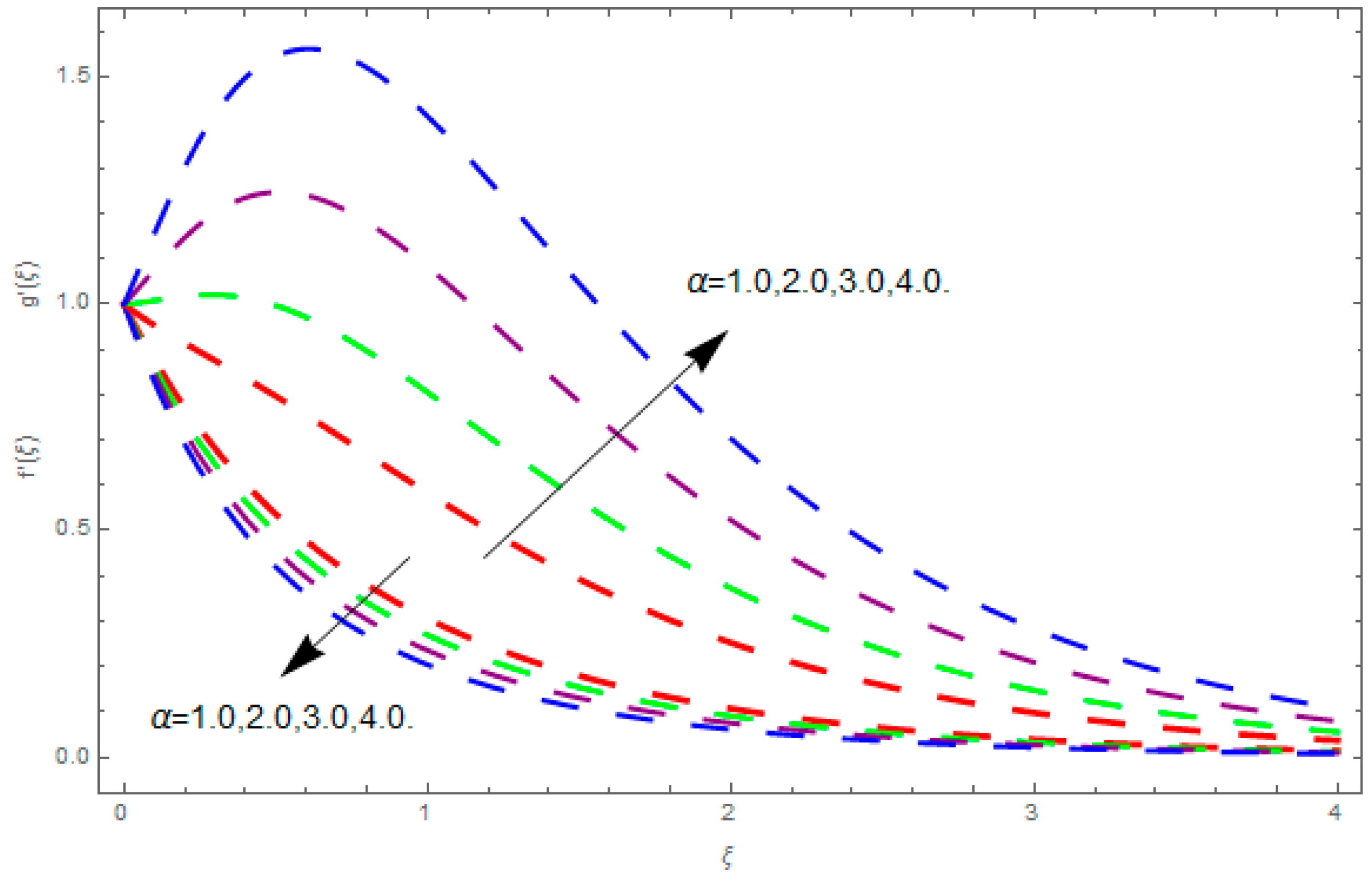
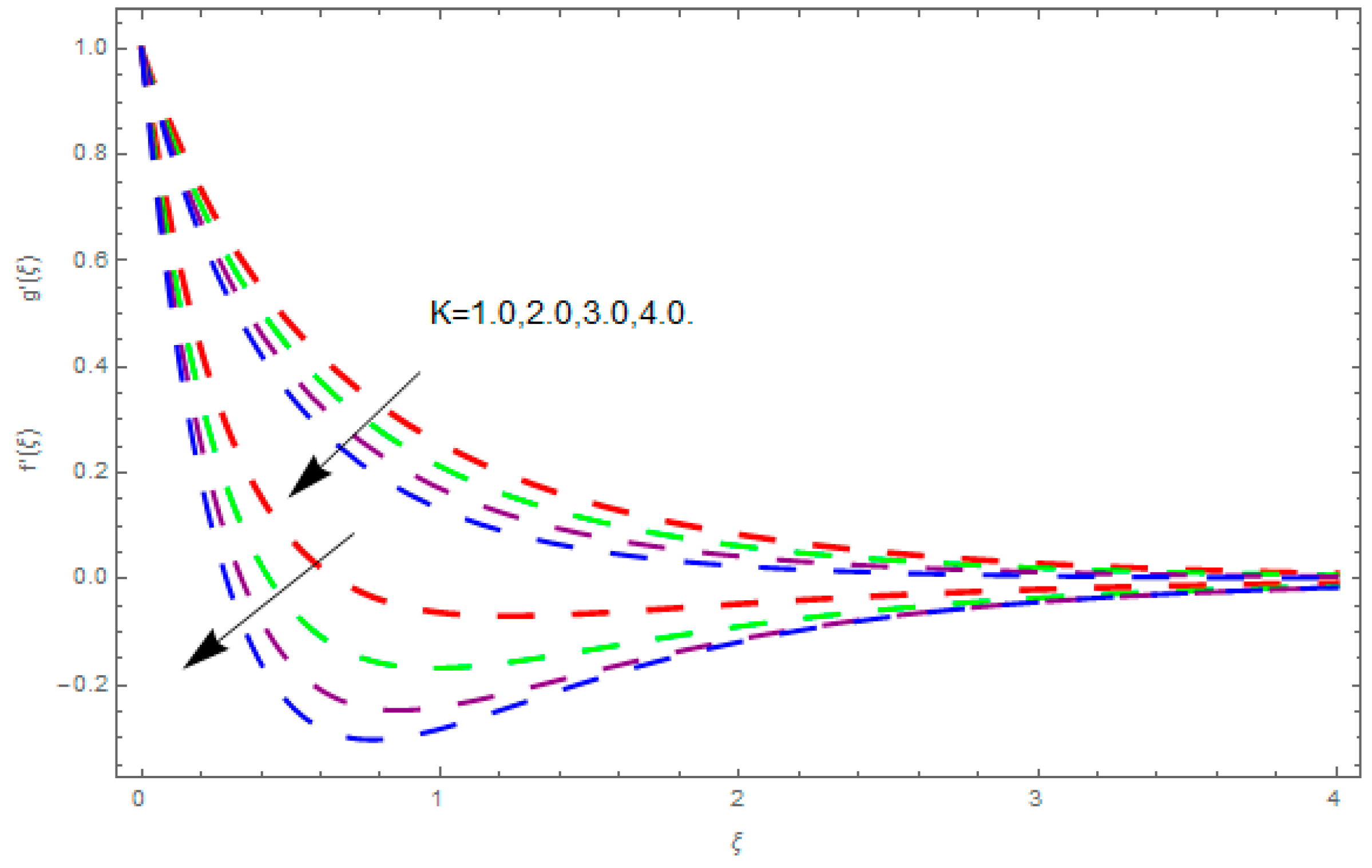
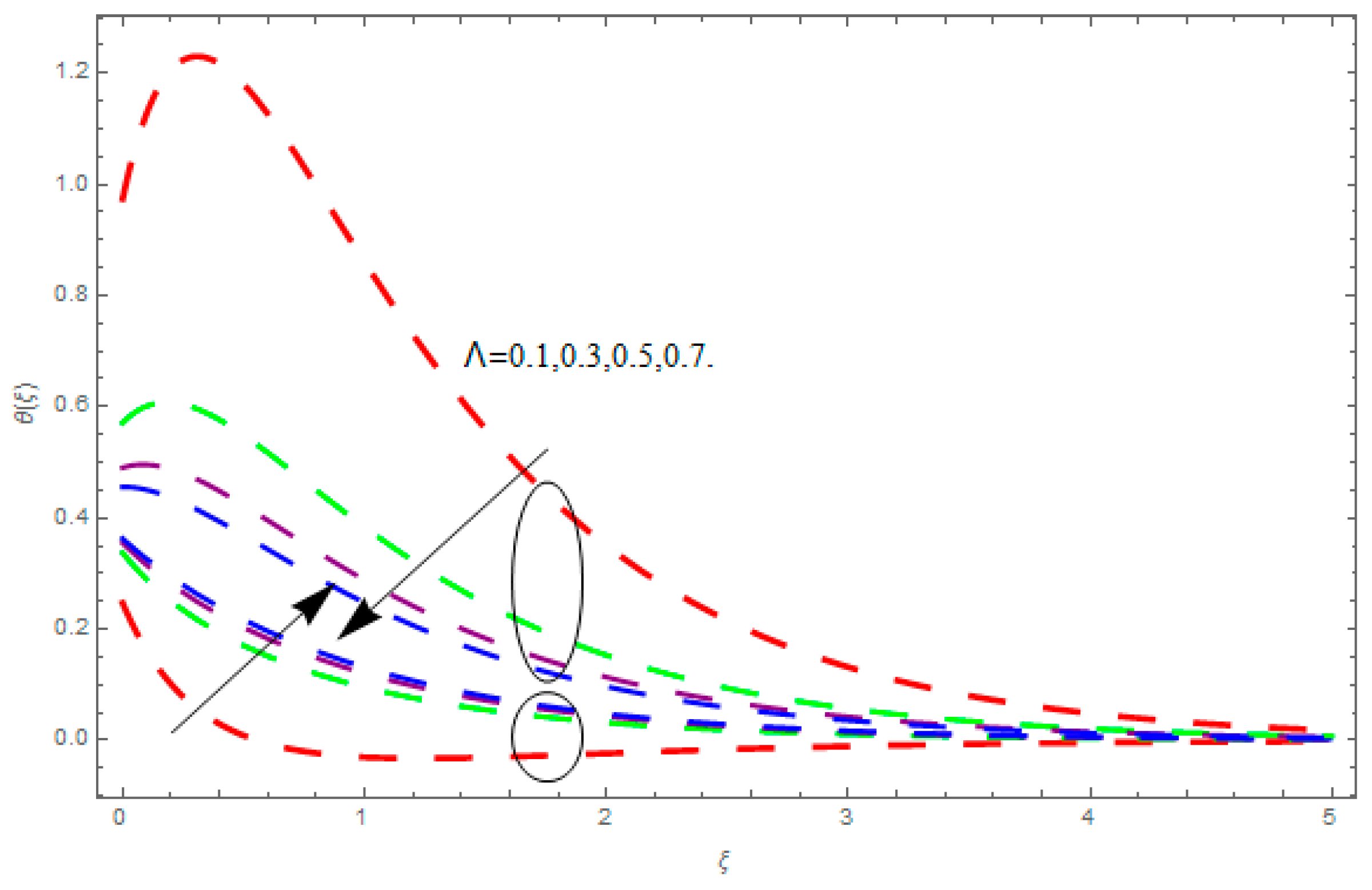
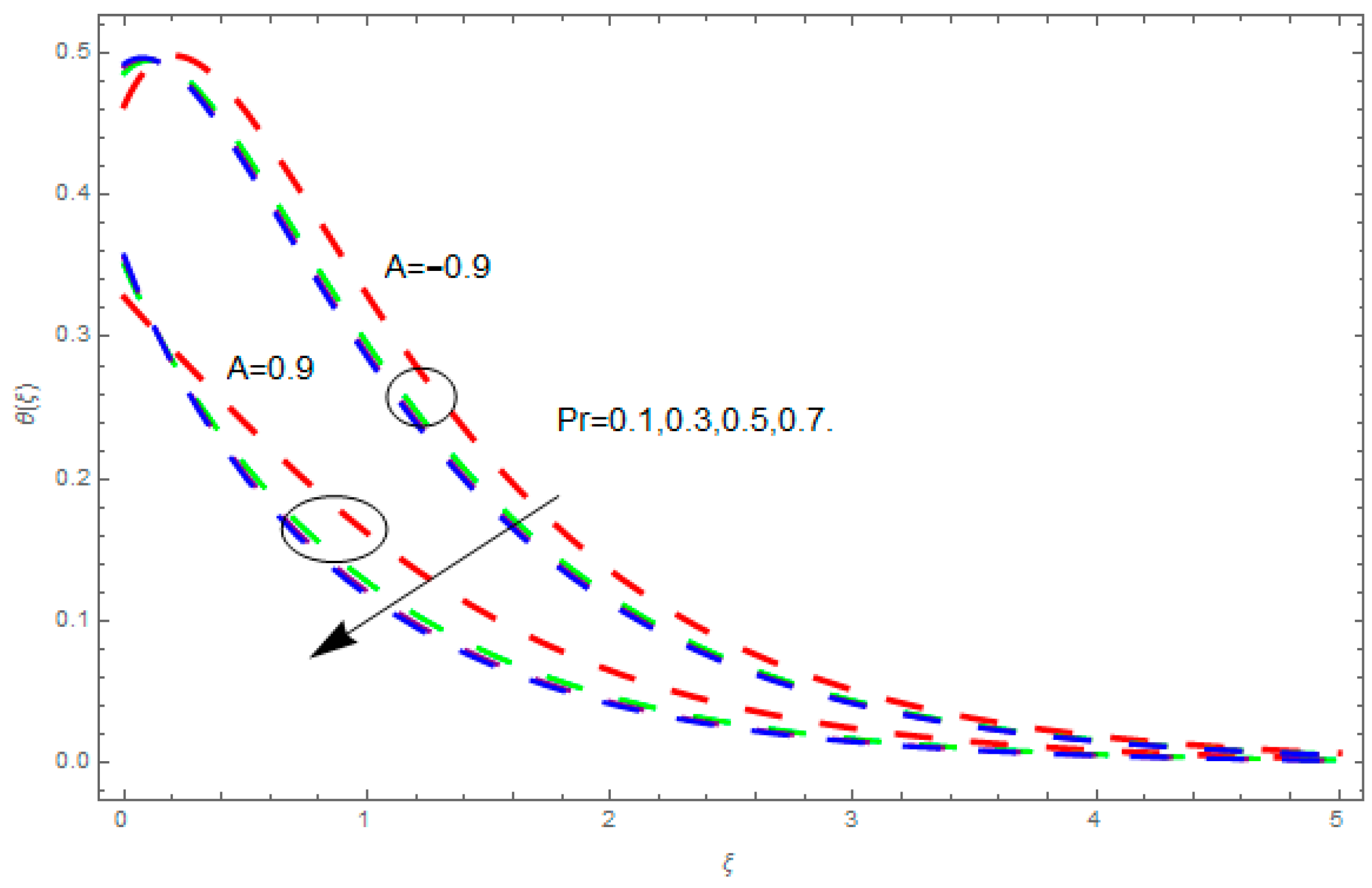
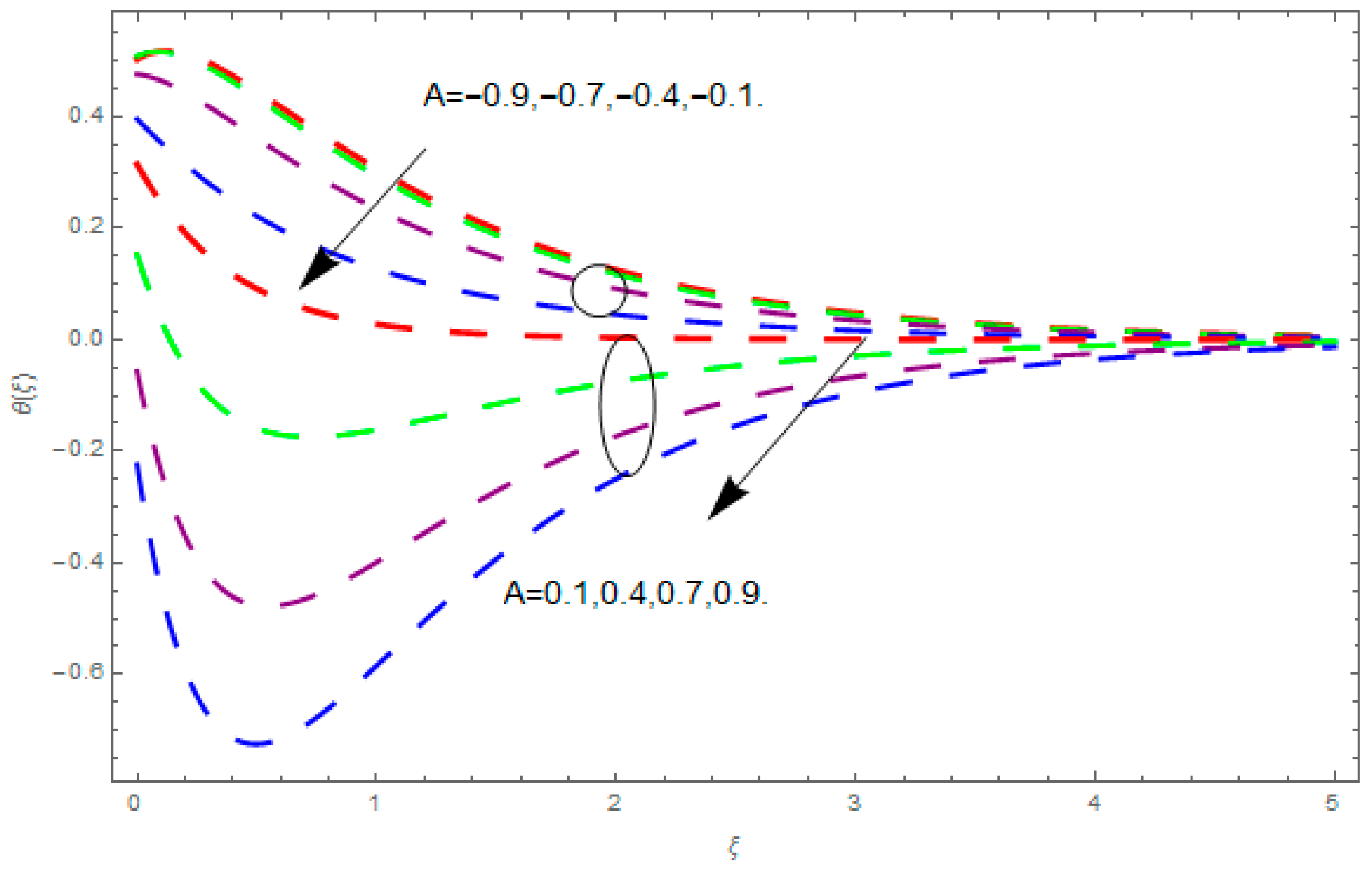
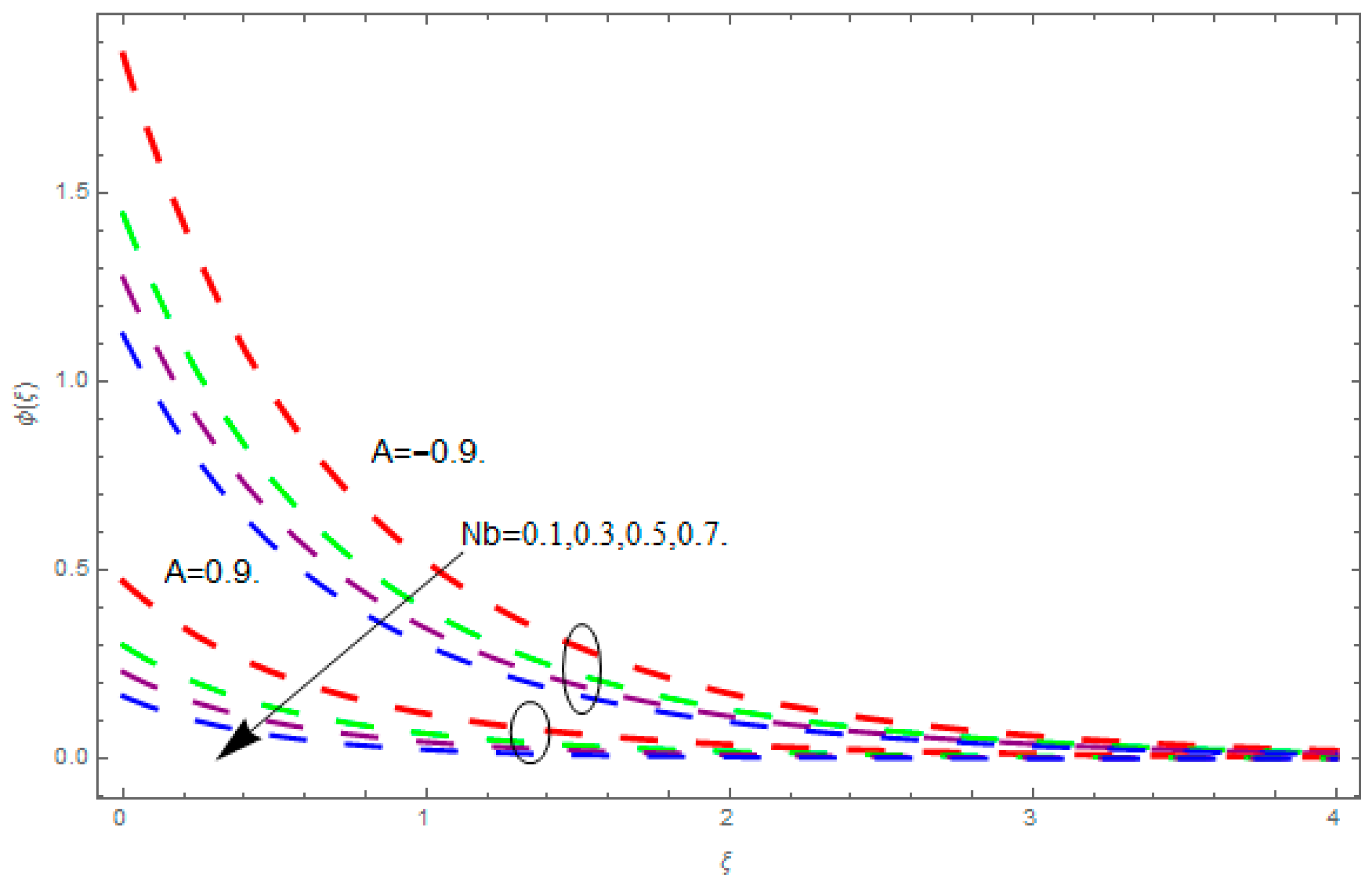
5. Results and Discussion
6. Tables Discussion
7. Conclusions
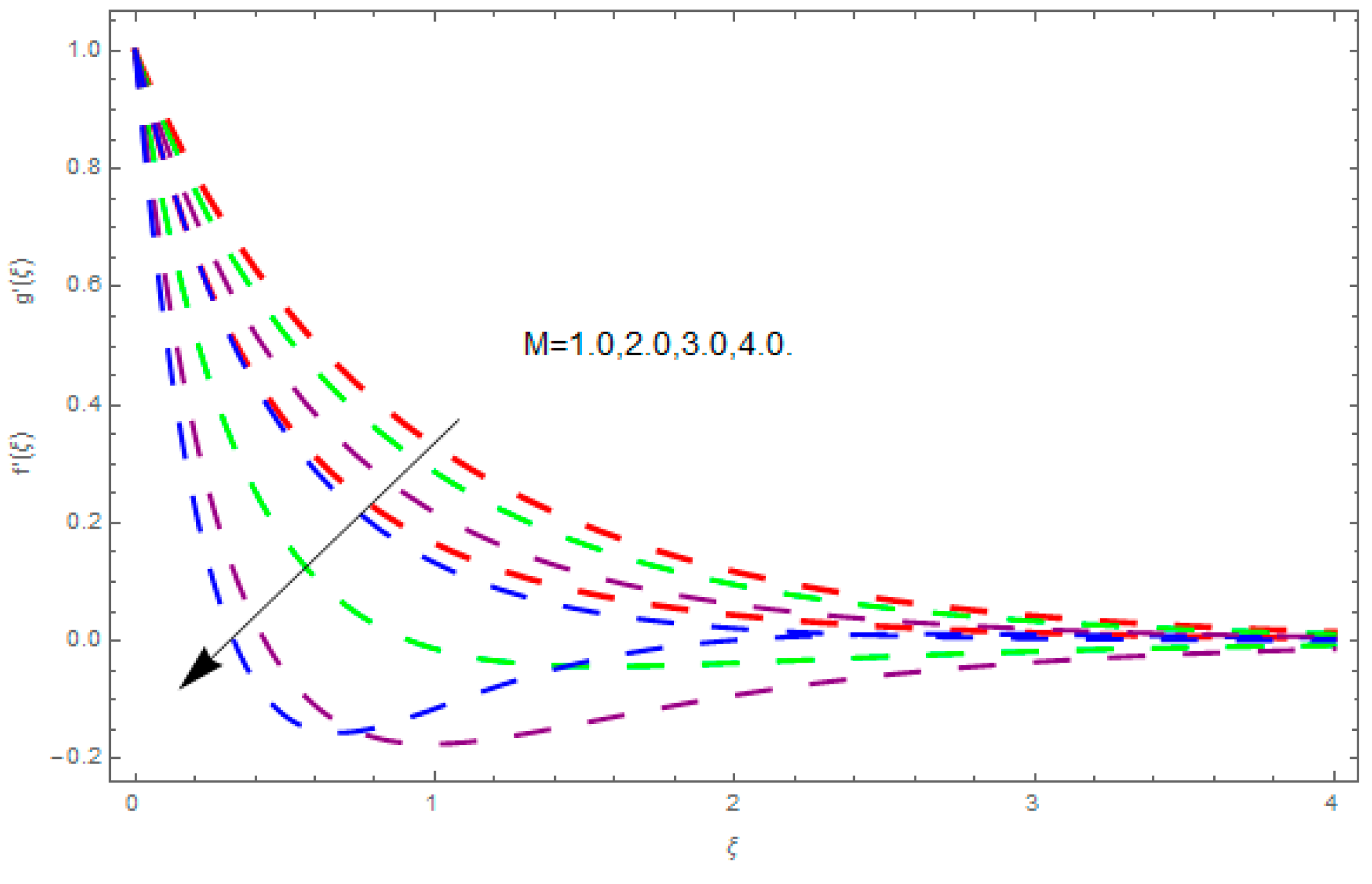
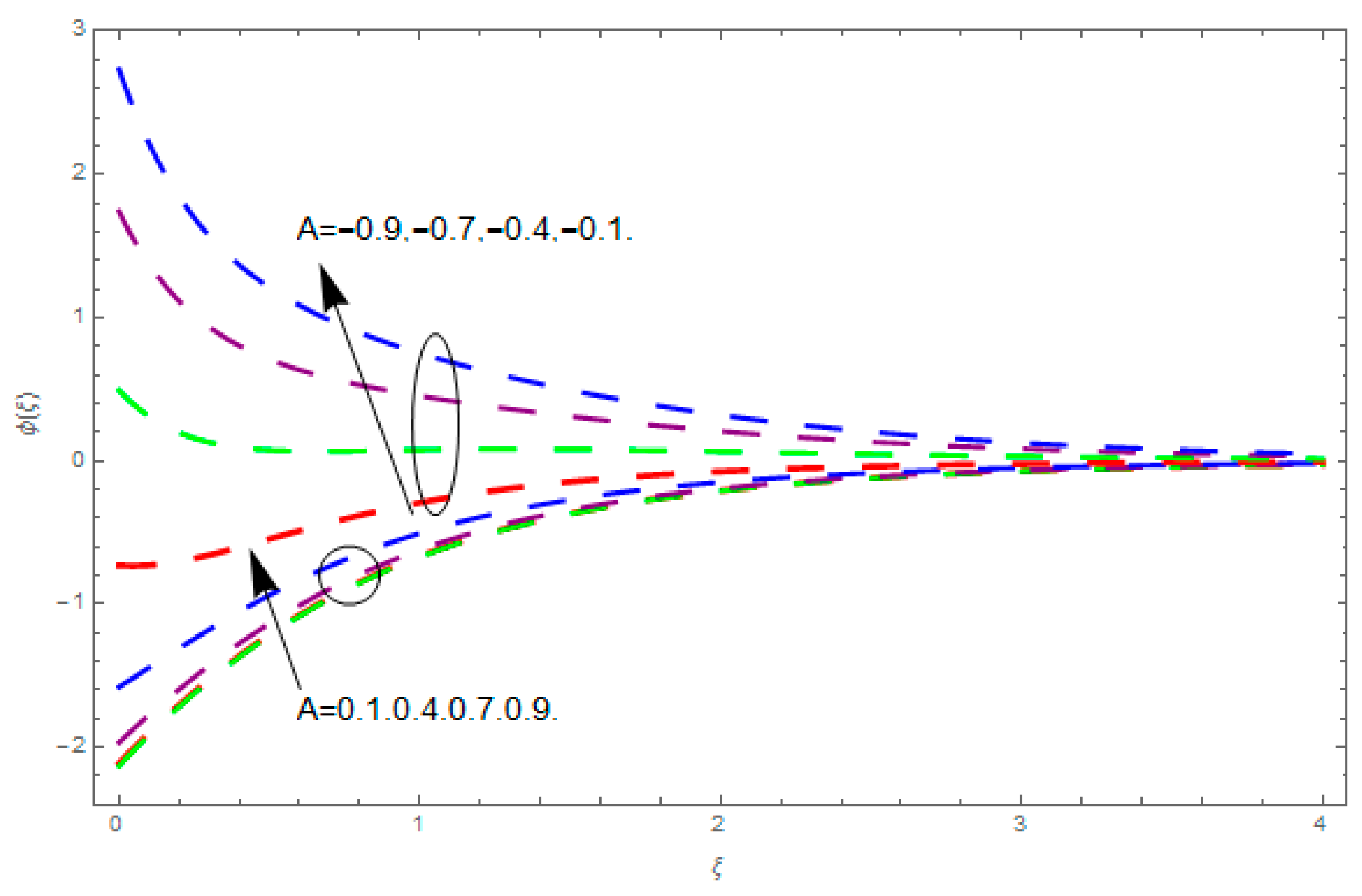
- The augmented ratio of rates parameter increases the velocity profile in the x-direction.
- The augmented magnetic field, porosity parameter, coefficient of inertia, and couple stress parameter diminishes the velocity field along the direction.
- The augmented magnetic field, porosity parameter, coefficient of inertia, ratio of rates parameter, and couple stress parameter reduces the velocity field along the axis.
- The enhancement in Prandtl number, time relaxation, and temperature exponent reduces the temperature field.
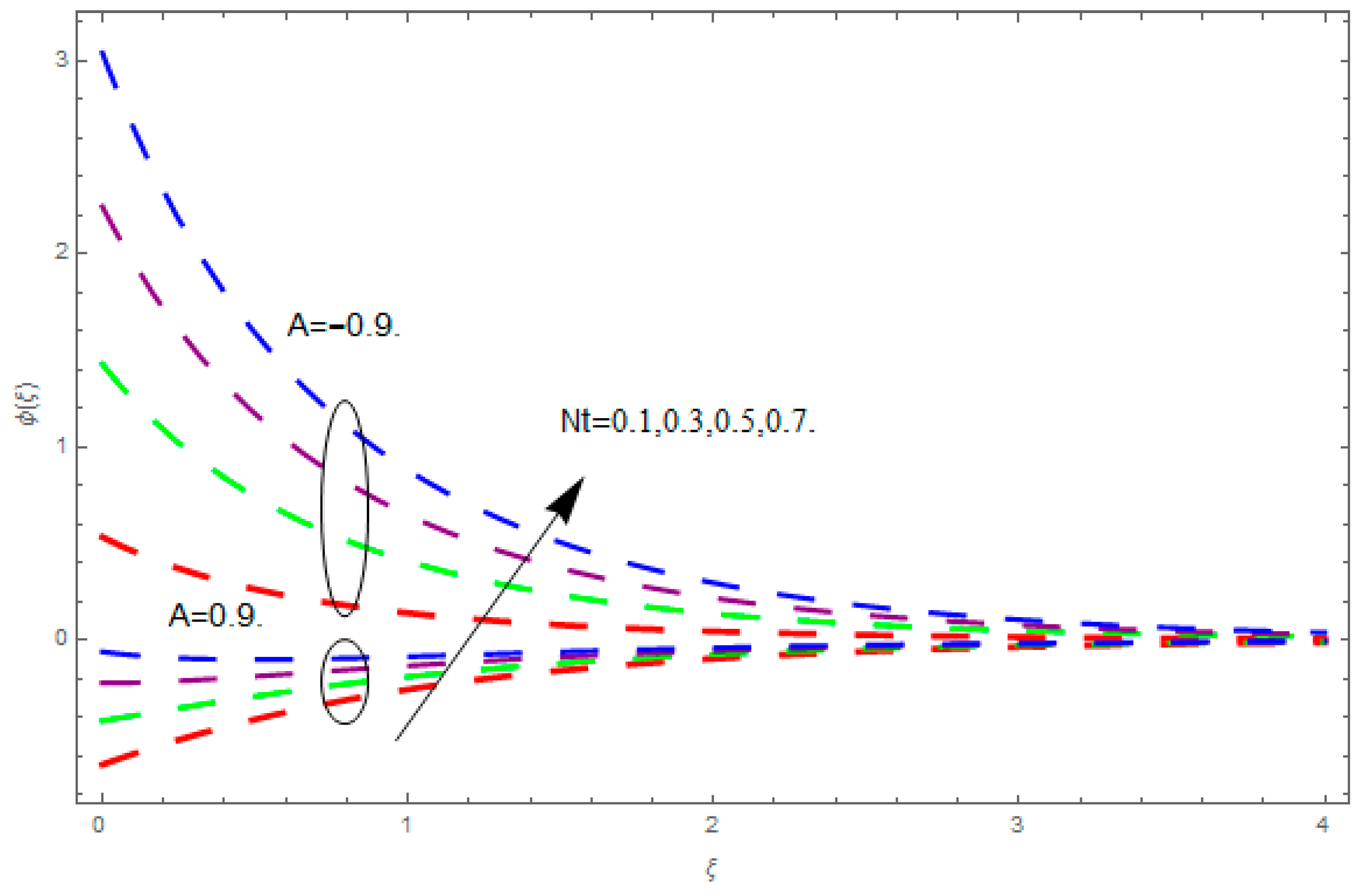
- The augmented thermophoresis and temperature exponent upsurges the concentration field.
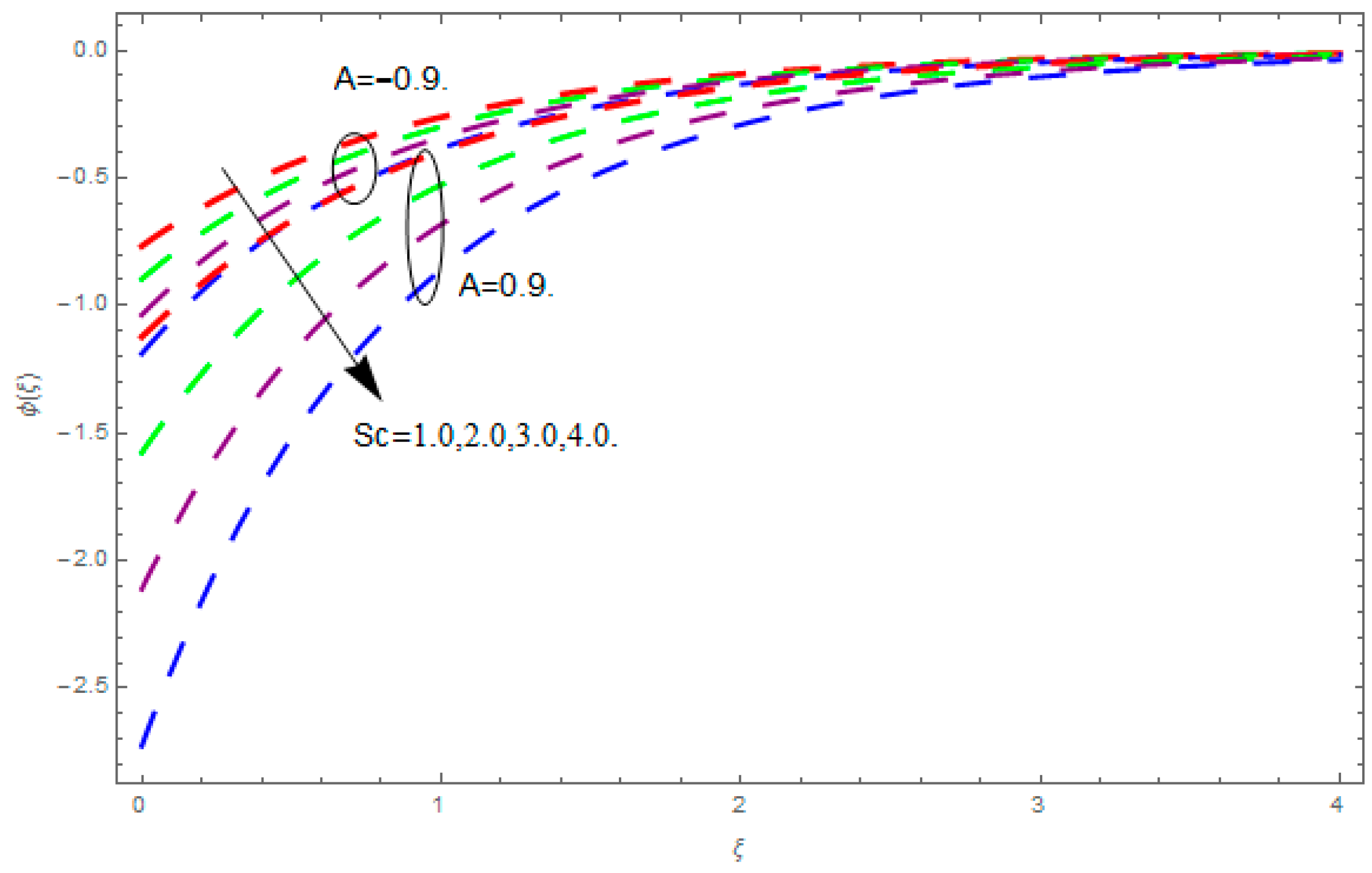
- The augmented Brownian motion and Schmidt number reduces the concentration field.
- The augmented ratio of rates, couple stress, magnetic field, and porosity parameters upsurges the skin friction coefficient.
- The augmented coefficient of inertia diminishes the skin friction coefficient.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Temperature exponent | |
| Constants | |
| Magnetic field strength | |
| Coefficient of concentration | |
| Skin friction coefficient | |
| Specific heat | |
| Brownian diffusion of nanofluids | |
| Thermophoretic diffusion of nanofluids | |
| Electric field | |
| Dimensional velocity profiles | |
| Couple stress parameter | |
| Reference length | |
| Hartmann number | |
| Brownian motion | |
| Thermophoretic parameter | |
| Nusselt number | |
| Prandtl number | |
| Heat flux | |
| Local Reynolds number | |
| Schmidt number | |
| Sherwood number | |
| Fluid temperature | |
| Velocity components | |
| Coordinates | |
| Constants | |
| Greek Letters | |
| Ratio of rates parameter | |
| Thermal relaxation time | |
| Biot number | |
| Dimensional heat profile | |
| Dimensional concentration profile | |
| Similarity variable | |
| Kinematic viscosity | |
| Porosity parameter | |
| Fluid density | |
| Electrical conductivity |
References
- Choi, S.U.S.; Estman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed. 1995, 231, 99–106. [Google Scholar]
- Wang, X.Q.; Mujumdar, A.S. Heat transfer characteristics of nanofluids: A review. Int. J. Therm. Sci. 2007, 46, 1–19. [Google Scholar] [CrossRef]
- Eastman, J.A.; Phillpot, S.R.; Choi, S.U.S.; Keblinski, P. Thermal transport in nanofluids. Annu. Rev. Mater. Res. 2004, 34, 219–246. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.U.S.; Li, S.; Yu, W.; Thompson, L.J. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Tiwari, R.K.; Das, M.K. Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. Int. J. Heat Mass Transf. 2007, 50, 2002–2018. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Kasaeian, A.; Daneshazarian, R.; Mahian, O.; Chamkha, A.J.; Wingwises, S.; Pop, I. Nanofluid flow and heat transfer in porous media: A review of the latest developments. Int. J. Heat Mass Transf. 2017, 107, 778–791. [Google Scholar] [CrossRef]
- Ramzan, M.; Chung, J.D.; Ullah, N. Radiative magnetohydrodynamic nanofluid flow due to gyrotactic microorganisms with chemical reaction and non-linear thermal radiation. Int. J. Mech. Sci. 2017, 130, 31–40. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafi, A.; Khan, I.; Itili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1196. [Google Scholar] [CrossRef]
- Besthapu, P.; Haq, R.U.; Bandari, S.; Al-Mdallal, Q.M. Mixed convection flow of thermally stratified MHD nanofluid over an exponentially stretching surface with viscous dissipation effect. J. Taiwan Inst. Chem. E 2017, 71, 307–314. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Idress, M.; Khan, W.; Islam, S.; Gul, T. Impact of thermal radiation and heat source/sink on eyring–powell fluid flow over an unsteady oscillatory porous stretching surface. Math. Comput. Appl. 2018, 23, 20. [Google Scholar] [CrossRef]
- Alharbi, S.O.; Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S.; Khan, I. Entropy generation in MHD eyring–powell fluid flow over an unsteady oscillatory porous stretching surface under the impact of thermal radiation and heat source/sink. Appl. Sci. 2018, 8, 2588. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer flow of radiative carbon nanotubes with microstructure and inertial characteristics in the rotating frame. Stud. Therm. Eng. 2018, 12, 823–832. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Dawar, A.; Bonyah, E.; Ullah, H.; Khan, A. Darcy-Forchheimer flow of MHD CNTs nanofluid radiative thermal behaviour and convective non uniform heat source/sink in the rotating frame with microstructure and inertial characteristics. AIP Adv. 2018, 8, 125024. [Google Scholar] [CrossRef]
- Zubair, M.; Shah; Islam, S.; Khan, W.; Dawar, A. 3D Darcy-Forchhemier squeezing nanofluid flow with Cattaneo-Christov heat flux through porous medium in spinning coordinates. Adv. Mech. Eng. 2019, 11, 1–17. [Google Scholar] [CrossRef]
- Khan, A.S.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-dimensional nanofluid flow with heat and mass transfer analysis over a linear stretching surface with convective boundary conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S. Unsteady squeezing flow of magnetohydrodynamic carbon nanotube nanofluid in rotating channels with entropy generation and viscous dissipation. Adv. Mech. Eng. 2019, 11, 1–18. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical investigation of nanofluid free convection under the influence of electric field in a porous enclosure. J. Mol. Liq. 2018, 249, 1212–1221. [Google Scholar] [CrossRef]
- Sheikholeslami, M. CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion. J. Mol. Liq. 2018, 249, 921–929. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Khan, W.; Islam, S.; Idrees, M. An optimal analysis for Darcy-Forchheimer 3-D Williamson Nanofluid Flow over a stretching surface with convective conditions. Adv. Mech. Eng. 2019, 11, 1–15. [Google Scholar] [CrossRef]
- Ramzan, M.; Sheikholeslami, M.; Saeed, M.; Chung, J.D. On the convective heat and zero nanoparticle mass flux conditions in the flow of 3D MHD Couple Stress nanofluid over an exponentially stretched surface. Sci. Rep. 2019, 9, 562. [Google Scholar] [CrossRef]
- Fourier, J.B.J. Théorie Analytique De La Chaleur; Didot: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione del calore. Atti Sem. Mat. Fis. Univ. Modena 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Straughan, B. Stability and Wave Motion in Porous Media; Springer: New York, NY, USA, 2008; Volume 165. [Google Scholar]
- Straughan, B. Thermal convection with the Cattaneo-Christov model. Int. J. Heat Mass Transf. 2010, 53, 95–98. [Google Scholar] [CrossRef]
- Han, S.; Zheng, L.; Li, C.; Zhang, X. Coupled flow, and heat transfer in viscoelastic fluid with Cattaneo-Christov heat flux model. Appl. Math. Lett. 2014, 38, 87–93. [Google Scholar] [CrossRef]
- Khan, J.A.; Mustafa, M.; Hayat, T.; Alsaedi, A. Numerical study of Cattaneo-Christov heat flux model for viscoelastic flow due to an exponentially stretching surface. PLoS ONE 2015, 10, e0137363. [Google Scholar]
- Hayat, T.; Nadeem, S. Aspects of developed heat and mass flux models on 3D flow of Eyring-Powell fluid. Results Phys. 2017, 7, 3910–3917. [Google Scholar] [CrossRef]
- Tibullo, V.; Zampoli, V. A uniqueness result for the Cattaneo-Christov heat conduction model applied to incompressible fluids. Mech. Res. Commun. 2011, 38, 77–79. [Google Scholar] [CrossRef]
- Ciarletta, M.; Straughan, B. Uniqueness and structural stability for the Cattaneo-Christov equations. Mech. Res. Commun. 2010, 37, 445–447. [Google Scholar] [CrossRef]
- Haddad, S.A.M. Thermal instability in Brinkman porous media with Cattaneo-Christov heat flux. Int. J. Heat Mass Transf. 2014, 68, 659–668. [Google Scholar] [CrossRef]
- Mustafa, M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Adv. 2015, 5, 047109. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, M.; Alsaedi, A.; Al-Solamym, F. Impact of Cattaneo-Christov heat flux in the flow over a stretching sheet with variable thickness. AIP Adv. 2015, 5, 087159. [Google Scholar] [CrossRef]
- Waqas, M.; Hayat, T.; Farooq, M.; Shehzad, S.A.; Alsaedi, A. Cattaneo-Christov heat flux model for flow of variable thermal conductivity generalized Burgers fluid. J. Mol. Liq. 2016, 220, 642–648. [Google Scholar] [CrossRef]
- Li, J.; Zheng, L.; Liu, L. MHD viscoelastic flow and heat transfer over a vertical stretching with Cattaneo- Christov heat flux. J. Mol. Liq. 2016, 221, 19–25. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Khan, I.; Islam, S.; Ching, D.L.C.; Khan, A.Z. Cattaneo-Christov model for electrical magnetite micropoler Casson ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. Case Stud. Therm. Eng. 2019, 13, 100352. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Flow of 3D Eyring-Powell fluid by utilizing Cattaneo-Christov heat flux model and chemical processes over an exponentially stretching surface. Results Phys. 2018, 8, 397–403. [Google Scholar] [CrossRef]
- Muskat, M. The Flow of Homogeneous Fluids through Porous Media; Edwards: Ann Arbor, MI, USA, 1946. [Google Scholar]
- Seddeek, M.A. Influence of viscous dissipation and thermophoresis on Darcy-Forchheimer mixed convection in a fluid saturated porous media. J. Colloid Interface Sci. 2006, 293, 137–142. [Google Scholar] [CrossRef]
- Pal, D.; Mondal, H. Hydromagnetic convective diffusion of species in Darcy-Forchheimer porous medium with non-uniform heat source/sink and variable viscosity. Int. Commun. Heat Mass Transf. 2012, 39, 913–917. [Google Scholar] [CrossRef]
- Sadiq, M.A.; Hayat, T. Darcy-Forchheimer flow of magneto Maxwell liquid bounded by convectively heated sheet. Results Phys. 2016, 6, 884–890. [Google Scholar] [CrossRef]
- Abderrahim, W.; Zoubair, B.; Rachid, S. Numerical analysis of the onset of longitudinal convective rolls in a porous medium saturated by an electrically conducting nanofluid in the presence of an external magnetic field. Results Phys. 2017, 7, 2134–2152. [Google Scholar]
- Wakif, A.; Boulahia, Z.; Ali, F.; Mohamed, R.E.; Rachid, S. Numerical Analysis of the Unsteady Natural Convection MHD Couette Nanofluid Flow in the Presence of Thermal Radiation Using Single and Two-Phase Nanofluid Models for Cu–Water Nano fluids. Int. J. Appl. Comput. Math. 2018, 4, 81. [Google Scholar] [CrossRef]
- Wakif, A.; Boulahia, Z.; Mishra, S.R.; Rashidi, M.M.; Sehaqui, R. Influence of a uniform transverse magnetic field on the thermo-hydrodynamic stability in water-based nanofluids with metallic nanoparticles using the generalized Buongiorno’s mathematical model. Eur. Phys. J. Plus 2018, 133, 181. [Google Scholar] [CrossRef]
- Abderrahim, W.; Zoubair, B.; Rachid, S. Numerical Study of the Onset of Convection in a Newtonian Nanofluid Layer with Spatially Uniform and Non Uniform Internal Heating. J. Nanofluids 2017, 6, 136–148. [Google Scholar]
- Abderrahim, W.; Zoubair, B.; Rachid, S. A semi-analytical analysis of electro-thermo hydrodynamic stability in dielectric nanofluids using Buongiorno’s mathematical model together with more realistic boundary conditions. Results Phys. 2018, 9, 1438–1454. [Google Scholar]
- Wakif, A.; Boulahia, Z.; Amine, A.; Animasaun, I.L.; Afridi, M.I.; Qasimd, M.; Sehaqui, R. Magneto-convection of alumina-water nanofluid within thin horizontal layers using the reccised generalized Buongiorno’s model. Front. Heat Mass Transf. (FHMT) 2019, 12, 3. [Google Scholar]
- Wakif, A.; Qasim, M.; Afridi, M.; Saleem, S.; Al-Qarni, M.M. Numerical examination of the entropic energy harvesting in a magnetohydrodynamic dissipative flow of stokes’ second problem: utilization of the gear-generalized differential quadrature method. J. Non-Equilib. Thermodyn. 2019. [Google Scholar] [CrossRef]
- Zubair, M.; Shah, Z.; Dawar, A.; Islam, S.; Kumam, P.; Khan, A. Entropy generation optimization in squeezing magnetohydrodynamics flow of casson nanofluid with viscous dissipation and joule heating effect. Entropy 2019, 21, 747. [Google Scholar] [CrossRef]
| Ramzan et al. [21] | Present Study | |||||
|---|---|---|---|---|---|---|
| 0.1 | 1.43588 | 1.435881 | ||||
| 0.2 | 1.45336 | 1.453367 | ||||
| 0.3 | 1.51480 | 1.514801 | ||||
| 0.1 | 0.02 | 1.48241 | 1.482410 | |||
| 0.03 | 1.58900 | 1.589002 | ||||
| 0.01 | 0.1 | 1.37723 | 1.377231 | |||
| 0.2 | 1.38939 | 1.389390 | ||||
| 0.3 | 1.40891 | 1.408911 | ||||
| 0.1 | 0.2 | - | 1.268100 | |||
| 0.3 | - | 1.265650 | ||||
| 0.4 | - | 1.263190 | ||||
| 0.1 | 0.1 | - | 1.273000 | |||
| 0.2 | - | 1.275451 | ||||
| 0.3 | - | 1.277892 |
| Ramzan et al. [21] | Current Study | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.143578 | 0.143577 | ||||
| 0.2 | 0.299583 | 0.299582 | ||||
| 0.3 | 0.467421 | 0.467420 | ||||
| 0.4 | 0.646402 | 0.646401 | ||||
| 0.1 | 0.02 | 0.147835 | 0.147834 | |||
| 0.03 | 0.154193 | 0.154192 | ||||
| 0.04 | 0.164693 | 0.164692 | ||||
| 0.01 | 0.5 | 0.146938 | 0.146937 | |||
| 0.6 | 0.150971 | 0.150970 | ||||
| 0.7 | 0.155608 | 0.155607 | ||||
| 0.2 | - | 0.331610 | ||||
| 0.3 | - | 0.330969 | ||||
| 0.4 | - | 0.330280 | ||||
| 0.1 | - | 0.330966 | ||||
| 0.2 | - | 0.331603 | ||||
| 0.3 | - | 0.332237 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, M.W.; Kumam, P.; Shah, Z.; Farooq, A.A.; Nawaz, R.; Dawar, A.; Islam, S.; Thounthong, P. Darcy–Forchheimer MHD Couple Stress 3D Nanofluid over an Exponentially Stretching Sheet through Cattaneo–Christov Convective Heat Flux with Zero Nanoparticles Mass Flux Conditions. Entropy 2019, 21, 867. https://doi.org/10.3390/e21090867
Ahmad MW, Kumam P, Shah Z, Farooq AA, Nawaz R, Dawar A, Islam S, Thounthong P. Darcy–Forchheimer MHD Couple Stress 3D Nanofluid over an Exponentially Stretching Sheet through Cattaneo–Christov Convective Heat Flux with Zero Nanoparticles Mass Flux Conditions. Entropy. 2019; 21(9):867. https://doi.org/10.3390/e21090867
Chicago/Turabian StyleAhmad, Muhammad Wakeel, Poom Kumam, Zahir Shah, Ali Ahmad Farooq, Rashid Nawaz, Abdullah Dawar, Saeed Islam, and Phatiphat Thounthong. 2019. "Darcy–Forchheimer MHD Couple Stress 3D Nanofluid over an Exponentially Stretching Sheet through Cattaneo–Christov Convective Heat Flux with Zero Nanoparticles Mass Flux Conditions" Entropy 21, no. 9: 867. https://doi.org/10.3390/e21090867
APA StyleAhmad, M. W., Kumam, P., Shah, Z., Farooq, A. A., Nawaz, R., Dawar, A., Islam, S., & Thounthong, P. (2019). Darcy–Forchheimer MHD Couple Stress 3D Nanofluid over an Exponentially Stretching Sheet through Cattaneo–Christov Convective Heat Flux with Zero Nanoparticles Mass Flux Conditions. Entropy, 21(9), 867. https://doi.org/10.3390/e21090867







