Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy
Abstract
1. Introduction
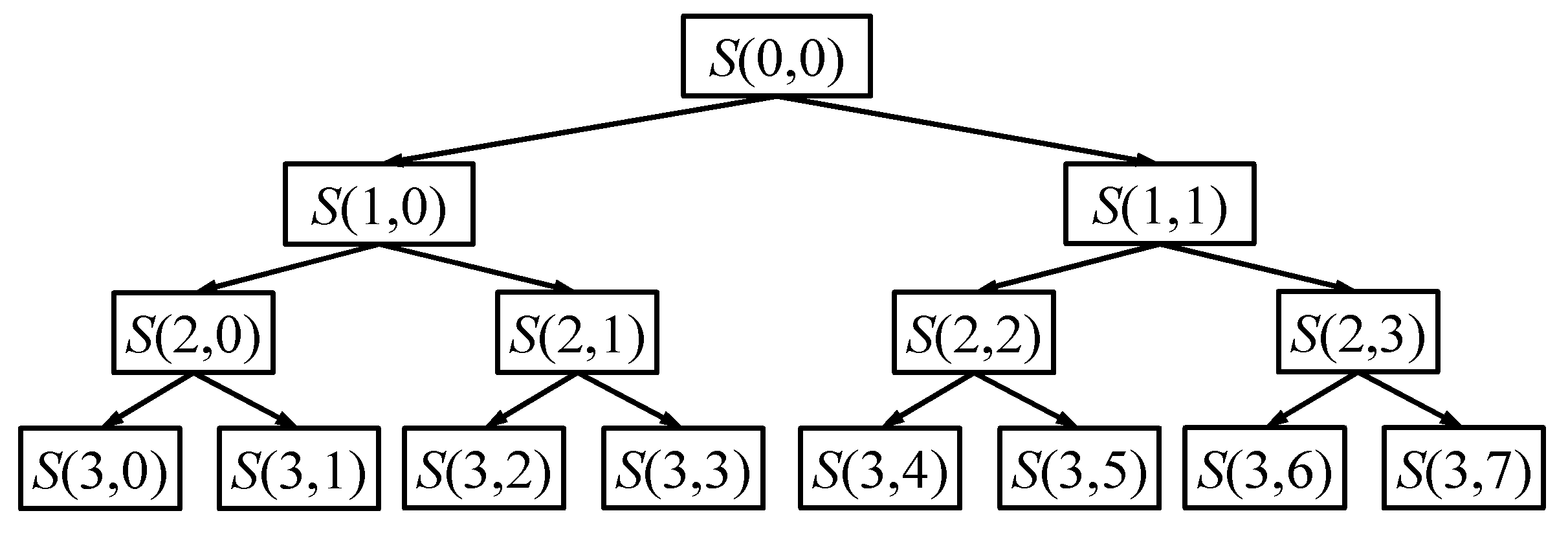
2. WPT-Based Energy Feature Reconstruction
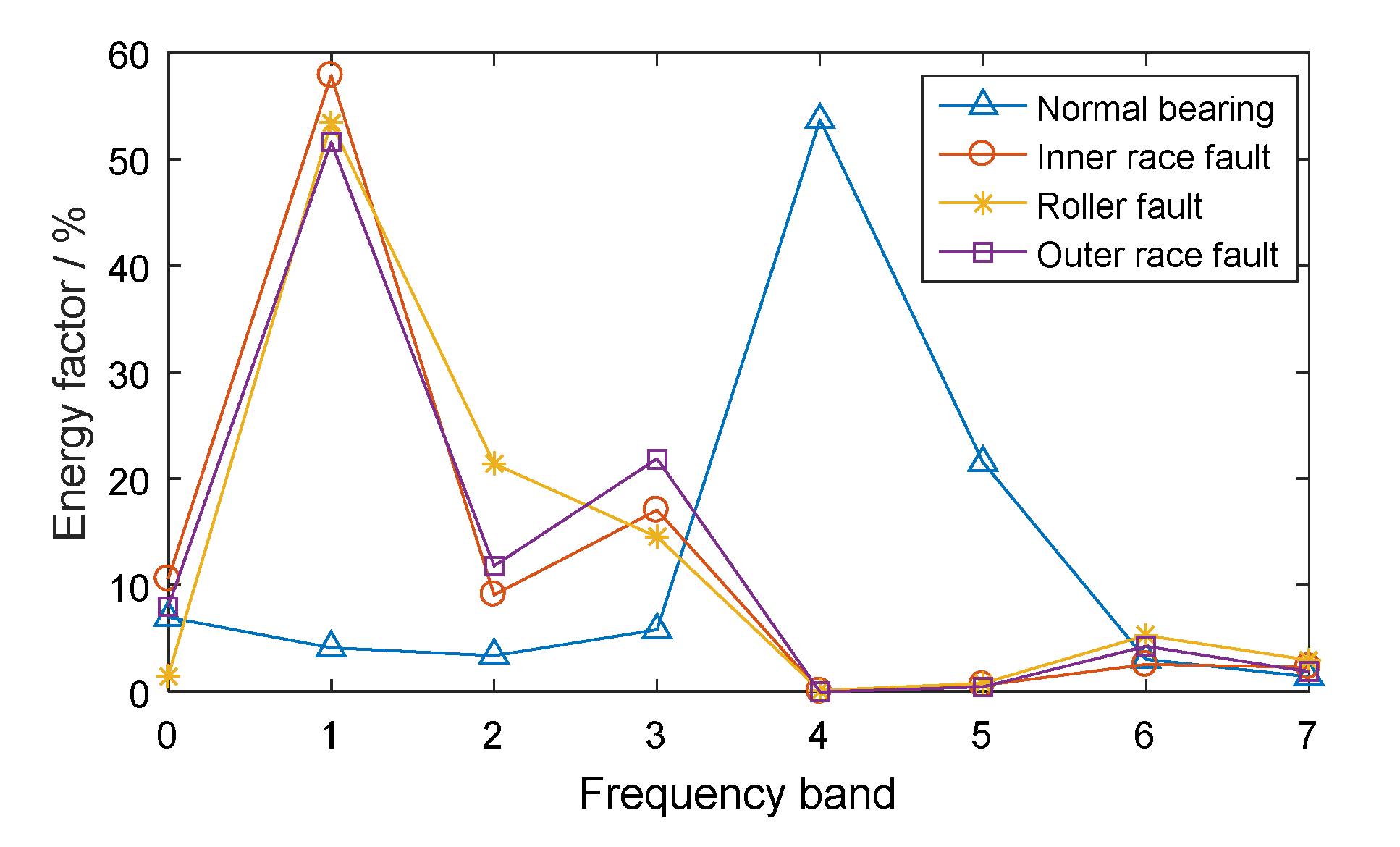
2.1. WPT and Energy Feature Extraction Algorithm
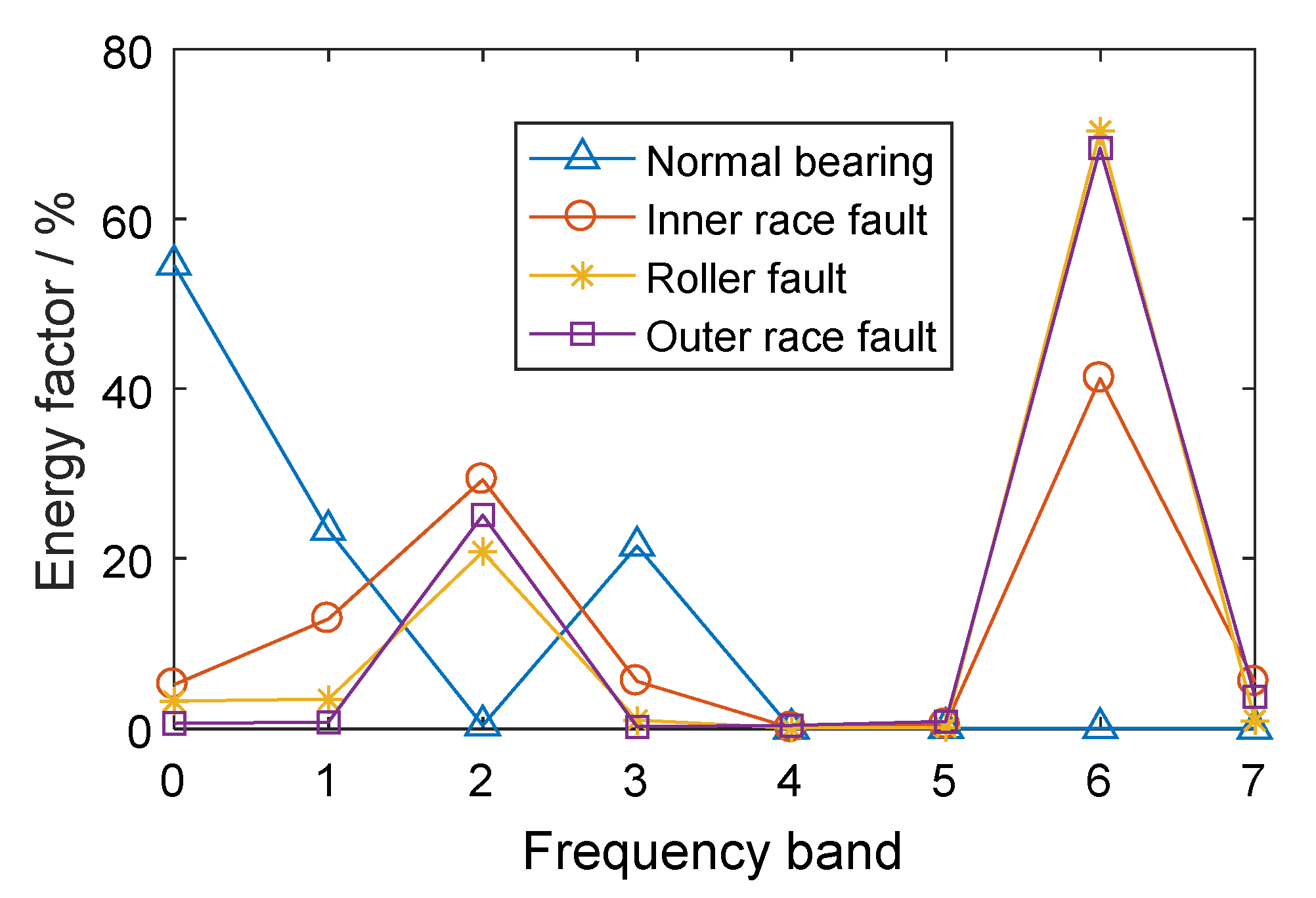
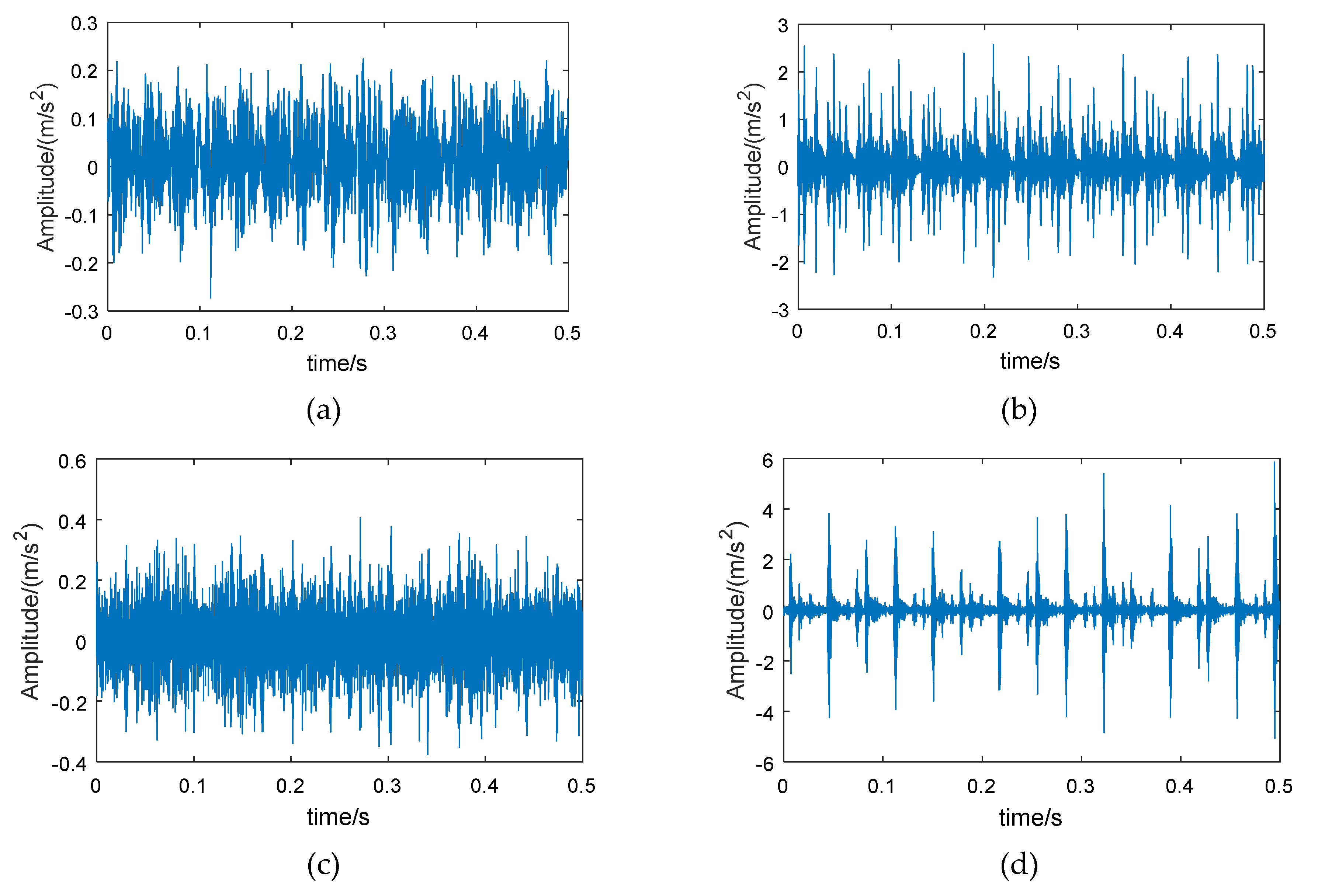
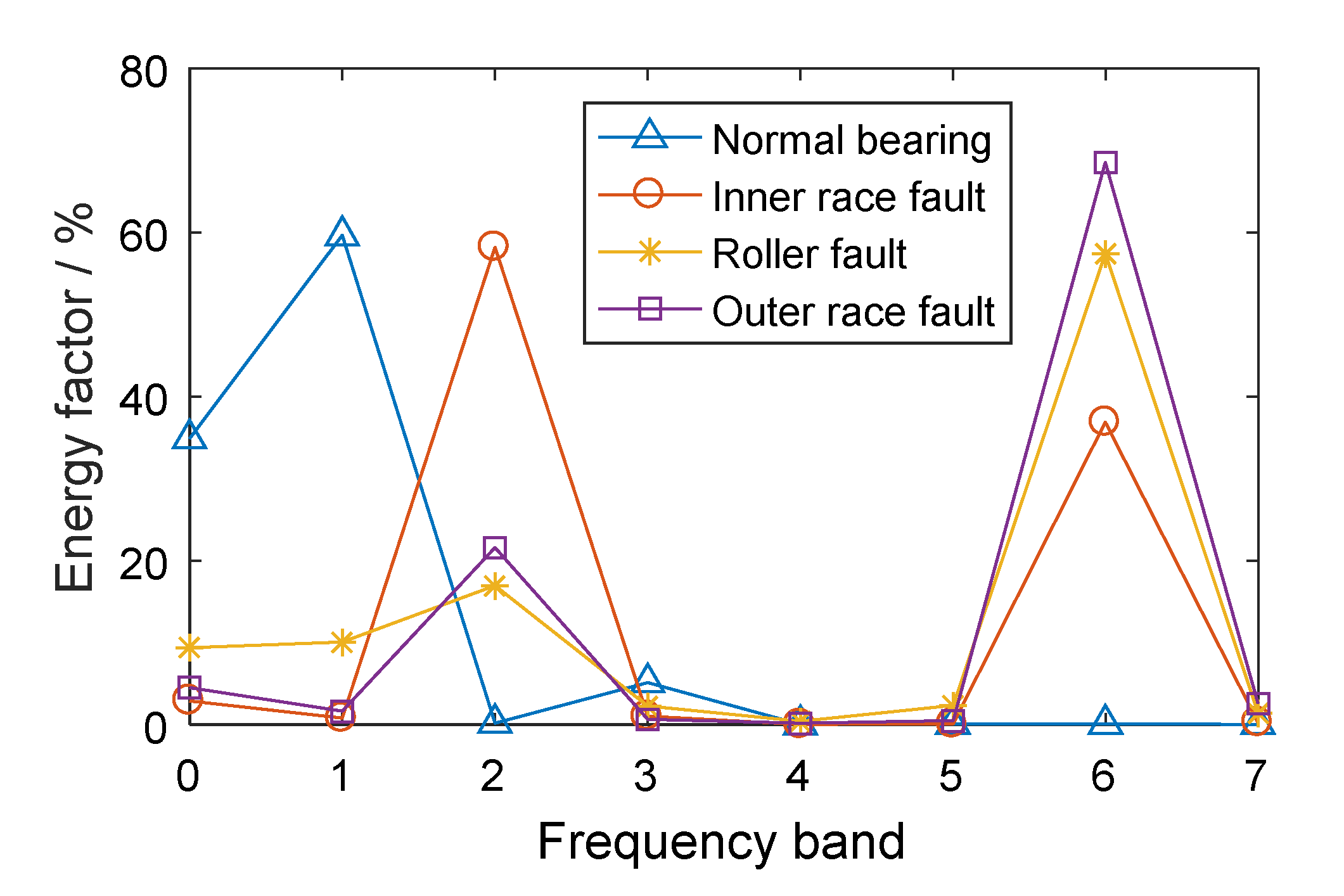
2.2. Experimental Verification
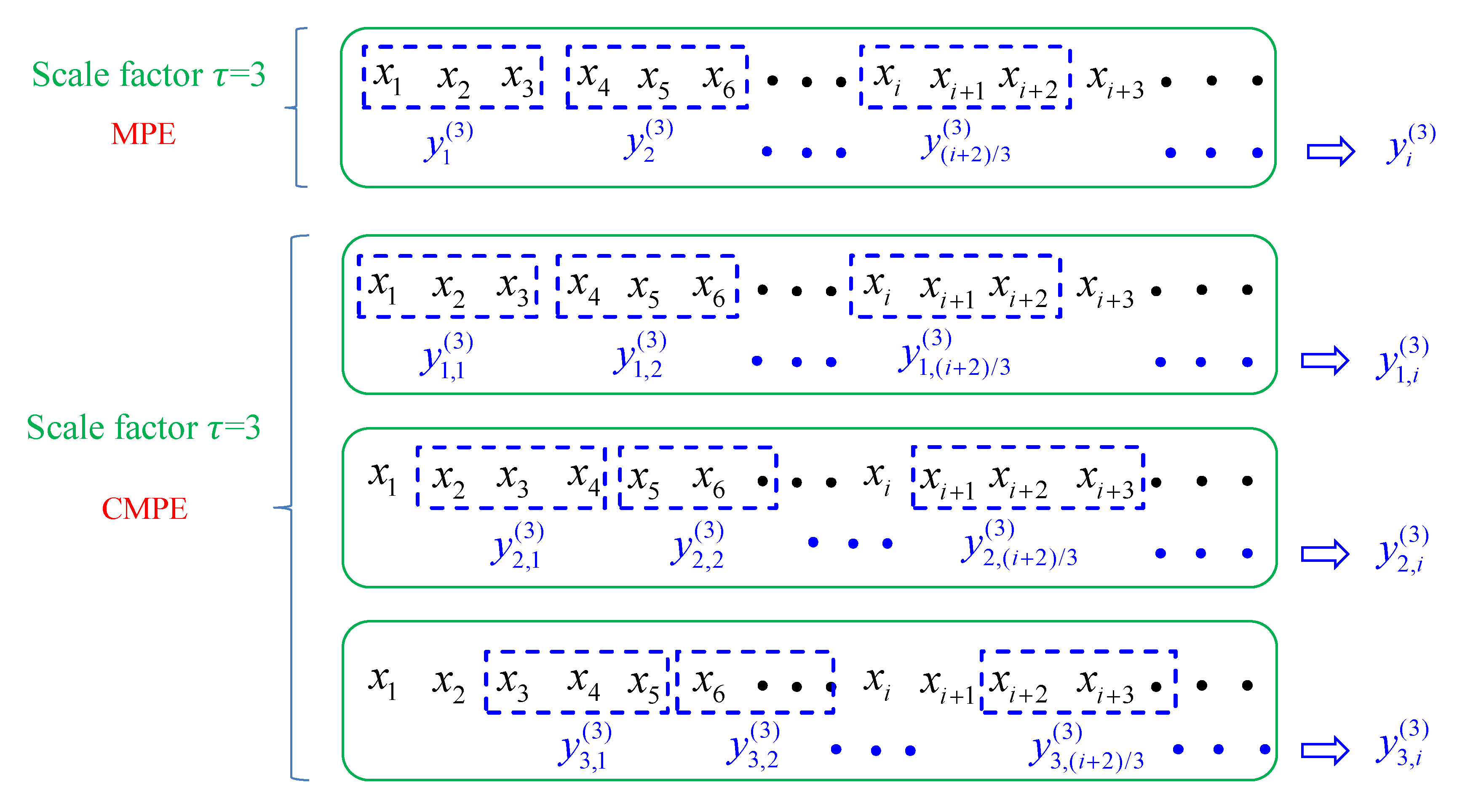
3. Composite Multiscale Permutation Entropy
3.1. Permutation Entropy
3.2. MPE and CMPE
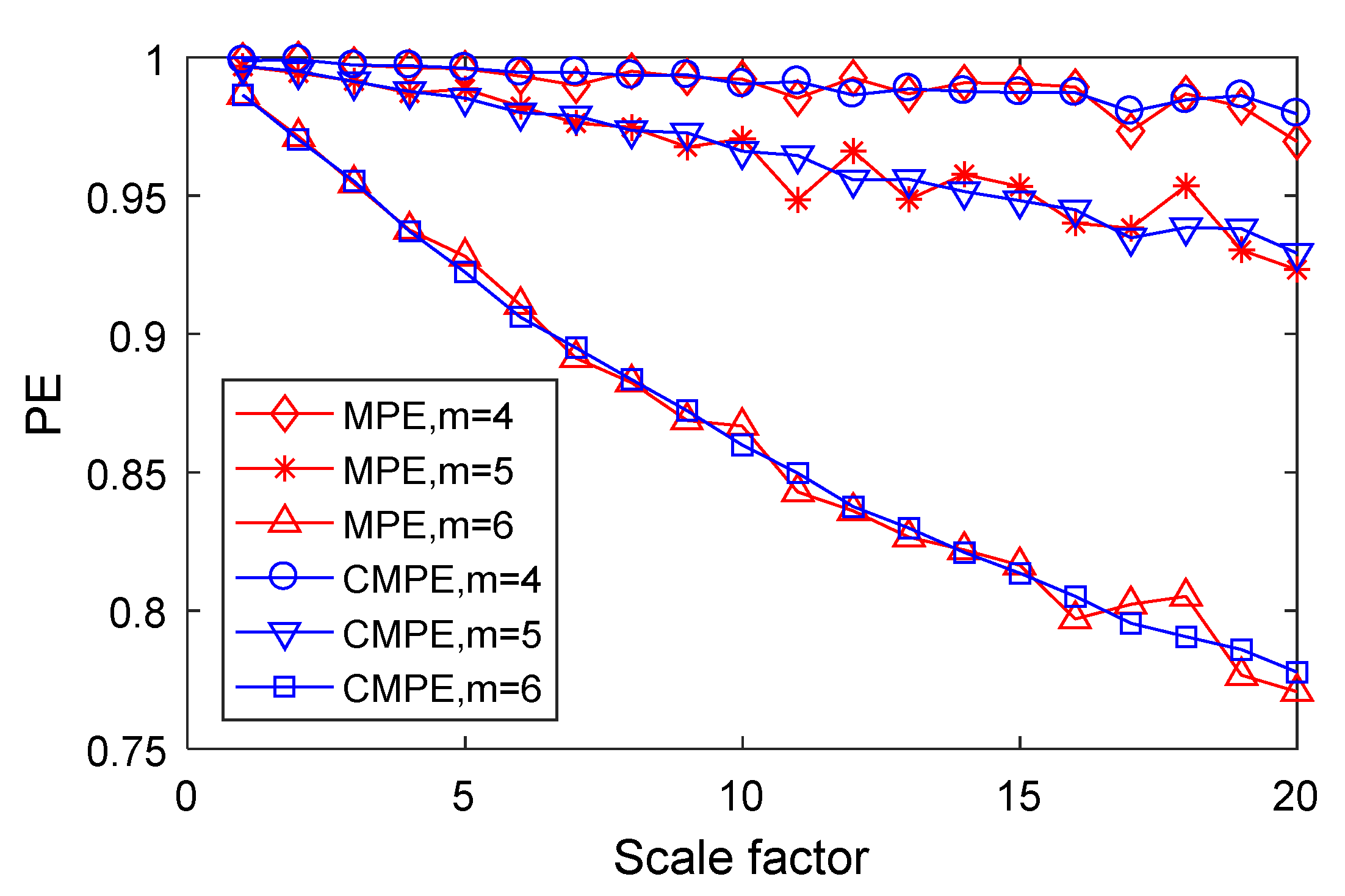
3.3. Simulation Contrast between MPE and CMPE
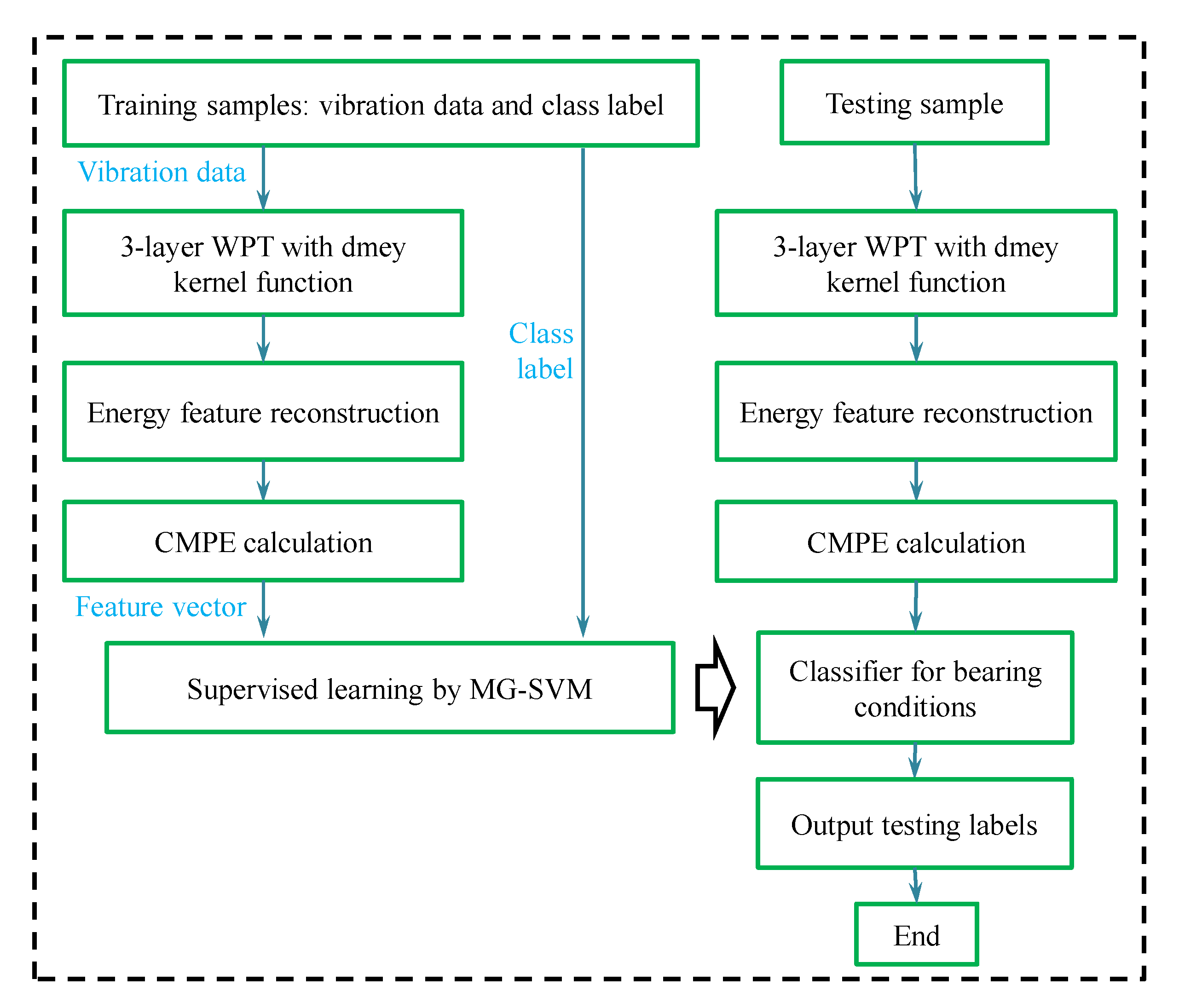
4. The Proposed Fault Diagnosis Method
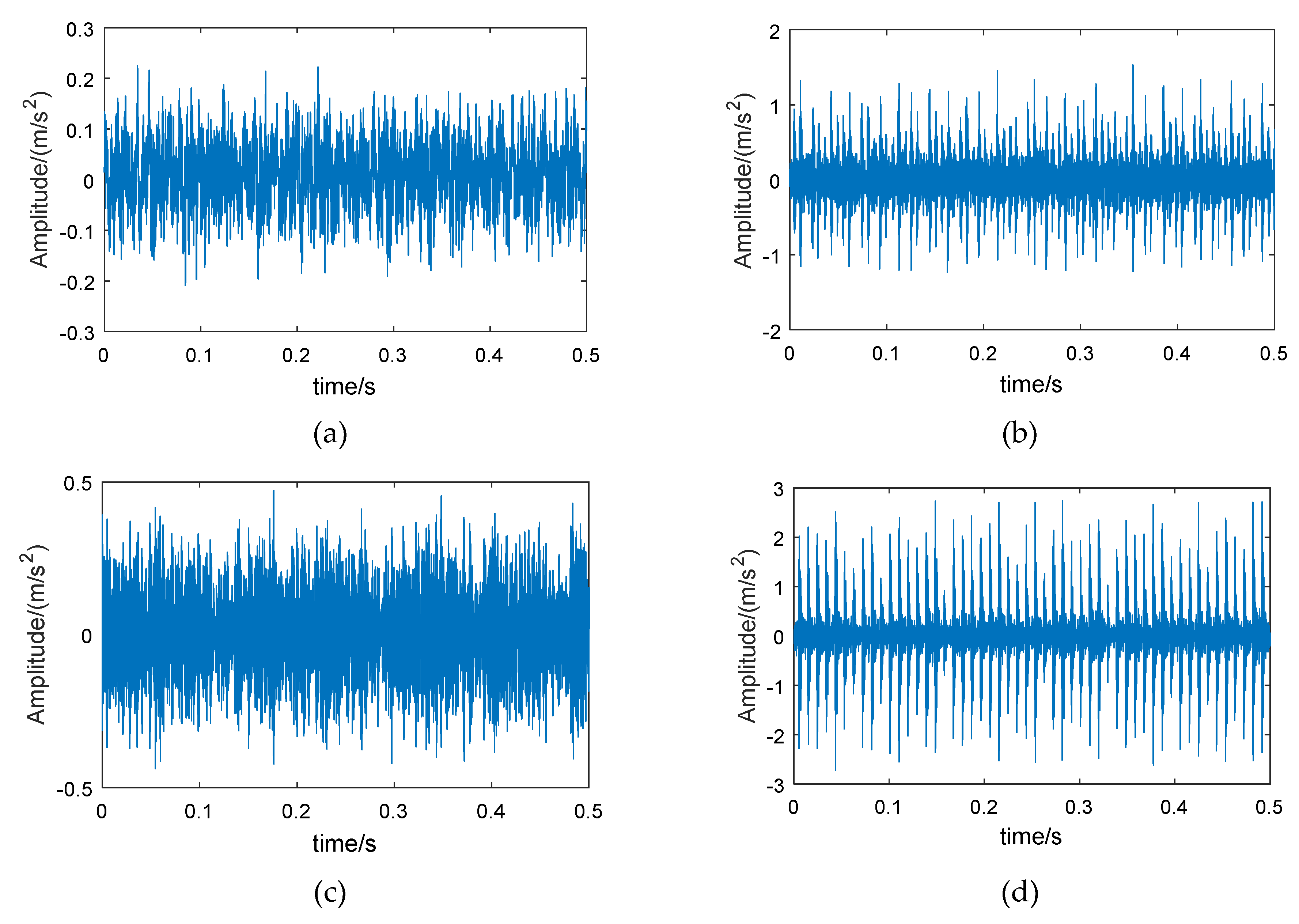
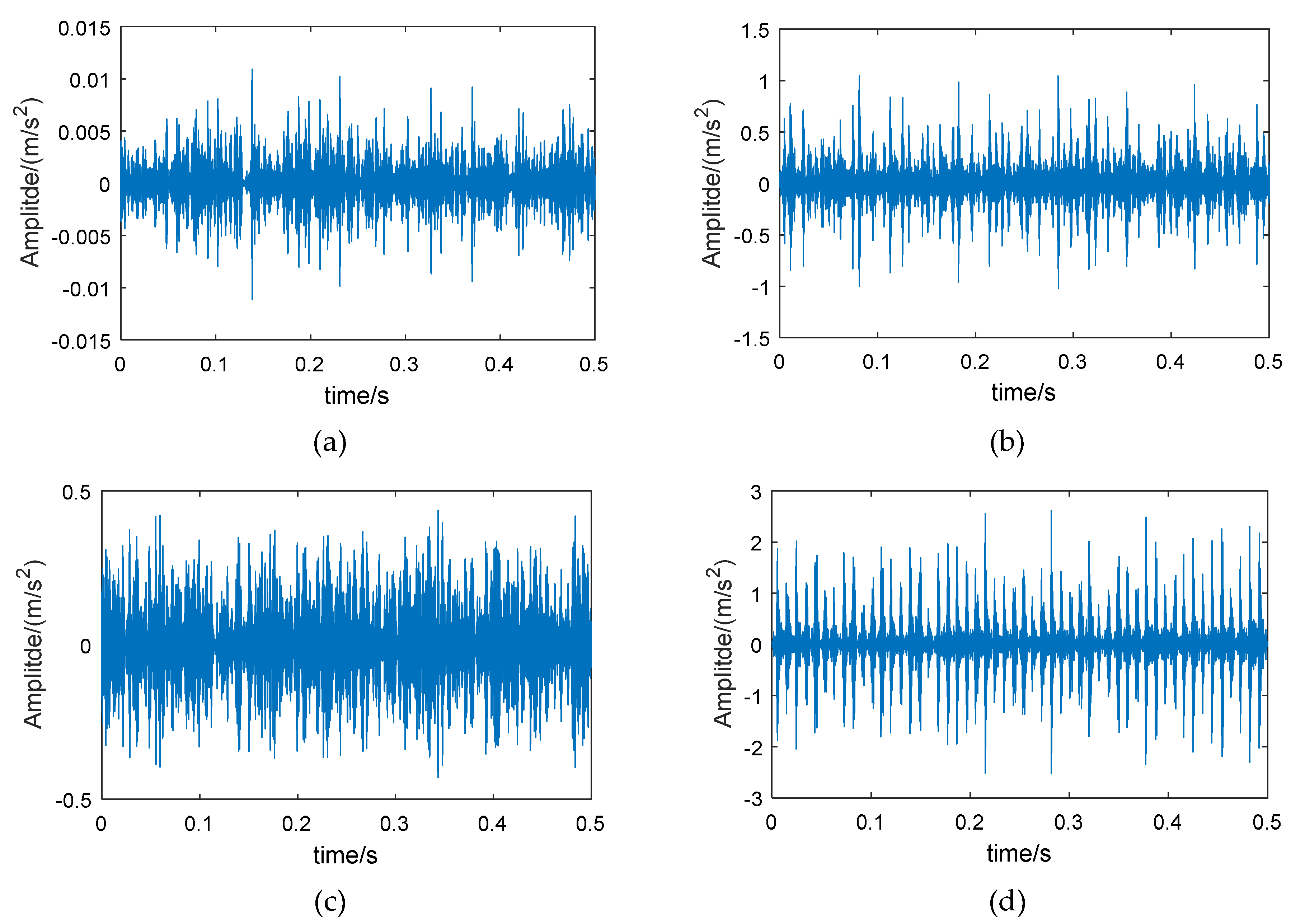
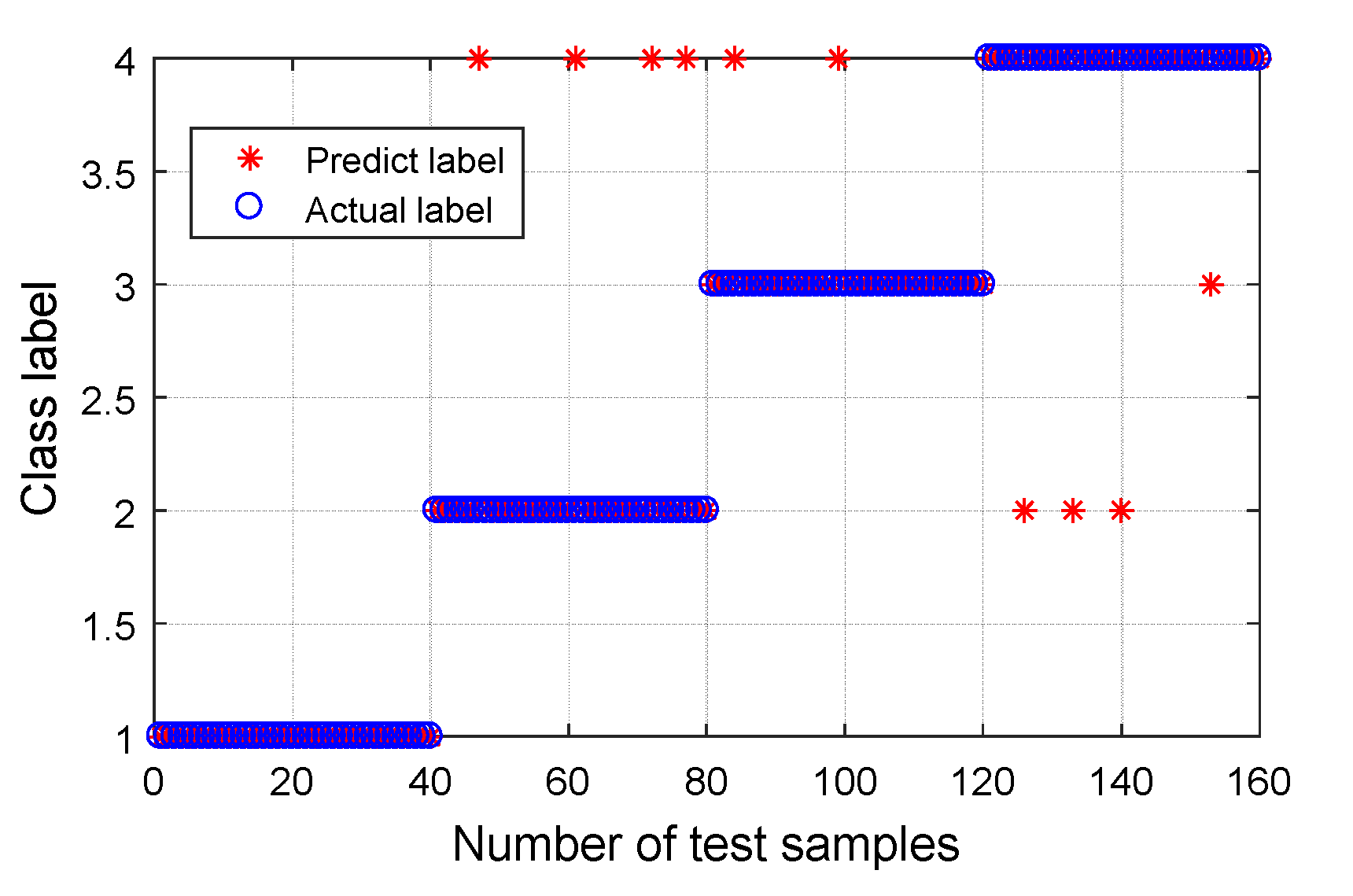
5. Experimental Results and Analysis
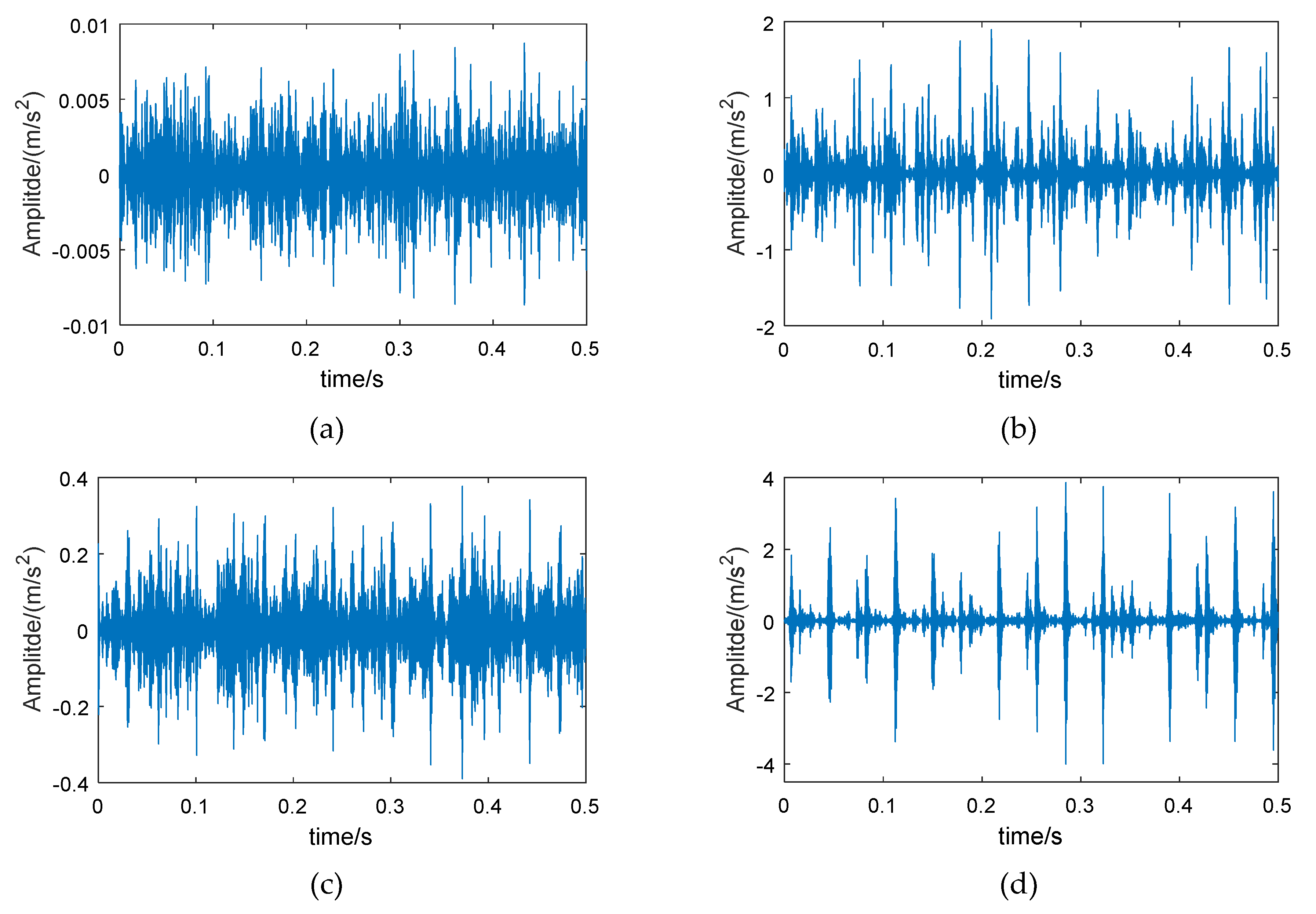
5.1. Experimental Validation 1
5.2. Performance Comparison 1
5.3. Experimental Validation 2
5.4. Performance Comparison 2
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Acronym | Signification |
|---|---|
| WT | Wavelet Transform |
| WPT | Wavelet Packet Transform |
| EF | Energy Feature |
| EFR | Energy Feature Reconstruction |
| PE | Permutation Entropy |
| MPE | Multiscale Permutation Entropy |
| CMPE | Composite Multiscale Permutation Entropy |
| EMD | Empirical Mode Decomposition |
| EEMD | Ensemble Empirical Mode Decomposition |
| CEEMD | Complementary Ensemble Empirical Mode Decomposition |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| LMD | Local Mean Decomposition |
| EWT | Empirical Wavelet Transform |
| VMD | Variational Mode Decomposition |
| ApEn | Approximate Entropy |
| SampEn | Sample Entropy |
| MSE | Multiscale Entropy |
References
- Li, Y.B.; Yang, Y.T.; Wang, X.Z.; Liu, B.B.; Liang, X.H. Early fault diagnosis of rolling bearings based on hierarchical symbol dynamic entropy and binary tree support vector machine. J. Sound Vib. 2018, 428, 72–86. [Google Scholar] [CrossRef]
- Li, Q.; Ji, X.; Liang, S.Y. Incipient fault feature extraction for rotating machinery based on improved ar-minimum entropy deconvolution combined with variational mode decomposition approach. Entropy 2017, 19, 317. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.Q.; Xu, M.Q.; Huang, W.H. A review of early fault diagnosis approaches and their applications in rotating machinery. Entropy 2019, 21, 409. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Smith, J. The local mean decomposition and its application to EEG perception data. J. R. Soc. Interface 2005, 23, 443–454. [Google Scholar] [CrossRef]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Amin, J.; Sharif, M.; Raza, M.; Saba, T.; Anjum, M.A. Brain tumor detection using statistical and machine learning method. Comput. Methods Programs Biomed. 2019, 177, 69–79. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time-frequency analysis methods for machinery fault diagnosis: A review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Huang, N.E.; Wu, Z. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Li, Y.X.; Chen, X.; Yu, J. A hybrid energy feature extraction approach for ship-radiated noise based on CEEMDAN combined with energy difference and energy entropy. Processes 2019, 7, 69. [Google Scholar] [CrossRef]
- Li, Y.X.; Li, Y.; Chen, X.; Yu, J.; Yang, H.; Wang, L. A New Underwater Acoustic Signal Denoising Technique Based on CEEMDAN, Mutual Information, Permutation Entropy, and Wavelet Threshold Denoising. Entropy 2018, 20, 563. [Google Scholar] [CrossRef]
- Li, Y.X.; Chen, X.; Yu, J.; Yang, X.H. A fusion frequency feature extraction method for underwater acoustic signal based on variational mode decomposition, duffing chaotic oscillator and a kind of permutation entropy. Electronics 2019, 8, 61. [Google Scholar] [CrossRef]
- Fan, W.; Zhou, Q.; Li, J.; Zhu, Z. A wavelet-based statistical approach for monitoring and diagnosis of compound faults with application to rolling bearings. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1563–1572. [Google Scholar] [CrossRef]
- Bin, G.F.; Gao, J.J.; Li, X.J.; Dhillon, B.S. Early fault diagnosis of rotating machinery based on wavelet packets-Empirical mode decomposition feature extraction and neural network. Mech. Syst. Signal Process. 2012, 27, 696–711. [Google Scholar] [CrossRef]
- Bastam, A.R.; Aasi, A.; Arghand, H.A. Estimation of remaining useful life of rolling element bearings using wavelet packet decomposition and artificial neural network. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, S233–S245. [Google Scholar] [CrossRef]
- Wang, C.; Gan, M.; Zhu, C.A. Fault feature extraction of rolling element bearings based on wavelet packet transform and sparse representation theory. J. Intell. Manuf. 2018, 29, 937–951. [Google Scholar] [CrossRef]
- Wan, S.T.; Zhang, X.; Dou, L.J. Shannon entropy of binary wavelet packet subbands and its application in bearing fault extraction. Entropy 2018, 20, 260. [Google Scholar] [CrossRef]
- Chen, G.; Li, Q.Y.; Li, D.Q.; Wu, Z.Y.; Liu, Y. Main frequency band of blast vibration signal based on wavelet packet transform. Appl. Math. Model. 2019, 74, 569–585. [Google Scholar] [CrossRef]
- Huang, L.P.; Huang, H.; Liu, Y.H. A fault diagnosis approach for rolling bearing based on wavelet packet decomposition and GMM-HMM. Int. J. Acoust. Vib. 2019, 24, 199–209. [Google Scholar] [CrossRef]
- Ma, J.; Wu, J.D.; Wang, X.D. Fault diagnosis method based on wavelet packet-energy entropy and fuzzy kernel extreme learning machine. Adv. Mech. Eng. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J. Bearing Fault Diagnosis Based on Multiscale Permutation Entropy and Support Vector Machine. Entropy 2012, 14, 2650–2654. [Google Scholar] [CrossRef]
- Zhang, W.B.; Zhou, J.Z. Fault diagnosis for rolling element bearings based on feature space reconstruction and multiscale permutation entropy. Entropy 2019, 21, 519. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X. Approximate entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhuang, J.; Yu, W. Measuring complexity using FuzzyEn, ApEn, and SampEn. Med. Eng. Phys. 2009, 31, 61–68. [Google Scholar] [CrossRef]
- Nicoletti, R.; Cavalini, A.A.; Steffen, V. Detection of cracks in rotating shafts by using the combination resonances approach and the approximated entropy algorithm. Shock Vib. 2018, 2018, 14. [Google Scholar] [CrossRef]
- Li, Y.B.; Feng, K.; Liang, X.H.; Zuo, M.J. A fault diagnosis method for planetary gearboxes under non-stationary working conditions using improved Vold-Kalman filter and multi-scale sample entropy. J. Sound Vib. 2019, 439, 271–286. [Google Scholar] [CrossRef]
- Hsieh, N.K.; Lin, W.Y.; Young, H.T. High-speed spindle fault diagnosis with the empirical mode decomposition and multiscale entropy method. Entropy 2015, 17, 2170–2183. [Google Scholar] [CrossRef]
- Zheng, J.D.; Jiang, Z.W.; Pan, H.Y. Sigmoid-based refined composite multiscale fuzzy entropy and t-SNE based fault diagnosis approach for rolling bearing. Measurement 2018, 129, 332–342. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.X.; Zhou, G.W.; Li, D.D. Application of Variational Mode Decomposition and Permutation Entropy for Rolling Bearing Fault Diagnosis. Int. J. Acoust. Vib. 2019, 24, 303–311. [Google Scholar] [CrossRef]
- Xiao, L.J.; Lv, Y.; Fu, G.Z. Fault Classification of Rotary Machinery Based on Smooth Local Subspace Projection Method and Permutation Entropy. Appl. Sci. 2019, 9, 2102. [Google Scholar] [CrossRef]
- Tian, Y.; Wang, Z.L.; Lu, C. Self-adaptive bearing fault diagnosis based on permutation entropy and manifold-based dynamic time warping. Mech. Syst. Signal Process. 2019, 114, 658–673. [Google Scholar] [CrossRef]
- Aziz, W.; Arif, M. Multiscale permutation entropy of physiological time series. In Proceedings of the 9th International Multitopic Conference (INMIC ’05), Karachi, Pakistan, 24–25 December 2005. [Google Scholar]
- Zheng, J.D.; Pan, H.Y.; Yang, S.B.; Cheng, J.S. Generalized composite multiscale permutation entropy and Laplacian score based rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2018, 99, 229–243. [Google Scholar] [CrossRef]
- Azami, H.; Escudero, J. Improved multiscale permutation entropy for biomedical signal analysis: Interpretation and application to electroencephalogram recordings. Biomed. Signal Process. Control 2016, 23, 28–41. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.; Xiong, Q.; Luo, D.; Mei, G.; Zhang, T. A rolling bearing fault diagnosis strategy based on improved multiscale permutation entropy and least squares SVM. J. Mech. Sci. Technol. 2017, 31, 2711–2722. [Google Scholar] [CrossRef]
- Si, L.; Wang, Z.B.; Tan, C.; Liu, X.H. A feature extraction method based on composite multi-scale permutation entropy and Laplacian score for shearer cutting state recognition. Measurement 2019, 145, 84–93. [Google Scholar] [CrossRef]
- Yin, Z.D.; Wang, L.; Zhang, Y.J.; Gao, Y. A novel arc fault detection method integrated random forest, improved multi-scale permutation entropy and wavelet packet transform. Electronics 2019, 8, 396. [Google Scholar] [CrossRef]
- Case Western Reserve University Bearing Data Center Website. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 4 September 2019).
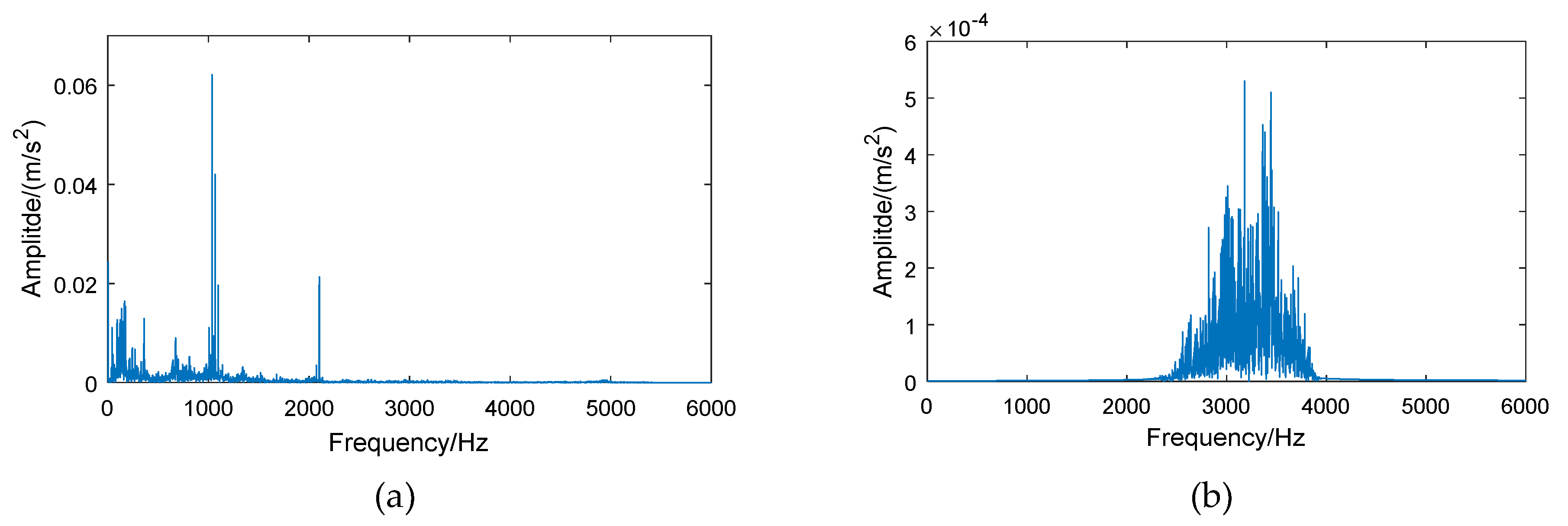
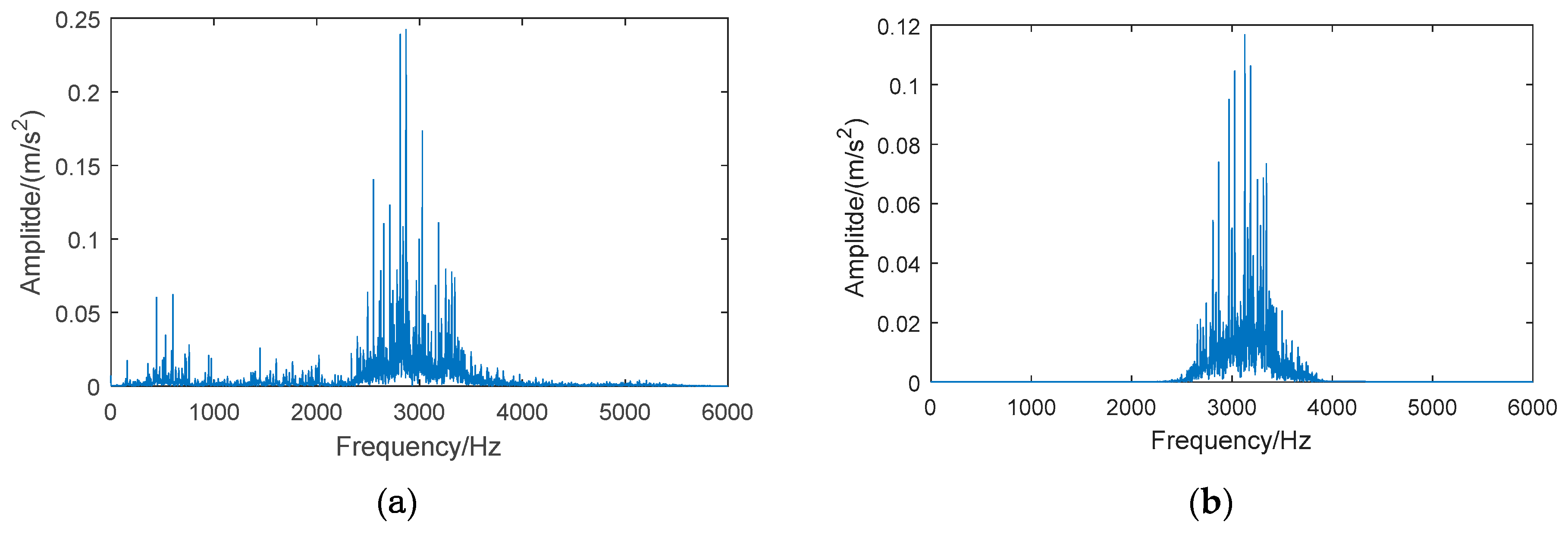

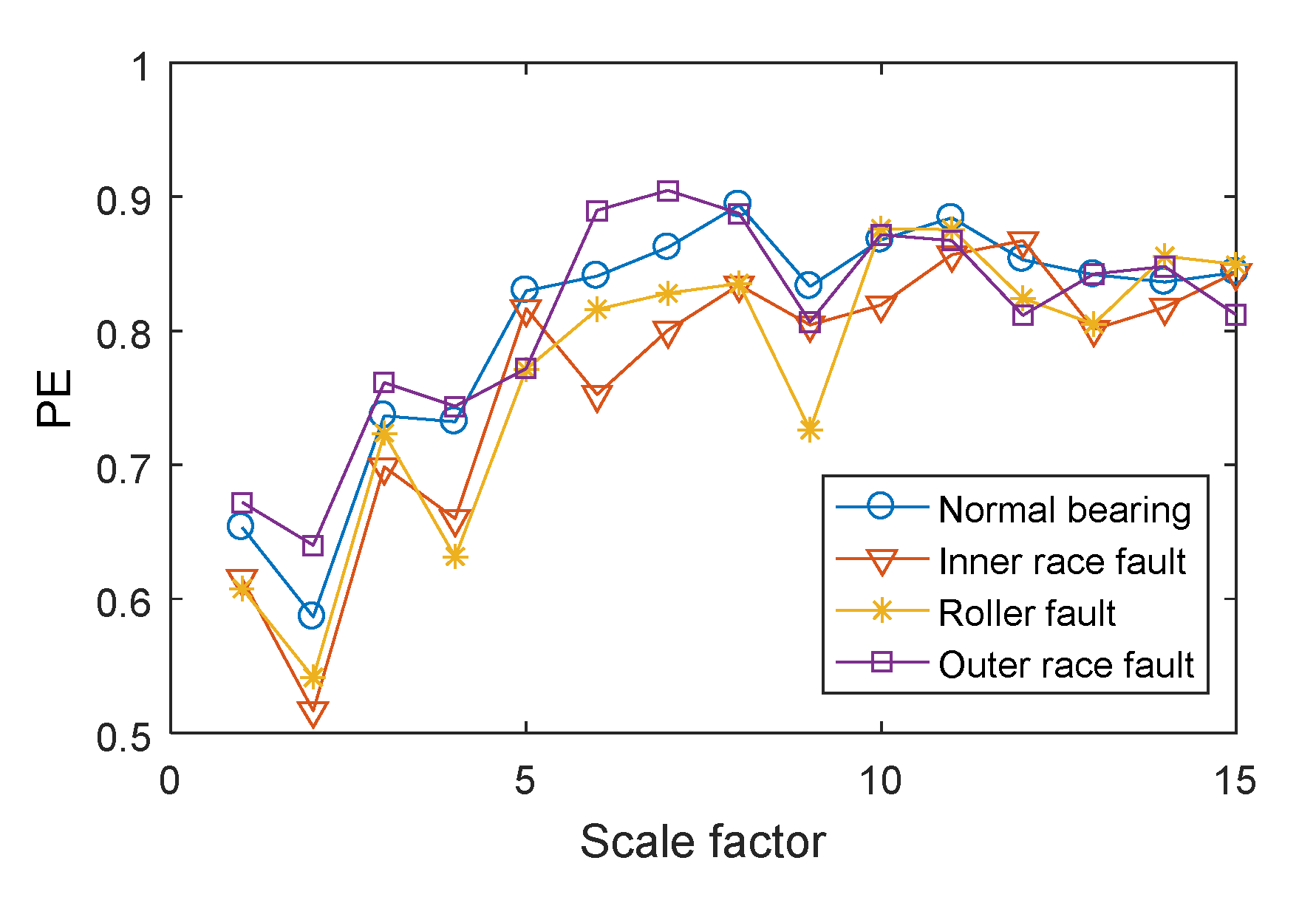
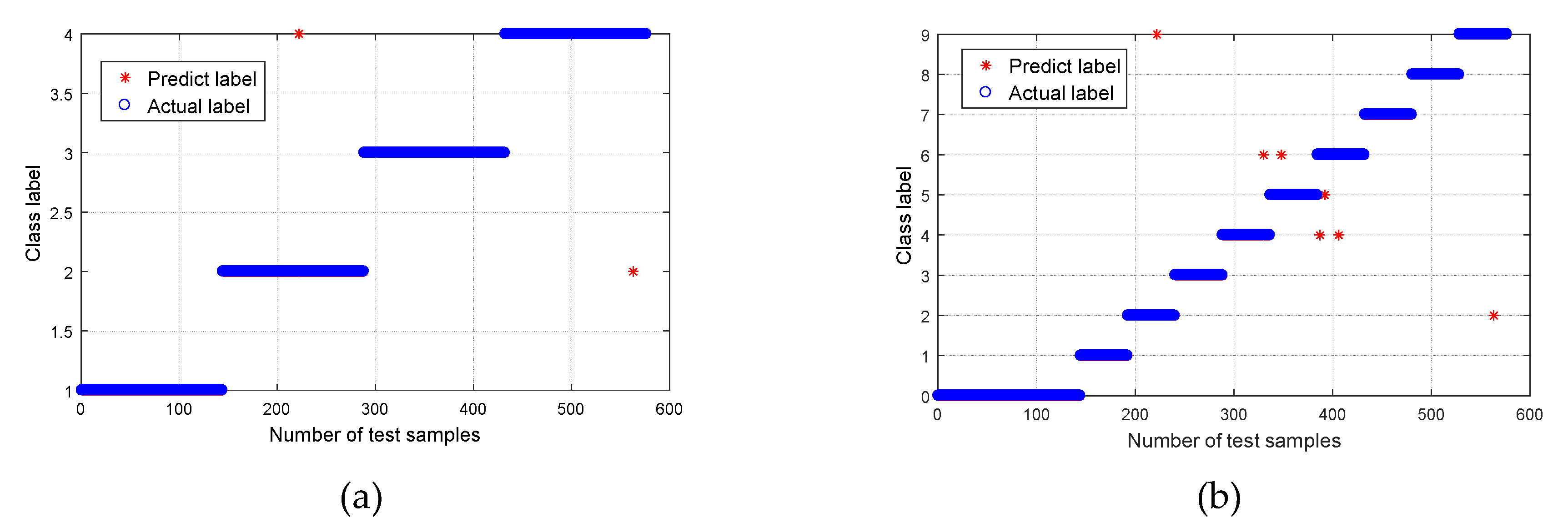
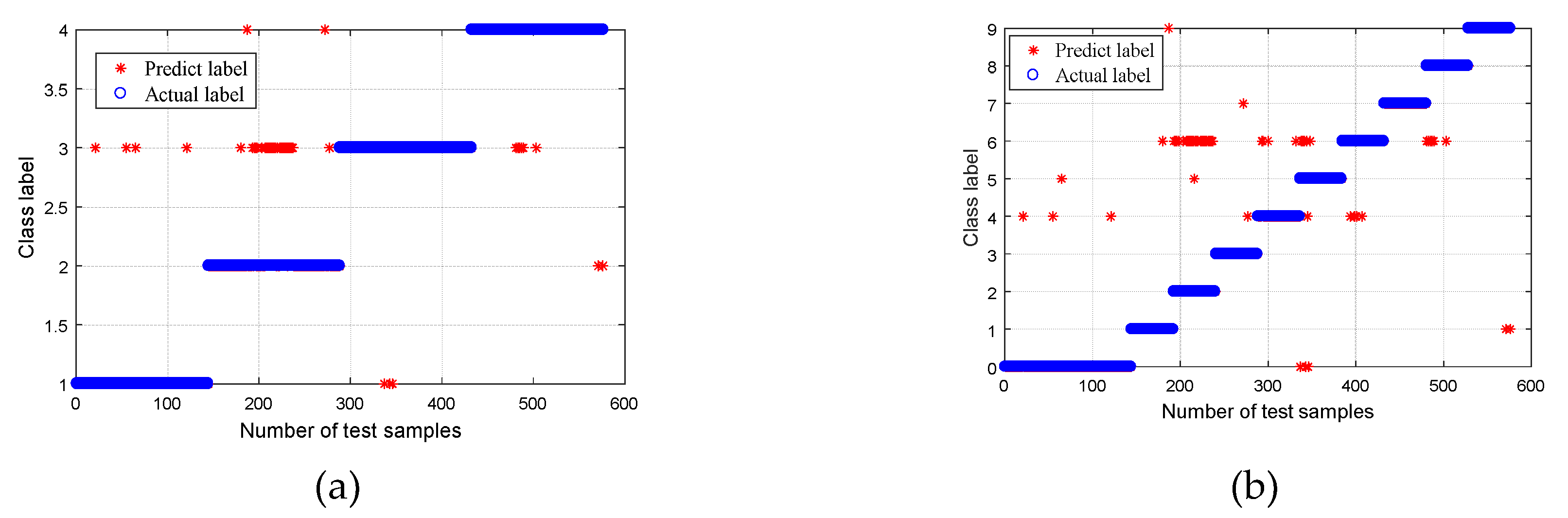
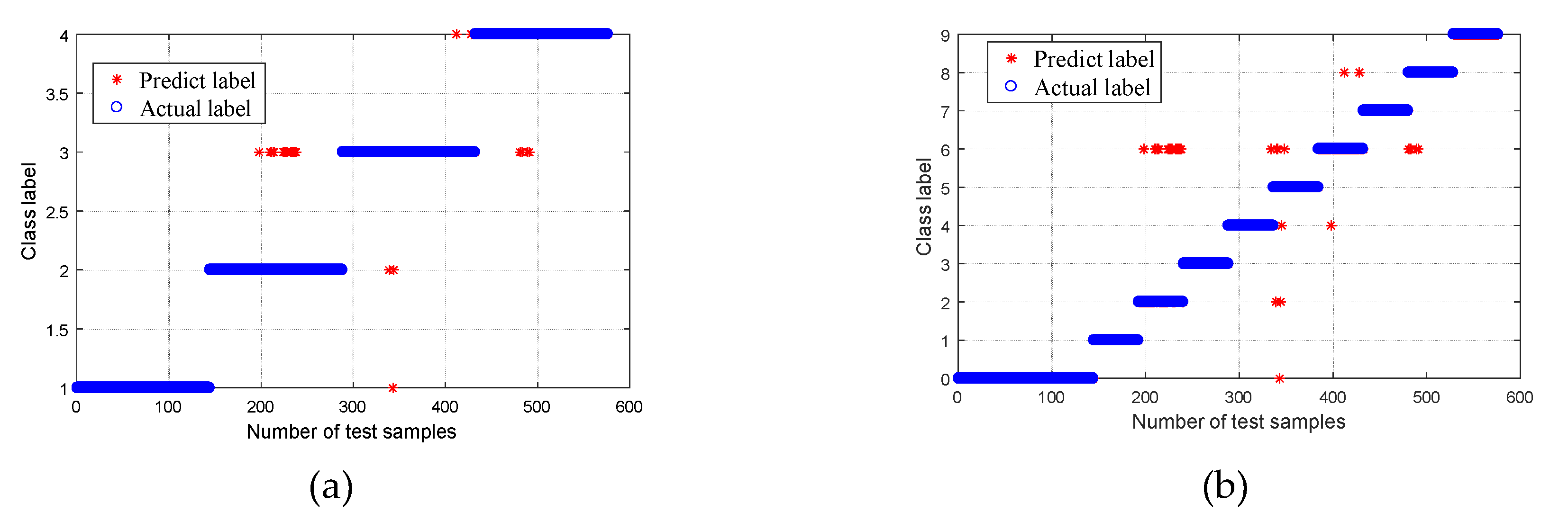
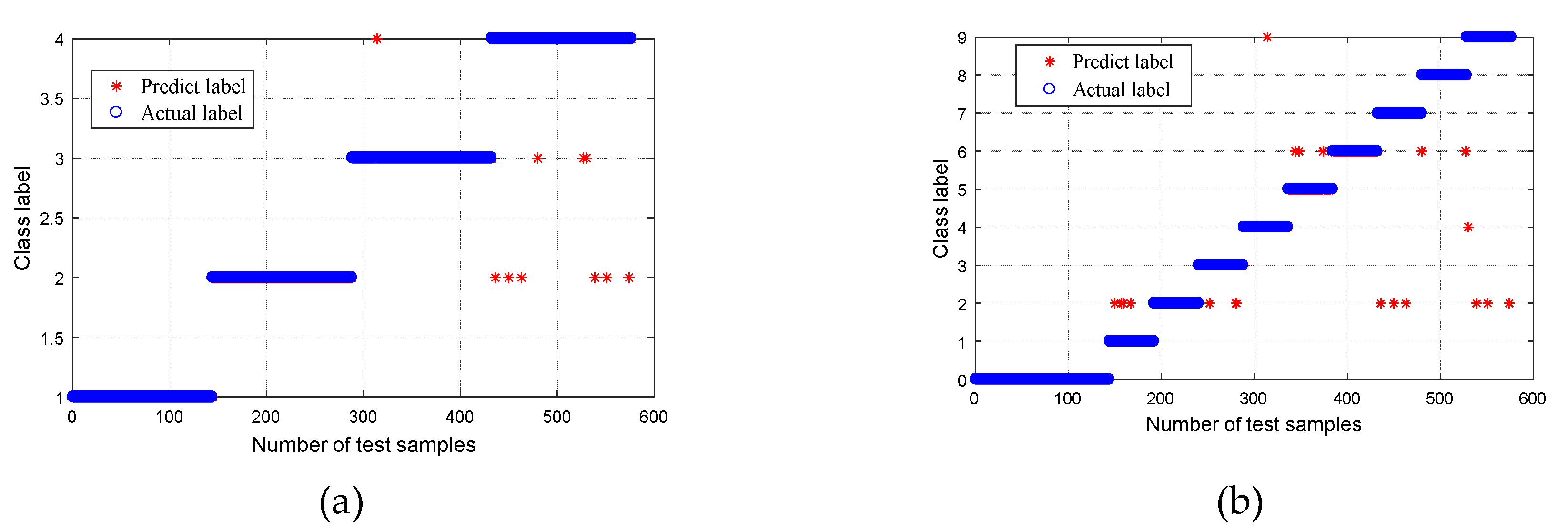
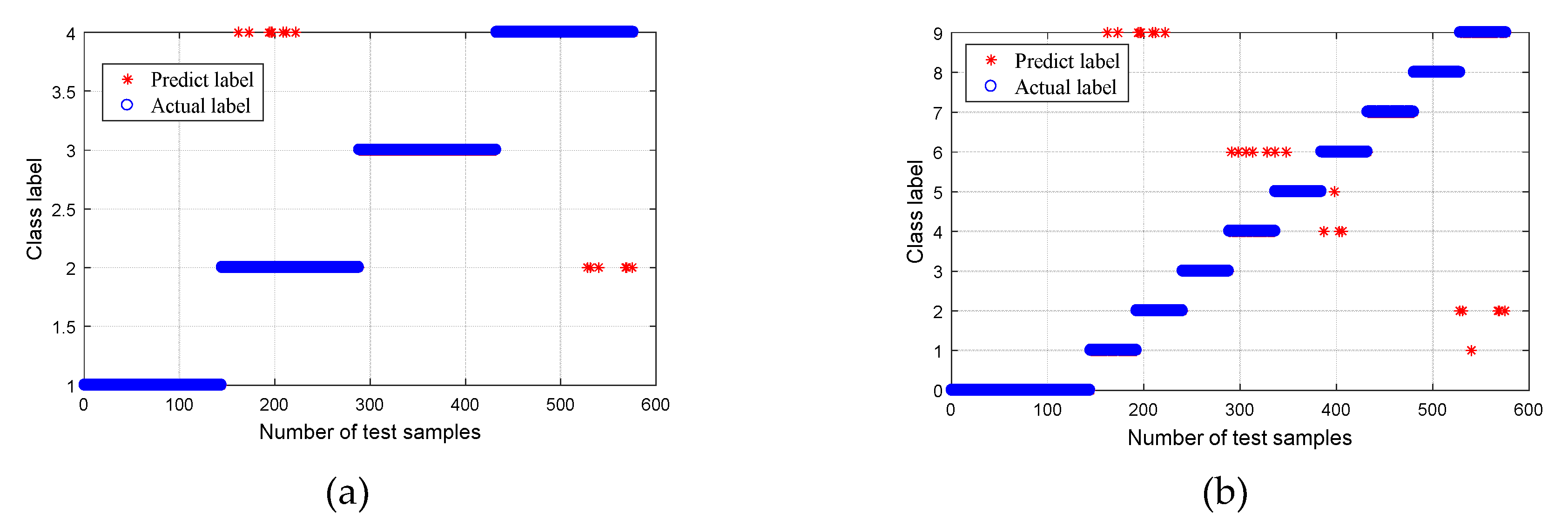

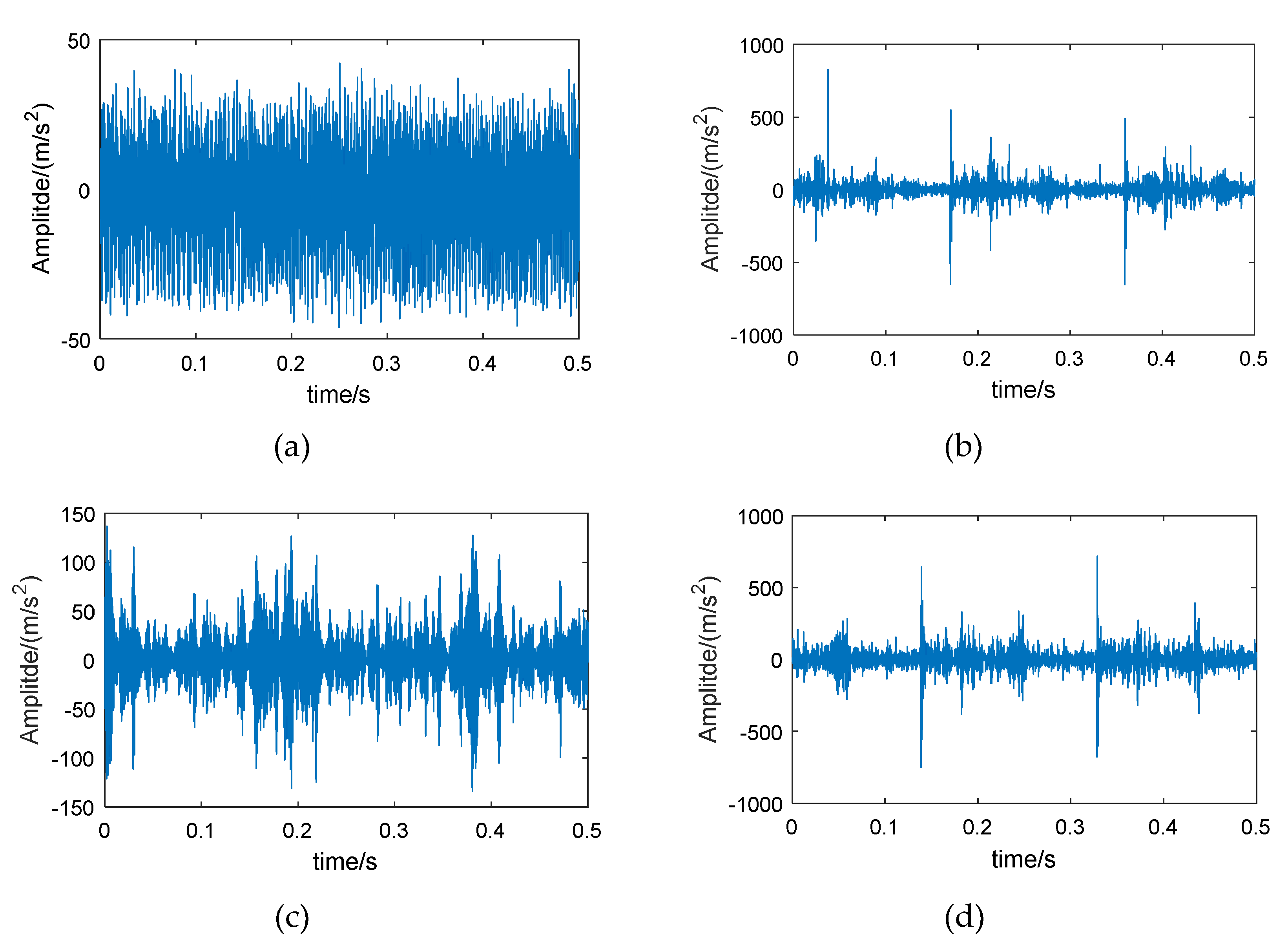
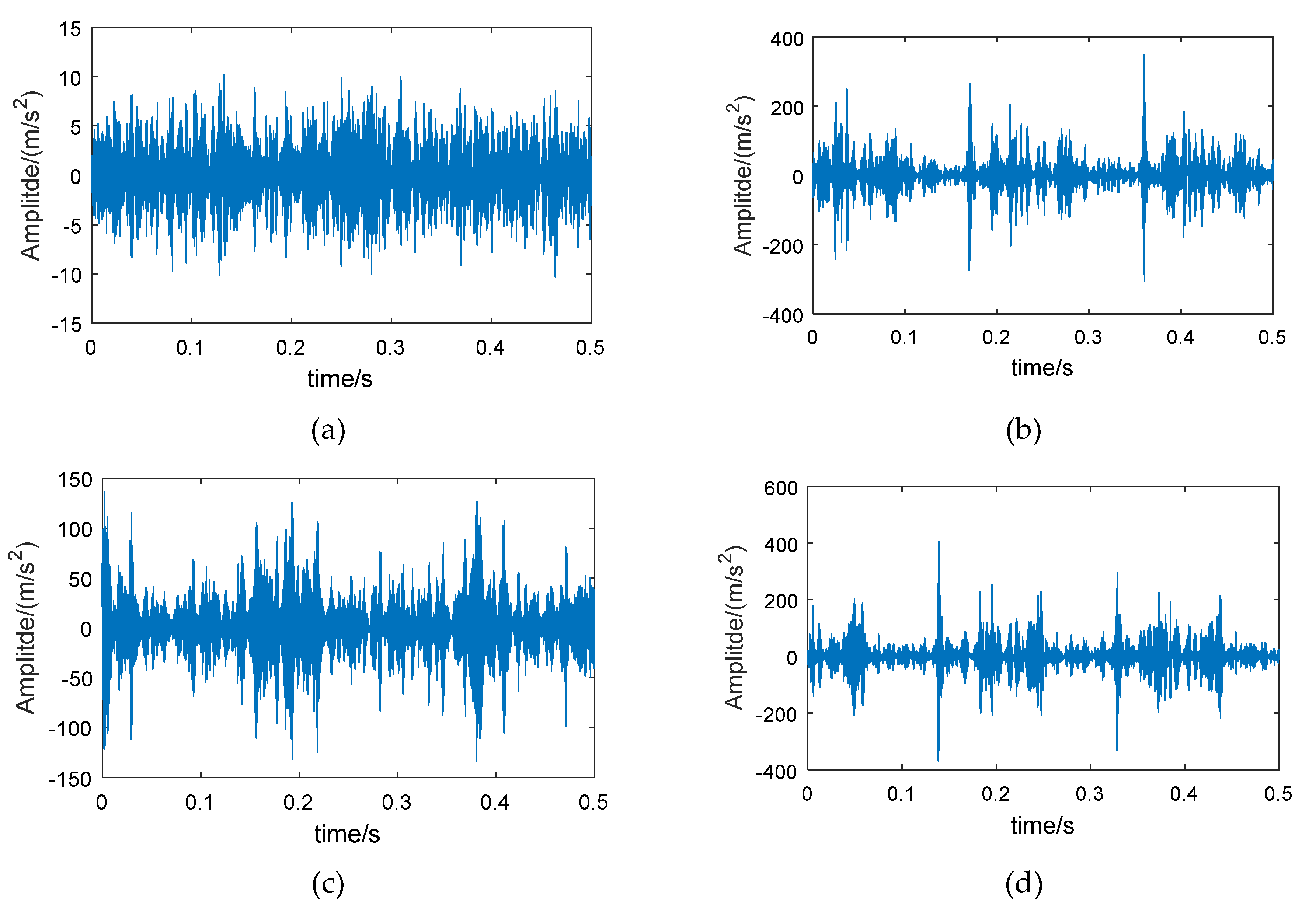
| Bearing Condition | Fault Diameter (mm) | Number of Training Samples | Number of Testing Samples | Group II Class Label | Group I Class Label |
|---|---|---|---|---|---|
| Normal | 0 | 36 | 144 | 0 | 1 |
| IRF1 | 0.1778 | 12 | 48 | 1 | 2 |
| IRF2 | 0.3556 | 12 | 48 | 2 | |
| IRF3 | 0.5334 | 12 | 48 | 3 | |
| BF1 | 0.1778 | 12 | 48 | 4 | 3 |
| BF2 | 0.3556 | 12 | 48 | 5 | |
| BF3 | 0.5334 | 12 | 48 | 6 | |
| ORF1 | 0.1778 | 12 | 48 | 7 | 4 |
| ORF2 | 0.3556 | 12 | 48 | 8 | |
| ORF3 | 0.5334 | 12 | 48 | 9 |
| Item | Fault Diameter (mm) | Accuracy (%) (Correct Number/Testing Number) | Total Accuracy (%) | |||
|---|---|---|---|---|---|---|
| Normal | IRF | BF | ORF | |||
| Group I | 0.1778 | 100 (144/144) | 100 (48/48) | 97.9 (47/48) | 100 (48/48) | 98.54 |
| 0.3556 | 97.9 (47/48) | 97.9 (47/48) | 100 (48/48) | |||
| 0.5334 | 100 (48/48) | 93.8 (45/48) | 97.9 (47/48) | |||
| Group II | Different diameter | 100 (144/144) | 99.31 (143/144) | 100 (144/144) | 99.31 (143/144) | 99.66 |
| Different Approaches | Accuracy (%) | |
|---|---|---|
| Group I | Group II | |
| MPE + MG-SVM | 86.60 | 91.15 |
| CMPE + MG-SVM | 93.33 | 95.49 |
| WPT-EF + MG-SVM | 95.63 | 98.26 |
| WPT-EFR-MPE + MG-SVM | 94.79 | 97.57 |
| Proposed method | 98.54 | 99.66 |
| Pitch Diameter (mm) | Roller Diameter (mm) | Roller Number | Contact Angle (rad) | Rotation Velocity (rpm) | Load (kN) |
|---|---|---|---|---|---|
| 176 | 26 | 18 | 0 | 300 | 70 |
| Accuracy (%) (Correct Number/Testing Number) | Total Accuracy (%) | |||
|---|---|---|---|---|
| Normal | IRF | BF | ORF | |
| 100 (40/40) | 90 (36/40) | 95 (38/40) | 90 (36/40) | 93.75 |
| Different Approaches | Accuracy (%) (Correct Number/Testing Number) | Total Accuracy (%) | |||
|---|---|---|---|---|---|
| Normal | IRF | BF | ORF | ||
| MPE + MG-SVM | 100 (40/40) | 65 (26/40) | 88 (35/40) | 83 (33/40) | 83.75 |
| CMPE + MG-SVM | 100 (40/40) | 73(29/40) | 95 (38/40) | 97 (39/40) | 91.25 |
| WPT-EF + MG-SVM | 100 (40/40) | 78 (31/40) | 95 (38/40) | 85 (34/40) | 89.37 |
| WPT-EFR-MPE + MG-SVM | 95 (38/40) | 63 (25/40) | 90 (36/40) | 83 (33/40) | 82.50 |
| Proposed method | 100 (40/40) | 90 (36/40) | 95 (38/40) | 90 (36/40) | 93.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lu, Z.; Wei, J.; Zhang, Y. Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy. Entropy 2019, 21, 865. https://doi.org/10.3390/e21090865
Wang X, Lu Z, Wei J, Zhang Y. Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy. Entropy. 2019; 21(9):865. https://doi.org/10.3390/e21090865
Chicago/Turabian StyleWang, Xiaochao, Zhenggang Lu, Juyao Wei, and Yuan Zhang. 2019. "Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy" Entropy 21, no. 9: 865. https://doi.org/10.3390/e21090865
APA StyleWang, X., Lu, Z., Wei, J., & Zhang, Y. (2019). Fault Diagnosis for Rail Vehicle Axle-Box Bearings Based on Energy Feature Reconstruction and Composite Multiscale Permutation Entropy. Entropy, 21(9), 865. https://doi.org/10.3390/e21090865





