A Physically-Motivated Quantisation of the Electromagnetic Field on Curved Spacetimes
Abstract
1. Introduction
2. Gauge-Independent Quantisation of the Electromagnetic Field
2.1. Classical Electrodynamics
2.2. Gauge Dependence in Electromagnetic Field Quantisation
2.3. Physically-Motivated Gauge-Independent Method
3. Gauge-Independent Quantisation of the Electromagnetic Field in Curved Spacetimes
3.1. Classical Electrodynamics in Curved Space
3.2. Particles in Curved Spacetimes
3.3. Covariant and Gauge-Independent Electromagnetic Field Quantisation Scheme
3.3.1. Hilbert Space
3.3.2. Hamiltonian
3.3.3. Electromagnetic Field Observables
3.3.4. Summary of Scheme
4. Electromagnetic Field Quantisation in an Accelerated Frame
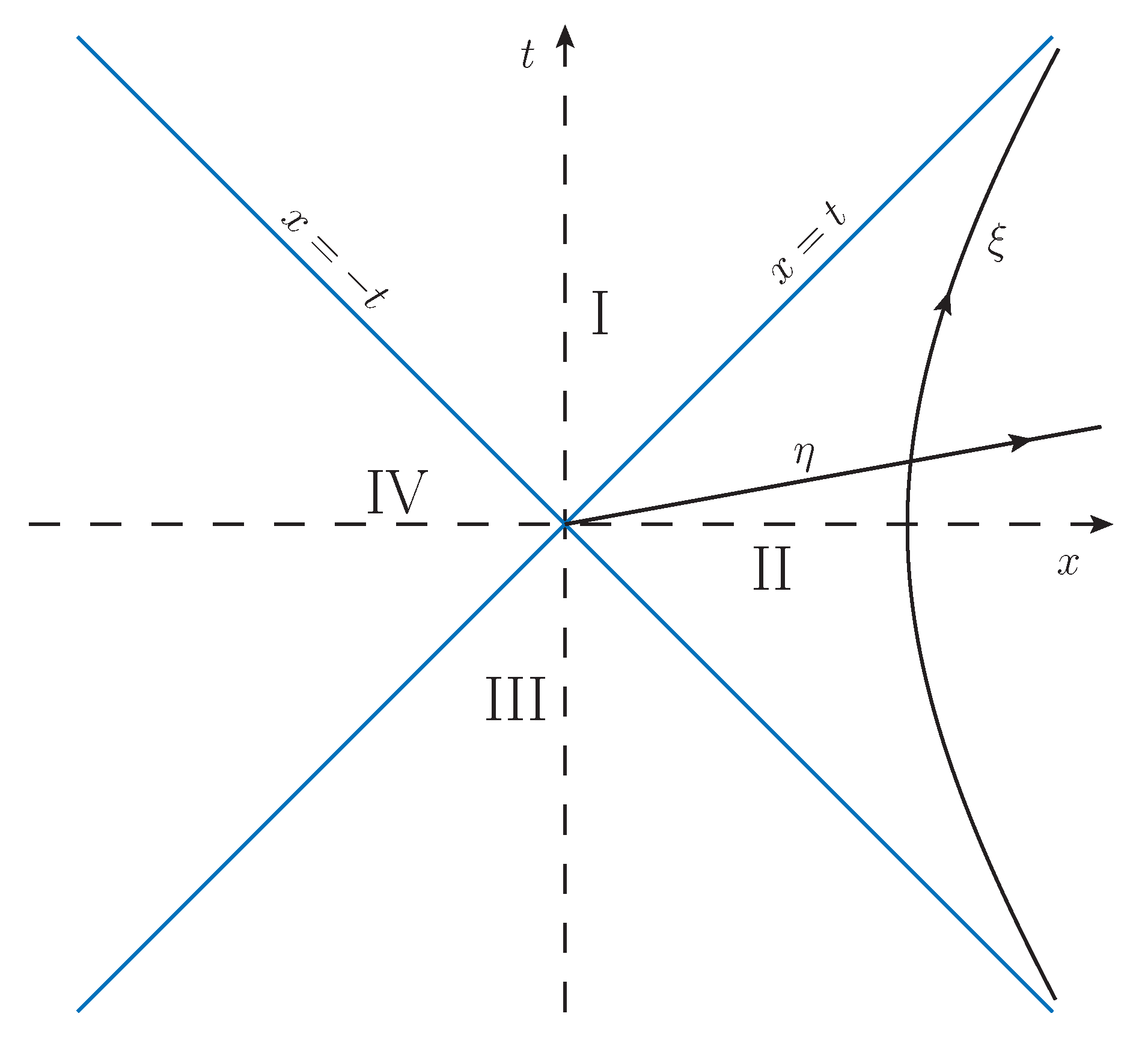
4.1. Rindler Space
4.2. Electromagnetism in Rindler Space
4.3. Field Quantisation in Rindler Space
4.4. The Unruh Effect
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Further Results of Electromagnetism in Rindler Space
References
- Roychoudhuri, C.; Kracklauer, A.F.; Creath, K. The Nature of Light: What Is a Photon? CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Stokes, A. On Gauge Freedom and Subsystems in Quantum Electrodynamics. Ph.D. Thesis, School of Physics and Astronomy, University of Leeds, Leeds, UK, January 2014. [Google Scholar]
- Andrews, D.L. Physicality of the photon. J. Phys. Chem. Lett. 2013, 4, 3878–3884. [Google Scholar] [CrossRef]
- Barlow, T.M.; Bennett, R.; Beige, A. A master equation for a two-sided optical cavity. J. Mod. Opt. 2015, 62, S11–S20. [Google Scholar] [CrossRef] [PubMed]
- Furtak-Wells, N.; Clark, L.A.; Purdy, R.; Beige, A. Quantising the electromagnetic field near two-sided semitransparent mirrors. Phys. Rev. 2018, 97, 043827. [Google Scholar] [CrossRef]
- Nisbet-Jones, P.B.R.; Dilley, J.; Ljunggren, D.; Kuhn, A. Highly efficient source for indistinguishable single photons of controlled shape. New J. Phys. 2011, 13, 103036. [Google Scholar] [CrossRef]
- Milburn, G.J.; Basiri-Esfahani, S. Quantum optics with one or two photons. Proc. R. Soc. A 2015, 471, 20150208. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, A.; Hennrich, M.; Rempe, G. Deterministic Single-Photon Source for Distributed Quantum Networking. Phys. Rev. Lett. 2002, 89, 067901. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.W.; Bouwmeester, D.; Daniell, M.; Weinfurter, H.; Zeilinger, A. Experimental test of quantum nonlocality in three-photon Greenberger-Horne-Zeilinger entanglement. Nature 2000, 403, 515–519. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Fan, J.; Migdall, A.; Polyakov, S.V. Invited review article: Single-photon sources and detectors. Rev. Sci. Instrum. 2011, 82, 071101. [Google Scholar] [CrossRef]
- Giustina, M.; Versteegh, M.A.M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.A.; Abellan, C.; et al. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellan, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- Villoresi, P.; Jennewein, T.; Tamburini, F.; Aspelmeyer, M.; Bonato, C.; Ursin, R.; Pernechele, C.; Luceri, V.; Bianco, G.; Zeilinger, A.; et al. Experimental verification of the feasibility of a quantum channel between space and earth. New J. Phys. 2008, 10, 033038. [Google Scholar] [CrossRef]
- Vallone, G.; Bacco, D.; Dequal, D.; Gaiarin, S.; Luceri, V.; Bianco, G.; Villoresi, P. Experimental Satellite Quantum Communications. Phys. Rev. Lett. 2015, 115, 040502. [Google Scholar] [CrossRef] [PubMed]
- Rideout, D.; Jennewein, T.; Amelino-Camelia, G.; Demarie, T.F.; Higgins, B.L.; Kempf, A.; Kent, A.; Laflamme, R.; Ma, X.; Mann, R.B.; et al. Fundamental quantum optics experiments conceivable with satellites reaching relativistic distances and velocities. Class. Quantum Gravity 2012, 29, 224011. [Google Scholar] [CrossRef]
- Friis, N.; Lee, A.R.; Louko, J. Scalar, spinor, and photon fields under relativistic cavity motion. Phys. Rev. D 2013, 88, 064028. [Google Scholar] [CrossRef]
- Friis, N.; Lee, A.R.; Truong, K.; Sabín, C.; Solano, E.; Johansson, G.; Fuentes, I. Relativistic quantum teleportation with superconducting circuits. Phys. Rev. Lett. 2013, 110, 113602. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, M.; Bruschi, D.E.; Fuentes, I. Quantum metrology for relativistic quantum fields. Phys. Rev. D 2014, 89, 065028. [Google Scholar] [CrossRef]
- Bruschi, D.E.; Sabín, C.; Kok, P.; Johansson, G.; Delsing, P.; Fuentes, I. Towards universal quantum computation through relativistic motion. Sci. Rep. 2016, 6, 18349. [Google Scholar] [CrossRef] [PubMed]
- Kravtsov, K.S.; Radchenko, I.V.; Kulik, S.P.; Molotkov, S.N. Relativistic quantum key distribution system with one-way quantum communication. Sci. Rep. 2018, 8, 6102. [Google Scholar] [CrossRef]
- Lopp, R.; Martín-Martínez, E. Light, matter, and quantum randomness generation: A relativistic quantum information perspective. Opt. Commun. 2018, 423, 29–47. [Google Scholar] [CrossRef]
- Bruschi, D.E.; Fuentes, I.; Louko, J. Voyage to alpha centauri: Entanglement degradation of cavity modes due to motion. Phys. Rev. D 2012, 85, 061701. [Google Scholar] [CrossRef]
- Bruschi, D.E.; Ralph, T.C.; Fuentes, I.; Jennewein, T.; Razavi, M. Spacetime effects on satellite-based quantum communications. Phys. Rev. D 2014, 90, 045041. [Google Scholar] [CrossRef]
- Bruschi, D.E.; Sabín, C.; White, A.; Baccetti, V.; Oi, D.K.L.; Fuentes, I. Testing the effects of gravity and motion on quantum entanglement in space-based experiments. New J. Phys. 2014, 16, 053041. [Google Scholar] [CrossRef]
- Calmet, X.; Dunningham, J. Transformation properties and entanglement of relativistic qubits under space-time and gauge transformations. Phys. Rev. A 2017, 95, 042309. [Google Scholar] [CrossRef]
- Bruschi, D.E.; Datta, A.; Ursin, R.; Ralph, T.C.; Fuentes, I. Quantum estimation of the Schwarzschild spacetime parameters of the earth. Phys. Rev. D 2014, 90, 124001. [Google Scholar] [CrossRef]
- Alsing, P.M.; Milburn, G.J. Teleportation with a uniformly accelerated partner. Phys. Rev. Lett. 2003, 91, 180404. [Google Scholar] [CrossRef] [PubMed]
- Bruschi, D.E.; Louko, J.; Martín-Martínez, E.; Dragan, A.; Fuentes, I. Unruh effect in quantum information beyond the single-mode approximation. Phys. Rev. A 2010, 82, 042332. [Google Scholar] [CrossRef]
- Bruschi, D.E.; Dragan, A.; Lee, A.R.; Fuentes, I.; Louko, J. Relativistic motion generates quantum gates and entanglement resonances. Phys. Rev. Lett. 2013, 111, 090504. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.Y.; Ma, W.; Wang, D.; Ye, L. How the relativistic motion affect quantum Fisher information and Bell non-locality for multipartite state. Sci. Rep. 2017, 7, 38456. [Google Scholar] [CrossRef]
- Schützhold, R.; Schaller, G.; Habs, D. Signatures of the Unruh Effect from Electrons Accelerated by Ultrastrong Laser Fields. Phys. Rev. Lett. 2006, 97, 121302. [Google Scholar] [CrossRef]
- Schützhold, R.; Schaller, G.; Habs, D. Tabletop Creation of Entangled Multi-keV Photon Pairs and the Unruh Effect. Phys. Rev. Lett. 2008, 100, 091301. [Google Scholar]
- Hawton, M. Photon counting by inertial and accelerated detectors. Phys. Rev. A 2013, 87, 042116. [Google Scholar] [CrossRef]
- Soldati, R.; Specchia, C. On the Massless Vector Fields in a Rindler Space. J. Mod. Phys. 2015, 6, 1743–1755. [Google Scholar] [CrossRef]
- Bennett, R.; Barlow, T.M.; Beige, A. A physically motivated quantization of the electromagnetic field. Eur. J. Phys. 2016, 37, 014001. [Google Scholar] [CrossRef]
- Stokes, A.; Kurcz, A.; Spiller, T.P.; Beige, A. Extending the validity range of quantum optical master equations. Phys. Rev. A 2010, 85, 053805. [Google Scholar] [CrossRef]
- Stokes, A. Noncovariant gauge fixing in the quantum Dirac field theory of atoms and molecules. Phys. Rev. A 2012, 86, 012511. [Google Scholar] [CrossRef]
- Stokes, A.; Deb, P.; Beige, A. Using thermodynamics to identify quantum subsystems. J. Mod. Opt. 2017, 64, S7–S19. [Google Scholar] [CrossRef]
- Parker, L.E.; Toms, D.J. Quantum Field Theory in Curved Spacetime: Quantized Fields and Gravity; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Casals, M.; Dolan, S.R.; Nolan, B.C.; Ottewill, A.C.; Winstanley, E. Quantization of fermions on Kerr space-time. Phys. Rev. D 2013, 87, 064027. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Gauge-invariant formulation of quantum electrodynamics. Can. J. Phys. 1955, 33, 650–660. [Google Scholar] [CrossRef]
- DeWitt, B.S. Quantum Theory without Electromagnetic Potentials. Phys. Rev. 1962, 125, 2189–2191. [Google Scholar] [CrossRef]
- Gray, R.D.; Kobe, D.H. Gauge-invariant canonical quantisation of the electromagnetic field and duality transformations. J. Phys. A Math. Gen. 1982, 15, 3145–3155. [Google Scholar] [CrossRef]
- Menikoff, R.; Sharp, D.H. A gauge invariant formulation of quantum electrodynamics using local currents. J. Math. Phys. 1977, 18, 471–482. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Lectures on Quantum Mechanics; Dover Publications Inc.: Mineola, NY, USA, 2001. [Google Scholar]
- Loudon, R. The Quantum Theory of Light; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Macmillan: London, UK, 1973. [Google Scholar]
- Carroll, S.M. Spacetime and Geometry: An Introduction to General Relativity; Addison Wesley: Boston, MA, USA, 2004. [Google Scholar]
- Lawrie, I.D. A Unified Grand Tour of Theoretical Physics, 2nd ed.; Institute of Physics Publishing: Bristol, UK, 2002. [Google Scholar]
- Martín-Martínez, E.; Rodriguez-Lopez, P. Relativistic quantum optics: The relativistic invariance of the light–Matter interaction models. Phys. Rev. D 2018, 97, 105026. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Fulling, S.A. Nonuniqueness of canonical field quantization in Riemannian space-time. Phys. Rev. D 1973, 7, 2850–2862. [Google Scholar] [CrossRef]
- Alsing, P.M.; Fuentes, I. Observer-dependent entanglement. Class. Quantum Gravity 2012, 29, 224001. [Google Scholar] [CrossRef]
- Hollands, S.; Wald, R.M. Quantum fields in curved spacetime. Phys. Rep. 2015, 574, 1–35. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870–892. [Google Scholar] [CrossRef]
- Unruh, W.G.; Weiss, N. Acceleration radiation in interacting field theories. Phys. Rev. D 1984, 29, 1656–1662. [Google Scholar] [CrossRef]
- Takagi, S. Vacuum Noise and Stress Induced by Uniform Acceleration: Hawking-Unruh Effect in Rindler Manifold of Arbitrary Dimension. Prog. Theor. Phys. Suppl. 1986, 88, 1–142. [Google Scholar] [CrossRef]
- Crispino, L.C.B.; Higuchi, A.; Matsas, G.E.A. The Unruh effect and its applications. Rev. Mod. Phys. 2008, 80, 787–838. [Google Scholar] [CrossRef]
- Buchholz, D.; Verch, R. Unruh versus Tolman: On the heat of acceleration. Gen. Relativ. Gravit. 2016, 48, 1–9. [Google Scholar] [CrossRef][Green Version]
- Acedo, L.; Tung, M.M. Electromagnetic waves in a uniform gravitational field and Planck’s postulate. Eur. J. Phys. 2012, 33, 1073. [Google Scholar] [CrossRef][Green Version]
- de Almeida, C.; Saa, A. The radiation of a uniformly accelerated charge is beyond the horizon: A simple derivation. Am. J. Phys. 2006, 74, 154–158. [Google Scholar] [CrossRef]
- Desloge, E.A. Nonequivalence of a uniformly accelerating reference frame and a frame at rest in a uniform gravitational field. Am. J. Phys. 1989, 57, 1121–1125. [Google Scholar] [CrossRef]
- Rindler, W. Kruskal space and the uniformly accelerated frame. Am. J. Phys. 1966, 34, 1174–1178. [Google Scholar] [CrossRef]
- Semay, C. Observer with a constant proper acceleration. Eur. J. Phys. 2006, 27, 1157–1167. [Google Scholar] [CrossRef]
- Ornigotti, M.; Aiello, A. The Faddeev-Popov Method Demystified. arXiv 2014, arXiv:1407.7256. [Google Scholar]
- Andrews, D.L.; Romero, L.C.D. A back-to-front derivation: the equal spacing of quantum levels is a proof of simple harmonic oscillator physics. Eur. J. Phys. 2009, 30, 1371–1380. [Google Scholar] [CrossRef]
- Ballentine, L.E. Quantum Mechanics: A Modern Development; World Scientific Publishing Company: Singapore, 1998. [Google Scholar]
- Nikolić, H. Horava-Lifshitz gravity, absolute time, and objective particles in curved space. Mod. Phys. Lett. A 2010, 25, 1595–1601. [Google Scholar] [CrossRef]
- Peres, A.; Terno, D.R. Quantum information and relativity theory. Rev. Mod. Phys. 2004, 76, 93–123. [Google Scholar] [CrossRef]
- Brown, J.D.; York, J.W., Jr. Quasilocal energy and conserved charges derived from the gravitational action. Phys. Rev. D 1993, 47, 1407–1419. [Google Scholar] [CrossRef]
- Bogolubov, N.N.; Shirkov, D.V. Introduction to the Theory of Quantized Fields; Wiley-Interscience: New York, NY, USA, 1980. [Google Scholar]
- Schwinger, J. Quantum Electrodynamics. I. A Covariant Formulation. Phys. Rev. 1948, 74, 1439–1461. [Google Scholar] [CrossRef]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Kasper, U.; Kreisel, E.; Treder, H.J. On the Covariant Formulation of Quantum Mechanics. Found. Phys. 1977, 7, 375–389. [Google Scholar] [CrossRef]
- Crawford, J.P. Spinor Matter in a gravitational field: Covariant equations àla Heisenberg. Found. Phys. 1998, 28, 457–470. [Google Scholar] [CrossRef]
- Susskind, L. Black Holes and Holography. Available online: https://www.perimeterinstitute.ca/video-library/collection/black-holes-and-holography-mini-course-2007 (accessed on 29 August 2019).
- Iorio, A.; Lambiase, G.; Vitiello, G. Quantization of Scalar Fields in Curved Background and Quantum Algebras. Ann. Phys. 2001, 294, 234–250. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maybee, B.; Hodgson, D.; Beige, A.; Purdy, R. A Physically-Motivated Quantisation of the Electromagnetic Field on Curved Spacetimes. Entropy 2019, 21, 844. https://doi.org/10.3390/e21090844
Maybee B, Hodgson D, Beige A, Purdy R. A Physically-Motivated Quantisation of the Electromagnetic Field on Curved Spacetimes. Entropy. 2019; 21(9):844. https://doi.org/10.3390/e21090844
Chicago/Turabian StyleMaybee, Ben, Daniel Hodgson, Almut Beige, and Robert Purdy. 2019. "A Physically-Motivated Quantisation of the Electromagnetic Field on Curved Spacetimes" Entropy 21, no. 9: 844. https://doi.org/10.3390/e21090844
APA StyleMaybee, B., Hodgson, D., Beige, A., & Purdy, R. (2019). A Physically-Motivated Quantisation of the Electromagnetic Field on Curved Spacetimes. Entropy, 21(9), 844. https://doi.org/10.3390/e21090844





