Sensor Control in Anti-Submarine Warfare—A Digital Twin and Random Finite Sets Based Approach
Abstract
1. Introduction
- Digital twin breaks the barriers between the real ASW and the simulated ASW, and enables real-time communication in both directions.
- Digital twin can make full use of the prediction, evaluation, and analysis ability of simulation system to evaluate available courses of actions for sensor control.
- Digital twin paves a way for the cyber-physical integration of ASW, which is an important bottleneck to enable intelligent and adaptive decision making.
- Digital twin can enable the integrated application of new-generation information technologies, such as internet of things (IoT), 5G, AI, cloud, edge computing, and so on.
- Digital twin can take full advantage of POMDP and the simulation-based approach to support more complex application scenarios.
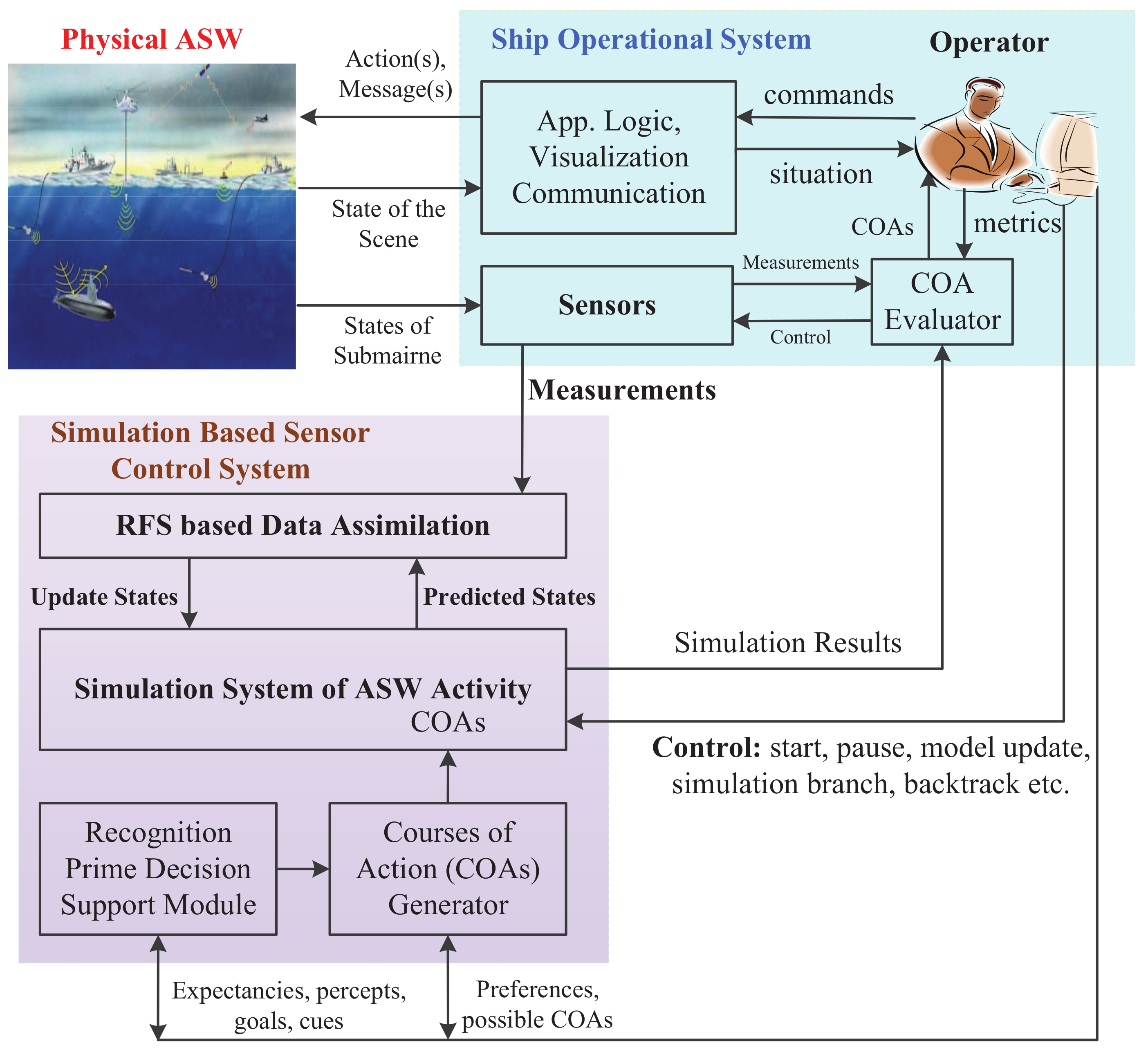
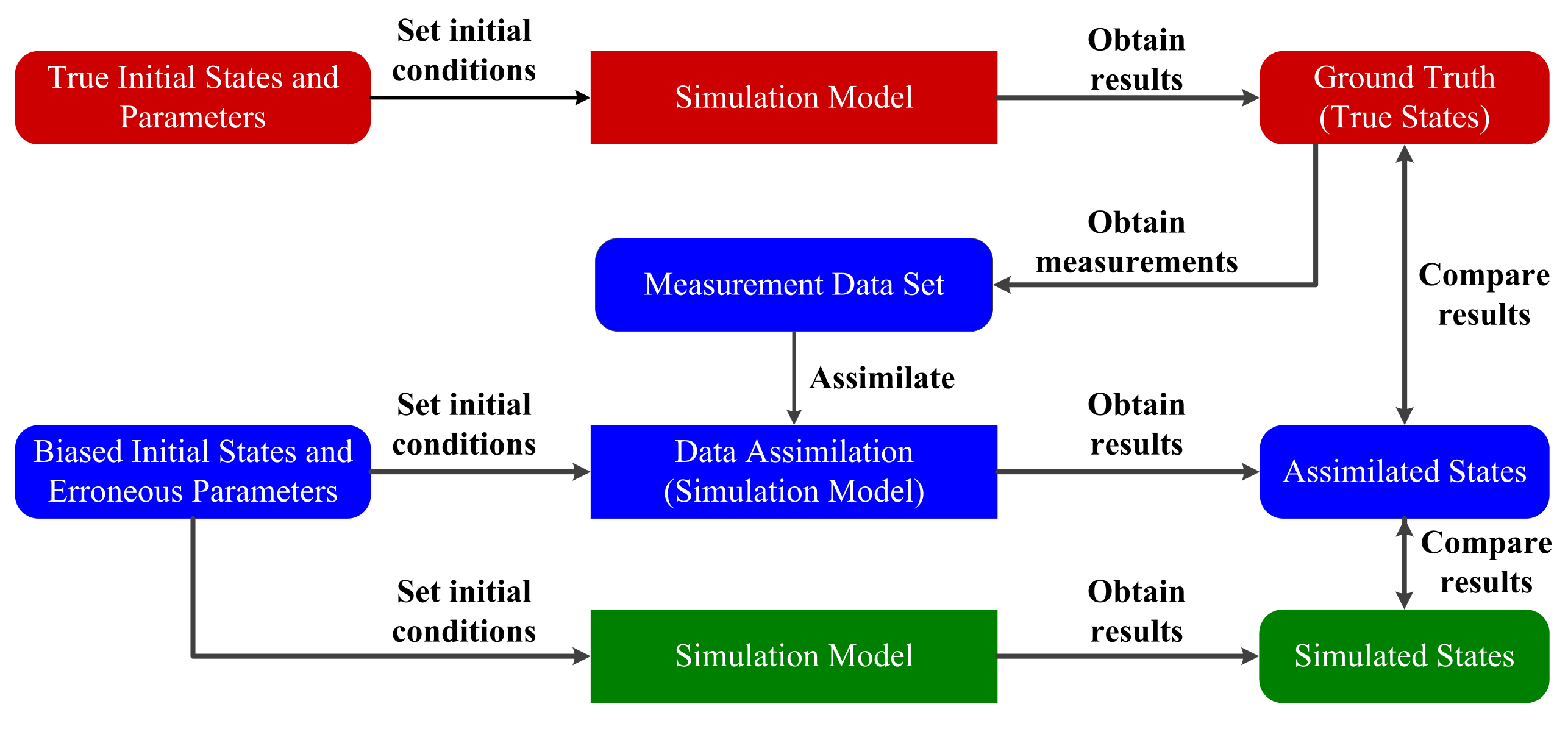
2. Digital Twin and RFS-Based Framework of Online Sensor Control
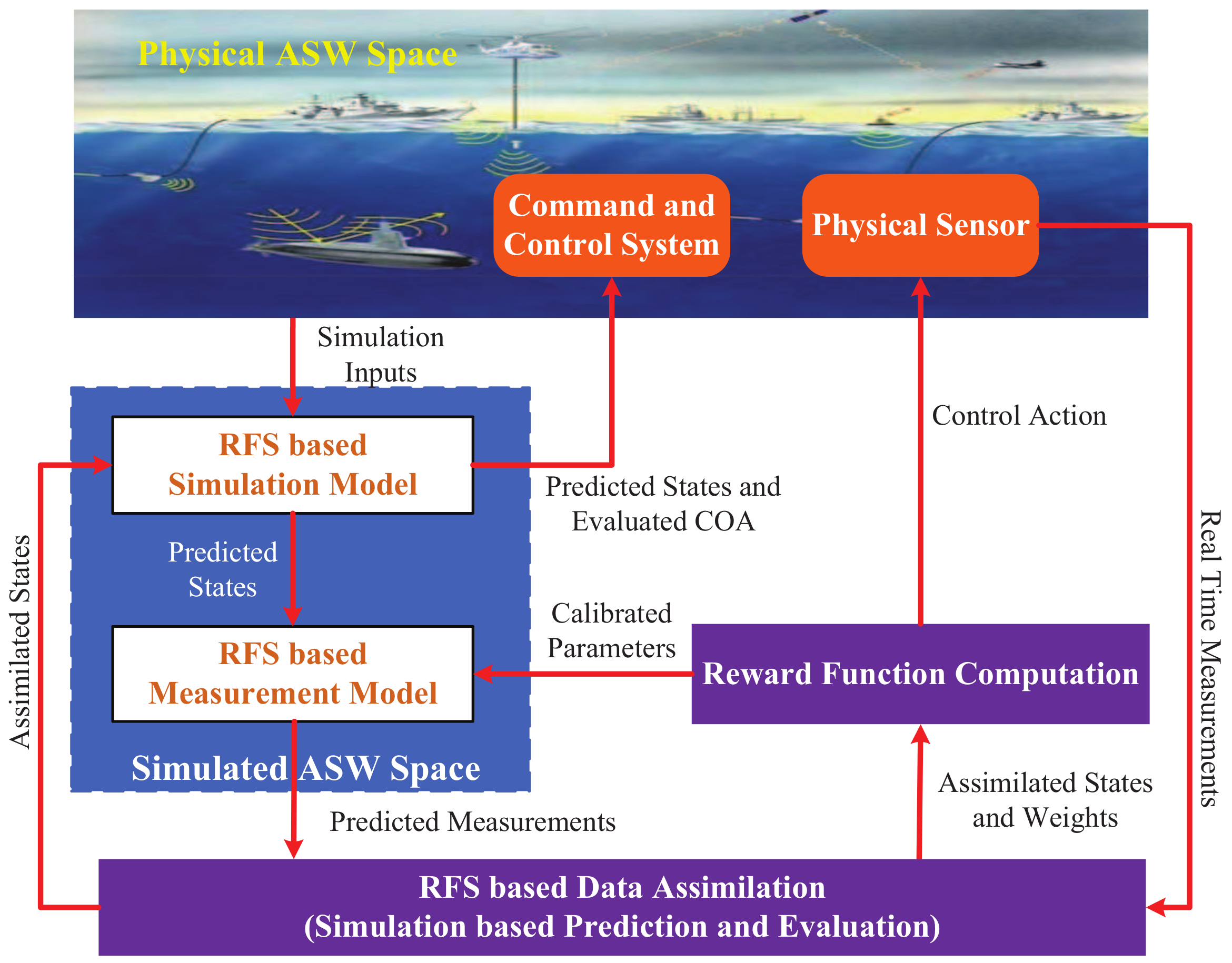
3. RFS-Based Modeling of the Simulated ASW
3.1. RFS-Based Data Model
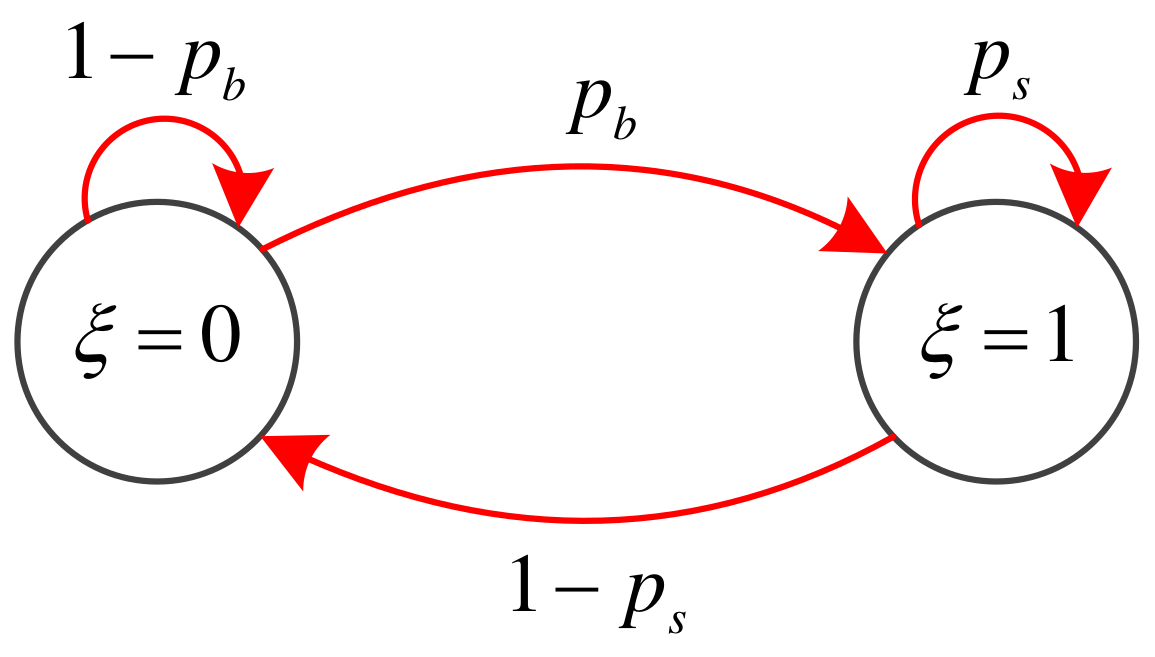
- It is based on the assumption that the studied system is a single dynamic system that is permanently active. It cannot be used for the dynamic system that switches on and off randomly. Switching is quite common for submarine activity, for example, a submarine may enter and leave a battle area at random instance.
- It is based on the assumption that the detection is perfect with no false detections and no missed detections, and it also needs the number and ordering of measurements to be previously designated. Furthermore, it cannot jointly estimate the number of submarines and the states of each submarine.
3.2. RFS-Based Measurement Model
3.3. RFS-Based Simulation Model
4. RFS-Based Data-Assimilation Algorithm
4.1. Data Assimilation with RFS-Based Models
- the posterior submarine’s existence probability ;
- the posterior spatial PDF of denoted by .
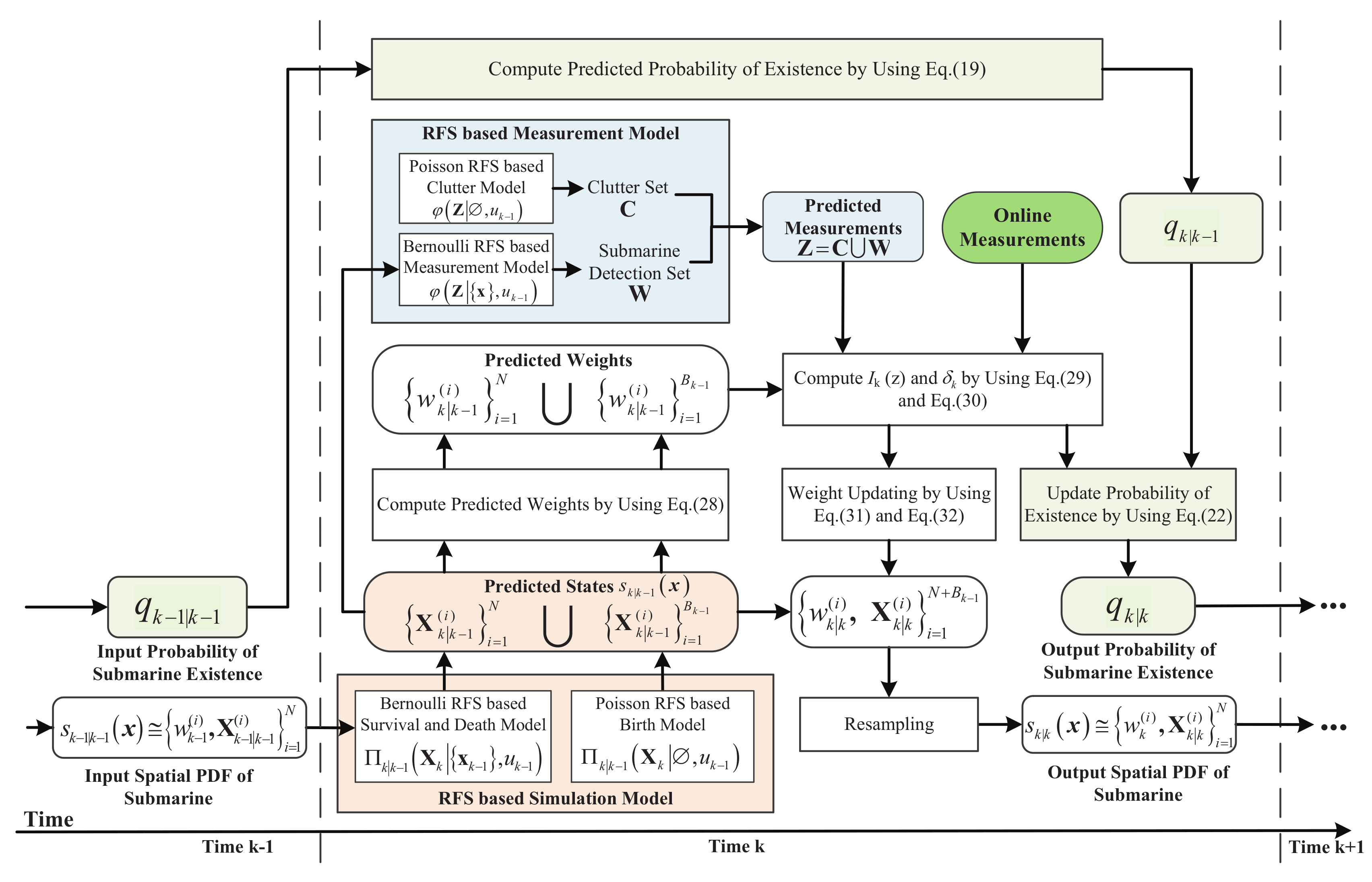
4.2. SMC-Based Calculation
5. Computation of Reward Function
5.1. Derivation of Reward Function
5.2. Data-Assimilation-Based Computation
6. Simulation Experiments
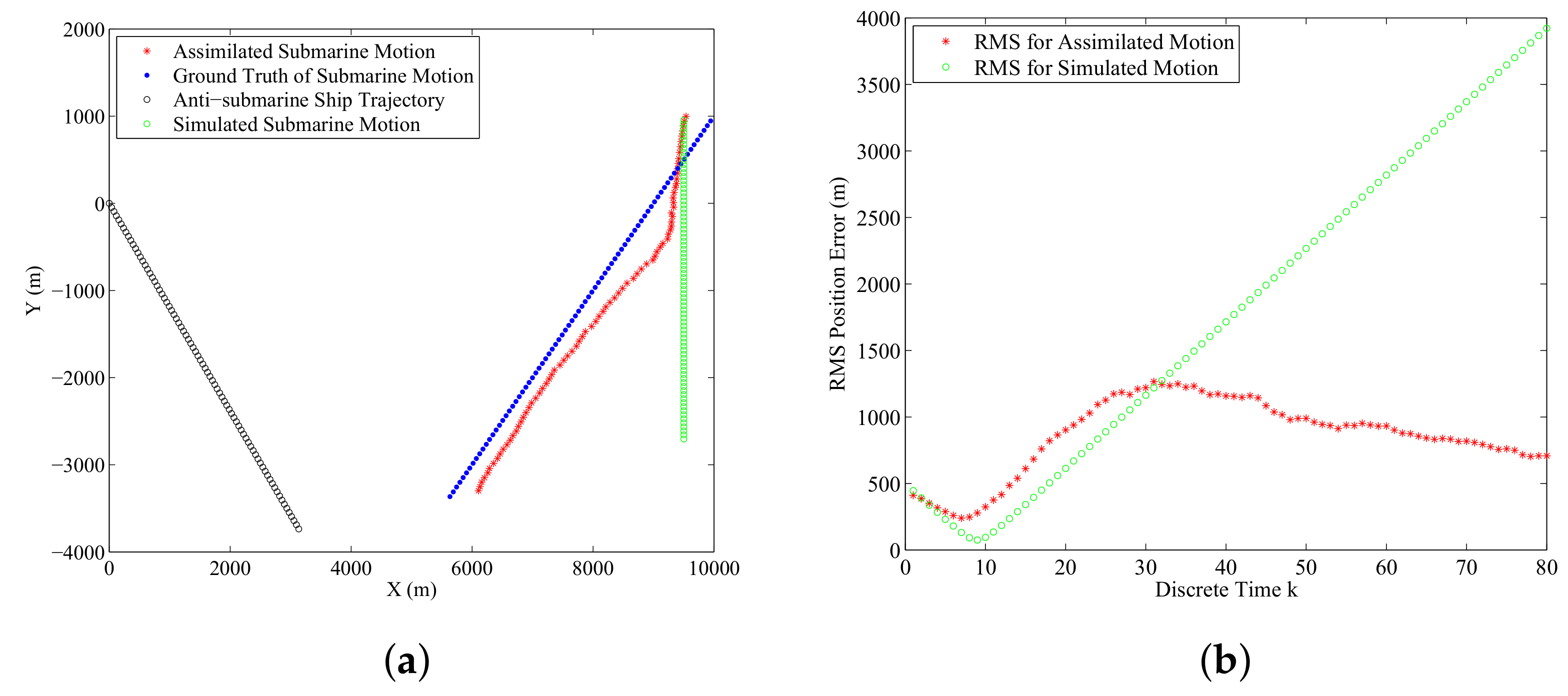
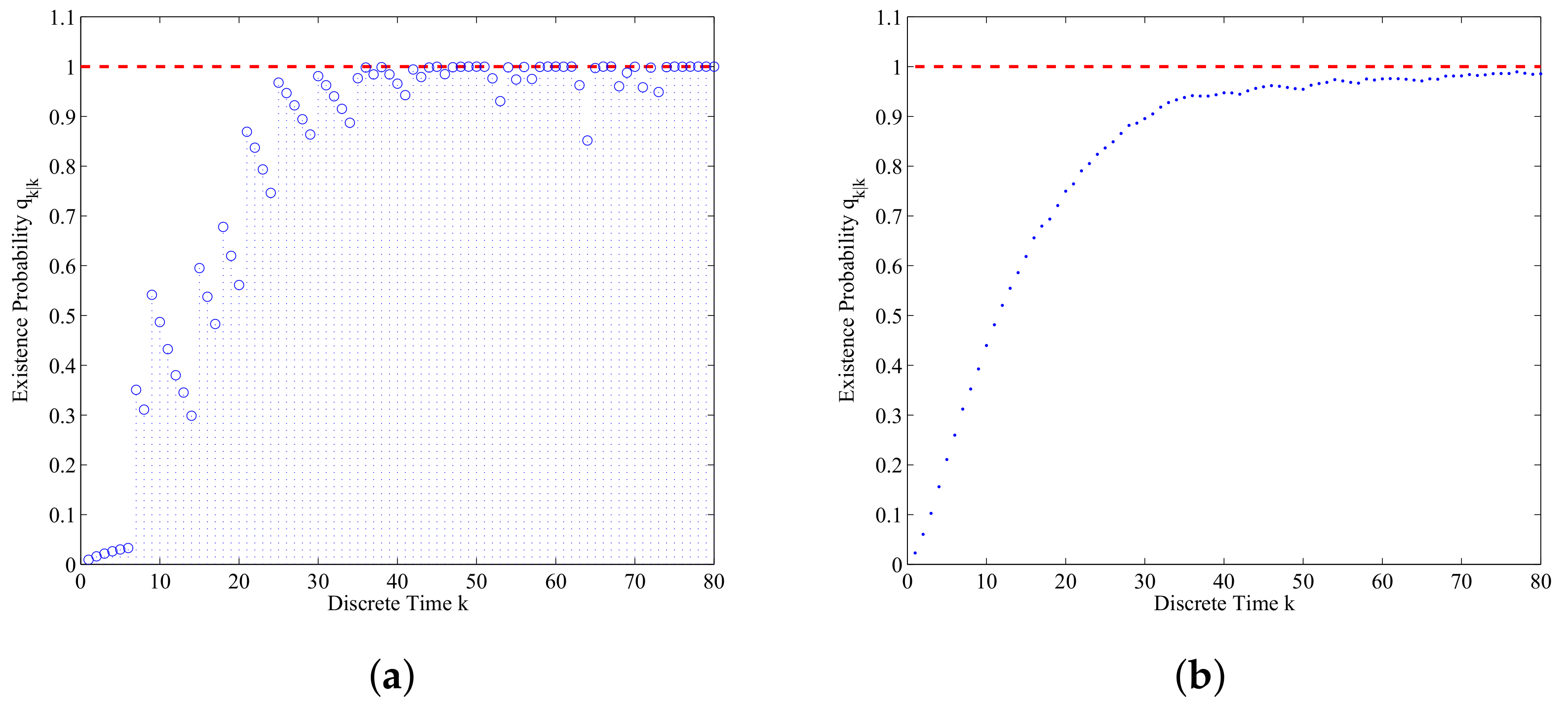
6.1. Data-Assimilation Experiment
6.1.1. Experimental Setup
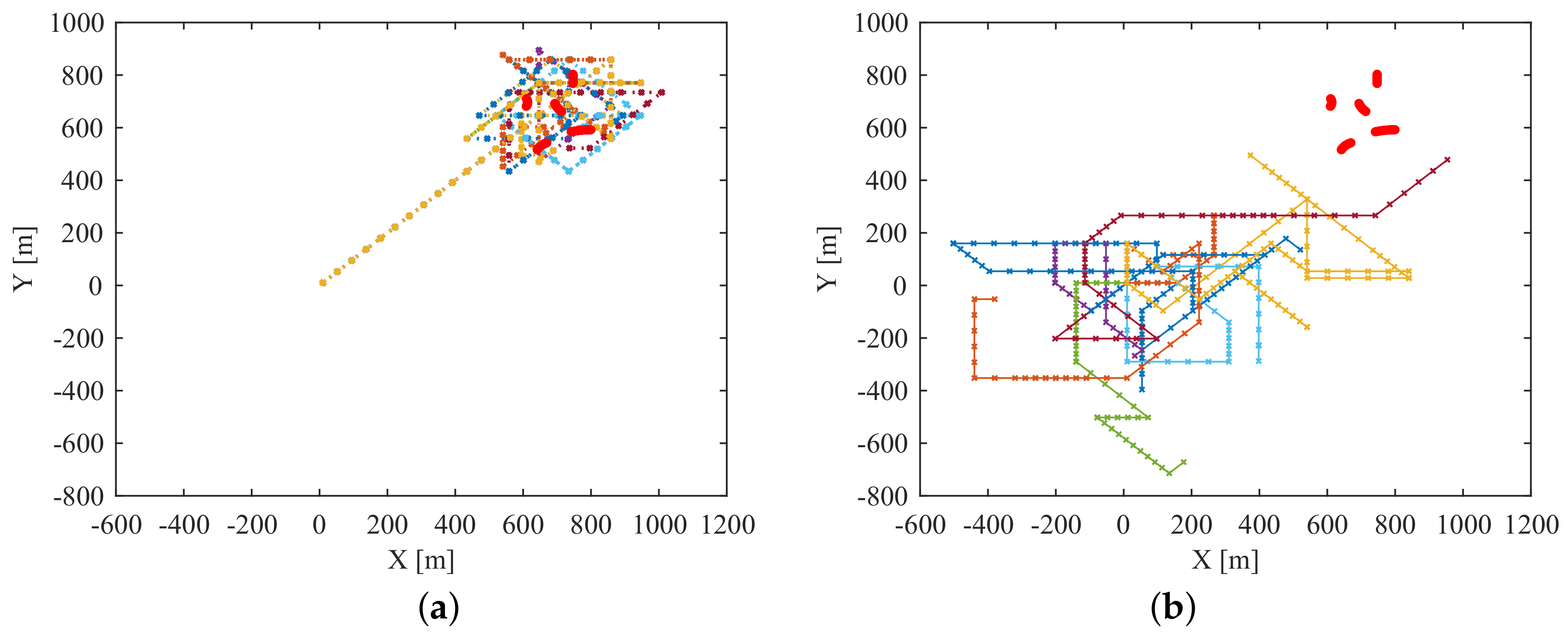
6.1.2. Experimental Results
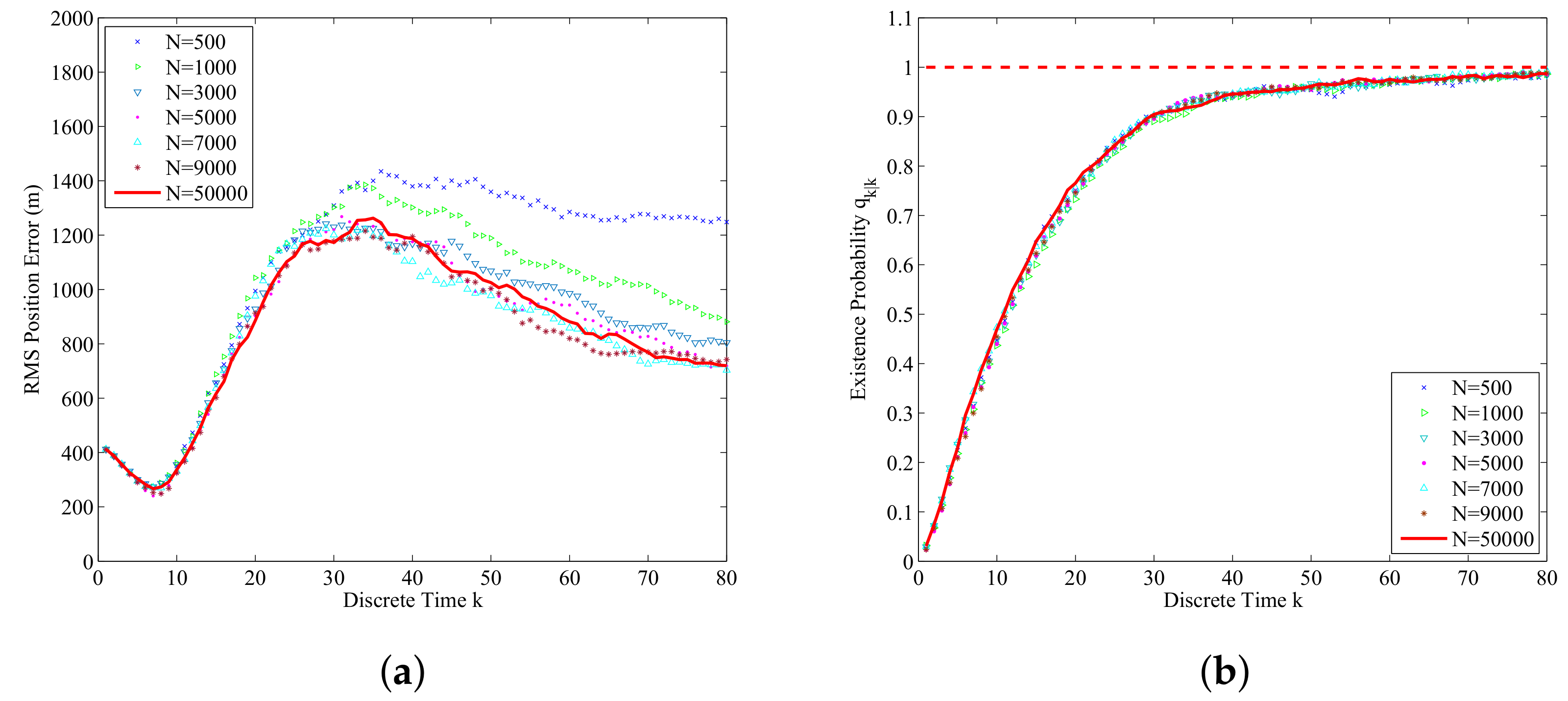
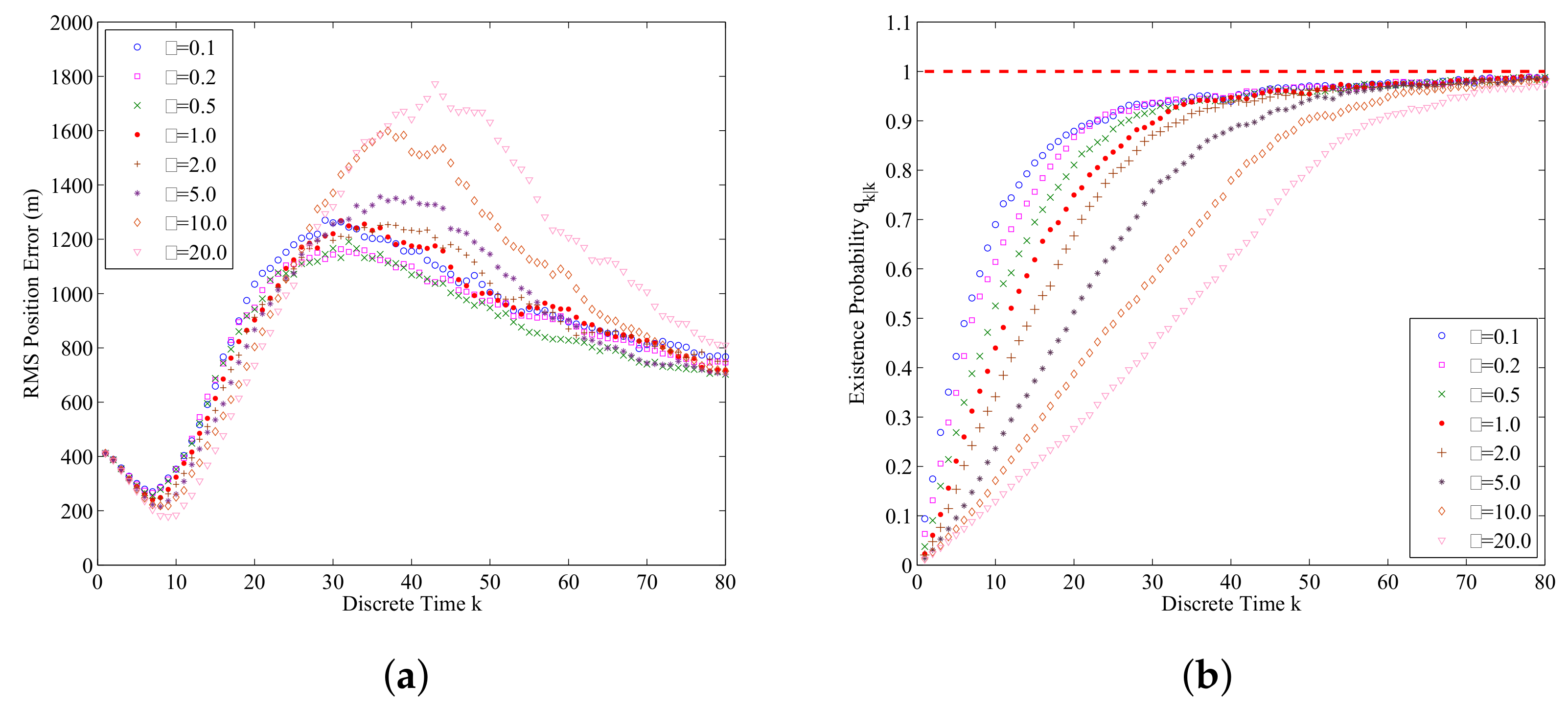
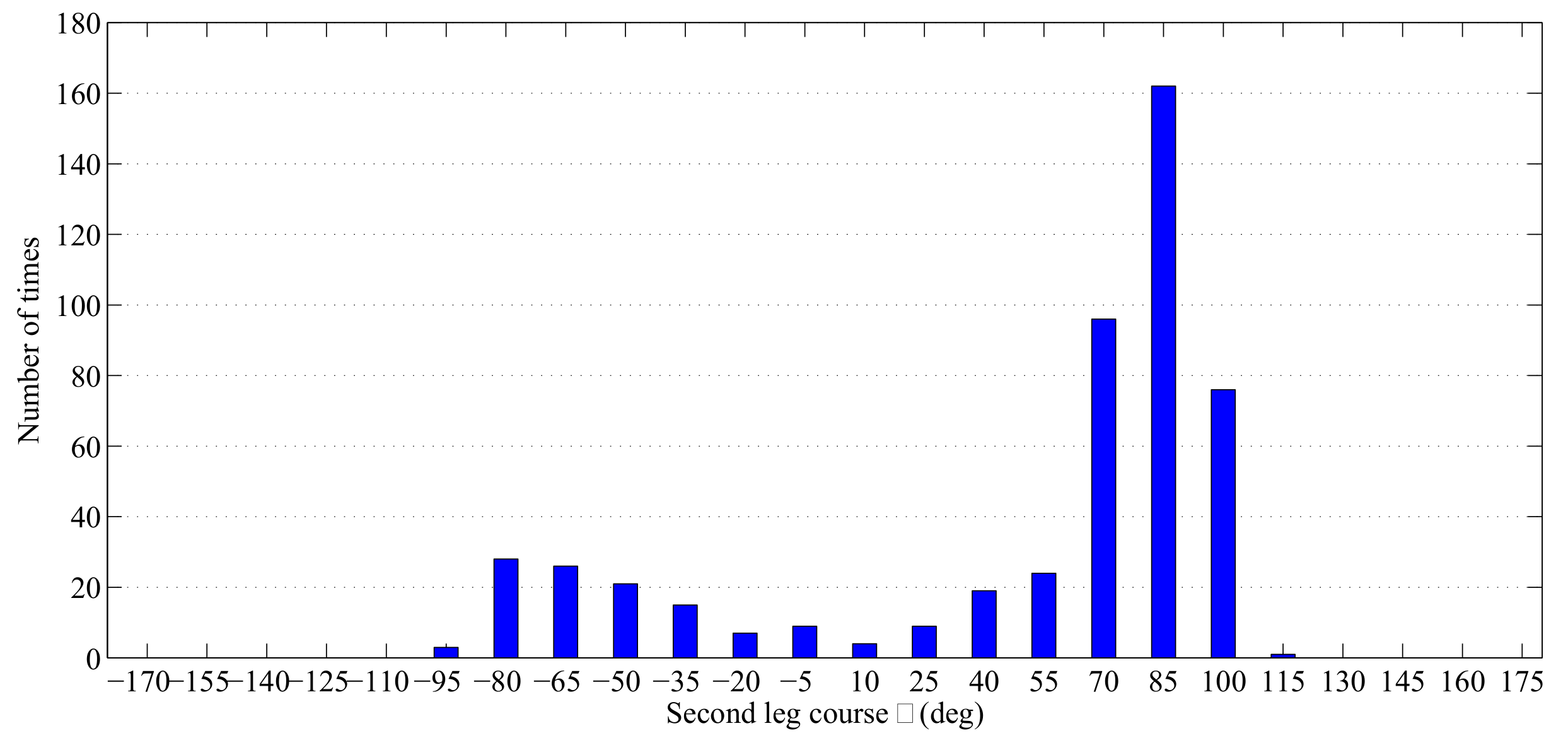
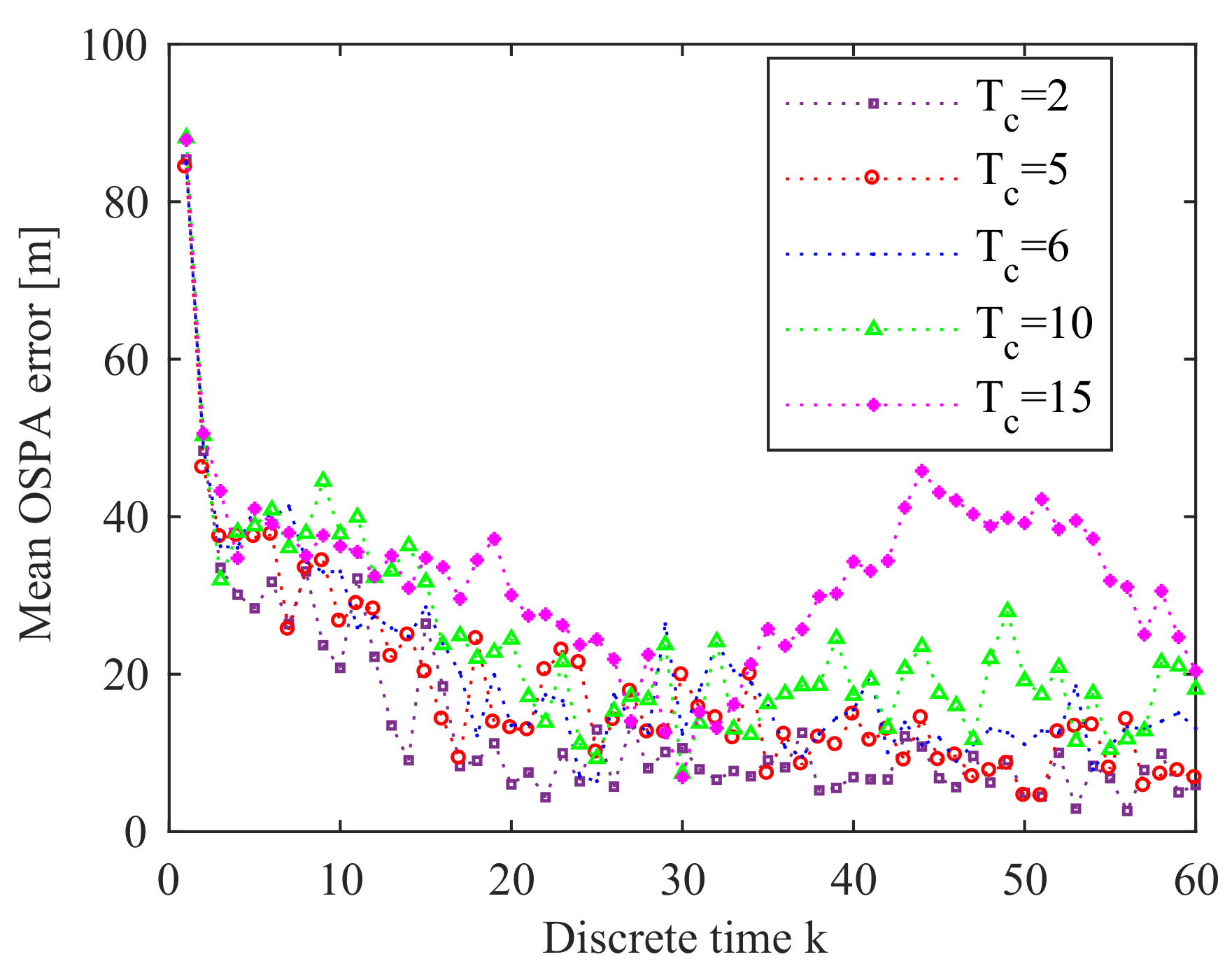
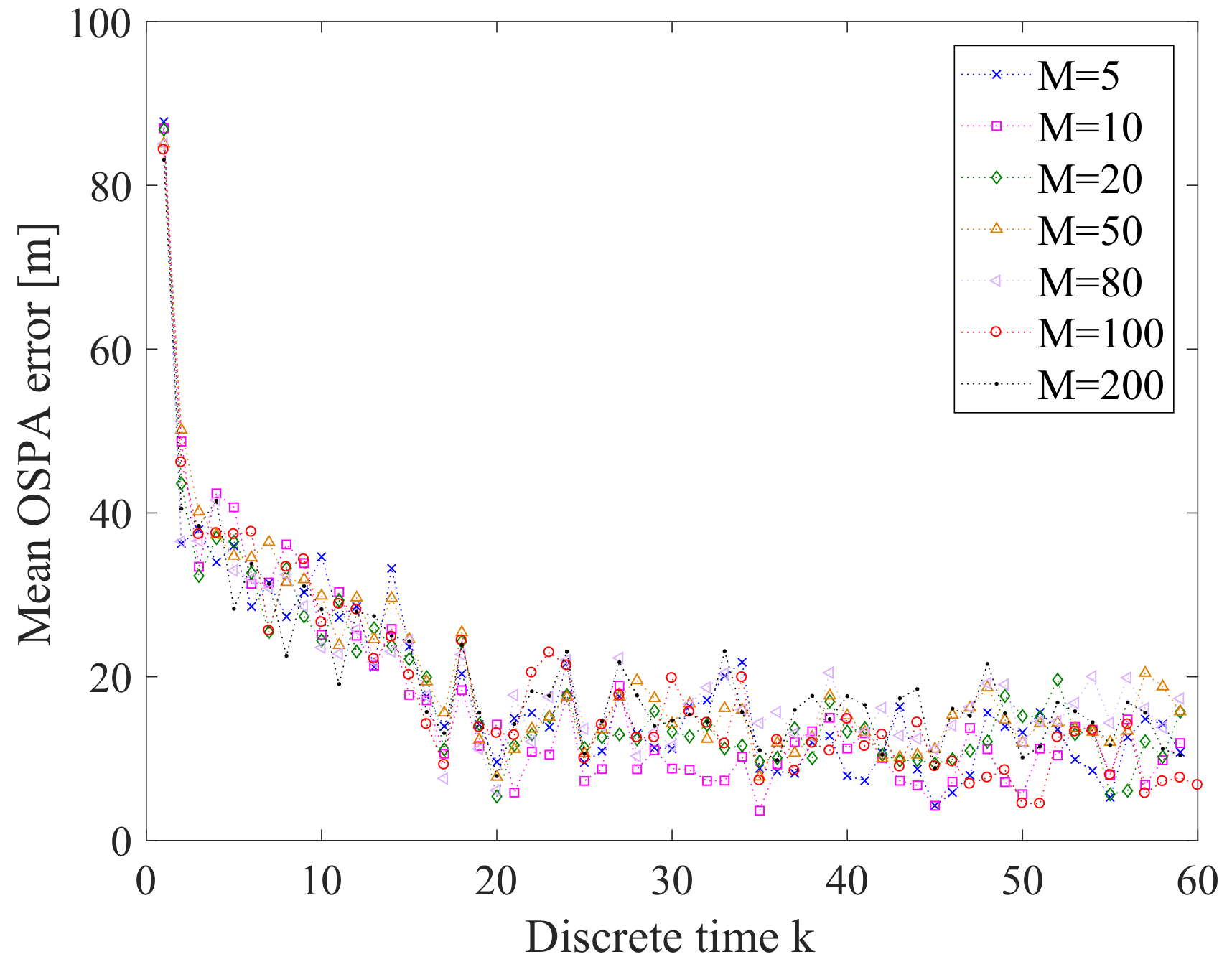
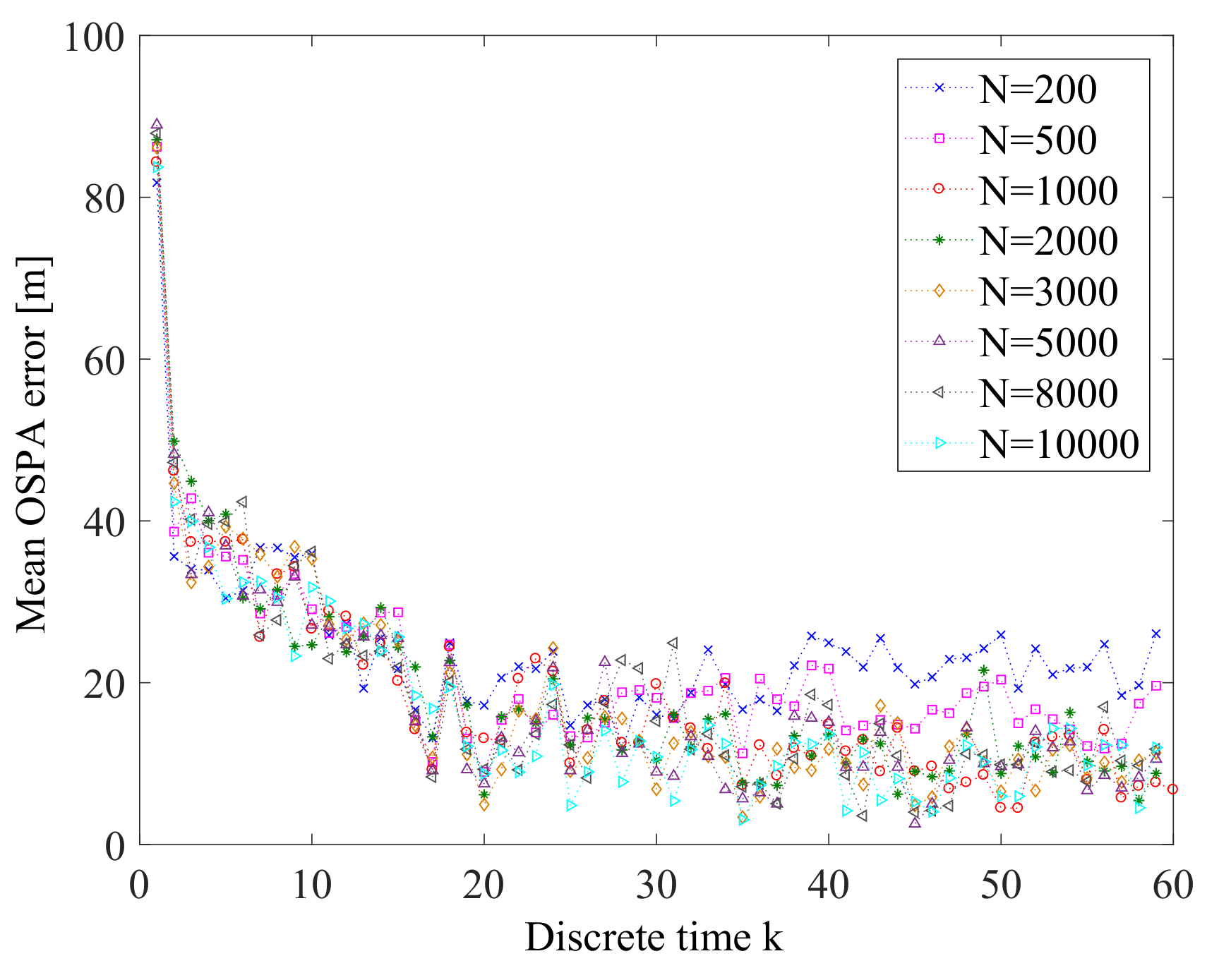
6.1.3. Sensitivity Analysis
6.2. Online Sensor Control Experiment with Single Submarine
6.2.1. Experimental Setup
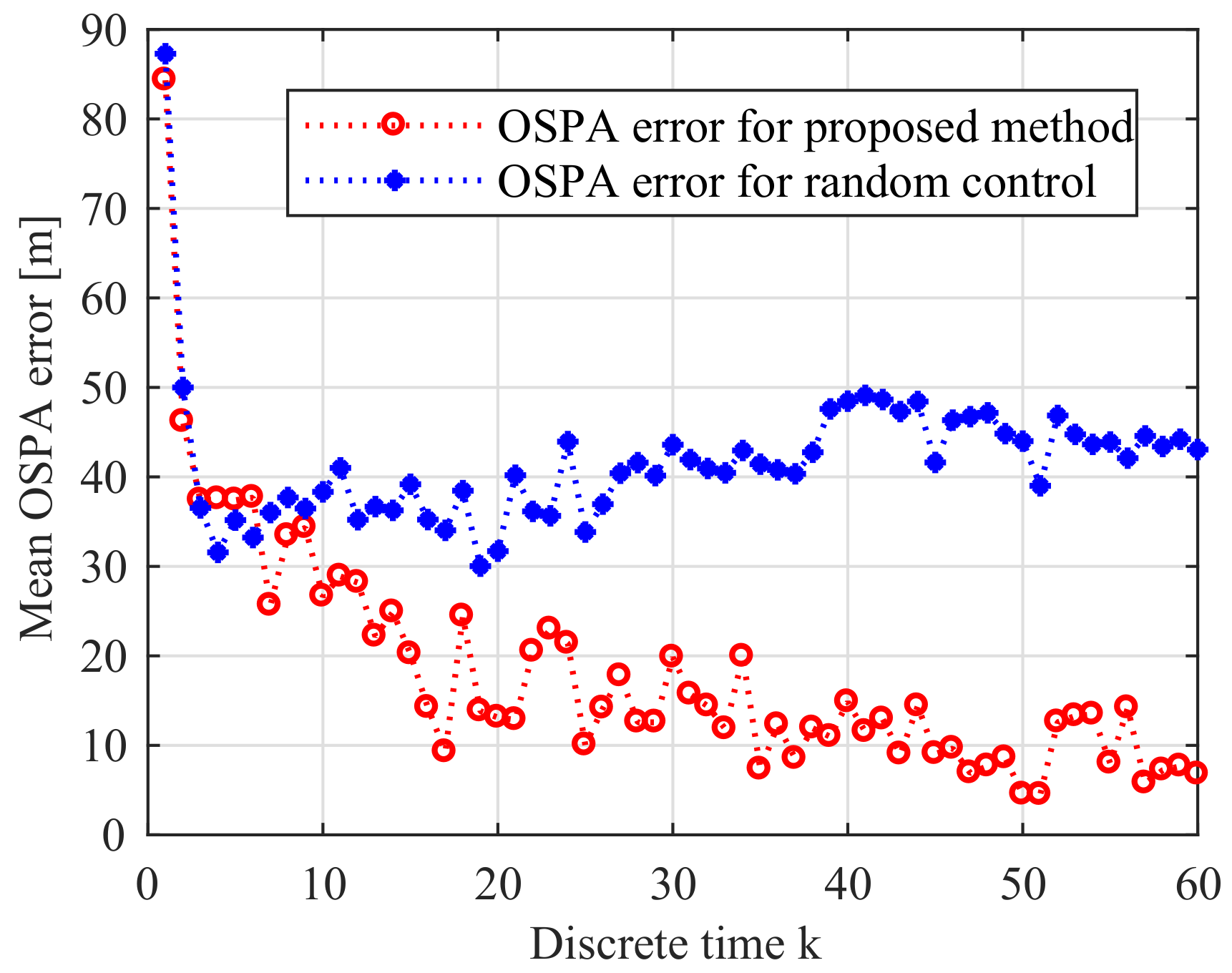
6.2.2. Experimental Results
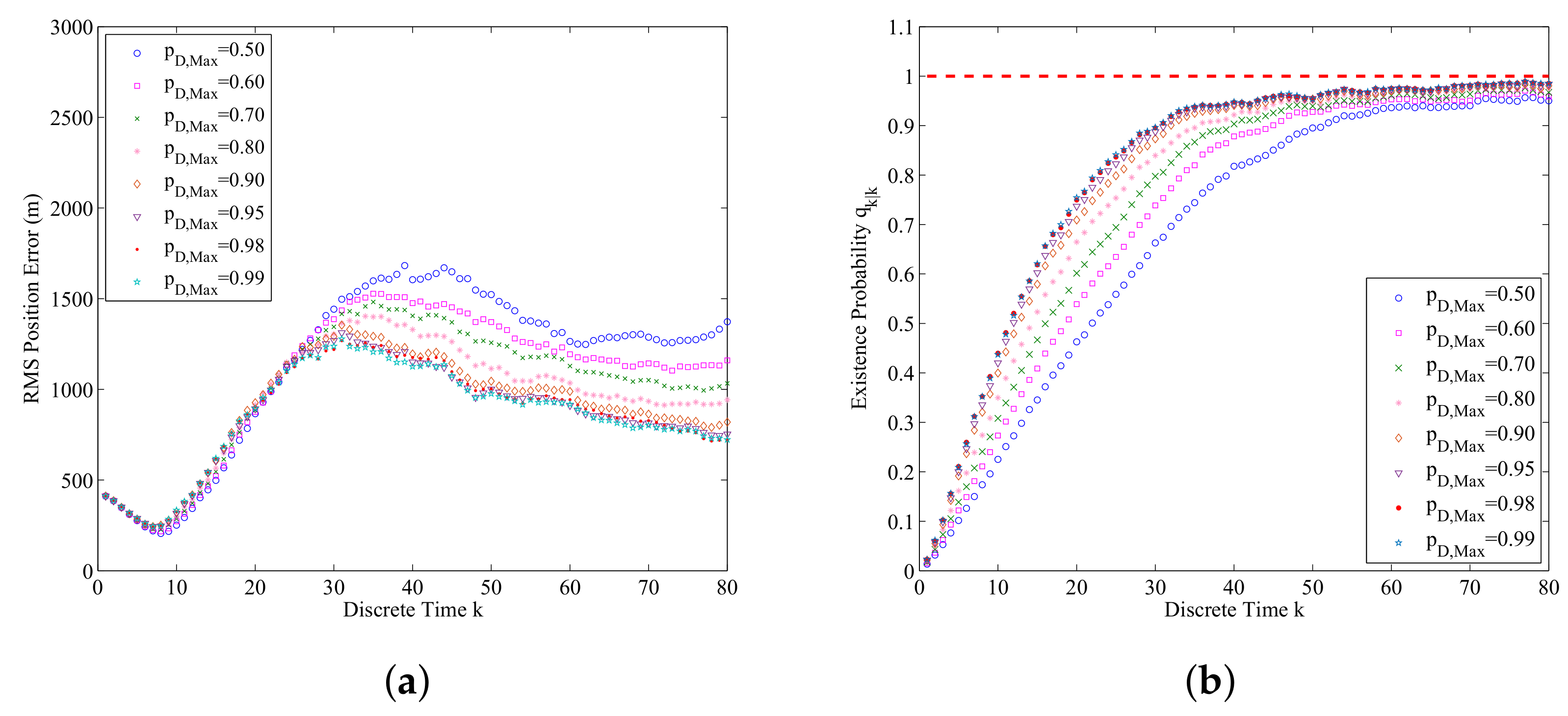
6.2.3. Sensitivity Analysis
6.3. Online Sensor Control Experiment with Multiple Submarines
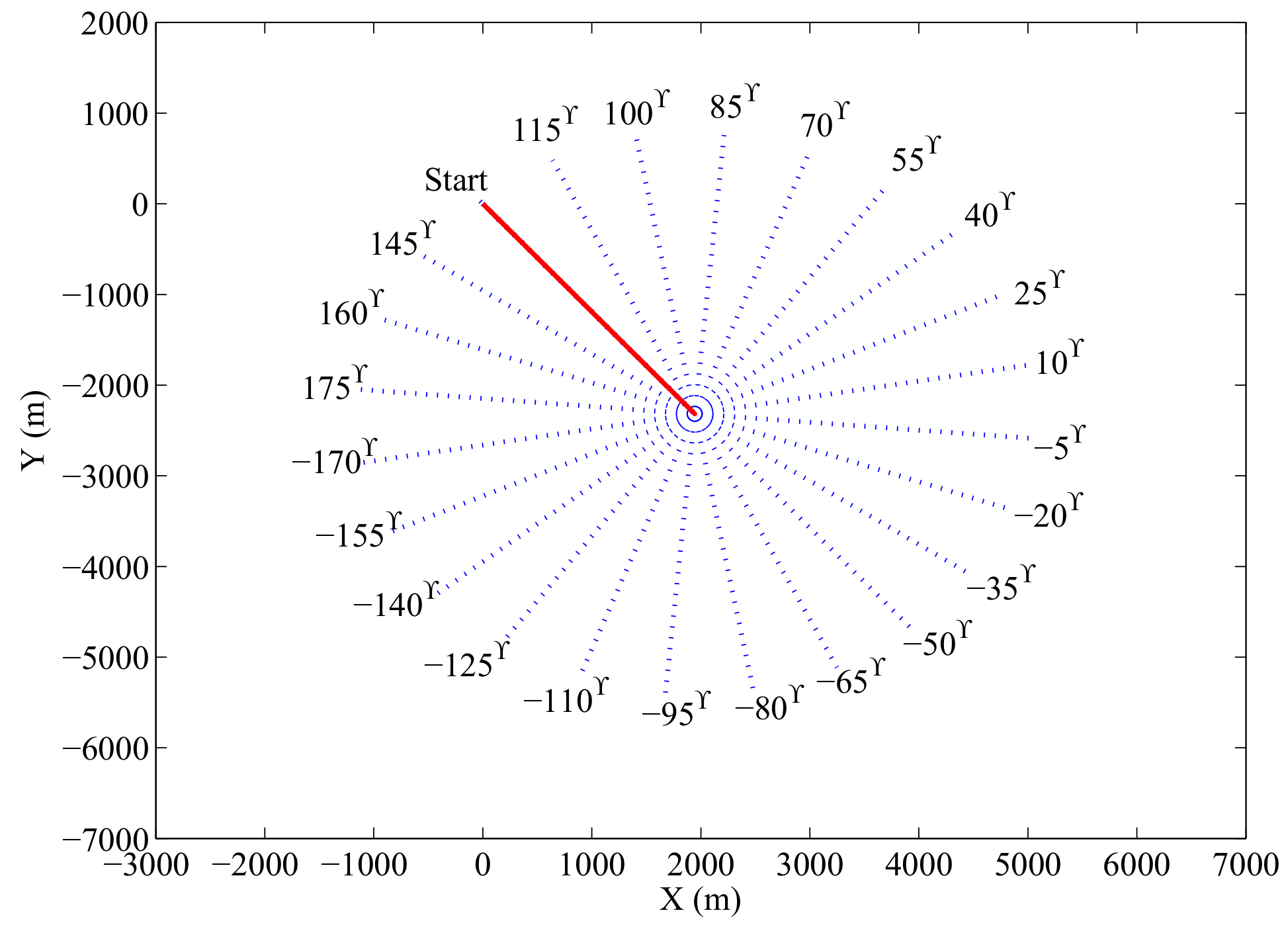
6.3.1. Experimental Setup
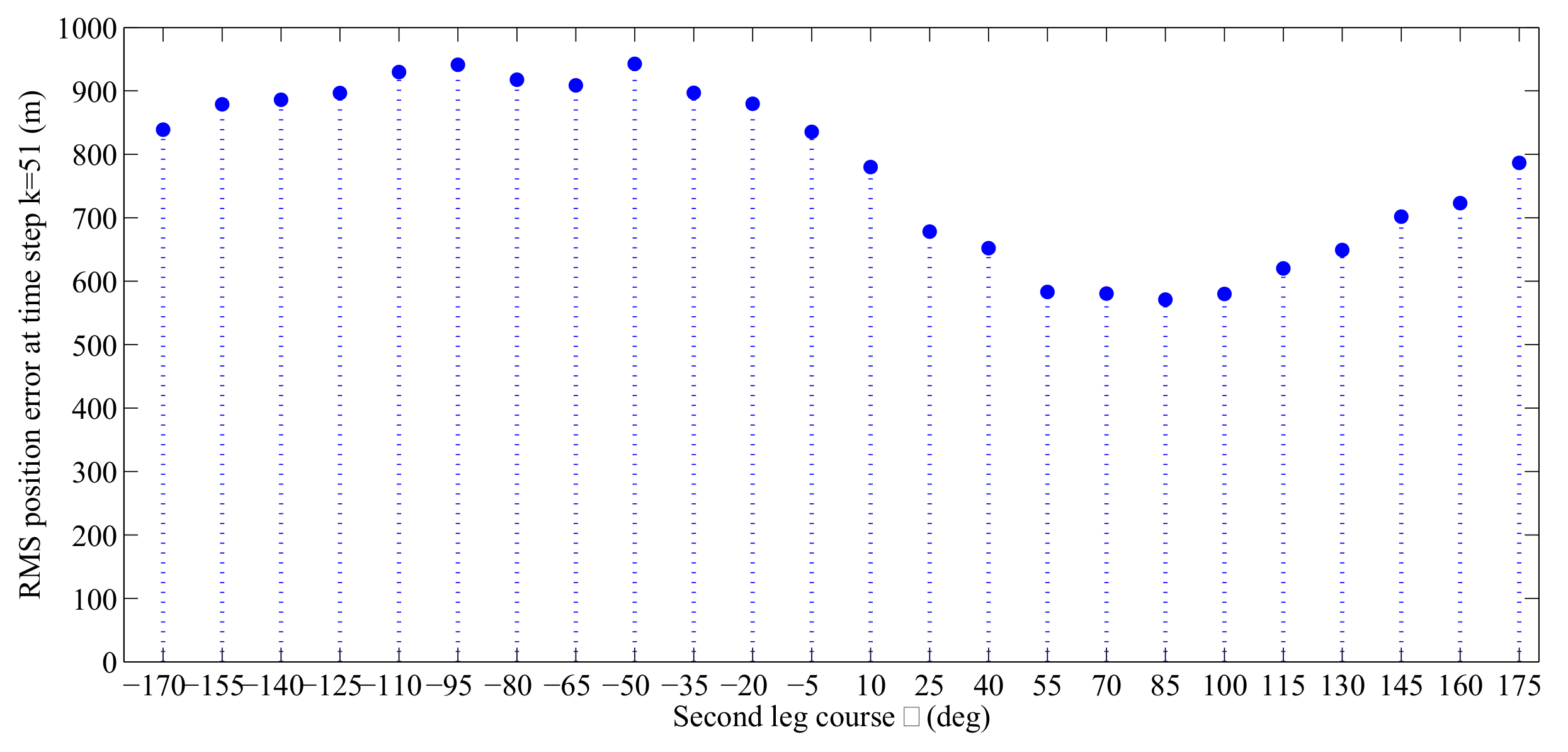
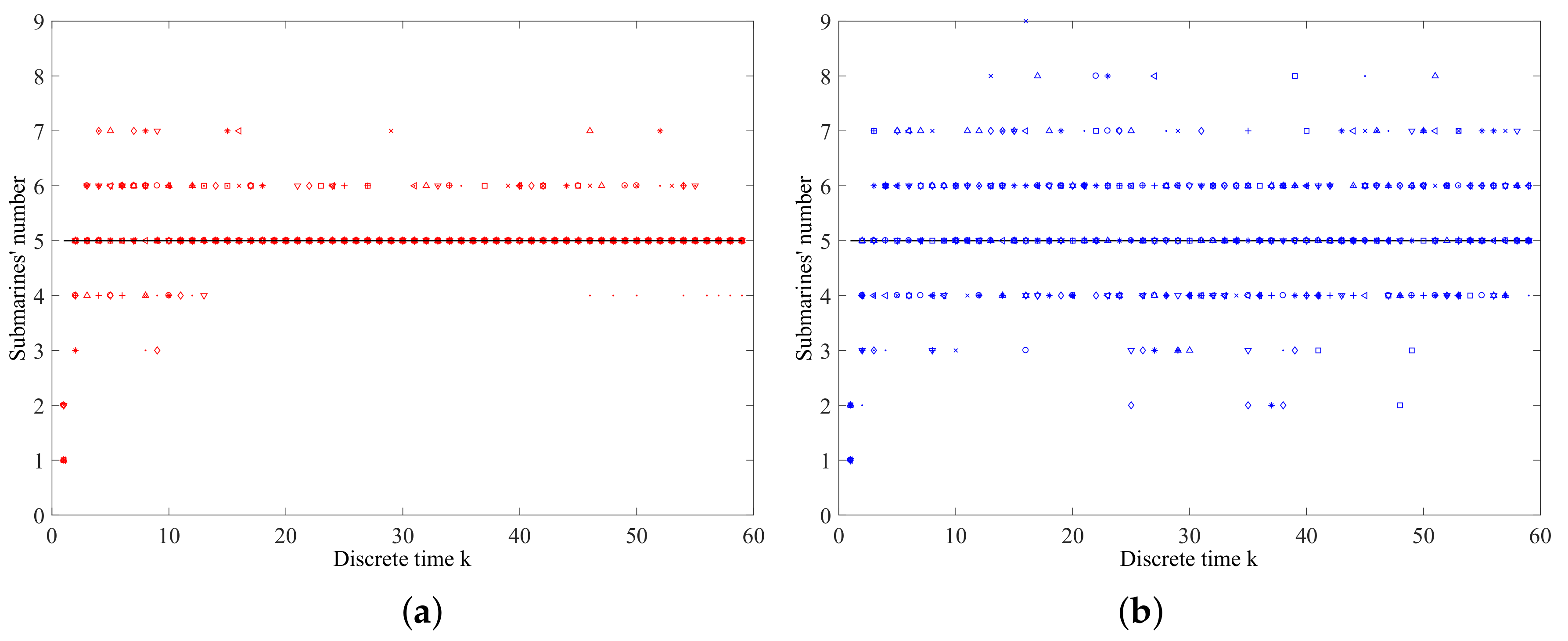
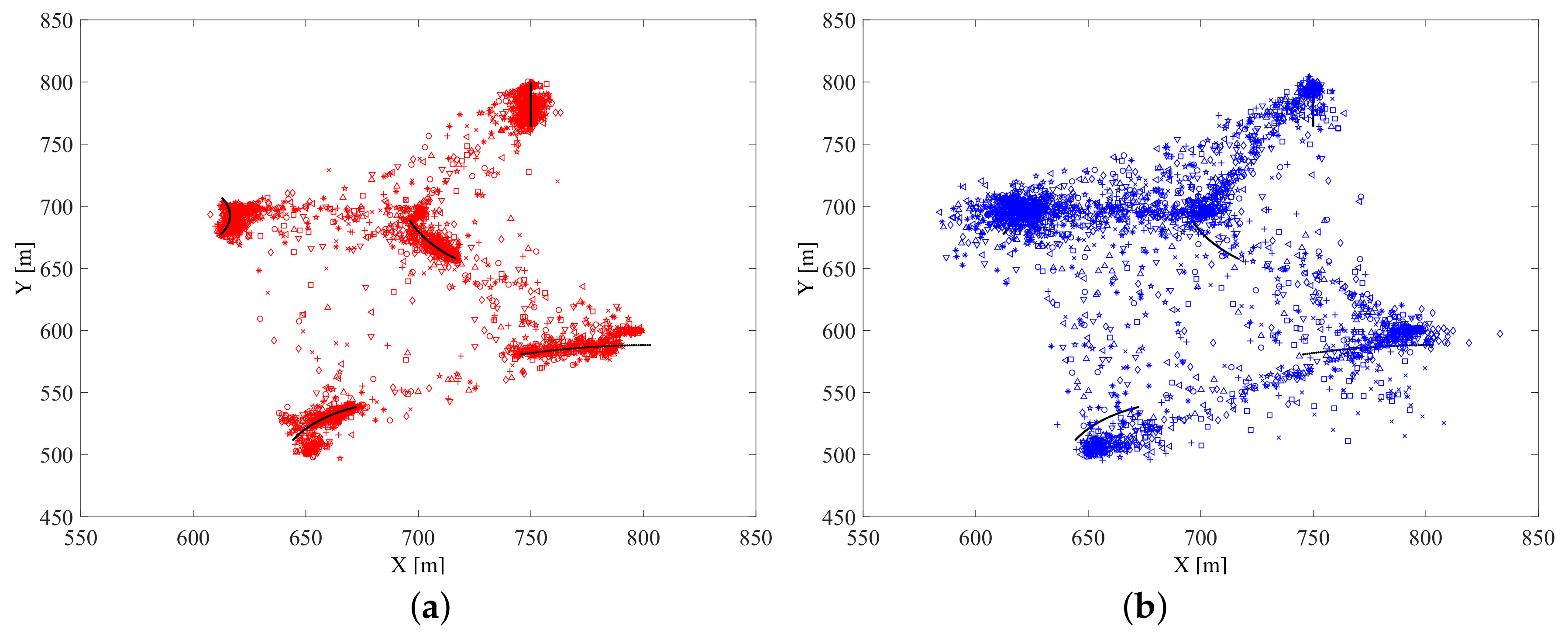
6.3.2. Experimental Results
6.3.3. Sensitivity Analysis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ASW | Anti-submarine Warfare |
| FISST | Finite Set Statistics |
| Probability Density Function | |
| PF | Particle Filter |
| POMDP | Partially Observed Markov Decision Process |
| RFS | Random Finite Set |
| RMS | Root Mean Square |
| SMC | Sequential Monte Carlo |
References
- Jauffret, C.; Pillon, D. Observability in passive target motion analysis. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1290–1300. [Google Scholar] [CrossRef]
- Nardone, S.C.; Aidala, V.J. Observability criteria for bearing-only target motion analysis. IEEE Trans. Aerosp. Electron. Syst. 1981, 17, 162–166. [Google Scholar] [CrossRef]
- Fogel, E.; Gavish, M. Nth-order dynamics target observability from angle measurements. IEEE Trans. Aerosp. Electron. Syst. 1988, AES-24, 305–308. [Google Scholar] [CrossRef]
- Doucet, A.; Vo, B.-N.; Andrieu, C.; Navy, M. Particle filtering for multi-target tracking and sensor management. In Proceedings of the 5th Annual Conference on Information Fussion (FUSION 2002), Annapolis, MD, USA, 8–11 July 2002; pp. 474–481. [Google Scholar]
- Aughenbaugh, J.M.; La Cour, B.R. Metric selection for information theoretic sensor management. In Proceedings of the 2008 11th International Conference on Information Fusion, Cologne, Germany, 30 June–3 July 2008. [Google Scholar]
- Mahler, R. Global posterior densities for sensor management. Proc. SPIE 1998, 3365, 252–263. [Google Scholar]
- Mahler, R. Multitarget sensor management of dispersed mobile sensors. In Theory and Algorithms for Cooperative Systems; Grundel, D., Murphey, R., Pardalos, P., Eds.; World Scientific Books: Singapore, 2004; pp. 239–310. [Google Scholar]
- El-Fallah, A.; Zatezalo, A.; Mahler, R.; Donatelli, D. Dynamic sensor management of dispersed and disparate sensors for tracking resident space objects. Proc. SPIE 2008, 6968. [Google Scholar] [CrossRef]
- Witkoskie, J.; Kuklinski, W.; Theophanis, S.; Otero, M. Random set tracker experimen on a road constrained network with resource management. In Proceedings of the 2006 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006. [Google Scholar]
- Jenssen, R.; Principe, J.C.; Erdognus, D.; Eltoft, T. The Cauchy-Schwarz divergence and Parzen windowing: connections to graph theory and Mercer kernels. J. Frankl. Inst. 2006, 343, 614–629. [Google Scholar] [CrossRef]
- Ristic, B.; Vo, B. Sensor control for multi-object state-space estimation using random finite sets. Automatica 2014, 46, 1812–1818. [Google Scholar] [CrossRef]
- Hoang, H.G.; Vo, B.T. Sensor management for multi-target tracking via multi-Bernoulli filtering. Automatica 2014, 50, 1135–1142. [Google Scholar] [CrossRef]
- Hoang, H.G.; Vo, B.N.; Vo, B.T.; Mahler, R. The Cauchy-Schwarz divergence for Poinsson point processes. IEEE Trans. Inf. Theory 2015, 61, 4475–4485. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.; Vo, B.; Arulanpalam, S. Sensor Control for Multi-target Tracking using Cauchy-Schwarz Divergenc. In Proceedings of the 2015 18th International Conference on Information Fusion (Fusion), Washington, DC, USA, 6–9 July 2015; pp. 937–944. [Google Scholar]
- Gostar, A.K.; Hoseinnezhad, R.; Rathnayake, T.; Wang, X.; Bab-Hadiashar, A. Constrained sensor control for Labeled Multi-Bernoulli filter using Cauchy-Schwarz divergenc. IEEE Signal Process. Lett. 2017, 24, 1313–1317. [Google Scholar] [CrossRef]
- Gomes-Borges, M.E.; Maltese, D.; Vanheeghe, P.; Duflos, E. A risk-based sensor management using random finite sets and POMDP. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017. [Google Scholar]
- Castanon, D.A.; Carin, L. Stochastic control theory for sensor management. In Foundations and Applications of Sensor Management; Hero, A.O., III, Castanon, D.A., Cochran, D., Kastella, K., Eds.; Springer: Boston, MA, USA, 2008; pp. 7–32. [Google Scholar]
- Qi, Q.; Zhao, D.; Liao, T.W.; Tao, F. Modeling of Cyber-physical Systems and Digital Twin Based on Edge Computing, Fog Computing and Cloud Computing Towards Smart Manufacturing. In Proceedings of the ASME 2018 13th International Manufacturing Science and Engineering Conference, College Station, TX, USA, 18–22 June 2018; pp. 1–7. [Google Scholar]
- Grieves, M.; Vickers, J. Digital Twin: Mitigating Unpredictable, Undesir-able Emergent Behavior in Complex Systems. In Transdisciplinary Perspectives on Complex Systems: New Findings and Approaches; Kahlen F-JFlumerfelt, S., Alves, A., Eds.; Springer: Boston, MA, USA, 2017; pp. 85–113. [Google Scholar]
- Abramovici, M.; Gobel, J.C.; Dang, H.B. Semantic data management for the development and continuous reconfiguration of smart products and systems. Cirp Ann. Manuf. Technol. 2016, 65, 185–188. [Google Scholar] [CrossRef]
- Rosen, R.; Von Wichert, G.; Lo, G.; Bettenhausen, K.D. About the importance of autonomy and digital twins for the future of manufacturing. IFAC-PaperOnLine 2015, 48, 567–572. [Google Scholar] [CrossRef]
- Schlus, M.; Rossmann, J. From simulation to experimentable digital twins: Simulation-based development and operation of complex technical systems. In Proceedings of the 2016 IEEE International Symposium on Systems Engineering (ISSE), Edinburgh, UK, 3–5 October 2016. [Google Scholar]
- Schroeder, G.N.; Steinmetz, C.; Pereira, C.E.; Espindola, D.B. Digital twin data modeling with automationML and a communication methodology for data exchange. Int. Fed. Autom. Control. 2016, 012–017. [Google Scholar] [CrossRef]
- Hochhalter, J.D.; Leser, W.P.; Newman, J.A.; Glaessgen, E.H.; Gupta, V.K.; Yamakov, V.I. Coupling Damage-Sensing Particles to the Digitial Twin Concept. Available online: https://ntrs.nasa.gov/search.jsp?R=20140006408 (accessed on 15 April 2014).
- Glaessgen, E.H.; Stargel, D.S. The Digital Twin Paradigm for Future NASA and U.S. Air Force Vehicles. In Proceedings of the 53rd AIAA Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012. [Google Scholar]
- Boschert, S.; Christoph, H.; Rosen, R. Next Generation Digital Twin. In Proceedings of TMCE 2018; Horvath, J.P., Suarez Rivero, P.M., Castellano, H., Eds.; Taylor and Francis: Las Palmas de Gran Canaria, Spain, 2018; pp. 209–218. ISBN 978-94-6186-910-4. [Google Scholar]
- Rao, V.; Sandu, A. A posteriori error estimates for DDDAS inference problems. Procedia Comput. Sci. 2014, 29, 1256–1265. [Google Scholar] [CrossRef][Green Version]
- GE. The Digital Twin: Compressing Time-to-Value for Digital Industrial Companies, White Paper. Available online: https://www.ge.com/digital/sites/default/files/The-Digital-Twin-Compressing-Time-to-Value-for-Digital-Industrial-Companies.pdf (accessed on 8 May 2016).
- Hu, X. Dynamic data driven simulation. Scs Model. Simul. Mag. 2011, 1, 16–22. [Google Scholar]
- Douglas, C.C. An Open Framework for Dynamic Big-Data-Driven Application Systems (DBDDAS) Development. Procedia Comput. Sci. 2014, 29, 1246–1255. [Google Scholar] [CrossRef][Green Version]
- Xie, X.; Verbraeck, A.; Gu, F. Data Assimilation in Discrete Event Simulations—A Rollback based Sequential Monte Carlo Approach. In Proceedings of the 2016 Spring Simulation Conference (SpringSim 2016), Pasadena, CA, USA, 3–6 April 2016; pp. 522–529. [Google Scholar] [CrossRef]
- Wu, P.; Xue, H.; Hu, X. Particle Filter Based Traffic Data Assimilation with Sensor Informed Proposal Distribution. In Proceedings of the 2015 Spring Simulation Conference (SpringSim 2015), Alexandria, VA, USA, 12–15 April 2015; pp. 264–271. [Google Scholar]
- Xue, H.; Gu, F.; Hu, X. Data Assimilation Using Sequential Monte Carlo Methods in Wildfire Spread Simulation. Acm Trans. Model. Comput. Simul. 2012, 22, 1–25. [Google Scholar] [CrossRef]
- Xue, H.; Hu, X. An Effective Proposal Distribution for Sequential Monte Carlo Methods-Based Wildfire Data Assimilation. In Proceedings of the 2013 Winter Simulations Conference (WSC), Washington, DC, USA, 8–11 December 2013; pp. 1938–1949. [Google Scholar] [CrossRef]
- Vo, B.T.; Vo, B.-N.; Cantoni, A. Bayesian filtering with random finite set observations. IEEE Trans. Signal Process. 2008, 56, 1313–1326. [Google Scholar] [CrossRef]
- Blackman, S.S.; Popoli, R. Design and Analysis of Modern Tracking Systems; Artech House, Library: Norwood, MA, USA, 1999; ISBN 978-1580530064. [Google Scholar]
- La Scala, B.F.; Mallick, M.; Arulampalam, S. Differential geometry measures of nonlinearity for filtering with nonlinear dynamic and linear measurement models. SPIE Proc. 2007, 6699. [Google Scholar] [CrossRef]
- Chen, W.; Kesidis, G.; Morrison, T.; Tinsley, J. Uncertainty in Modeling and Simulation. In Research Challenges in Modeling and Simulation for Engineering Complex Systems; Fujimoto, R., Bock, C., Chen, W., Page, E., Panchal, J.H., Eds.; Springer: Boston, MA, USA, 2017; pp. 75–85. [Google Scholar]
- van Leeuwen, P.J.; Cheng, Y.; Reich, S. Nolinear data assimilation for high-dimensional sytems. In Nonlinear Data Assimilation; Jones, C.K.R.T., Young, L.-S., Eds.; Springer: Boston, MA, USA, 2010; pp. 1–74. [Google Scholar]
- Vo, B.-T.; Vo, D.C.B.-N.; Ristic, B. Bernoulli forward-backward smoothing for joint target detection and tracking. IEEE Trans. Signal Proces. 2011, 59, 4473–4477. [Google Scholar] [CrossRef]
- Hero, A.O.; Kreucher, C.M.; Blatt, D. Information theoretic approaches to sensor management. In Foundations and Applications of Sensor Management; Hero, A.O., Castanon, D., Cochran, D., Kastella, K., Eds.; Springer: Boston, MA, USA, 2008; pp. 33–57. [Google Scholar]
- Passerieux, J.M.; Cappel, D.V. Optimal observer maneuver for bearings-only tracking. IEEE Trans. Aerosp. Electr. Syst. 1998, 34, 777–788. [Google Scholar] [CrossRef]
- Cadre, J.-P.L.; Laurent-Michel, S. Optimizing the receiver maneuvers for bearings-only tracking. Automatica 1999, 35, 591–606. [Google Scholar] [CrossRef]
- Oshman, Y.; Davidson, P. Optimization of observer trajectories for bearings only target localization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 892–902. [Google Scholar] [CrossRef]
- Kreucher, C.M.; Hero, A.O.; Kastella, K.D.; Morelande, M.R. An information based approach to sensor management in large dynamic networks. Proc. IEEE 2007, 95, 978–999. [Google Scholar] [CrossRef]
- Nakamura, K.; Yamamoto, S.; Honda, M. Sequential Data Assimilation in Geotechnical Engineering and Its Application to Seepage Analysis. In Proceedings of the 14th International Conference on Information Fusion, Chicago, IL, USA, 5–8 July 2011; pp. 544–549, ISBN 978-1-4577-0267-9. [Google Scholar]


| Name | Parameter | True Value | Biased Value |
|---|---|---|---|
| Enemy submarine | Initial speed | 5 knot | 3 knot |
| Process noise intensity | 0.0 | 0.2 | |
| Initial position | (10,000, 1000) m | (9500, 1000) m | |
| Initial heading | −135 deg | −90 deg | |
| Survival Probability | 0.99 | - | |
| Anti-submarine ship | Initial speed | 4 knot | - |
| Initial heading | −50 deg | - | |
| Initial position | (0, 0) m | - | |
| Detection probability | - | ||
| Max detection probability | 0.98 | - | |
| Measurement standard deviation | 1 deg | - |
| 1 | 5 | 10 | 20 | 50 | 80 | 100 | 200 | 500 | 800 | 900 | 1000 | 1500 | 2000 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 25 | 11 | 11 | 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 45 | 23 | 37 | 28 | 22 | 15 | 17 | 11 | 9 | 5 | 7 | 6 | 8 | 2 | |
| 45 | 42 | 27 | 25 | 32 | 30 | 32 | 33 | 30 | 29 | 30 | 30 | 31 | 32 | |
| 22 | 30 | 29 | 22 | 20 | 16 | 20 | 19 | 19 | 26 | 18 | 15 | 20 | 17 | |
| 19 | 17 | 14 | 15 | 8 | 12 | 10 | 7 | 12 | 12 | 12 | 10 | 8 | 12 | |
| 2 | 7 | 10 | 7 | 7 | 8 | 6 | 8 | 6 | 4 | 5 | 8 | 6 | 5 | |
| 7 | 9 | 5 | 9 | 6 | 6 | 6 | 8 | 6 | 6 | 5 | 4 | 5 | 4 | |
| 4 | 3 | 6 | 4 | 3 | 5 | 3 | 2 | 3 | 6 | 1 | 7 | 4 | 7 | |
| 9 | 12 | 9 | 9 | 9 | 8 | 6 | 4 | 5 | 4 | 4 | 3 | 6 | 5 | |
| 18 | 10 | 12 | 19 | 14 | 13 | 13 | 9 | 11 | 9 | 16 | 13 | 12 | 11 | |
| 26 | 30 | 28 | 24 | 39 | 32 | 32 | 35 | 30 | 34 | 39 | 28 | 26 | 22 | |
| 65 | 90 | 82 | 96 | 108 | 120 | 110 | 108 | 104 | 102 | 92 | 106 | 94 | 91 | |
| 111 | 125 | 142 | 162 | 175 | 192 | 207 | 225 | 242 | 256 | 263 | 266 | 276 | 290 | |
| 64 | 77 | 81 | 76 | 56 | 43 | 38 | 31 | 23 | 7 | 8 | 4 | 4 | 2 | |
| 22 | 13 | 7 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, P.; Yang, M.; Peng, Y.; Zhu, J.; Ju, R.; Yin, Q. Sensor Control in Anti-Submarine Warfare—A Digital Twin and Random Finite Sets Based Approach. Entropy 2019, 21, 767. https://doi.org/10.3390/e21080767
Wang P, Yang M, Peng Y, Zhu J, Ju R, Yin Q. Sensor Control in Anti-Submarine Warfare—A Digital Twin and Random Finite Sets Based Approach. Entropy. 2019; 21(8):767. https://doi.org/10.3390/e21080767
Chicago/Turabian StyleWang, Peng, Mei Yang, Yong Peng, Jiancheng Zhu, Rusheng Ju, and Quanjun Yin. 2019. "Sensor Control in Anti-Submarine Warfare—A Digital Twin and Random Finite Sets Based Approach" Entropy 21, no. 8: 767. https://doi.org/10.3390/e21080767
APA StyleWang, P., Yang, M., Peng, Y., Zhu, J., Ju, R., & Yin, Q. (2019). Sensor Control in Anti-Submarine Warfare—A Digital Twin and Random Finite Sets Based Approach. Entropy, 21(8), 767. https://doi.org/10.3390/e21080767





