A New Surrogating Algorithm by the Complex Graph Fourier Transform (CGFT)
Abstract
1. Introduction
1.1. Statement of the Problem and Related Works
1.2. New Contributions and Paper Organization
1.3. Notation
2. The Hermitian Laplacian Matrix
2.1. Definition and Properties
2.2. The Complex Graph Fourier Transform (CGFT)
3. Graph Spectrum Amplitude Invariants
4. Surrogating Algorithms
4.1. Iterative Surrogate Graph Signal Algorithm
| Algorithm 1: Iterative surrogating complex graph signals by means of the CGFT (ICGFT). |
| 1: Input: Graph signal , Hermitian Laplacian , number of surrogates K, maximum number of iterations I, convergence threshold 2: Compute eigenvector matrix 3: for k = 1, 2, …, K do: 4: Generate graph spectrum random phases 5: Compute initial surrogate, Equation (16a,b) 6: for i = 1, 2, …, I do: 7: Compute surrogate, Equation (17a,b) where 8: If and go to 11 9: end for 10: 11: end for 12: Output: |
4.2. Selecting the Hermitian Laplacian
5. Experiments
5.1. Automatic Hand Gesture Recognition
- OTS, the original training set formed by only original instances.
- ETS-ICGFT, an enlarged training set formed by only a reduced number of original instances enlarged by a varying number of surrogates obtained from them by the ICGFT method (Algorithm 1).
- ETS-IAAFT, an enlarged training set formed by only a reduced number of original instances (real part) enlarged by a varying number of surrogates obtained from them by the IAAFT method.
- ETS-nIGFT, an enlarged training set formed by only a reduced number of the original instances (real part) enlarged by a varying number of surrogates obtained from them by the method proposed in [11], which uses the (real) GFT. This method does not iterate as no corrections are made in the original graph domain, so we call it non-Iterative GFT (nIGFT).
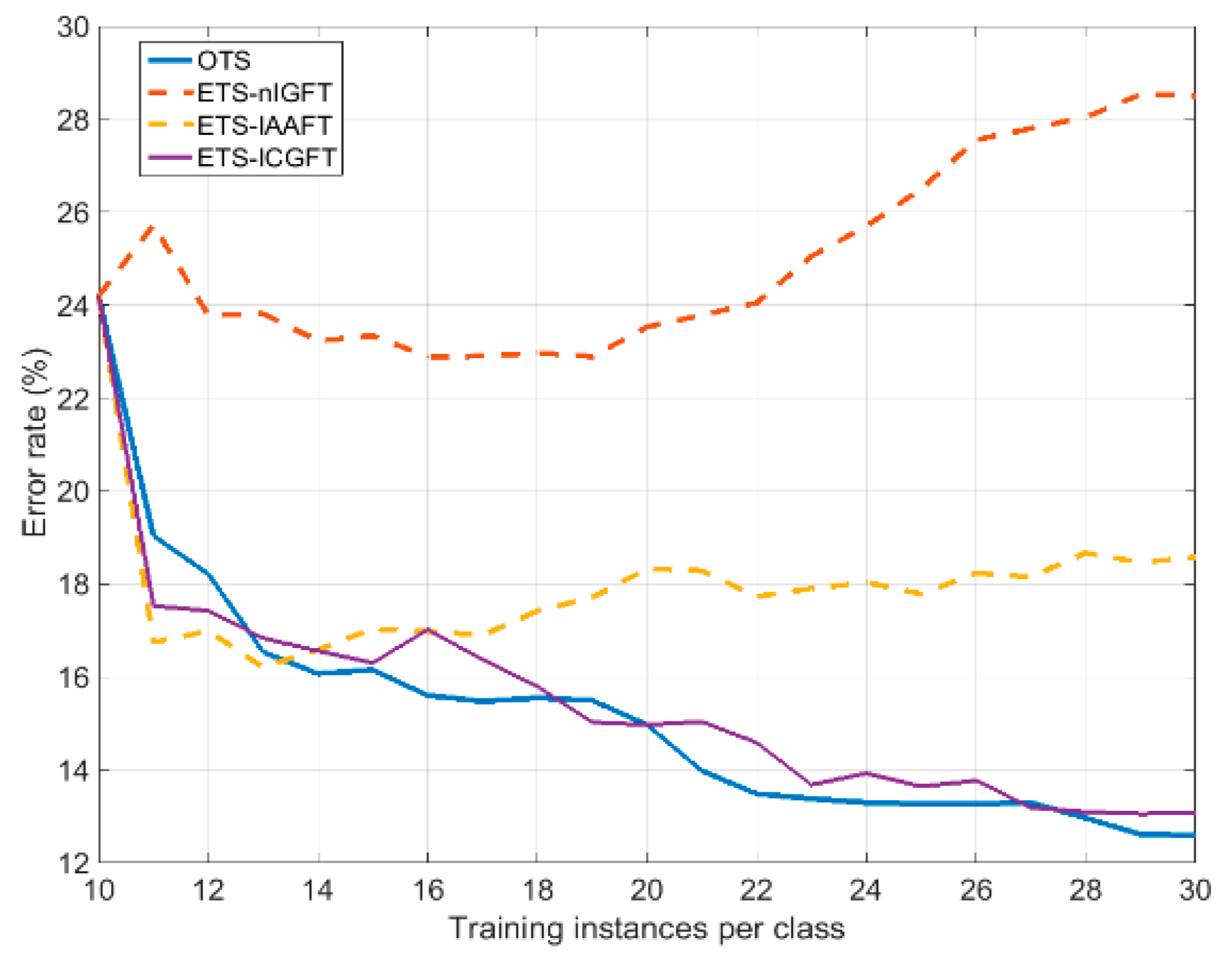
5.2. Experiment 1. Enlarging the Original Training Set: Overall Scarcity
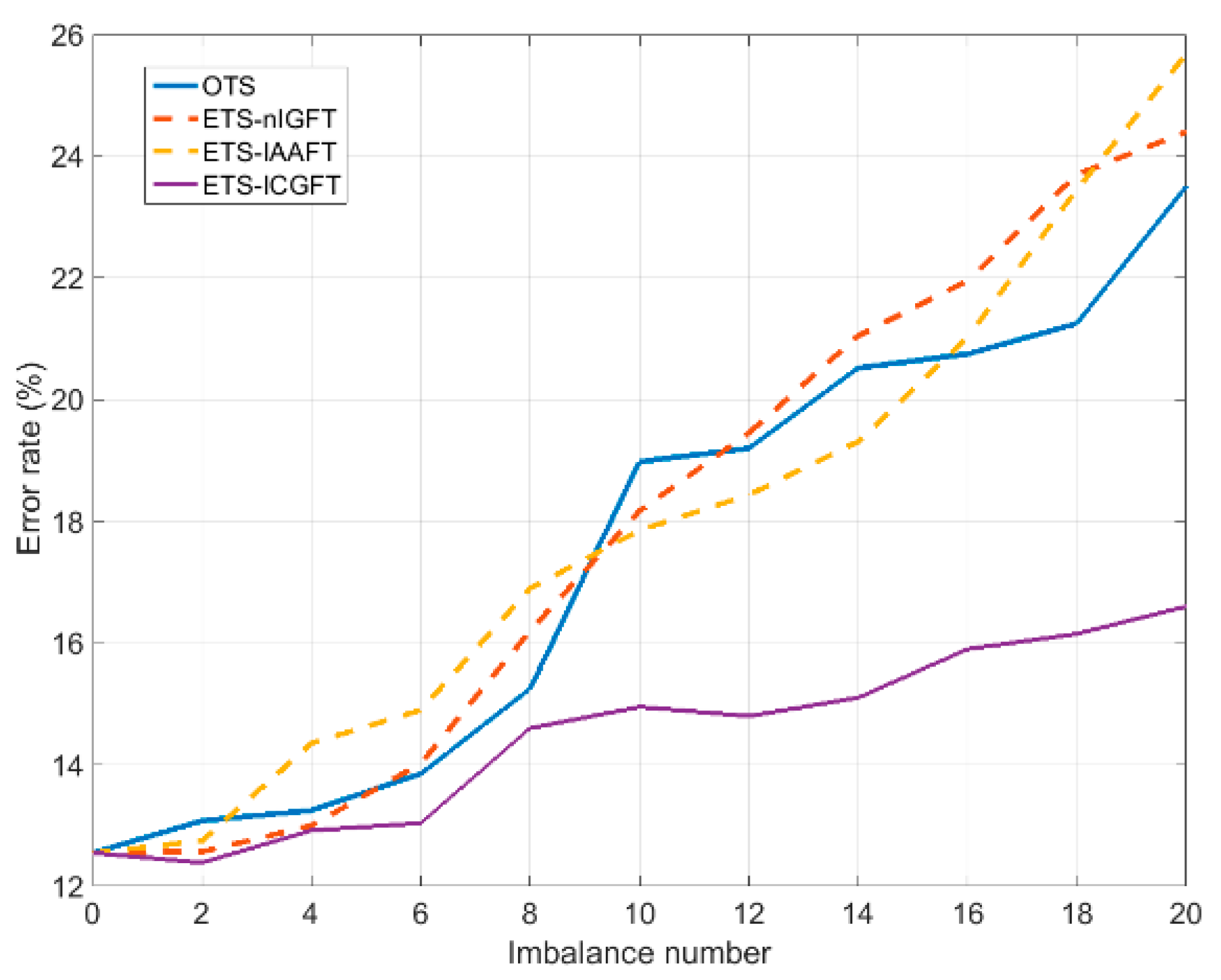
5.3. Experiment 2. Enlarging the Original Training Set: Imbalanced Classes
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Derivation of Equation (2)
Appendix B. Derivation of Equation (18)
Appendix C. List of Acronyms
| FT | Fourier Transform |
| GSP | Graph Signal Processing |
| GFT | Graph Fourier Transform |
| CGFT | Complex Graph Fourier Transform |
| GSA | Graph Spectrum Amplitude |
| GWSS | Graph Wide-Sense Stationary |
| AAFT | Amplitude Adjusted Fourier Transform surrogating algorithm |
| IAAFT | Iterative AAFT surrogating algorithm |
| ICGFT | Iterative CGFT surrogating algorithm |
| nIGFT | non-Iterative GFT surrogating algorithm |
| DFT | Discrete Fourier Transform |
| HMM | Hidden Markov Models |
| OTS | Original Training Set |
| ETS | Enlarged Training Set |
| GMM | Gaussian Mixture Model |
References
- Schreiber, T.; Schmitz, A. Surrogate time series. Phys. D Nonlinear Phenom. 2000, 142, 346–382. [Google Scholar] [CrossRef]
- Maiwald, T.; Mammen, E.; Nandi, S.; Timmer, J. Surrogate data—A qualitative and quantitative analysis. In Mathematical Methods in Signal Processing and Digital Image Analysis; Dahlhaus, R., Kurths, J., Maass, P., Timmer, J., Eds.; Springer: New York, NY, USA, 2008; pp. 41–74. [Google Scholar]
- Miralles, R.; Vergara, L.; Salazar, A.; Igual, J. Blind Detection of Nonlinearities in Ultrasonic Grain Noise. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2008, 55, 637–647. [Google Scholar] [CrossRef] [PubMed]
- Mandic, D.P.; Chen, M.; Gautama, T.; Van Hulle, M.M.; Constantinides, A. On the characterization of the deterministic/stochastic and linear/nonlinear nature of time series. Proc. R. Soc. A 2008, 464, 1141–1160. [Google Scholar] [CrossRef]
- Araújo, R.; Small, M.; Fernandes, R. Testing for Linear and Nonlinear Gaussian Processes in Nonstationary Time Series. Int. J. Bifurc. Chaos 2015, 25, 1550013. [Google Scholar]
- Jelfs, B.; Vayanos, P.; Javidi, S.; Goh, V.S.L.; Mandic, D.P. Collaborative adaptive filters for online knowledge extraction and information fusion. In Signal Processing Techniques for Knowledge Extraction and Information Fusion; Mandic, D., Golz, M., Kuh, A., Obradovic, D., Tanaka, T., Eds.; Springer: Boston, MA, USA, 2007; pp. 3–21. [Google Scholar]
- Borgnat, P.; Flandrin, P.; Honeine, P.; Richard, C.; Xiao, J. Testing stationarity with surrogates: A time-frequency approach. IEEE Trans. Signal Process. 2010, 58, 3459–3470. [Google Scholar] [CrossRef]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Sandryhaila, A.; Moura, J.M.F. Discrete signal processing on graphs. IEEE Trans. Signal Process. 2013, 61, 1644–1656. [Google Scholar] [CrossRef]
- Sandryhaila, A.; Moura, J.M.F. Big Data Analysis with signal processing on graphs. IEEE Signal Process. Mag. 2014, 31, 80–90. [Google Scholar] [CrossRef]
- Pirondini, E.; Vybornova, A.; Coscia, M.; Van De Ville, D. A Spectral Method for Generating Surrogate Graph Signals. IEEE Signal Process. Lett. 2016, 13, 1275–1278. [Google Scholar] [CrossRef]
- Sandryhaila, A.; Moura, J.M.F. Discrete signal processing on graphs: Frequency analysis. IEEE Trans. Signal Process. 2014, 62, 3042–3054. [Google Scholar] [CrossRef]
- Shuman, D.I.; Ricaud, B.; Vandergheynst, P. Vertex-frequency analysis on graphs. Appl. Comput. Harmonic Anal. 2016, 40, 260–291. [Google Scholar] [CrossRef]
- Spielman, D. Spectral graph theory. In Combinatorial Scientific Computing; Naumann, U., Schnek, O., Eds.; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2012; Chapter 16; pp. 1–23. [Google Scholar]
- Hu, C.; Cheng, L.; Sepulcre, J.; Fakhri, G.E.; Lu, Y.M.; Li, Q. A graph theoretical regression model for brain connectivity learning of Alzheimer’s disease. In Proceedings of the IEEE 10th International Symposium on Biomedical Imaging, California, CA, USA, 7–11 April 2013; pp. 616–619. [Google Scholar]
- Dong, X.; Thanou, D.; Frossard, P.; Vandergheynst, P. Learning Laplacian matrix in smooth graph signal representations. IEEE Trans. Signal Process. 2016, 64, 6160–6173. [Google Scholar] [CrossRef]
- Zhang, C.; Florencio, D.; Chou, P.A. Graph Signal Processing-A Probabilistic Framework; Technical Report MSR-TR-2015–31; Microsoft Res.: Redmond, WA, USA, 2015. [Google Scholar]
- Pávez, E.; Ortega, A. Generalized precision matrix estimation for graph signal processing. In Proceedings of the IEEE International Conference on Acoustics, Speech Signal Process (ICASSP), Sanghai, China, 20–25 March 2016; pp. 6350–6354. [Google Scholar]
- Girault, B. Stationary graph signals using an isometric graph translation. In Proceedings of the 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 September 2015; pp. 1516–1520. [Google Scholar]
- Perraudin, N.; Vandergheynst, P. Stationary Signal processing on graphs. IEEE Trans. Signal Process. 2017, 65, 3462–3477. [Google Scholar] [CrossRef]
- Yu, G.; Qu, H. Hermitian Laplacian Matrix and positive of mixed graphs. Appl. Math. Comput. 2015, 269, 70–76. [Google Scholar] [CrossRef]
- Wilson, R.C.; Hancock, E.R. Spectral Analysis of Complex Laplacian Matrices. In Structural, Syntactic and Statistical Pattern Recognition LNCS; Fred, A., Caelli, T.M., Duin, R.P.W., Campilho, A., de Ridder, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 57–65. [Google Scholar]
- Gilbert, G.T. Positive definite matrices and Sylvester’s criterion. Am. Math. Mon. 1991, 98, 44–46. [Google Scholar] [CrossRef]
- Merris, R. Laplacian matrices of a graph: A survey. Linear Algebra Appl. 1994, 197, 143–176. [Google Scholar] [CrossRef]
- Zhang, X.D. The Laplacian Eigenvalues of Graphs: A Survey. In Linear Algebra Research Advances; Ling, G.D., Ed.; Nova Science Publishers Inc.: New York, NY, USA, 2007; pp. 201–228. [Google Scholar]
- Shapiro, H. A survey of canonical forms and invariants for unitary similarity. Linear Algebra Appl. 1991, 147, 101–167. [Google Scholar] [CrossRef]
- Futorny, V.; Horn, R.A.; Sergeichuk, V.V. Spetch’s criterion for systems of linear mapping. Linear Algebra Appl. 2017, 519, 278–295. [Google Scholar] [CrossRef]
- Mazumder, R.; Hastie, T. The graphical lasso: New insights and alternatives. Electr. J. Stat. 2012, 6, 2125–2149. [Google Scholar] [CrossRef]
- Baba, K.; Shibata, R.; Sibuya, M. Partial correlation and conditional correlation as measures of conditional independence. Austr. New Zeal. J. Stat. 2004, 46, 657–664. [Google Scholar] [CrossRef]
- Chen, X.; Xu, M.; Wu, W.B. Covariance and precision matrix estimation for high-dimensional time series. Ann. Stat. 2013, 41, 2994–3021. [Google Scholar] [CrossRef]
- Öllerer, V.; Croux, C. Robust high-dimensional precision matrix estimation. In Modern Multivariate and Robust Methods; Nordhausen, K., Taskinen, S., Eds.; Springer: New York, NY, USA, 2015; pp. 329–354. [Google Scholar]
- Theiler, J.; Eubank, S.; Longtin, A.; Galdrikian, B.; Farmer, J.D. Testing for nonlinearity in time series: The method of surrogate data. Phys. D 1992, 58, 77–94. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635–638. [Google Scholar] [CrossRef] [PubMed]
- Mammen, E.; Nandi, S.; Maiwald, T.; Timmer, J. Effect of Jump Discontinuity for Phase-Randomized Surrogate Data Testing. Int. J. Bifurc. Chaos 2009, 19, 403–408. [Google Scholar] [CrossRef]
- Lucio, J.H.; Valdes, R.; Rodriguez, L.R. Improvements to surrogate data methods for nonstationary time series. Phys. Rev. E 2012, 85, 056202. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, T. Constrained randomization of time series data. Phys. Rev. Lett. 1998, 80, 2105–2108. [Google Scholar] [CrossRef]
- Prichard, D.; Theiler, J. Generating surrogate data for time series with several simultaneously measured variables. Phys. Rev. Lett. 1994, 73, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Borgnat, P.; Abry, P.; Flandrin, P. Using surrogates and optimal transport for synthesis of stationary multivariate series with prescribed covariance function and non-Gaussian joint distribution. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 3729–3732. [Google Scholar]
- Salazar, A.; Safont, G.; Vergara, L. Surrogate Techniques for Testing Fraud Detection Algorithms in Credit Card Operations. In Proceedings of the IEEE International Carnahan Conference on Security Technology (ICCSR), Rome, Italy, 13–16 September 2014. [Google Scholar]
- Hirata, Y.; Suzuki, H.; Aihara, K. Wind Modelling and its Possible Application to Control of Wind Farms. In Signal Processing Techniques for Knowledge Extration and Information Fusion; Mandic, D., Golz, M., Kuh, A., Obradovic, D., Tanaka, T., Eds.; Springer: New York, NY, USA, 2008; pp. 23–35. [Google Scholar]
- Belda, J.; Vergara, L.; Salazar, A.; Safont, G. Estimating the Laplacian matrix of Gaussian mixtures for signal processing on graphs. Signal Process. 2018, 148, 241–249. [Google Scholar] [CrossRef]
- Belda, J.; Vergara, L.; Safont, G.; Salazar, A. Computing the Partial Correlation of ICA Models for Non-Gaussian Graph Signal Processing. Entropy 2019, 21, 22. [Google Scholar] [CrossRef]
- Gray, R.M. Toeplitz and Circulant Matrices: A Review; Information System Laboratory, Stanford University: Stanford, CA, USA, 1971. [Google Scholar]
- Liao, T.W. Classification of weld flaws with imbalanced class data. Expert Syst. Appl. 2008, 35, 1041–1052. [Google Scholar] [CrossRef]
- Song, S.J.; Shin, Y.G. Eddy current flaw characterization in tubes by neural networks and finite element modeling. NDT&E Int. 2000, 33, 233–243. [Google Scholar]
- Bhattacharyya, S.; Jha, S.; Tharakunnel, K.; Westland, J.C. Data mining for credit card fraud: A comparative study. Decis. Support Syst. 2011, 50, 602–613. [Google Scholar] [CrossRef]
- Kumar, M.N.A.; Sheshadri, H.S. On the classification of imbalanced datasets. Int. J. Comput. Appl. 2012, 44, 1–7. [Google Scholar]
- Bardet, J.; Lang, G.; Oppenheim, G.; Philippe, A.; Taqqu, M. Generators of Long-Range Dependent Processes: A Survey. In Long-Range Dependence: Theory and Applications; Doukhan, P., Oppenheim, G., Taqqu, M., Eds.; Birkhauser: Boston, MA, USA, 2003; pp. 579–623. [Google Scholar]
- Mitra, S.; Acharya, T. Gesture Recognition: A Survey. IEEE Trans. Syst. Man Cybern. 2007, 37, 311–324. [Google Scholar] [CrossRef]
- Marin, G.; Dominio, F.; Zanuttigh, P. Hand Gesture Recognition with Leap Motion and Kinect Devices. In Proceedings of the IEEE International Conference on Image Processing (ICIP), París, France, 27–30 October 2014; pp. 1565–1569. [Google Scholar]
- Moni, M.A.; Shawkat, A.B.M. HMM based hand gesture recognition: A review on techniques and approaches. In Proceedings of the IEEE International Conference on Computer Science and Information Technology (ICCSIT), Beijing, China, 8–12 August 2009; pp. 433–437. [Google Scholar]
- Dardas, N.H.; Georganas, N.D. Real-Time Hand Gesture Detection and Recognition Using Bag-of-Features and Support Vector Machine Techniques. IEEE Trans. Instrum. Meas. 2011, 60, 3592–3606. [Google Scholar] [CrossRef]
- Parcheta, Z.; Martínez-Hinarejos, C.D. Sign language gesture recognition using HMM. In Pattern Recognition and Image Analysis: 8th Iberian Conference, Proceedings of the Iberian Conference on Pattern Recognition and Image Analysis (IbPRIA), Faro, Portugal, 20–23 June 2017; Springer: Cham, Switzerland, 2017; pp. 419–426. [Google Scholar]
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal–part 1: Fundamentals. Proc. IEEE 1992, 80, 520–538. [Google Scholar] [CrossRef]
- Horn, A. Doubly Stochastic Matrices and the Diagonal of a Rotation Matrix. Am. J. Math. 1954, 76, 620–630. [Google Scholar] [CrossRef]
| Invariant | Equation |
|---|---|
| Signal energy | |
| Frobenious norm of the sample correlation matrix | |
| Traces of the sample correlation matrix powers | |
| Smoothness | |
| Precision matrix | If then |
| Graph Wide-Sense Stationarity | If then |
| OTS10 | ETS-nIGFT | ETS-IAAFT | ETS-ICGFT | OTS30 | |
|---|---|---|---|---|---|
| Error rate (%) | 24.1 | 28.5 | 18.58 | 13.07 | 12.6 |
| OTS | ETS-nIGFT | ETS-IAAFT | ETS-ICGFT | |
|---|---|---|---|---|
| Error rate (%) | 17.47 | 17.91 | 17.92 | 14.82 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belda, J.; Vergara, L.; Safont, G.; Salazar, A.; Parcheta, Z. A New Surrogating Algorithm by the Complex Graph Fourier Transform (CGFT). Entropy 2019, 21, 759. https://doi.org/10.3390/e21080759
Belda J, Vergara L, Safont G, Salazar A, Parcheta Z. A New Surrogating Algorithm by the Complex Graph Fourier Transform (CGFT). Entropy. 2019; 21(8):759. https://doi.org/10.3390/e21080759
Chicago/Turabian StyleBelda, Jordi, Luis Vergara, Gonzalo Safont, Addisson Salazar, and Zuzanna Parcheta. 2019. "A New Surrogating Algorithm by the Complex Graph Fourier Transform (CGFT)" Entropy 21, no. 8: 759. https://doi.org/10.3390/e21080759
APA StyleBelda, J., Vergara, L., Safont, G., Salazar, A., & Parcheta, Z. (2019). A New Surrogating Algorithm by the Complex Graph Fourier Transform (CGFT). Entropy, 21(8), 759. https://doi.org/10.3390/e21080759





