Minimum Memory-Based Sign Adjustment in Signed Social Networks
Abstract
1. Introduction
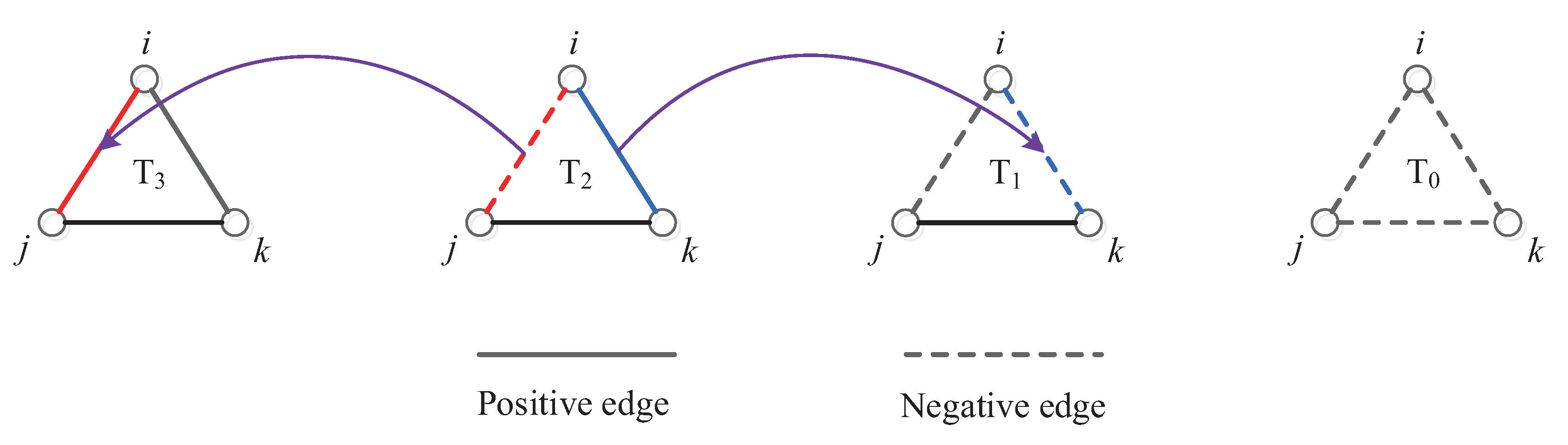
2. The Network Model and Sign Adjustment Rules
2.1. The Signed Social Network Model
- The network is assigned n nodes and a regular ring lattice is constructed on the nodes, where each node is connected to a total of K neighbours, each side with neighbours (where K is even integer).
- Select all node pairs in turn.
- Add links between the selected node pairs with probability , if no self-loops and link duplication. We name the probability as the rewiring probability.
- Each symmetric link is randomly set to a positive sign with a probability of and to negative with a probability of .
2.2. Random Adjustment Rule
- Randomly select a three-cycle from the network.
- If the selected cycle is balanced, then return to step 1.
- If the cycle is imbalanced, select any one of its constituent nodes as the “duty node” and change the sign of any one of duty node’s two links, in order to achieve balance in the cycle.
2.3. Minimum Memory-Based Sign Adjustment Rules
- Set all nodes to remember only one of their most important neighbours (regardless of whether it is friend or enemy). At the beginning of the simulation, each node randomly selects one neighbour from amongst all of its neighbours to compose its close neighbour set.
- Select a three-cycle at random from the network.
- If the cycle is balanced, then return to step 2.
- If the cycle is imbalanced, randomly select one of its nodes as the duty node.
- Change the sign of any one of the two edges which link the duty node in the cycle if the sign change can strictly increase the balance ratio of the duty node with his best neighbour.
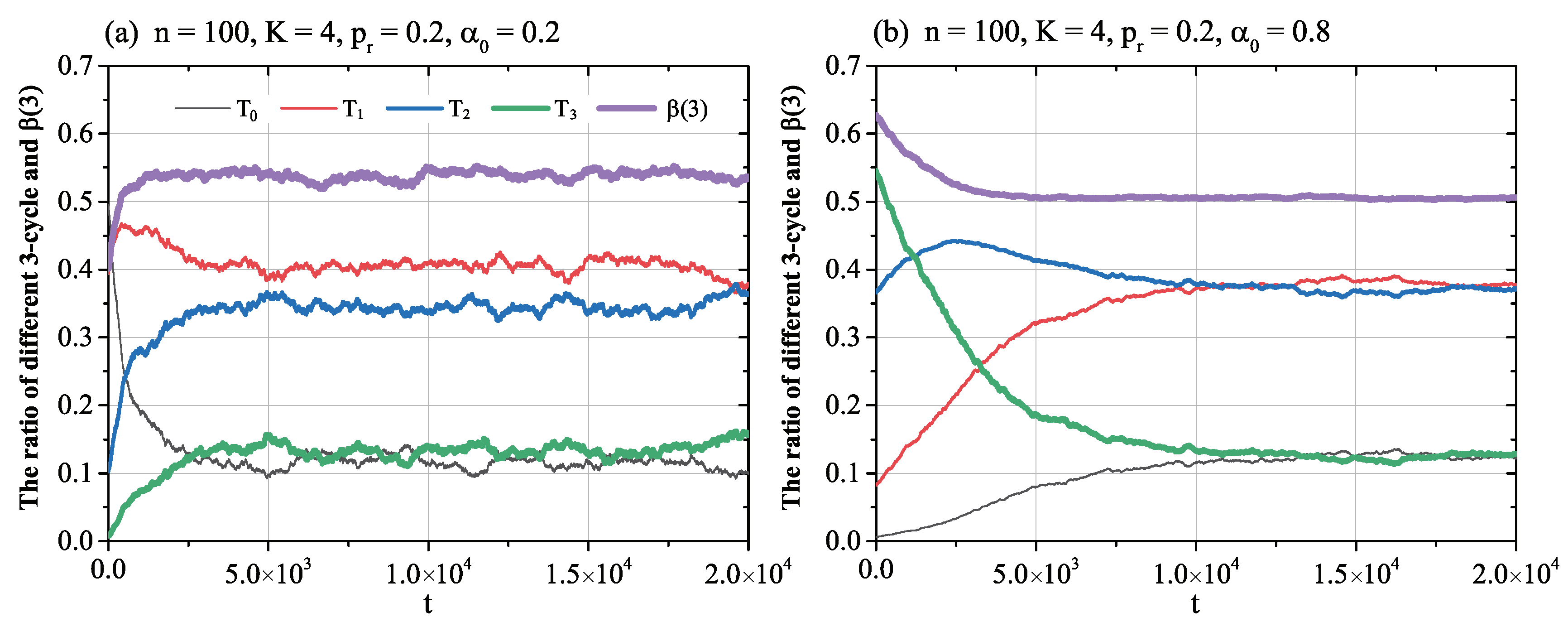
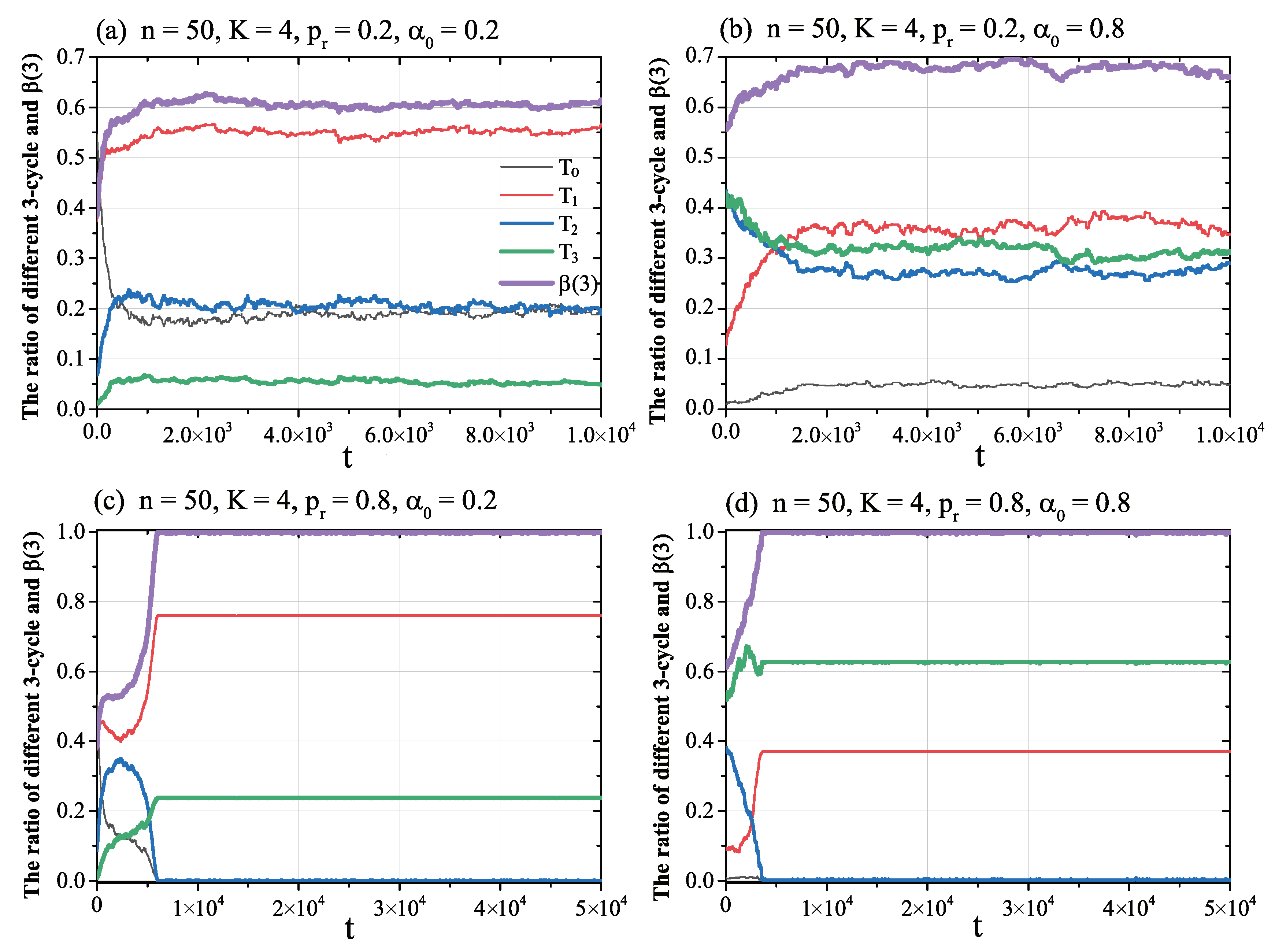
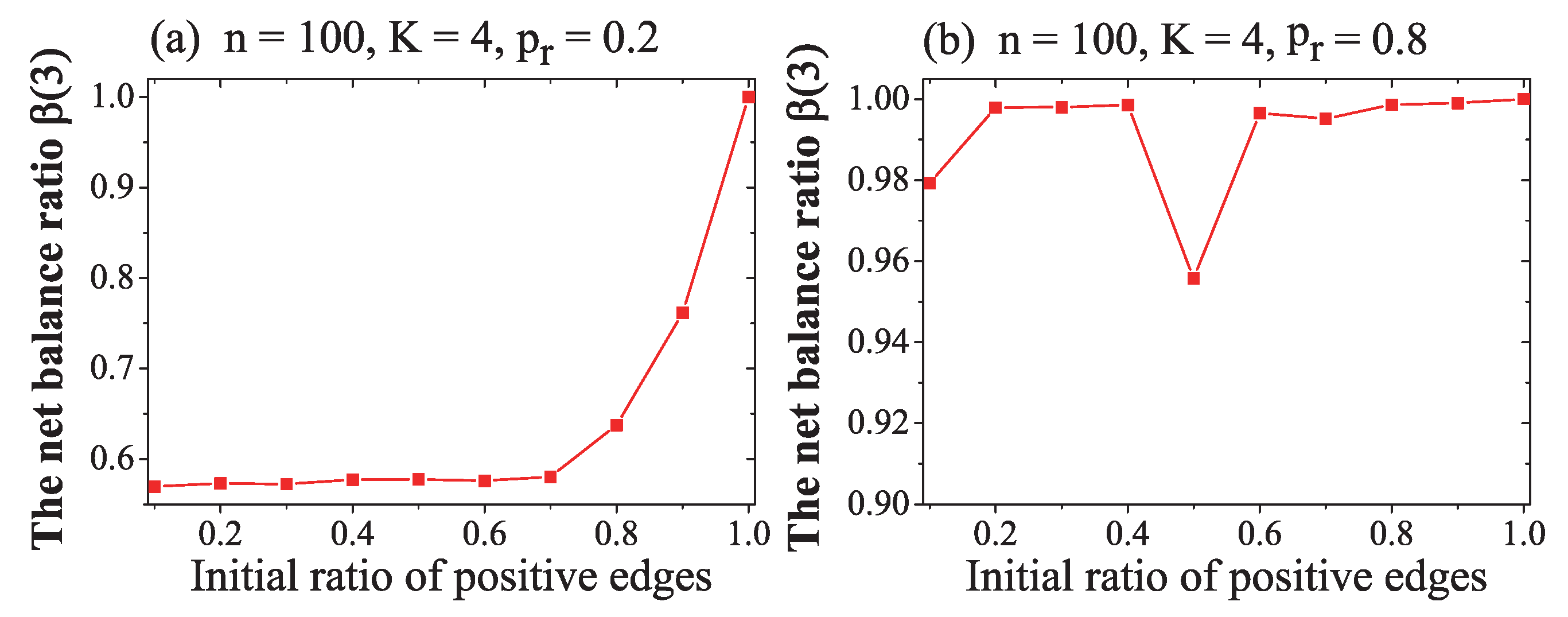
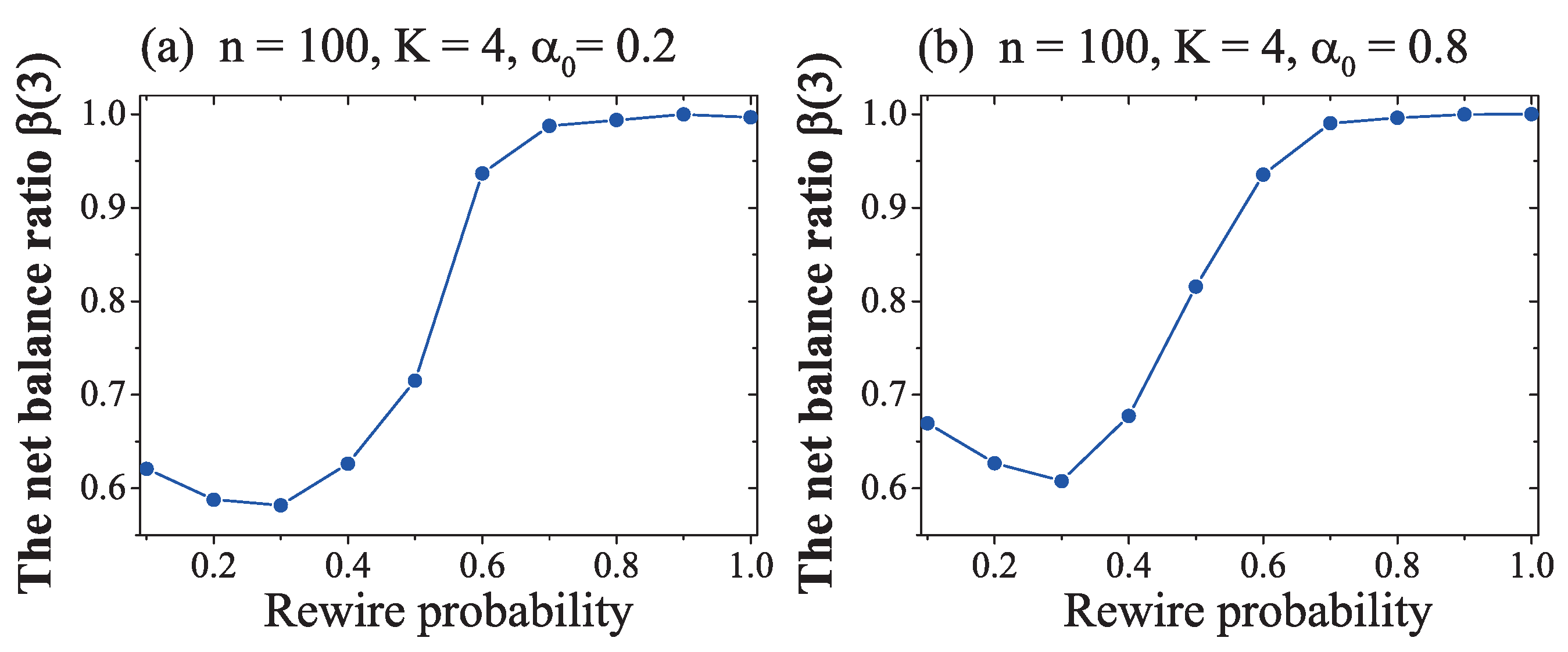
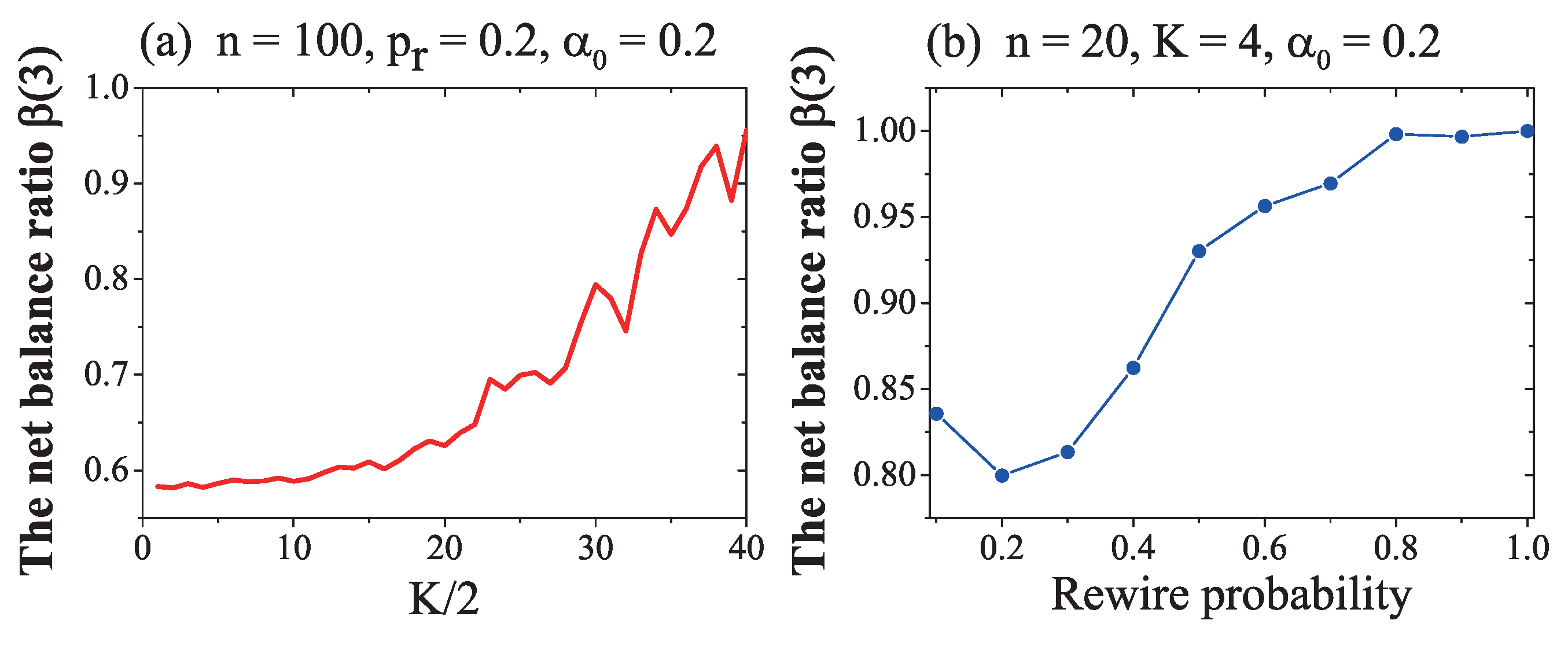
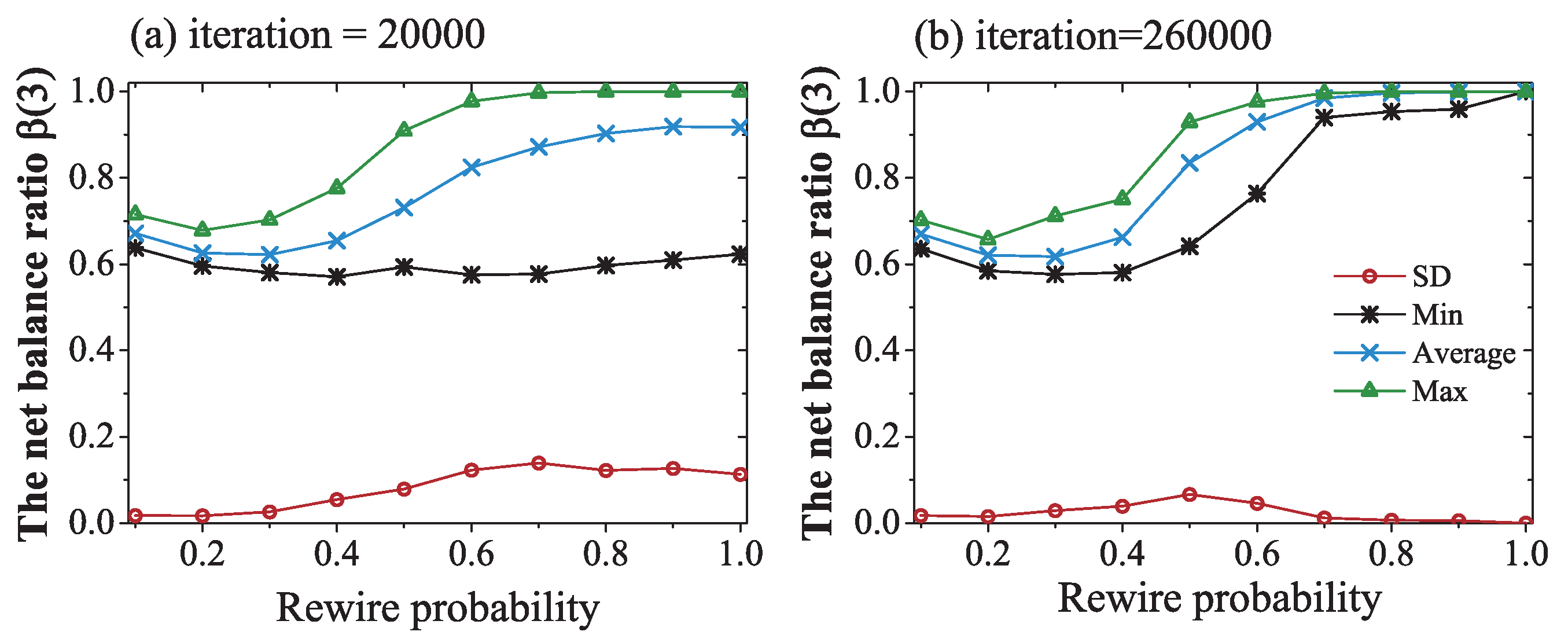
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Heider, F. Attitudes and cognitive organization. J. Psychol. 1946, 21, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, D.; Harary, F. Structural balance: A generalization of Heider’s theory. Psychol. Rev. 1956, 63, 277–293. [Google Scholar] [CrossRef] [PubMed]
- Opp, K.D. Balance Theory: Progress and Stagnation of a Social Psychological Theory. Philos. Soc. Sci. 1984, 14, 27–49. [Google Scholar] [CrossRef]
- Hallinan, M.T.; Hutchins, E.E. Structural Effects on Dyadic Change. Soc. Forces 1980, 59, 225–245. [Google Scholar] [CrossRef]
- Deng, H.; Abell, P. A Study of Local Sign Change Adjustment in Balancing Structures. J. Math. Sociol. 2010, 34, 253–282. [Google Scholar] [CrossRef]
- Deng, H.; Abell, P.; Li, J.; Wu, J. A study of sign adjustment in weighted signed networks. Soc. Netw. 2012, 34, 253–263. [Google Scholar] [CrossRef]
- Lewis, K. How Networks Form: Homophily, Opportunity, and Balance. In Emerging Trends in the Social and Behavioral Sciences: An Interdisciplinary, Searchable, and Linkable Resource; Wiley Online Library: Hoboken, NJ, USA, 2015; pp. 1–14. [Google Scholar]
- Deng, H.; Abell, P.; Engel, O.; Wu, J.; Tan, Y. The influence of structural balance and homophily/heterophobia on the adjustment of random complete signed networks. Soc. Netw. 2016, 44, 190–201. [Google Scholar] [CrossRef][Green Version]
- Rawlings, C.M.; Friedkin, N.E. The structural balance theory of sentiment networks: Elaboration and test. Am. J. Sociol. 2017, 123, 510–548. [Google Scholar] [CrossRef]
- Kirkley, A.; Cantwell, G.T.; Newman, M.E.J. Balance in signed networks. Phys. Rev. E 2019, 99, 012320. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, A.B.; Hallinan, M.T. A stochastic model for change in group structure. Sociol. Rev. 1976, 24, 143–166. [Google Scholar] [CrossRef]
- Doreian, P.; Krackhardt, D. Pre-transitive balance mechanisms for signed networks. Math. Sociol. 2001, 25, 43–67. [Google Scholar] [CrossRef]
- Macy, M.W.; Willer, R. From factors to actors: Computational sociology and agent-based modeling. Rev. Sociol. 2002, 28, 143–166. [Google Scholar] [CrossRef]
- Ilany, A.; Barocas, A.; Koren, L.; Kam, M.; Geffen, E. Structural balance in the social networks of a wild mammal. Anim. Behav. 2013, 85, 1397–1405. [Google Scholar] [CrossRef]
- Yap, J.; Harrigan, N. Why does everybody hate me? Balance, status, and homophily: The triumvirate of signed tie formation. Soc. Netw. 2015, 40, 103–122. [Google Scholar] [CrossRef]
- Hummon, N.P.; Doreian, P. Some dynamics of social balance processes: Bringing Heider back into balance theory. Soc. Netw. 2003, 25, 17–49. [Google Scholar] [CrossRef]
- Antal, T.; Krapivsky, P.L.; Redner, S. Dynamics of social balance on networks. Phys. Rev. E 2005, 72, 36121. [Google Scholar] [CrossRef] [PubMed]
- Kulakowski, K.; Gawronski, P.; Gronek, P. The Heider Balance: A Continuous Approach. Int. J. Mod. Phys. C 2005, 16, 707–716. [Google Scholar] [CrossRef]
- Ludwig, M.; Abell, P. An evolutionary model of social networks. Eur. Phys. J. B 2007, 58, 97–105. [Google Scholar] [CrossRef]
- Montgomery, J.D. Balance Theory with Incomplete Awareness. J. Math. Sociol. 2009, 33, 69–96. [Google Scholar] [CrossRef]
- Marvel, S.A.; Kleinberg, J.M.; Kleinberg, R.D.; Strogatz, S.H. Continuous-time model of structural balance. Proc. Natl. Acad. Sci. USA 2011, 108, 1771–1776. [Google Scholar] [CrossRef]
- Kossinets, G.; Watts, D.J. Origins of Homophily in an Evolving Social Network. Am. J. Sociol. 2009, 115, 405–450. [Google Scholar] [CrossRef]
- Mei, W.; Cisneros-Velarde, P.; Friedkin, N.E.; Bullo, F. Dynamic Social Balance and Convergent Appraisals via Homophily and Influence Mechanisms. arXiv 2017, arXiv:1710.09498. [Google Scholar]
- Rijt, A.V.D. The Micro-Macro Link for the Theory of Structural Balance. J. Math. Sociol. 2011, 35, 94–113. [Google Scholar] [CrossRef]
- Volstorf, J.; Rieskamp, J.; Stevens, J.R. The Good, the Bad, and the Rare: Memory for Partners in Social Interactions. PLoS ONE 2011, 6, e18945. [Google Scholar] [CrossRef] [PubMed]
- Brashears, M.E.; Brashears, L.A. The Enemy of My Friend Is Easy to Remember: Balance as a Compression Heuristic. In Advances in Group Processes; Emerald Group Publishing Limited: Bingley, UK, 2016; Volume 33. [Google Scholar]
- Hassanibesheli, F.; Hedayatifar, L.; Safdari, H.; Ausloos, M.; Jafari, G. Glassy States of Aging Social Networks. Entropy 2017, 19, 246. [Google Scholar] [CrossRef]
- Kottonau, J.; Burse, J.; Pahl-Wostl, C. A consumer memory-based model of new product diffusion within a social network. In Proceedings of the 10th Meeting of the Annual Workshop on Computational and Mathematical Organisation Theory, CMOT, Computational Social Organisational Science Conference, CASOS, CMU, Pittsburgh, PA, USA, 21–24 July 2000. [Google Scholar]
- Winke, T.; Stevens, J.R. Is cooperative memory special? The role of costly errors, context, and social network size when remembering cooperative actions. Front. Robot. AI 2017, 4, 52. [Google Scholar] [CrossRef]
- Milgram, S. The small world problem. Psychol. Today 1967, 2, 60–67. [Google Scholar]
- Guare, J. Six Degrees of Separation: A Play; Vintage: New York, NY, USA, 1990. [Google Scholar]
- Adamic, L.A.; Huberman, B.A. Power-Law Distribution of the World Wide Web. Science 2000, 287, 2115. [Google Scholar] [CrossRef]
- Amaral, L.A.N.; Scala, A.; Barthelemy, M.; Stanley, H.E. Classes of small-world networks. Proc. Natl. Acad. Sci. USA 2000, 97, 11149–11152. [Google Scholar] [CrossRef]
- Davis, G.F.; Yoo, M.; Baker, W.E. The Small World of the American Corporate Elite, 1982–2001. Strateg. Organ. 2003, 1, 301–326. [Google Scholar] [CrossRef]
- Davis, G.F.; Greve, H.R. Corporate Elite Networks and Governance Changes in the 1980s. Am. J. Sociol. 1997, 103, 1–37. [Google Scholar] [CrossRef]
- Bordons, M.; Gomez, I. Collaboration networks in science. In The Web of Knowledge: A Festschrift in Honor of Eugene Garfield; Information Today Inc.: Medford, NJ, USA, 2000; pp. 197–213. [Google Scholar]
- Barabasi, A.; Jeong, H.; Neda, Z.; Ravasz, E.; Schubert, A.; Vicsek, T. Evolution of the social network of scientific collaborations. Phys. A-Stat. Mech. Appl. 2002, 311, 590–614. [Google Scholar] [CrossRef]
- Aiello, W.; Chung, F.R.K.; Lu, L. A random graph model for massive graphs. In Proceedings of the Thirty-Second Annual Acm Symposium on Theory of Computing, Portland, OR, USA, 21–23 May 2000; pp. 171–180. [Google Scholar]
- Aiello, W.; Chung, F.R.K.; Lu, L. Random evolution in massive graphs. In Proceedings of the 42nd IEEE Symposium on Foundations of Computer Science, Newport Beach, CA, USA, 7 August 2002; pp. 97–122. [Google Scholar]
- Ebel, H.; Mielsch, L.I.; Bornholdt, S. Scale-free topology of e-mail networks. Phys. Rev. E 2002, 66, 35103. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.; Watts, D. Renormalization Group Analysis of the Small-World Network Model. Phys. Lett. A 1999, 263, 341–346. [Google Scholar] [CrossRef]
- Abell, P.; Ludwig, M. Structural Balance: A Dynamic Perspective. J. Math. Sociol. 2009, 33, 129–155. [Google Scholar] [CrossRef]
- Deng, H.Z.; Abell, P.; Li, Y.; Wu, J.; Tan, Y.J. Network Size Impact upon Global Balance Structure in Small Complete Network. Appl. Mech. Mater. 2015, 713, 2276–2279. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, M.; Deng, H.; Li, Y. Minimum Memory-Based Sign Adjustment in Signed Social Networks. Entropy 2019, 21, 728. https://doi.org/10.3390/e21080728
Qi M, Deng H, Li Y. Minimum Memory-Based Sign Adjustment in Signed Social Networks. Entropy. 2019; 21(8):728. https://doi.org/10.3390/e21080728
Chicago/Turabian StyleQi, Mingze, Hongzhong Deng, and Yong Li. 2019. "Minimum Memory-Based Sign Adjustment in Signed Social Networks" Entropy 21, no. 8: 728. https://doi.org/10.3390/e21080728
APA StyleQi, M., Deng, H., & Li, Y. (2019). Minimum Memory-Based Sign Adjustment in Signed Social Networks. Entropy, 21(8), 728. https://doi.org/10.3390/e21080728




