1. Introduction
Quantum information processing can be achieved by discriminating quantum states, where classical information is encoded. Quantum states which are orthogonal to each other can be perfectly distinguishable. However, non-orthogonal quantum states cannot be perfectly discriminated. Therefore, one needs to have a discrimination strategy for non-orthogonal quantum states, and there are various strategies [
1,
2,
3,
4] such as minimum error discrimination (MD) [
4,
5,
6,
7], unambiguous discrimination [
8,
9,
10,
11,
12], maximum confidence discrimination [
13], and discrimination of fixed rate inconclusive result [
14,
15,
16,
17,
18]. Unambiguous discrimination is a strategy where there is no error in the conclusive result by allowing an inconclusive result. Maximum confidence is a strategy where one maximizes the confidence of a conclusive result. Discrimination of fixed rate inconclusive result is a strategy where one may fix the rate of an inconclusive result. Among these strategies, the MD strategy can conclusively discriminate quantum states with a prior probability.
The MD strategy is employed for quantum states with a given prior probability, and the quantum states are optimally measured. MD strategy is that one maximizes the probability that the result of measurement of a receiver correctly points out the quantum state that a sender transmitted when only a conclusive result is permitted. The maximum probability is called guessing probability. One can investigate the behavior of MD in terms of a prior probability when quantum states are given.
Because the guessing probability is obtained based on prior probability, a change in prior probability results in different guessing probabilities, which implies that prior probabilities can be considered as a strategy of a sender. Even though one has discussed the uniqueness of measurement strategy in discrimination of two quantum states, the strategy of preparation such as a prior probability, which can be a strategy of a sender, has not been discussed in terms of identical guessing probability and optimal measurement strategy.
Quantum minimax approach is obtained by applying the minimax approach of a statistical decision to quantum state discrimination. Von Neumann, the inventor of game theory, showed that there exists a solution to the minimax problem when sender and receiver can choose a finite number of strategies in a two-person zero-sum game. Wald proved that the necessary and sufficient condition to the existence of a solution to the minimax problem is that the set of strategy for sender and receiver is countable [
19]. Hirota and Ikehara discussed quantum minimax theorem, using the fact that the set of measurement strategy satisfies compactness [
20]. They suggested the necessary and sufficient condition for minimax strategy in quantum state discrimination.
Further, by mean value theorem D’Ariano showed that there exists a quantum minimax strategy for two quantum state discrimination and provided a sufficient condition for the strategy [
21]. However, in spite of these studies, the necessary and sufficient condition for uniqueness of minimax strategy in two quantum state discrimination is not known yet. Even more, the uniqueness of minimax strategy in two quantum state discrimination is not understood in terms of sender’s strategy, which is a selection of prior probability.
This study investigates a two-person zero-sum game where the payoff is defined by the correct probability of two quantum states [
19,
20,
21,
22]. The optimal strategy of the game is a minimax strategy, where the minimax strategy of a receiver is to select the optimal measurement providing MD and the minimax strategy of a sender is to choose the prior probability providing the minimum of guessing probability, which is displayed in
Figure 1.
In this scenario, the prior probability and the measurement in MD are constructed as the strategy of a sender Alice and a receiver Bob [
20,
21]. First, Alice sends the quantum states, where classical information
is encoded, to Bob. Because the quantum states are not orthogonal to each other, a single measurement of Bob cannot perfectly discriminate the quantum states. Therefore, a suitable strategy is needed. Here Bob should choose a measurement strategy that can perform MD.
Meanwhile, a suitable selection of prior probability can be obtained by Alice, as a sender’s strategy. Alice’s strategy is to interfere with the minimum error strategy of Bob to minimize the guessing probability. Because Bob should perform MD without noticing Alice’s strategy, Bob tries to find an optimal strategy to obtain a payoff. Therefore, the minimum of guessing probability implies that a suitable selection of prior probability lets Bob obtain the minimum of guessing probability when Bob performs an optimal measurement. Furthermore, if Bob cannot perform an optimal measurement, he obtains a probability less than the guessing probability.
The quantum minimax theorem [
20,
21] can be used to prove that Alice and Bob can set up an optimal strategy on both sides. However, it is not known whether the minimax strategy is unique or not. The uniqueness of the optimal strategy of the game is important in performing the game. There is no alternative to a unique optimal strategy. Therefore, a strategy cannot be optimal if an error occurs when performing the strategy. However, a strategy can still be optimal if it is not unique, even though an error occurs in the strategy. In this light, it is crucial to know whether the minimax strategy is unique, when the strategy is optimal in the game. Here, we investigate the condition for uniqueness of the optimal strategy of a sender. The condition is described by the quantum states and the minimax strategy of a receiver. More explicitly, we study the necessary and sufficient condition for the uniqueness of a sender’s strategy. Using the condition, we investigate the quantum states that exhibit the minimum of guessing probability when a sender’s minimax strategy is unique.
Also, we show that a sender’s minimax strategy and a receiver’s minimum error strategy cannot be unique if two quantum states are simultaneously diagonalized with the optimal measurement of minimax strategy. Therefore, a sender can make the optimal strategy of only a single side unique by preparing specific quantum states. Our investigation can be applied to various fields. As the first example of our investigation, we explain how the BB84 protocol [
23] with equal prior probability is optimal in terms of the minimax strategy. We also discuss how the results of this study can be applied to building a quantum random number generator(QRNG) [
24,
25,
26].
This paper is organized as follows. In
Section 2, we explain the necessary background of our investigation. In
Section 3, for the minimax strategy of a sender, we provide the necessary and sufficient condition for uniqueness of the optimal strategy. We investigate the uniqueness of the strategy of the sender for some quantum states by using this condition. Furthermore, we obtain the condition under which both the sender’s minimax strategy and the receiver’s optimal minimum error strategy cannot be unique. Finally, we discuss the results and conclusions in
Section 4.
2. Preliminaries
For two quantum states and , the minimal subspace for discriminating and should satisfy . In this study, we assume that the rank of quantum state is finite. Then, by the relation , a quantum state or an optimal measurement can be represented as an operator on finite dimensional Hilbert space.
The MD of two quantum states
and
is a strategy to determine the maximum value of correct probability
, which is called guessing probability, by performing an optimal measurement. The maximum value of the correct probability is known as Helstrom bound [
27].
Assuming that the prior probabilities of two quantum states
and
are
q and
, respectively, one can obtain the following lemma in the MD of the two quantum states. (The proof can be found in the
Appendix A).
Lemma 1 (Optimal condition of MD for two quantum states [
27,
28])
. The necessary and sufficient condition for optimal measurement is given by In general, the optimal measurement in MD is not unique. If the nullity of operator
is
d, there exist at least
number of optimal extreme POVMs. A convex combination of these POVM also provides an optimal measurement of MD. When
has full rank, the optimal measurement is unique. Quantum minimax theorem tells that among optimal MD strategies there is at least a POVM of minimax strategy in a prior probability providing the minimum of guessing probability [
20,
21].
Theorem 1 (Quantum minimax theorem [
20,
21])
. There exists an a priori probability for the states and , and a measurement such thatwhere . Note that when quantum states are prepared in a prior probability
,
implies that the measurement of
is optimal and
implies that the prior probability of
provides the minimum of guessing probability. However, every optimal MD in the prior probability of
is not a minimax strategy of Bob. Suppose that a measurement of
in the prior probability of
is an optimal strategy of MD, satisfying
. Then, the strategy of Alice in
cannot be a prior probability for the minimax strategy, as
of Alice’s strategy provides a lower guessing probability than that of
:
Therefore, the first condition that the minimax strategy
of Bob should satisfy is
. Because the measurement of
is an optimal strategy for the prior probability of
, it satisfies the optimal condition of MD, which is the second condition. Inversely, the fulfillment of the two conditions is the sufficient condition for the minimax strategy.
Here, the conditions can be explained as follows. Suppose that a measurement
satisfies
and is optimal for the prior probability of
. Then, we find the following relation:
The last equality holds by
. Because of
, we find
. And the following relation holds:
The first equality is obtained by
. Because of
, we obtain
and
. It implies that
is a minimax strategy. Then, one can obtain the following lemma.
Lemma 2. When MD is performed for a given prior probability, the minimum of guessing probability is obtained iff an optimal measurement satisfies .
3. Results
This section presents the necessary and sufficient condition that ensures the uniqueness of the minimax strategy of a sender. Because there always exists a minimax strategy for the quantum minimax theorem, when one finds a minimax strategy, one can obtain the condition by which the strategy is unique. When MDs with different prior probabilities can provide the same guessing probability, the following lemma provides the condition by which the MDs with different prior probabilities can have the same optimal measurement (The proof of this lemma can be found in the
Appendix A).
Lemma 3. The quantum ensembles of and are given as and , respectively, where . Suppose that in the MD of a quantum ensemble , the guessing probability is and the minimum value of guessing probability is . Then, when , if there exists an measurement that can simultaneously perform MD on two quantum ensembles and , one can obtain .
Note that the optimal measurement performing simultaneous MD on two quantum ensemble
and
satisfies the equal probabilities of correct detection. It is the minimax strategy of the receiver. Here, the set of prior probability providing the minimum of guessing probability is a convex set. It can be shown in the following way. Suppose that the prior probabilities of
and
provide the minimum of guessing probability
. Then, by Lemma 3 there exists a measurement
that can perform MD on both the quantum states, satisfying
. Now, one can see that the relation of
holds for
. If one assumes that the minimax strategy
is not unique and there is another strategy
for a sender, then the minimax strategy of the sender forms a convex set, and one can find the prior probability where
is optimal in the
-neighborhood of
for an arbitrary positive number of
. Therefore, one can check the uniqueness of the prior probability of
providing the minimum of guessing probability, by deciding whether there exists a prior probability exhibiting optimal
in the
neighborhood of
after finding the optimal POVM
for minimax strategy in the prior probability of
providing the minimum of guessing probability. Proposition 1 shows the necessary and sufficient condition for the non-uniqueness of a prior probability
of which
is optimal in the
neighborhood (The proof of this proposition can be found in the
Appendix A).
Proposition 1. The prior probability providing the minimum of guessing probability is not unique if and only if satisfies the following conditions.
- 1.
,
- 2.
For some , every satisfies .
where .
Lemma 2 and Proposition 1 can be applied to check whether the strategy under a situation is unique. By applying Lemma 2, one can explain why the identical prior probability in the BB84 protocol is the best strategy of a sender. The quantum states used in the BB84 protocol are
[
23]. Alice encodes
into quantum states and sends them to Bob. In general,
is selected by Alice, but
is randomly chosen. Suppose that
Table 1 is used for encoding bit. Here, encoding means that a quantum state corresponding to
is prepared for communication.
When Alice chooses 0 as the value of
, the quantum state is determined by
. If the value of
is 0, the quantum state becomes
. However, when
is 1,
is prepared for the quantum state. If the quantum state does not interact with the environment, Bob receives the quantum state prepared by Alice. Then, Bob performs the following measurements:
When for the quantum states
the prior probability of the quantum states is identical, the optimal measurement becomes
The optimal measurement satisfies the following relation:
It implies that the identical prior probability provides the minimum of guessing probability. It is because if there exists an optimal measurement satisfying the above condition, the prior probability provides the minimum of guessing probability. It should be noted that Lemma 3 implies that the measurement of
M is optimal for every prior probability providing the minimum of guessing probability. Meanwhile, if the prior probability is not identical, all the quantum states in the BB84 protocol does not have
M as an optimal measurement. It can be shown in the following way. Let us assume that the probability of
to become 0 or 1 is equal, and the probability of
to become 0 or 1 is
q. Then, the prior probability of each quantum state becomes
. We can show that if the measurement
M is optimal at
, the following inequalities should be satisfied [
2,
28]:
However, when
, one of these inequalities cannot be satisfied. Therefore, the prior probability providing the minimum of the guessing probability is only the case of
.
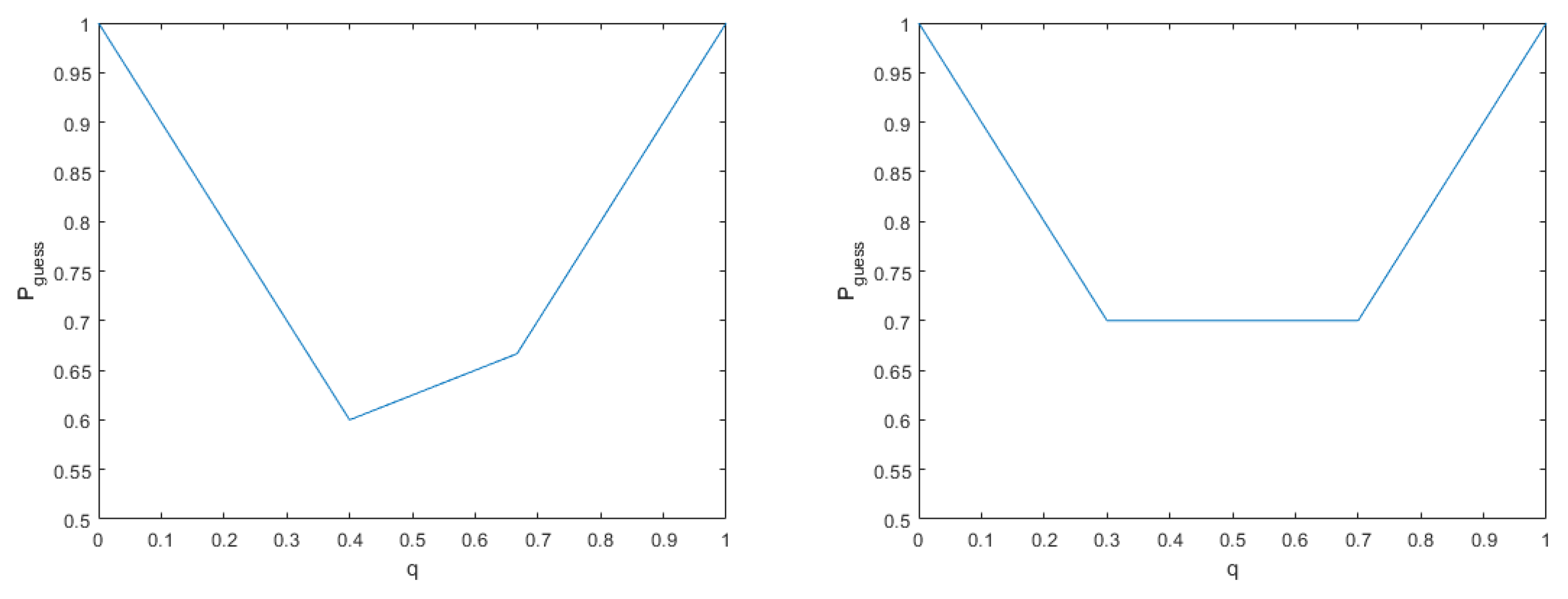
Using Proposition 1, we can investigate the quantum states of the unique prior probability, which provides the minimum of the guessing probability. Here we consider the MD of the following two quantum states:
From
Figure 2, we can check whether the prior probability providing the minimum of guessing probability is unique. We can see that the prior probabilities providing the minimum of guessing probability are
and
. The optimal measurement for the quantum ensemble is
, since the measurement satisfies Lemma 1 as follows:
In addition,
satisfies the relation of
. From Lemma 2, the prior probability of
and
provides the minimum of guessing probability. Now, we verify the uniqueness of the prior probability which provides the minimum of the guessing probability for the given quantum states. The following relations show
, which is the first condition of Proposition 1:
However,
which is the support of
and
, satisfies the following relation:
Because the second condition of Proposition 1 cannot be satisfied, the prior probability providing the minimum of the guessing probability is unique.
Now, to investigate the case of non-unique prior probability, which provides the minimum of the guessing probability, we consider the following quantum states:
From
Figure 2, we can see non-uniqueness of the prior probability, which can provide the minimum of guessing probability.
For
and
with the prior probability of
, we can obtain the minimum of the guessing probability, which is
. Then, the optimal measurements are
. Because of
, the minimum of the guessing probability becomes
at
. And because of
, the support of
is
, which is unique. Then, one has
Further, because of
, the support of
is
, which is unique. We have
Then, the prior probability providing the minimum of the guessing probability is not unique.
From Proposition 1, the unique prior probability providing the minimum of the guessing probability has two cases. The interesting case of the two cases is one where the prior probability providing the minimum of the guessing probability is unique, with the condition that the second inequality of Proposition 1 does not hold. This is because, in this case, Bob’s optimal MD strategy is not unique. When the second condition of Proposition 1 is satisfied, an element
in the support of
satisfies the relation of
. Then, from Lemma A1 in
Appendix B, there exists
providing
. Now, we define
and
as
and
, respectively. Then,
and
are positive semidefinite operators. Because of
,
is a POVM. We can verify whether
is an optimal measurement at
. First, from the relation of
, we have
. For
, by Lemma A2, we can obtain
. Then, we have the following relations that show that
is an optimal measurement at
:
According to Lemma A3 in the
Appendix B, the necessary and sufficient condition that two conditions of
and
are satisfied is that the optimal measurement
of a receiver can be simultaneously diagonalized with two quantum states
and
. Therefore, if the optimal measurement
of a receiver is simultaneously diagonalized with two quantum states
and
, the uniqueness of the sender’s minimax strategy cannot be compatible with the uniqueness of the receiver’s MD strategy. The following Corollary summarizes this result.
Corollary 1. If the optimal measurement can be simultaneously diagonalized with two quantum states and , the uniqueness of minimax strategy of a sender and the uniqueness of MD of a receiver cannot be compatible.
The above result can be applied to cases of building quantum random number generator(QRNG). Suppose that only one side’s strategy is unique. Therefore, either the minimax strategy of a sender or the minimum error strategy is unique. The randomness in QRNG is defined as the min-entropy to the classical bit in the quantum-classical state and depends on the prior probability [
25,
29]. If the prior probability providing minimum guessing probability is not unique, we can build QRNG that is not sensitive to the prior probability. When QRNG is built such that the receiver’s strategy is unique, even a slight error in the measurement leads to the loss of the optimality of the receiver’s strategy. The quantum states with a unique receiver’s strategy in QRNG can be found by using Corollary 1.