Flow Regime Recognition and Dynamic Characteristics Analysis of Air-Water Flow in Horizontal Channel under Nonlinear Oscillation Based on Multi-Scale Entropy
Abstract
1. Introduction
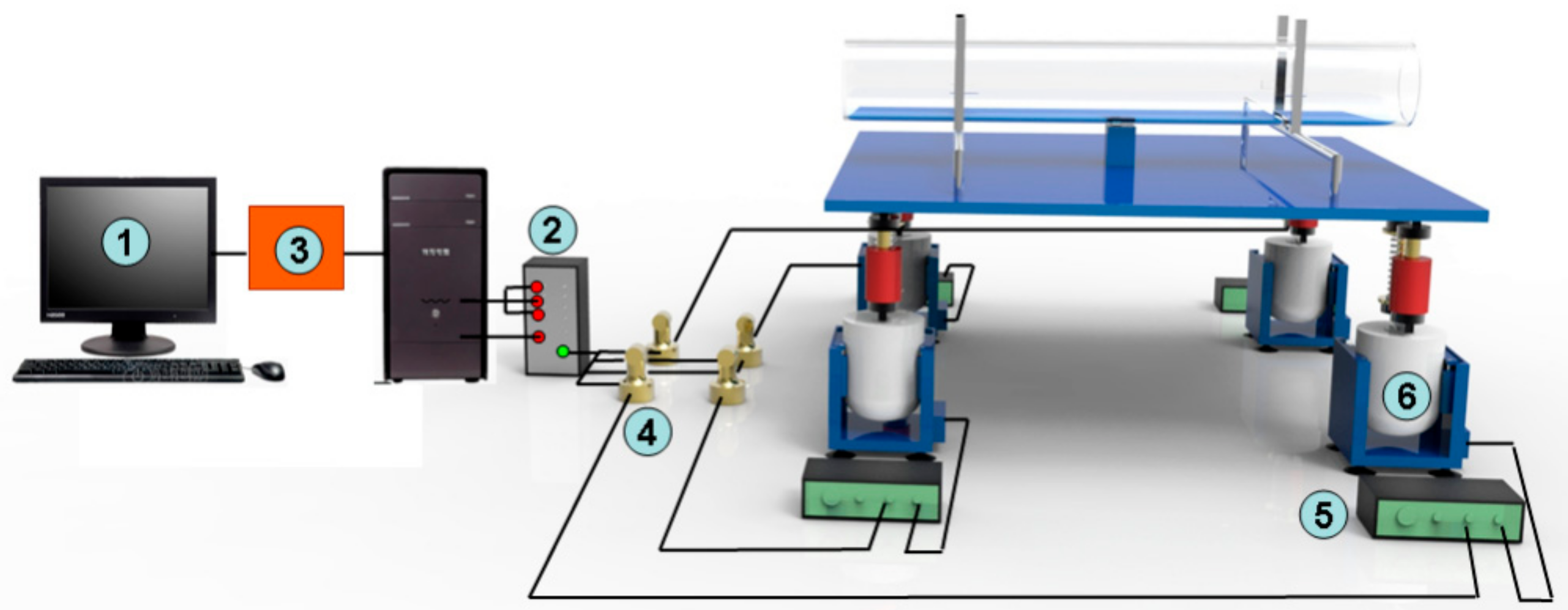
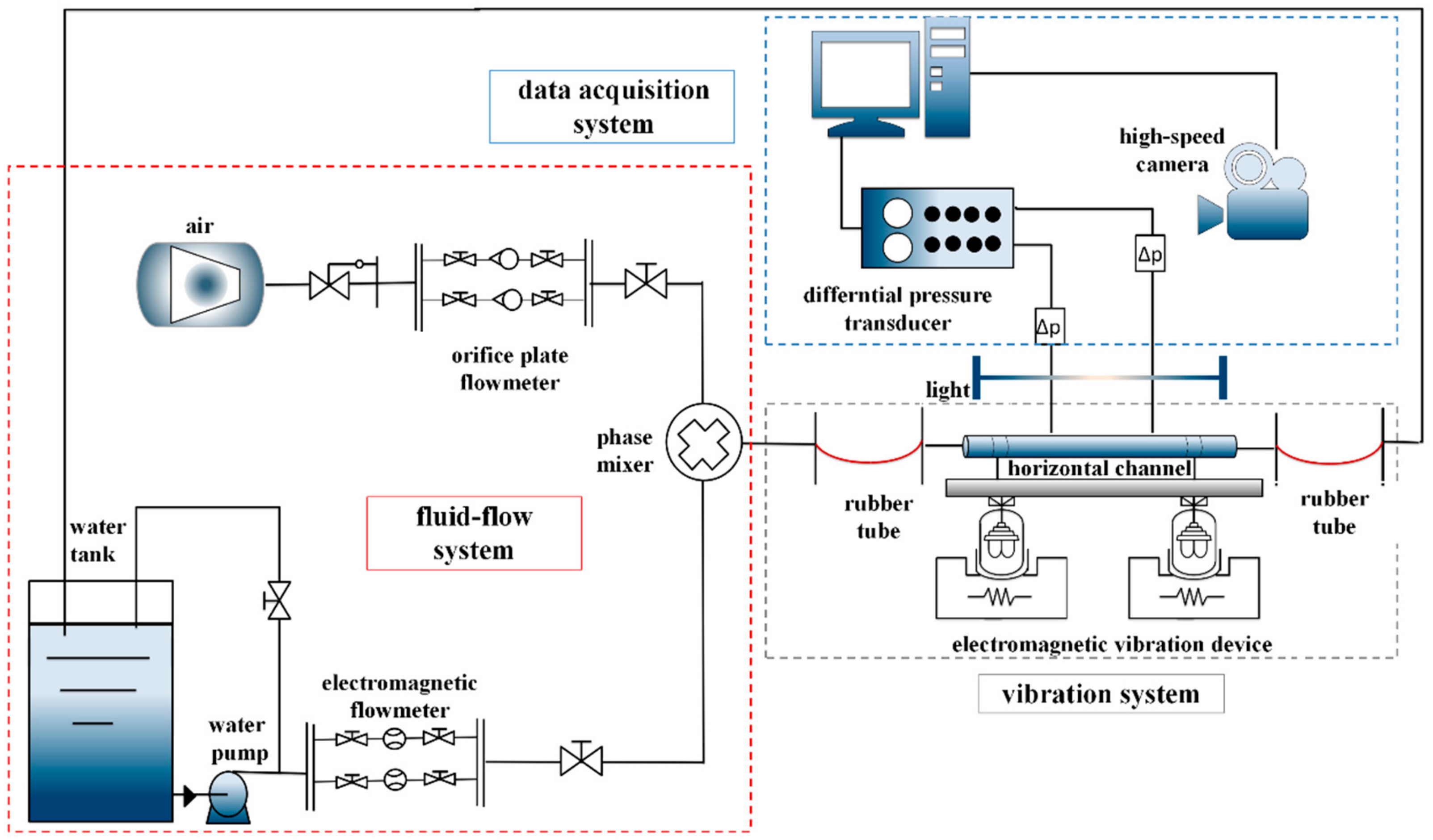
2. Experimental Setup
2.1. Vibration Platform
2.2. Experimental Loop
2.3. Instrumentations
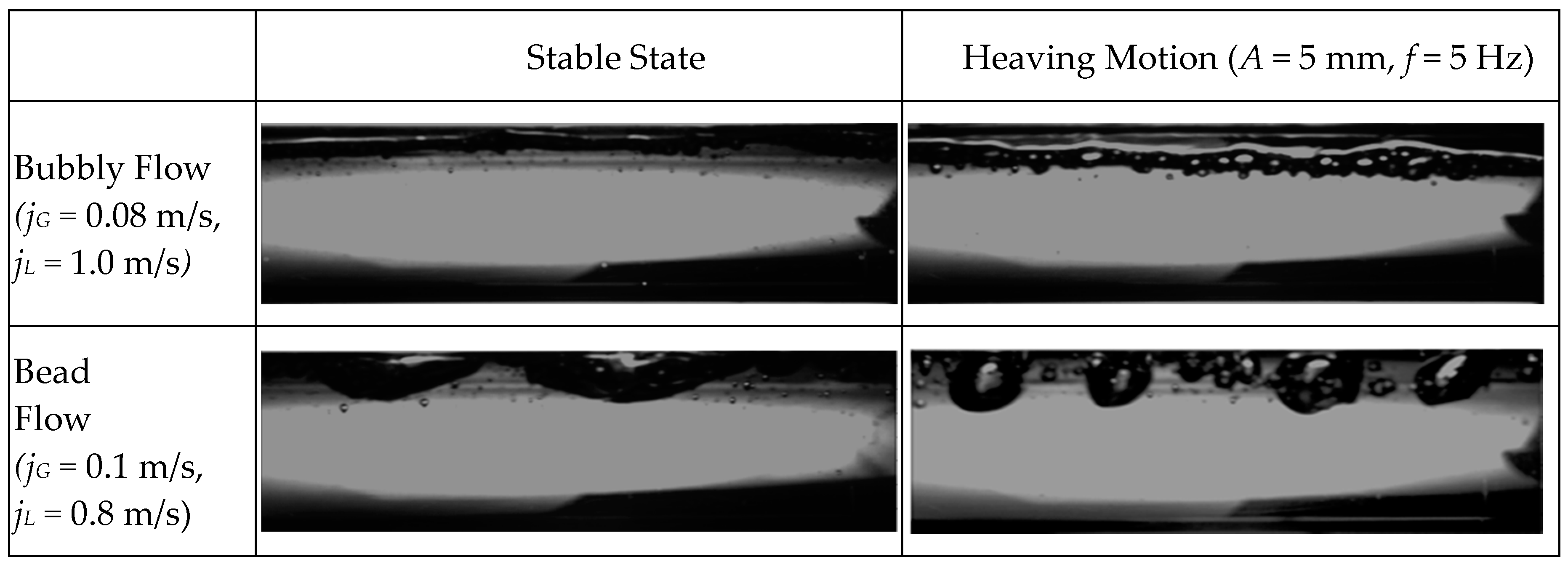
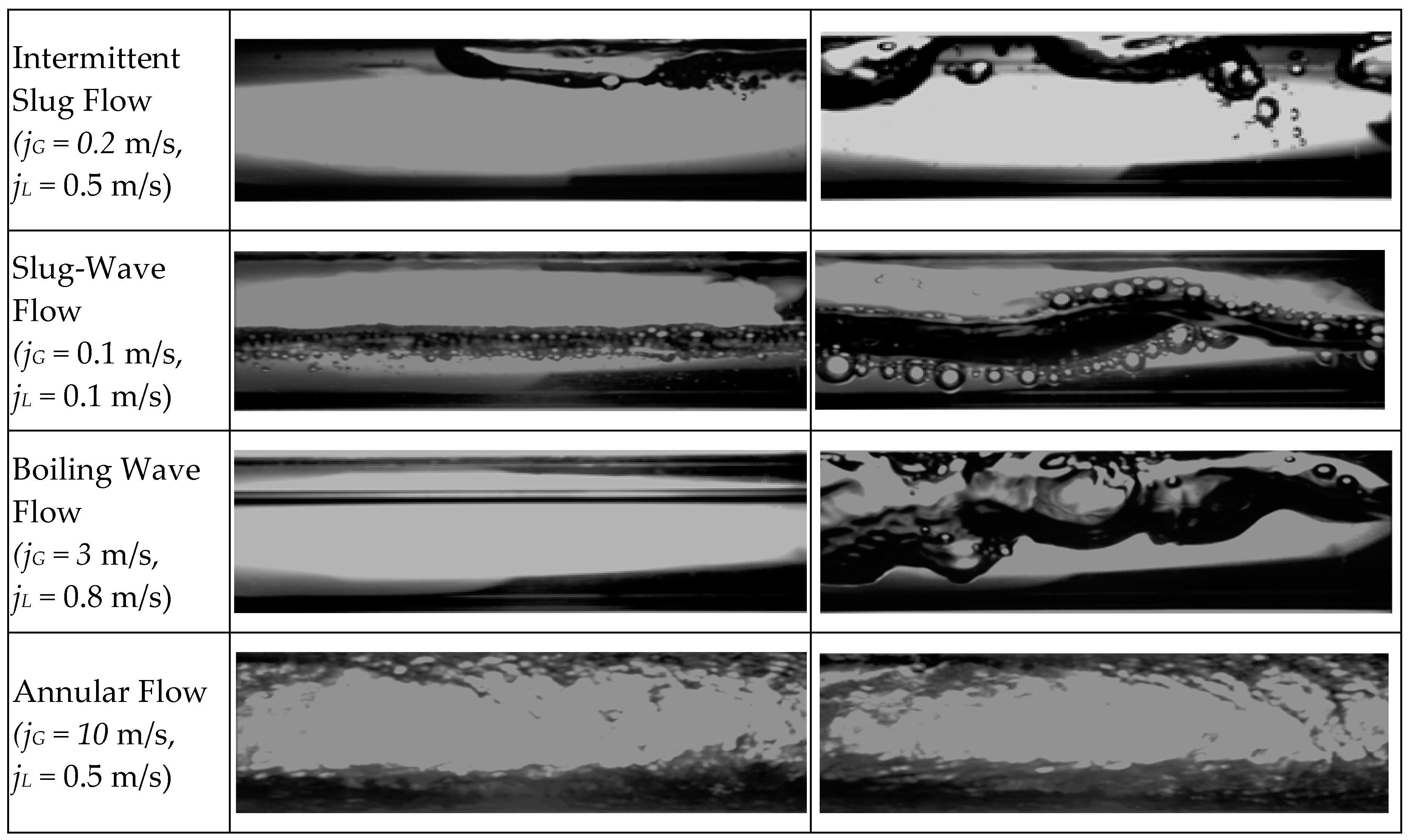
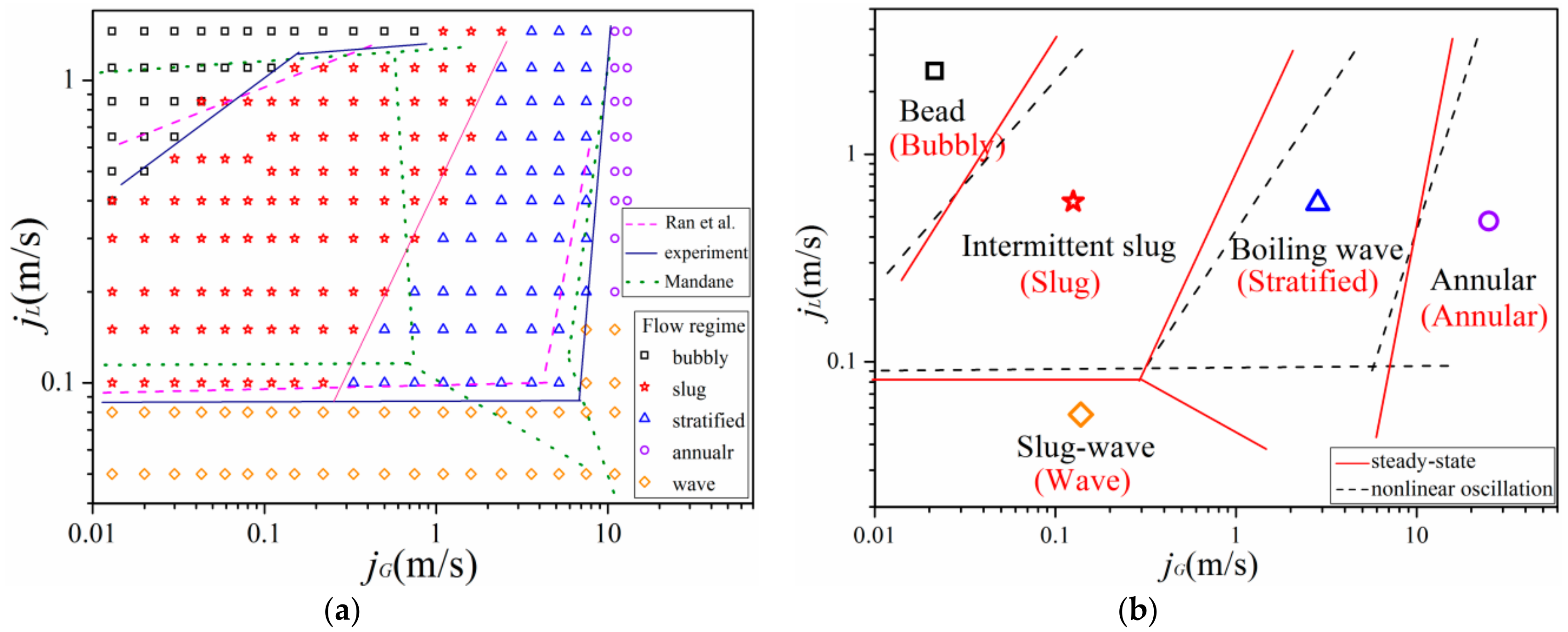
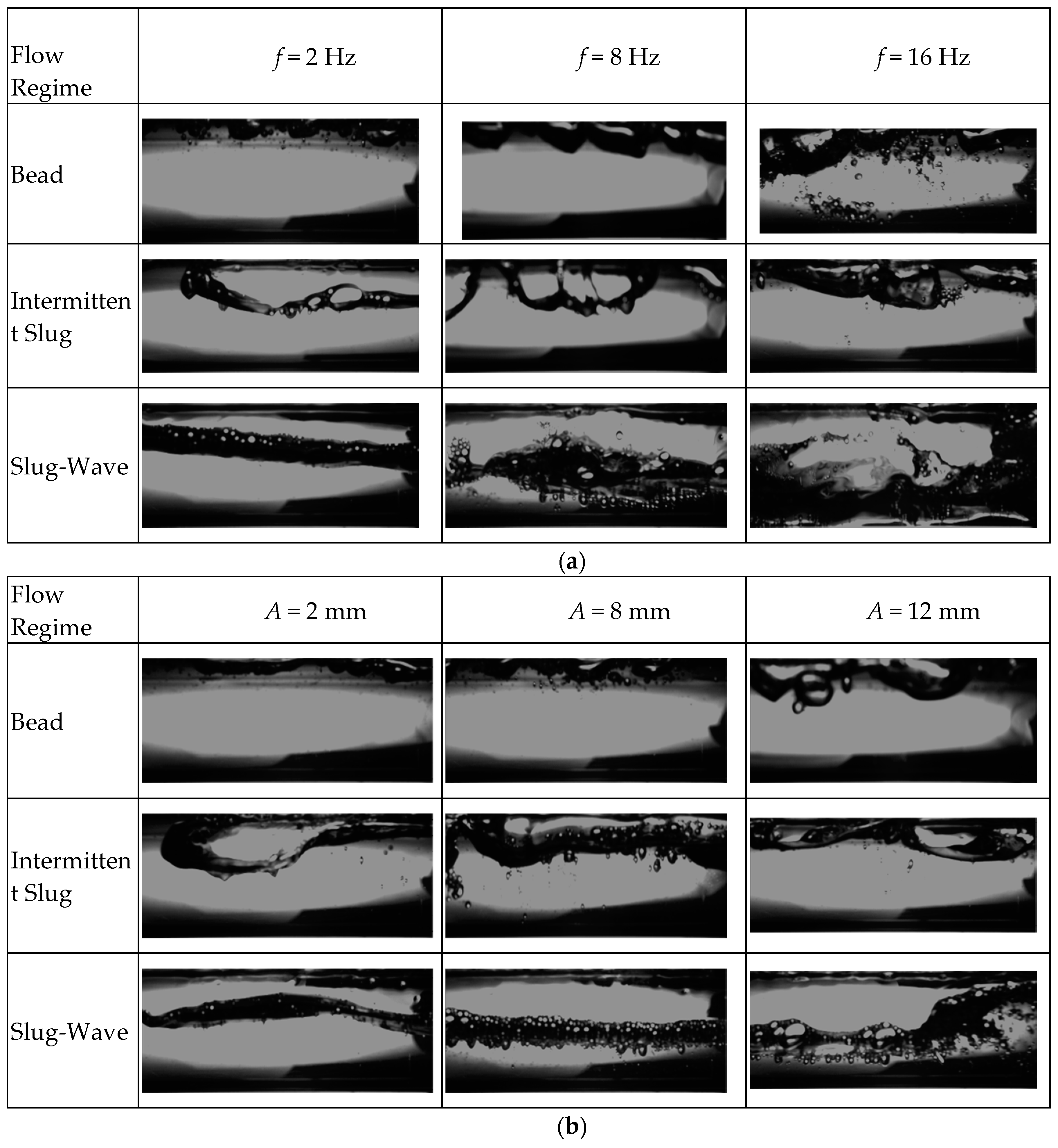
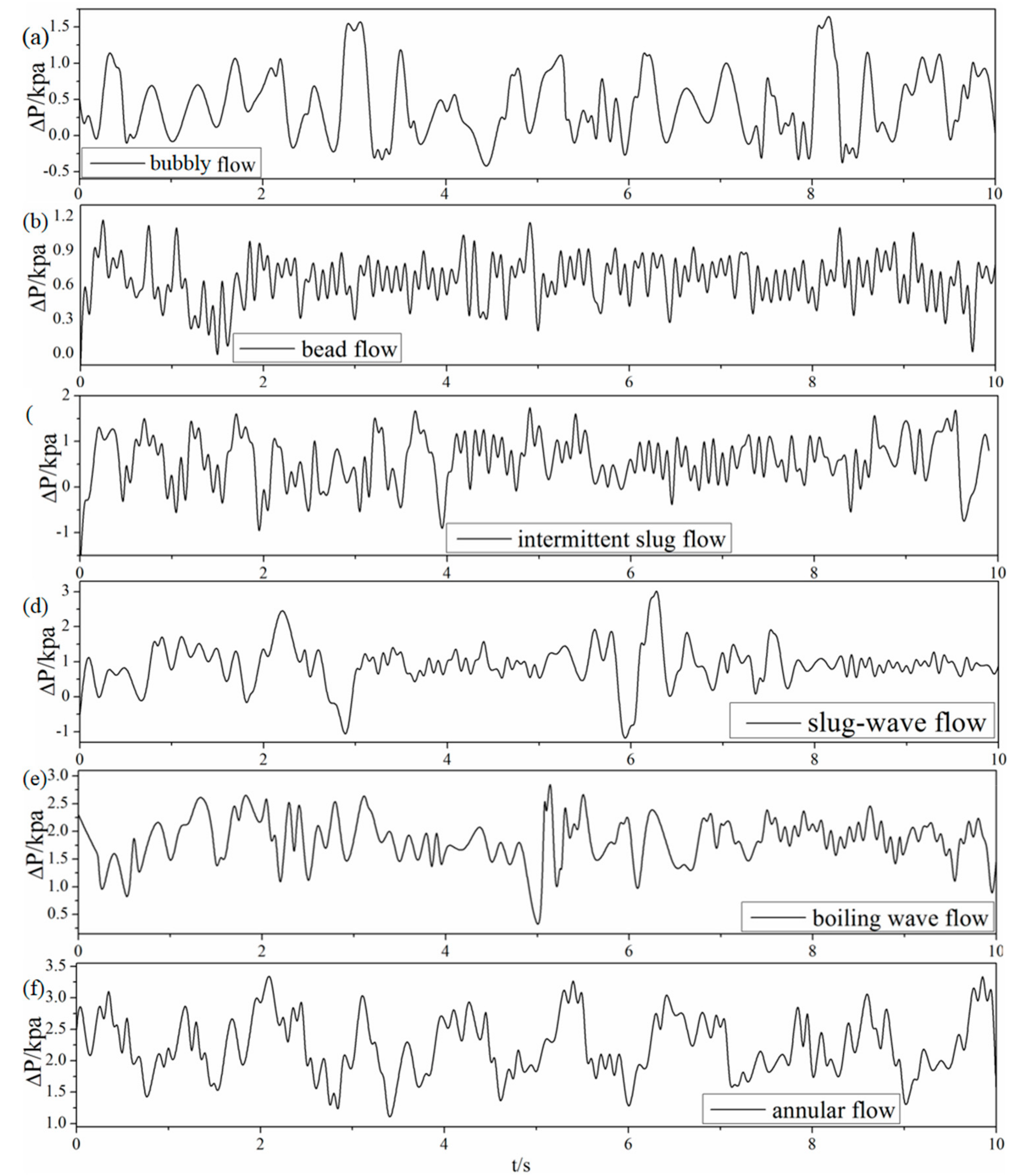
2.4. Experimental Results
3. Analysis of Flow Pattern Based on Multi-Scale Entropy
3.1. Theory Basis
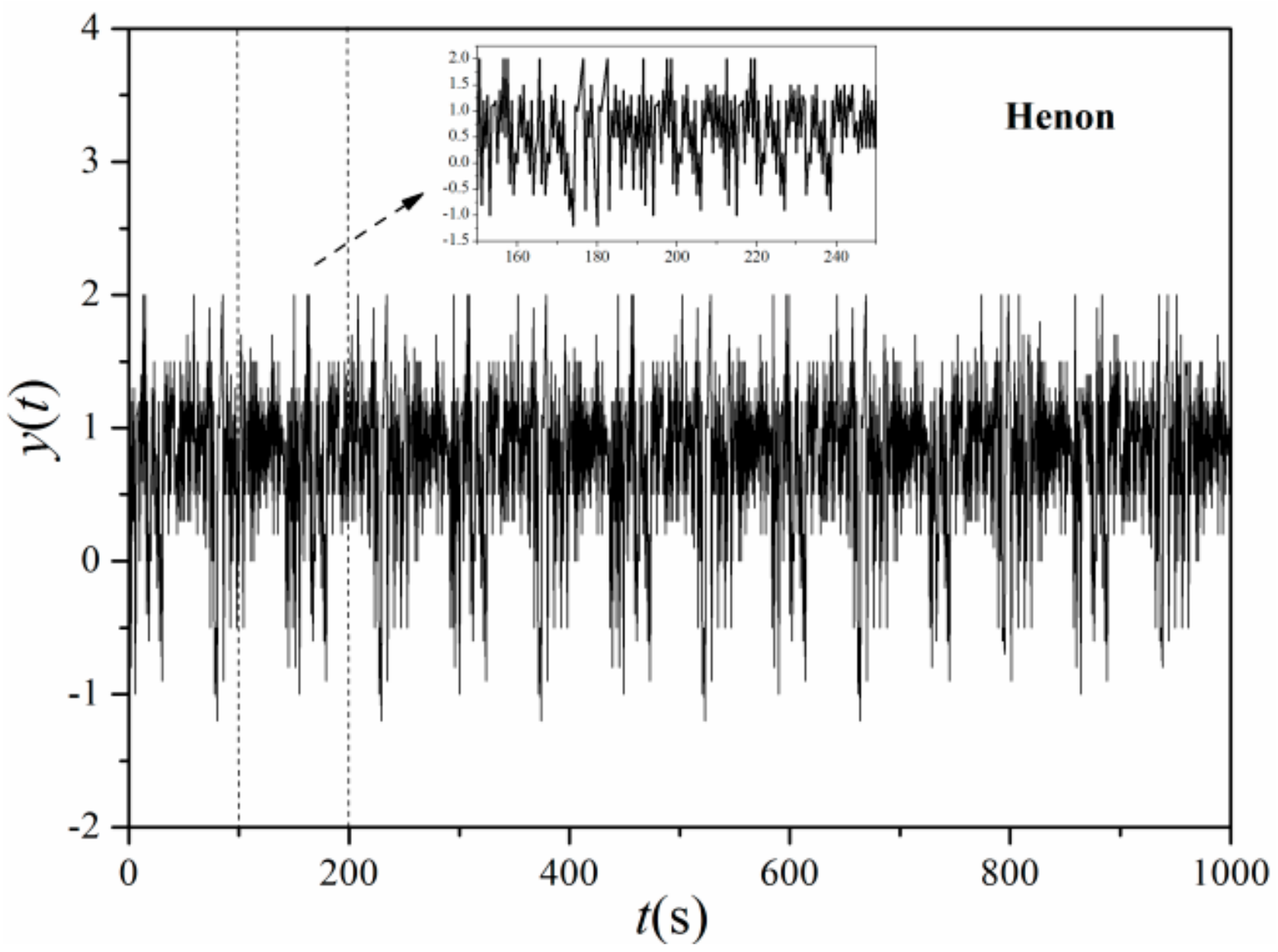
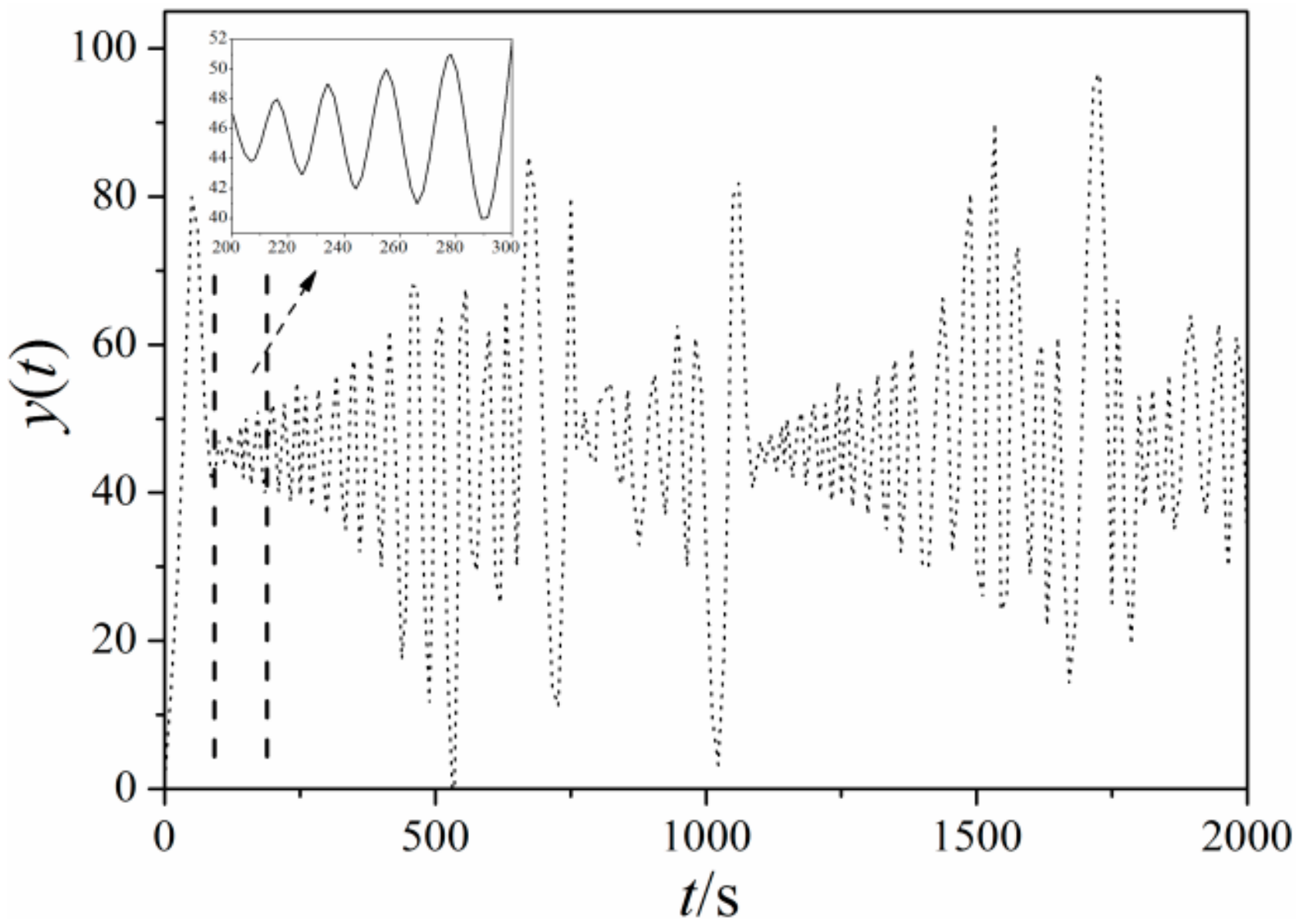
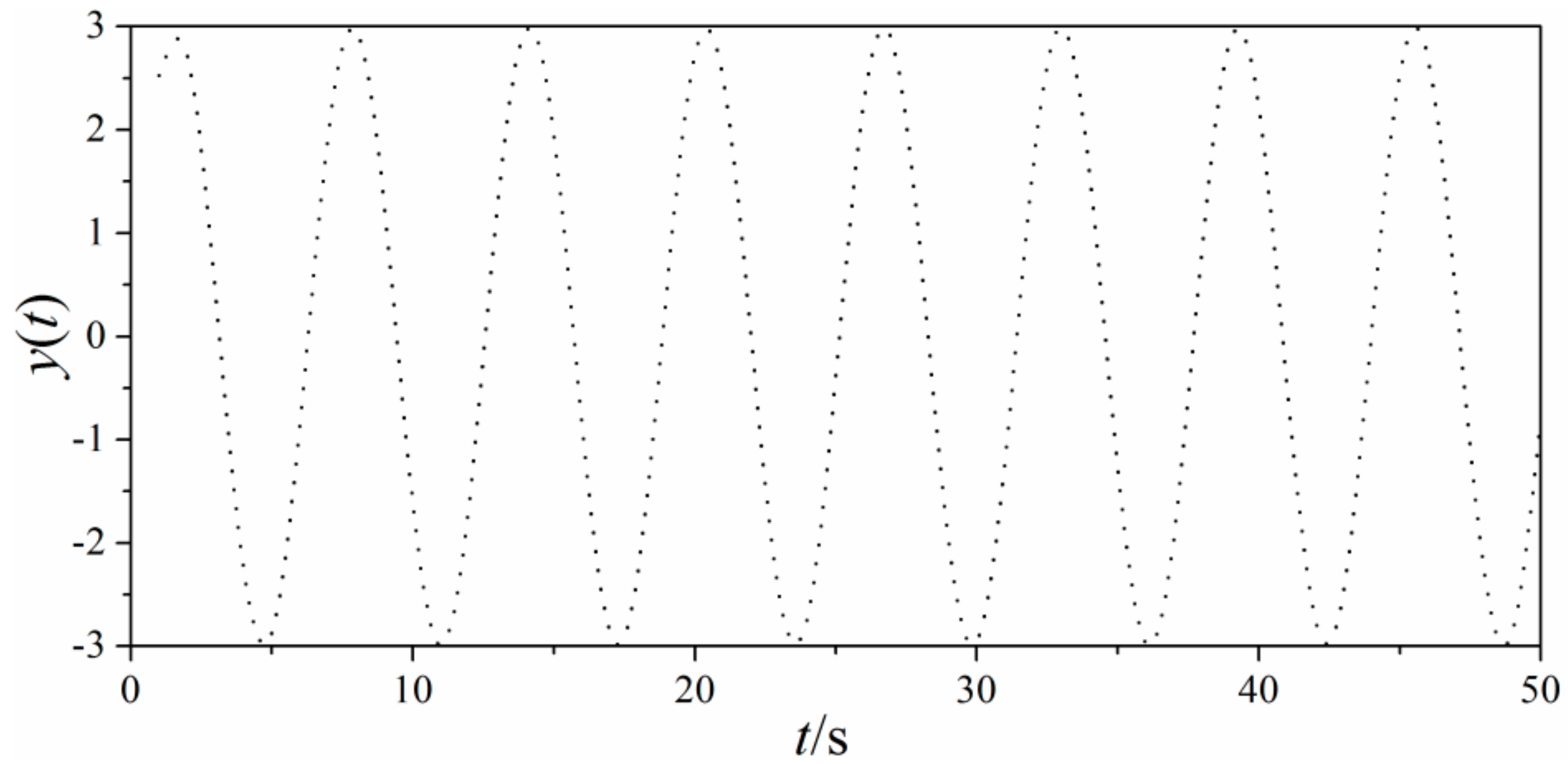
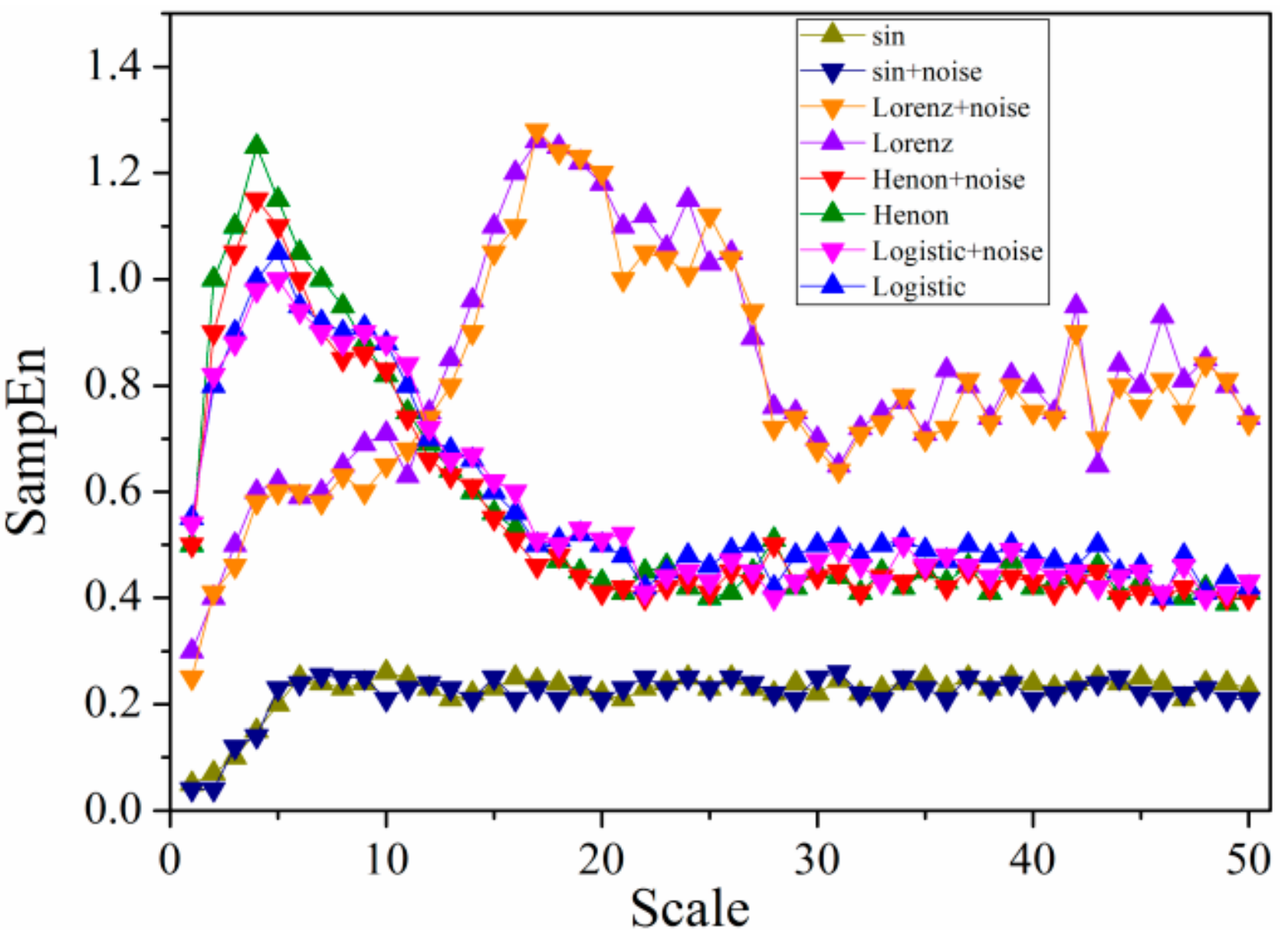
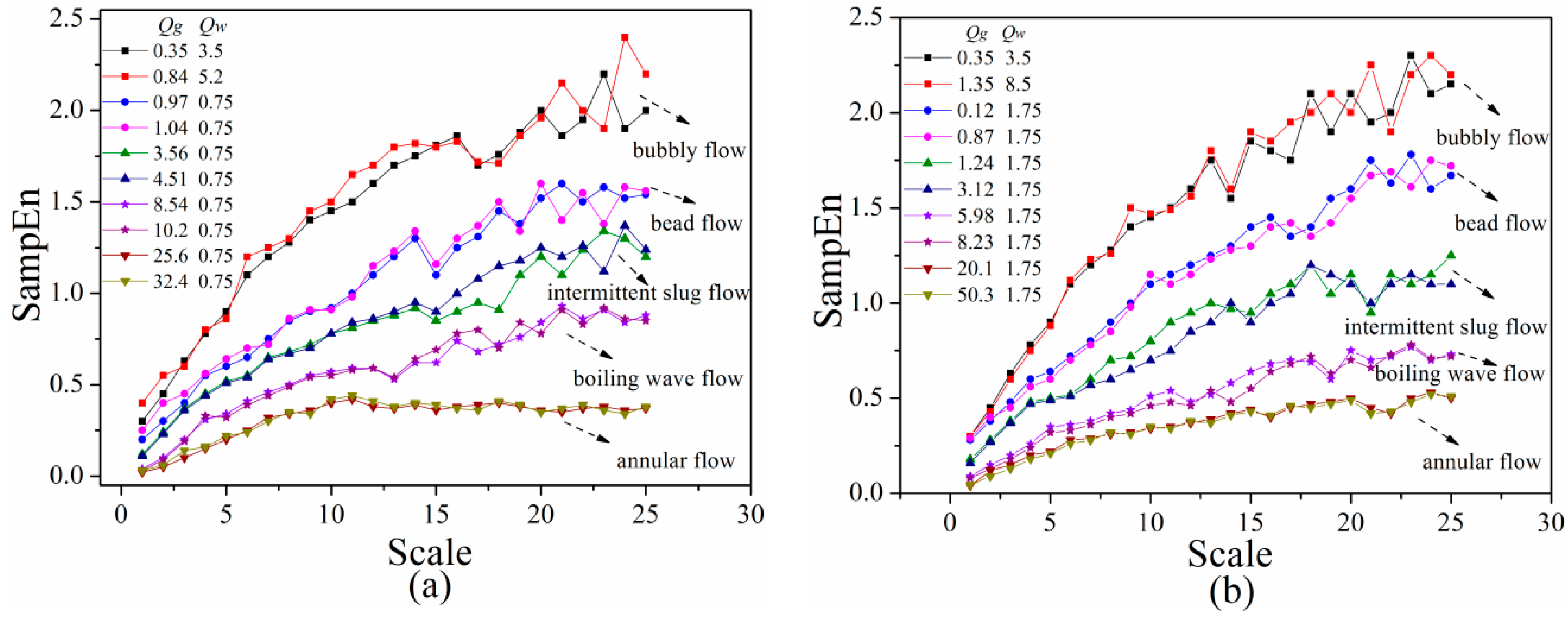
3.2. Multi-Scale Entropy of Typical Signals
3.3. Analysis of Flow Characteristics
3.3.1. Frequency Analysis of Differential Pressure Signal
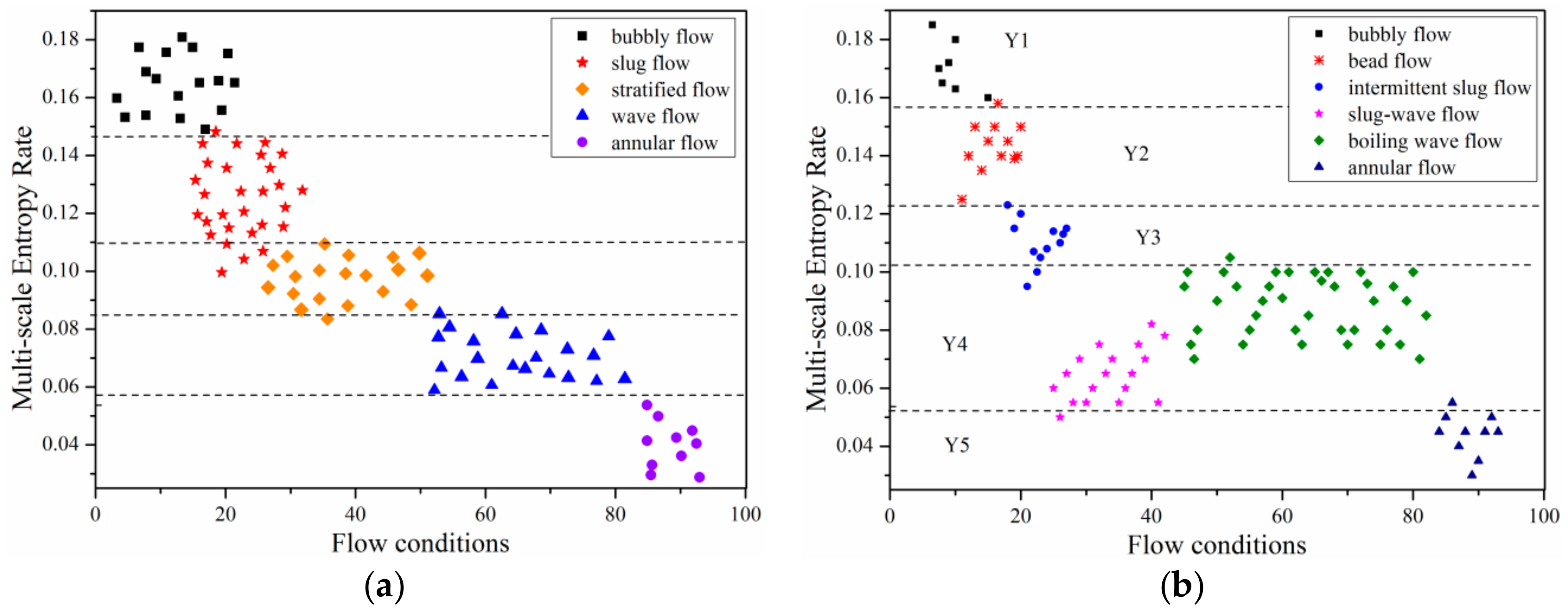
3.3.2. Analysis of Flow Patterns
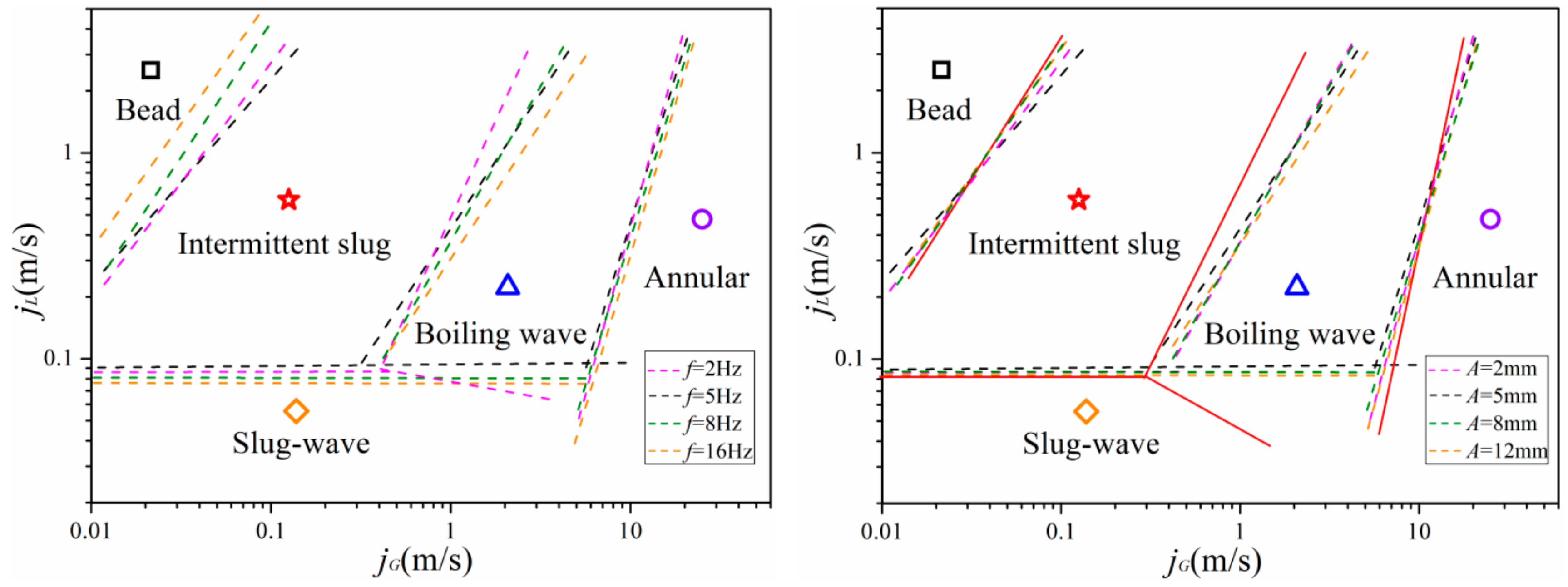
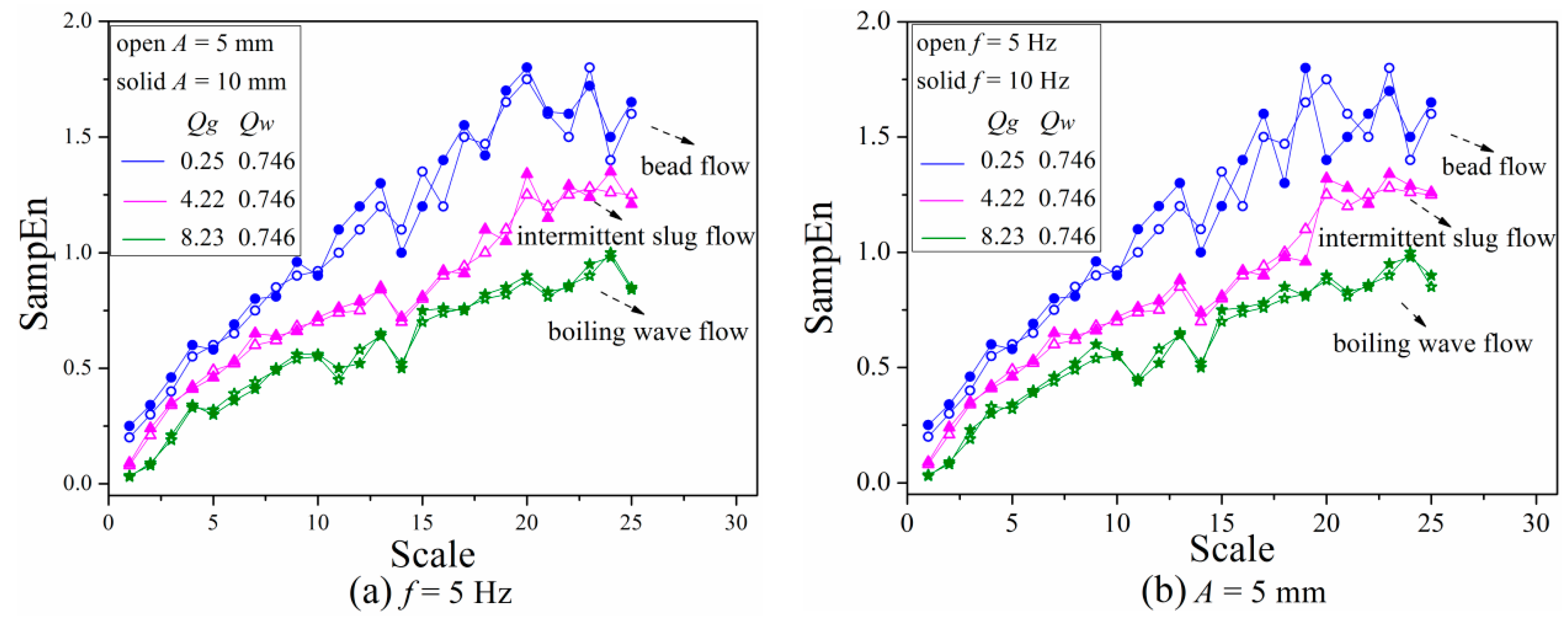
3.3.3. Analysis of Flow Patterns with Different Vibration Parameters
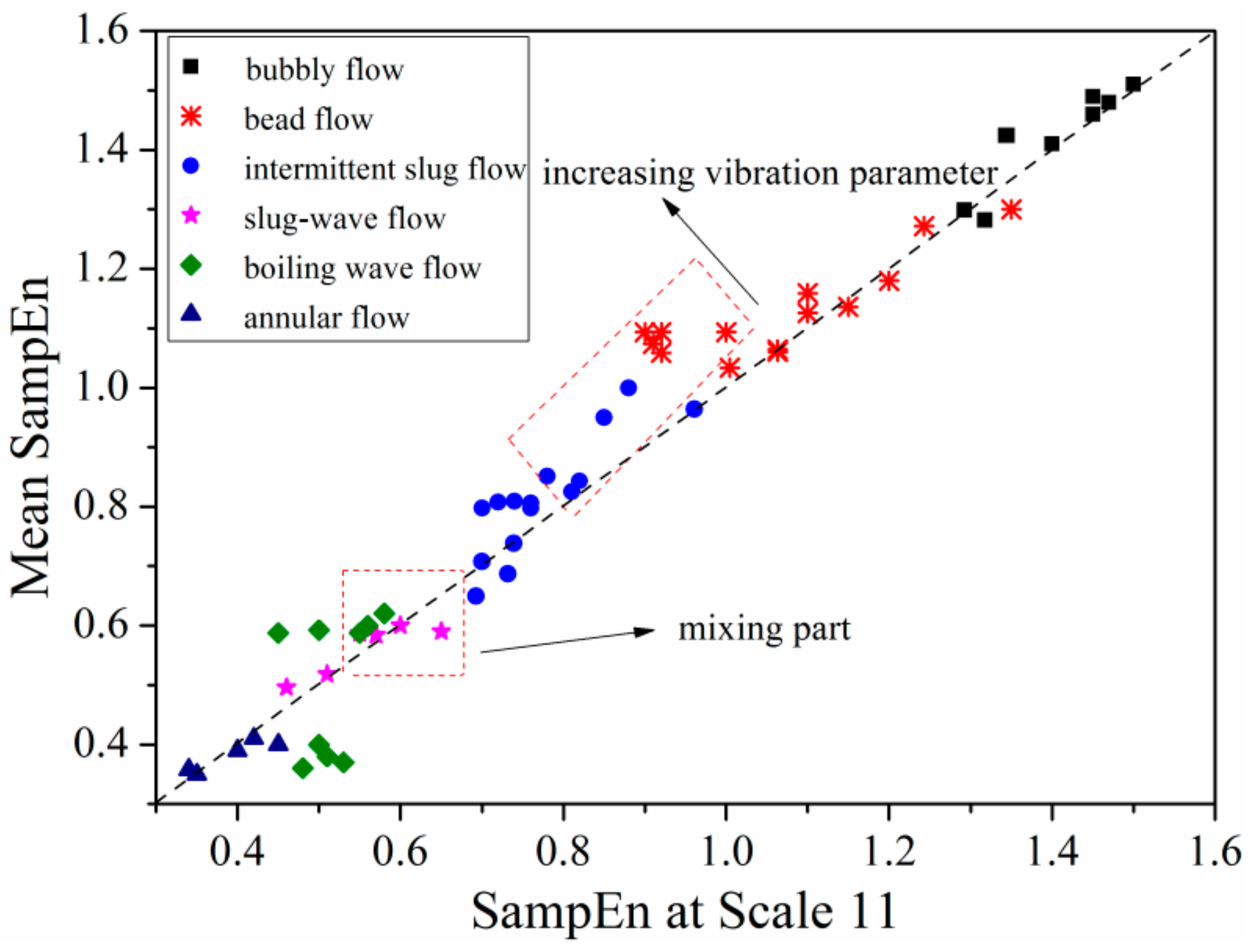
3.4. Flow Pattern Separation
4. Analysis of Flow Pattern Based on Multi-Scale Marginal Spectrum Entropy
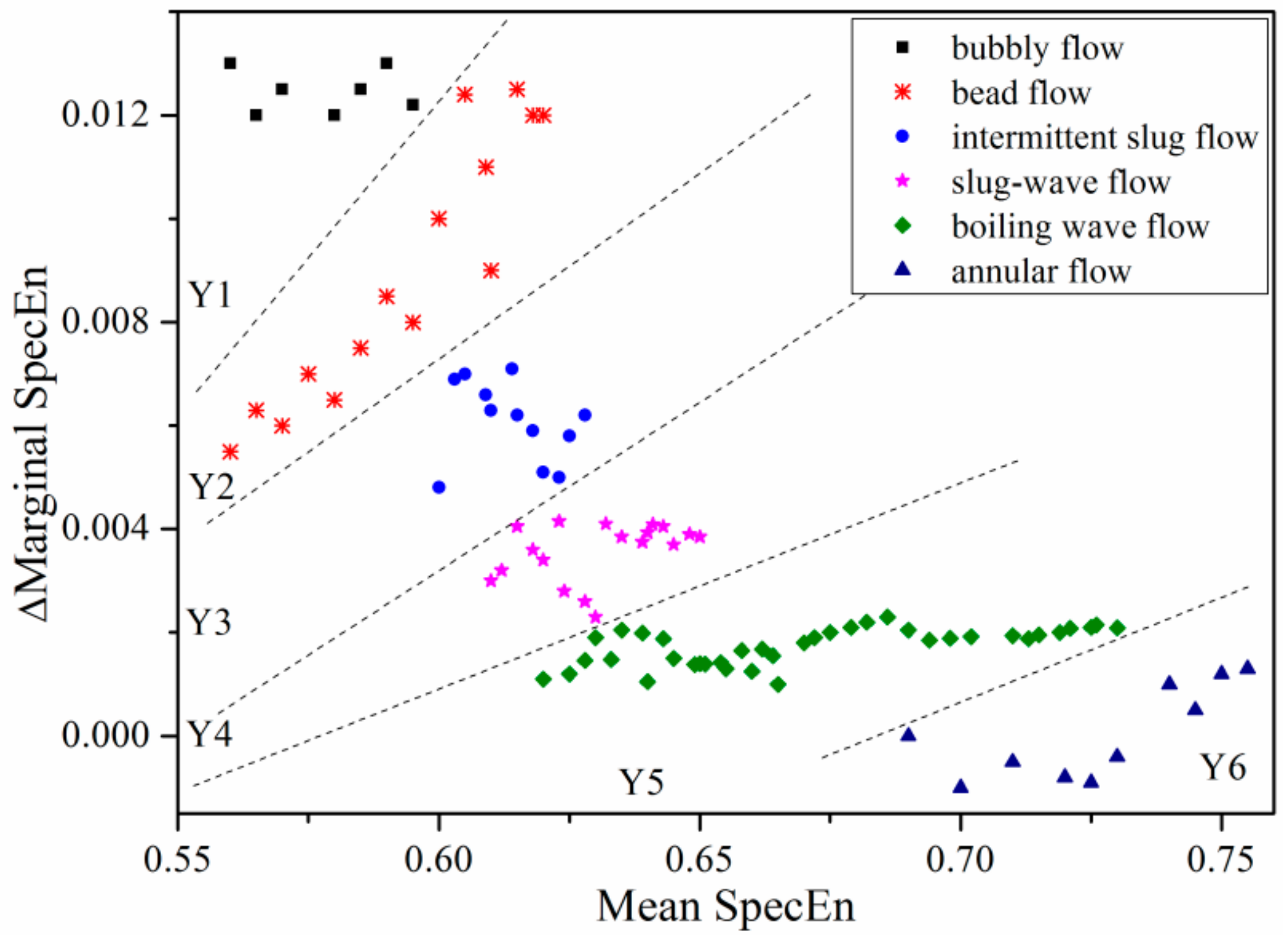
4.1. Theory Basis
4.2. Flow Pattern Separation
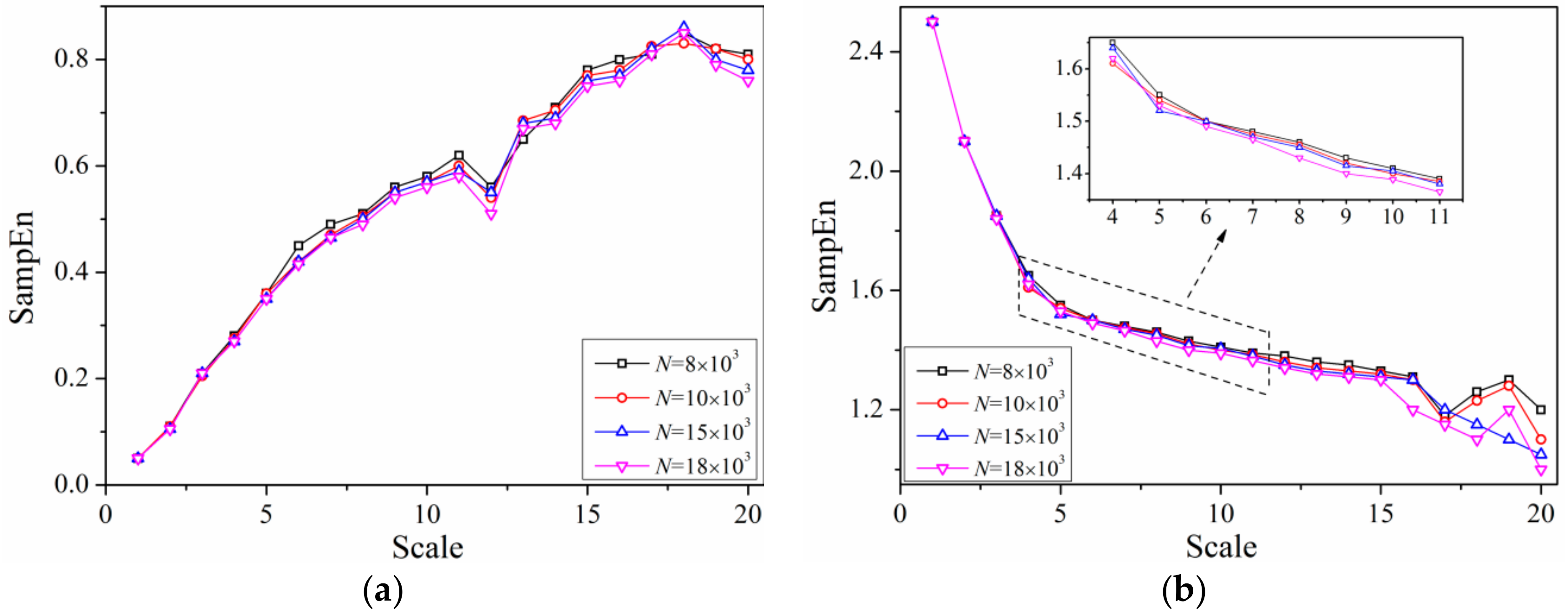
5. Error Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brook, B.W.; Alonso, A.; Meneley, D.A.; Misak, J. Why nuclear energy is sustainable and has to be part of the energy mix. Sustain. Mater. Technol. 2014, 1–2, 8–16. [Google Scholar] [CrossRef]
- Ishida, I.; Kusunoki, T.; Murata, H. Thermal-hydraulic behavior of a marine reactor during oscillations. Nucl. Eng. Des. 1990, 120, 213–225. [Google Scholar] [CrossRef]
- Ishida, I.; Kusunoki, T.; Ochiai, M. Effects by sea wave on thermal hydraulics of marine system. Nucl. Eng. Des. 1995, 32, 740–751. [Google Scholar] [CrossRef]
- Pendyala, R.; Jayanti, S.; Balakrishnan, A.R. Flow and pressure drop fluctuations in a vertical tube subject to low frequency oscillations. Nucl. Eng. Des. 2008, 238, 178–187. [Google Scholar] [CrossRef]
- Cao, X.X.; Yan, C.Q.; Sun, L.C. The transition analysis of air-water flow patterns in inclined pipe. Nucl. Sci. Eng. 2005, 25, 45–49. [Google Scholar]
- Islam, A.; Sun, A.; Sepehrnoori, K. An Efficient Computational Scheme for Two-Phase Steam Condensation in the Presence of CO2 for Wellbore and Long-Distance Flow. Chem. Eng. 2019, 3, 4. [Google Scholar] [CrossRef]
- Xing, D.; Yan, C.; Sun, L.; Jin, G.; Tan, S. Frictional resistance of adiabatic two-phase flow in narrow rectangular duct under rolling condition. Ann. Nucl. Energy 2013, 53, 109–119. [Google Scholar] [CrossRef]
- Xing, D.; Yan, C.; Sun, L.; Liang, L.; Zan, Y. A theoretical analysis about the mechanism of the effect of rolling motion on single-phase flow resistance in rectangular duct. Prog. Nucl. Energy 2014, 74, 53–60. [Google Scholar] [CrossRef]
- Li, S.; Tan, S.; Xu, C.; Gao, P. Visualization study of bubble behavior in a subcooled flow boiling channel under rolling motion. Ann. Nucl. Energy 2016, 76, 390–400. [Google Scholar] [CrossRef]
- Li, H.W.; Zhou, Y.L.; Sun, B. Multi-scale chaotic analysis of the characteristics of gas-liquid two-phase flow patterns. Chin. J. Chem. Eng. 2010, 18, 880–888. [Google Scholar] [CrossRef]
- Bai, B.F.; Zhang, S.J.; Zhang, X.M.; Guo, L.J. Online recognition of the multiphase flow regime. Sci. China Technol. Sci. 2008, 51, 1186–1194. [Google Scholar] [CrossRef]
- Du, M.; Jin, N.D.; Gao, Z.K.; Sun, B. Analysis of tatal energy and time-frequency entropy of gas-liquid two-phase flow pattern. Chem. Eng. Sci. 2012, 82, 144–158. [Google Scholar] [CrossRef]
- Xu, C.; Liang, C.; Zhou, B.; Wang, S. HHT analysis of electrostatic fluctuation signals in dense-phase pneumatic conveying of pulverized coal at high pressure. Chem. Eng. Sci. 2010, 65, 1334–1344. [Google Scholar] [CrossRef]
- Tuan, D.P.; Yan, H. Spatial-dependence recurrence sample entropy. Phys. Rev. A 2018, 494, 581–590. [Google Scholar]
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Zhuang, J.J.; Ningm, X.B. Agreement of two entropy-based measures on quantifying the complexity of short-term heart rate variability signals from professional shootersm. Acta Phys. Sin. 2008, 57, 2805–2811. [Google Scholar]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multi-scale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multi-scale entropy analysis of biological signals. Pyhs. Rev. A 2005, 71, 021906. [Google Scholar]
- Chen, S.W.; Liu, Y.; Hibiki, T. Experimental study of air-water two-phase flow in an 8×8 rod bundle under pool condition for one-dimensional drift0flux analysis. Int. J. Heat Fluid Flow 2012, 33, 168–181. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Hou, Y.D.; Li, H.W. Flow pattern map and multi-scale entropy analysis in 3×3 rod bundle channel. Ann. Nucl. Energy 2015, 80, 144–150. [Google Scholar] [CrossRef]
- Li, H.W.; Zhou, Y.L.; Yang, Y. Time-frequency characteristics of smoothed Winger tri-spectrum slices of nitrogen-water two-phase flow patterns. CIESC J. 2013, 64, 3571–3580. [Google Scholar]
- Tan, C.; Zhao, J.; Dong, F. Gas-water two-phase flow characterization with electrical resistance tomography and multivariate multi-scale entropy analysis. ISA Trans. 2015, 55, 241–249. [Google Scholar] [CrossRef] [PubMed]
- Deabes, W.A.; Abdelrahman, M.A. A nonlinear fuzzy assisted image reconstruction algorithm for electrical capacitance tomography. ISA Trans. 2010, 49, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.L.; Fu, Z.T.; Yuan, N.M. Beyond Benford’s law: Distinguishing noise from chaos. PLoS ONE 2015, 10, e0129161. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.P. Performance comparison research of various chaotic systems. Microcomput. ITS Appl. 2016, 35, 4–9. [Google Scholar]
- Zhou, Y.L.; Li, S.S. Multi-scale entropy analysis of two-phase flow in inclined pipe under vibration condition. J. Chem. Ind. Eng. 2018, 69, 1884–1891. [Google Scholar]
- Zhou, Y.L.; Chang, H.; Qi, T.Y. Gas-liquid two phase flow in serpentine microchannel with different wall wettability. Chin. J. Chem. Eng. 2017, 25, 874–881. [Google Scholar] [CrossRef]
- Ran, K.; Kim, S.; Bajorek, S.; Tien, K.; Hoxie, C. Effects of pipe size on horizontal two-phase flow: Flow regimes, pressure drop, two-phase flow parameters, and drift-flux analysis. Exp. Therm. Fluid Sci. 2018, 96, 75–89. [Google Scholar] [CrossRef]
- Mandhane, J.M.; Gregory, G.A.; Aziz, K. A flow pattern map for gas-liquid flow in horizontal pipes. Int. J. Multiph. Flow 1974, 1, 537–553. [Google Scholar] [CrossRef]
- Zhu, L.; Jin, N.D.; Gao, Z.K.; Zhong, Y.B. Multi-scale cross entropy analysis for inclined oil-water two-phase countercurrent flow patterns. Chem. Eng. Sci. 2011, 66, 6099–6108. [Google Scholar] [CrossRef]
- Zheng, G.B.; Jin, N.D. Multi-scale entropy and dynamic characteristics of two-phase flow patterns. Acta Phys. Sin. 2009, 58, 4485–4492. [Google Scholar]
- Henon, M.; Heiles, C. The applicability of the third integral of motion: Some numerical experimens. Astron. J. 1964, 69, 73–79. [Google Scholar] [CrossRef]
- Gao, Z.K.; Jin, N.D. Complex network community structure of two-phase flow pattern and its statistical characteristics. Acta Phys. Sin. 2008, 57, 2567–2573. [Google Scholar]
- Li, H.W.; Hao, P.F.; Yang, D.; Sun, B.; Zhou, Y.L. Analysis of the dynamic characteristics of air-water two-phase flow in small channel based on multi-scale normalized Benford probability distribution. Chem. Eng. Sci. 2018, 179, 161–171. [Google Scholar] [CrossRef]
| Parameter | ETS MPA101A/L215M |
|---|---|
| Rated thrust peak | 1964.33 n |
| Rated peak ground acceleration | 100.034 g |
| Rated peak velocity | 2 m/s |
| Rated displacement peak | 25.4 mm |
| Vibration frequency | 2.00~4500 Hz |
| Maximum input voltage of amplifier | 10 V |
| Equivalent mass of moving parts | 2 kg |
| Total load | 2 kg |
| ΔSampEn | Bead Flow | Fluctuant-Slug Flow | Boiling-Wave Flow | Annular Flow | |
|---|---|---|---|---|---|
| scale 0–14 | Qw = 0.75 | 0.780 | 0.610 | 0.412 | 0.254 |
| Qw = 1.75 | 0.833 | 0.620 | 0.363 | 0.264 | |
| Scale 15–25 | Qw = 0.75 | 1.430 | 1.129 | 0.806 | 0.373 |
| Qw = 1.75 | 1.545 | 1.088 | 0.691 | 0.464 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Chang, H.; Zhou, Y.-L. Flow Regime Recognition and Dynamic Characteristics Analysis of Air-Water Flow in Horizontal Channel under Nonlinear Oscillation Based on Multi-Scale Entropy. Entropy 2019, 21, 667. https://doi.org/10.3390/e21070667
Sun B, Chang H, Zhou Y-L. Flow Regime Recognition and Dynamic Characteristics Analysis of Air-Water Flow in Horizontal Channel under Nonlinear Oscillation Based on Multi-Scale Entropy. Entropy. 2019; 21(7):667. https://doi.org/10.3390/e21070667
Chicago/Turabian StyleSun, Bo, He Chang, and Yun-Long Zhou. 2019. "Flow Regime Recognition and Dynamic Characteristics Analysis of Air-Water Flow in Horizontal Channel under Nonlinear Oscillation Based on Multi-Scale Entropy" Entropy 21, no. 7: 667. https://doi.org/10.3390/e21070667
APA StyleSun, B., Chang, H., & Zhou, Y.-L. (2019). Flow Regime Recognition and Dynamic Characteristics Analysis of Air-Water Flow in Horizontal Channel under Nonlinear Oscillation Based on Multi-Scale Entropy. Entropy, 21(7), 667. https://doi.org/10.3390/e21070667




