1. Introduction
Dry sliding friction is a universal phenomenon observed at the scales ranging from nano-newtons to billions of tons for all classes of materials (polymers, metals, ceramics, composites, etc.) and their combinations. However, the way of how friction is treated in physics is far from general or universal. The so-called Amontons–Coulomb laws of dry friction were formulated by the 18th century, and they describe a theory which is referred to as “the Coulomb friction.” These laws state that the friction force between two contacting bodies,
F, is independent of the nominal area of contact, sliding velocity, and that
F is linearly proportional to the normal force,
W, acting between the two bodies. In the form of an equation this is formulated as
where
μ is the coefficient of friction (COF), which is independent of the normal force, sliding velocity, and the nominal area of contact between the bodies.
The physical foundations of the Coulomb friction theory have been discussed and criticized in literature [
1], while various modifications of the friction laws have been suggested including, for instance, the rate-and-state models with internal variables [
2] or the “friction is fracture” concept [
3]. However, the Coulomb law in the form of Equation (1) and its version for the normal and shear stress components,
τxy =
μσyy, still remain the most common way to introduce friction into mechanical analysis of both rigid and deformable systems.
Usually, the Amontons–Coulomb laws of dry friction are introduced in an ad hoc manner, without any justification from the deeper principles of physics, although some attempts to either derive the laws of friction from more fundamental principles, such as the second law of thermodynamics or principles of brittle fracture are sometimes introduced. However, in most textbooks the Amontons–Coulomb laws are treated as approximate empirical rules rather than exact laws of nature.
Due to this ambiguous status of friction in physics—universal on the one hand and unrelated to the fundamental principles of physics on the other hand—and despite the successful application of the Amontons–Coulomb friction laws, combining friction with the rest of mechanics and physics involves a number of interesting logical paradoxes. The best-known family of frictional paradoxes are the Painlevé paradoxes involving rigid (non-deformable) bodies [
4,
5,
6,
7,
8,
9,
10,
11]. When a solution of equations of motion with friction is obtained, it may turn out that the assumed direction of the friction force contradicts the direction of the velocities in the system, therefore resulting in a paradox. The Painlevé paradox indicates that the Coulomb friction is not always logically compatible with the rest of the equations of mechanics. The differential equations of motion in mechanics are supposed to have a unique solution corresponding to any reasonable set of initial conditions. However, a system with the paradox either has no solution or it has more than one solution.
The original 1885 publication by Painlevé [
12] caused a long discussion, in which participated prominent physicists and mechanicians such as L. Prandtl, F. Klein, R. Von Mises, and Lecornu. L. Lecornu [
13,
14] suggested abandoning the model of the absolute rigid body, while F. Klein [
15] insisted that the Coulomb friction is not in contradiction neither with principles of mechanics nor with the phenomena observable in nature, and Von Mises stated that the methodology of Newtonian mechanics compels us to modify the Coulomb law [
16].
There is significant literature about the nature of the Painlevé paradox and various approaches to resolve it [
17,
18]. These approaches typically modify the law of friction [
19] by suggesting a non-Coulombian friction law, e.g., velocity dependent [
4], or they consider deformable bodies instead of rigid ones [
5,
6,
7]. Some approaches concentrate on computational schemes, including the use of Convex Analysis [
8] and the variational inequality approaches [
9]. The relationship of the Painlevé paradoxes to other mathematical problems, such as the linear complementary problem, has also been investigated [
10], as well as the relationship between the paradoxes to the friction-induced dynamic instabilities and self-excited vibrations [
11,
20].
Besides the Painlevé paradoxes, there are several other types of frictional paradoxes [
21,
22]. Some of these paradoxes emerge because in general the introduction of the compliance does not resolve the Painlevé paradoxes. Dynamic effects in elastically deformable systems lead to different types of frictional paradoxes with the assumed direction of sliding used for the Coulomb friction opposite to the resulting slip velocity [
21]. This suggests that the Coulomb friction is inconsistent not only with the rigid body dynamics, but also with the dynamics of the elastically deformable bodies.
In a formal logical sense, there are several ways of resolving logical paradoxes. One method is to introduce a multi-valued logic, in which the law of excluded middle does not apply, and unlike in the regular binary logic, logical variables can attain values beyond
true and
false. Note that different interpretations of the third truth value have been suggested including
unknown,
possible,
undefined,
half-true,
irrelevant, and
inconsistent [
23]. Despite that, ternary logic has been applied successfully to various problems ranging from computer science to oscillating chemical reactions [
24]. The idea that some parts of mechanics can be represented by means of pure symbolic logic has also been suggested, for example, by A. Zinov’ev [
25]. However, nowadays this idea is often connected to the paradigm of unconventional computing, according to which different natural systems have their different own symbolic logics [
26,
27]. Therefore, a three-valued symbolic logic can also be applied to mechanical problems with friction.
In this paper, we will discuss the application of ternary logic to the frictional paradoxes, its productivity for the analysis of mechanical problems, and how it can affect the fundamental mechanical concepts of “motion”, “rest”, and “stability”.
2. Examples of Frictional Paradoxes
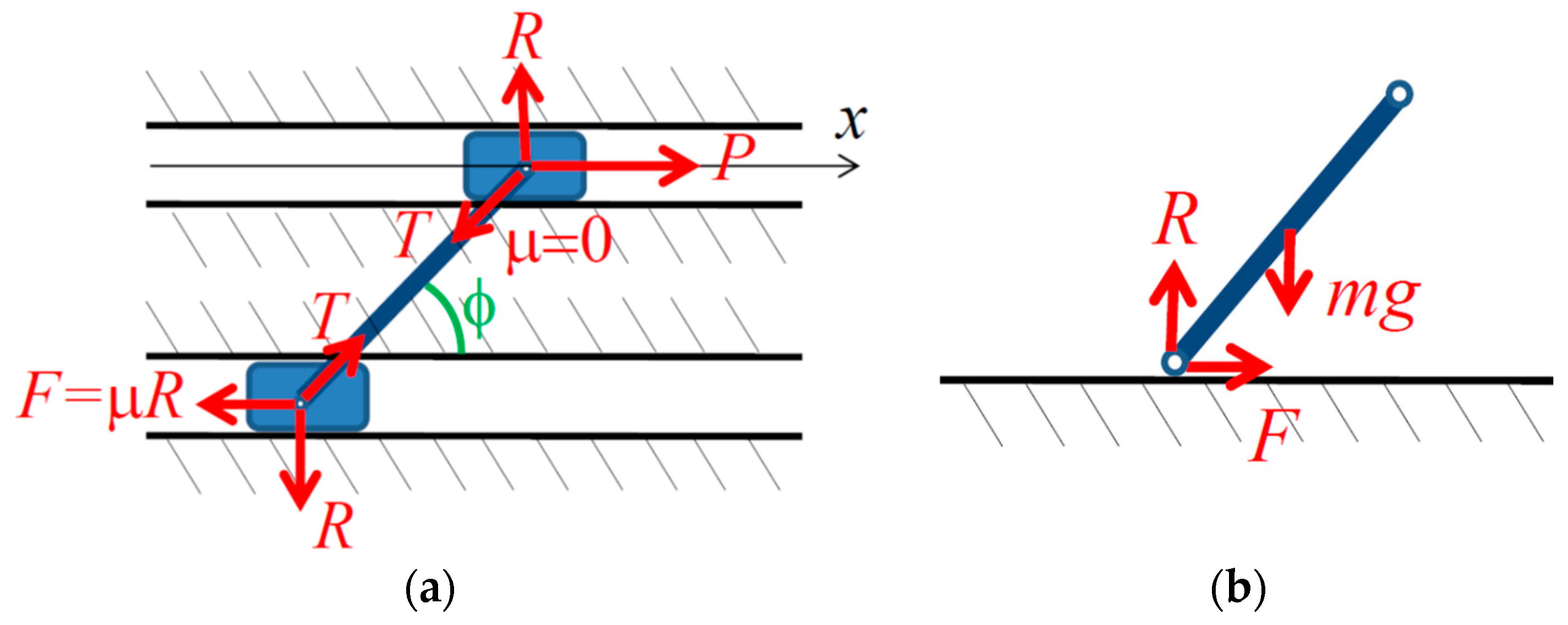
An example is in
Figure 1a, showing two sliders of equal mass
m connected by a rigid link with a constant length
l at an angle
with the sliding surface. The upper slider is frictionless while the lower slider is frictional with the COF
μ. An external positive force
P is applied to the upper slider. The normal force
R acts at the first slider, so that
T =
R/sin
is the tension/compression force in the link, and
is the friction force on the second slider. The motion of this system is governed by the equation
with two unknowns,
and
R, related by the equation of motion for the upper body,
. Note that for
P > 0,
,
, and the sign of
R depends on the sign of
, In order to solve Equation (2), one should assume a value of
. Substituting
into Equation (2) and we obtain four possible cases:
- (a)
If and then , which is possible only for (otherwise ).
- (b)
If and then .
- (c)
If and then , which contradicts .
- (d)
If and then , which is possible only for .
Therefore, two solutions (cases b and d) exist when and , one solution (case b) when and , one solution (case a) when and , and no solution when and .
A slightly different version of the paradox, close to the original problem studied by Painlevé in 1905 [
28], involves a rigid slender rod of mass
m in contact with a rigid surface and falling under gravity (
Figure 1b).
3. Ternary Logic of Motion and Rest
The Painlevé paradox indicates that the Coulomb friction is not always logically compatible with the rest of the equations of mechanics. To express this situation in a formal manner, we can introduce a logical predicate
P(
m,
F,
μ,
) defined over a system of mechanical equations (Equation (2)) [
11]. The predicate can attain two values,
P =
true, when the system is at rest, or
P =
false when the system is in motion.
In a regular mechanical system without friction, there are only two possible states of the system: it is either at rest or in motion, or
where
stands for the exclusive disjunction (“exclusive or”) operator and
is the negation. However, in a system with paradoxes, the classical logical law of the excluded middle (
tertium non datur) of the binary Aristotelean logic is not valid anymore. Besides the state of the rest and the state of the motion, there are values of the parameters
m,
F,
μ, and
which correspond to the paradox. In the context of friction, the states of rest and motion are typically called the
slip and
stick states.
For a system with the Coulomb friction, such as in
Figure 1, the solution exists when and only when parameters are within the specified range, for example
which is equivalent to
To accommodate the undefined state, we will use the following relationships of the Łukasiewicz logic [
29].
We suggest the following physical interpretation of these logical operations. The value
P =
true is the rest,
P =
false is the motion, and
P =
undefined is the paradox. The Conjunction (
Table 1) corresponds to a situation, when a larger system consists of several parts. Only if all parts of a system are at rest, the entire system will be at rest. If at least one part of the system is in motion, then the entire system is in motion. If some parts of the system are at rest, while others have a paradox, the entire system is in paradox. If some parts of the system are in motion, while others have a paradox, the entire system is in motion.
The Disjunction (
Table 2) can be defined as a situation when at least one part of the system has a part in a given state. If one part of the system is at rest and another is in motion or has a paradox, then a resting part is present. If one part of the system is in motion, and another has a paradox, then a paradoxical part is present.
Negation rules (
Table 3) in the Łukasiewicz logic imply an opposite state: a resting system is opposite to a moving system, while the undefined state is opposite to itself. Other logical functions, such as the exclusive or and the Implication, can be defined as well.
5. Discussion
Besides its importance to the resolution of frictional paradoxes, the logical juxtaposition of the three types of solutions of mechanical equations—rest, stable motion, and unstable motion—has interesting parallels in the history of mechanics and it has relevance to emerging new areas.
5.1. Note on the History of Mechanics
Throughout the history of pre-modern mechanics, the state of
rest and the state of
motion were considered two opposite states of a mechanical system, rather than
rest being a special case of
motion. This is because in Aristotle’s physics, no motion by inertia was possible, and motion always implied the presence of a moving force or an effective cause of motion [
33].
Several paradoxes have emerged accompanying the opposition of
rest vs.
motion, including the classical Zeno’s arrow paradox, formulated by Aristotle as “If everything when it occupies an equal space is at rest, and if that which is in locomotion is always occupying such a space at any moment, the flying arrow is therefore motionless.” [
25,
33]
Furthermore, it was a matter of discussion, whether rest can be obtained as a combination of two uniform motions, until the so-called Tusi couple was discovered in the 13th century. The Tusi couple is an imaginary device used for the Copernican astronomical model. The Tusi couple consists of two spheres with a smaller sphere rolling inside a larger sphere having twice the same diameter. A point on a smaller sphere performs an oscillatory motion. At an extreme point of its trajectory, the point changes its direction for an opposite one, so that the instantaneous velocity is zero. While the mechanism is similar to the crank-slider linkage, which converts rotation into the reciprocating motion, and it was known from ancient times, the Tusi couple demonstrated that continuous rotation can produce motion with instantaneous zero velocity, which was not obvious until the concept of instantaneous velocity was suggested [
34].
It took significant efforts, until the motion by inertia (without cause) was discovered by Galileo in the early 1600s (in fact, Giuseppe Moletti had already established that objects of different weight fall with the same acceleration [
35]). This required the realization that friction is what prevents moving objects from continuous motion by inertia. Therefore, friction and inertia were in a complimentary relationship: without identifying friction, inertia could not be recognized.
H.A. Wiltsche pointed out that pre-Galilean Aristotelian mechanics studied natural
occurrences as opposed to the study of
phenomena (“the invariant forms that allegedly underline natural occurrences”) introduced by Galileo. The latter systematically excluded causal accidents as impediments, and friction largely fell as a victim in the search of refined and purified phenomena [
36]. Even today, despite almost universal occurrence of friction, it is studied by materials scientists and engineers much more often than by physicists.
After calculus was also created in the 17th century by Newton and Leibnitz, it became possible to introduce the concept of instantaneous velocity as a derivative of coordinate, and consider rest as a special zero-velocity case of motion. Since then, it has been established that the positions and velocities corresponding to degrees of freedom of a mechanical system characterize a state of that system. The approach was extended in a formal way by the Lagrange mechanics, which views the law of motion as a local extremum of a functional depending on the generalized coordinates in the configurational space of the system, and further by the Hamilton mechanics, which defines the law of motion in the phase space of a mechanical system (a cotangential bundle of the configurational space) given by coordinates and momenta.
5.2. Ultraslow Frictional Sliding between Motion and Rest
While most traditional mechanical systems possess a clear distinction between the states of motion and rest, some systems can be characterized by an intermediate state between motion and rest, including the so-called
ultraslow or
super-slow motion. Ultraslow processes are defined as processes with the rate of change of the parameters comparable or smaller than the fluctuations of their measurements. An example is supplied by ultra-slow frictional sliding, which is defined as sliding with the velocity comparable with the relaxation rate of the processes in the material [
37]. Practically speaking, this is a nanovelocity, typically in the range of nanometers per second (
Figure 4).
In the context of friction, motion and rest are often called
slip and
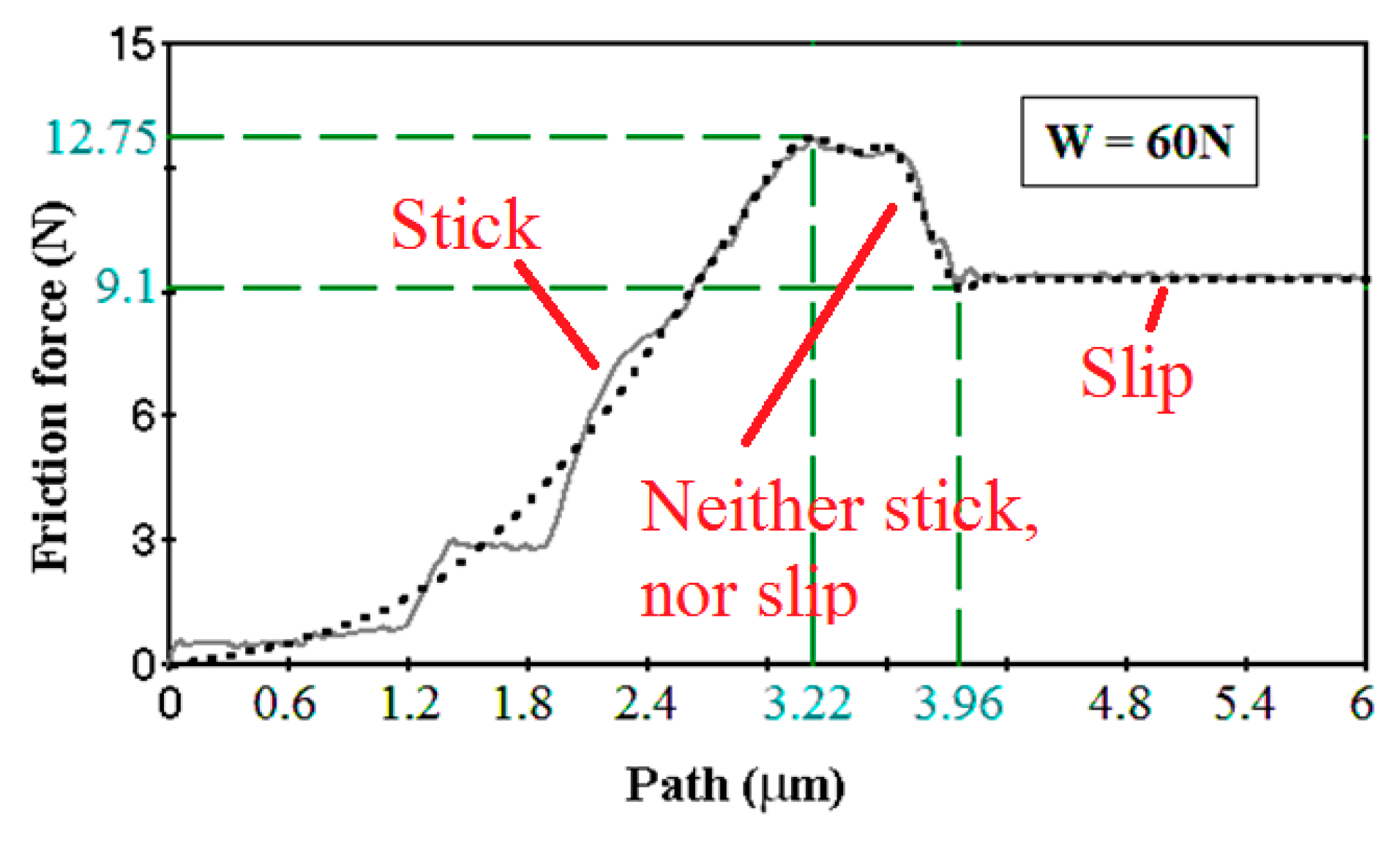
stick, while the static COF in the stick state is typically larger than the kinetic COF in the slip state. The ultraslow sliding friction is, in a sense, between the static friction and kinetic friction. For friction between two very smooth steel samples (so-called Jo blocks) at the sliding velocity of 37 nm/s, the force-displacement dependencies suggest that the onset of sliding is a gradual transition between two regimes rather than an abrupt irreversible transition from static to kinetic friction observed at higher sliding velocities (
Figure 5). Thus, ultraslow sliding can be interpreted as a state which is neither stick nor slip.
5.3. Mechanics of Instabilities
Traditionally, mechanics studies stable processes and stable solutions of the equations of motion, with unstable solutions considered non-physical and thus irrelevant. However, unstable processes and regimes of motion play a role in various situations, from flight aerodynamics (flying objects, from insects to fighter jets, may have unstable phases of motion when they maneuver) to rapid processes such as explosions or crack propagations during fracture. Non-stable solutions are usually just sorted out and not considered. While unstable processes are qualitatively different from stable processes, traditional mechanics has limited tools to adequately reflect this difference. The proposed logical formalism can fill this gap.
Investigating unstable motion introduces a new and diverse class of mechanical phenomena, which have rarely been investigated by mechanicians until the end of the 20th century, including those leading to the self-organization and hierarchical structures.
The advances of recent decades in studying non-equilibrium processes made it clear that “unstable motion” is a very important area of research and that it can lead to engineering applications, such as the development of new materials. Note that frictional systems can lead to new logical and informational devices, if friction is viewed from the viewpoint of information production, rather than from the view point of energy dissipation [
11].
6. Conclusion
In the classical Newtonian and Lagrangian mechanics of particles, a state of the system with N degrees of freedom is characterized by a set of coordinates and velocities , . We have suggested an extension of this description, , where is a logical variable, which may attain three values: true (the system at rest), false (the system in motion, which is assumed stable), and undefined. The undefined state can be interpreted as a paradoxical situation (when no solution or non-unique solution exists), as an instability, or as an intermediate state between rest and motion in a certain sense (e.g., the ultraslow sliding). The overall state of the system is given by the conjunction of the degrees of freedom . Thus, the system is at rest if all velocities are defined and equal to zero, the system is moving if at least one velocity is defined and non-zero, and the system is undefined otherwise. For example, the stability of the system can be defined as , where .
Certainly, the actual behavior of a mechanical system does not depend on the logical apparatus used. The paradoxes are related to shortcomings of the models, which describe mechanical systems with friction. The main advantage of the proposed three-valued logical description is that it formally addresses and often resolves frictional paradoxes in mechanical models (when no solution exists or a solution is non-unique) in a natural way, and allows to clearly distinguish between stable motion, unstable solutions, and rest as qualitatively different states of a mechanical system. The proposed method can be applied to the analysis of unstable motion and to the analysis of situations, when intermediate states between rest and motion exist, such as the ultraslow motion.