Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method
Abstract
1. Introduction
2. Preliminaries
3. Idea of the Fractional Natural Transform Decomposition Method
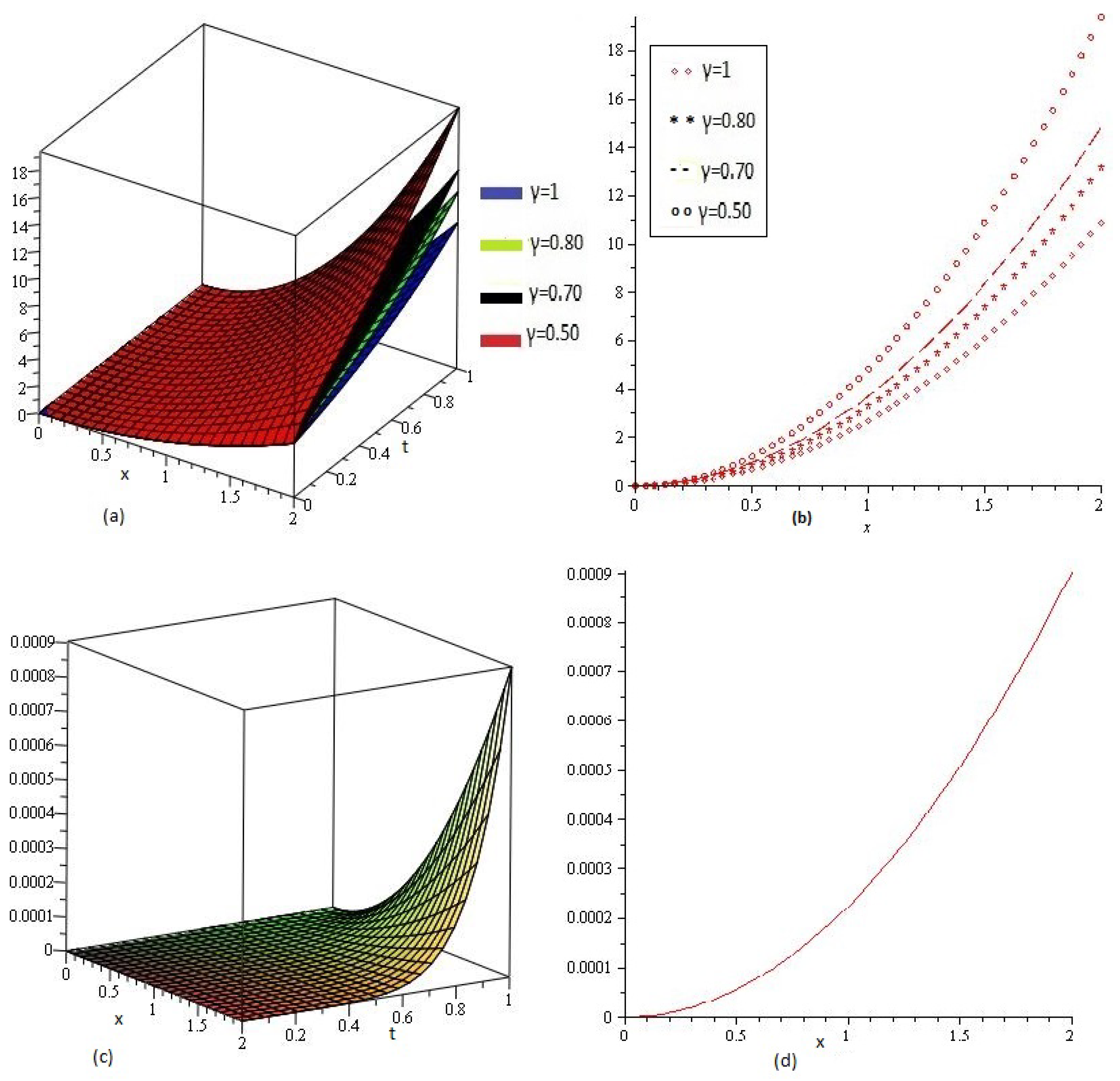
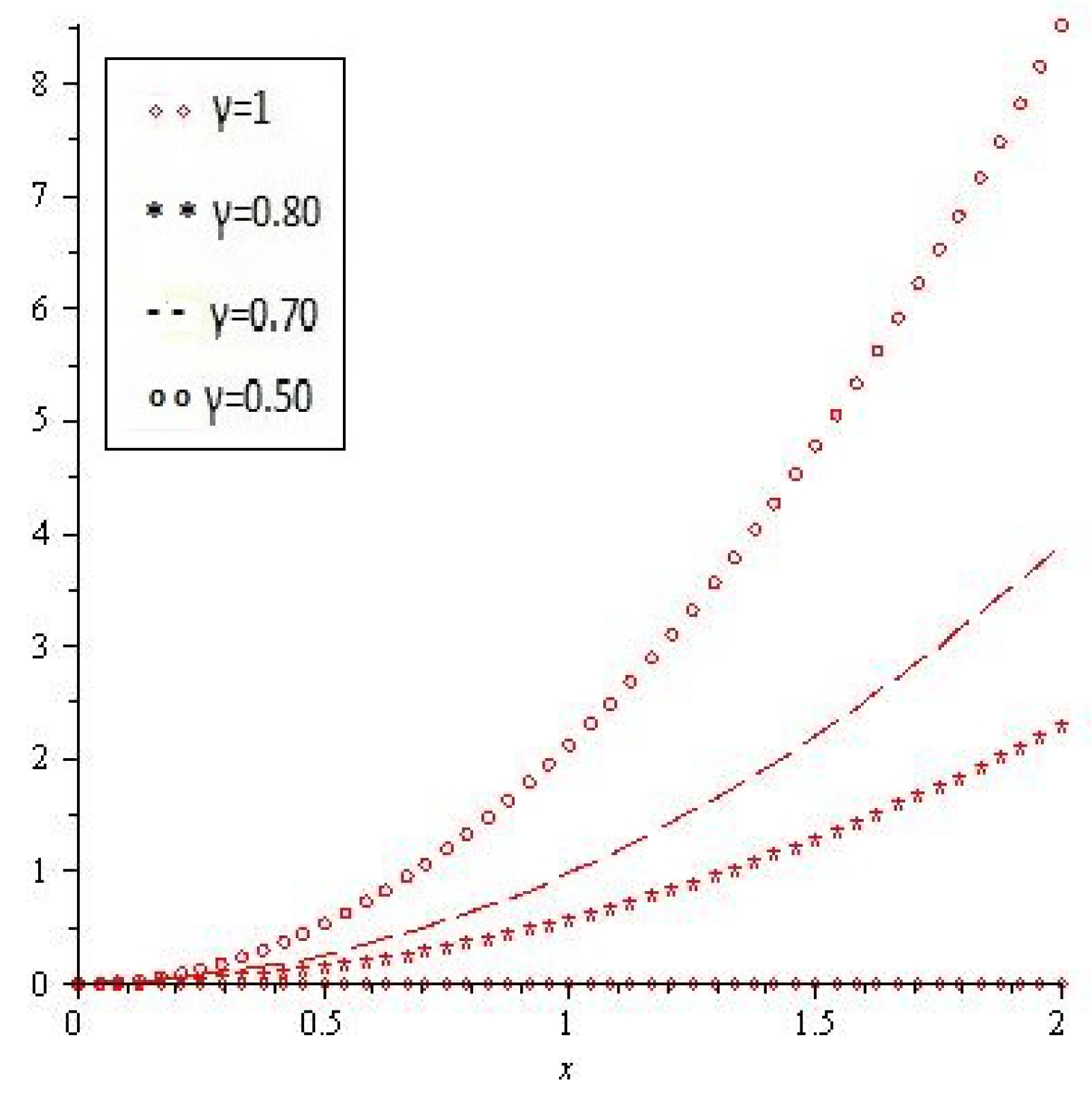
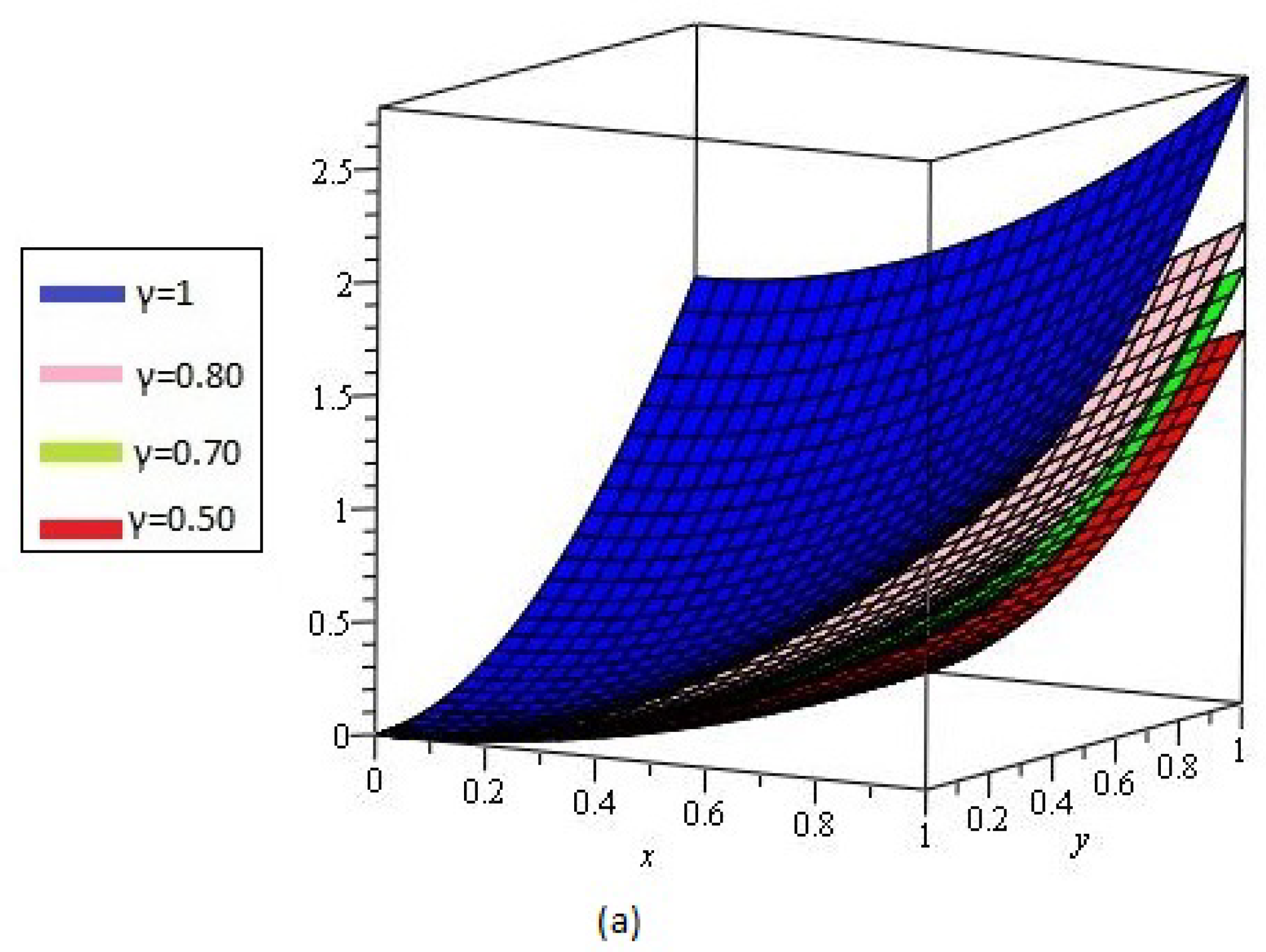
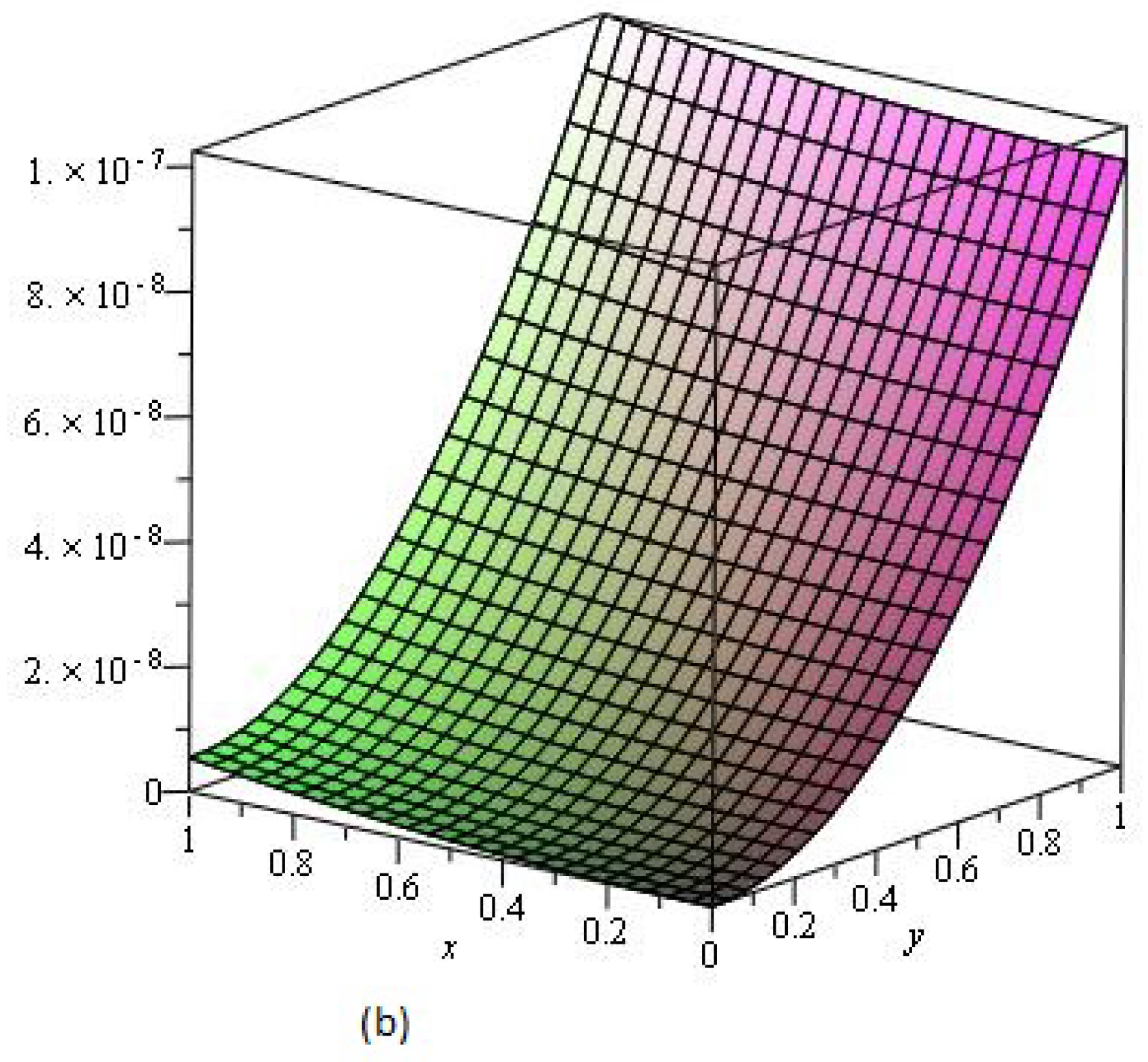
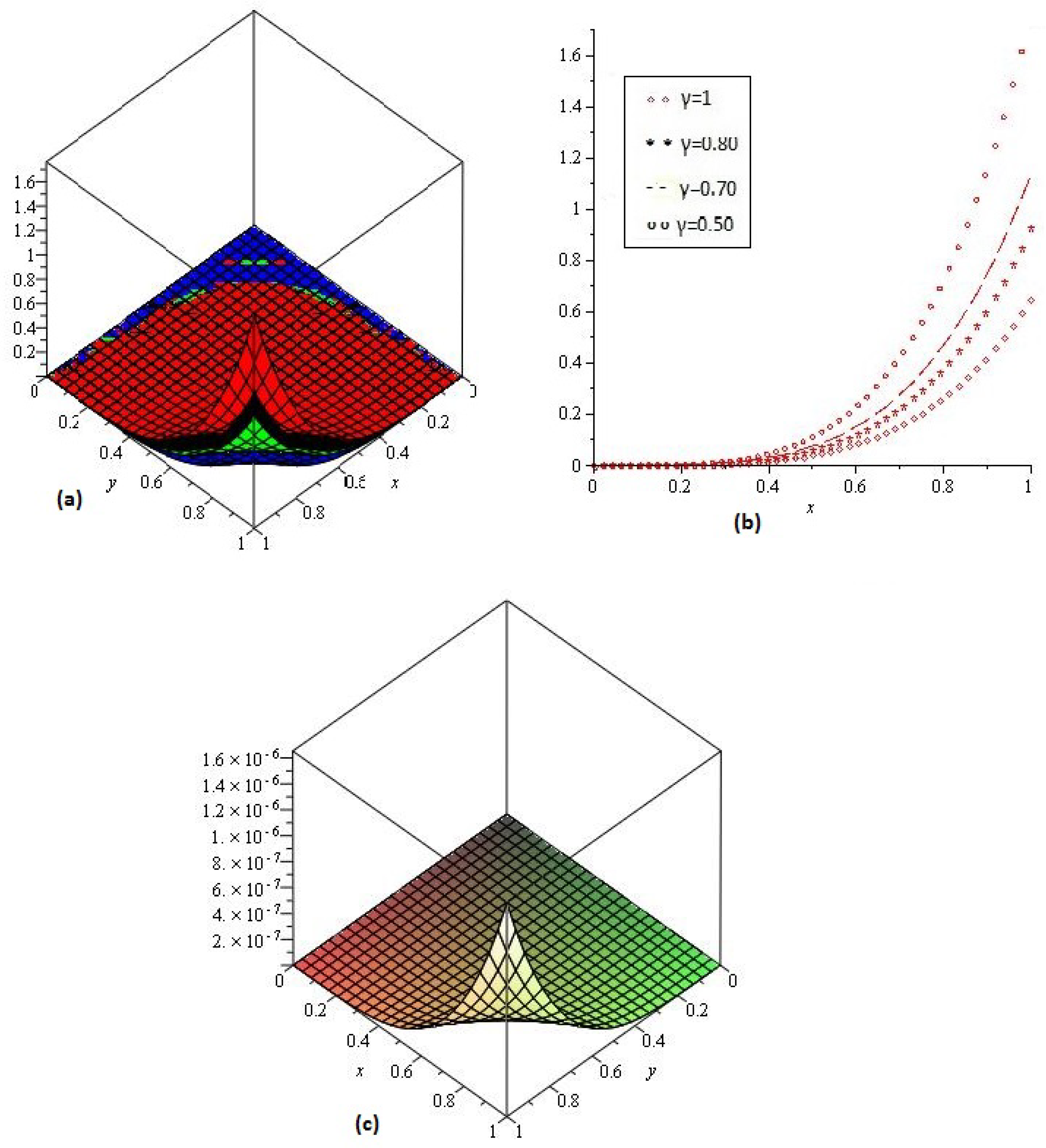
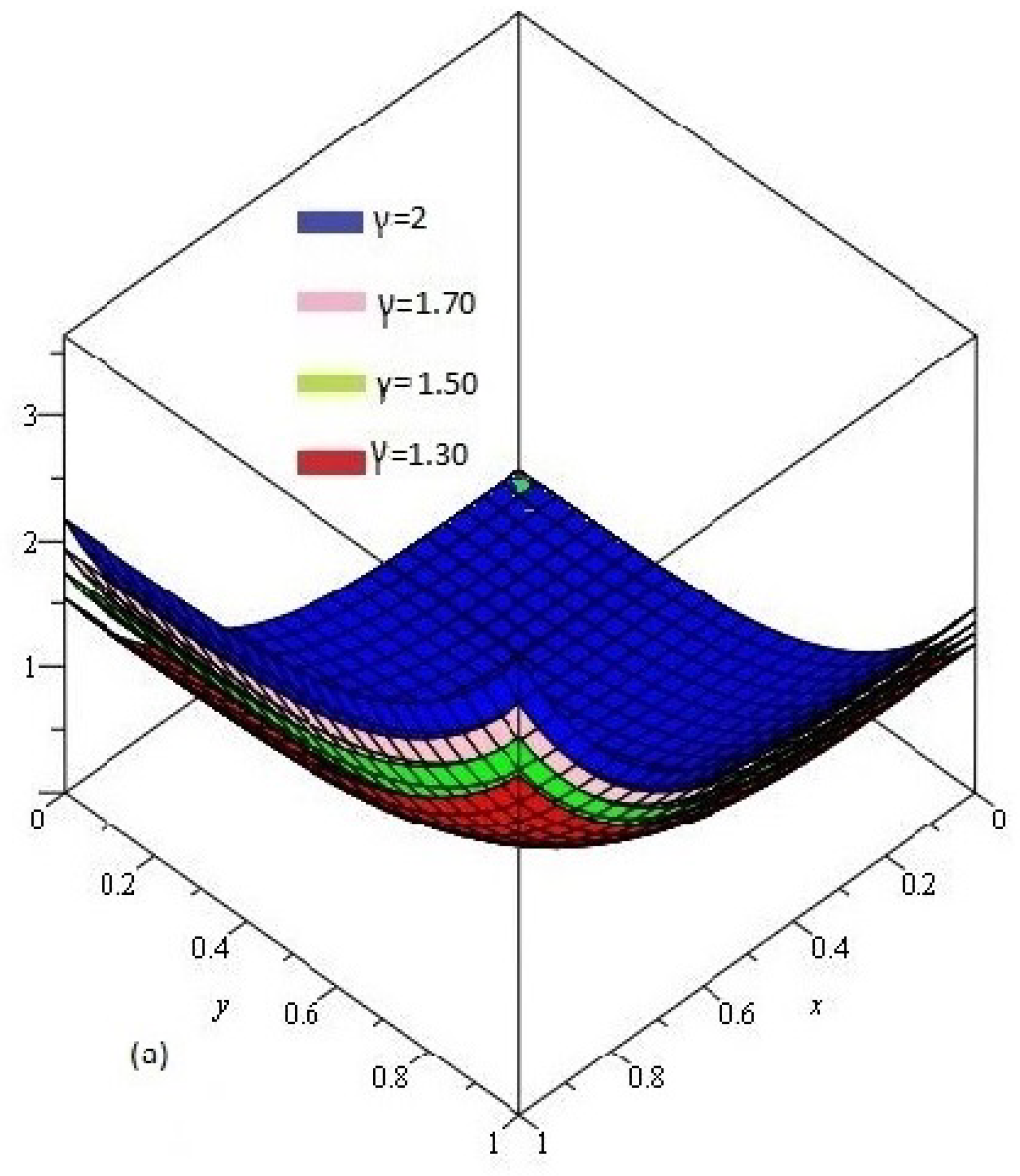
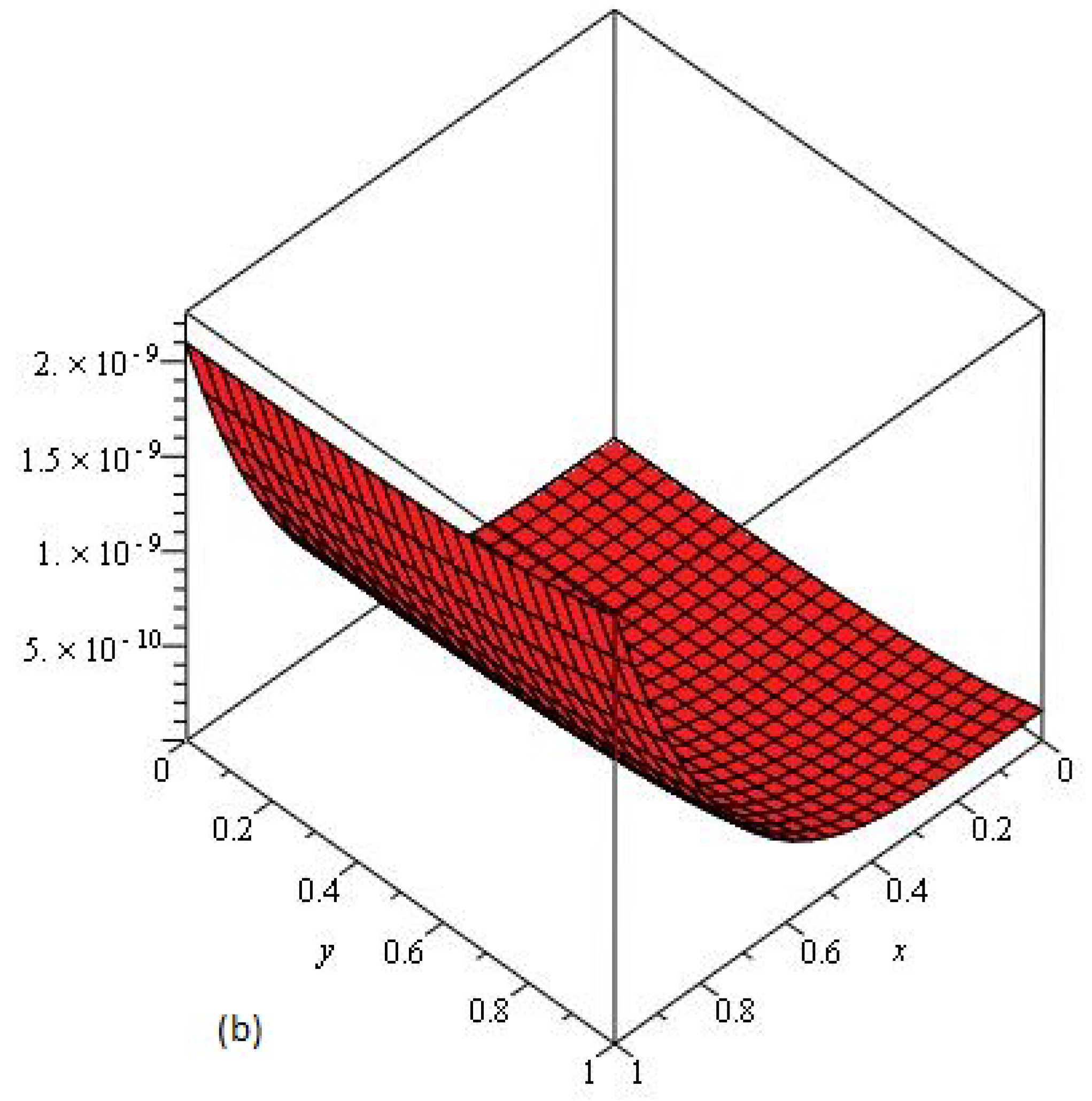
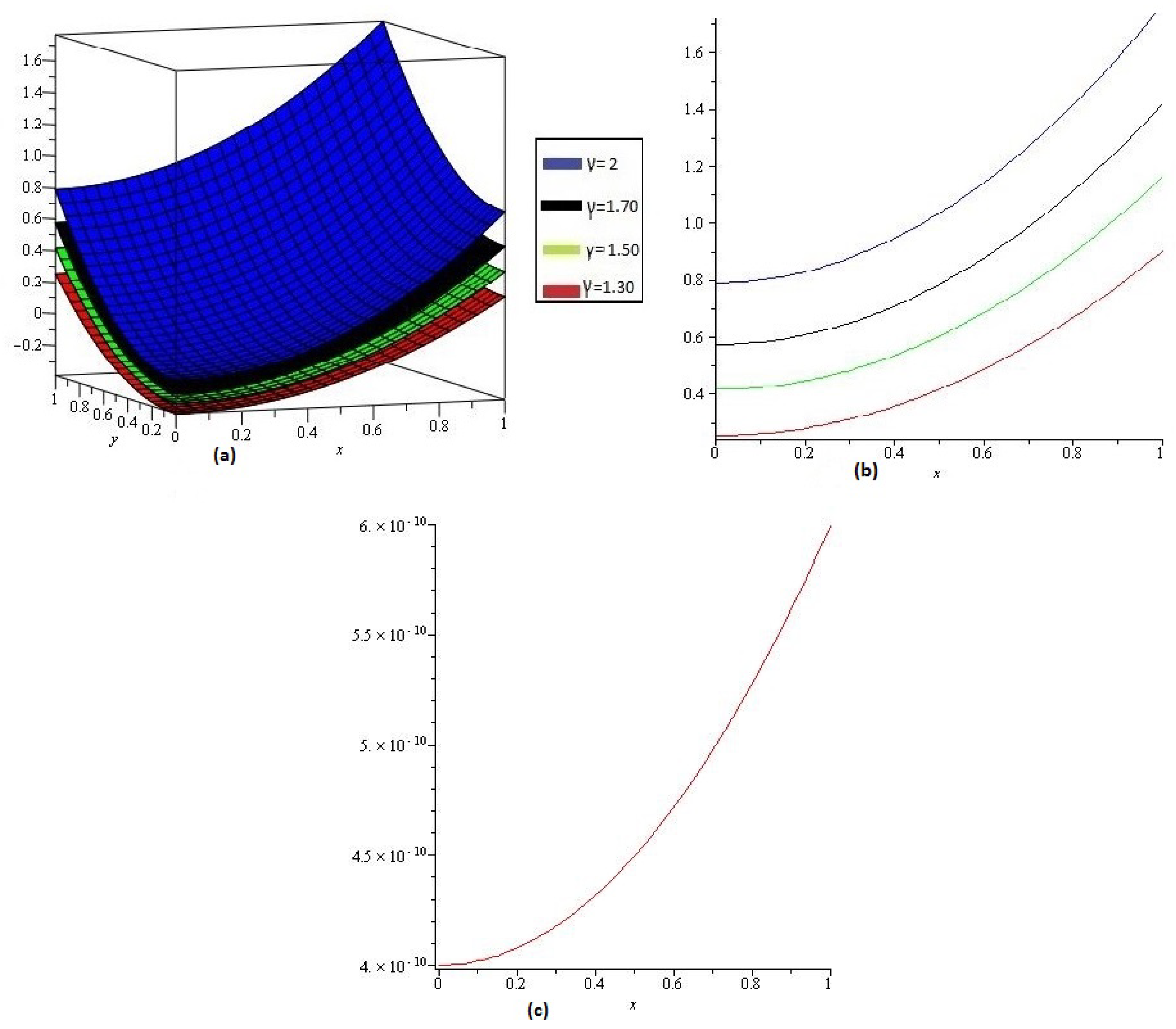
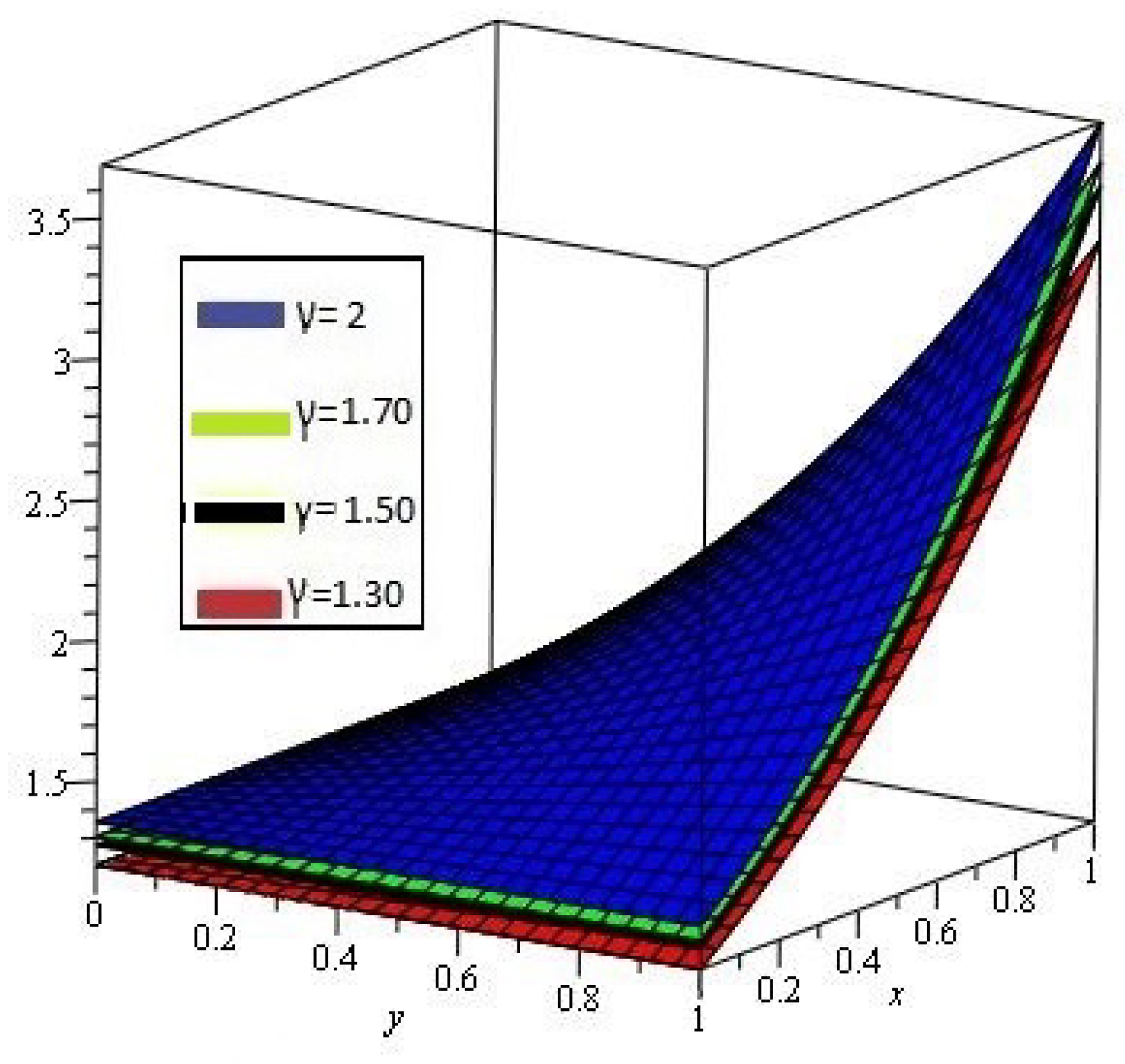
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ibrahim, R.; Jalab, H. Existence of Ulam stability for iterative fractional differential equations based on fractional entropy. Entropy 2015, 17, 3172–3181. [Google Scholar] [CrossRef]
- Arshad, S.; Baleanu, D.; Huang, J.; Qurashi, M.A.; Tang, Y.; Zhao, Y. Finite Difference Method for Time-Space Fractional Advection-Diffusion Equations with Riesz Derivative. Entropy 2018, 20, 321. [Google Scholar] [CrossRef]
- Povstenko, Y. Generalized boundary conditions for the time-fractional advection diffusion equation. Entropy 2015, 17, 4028–4039. [Google Scholar] [CrossRef]
- Hoffmann, H.K.; Essex, C.; Schulzky, C. Fractional diffusion and entropy production. J. Non-Equilib. Thermodyn. 1998, 23, 166–175. [Google Scholar] [CrossRef]
- Magin, R.L.; Ingo, C. Entropy and information in a fractional order model of anomalous diffusion. IFAC Proc. Vol. 2012, 45, 428–433. [Google Scholar] [CrossRef]
- Ubriaco, M.R. Entropies based on fractional calculus. Phys. Lett. A 2009, 373, 2516–2519. [Google Scholar] [CrossRef]
- Machado, J.T. Entropy analysis of integer and fractional dynamical systems. Nonlinear Dyn. 2010, 62, 371–378. [Google Scholar]
- Ball, J.M.; Chen, G.-Q. Entropy and convexity for nonlinear partial differential equations. Philos. Trans. R. Soc. A 2013. [Google Scholar] [CrossRef] [PubMed]
- Shah, R.; Khan, H.; Arif, M.; Kumam, P. Application of Laplace-Adomian Decomposition Method for the Analytical Solution of Third-Order Dispersive Fractional Partial Differential Equations. Entropy 2019, 21, 335. [Google Scholar] [CrossRef]
- Butusov, D.N.; Karimov, A.I.; Pesterev, D.O.; Tutueva, A.V.; Okoli, G. Bifurcation and recurrent analysis of memristive circuits. In Proceedings of the 2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Moscow, Russia, 29 Januanry–1 February 2018; pp. 178–183. [Google Scholar]
- Tutueva, A.V.; Butusov, D.N.; Karimov, A.I.; Andreev, V.S. Recurrence density analysis of multi-wing and multi-scroll chaotic systems. In Proceedings of the 2018 7th Mediterranean Conference on Embedded Computing (MECO), Budva, Montenegro, 10–14 June 2018; pp. 1–5. [Google Scholar]
- Butusov, D.; Karimov, A.; Tutueva, A.; Kaplun, D.; Nepomuceno, E.G. The effects of Padé numerical integration in simulation of conservative chaotic systems. Entropy 2019, 21, 362. [Google Scholar] [CrossRef]
- Sibatov, R.; Shulezhko, V.; Svetukhin, V. Fractional Derivative Phenomenology of Percolative Phonon- Assisted Hopping in Two-Dimensional Disordered Systems. Entropy 2017, 19, 463. [Google Scholar] [CrossRef]
- Jiang, J.; Feng, Y.; Li, S. Exact solutions to the fractional differential equations with mixed partial derivatives. Axioms 2018, 7, 10. [Google Scholar] [CrossRef]
- Prehl, J.; Essex, C.; Hoffmann, K.H. Tsallis relative entropy and anomalous diffusion. Entropy 2012, 14, 701–716. [Google Scholar] [CrossRef]
- Lopes, A.M.; Machado, J.T. Entropy Analysis of Soccer Dynamics. Entropy 2019, 21, 187. [Google Scholar] [CrossRef]
- Bejan, A. Second-law analysis in heat transfer and thermal design. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1982; Volume 15, pp. 1–58. [Google Scholar]
- Bejan, A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979, 101, 718–725. [Google Scholar] [CrossRef]
- Sarwar, S.; Alkhalaf, S.; Iqbal, S.; Zahid, M.A. A note on optimal homotopy asymptotic method for the solutions of fractional order heat-and wave-like partial differential equations. Comput. Math. Appl. 2015, 70, 942–953. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Mohammad, G.; Mustafa, M.T.; Zaman, F.D. Adomian decomposition method for a nonlinear heat equation with temperature dependent thermal properties. Math. Prob. Eng. 2009. [Google Scholar] [CrossRef]
- Shou, D.-H.; He, J.-H. Beyond Adomian method: The variational iteration method for solving heat-like and wave-like equations with variable coefficients. Phys. Lett. A 2008, 372, 233–237. [Google Scholar] [CrossRef]
- Secer, A. Approximate analytic solution of fractional heat-like and wave-like equations with variable coefficients using the differential transforms method. Adv. Differ. Equ. 2012, 2012, 198. [Google Scholar] [CrossRef][Green Version]
- Jin, L. Homotopy perturbation method for solving partial differential equations with variable coefficients. Int. J. Contemp. Math. Sci. 2008, 3, 1395–1407. [Google Scholar]
- Rostamy, D.; Karimi, K. Bernstein polynomials for solving fractional heat-and wave-like equations. Fract. Calculus Appl. Anal. 2012, 15, 556–571. [Google Scholar]
- Khalouta, A.; Kadem, A. Mixed of Elzaki Transform and Projected Differential Transform Method for a Nonlinear Wave-Like Equations with Variable Coefficients. Appl. Math. 2018. [Google Scholar] [CrossRef]
- Liu, C.-F.; Kong, S.-S.; Yuan, S.-J. Reconstructive schemes for variational iteration method within Yang-Laplace transform with application to fractal heat conduction problem. Therm. Sci. 2013, 17, 715–721. [Google Scholar] [CrossRef]
- Nuruddeen, R.I.; Nass, A.M. Exact solutions of wave-type equations by the Aboodh decomposition method. Stoch. Modell. Appl. 2017, 21, 23–30. [Google Scholar]
- Rawashdeh, M.S.; Maitama, S. Solving coupled system of nonlinear PDE’s using the natural decomposition method. Int. J. Pure Appl. Math. 2014, 92, 757–776. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud. 2018, 25, 753–764. [Google Scholar]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional Telegraph Equation and Its Solution by Natural Transform Decomposition Method. Symmetry 2015, 11, 334. [Google Scholar] [CrossRef]
- Abdel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedl-Rahim, H.R. Natural transform for solving fractional models. J. Appl. Math. Phys. 2015, 3, 1633. [Google Scholar] [CrossRef]
- Belgacem, F.B.M.; Silambarasan, R. Advances in the natural transform. AIP Conf. Proc. 2012, 1493, 106–110. [Google Scholar]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Sci. Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations, 1st ed.; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Shah, R.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy 2019, 21, 597. https://doi.org/10.3390/e21060597
Khan H, Shah R, Kumam P, Arif M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy. 2019; 21(6):597. https://doi.org/10.3390/e21060597
Chicago/Turabian StyleKhan, Hassan, Rasool Shah, Poom Kumam, and Muhammad Arif. 2019. "Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method" Entropy 21, no. 6: 597. https://doi.org/10.3390/e21060597
APA StyleKhan, H., Shah, R., Kumam, P., & Arif, M. (2019). Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy, 21(6), 597. https://doi.org/10.3390/e21060597






