A Correntropy-Based Proportionate Affine Projection Algorithm for Estimating Sparse Channels with Impulsive Noise
Abstract
1. Introduction
2. Review of the PAP Algorithm
2.1. AP Algorithm
2.2. PAP Algorithm
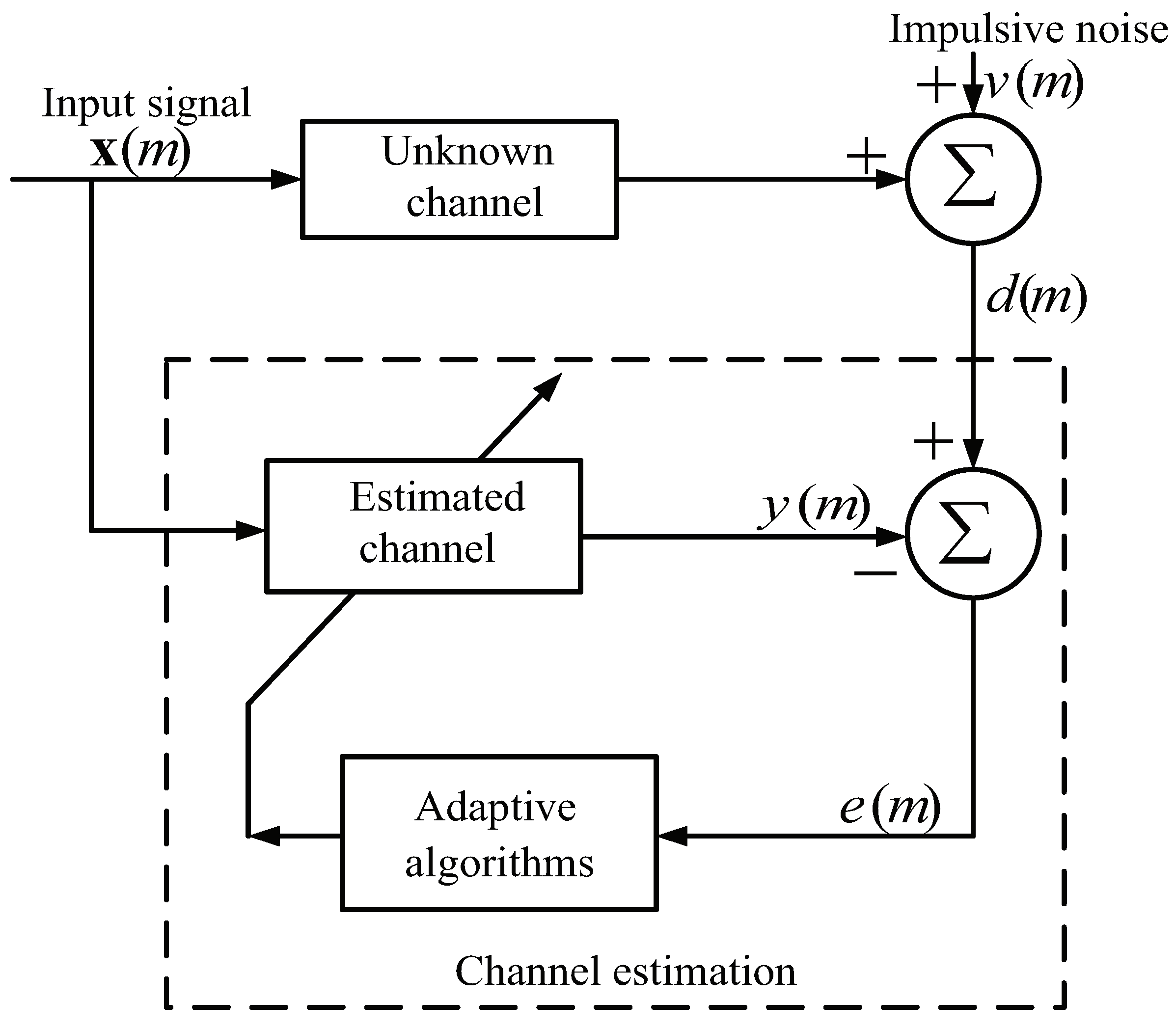
3. Proposed PAPMCC Algorithm
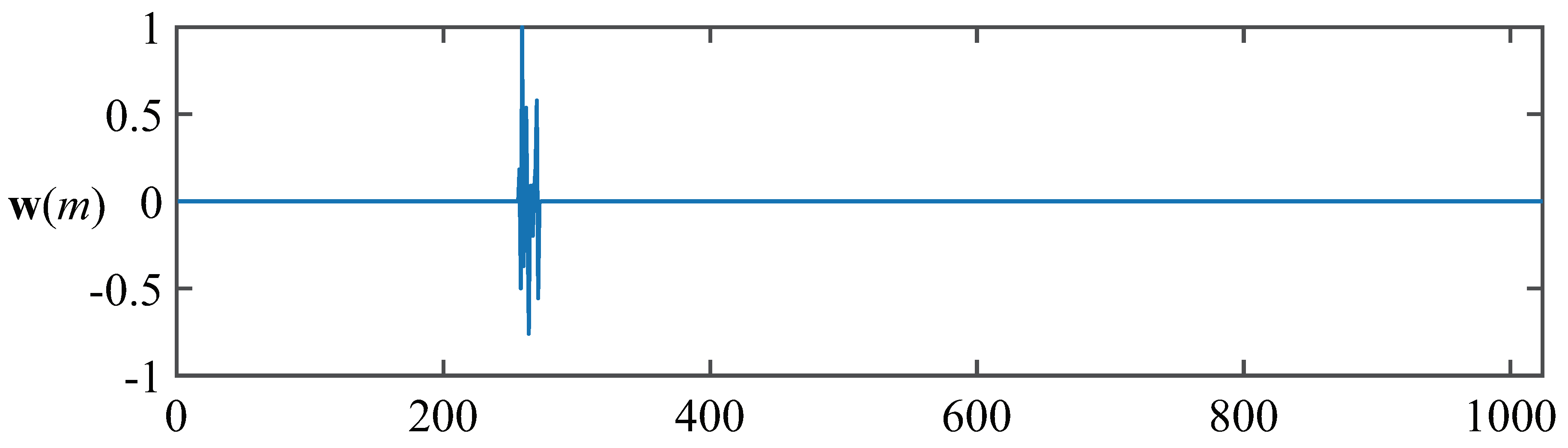
4. Experimental Results
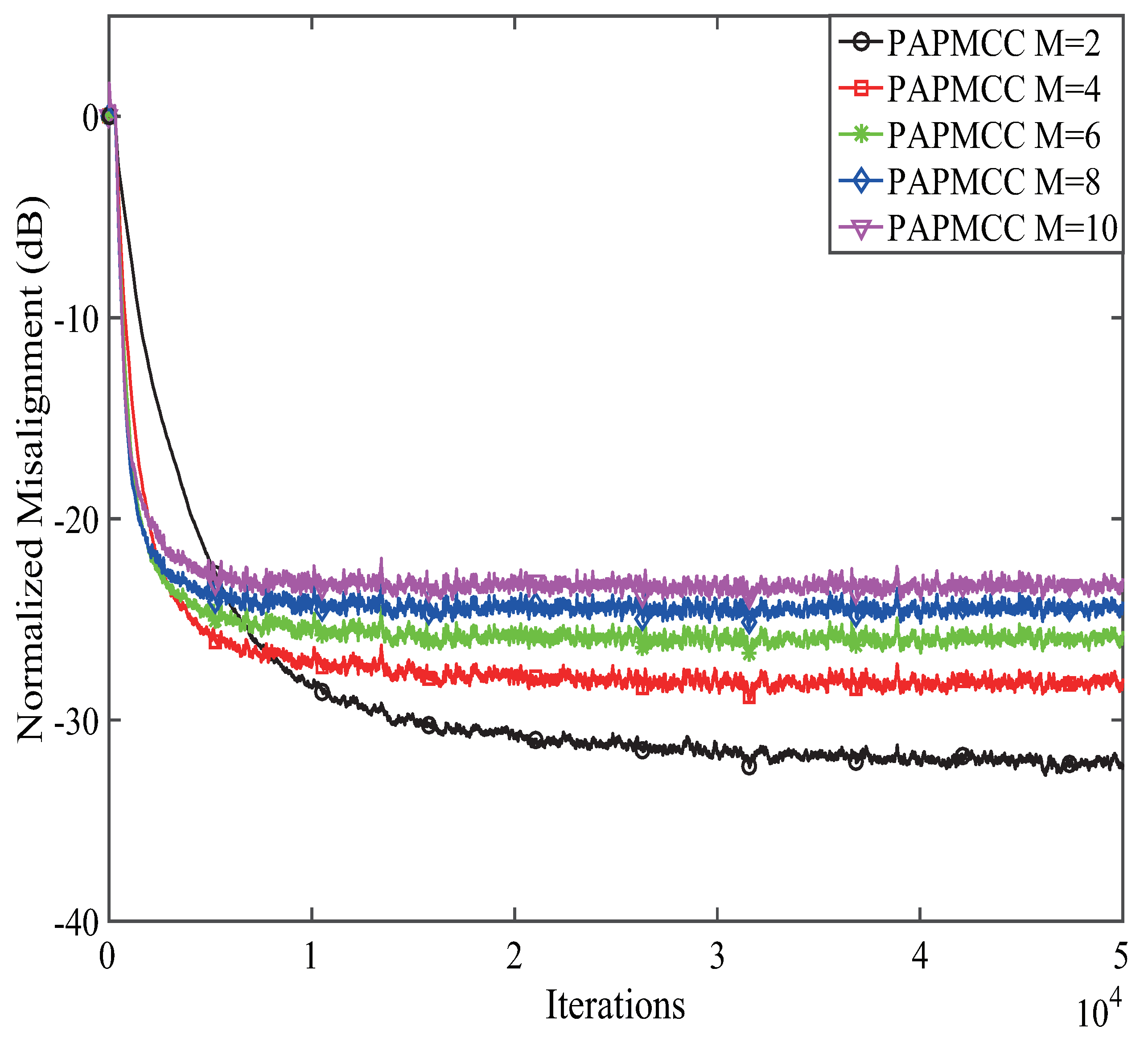
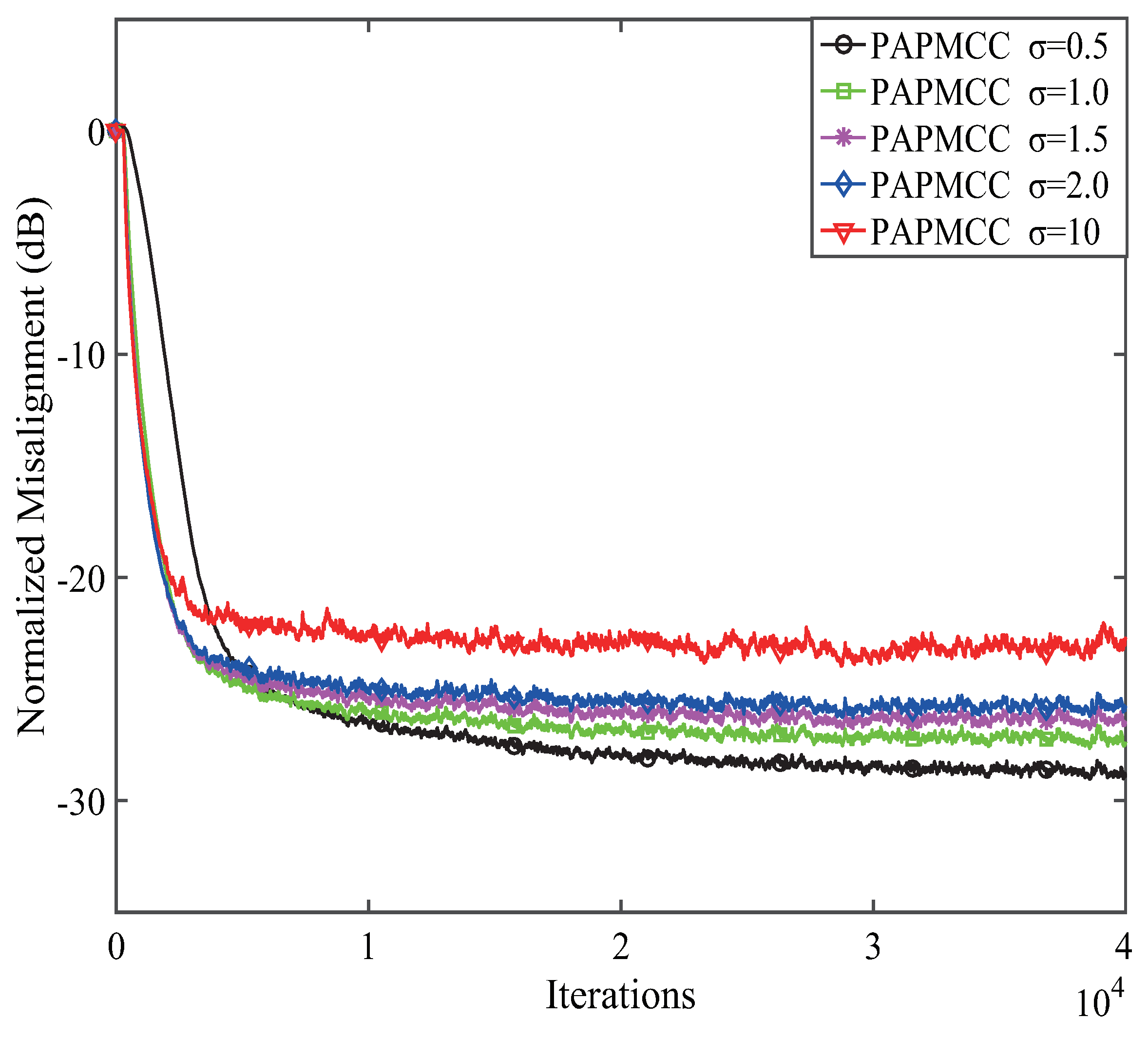
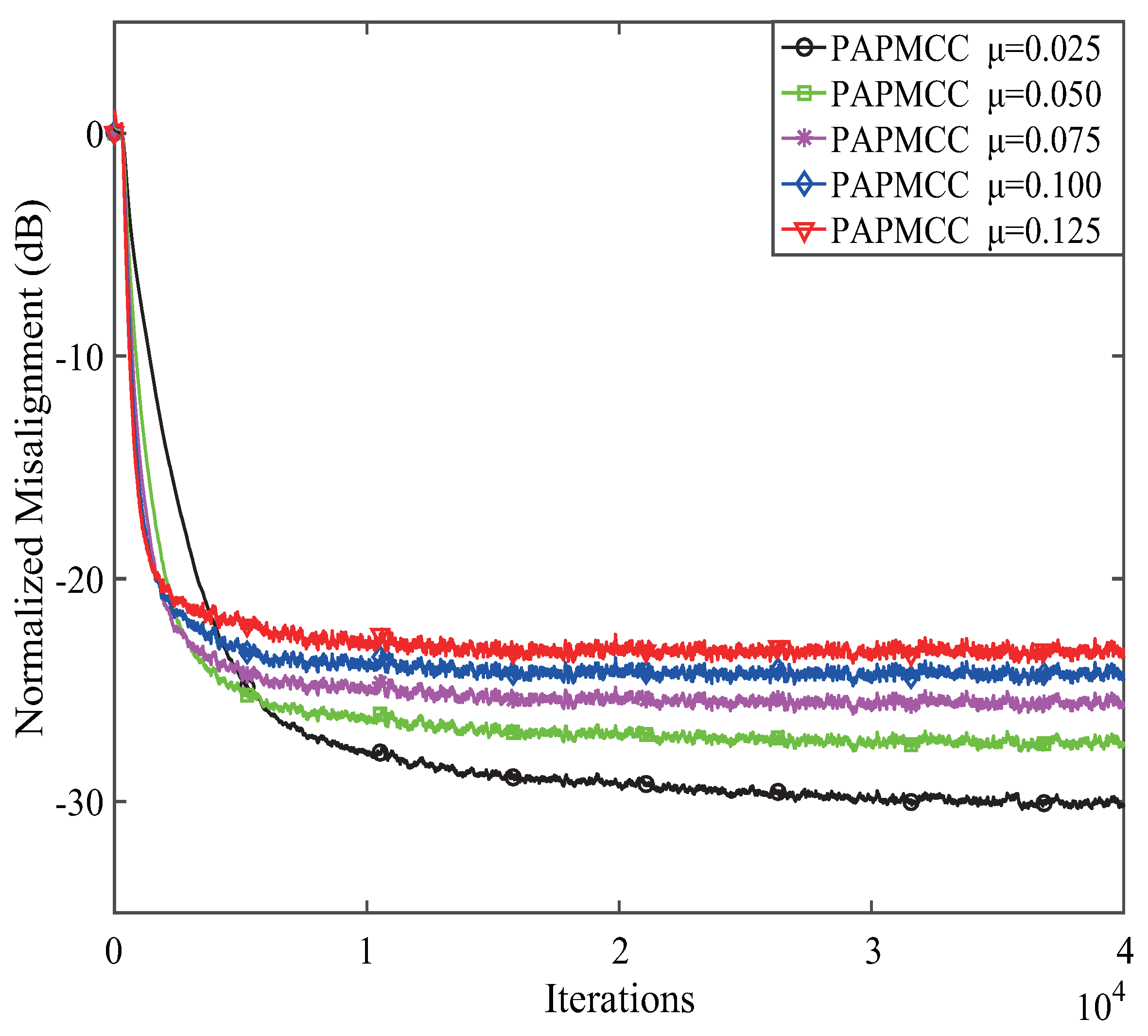
4.1. Performance of the PAPMCC Algorithm with Various Projection Orders M, Step-Sizes and Kernel Width
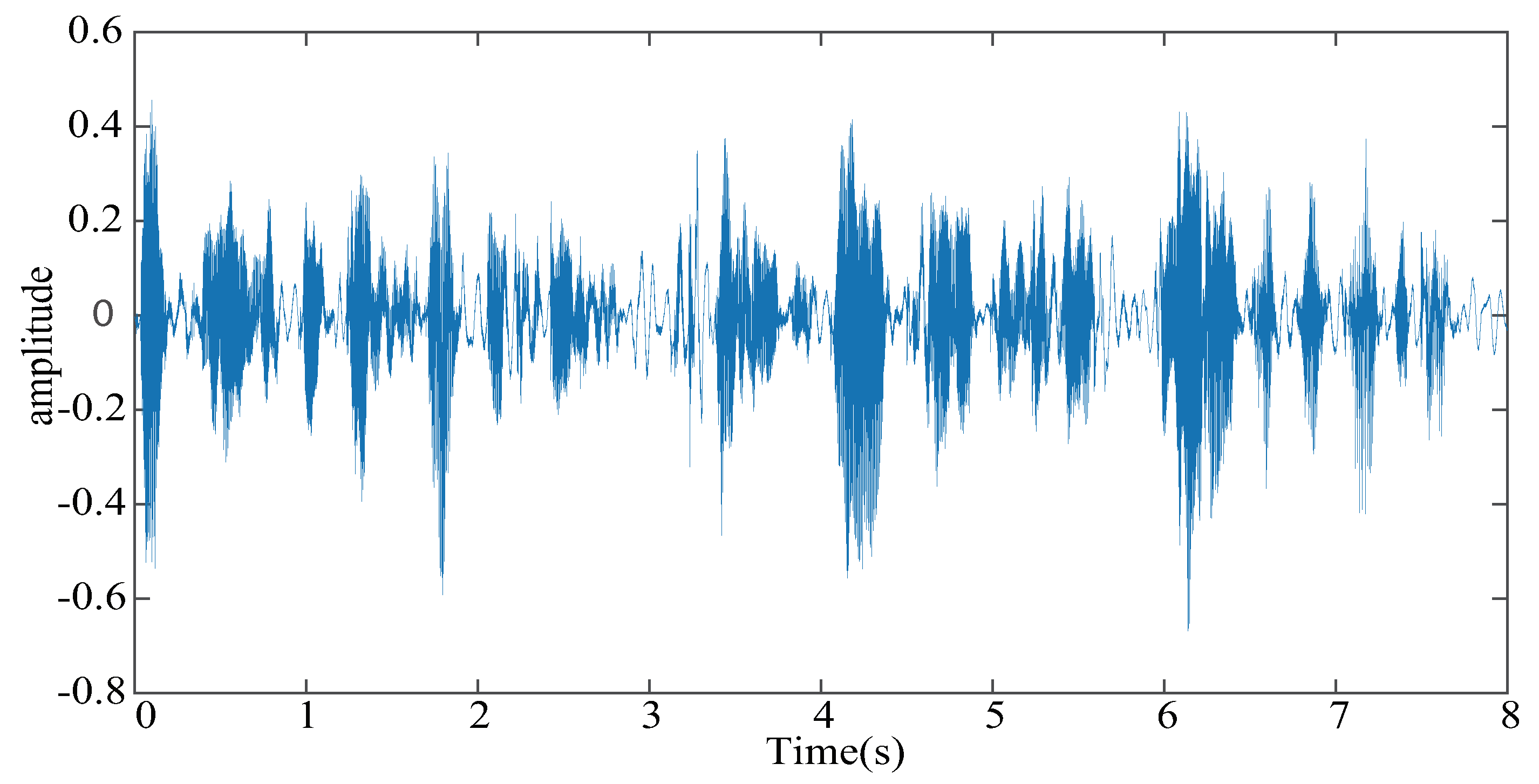
4.2. Performance Comparisons of the Proposed PAPMCC Algorithm under Different Input Signals
4.3. SNR vs. Normalized Misalignment (NM) of the PAPMCC Algorithm
4.4. Performance Comparisons of the Proposed PAPMCC Algorithm with the Conventional Robust AP Algorithms
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Haykin, S. Adaptive Filter Theory, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Benesty, J.; Gänsler, T.; Morgan, D.R.; Sondhi, M.M.; Gay, S.L. Advances in Network and Acoustic Echo Cancellation; Springer: Berlin, Germany, 2001. [Google Scholar]
- Shi, W.; Li, Y.; Wang, Y. Noise-free maximum correntropy criterion algorithm in non-Gaussian environment. IEEE Trans. Circuits Syst. II-Express Briefs 2019. [Google Scholar] [CrossRef]
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice-Hall: Upper Saddle River, NJ, USA, 1985. [Google Scholar]
- Douglas, S.C.; Meng, T.Y. Normalized data nonlinearities for LMS adaptation. IEEE Trans. Signal Process. 1994, 42, 1352–1365. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y.; Jiang, T. Sparse-aware set-membership NLMS algorithms and their application for sparse channel estimation and echo cancelation. AEU-Int. J. Electron. Commun. 2006, 70, 895–902. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Y. Sparse SM-NLMS algorithm based on correntropy criterion. Electron. Lett. 2016, 52, 1461–1463. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.; Yu, W.; Wan, J.; Li, Z. Sparse adaptive channel estimation based on -norm-penalized affine projection algorithm. Int. J. Antennas Propag. 2014, 2014, 1–13. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Jin, Z.; Han, X.; Yin, J. Cluster-sparse proportionate NLMS algorithm with the hybrid norm constraint. IEEE Access 2018, 6, 47794–47803. [Google Scholar] [CrossRef]
- Shi, W.; Li, Y.; Zhao, L.; Liu, X. Controllable sparse antenna array for adaptive beamforming. IEEE Access 2019, 7, 6412–6423. [Google Scholar] [CrossRef]
- Sayed, A.H. Fundamentals of Adaptive Filtering; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Ozeki, K.; Umeda, T. An adaptive filtering algorithm using an orthogonal projection to an affine subspace and its properties. Electr. Commun. Jpn. 1984, 67, 19–27. [Google Scholar] [CrossRef]
- Shin, H.-C.; Sayed, A.H.; Song, W.-J. Variable step-size NLMS and affine projection algorithms. IEEE Signal Process. Lett. 2004, 11, 132–135. [Google Scholar] [CrossRef]
- Vega, L.R.; Rey, H.; Benesty, J.; Tressens, S. A new robust variable step-size NLMS algorithm. IEEE Trans. Signal Process. 2008, 56, 1878–1893. [Google Scholar] [CrossRef]
- Vega, L.R.; Rey, H.; Benesty, J.; Tressens, S. A fast robust recursive least-squares algorithm. IEEE Trans. Signal Process. 2008, 57, 1209–1216. [Google Scholar] [CrossRef]
- Singh, A.; Principe, J.C. Using correntropy as a cost function in linear adaptive filters. In Proceedings of the 2009 International Joint Conference on Neural Networks, Atlanta, GA, USA, 14–19 June 2009; pp. 1209–1216. [Google Scholar]
- Peng, S.; Ser, W.; Chen, B.; Sun, L.; Lin, Z. Robust constrained adaptive filtering under minimum error entropy criterion. IEEE Trans. Circuits Syst. II-Express Briefs 2018, 65, 1119–1123. [Google Scholar] [CrossRef]
- Chen, B.; Wang, J.; Zhao, H.; Zheng, N.; Príncipe, J.C. Convergence of a fixed-point algorithm under maximum correntropy criterion. IEEE Signal Process. Lett. 2015, 22, 1723–1727. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Shi, W.; Han, X.; Chen, B. Blocked maximum correntropy criterion algorithm for cluster-sparse system identifications. IEEE Trans. Circuits Syst. II-Express Briefs 2019. [Google Scholar] [CrossRef]
- Ma, W.; Chen, B.; Zhao, H.; Gui, G.; Duan, J.; Principe, J.C. Sparse least logarithmic absolute difference algorithm with correntropy-induced metric penalty. Circuits Syst. Signal Process. 2016, 35, 1077–1089. [Google Scholar] [CrossRef]
- Pimenta, R.M.; Resende, L.C.; Siqueira, N.N.; Haddad, I.B.; Petraglia, M.R. A new proportionate adaptive filtering algorithm with coefficient reuse and robustness against impulsive noise. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; pp. 465–469. [Google Scholar]
- Kalouptsidis, N.; Mileounis, G.; Babadi, B.; Tarokh, V. Adaptive algorithms for sparse system identification. Signal Process. 2011, 91, 1910–1919. [Google Scholar] [CrossRef]
- Li, W.; Preisig, J.C. Estimation of rapidly time-varying sparse channels. IEEE J. Ocean. Eng. 2007, 32, 927–939. [Google Scholar] [CrossRef]
- Cotter, S.F.; Rao, B.D. Sparse channel estimation via matching pursuit with application to equalization. IEEE Trans. Commun. 2002, 50, 374–377. [Google Scholar] [CrossRef]
- Berger, C.R.; Zhou, S.; Preisig, J.C.; Willett, P. Sparse channel estimation for multicarrier underwater acoustic communication: From subspace methods to compressed sensing. IEEE Trans. Signal Process. 2010, 58, 1708–1721. [Google Scholar] [CrossRef]
- Duttweiler, D.L. Proportionate normalized least-mean-squares adaptation in echo cancelers. IEEE Trans. Speech Audio Process. 2000, 8, 508–518. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, Z.; Osman, O.M.O.; Han, X.; Yin, J. Mixed norm constrained sparse APA algorithm for satellite and network echo channel estimation. IEEE Access 2018, 6, 65901–65908. [Google Scholar] [CrossRef]
- Deng, H.; Doroslovački, M. Improving convergence of the PNLMS algorithm for sparse impulse response identification. IEEE Signal Process. Lett. 2005, 12, 181–184. [Google Scholar] [CrossRef]
- Li, Y.; Hamamura, M. An improved proportionate normalized least-mean-square algorithm for broadband multipath channel estimation. Sci. World J. 2014. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Fukumoto, M.; Saiki, S. An improved mu-law proportionate NLMS algorithm. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 3797–3800. [Google Scholar]
- Gansler, T.; Benesty, J.; Gay, S.L.; Sondhi, M.M. A robust proportionate affine projection algorithm for network echo cancellation. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; pp. 793–796. [Google Scholar]
- Paleologu, C.; Ciochina, S.; Benesty, J. An efficient proportionate affine projection algorithm for echo cancellation. IEEE Signal Process. Lett. 2009, 17, 165–168. [Google Scholar] [CrossRef]
- Liu, J.; Grant, S.L.; Benesty, J. A low complexity reweighted proportionate affine projection algorithm with memory and row action projection. EURASIP J. Adv. Signal Process. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Werner, S.; Apolinário, J.A., Jr.; Diniz, P.S.R. Set-membership proportionate affine projection algorithms. EURASIP J. Audio Speech Music Process. 2007, 2007, 1–10. [Google Scholar] [CrossRef][Green Version]
- Yang, J.; Sobelman, G.E. Efficient μ-law improved proportionate affine projection algorithm for echo cancellation. Electron. Lett. 2011, 47, 73–526. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhao, H. Memory improved proportionate M-estimate affine projection algorithm. Electron. Lett. 2015, 51, 525–526. [Google Scholar] [CrossRef]
- Benesty, J.; Gay, S.L. An improved PNLMS algorithm. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; pp. 1881–1884. [Google Scholar]
- Shao, T.; Zheng, Y.R.; Benesty, J. An affine projection sign algorithm robust against impulsive interferences. IEEE Signal Process. Lett. 2010, 17, 327–330. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, Y.R.; Grant, S.L. Proportionate affine projection sign algorithms for network echo cancellation. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 2283–2284. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Chen, Y.; Gu, Y.; Hero, A.O. Sparse LMS for system identification. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 3125–3128. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Norm-adaption penalized least mean square/fourth algorithm for sparse channel estimation. Signal Process. 2016, 128, 243–251. [Google Scholar] [CrossRef]
- Meng, R.; de Lamare, R.C.; Nascimento, V.H. Sparsity-aware affine projection adaptive algorithms for system identification. In Proceedings of the Sensor Signal Processing for Defence (SSPD 2011), London, UK, 27–29 September 2011; pp. 793–796. [Google Scholar]
- Li, Y.; Wang, Y.; Jiang, T. Sparse least mean mixed-norm adaptive filtering algorithms for sparse channel estimation applications. Int. J. Commun. Syst. 2016, 30, 1–14. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Wang, S. Low-complexity non-uniform penalized affine projection algorithm for sparse system identification. Circuits Syst. Signal Process. 2016, 35, 1–14. [Google Scholar] [CrossRef]
- Lima, M.V.; Ferreira, T.N.; Martins, W.A.; Diniz, P.S. Sparsity-aware data-selective adaptive filters. IEEE Trans. Signal Process. 2014, 62, 4557–4572. [Google Scholar] [CrossRef]
- Lima, M.V.; Martins, W.A.; Diniz, P.S. Affine projection algorithms for sparse system identification. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Benesty, J.; Paleologu, C.; Ciochina, S. On regularization in adaptive filtering. IEEE Trans. Audio Speech Lang. Process. 2011, 19, 1734–1742. [Google Scholar] [CrossRef]
- Hoshuyama, O.; Goubran, R.A.; Sugiyama, A. A generalized proportionate variable step-size algorithm for fast changing acoustic environments. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; pp. 161–164. [Google Scholar]





| Algorithm | Addition | Multiplication | Division |
|---|---|---|---|
| AP | 0 | ||
| ZA-AP | 0 | ||
| RZA-AP | K | ||
| PAP | K | ||
| PAPMCC |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Li, Y.; Huang, X. A Correntropy-Based Proportionate Affine Projection Algorithm for Estimating Sparse Channels with Impulsive Noise. Entropy 2019, 21, 555. https://doi.org/10.3390/e21060555
Jiang Z, Li Y, Huang X. A Correntropy-Based Proportionate Affine Projection Algorithm for Estimating Sparse Channels with Impulsive Noise. Entropy. 2019; 21(6):555. https://doi.org/10.3390/e21060555
Chicago/Turabian StyleJiang, Zhengxiong, Yingsong Li, and Xinqi Huang. 2019. "A Correntropy-Based Proportionate Affine Projection Algorithm for Estimating Sparse Channels with Impulsive Noise" Entropy 21, no. 6: 555. https://doi.org/10.3390/e21060555
APA StyleJiang, Z., Li, Y., & Huang, X. (2019). A Correntropy-Based Proportionate Affine Projection Algorithm for Estimating Sparse Channels with Impulsive Noise. Entropy, 21(6), 555. https://doi.org/10.3390/e21060555





