Entropy and Mixing Entropy for Weakly Nonlinear Mechanical Vibrating Systems
Abstract
1. Introduction
2. Motivation
3. Overview of Khinchin’s Entropy
3.1. Linear Systems
3.2. Nonlinear Systems
3.3. Mixing Entropy
4. Entropy of Duffing Oscillators
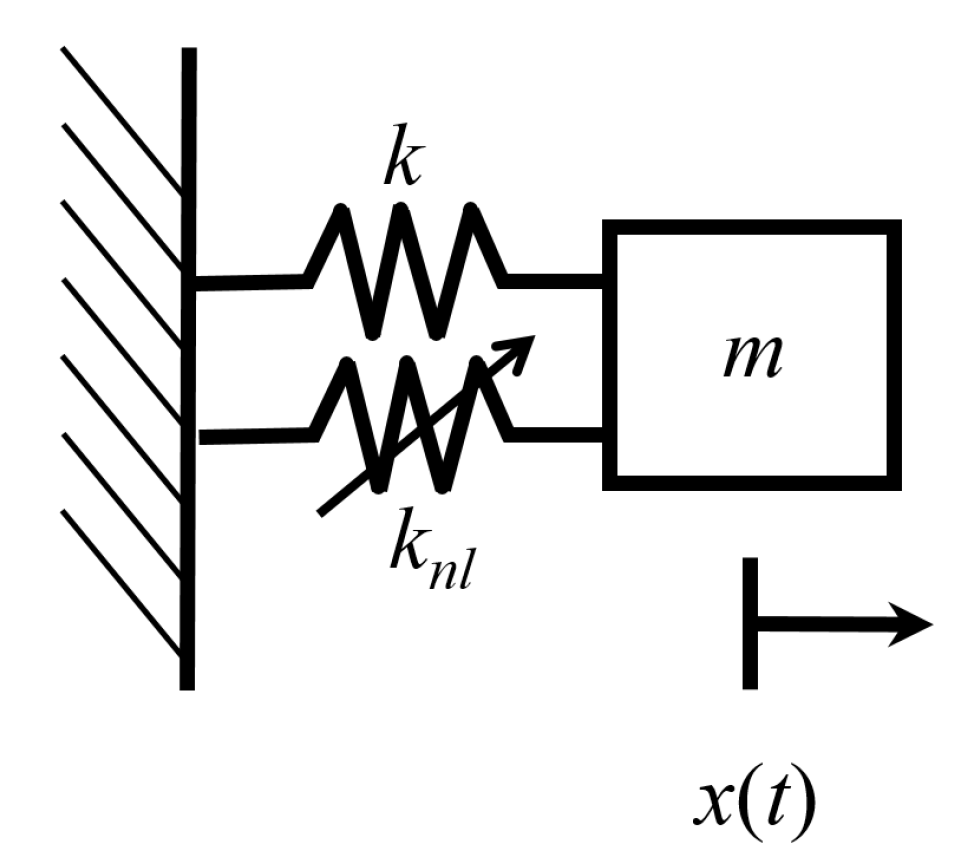
4.1. A Duffing Oscillator
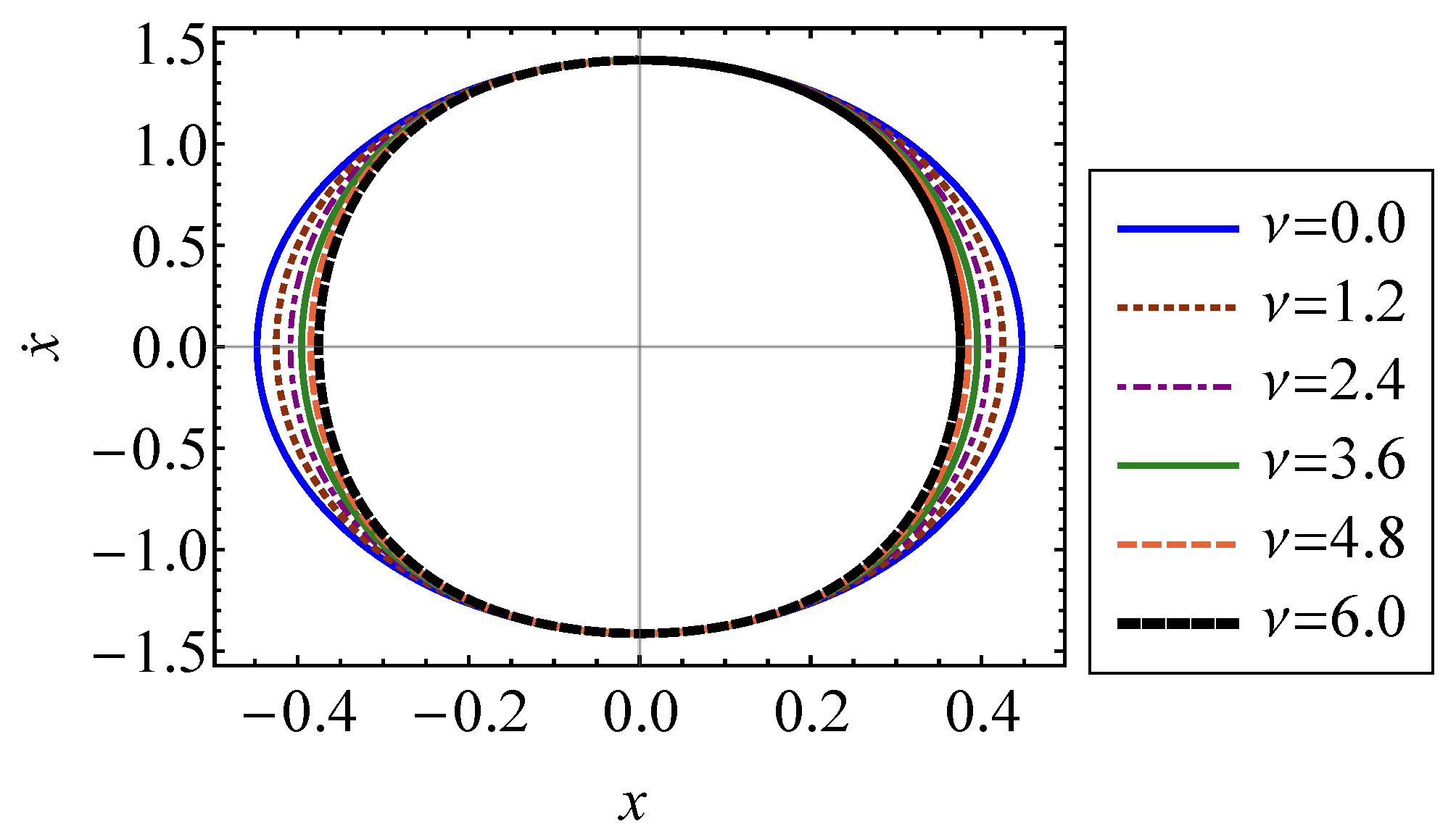
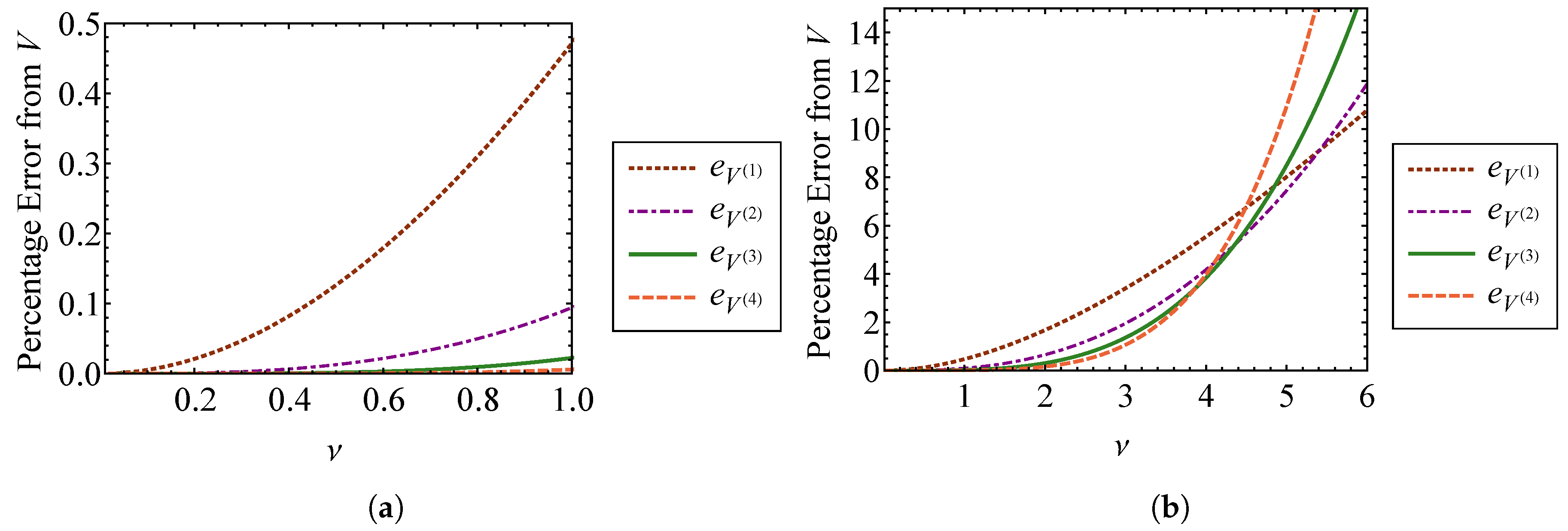
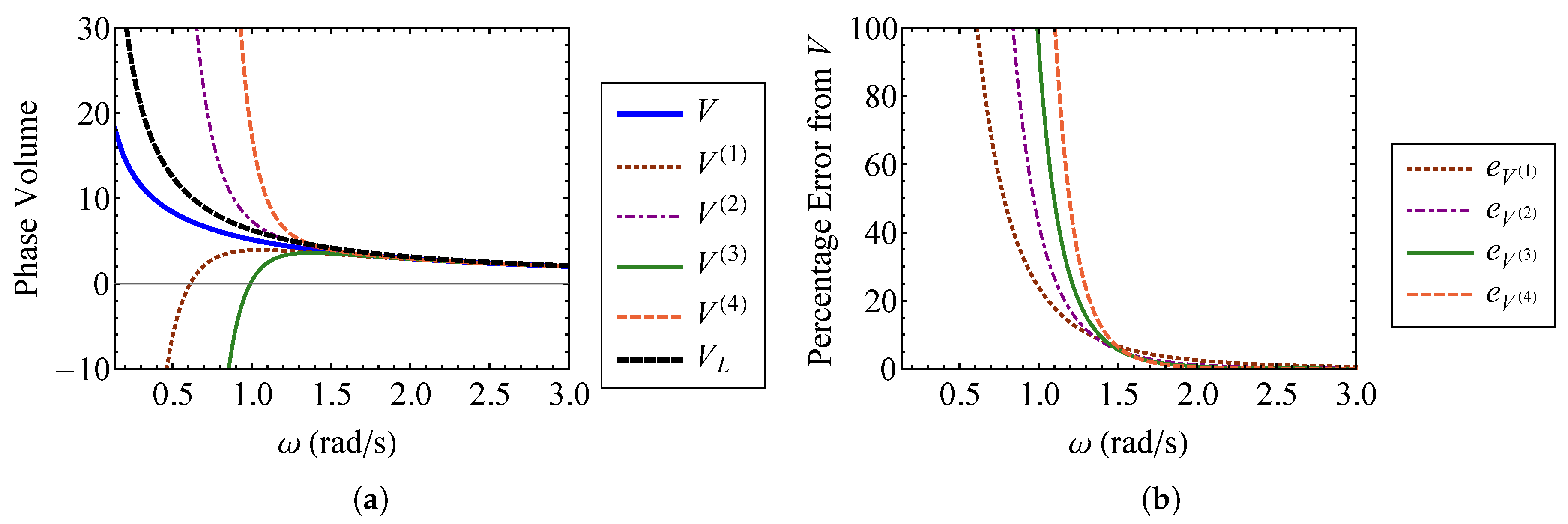
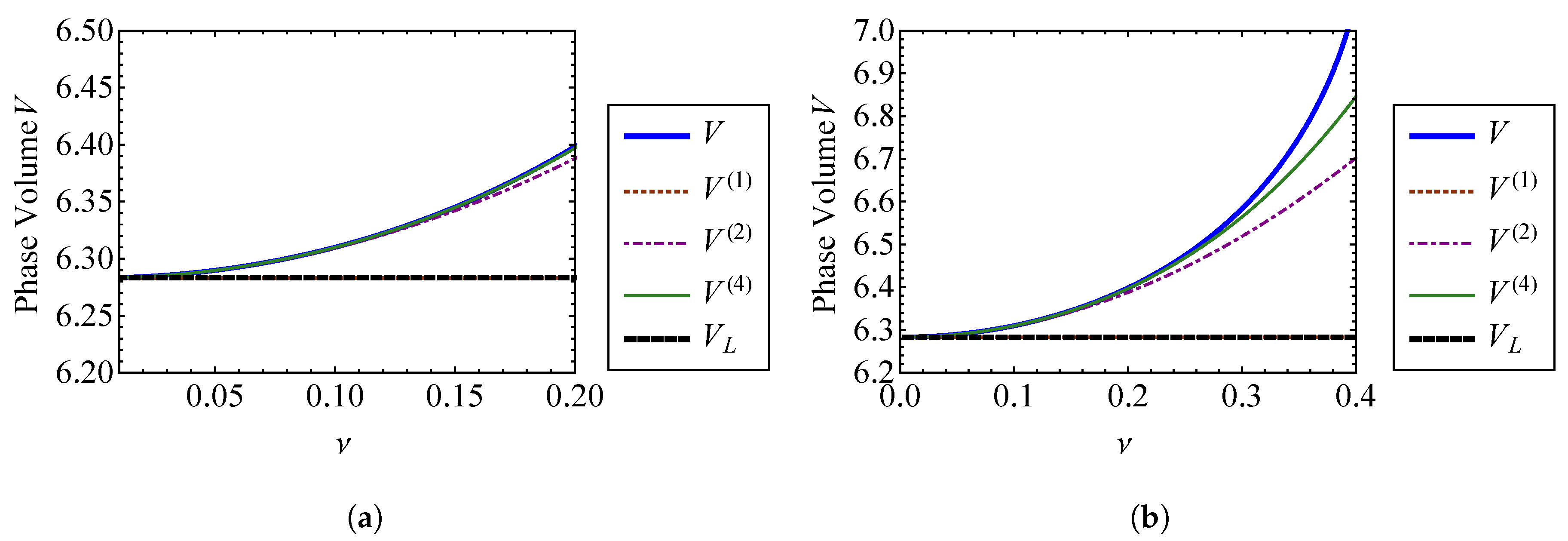
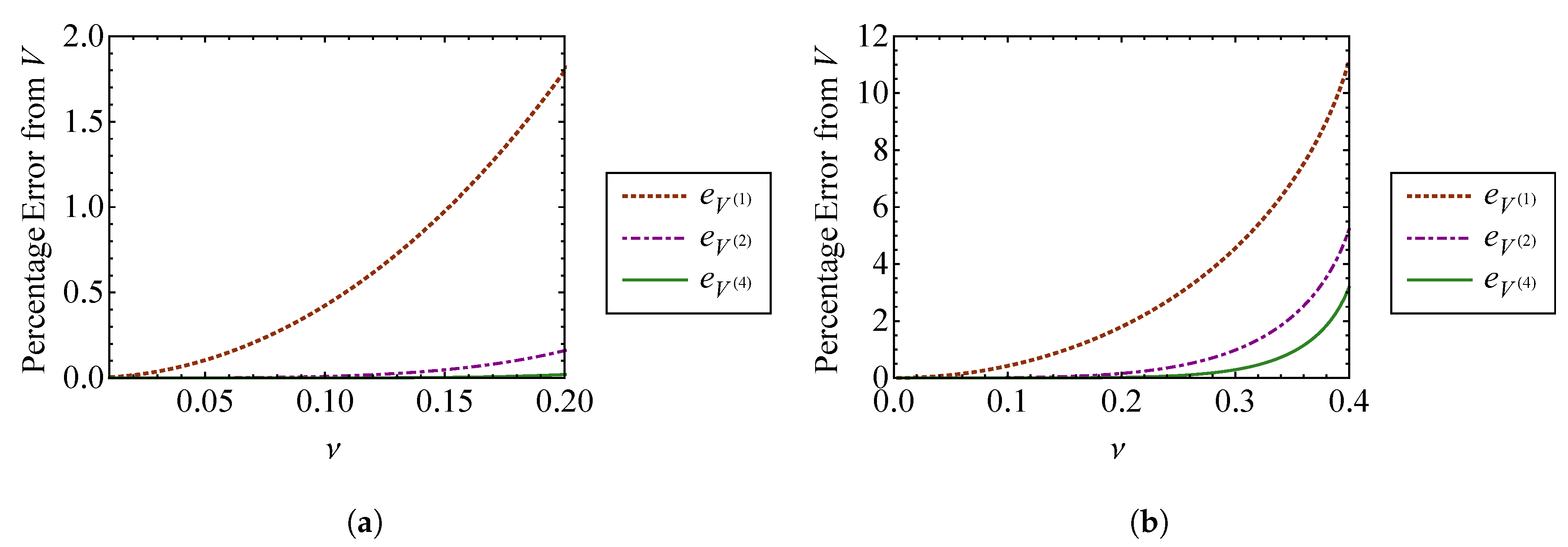
4.1.1. The Phase Volume
4.1.2. Khinchin’s Entropy
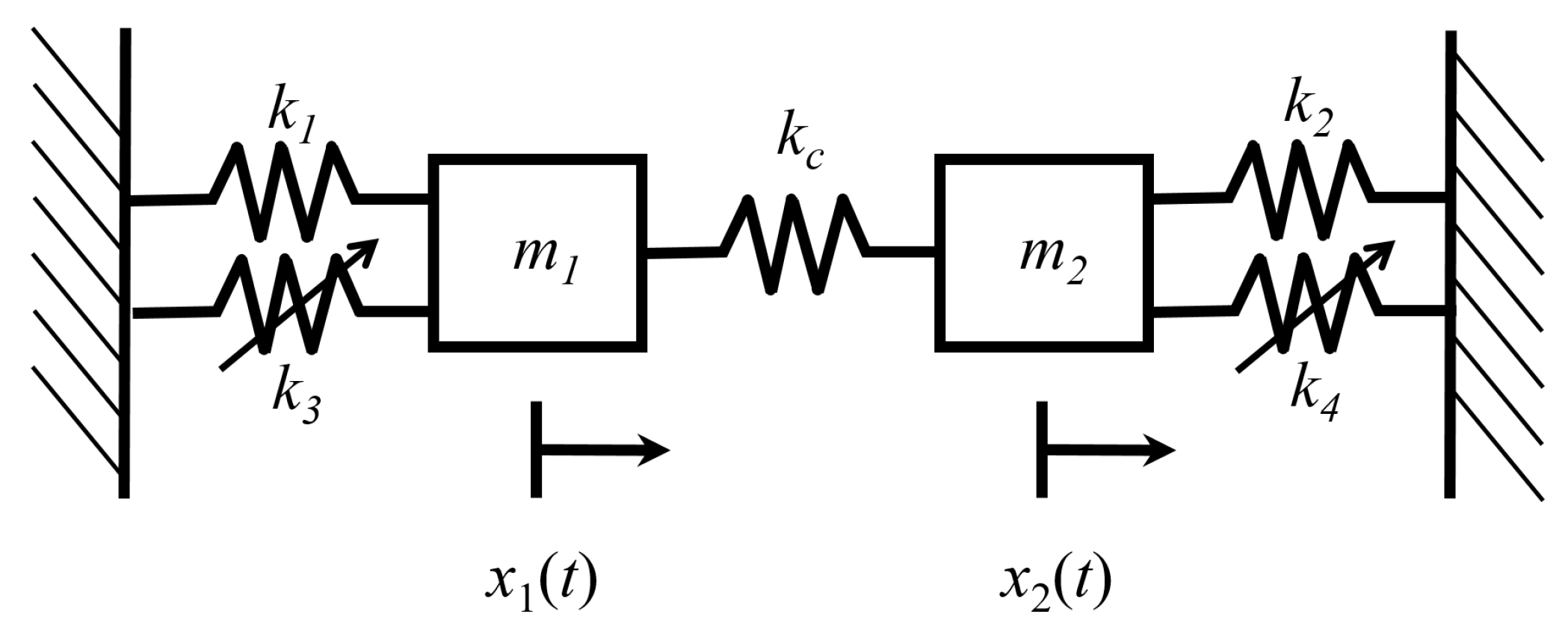
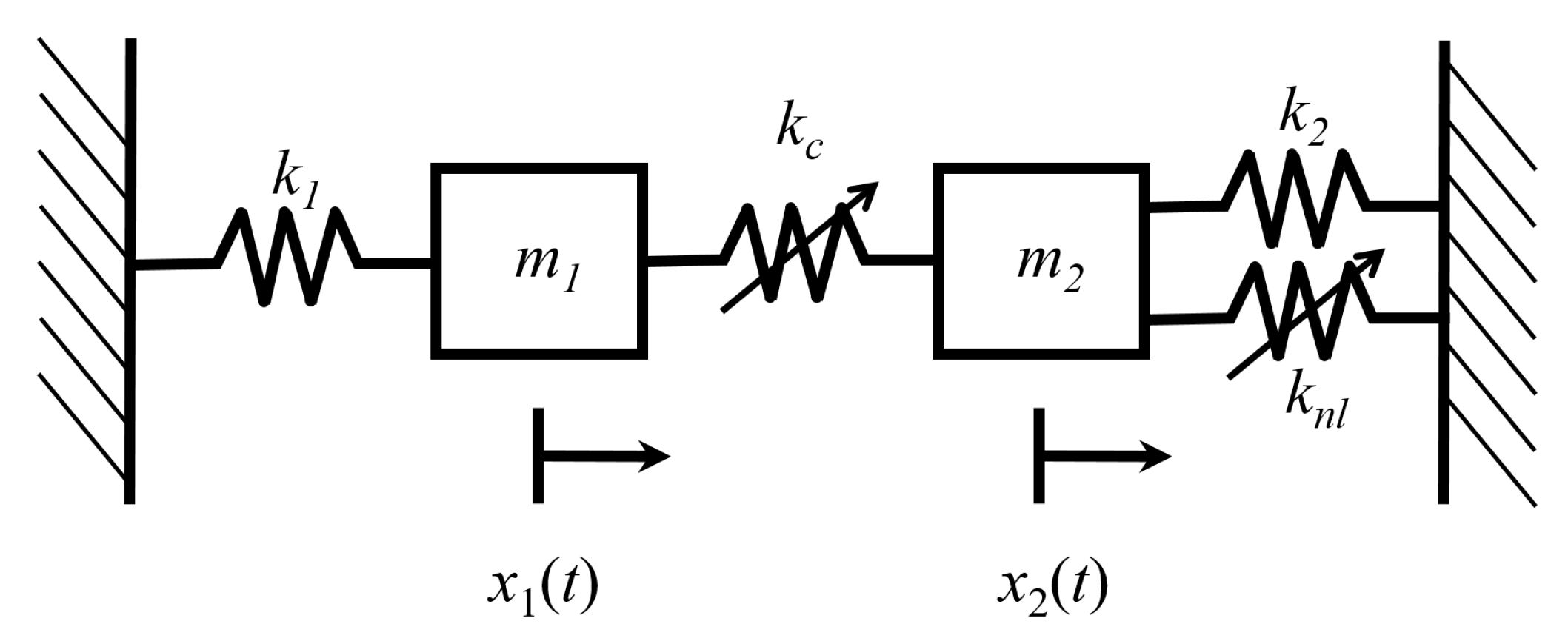
4.2. Coupled Duffing Oscillators
4.2.1. Entropy of the Coupled Duffing System
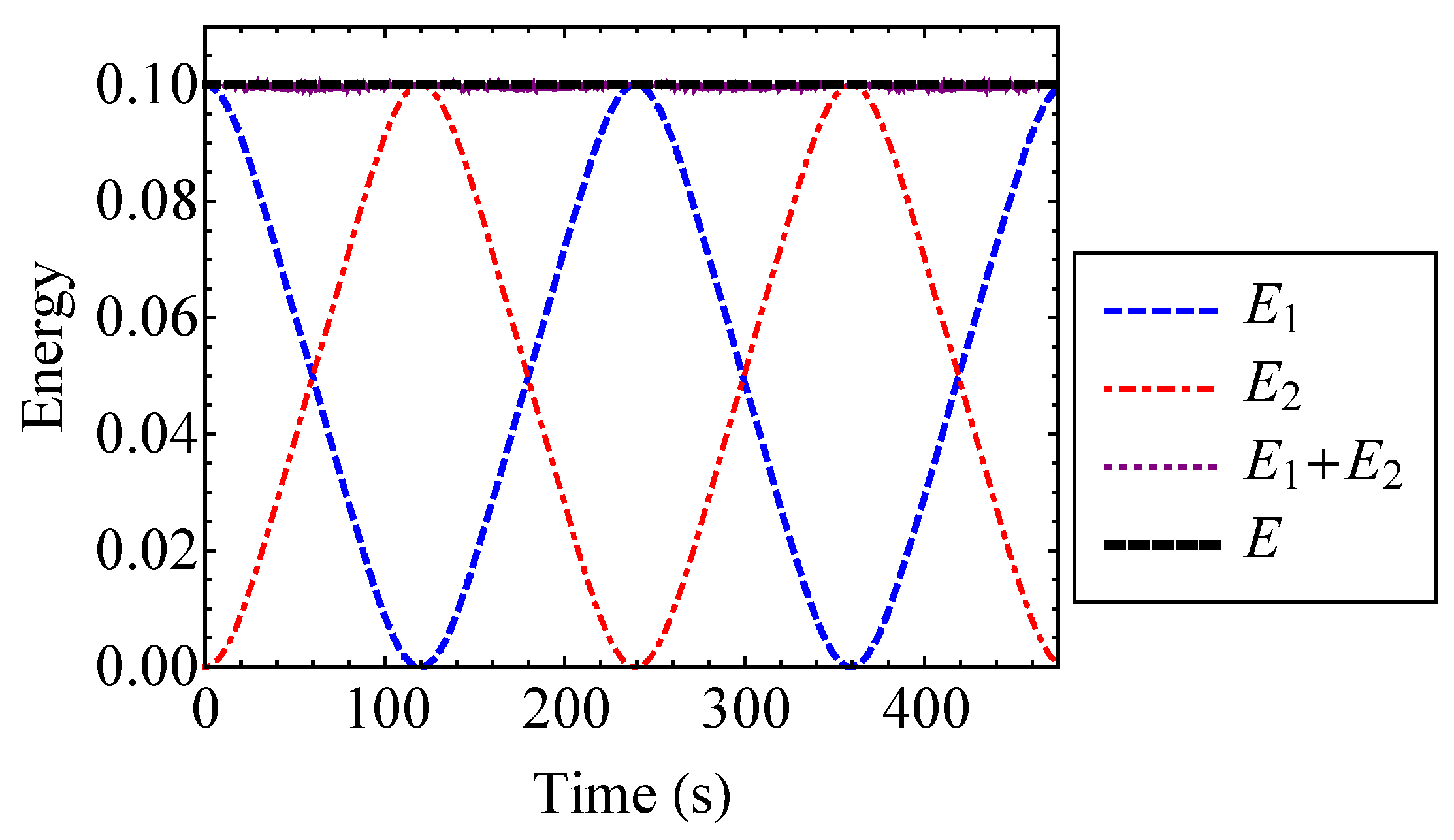
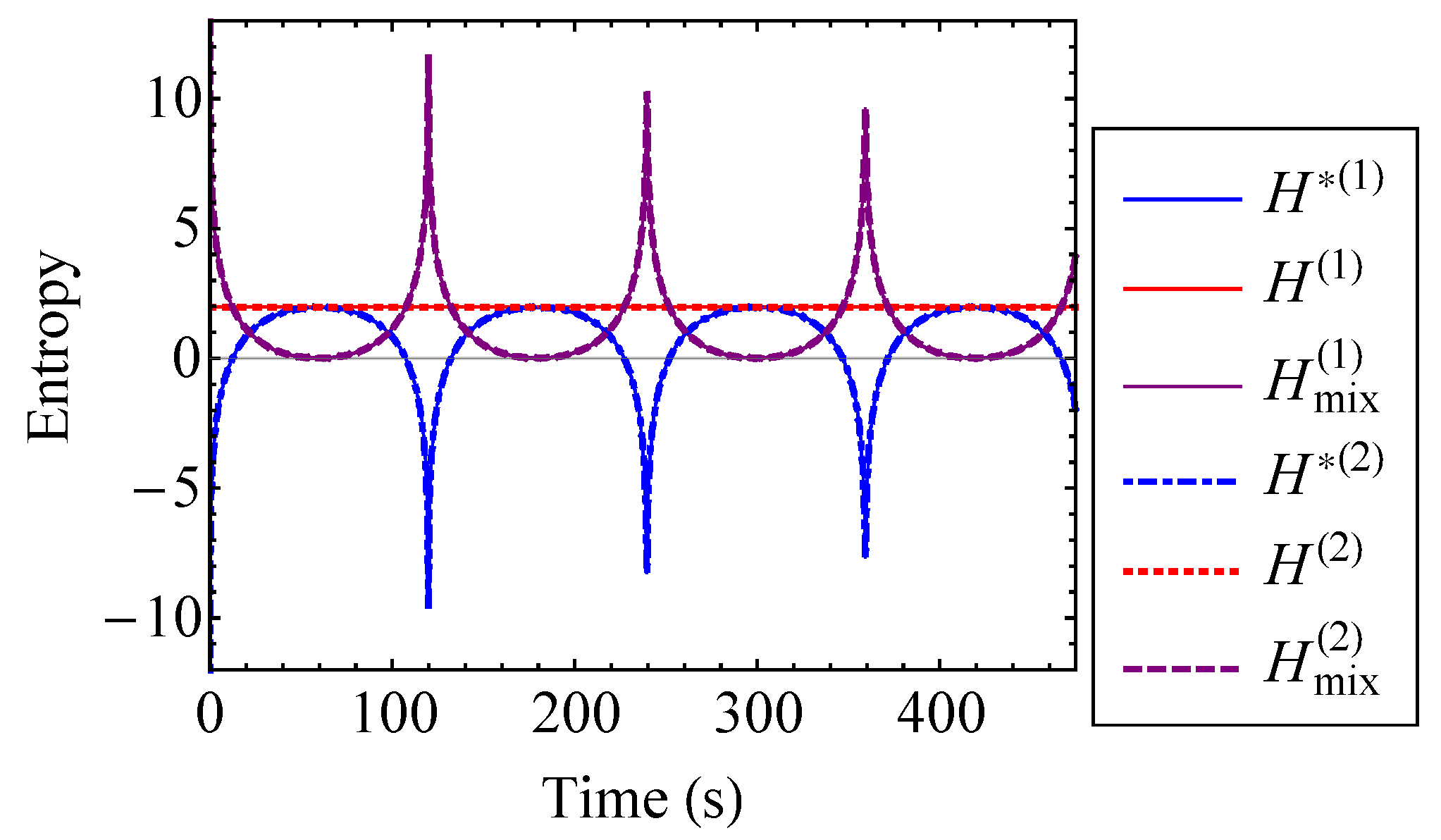
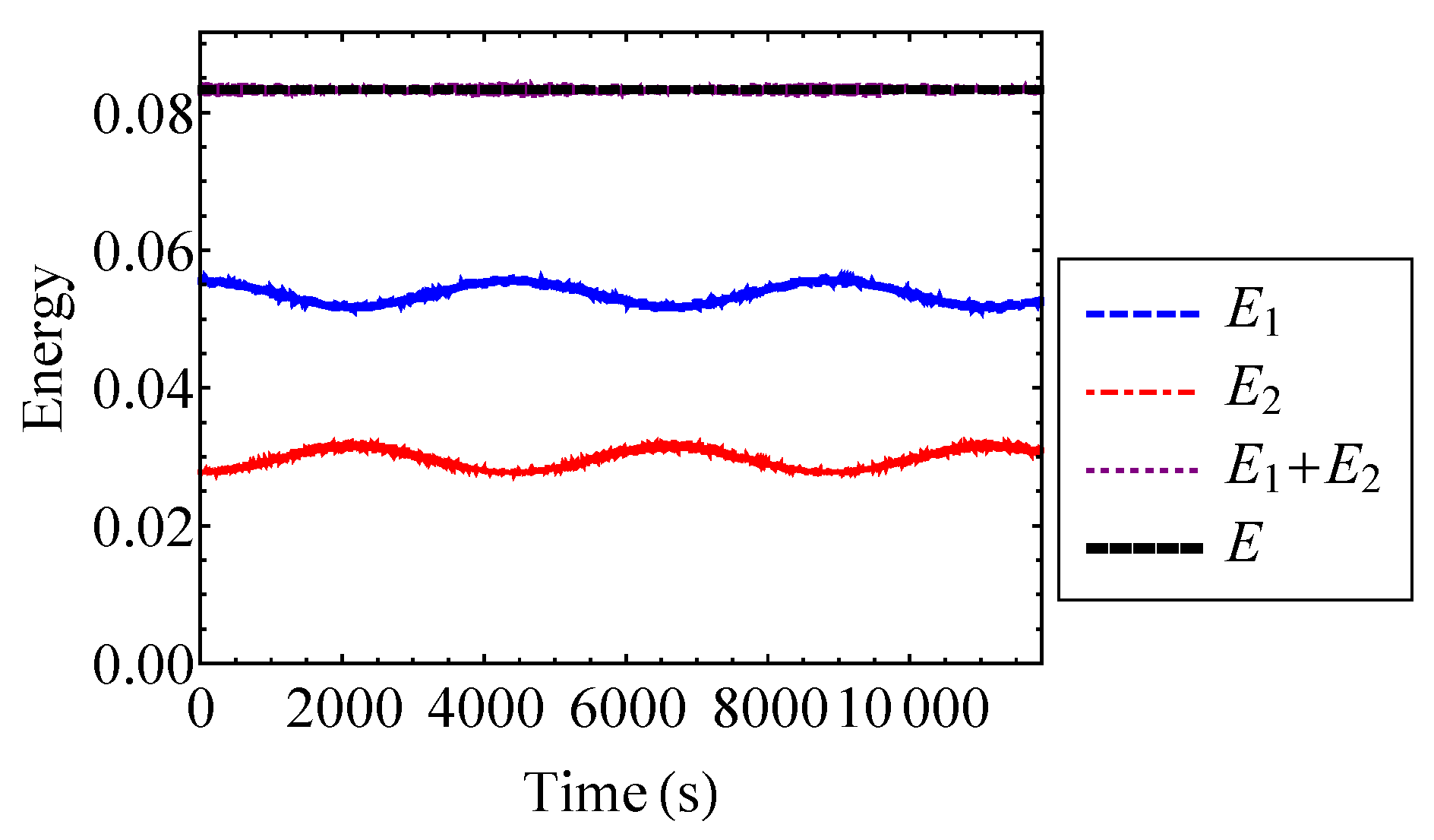
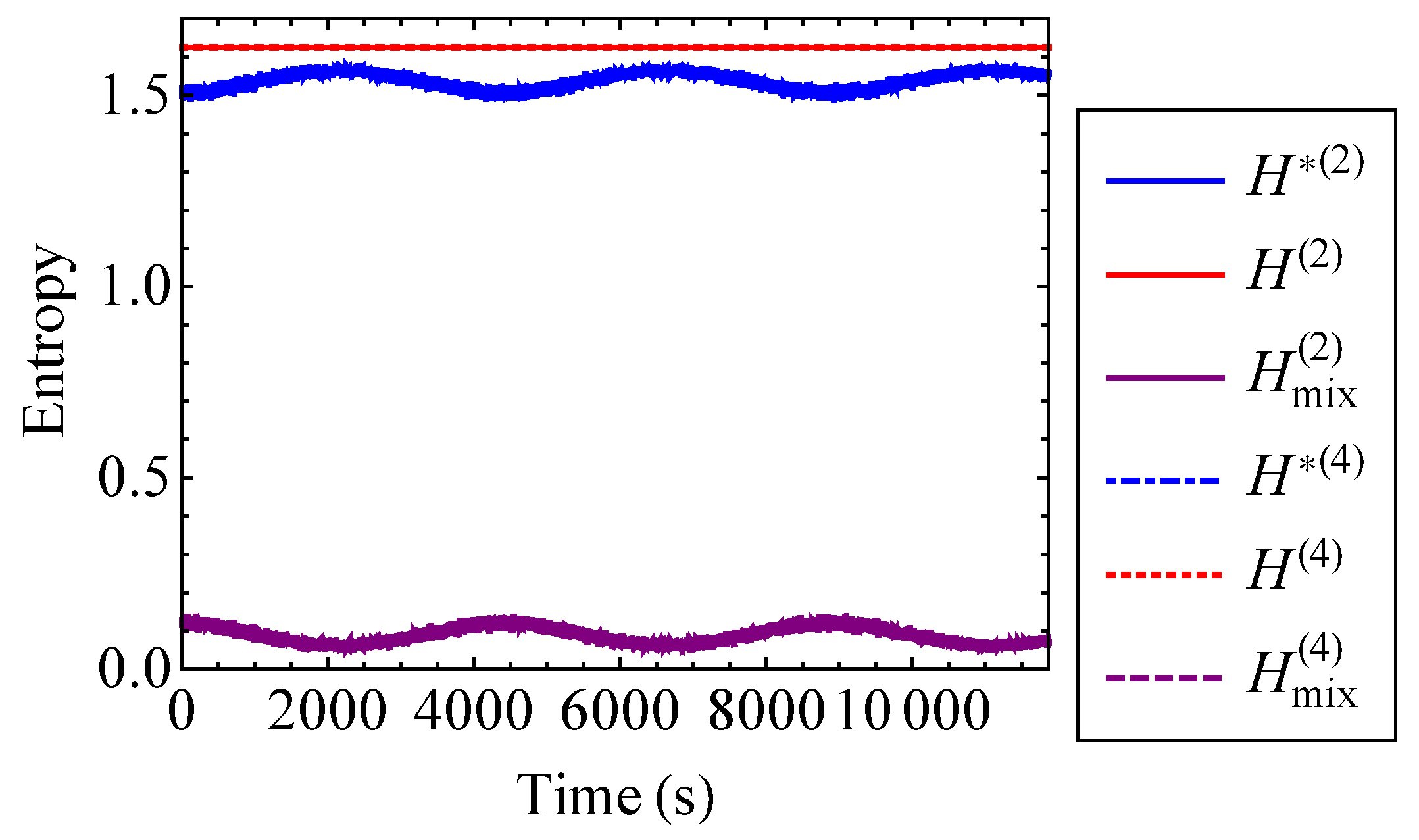
4.2.2. Mixing Entropy of the Coupled Duffing System
5. Entropy of Henon–Heiles Oscillators
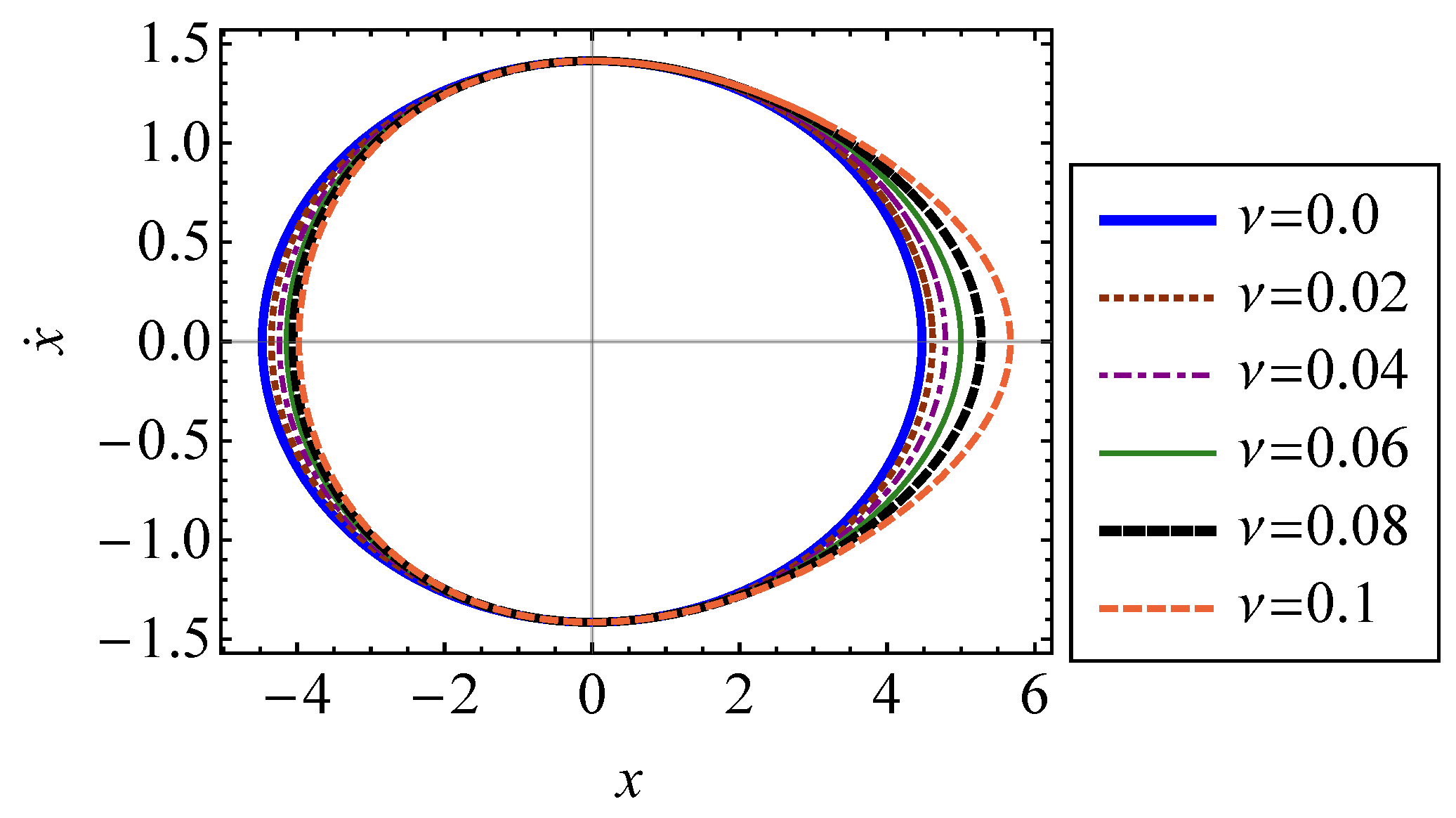
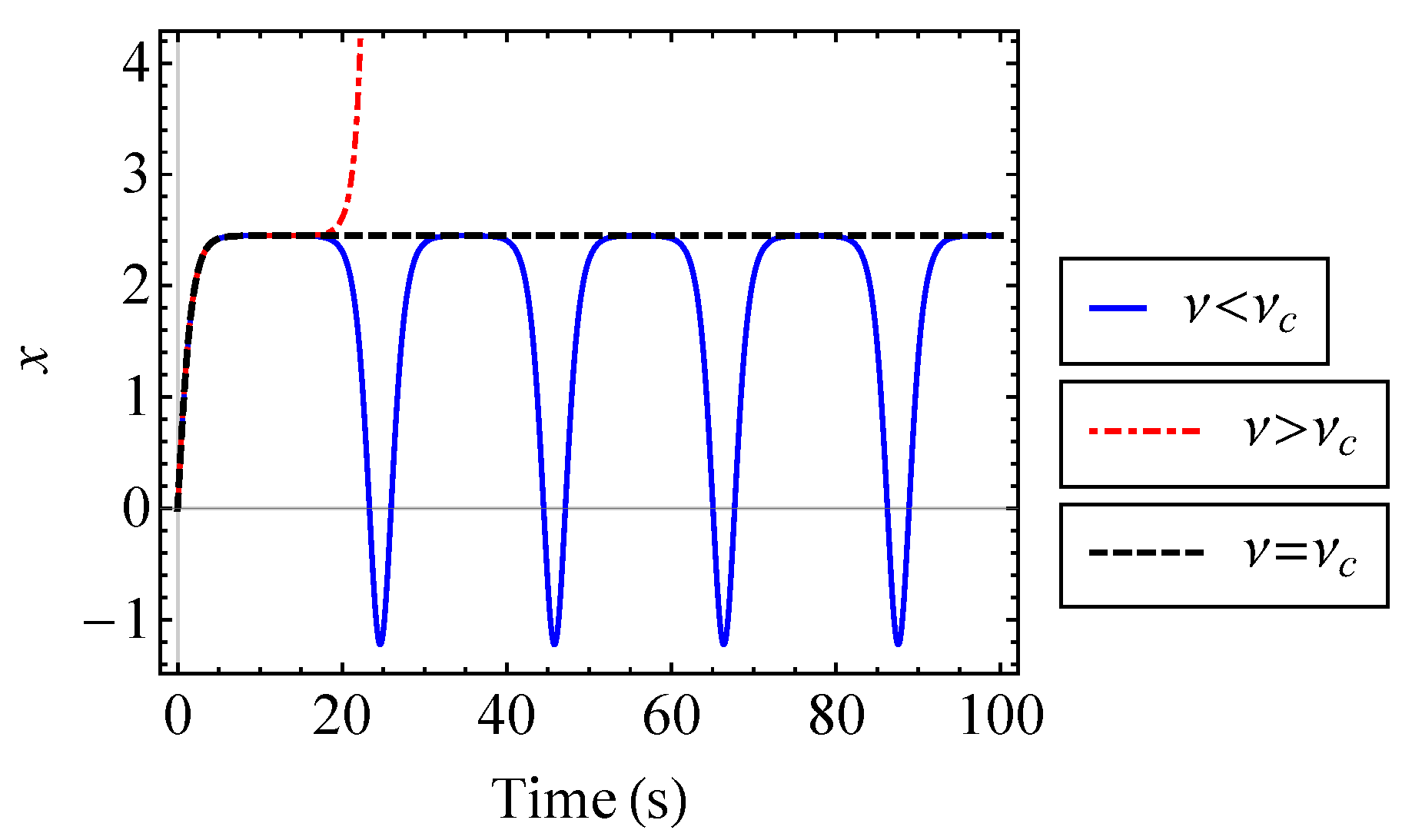
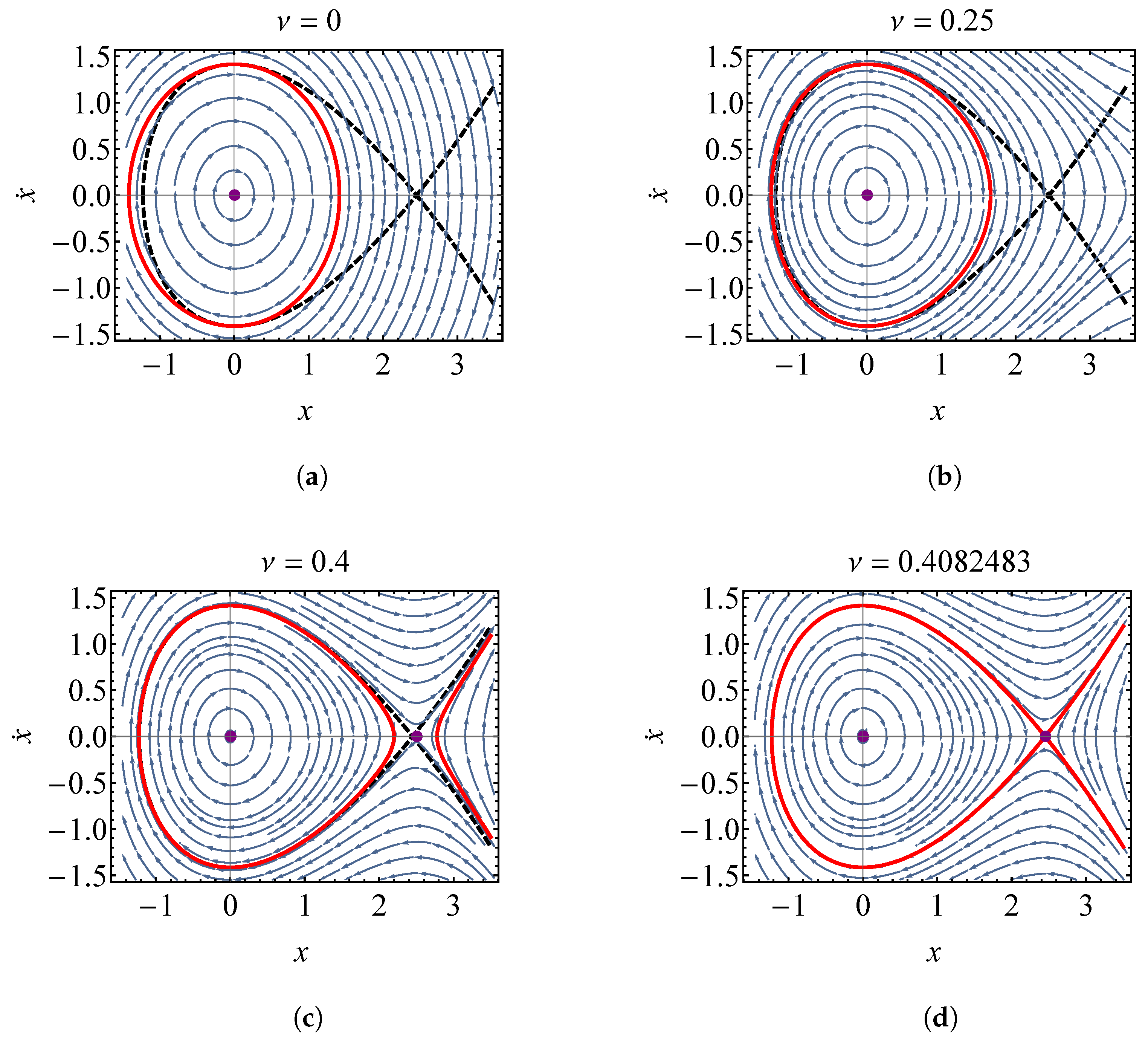
5.1. Single Degree of Freedom Oscillator with Third Order Anharmonic Potential
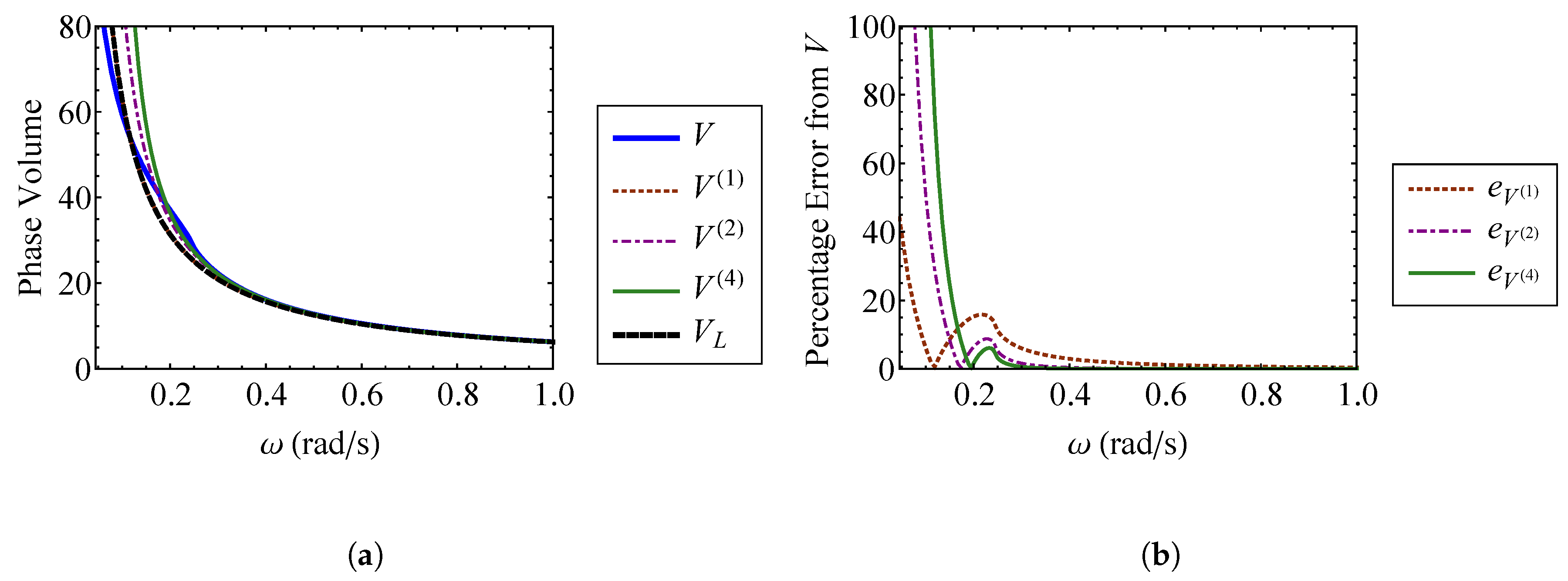
5.1.1. The Phase Volume
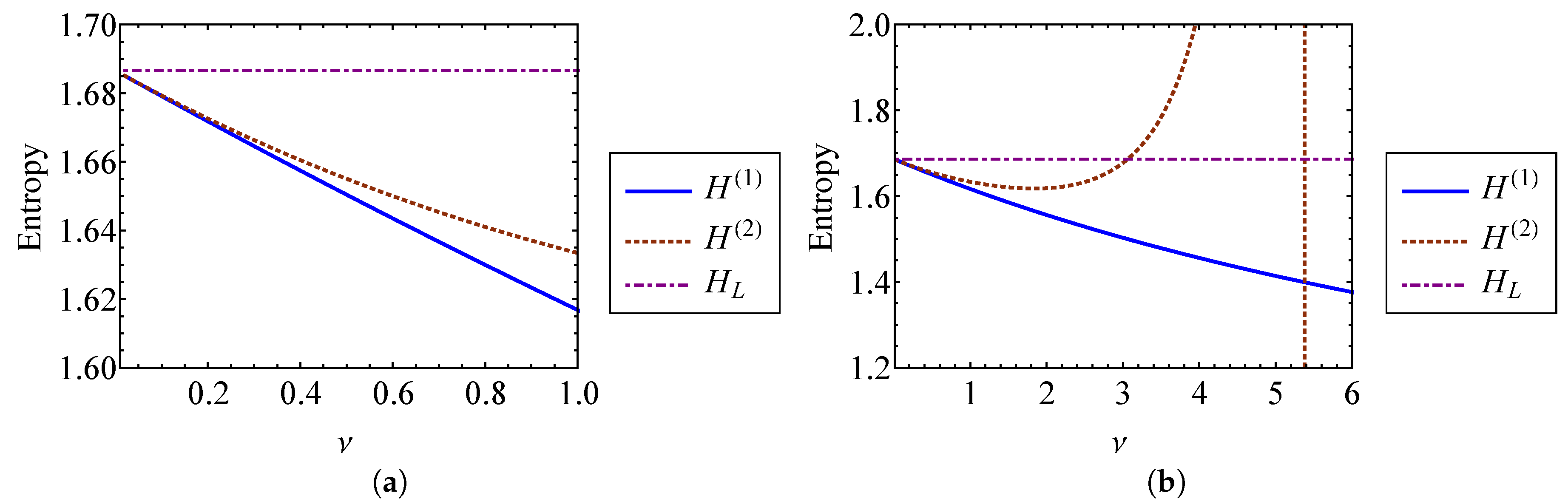
5.1.2. Khinchin’s Entropy
5.2. Henon–Heiles Oscillators
5.2.1. Entropy of the Henon–Heiles Oscillators
5.2.2. Mixing Entropy of the Henon–Heiles Oscillators
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Derivative of with respect to x | |
| Time-derivative of | |
| i-th displacement degree of freedom | |
| Maximum displacement over time | |
| i-th oscillator mass | |
| i-th spring stiffness | |
| Nonlinear spring stiffness | |
| Coupling spring stiffness | |
| q | Generalized coordinate |
| p | Generalized velocity |
| Nonlinearity multiplier | |
| i-th order approximation of with respect to | |
| i-th term in expansion of with respect to | |
| E | Energy |
| T | Thermodynamic temperature |
| System trajectory in phase space | |
| V | Equi-energy volume in phase space |
| Structure function | |
| Generating function | |
| H | Entropy |
| Decoupled entropy | |
| Mixing entropy | |
| Scalar constants | |
| Value that minimizes H | |
| Equal by definition | |
| Generalized coordinate matrix |
Appendix A
References
- Lyon, R.H. Theory and Application of Statistical Energy Analysis; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Crocker, M.; Price, A. Sound transmission using statistical energy analysis. J. Sound Vib. 1969, 9, 469–486. [Google Scholar] [CrossRef]
- Crandall, S.H.; Lotz, R. On the coupling loss factor in statistical energy analysis. J. Acoust. Soc. Am. 1971, 49, 352–356. [Google Scholar] [CrossRef]
- Fahy, F.J. Statistical energy analysis: A critical overview. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1994, 346, 431–447. [Google Scholar]
- Burroughs, C.B. An Introduction to Statistical Energy Analysis. J. Acoust. Soc. Am. 1997, 101, 1779–1789. [Google Scholar] [CrossRef]
- Lafont, T.; Totaro, N.; Le Bot, A. Review of statistical energy analysis hypotheses in vibroacoustics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20130515. [Google Scholar] [CrossRef]
- Carcaterra, A. An entropy formulation for the analysis of energy flow between mechanical resonators. Mech. Syst. Signal Process. 2002, 16, 905–920. [Google Scholar] [CrossRef]
- Newland, D. Power flow between a class of coupled oscillators. J. Acoust. Soc. Am. 1968, 43, 553–559. [Google Scholar] [CrossRef]
- Woodhouse, J. An introduction to statistical energy analysis of structural vibration. Appl. Acoust. 1981, 14, 455–469. [Google Scholar] [CrossRef]
- Norton, M.P.; Karczub, D.G. Fundamentals of Noise and Vibration Analysis for Engineers; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Tufano, D.; Sotoudeh, Z. Overview of coupling loss factors for damped and undamped simple oscillators. J. Sound Vib. 2016, 372, 223–238. [Google Scholar] [CrossRef]
- Spelman, G.; Langley, R. Statistical energy analysis of nonlinear vibrating systems. Phil. Trans. R. Soc. A 2015, 373, 20140403. [Google Scholar] [CrossRef] [PubMed]
- Soize, C. Coupling Between an Undamped Linear Acoustic Fluid and a Damped Nonlinear Structure—Statistical Energy Analysis Considerations. J. Acoust. Soc. Am. 1995, 98, 373–385. [Google Scholar] [CrossRef]
- Le Bot, A.; Carcaterra, A.; Mazuyer, D. Statistical vibroacoustics and entropy concept. Entropy 2010, 12, 2418–2435. [Google Scholar] [CrossRef]
- Carcaterra, A. Thermodynamic temperature in linear and nonlinear Hamiltonian Systems. Int. J. Eng. Sci. 2014, 80, 189–208. [Google Scholar] [CrossRef]
- Le Bot, A.; Carbonelli, A.; Liaudet, J.P. On the Usefulness of Entropy in Statistical Energy Analysis. Available online: https://hal.archives-ouvertes.fr/hal-00811020/ (accessed on 25 May 2019).
- Tufano, D.A.; Sotoudeh, Z. Introducing Entropy for the Statistical Energy Analysis of an Artificially Damped Oscillator. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition, Houston, TE, USA, 13–19 November 2015; p. V013T16A012. [Google Scholar]
- Khinchin, A.I. Mathematical Foundations of Statistical Mechanics; Courier Corporation: North Chelmsford, MA, USA, 1949. [Google Scholar]
- Carcaterra, A. Entropy in vibration: energy sharing among linear and nonlinear freely vibrating systems. In Proceedings of the Tenth International Congress on Sound and Vibration, Stockholm, Sweeden, 7–10 July 2003. [Google Scholar]
- Carcaterra, A. An entropy approach to statistical energy analysis. In Proceedings of the 1998 International Congress on Noise Control Engineering, Christchurch, New Zealand, 16–18 November 1998; pp. 1049–1052. [Google Scholar]
- Berdichevsky, V. Thermodynamics of Chaos and Order; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Le Bot, A. Entropy in statistical energy analysis. J. Acoust. Soc. Am. 2009, 125, 1473–1478. [Google Scholar] [CrossRef] [PubMed]
- Sotoudeh, Z. Exploring Different Definitions of Entropy for Statistical Energy Analysis. In Proceedings of the International Mechanical Engineering Congress & Exposition, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar]
- Berdichevsky, V.; Alberti, M. Statistical mechanics of Hénon-Heiles oscillators. Phys. Rev. A 1991, 44, 858. [Google Scholar] [CrossRef] [PubMed]
- Tufano, D.A.; Sotoudeh, Z. Entropy for Strongly Coupled Oscillators. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016. [Google Scholar]
- Tufano, D.; Sotoudeh, Z. Entropy for Nonconservative Vibrating Systems. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017; p. 0409. [Google Scholar]
- Tufano, D.; Sotoudeh, Z. Exploring the Entropy Concept for Coupled Oscillators. J. Int. Eng. Sci. 2016. submitted. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Introduction to Perturbation Methods; John Wiley & Sons: Hoboken, NJ, USA, 1981. [Google Scholar]
- Nagle, R.K.; Saff, E.B.; Snider, A.D. Fundamentals of Differential Equations; Addison-Wesley: Boston, MA, USA, 2000. [Google Scholar]
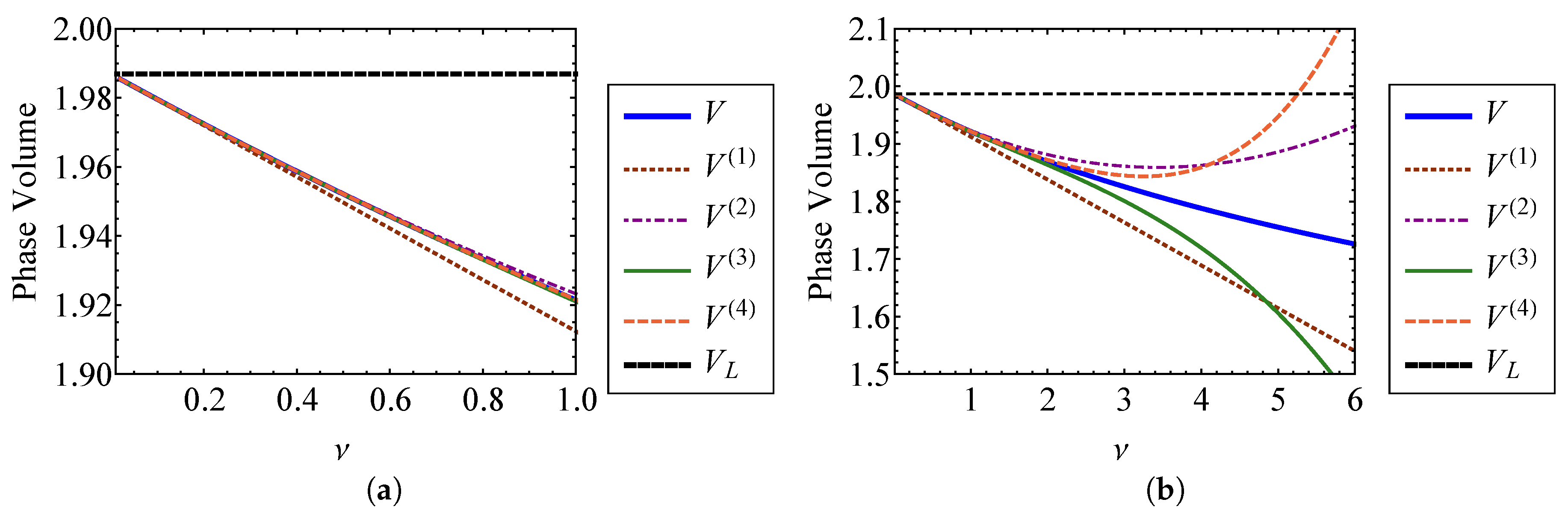
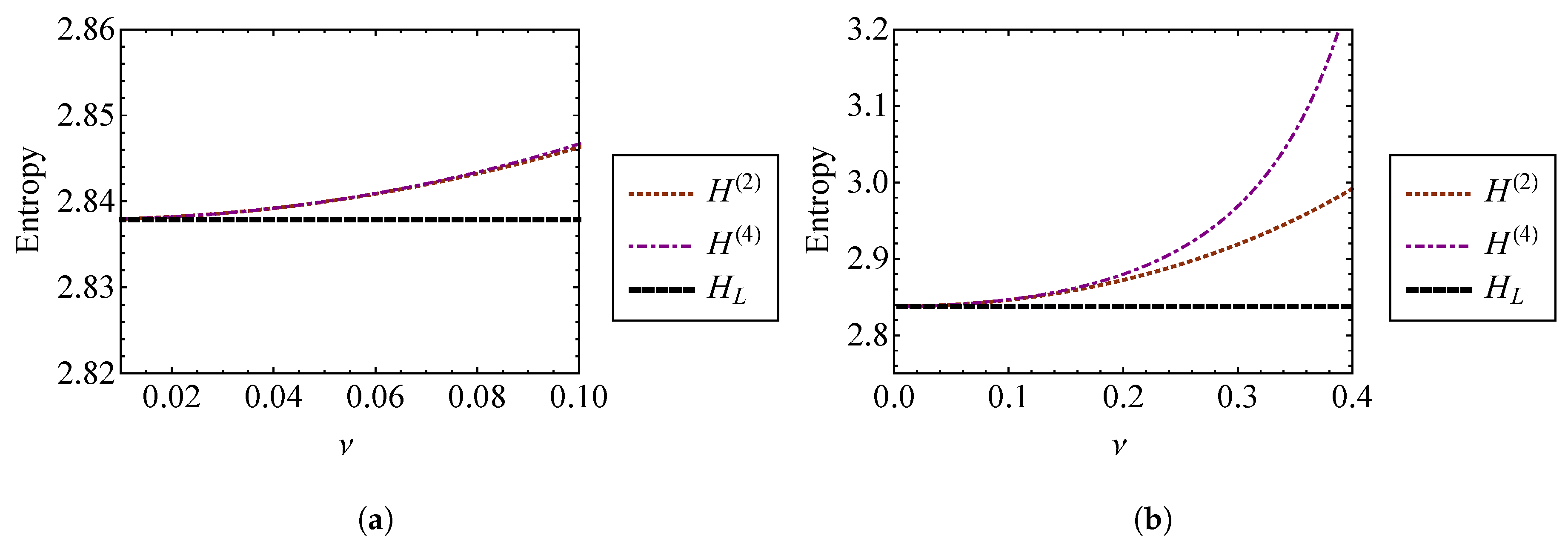
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sotoudeh, Z. Entropy and Mixing Entropy for Weakly Nonlinear Mechanical Vibrating Systems. Entropy 2019, 21, 536. https://doi.org/10.3390/e21050536
Sotoudeh Z. Entropy and Mixing Entropy for Weakly Nonlinear Mechanical Vibrating Systems. Entropy. 2019; 21(5):536. https://doi.org/10.3390/e21050536
Chicago/Turabian StyleSotoudeh, Zahra. 2019. "Entropy and Mixing Entropy for Weakly Nonlinear Mechanical Vibrating Systems" Entropy 21, no. 5: 536. https://doi.org/10.3390/e21050536
APA StyleSotoudeh, Z. (2019). Entropy and Mixing Entropy for Weakly Nonlinear Mechanical Vibrating Systems. Entropy, 21(5), 536. https://doi.org/10.3390/e21050536



