Entropy Generation via Ohmic Heating and Hall Current in Peristaltically-Flowing Carreau Fluid
Abstract
1. Introduction
2. Mathematical Model and Analysis
2.1. Flow Characteristics
2.2. Fluid Model
2.3. Development Problem
3. Analysis of Entropy Generation
4. Solution Methodology
4.1. Zeroth Order System and Boundary Conditions
4.2. First-Order System and Boundary Conditions
5. Discussion and Results
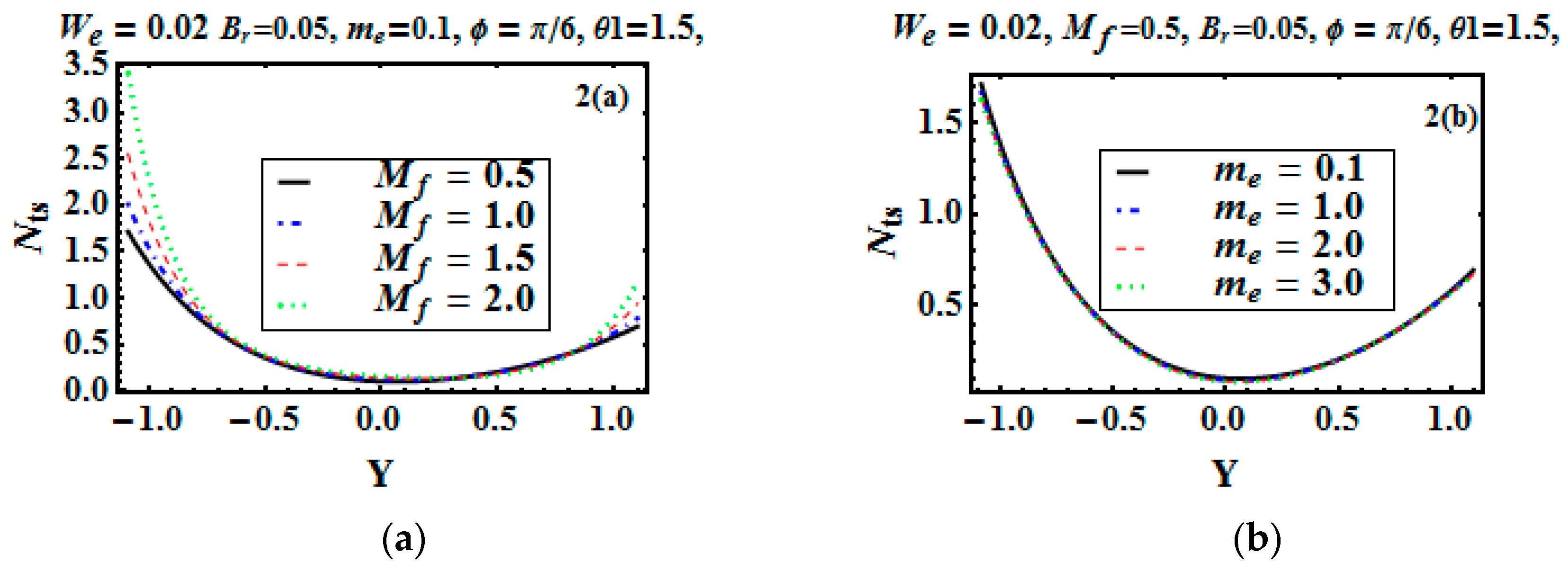
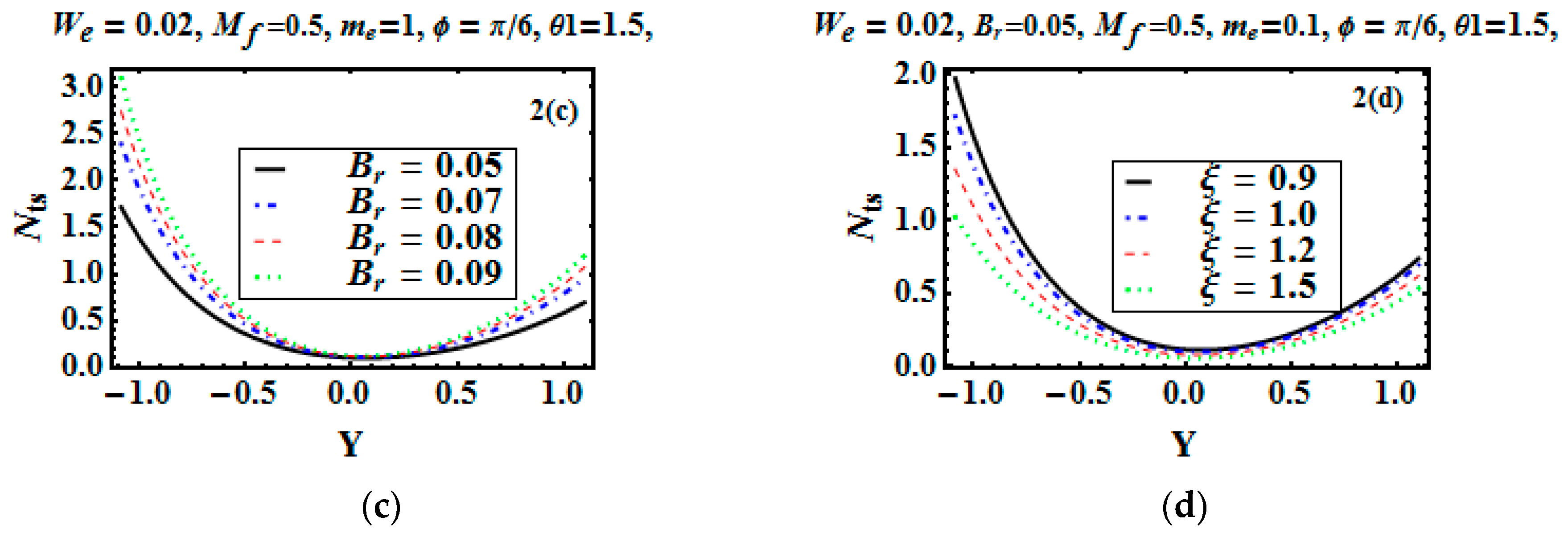
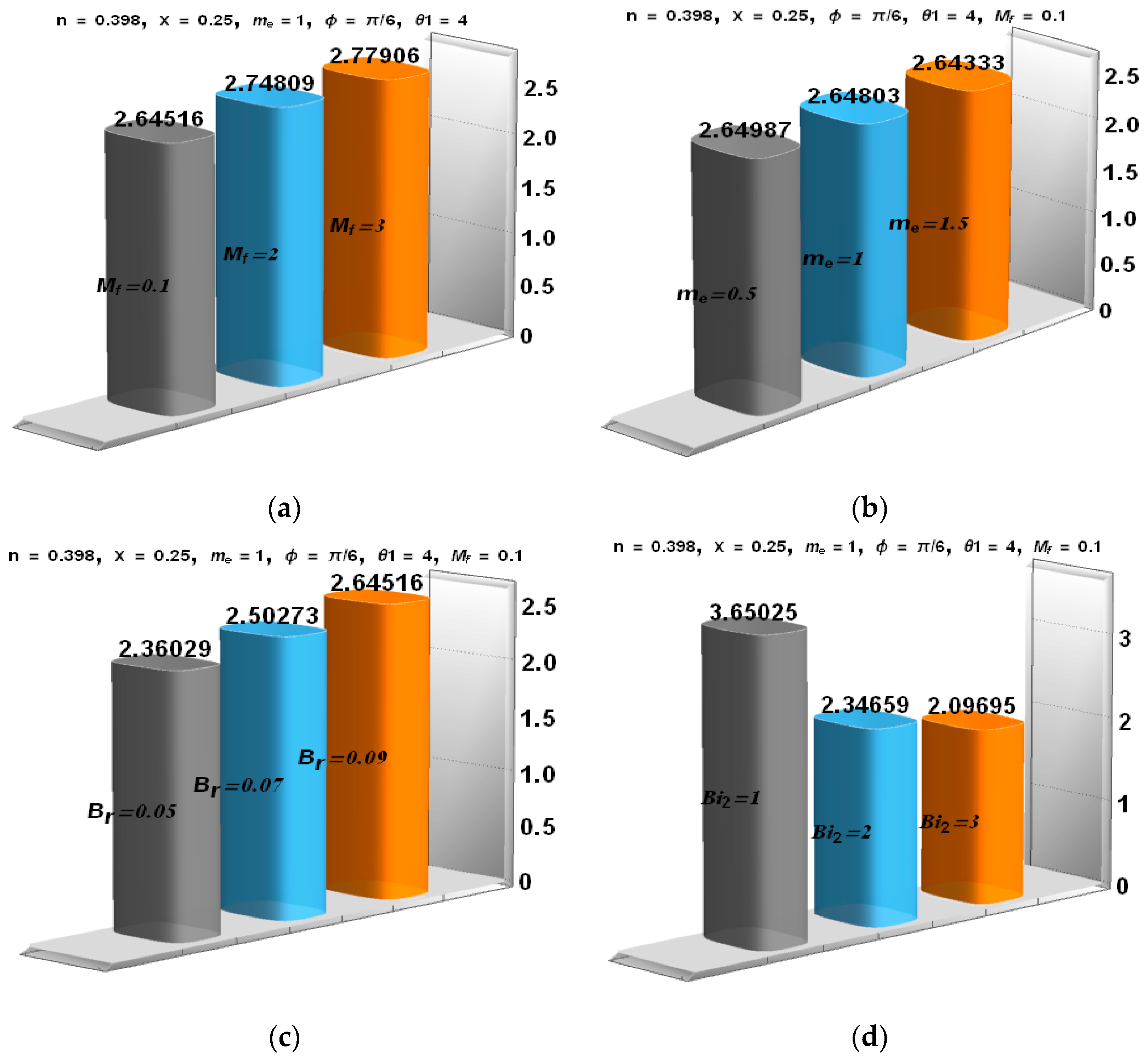
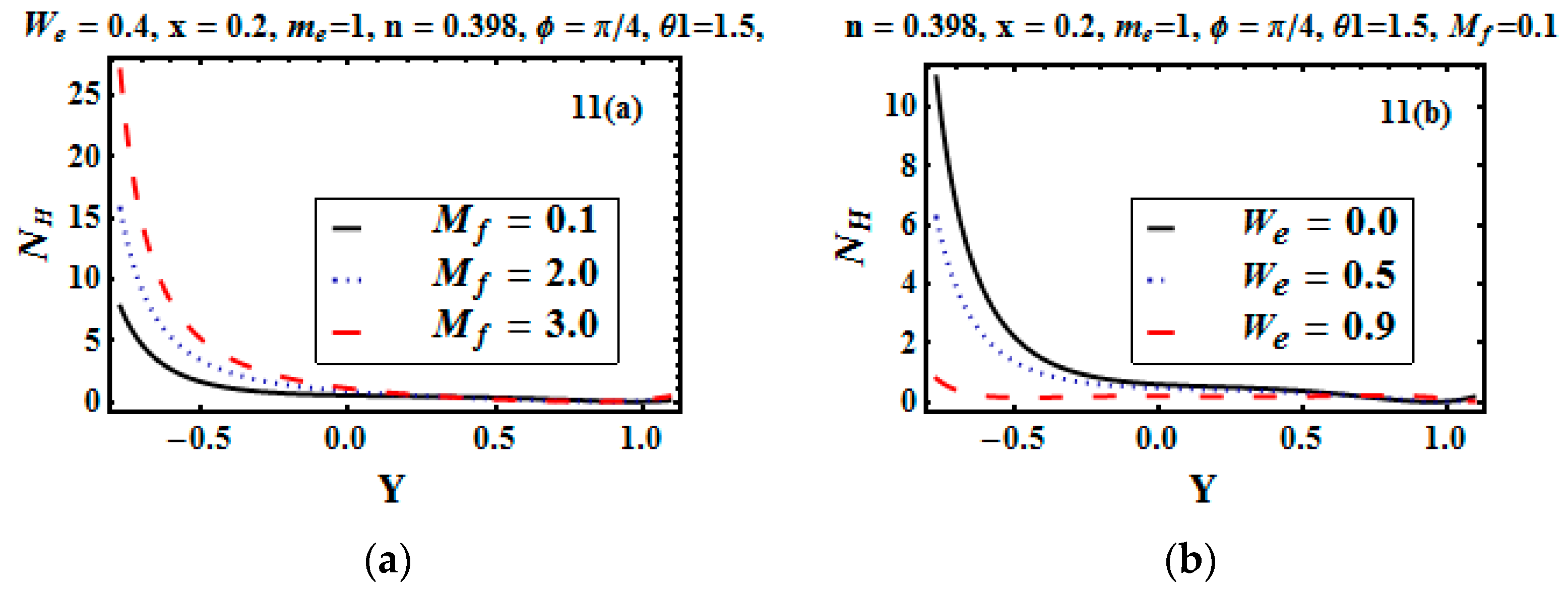
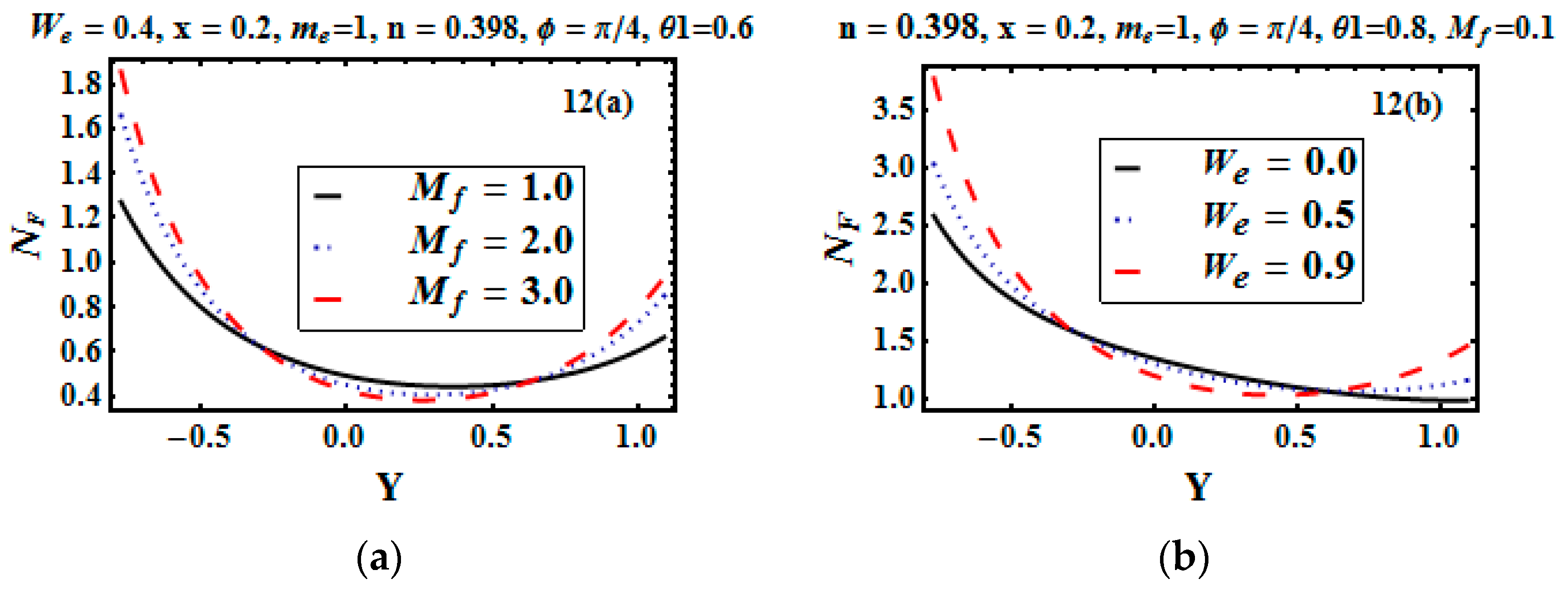
5.1. Analysis of Entropy Generation and Bejan Number
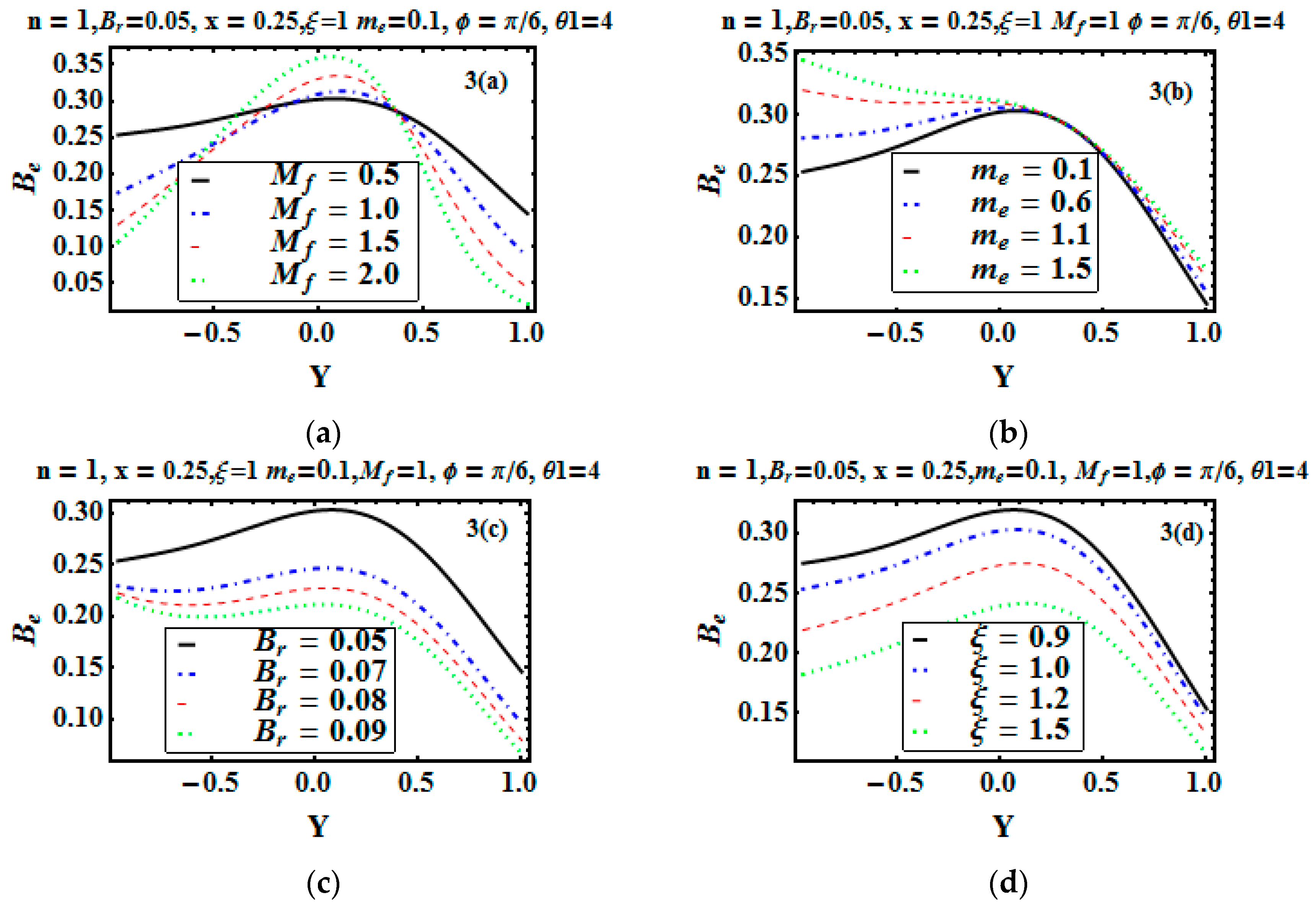
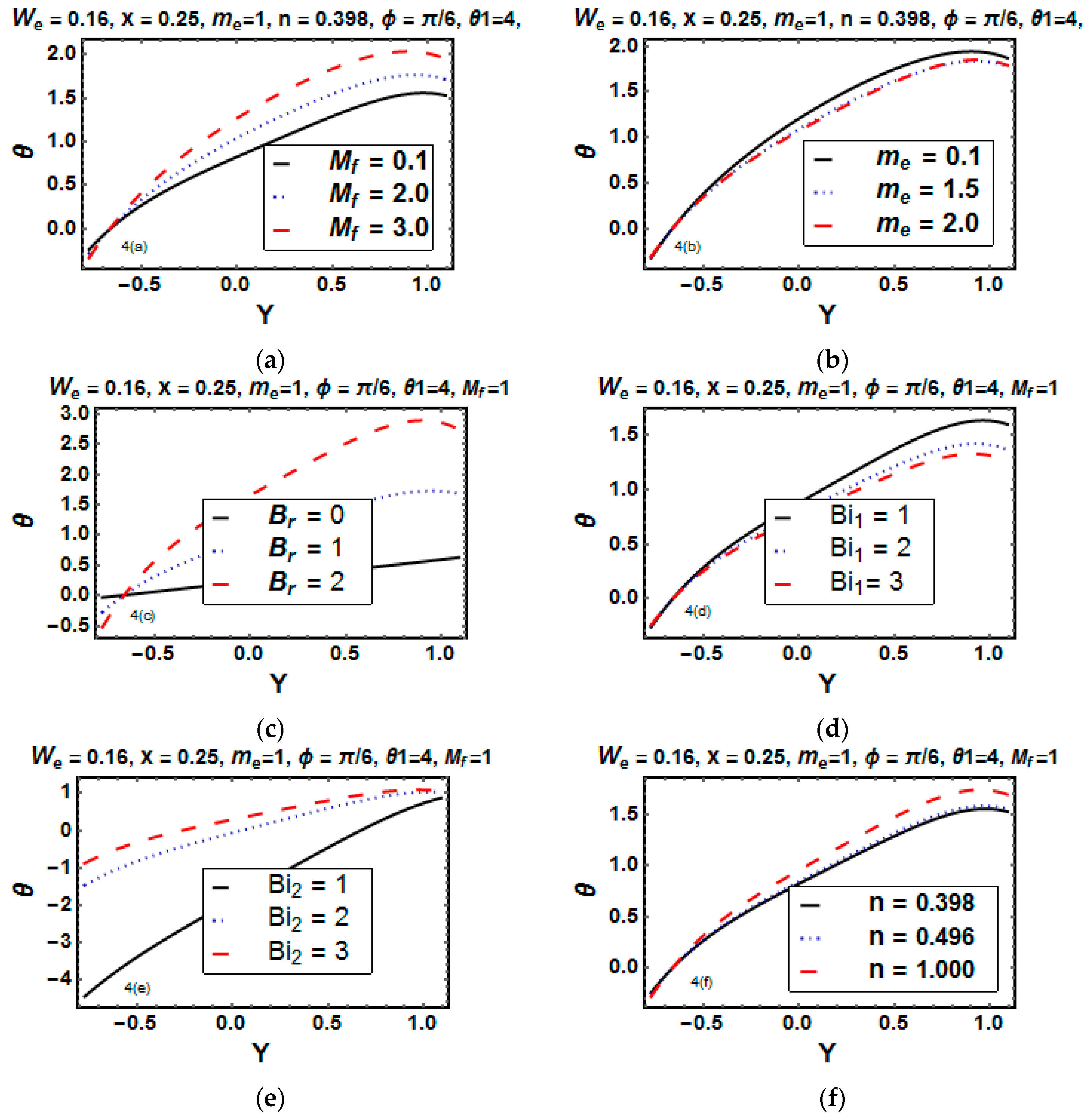
5.2. Analysis of Temperature
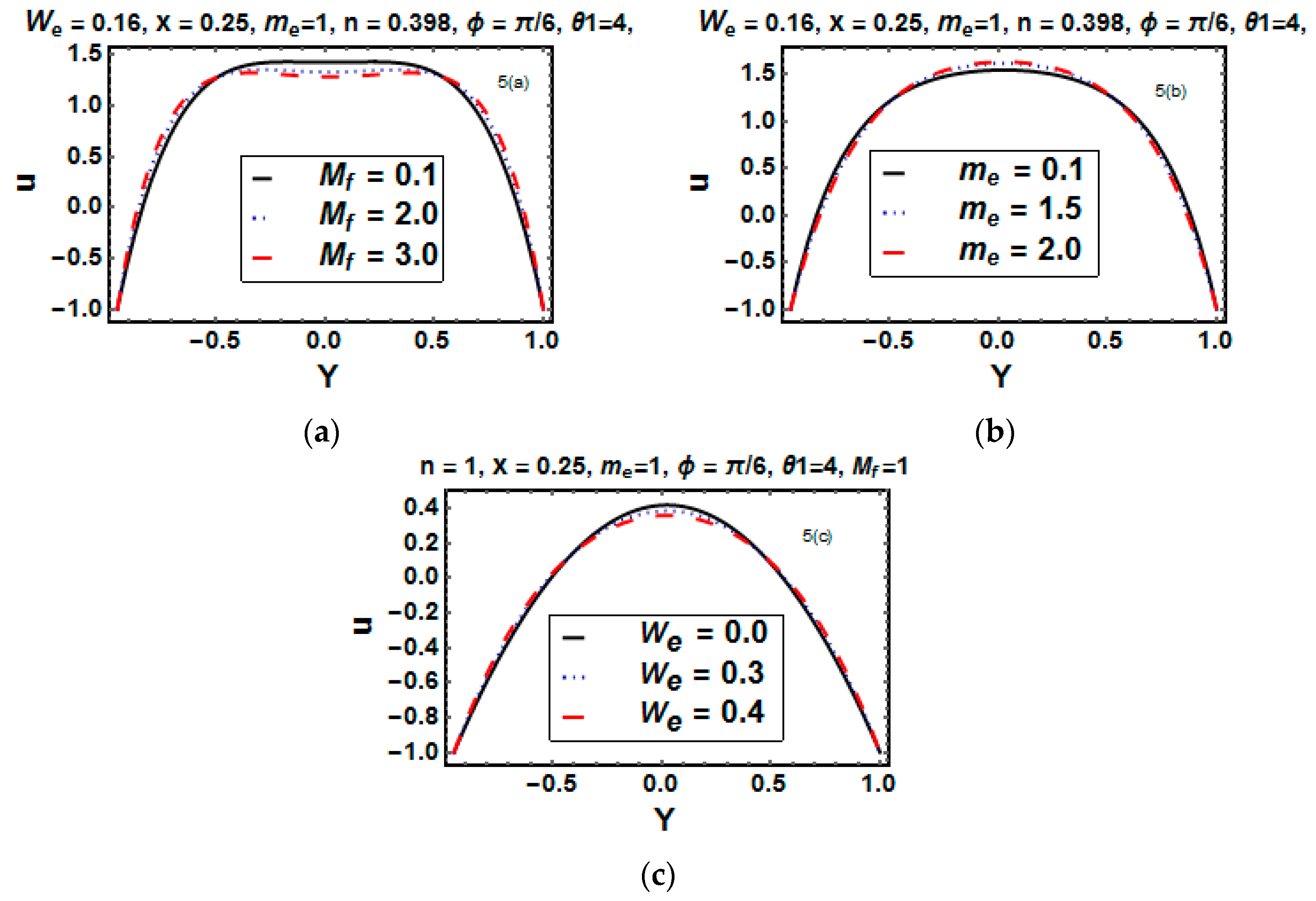
5.3. Analysis of Velocity
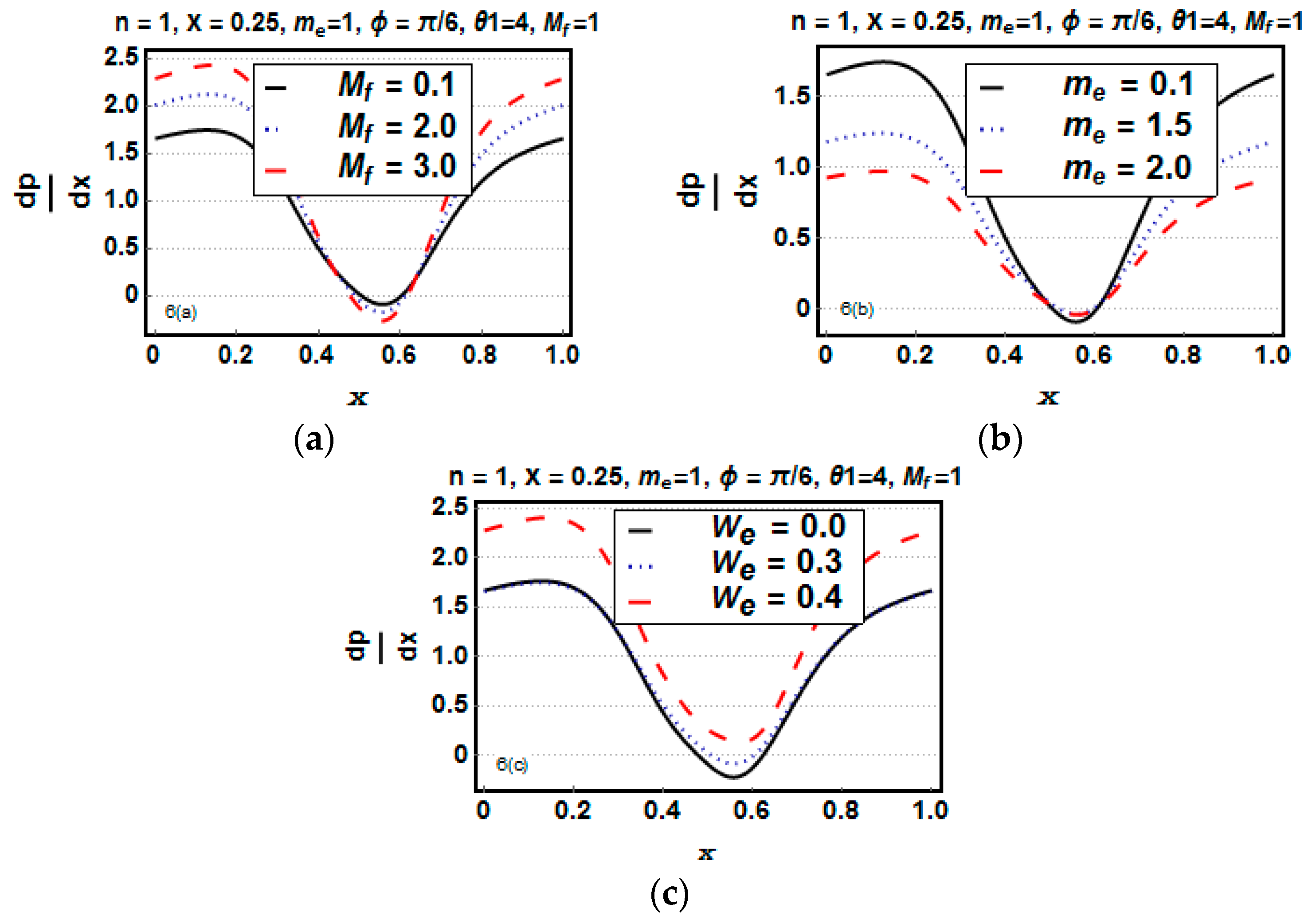
5.4. Analysis of the Pressure Gradient and the Rate of Heat Transfer
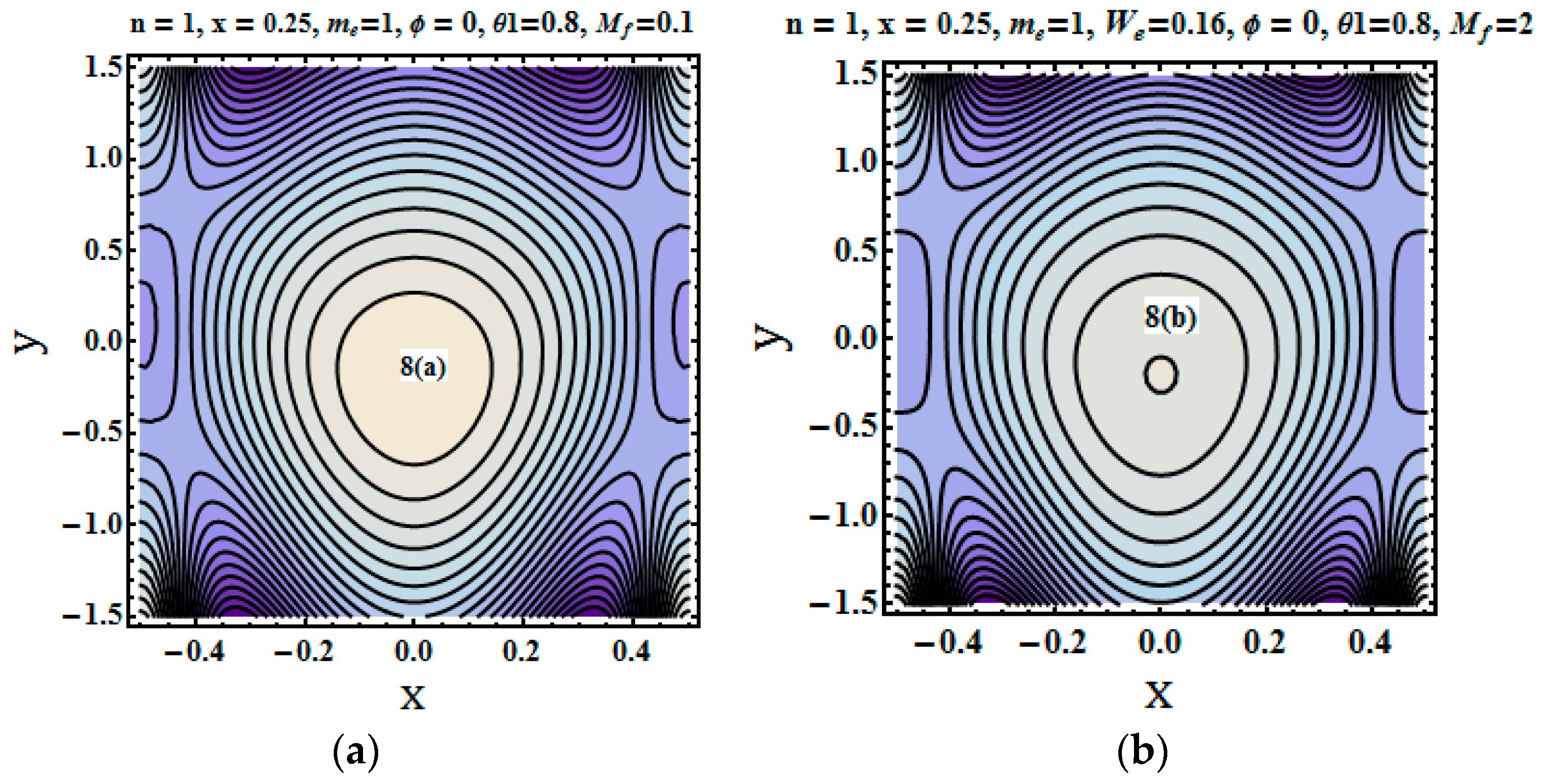
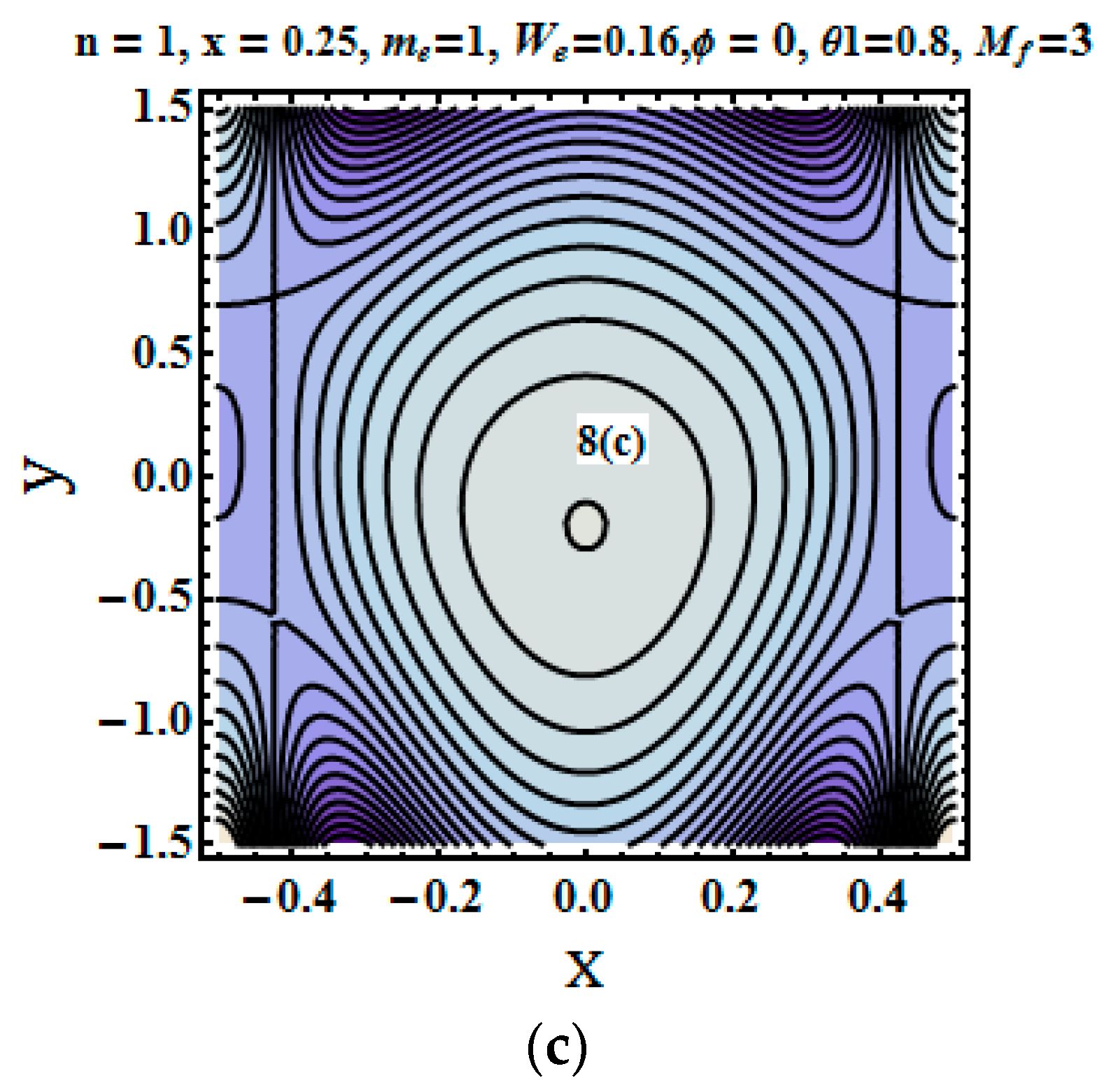
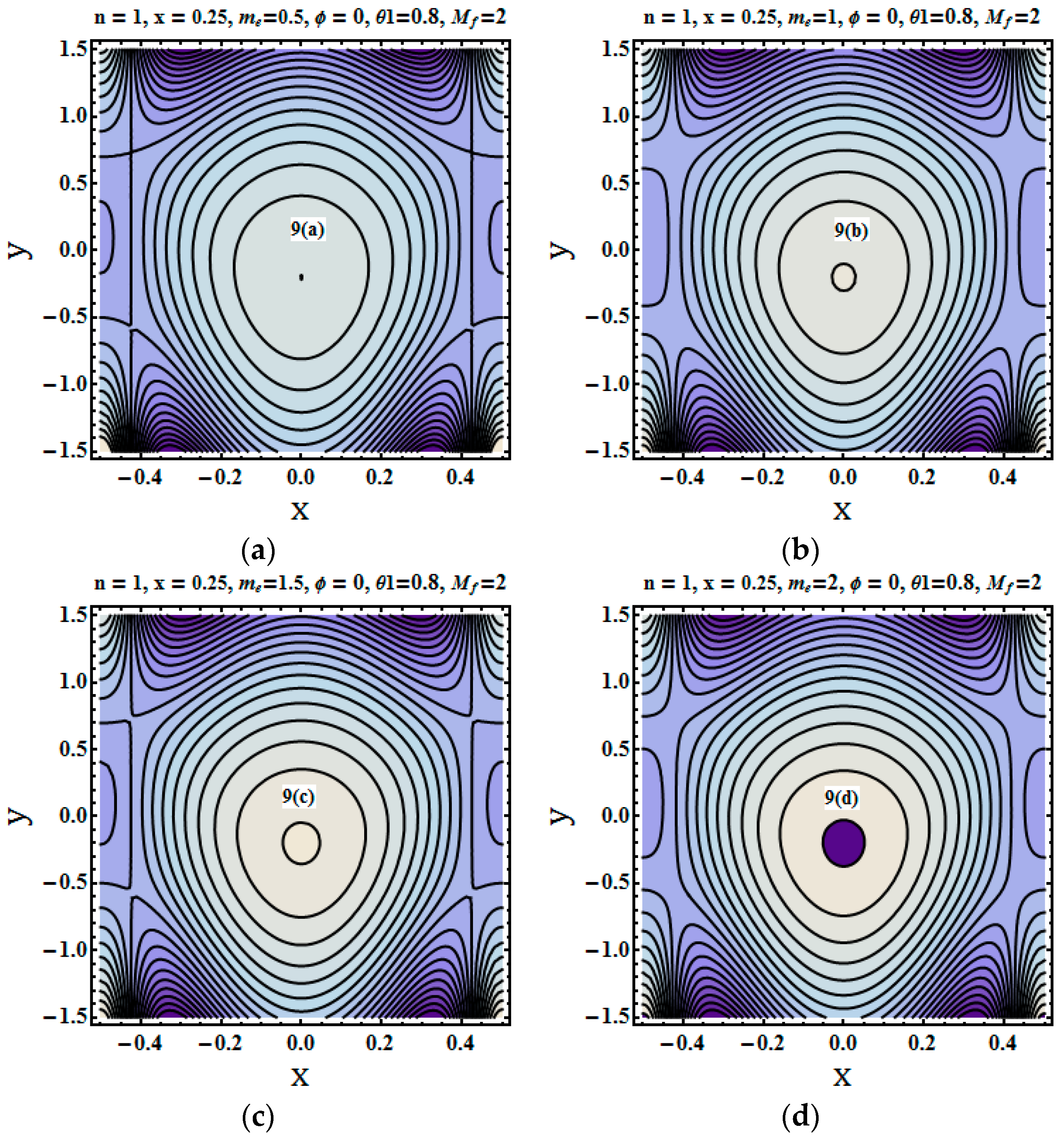
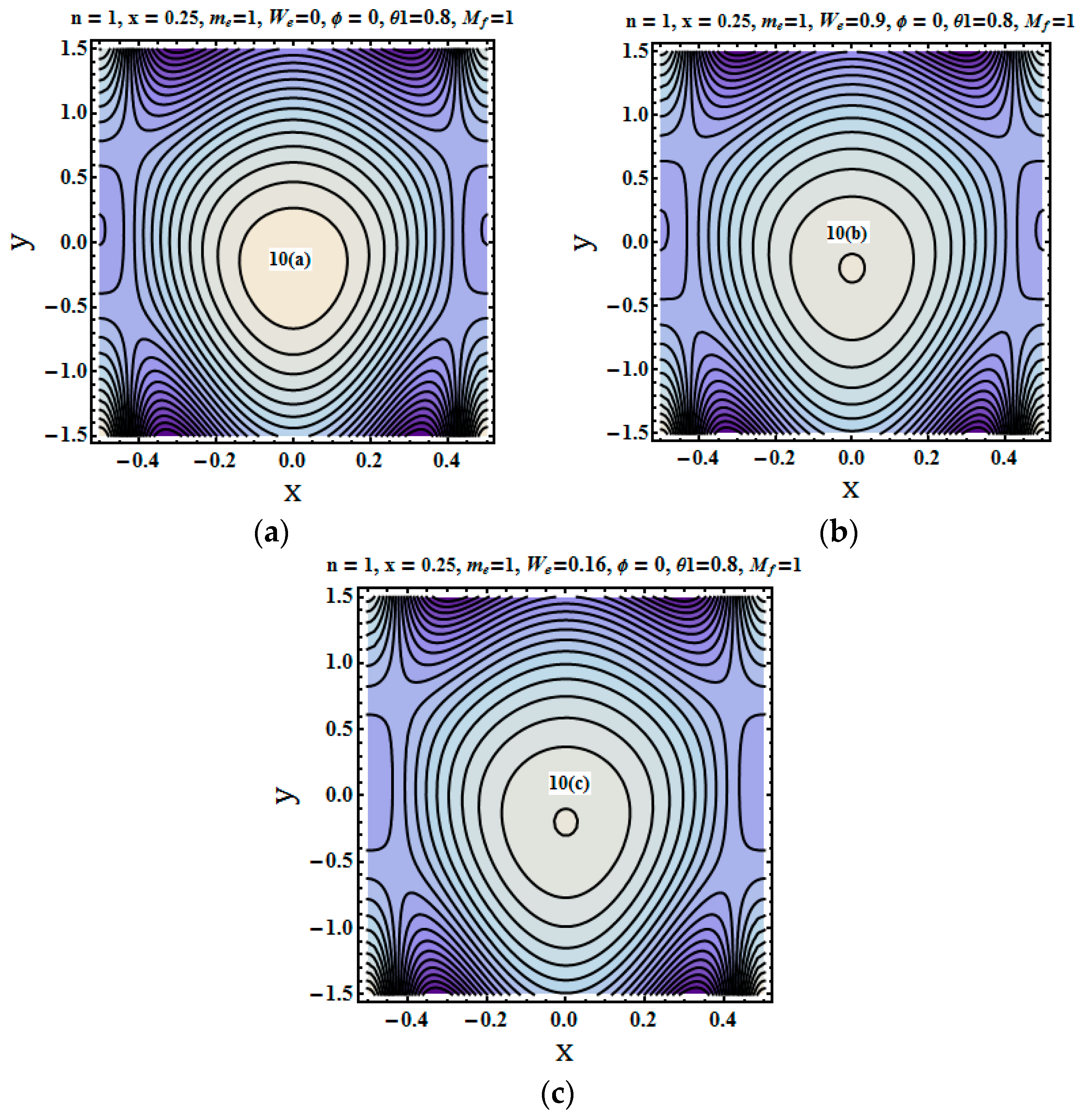
5.5. Trapping Phenomenon
5.6. Analysis of Entropy Generation Due to Heat Diffusion and Viscous Dissipation
6. Conclusions
- Entropy generation is not zero at the centerline y = 0.
- Heat irreversibility, at the bulk fluid region, is dominant, while at the edges, magnetic and viscous irreversibility dominates.
- The entropy generation profile is parabolic.
- Entropy production boosts for increasing values of the Hartman number and Brinkman number.
- Increasing the value of , which is the temperature difference parameter, reduces both the entropy generation and Bejan number.
- Due to the resistive nature of the magnetic field , the velocity profile decreases for the Hartman number, while for temperature, it increases.
- The velocity decreases due to the fluid’s Weissenberg number.
- The pressure gradient increases in a wider region for both the Hall parameter and the Hartman number.
- The number of closed circular stream lines encircling the bolus increases with an increase in the values of the Hall parameter.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Waqasas, M.; Yasmeen, T. Impact of Cattaneo—Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, M.; Hayat, T.; Alsaedi, A. A comparative study of Casson fluid with homogeneous-heterogeneous reactions. J. Colloid Interface Sci. 2017, 498, 85–90. [Google Scholar] [CrossRef] [PubMed]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Makinde, O.D. Entropy generation due to heat and mass transfer in a flow of dissipative elastic fluid through a porous medium. J. Heat Transf. 2019, 141. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Shafie, S. Entropy generation in hydromagnetic boundary flow under the effects of frictional and Joule heating: Exact solutions. Eur. Phys. J. Plus 2017, 132, 404. [Google Scholar] [CrossRef]
- Rashidi, M.; Bhatti, M.; Abbas, M.; Ali, M. Entropy generation on MHD blood flow of nanofluid due to peristaltic waves. Entropy 2016, 18, 117. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Bagheri, S.; Momoniat, E.; Freidoonimehr, N. Entropy analysis of convective MHD flow of third grade non-Newtonian fluid over a stretching sheet. Ain Shams Eng. J. 2017, 8, 77–85. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Qayyum, S.; Alsaedi, A. Entropy generation in flow with silver and copper nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2018, 539, 335–346. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Hayat, T.; Alsaedi, A. Entropy generation minimization and statistical declaration with probable error for skin friction coefficient and Nusselt number. Chin. J. Phys. 2018, 56, 1525–1546. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Alsaedi, A.; Qayyum, S.; Tamoor, S. Entropy optimization and quartic autocatalysis in MHD chemically reactive stagnation point flow of Sisko nanomaterial. Int. J. Heat Mass Transf. 2018, 127, 829–837. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Qian, Y. A Numerical Study on Entropy Generation in Two-Dimensional Rayleigh-Bénard Convection at Different Prandtl Number. Entropy 2017, 19, 443. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, Y.; Qian, Y.H. Numerical study on entropy generation in thermal convection with differentially discrete heat boundary conditions. Entropy 2018, 20, 351. [Google Scholar] [CrossRef]
- Yang, X.; He, H.; Xu, J.; Wei, Y.; Zhang, H. Entropy Generation Rates in Two-Dimensional Rayleigh-Taylor Turbulence Mixing. Entropy 2018, 20, 738. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Dou, S.H.; Qian, Y.H. A novel two-dimensional coupled lattice Boltzmann model for incompressible flow in application of turbulence Rayleigh-Taylor instability. Comput. Fluids 2017, 156, 97–102. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Dou, S.H.; Qian, Y.H.; Yan, W.W. Simulations of natural convection heat transfer in an enclosure at different Rayleigh number using lattice Boltzmann method. Comput. Fluids 2016, 124, 30–38. [Google Scholar] [CrossRef]
- Wei, Y.; Yang, H.; Lin, Z.; Wang, Z.; Qian, Y. A novel two-dimensional coupled lattice Boltzmann model for thermal incompressible flows. Appl. Math. Comput. 2018, 339, 556–567. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Hayat, T.; Alsaedi, A. Numerical analysis for MHD peristaltic transport of Carreau–Yasuda fluid in a curved channel with Hall effects. J. Magn. Magn. Mater. 2015, 382, 104–110. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Study of heat and mass transfer with Joule heating on magnetohydrodynamic (MHD) peristaltic blood flow under the influence of Hall effect. Propuls. Power Res. 2017, 6, 177–185. [Google Scholar] [CrossRef]
- Noreen, S.; Kousar, T.; Rashid, M.M. Hall, ion slip and ohmic heating effects in thermally active sinusoidal channel. Propuls. Power Res. 2019, in press. [Google Scholar] [CrossRef]
- Hayat, T.; Zahir, H.; Alsaedi, A.; Ahmad, B. Hall current and Joule heating effects on peristaltic flow of viscous fluid in a rotating channel with convective boundary conditions. Results Phys. 2017, 7, 2831–2836. [Google Scholar] [CrossRef]
- Noreen, S.; Qasim, M. Influence of Hall Current and Viscous Dissipation on Pressure Driven Flow of Pseudoplastic Fluid with Heat Generation: A Mathematical Study. PLoS ONE 2015, 10, e0129588. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, M.M.; Yang, Z.; Bhatti, M.M.; Abbas, M.A. Heat and mass transfer analysis on MHD blood flow of Casson fluid model due to peristaltic wave. Therm. Sci. 2018, 22, 2439–2448. [Google Scholar] [CrossRef]
- Mekheimer, K.S. Effect of the induced magnetic field on peristaltic flow of a couple stress fluid. Phys. Lett. A 2008, 372, 4271–4278. [Google Scholar] [CrossRef]
- Noreen, S.; Malik, A.; Rashidi, M.M. Peristaltic flow of shear thinning fluid via temperature dependent and thermal conductivity, communication in theoretical physics. Commun. Theor. Phys. 2019, 74, 4. [Google Scholar] [CrossRef]
- Latham, T.W. Fluid Motions in a Peristaltic Pump. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 1966. [Google Scholar]
- Shapiro, A.H.; Jaffrin, M.Y.; Weinberg, S.L. Peristaltic pumping with long wavelengths at low Reynolds number. J. Fluid Mech. 1969, 37, 799–825. [Google Scholar] [CrossRef]
- Asghar, S.; Hussain, Q.; Hayat, T. Peristaltic flow of reactive viscous fluid with temperature dependent viscosity. Math. Comput. Appl. 2013, 18, 198–220. [Google Scholar] [CrossRef]
- Vajravelu, K.; Sreenadh, S.; Lakshminarayana, P.; Sucharitha, G.; Rashidi, M.M. Peristaltic Flow of Phan-Thien-Tanner Fluid in an Asymmetric Channel with Porous Medium. J. Appl. Fluid Mech. 2016, 9. [Google Scholar] [CrossRef]
- Hayat, T.; Noreen, S.; Alsaedi, A. Effect of an induced magnetic field on peristaltic flow of non-Newtonian fluid in a curved channel. J. Mech. Med. Biol. 2012, 12. [Google Scholar] [CrossRef]
- Shit, G.C.; Ranjit, N.K.; Sinha, A.; Roy, M. Effect of induced magnetic field on peristaltic transport of a micropolar fluid in the presence of slip velocity. Int. J. Appl. Math. Mech. 2014, 10, 81–107. [Google Scholar]
- Ali, N.; Hayat, T. Peristaltic motion of a Carreau fluid in an asymmetric channel. Appl. Math. Comput. 2007, 193, 535–552. [Google Scholar] [CrossRef]
- Nadeem, S.; Akram, S. Peristaltic flow of a Williamson fluid in an asymmetric channel. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1705–1716. [Google Scholar] [CrossRef]
- Ellahi, R.; Riaz, A.; Nadeem, S.; Ali, M. Peristaltic flow of Carreau fluid in a rectangular duct through a porous medium. Math. Probl. Eng. 2012, 2012, 329639. [Google Scholar] [CrossRef]
- Noreen, S.; Hayat, T.; Alsaedi, A. Flow of MHD Carreau fluid in a curved channel. Appl. Bionics Biomech. 2013, 10, 29–39. [Google Scholar] [CrossRef]
- Hayat, T.; Yasmin, H.; Alsaedi, A. Peristaltic motion of Carreau fluid in a channel with convective boundary conditions. Appl. Bionics Biomech. 2014, 11, 157–168. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Noreen, S.; Abbas, A.; Hussanan, A. Entropy Generation via Ohmic Heating and Hall Current in Peristaltically-Flowing Carreau Fluid. Entropy 2019, 21, 529. https://doi.org/10.3390/e21050529
Noreen S, Abbas A, Hussanan A. Entropy Generation via Ohmic Heating and Hall Current in Peristaltically-Flowing Carreau Fluid. Entropy. 2019; 21(5):529. https://doi.org/10.3390/e21050529
Chicago/Turabian StyleNoreen, Saima, Asif Abbas, and Abid Hussanan. 2019. "Entropy Generation via Ohmic Heating and Hall Current in Peristaltically-Flowing Carreau Fluid" Entropy 21, no. 5: 529. https://doi.org/10.3390/e21050529
APA StyleNoreen, S., Abbas, A., & Hussanan, A. (2019). Entropy Generation via Ohmic Heating and Hall Current in Peristaltically-Flowing Carreau Fluid. Entropy, 21(5), 529. https://doi.org/10.3390/e21050529



